Theoretical study of some thermodynamical properties for solid under high pressure using finite-strain EOS

Abstract

This work involves the influence of high pressure on some thermodynamical properties of solid aluminum (Al) using a 3rd and 4th order Birch–Murnaghan equation of state based on the finite Eulerian strain theory.

Keywords:

• Aluminum
• Equation of state
• Melting
• Eulerian strain
• High pressure

1 Introduction

The equation of state (EOS) of a system basically describes the relationships among thermodynamic variables such as pressure, temperature and volume. The study of equation of state for solids has been extremely useful in the field of geophysics and condensed matter physics (Stacey et al., 1981; Anderson, 1995).

The isothermal EOS expresses the relation between pressure and volume at constant temperature while the relation between the volume and temperature at constant pressure is known as the isobaric EOS. However, the isochoric EOS relates temperature and pressure at constant volume (Tripathi et al., 2006).

It should be mentioned that the EOS expression for pressure (P), bulk modulus (K_T) and its derivatives () and () are not easy to obtain (Sushil et al., 2004).

The EOS has been derived by many authors based on different physical assumptions. Among these assumptions, the equation of state depends on finite-strain theory. This theory has played a very significant role in the development of equation of state (EOS) for solid (Stacey et al., 1981).

Stacey recently developed a method for obtaining higher order finite-strain equations which can be used for deriving and obtaining EOS. Other researches have obtained the EOS based on the finite Eulerian strain or the finite Lagrangian strain theories (Stacey, 2001). The equation of state based on the Eulerian strain yields good agreement with the EOS developed by Kushwah et al. (2007) and also with the generalized Rydberg EOS (Shanker et al., 2009). It is well known that the formulation based on the Eulerian strain is more appropriate than that based on the Lagrangian strain, since the Taylor series expansion for free energy in powers of the strain parameter is more convergent in the case of the Eulerian strain (Birch, 1952, 1986). The Lagrangian strain is the strain relative to the unstrained state, whereas the Eulerian strain represents the strain relative to the strained state (Sushil et al., 2004). The general form of strain (f) in terms of volume compression (V/V₀) is given by (Holzapfel, 1996)(1) where x = (V/V₀), V₀ is the volume at P₀, V is the volume at P. n is the power constant that depends upon the type of strain. For example, the value of n for the Eulerian strain is equal to 2 (Stacey, 2001).

The aim of this work is to study some thermodynamical properties for solid aluminum (Al) under high pressure using the 3rd and 4th order Birch–Murnaghan EOS based on the finite Eulerian strain theory. This study includes the variation of relative compression volume, isothermal bulk modulus (K_T) and the first derivative of bulk modulus () with pressure. Moreover, the effect of high pressure on the melting temperature of solid (Al) was investigated using the Mie–Gruneison–Debye equation based upon the 3rd and 4th order Birch–Murnaghan EOS, Lindemann and Kumar’s equations.

2 Theory

2.1 The isothermal Birch–Murnaghan EOS based on Eulerin strain

The Birch–Murnaghan EOS (B–M EOS) based on the Eulerian strain theory has been widely used for understanding high pressure behavior of solids (Gaurav et al., 2002). The Eulerian strain (f_e) can be obtained from Eq. (1)(1) by substituting n = 2. Therefore(2) The B–M EOS is obtained by expanding a series of powers of the Eulerian strain (Birch, 1952).

The 2nd order isothermal EOS is a function of two measurable parameters, x and isothermal bulk modulus (K₀) at P = 0, so that P = f(x, K₀).

Similarly, the 3rd and 4th order isothermal B–M EOS, have the forms and , respectively.

The coefficient of the term of degree 3 in the expansion can be neglected in many cases (corresponding to ) so that the equation of state at the 2nd order is good enough. However Stacey et al. (1981) and Anderson (1995) remarked that there is a truncation problem, since the coefficient of the term of degree 4 of the expansion is larger than that of the term of degree 3.

The 2nd, 3rd and 4th B–M EOS are written as below:(3) (4) (5) where(6) (7) (8) (9) where K₀ is the isothermal bulk modulus at P₀, is the first pressure derivative of bulk modulus and is the second pressure derivative of bulk modulus.

2.2 Isothermal bulk modulus (K_T) of 3rd and 4th order Birch–Murnghan EOS

Results obtained from the P–V relationship in a pressure study give information regarding higher order thermodynamic parameters. This isothermal P–V relationship yields bulk modulus and is defined as (Sushil et al., 2004)(10) the bulk modulus for 3rd and 4th B–M EOS is written as below:(11) and(12)

2.3 The pressure derivative of bulk modulus () at constant temperature

The pressure derivative of K_T for the 3rd and 4th order B–M EOS is given:(13) (14)

3 Result and discussion

The pressure has been calculated at different relative compression volumes ranging from 1 to 0.65 for solid aluminum (Al) using the 3rd and 4th order B–M EOS equations (4)(4) and (5)(5) . The input parameters V₀ = 10 cm³/mole, isothermal bulk modulus K₀ = 72.7 GPa at P₀ and its first pressure derivative are taken from Hänström and Lazor (2000). The value of the second pressure derivative of K₀ has been calculated from the following equation (Stacey, 2000, 2001):(15) where the value of is obtained from Hama and Suito (1996).

Fig. 1 shows a comparison between the calculated pressure (P) as a function of relative compression (V/V₀) for the 3rd and 4th order B–M EOS with experimental data obtained from Hänström and Lazor (2000) and Boehler and Ross (1997).

Figure 1 Comparison between the calculated isothermal compression curves for Al at room temperature using B–M EOS with experimental data.

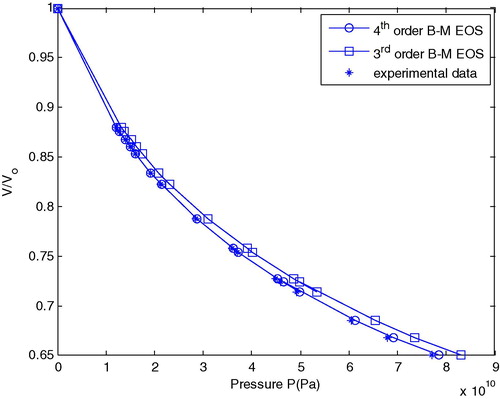
From this figure one can see that the relative compression volume decreases continually with the increase in pressure. It also indicates that up to 20 GPa, the compression curve coincides with experimental data. Beyond this and up to 100 GPa, the 3rd order B–M EOS diverges less than the 4th order B–M EOS in which it satisfies Eq. (5)(5) alongside experimental data.

The isothermal bulk modulus (K_T) and its first pressure derivative () have been calculated at different relative compression volumes from 1 to 0.65 for solid Al using the 3rd and 4th order B–M EOS according to Eqs. (11)–(14). The same input parameter values were used as above.

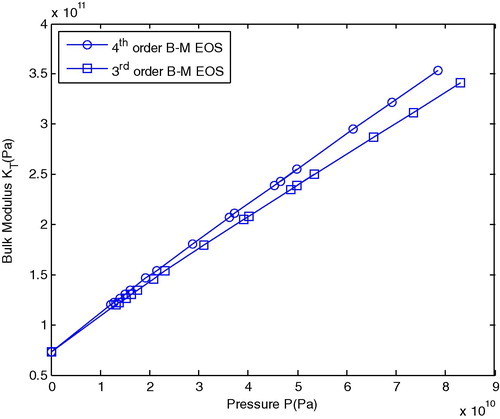
Fig. 2 shows the isothermal bulk modulus (K_T) versus pressure for the 3rd and 4th order B–M EOS at room temperature.

Figure 2 Isothermal curves K_T (GPa) versus P (GPa) for Al at room temperature.

Fig. 2 shows that the isothermal bulk modulus (K_T) increases continuously with an increase in pressure and which satisfies the equation of compressibility (10)(10) . The increase in pressure at constant temperature will reduce the volume for which dV will be negative. Thus K_T is increased above 20 GPa, the 3rd order B–M EOS slightly differs from the 4th order B–M EOS. This concept can be explained as due to the pressure of the term originally at the 4th order B–M EOS, while the 3rd order B–M EOS does not contain that term.

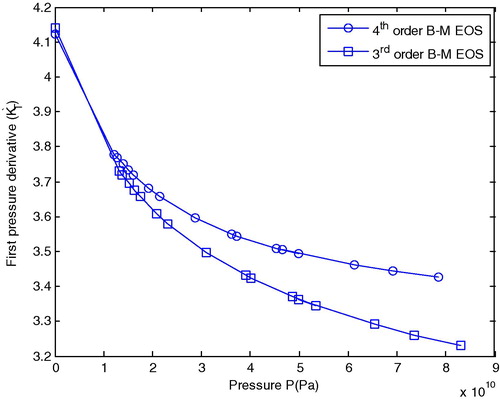
Fig. 3 shows the first pressure derivative () and isothermal bulk modulus (K_T) as a function of pressure for the 3rd and 4th order B–M EOS at room temperature.

Figure 3 Pressure versus first pressure derivative for Al at room temperature.

This figure shows that the first pressure derivative of isothermal bulk modulus () decreases as pressure increases for both Eqs. (13)(13) and (14)(14) and the results coincide with each other. It has been seen that above 20 GPa, the results of these equations do not coincide, but diverge away from each other. We can interpret this as the original 3rd order B–M EOS does not contain the term . The most important reason for this is that provides a close control of the curvature of the plot of versus P for the 4th order B–M EOS.

4 The effect of high pressure on melting temperature of solid

4.1 Preamble

The effect of pressure on melting temperature studied by Clapeyron was deduced a latent heat equation from Maxwell’s thermodynamical relation to obtain the following equation (Cohen and Weitz, 1996):(16) Determination of the pressure dependence of the melting temperature of solids is so important in condensed matter. A number of different theoretical expressions for the pressure dependence of melting temperature of solids have been discussed in the literature (Schlosser et al., 1989).

4.2 EOS of the melting curve of solid

Our calculation follows the recommendation of Gilvary (1956), who suggested that T_m(P) could be found by first calculating P(V_m) coupled with T_m(V_m), where T_m(V_m) is found by the Lindemann law. Gilvary used the Murnghan EOS and the Lindemann formula in its simplest form, i.e. where γ (first Grunisen parameter) is independent of V_m while in this work we do not assume that γ is independent of V_m.

The melting equation of state appropriate to temperature above T_m0 (T_m0 is the temperature of melting at ambient pressure, i.e. P = 0 GPa) is(17) which is the EOS of melting curve and called Mie–Grunisen–Debye EOS where(18) where E_D is the harmonic internal energy according to Debye theory and here(19) is given by Anderson (1995), where R is the gas constant and T_m is the melting temperature along melting curve at any P(20) where γ_m0 is the first Gruneisen parameter at zero pressure and melting temperature (T_m0), q is the second Gruneisen parameter = 1, the equation of state P(V, T₃₀₀) (Hofmeister, 1993; Hama and Suito, 1996) and equal isothermal EOS (4)(4) and (5)(5) .

V_m is melting molar volume at T_m and P_m (GPa) and is given by Kumer (1995, 1996)" and is equal to(21) where V_m0 is melting molar volume at T_m0 and P = 0 GPa, B₀ is bulk modulus at P = 0 GPa, A = δ_T + 1 and δ_T is Anderson Gruneisen parameter.

4.3 Lindemann’s equation

One of the oldest and most widely used attempts to predict the melting curves of solids is the Lindemann (1910) equation. Lindemann assumed that a solid melts when the mean-square amplitude of vibrations of atoms about their equilibrium position become larger than a certain fraction of the lattice spacing. Lindemann then straightforwardly arrived at a relationship between the melting temperature (T_m) and melting volume (V_m).

The famous Lindemann’s equation is written as below:(22) The melting gradient (dT_m/dP_m) can be obtained from Eq. (22)(22) as(23) where K_T is the bulk modules of solid and is a function of compression and temperature (Kumer, 1995, 1996).

5 Result and discussion

The melting pressure (P_m) and melting temperature (T_m) have been calculated for solid Al using the 3rd and 4th order B–M EOS.

To calculate the melting temperature (T_m), Eq. (22)(22) has been used. The melting pressure (P_m) has been worked out using Eq. (17)(17) . The first term of Eq. (17)(17) represented the value of P obtained from the 3rd and 4th order B–M EOS which is illustrated in Fig. 1. The second term of Eq. (17)(17) P_th(V_th, T_m) has been calculated using Eqs. (19)(19) and (20)(20) . To calculate the melting volume (V_m), Eq. (21)(21) has been used, while the melting gradient has been calculated by using Eq. (23)(23) . The basic physical specific values of Al are V_m0 = 10.65 cm³/mol, T_m0 = 933 K, γ_m0 = 2.42, q = 1, K_m0 = 58.71 GPa obtained from Kumer (1995, 1996)" and R = 8.31 J/mole.

Fig. 4 shows a comparison between the calculated melting temperature (T_m) versus (V_m/V_m0) using the 3rd and 4th order B–M EOS with experimental data obtained from Hänström and Lazor (2000) and Boehler and Ross (1997).

Figure 4 Comparison between calculated melting temperature versus V_m/V_m0 for Al with experimental data.

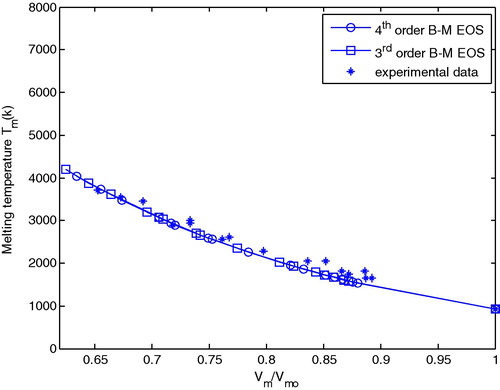
One can see from this figure that V_m/V_m0 decreases gradually with increasing melting temperature.

Fig. 5 shows a comparison between the calculated melting temperature (T_m) versus melting pressure (P_m) for Al using the Lindemann equation which involves the 3rd and 4th order B–M EOS with experimental data obtained from Hänström and Lazor (2000) and Boehler and Ross (1997).

Figure 5 Comparison between calculated melting temperature versus melting pressure for Al with experimental melting data.

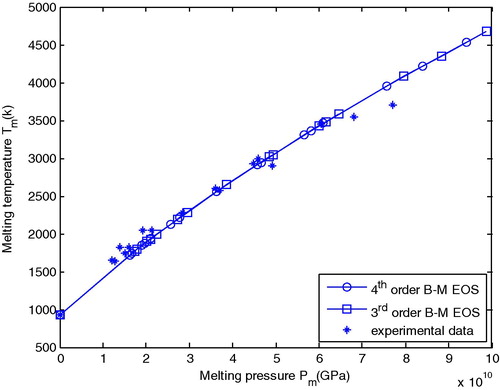
Fig. 5 exhibited that the results obtained from the 3rd and 4th order B–M EOS are quite matchable and they fit with experimental data.

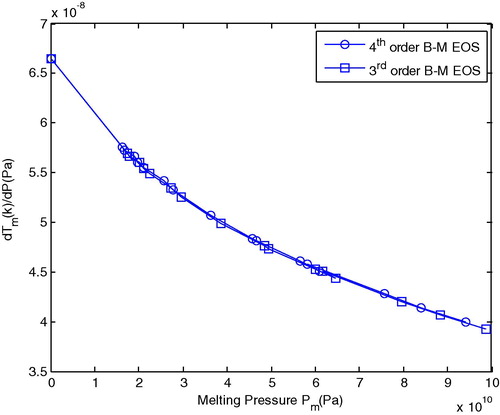
Fig. 6 shows the melting gradient with melting pressure (P_m) for Al using the 3rd and 4th order B–M EOS. In this figure we show that the rate of variation in melting temperature with melting pressure decrease gradually with increases melting pressure and at a high melting pressure the rate of melting gradient decreases.

Figure 6 Melting gradient versus melting pressure (P_m).

6 Conclusions

The results for (V/V_o) versus (P) obtained for 4th order B-M EOS are more agreement with experimental data than 3rd order B-M EOS. The isothermal bulk modulus (K_T) and its first pressure derivative () for the 3rd and 4th order B–M EOS give different results at high pressure, this difference is due to the 4th order B–M EOS containing the term ().

It has been found that the 3rd and 4th order B–M EOS gave same results with melting experiment data. The experimental melting compression curve was found in good agreement with the 3rd and 4th order B–M EOS. The melting temperature value obtained from Eq. (22)(22) as well as the experimental data at 0–100 GPa are in good matching to each other.

The Kumar equation gives the melting volume (V_m/V_m0) at any high pressure and temperature, which is far better than the other relation. At any high pressure the rate of variation of melting temperature with pressure decreases.