New ridge parameters for ridge regression

Peer review under responsibility of University of Bahrain.

Abstract

Hoerl and Kennard (1970a) introduced the ridge regression estimator as an alternative to the ordinary least squares (OLS) estimator in the presence of multicollinearity. In ridge regression, ridge parameter plays an important role in parameter estimation. In this article, a new method for estimating ridge parameters in both situations of ordinary ridge regression (ORR) and generalized ridge regression (GRR) is proposed. The simulation study evaluates the performance of the proposed estimator based on the mean squared error (MSE) criterion and indicates that under certain conditions the proposed estimators perform well compared to OLS and other well-known estimators reviewed in this article.

Keywords:

• Ridge regression
• Ridge parameter
• Multicollinearity

1 Introduction

In the presence of multicollinearity OLS estimator yields regression coefficients whose absolute values are too large and whose signs may actually reverse with negligible changes in the data (Buonaccorsi, 1996). Whenever the multicollinearity presents in the data, the OLS estimator performs ‘poorly’. The method of ridge regression, proposed by Hoerl and Kennard (1970a) is one of the most widely used tools to the problem of multicollinearity. In a ridge regression an additional parameter, the ridge parameter (k) plays an vital role to control the bias of the regression toward the mean of the response variable. In addition, they proposed the generalized ridge regression (GRR) procedure that allows separate ridge parameter for each regressor. Using GRR, it is easier to find optimal values of ridge parameter, i.e., values for which the MSE of the ridge estimator is minimum. In addition, if the optimal values for biasing constants differ significantly from each other then this estimator has the potential to save a greater amount of MSE than the OLS estimator (Stephen and Christopher, 2001). In both ORR and GRR as ‘k’ increases from zero and continues up to infinity, the regression estimates tend toward zero. Though these estimators result in biased, for certain value of k, they yield a minimum mean squared error (MMSE) compared to the OLS estimator (see Hoerl and Kennard, 1970a). Ridge parameter ‘k’ proposed by Hoerl et al. (1975) performs fairly well.

Much of the discussions on ridge regression concern the problem of finding good empirical value of k. Recently, many researchers have suggested various methods for choosing ridge parameter in ridge regression. These methods have been suggested by Hoerl and Kennard (1970a), Hoerl et al. (1975), McDonald and Galarneau (1975), Hocking et al. (1976), Lawless and Wang (1976), Gunst and Mason (1977), Lawless (1978), Nomura (1988)", Heath and co-workers (1979), Nordberg (1982), Saleh and Kibria (1993), Haq and Kibria (1996), Kibria (2003), Pasha and Shah (2004), Khalaf and Shukur (2005), Norliza et al. (2006), Alkhamisi and Shukur (2007), Mardikyan and Cetin (2008), Dorugade and Kashid (2010) and Al-Hassan (2010)" to mention a few. The objective of the article is to investigate some of the existing popular techniques that are available in the literature and to make a comparison among them based on mean square properties. Moreover, we suggested some methods for estimating ridge parameters in ORR and GRR which produce ridge estimators that yield minimum MSE than other estimators. The organization of the article is as follows.

In this article, we introduce alternative ordinary and generalized ridge estimators and study their performance by means of simulation techniques. Comparisons are made with other ridge-type estimators evaluated elsewhere, and the estimators to be included in this study are described in Section 2. In Section 3, we propose some new methods for estimating the ridge parameter. In Section 4, we illustrate the simulation technique that we have adopted in the study and related results of the simulations appear in the tables and figures. In Section 5, we give a brief summary and conclusion.

2 Model and estimators

Consider, a widely used linear regression model(1) where Y is a n × 1 vector of observations on a response variable. β is a p × 1 vector of unknown regression coefficients, X is a matrix of order (n × p) of observations on ‘p’ predictor (or regressor) variables and ε is an n × 1 vector of errors with E(ε) = 0 and V(ε) = σ ²I_n. For the sake of convenience, we assume that the matrix X and response variable Y are standardized in such a way that X′X is a non-singular correlation matrix and X′Y is the correlation between X and Y. The paper is concerned with data exhibited with multicollinearity leading to a high MSE for β meaning that is an unreliable estimator of β.

Let ∧ and T be the matrices of eigen values and eigen vectors of X′X, respectively, satisfying T′X′XT = ∧ = diagonal (λ₁, λ₂ , …, λ_p), where λi being the ith eigen value of X′X and T′T = TT′ =  I_p we obtain the equivalent model(2) where Z = XT, it implies that Z′Z = ∧, and α = T′β (see Montogomery et al. (2006)) Then OLS estimator of α is given by(3) Therefore, OLS estimator of β is given by

2.1 Generalized ridge estimator (GRR)

The GRR estimator of α is defined by(4) where K = diagonal(k₁,k₂ … k_p), k_i ⩾ 0, i = 1,2, …, p be the different ridge parameters for different regressors and A = ∧ + K.

Hence GRR estimator for β is .

and mean square error of is(5) In case of GRR, various methods are available in the literature to determine the separate ridge parameter for each regressor. Among these, well known methods for determination of ridge parameter which are used in the further study are given below.

(1)

1. Hoerl and Kennard (1970a) have proposed the following ridge parameter(6)

(2)

1. Nomura (1988) proposed a ridge parameter and it is given by(7)

(3)

1. Troskie and Chalton (1996) proposed a ridge parameter and it is given by(8)

(4)

1. Firinguetti (1999) proposed a ridge parameter and it is given by(9)

(5)

1. Batah et al. (2008) proposed a ridge parameter and it is given by(10) where, is the ith element of and is the OLS estimator of σ², i.e. .

2.2 Ordinary ridge estimator (ORR)

Setting k₁ = k₂ = … = k_p = k and k ⩾ 0, the Ordinary ridge regression (ORR) estimator of β is(11) and mean square error of is(12) We observe that, when k = 0 in (12)(12) , MSE of OLS estimator of α is recovered. HenceHoerl et al. (1975) suggested that, the value of ‘k’ is chosen small enough, for which the mean squared error of ridge estimator, is less than the mean squared error of OLS estimator.

In case of ORR also, many researchers have suggested different ways of estimating the ridge parameter. Some of the well known methods for choosing the ridge parameter value are listed below.

(1)	(13)
(2)	(14)
(3)	(15)
(4)	(16)
(5)	(17) where is the variance inflation factor of jth regressor.
(6)	(18)
(7)	(19)
(8)	(20)
(9)	(21)
(10)	(22)
(11)	(23)
(12)	(24)
(13)	(25)
(14)	(26)
(15)	(27) All the methods of estimating ridge parameter are used in Section 4.

3 Proposed ridge parameter

Hoerl and Kennard (1970a) conclude that, bias and total variance of the parameter estimates are, respectively monotonically increasing and decreasing functions of ridge parameters. They also suggested a value of ith ridge parameter k_i(HK) used in GRR given in (6)(6) . Hoerl et al. (1975) suggests the modification in k_i(HK) used in ORR which performs fairly well. Lawless and Wang (1976) suggest the modification in k_i(HK) to reduce the bias by multiplying the ith eigen value λ_i to the denominator of (6)(6) to keep the variation depends on the strength of the multicollinearity. Their estimator reduces the bias but results in greater total variance of the parameter estimates.

In this article, we suggest a estimator that takes a little bias than estimator given by Hoerl et al. (1975) and substantially reduces the total variance of the parameter estimates than the total variance using estimator given by Lawless and Wang (1976), thereby improving the mean square error of estimation and prediction. We suggest the modification by multiplying λ_max/2 to the denominator of (6)(6) . The suggested estimator is:(28) where λ_max is the largest eigen value of X′X.

This leads to the denominator of the alternative estimator given by (28)(28) being greater than that of Hoerl and Kennard (1970a) by λ_max/2. Hence, we can writeIt clearly indicates that our suggested estimator lies in between the estimators given by Hoerl et al. (1975) and Lawless and Wang (1976)". Kibria (2003) suggested optimal ridge parameters by proposing new ridge parameters by modifying the quantity . By adopting algorithms outlined in Kibria (2003), we propose new methods to determine ridge parameters in case of ORR for the ridge parameter k as below,(29) (30) (31) (32) From (29)–(31), (30) is the ith element of and is the OLS estimator of σ², i.e. .

Result 1

Result 2

If λ_max is close to ‘p’ then k₄(AD) ≅ 2k₁₄, and if λ_max is close to ‘1’ then k₄(AD) ≅ 2k₁.

Hoerl et al. (1975) have shown that . Using this, inequality from result 1, . Hence k₄(AD) satisfies the upper bound of ridge parameter stated by Hoerl and Kennard (1970a).

Proposed estimator is examined by means of a simulation technique which we present in the next section.

4 Performance of the proposed ridge parameter

In this section, we examined the performance of the ridge estimator using the proposed ridge parameters in both ORR and GRR over the different ridge parameters (k) reviewed in this article. We examined the average MSE (AMSE) ratio of the ridge estimator using proposed ridge parameters and other ridge parameters over OLS estimator. Performances of new ridge estimators given in (28)–(32) are studied in two parts. In part A, performance for proposed ridge estimators is evaluated through simulation in case of ORR. Whereas, in part B a simulation study is carried out for evaluating the performance of proposed ridge estimators in case of GRR.

4.1 Part A

We consider the true model as Y = Xβ + ε. Here ε follows a normal distribution N(0, σ²I_n) and the explanatory variables are generated (see Batah et al., 2008) fromwhere u_ij is an independent standard normal random number and ρ² is the correlation between x_ij and for j, j′ < p and j ≠ j′. j, j′ = 1,2, …, p. When j or j′ = p, the correlation will be ‘ρ’. Here we consider predictor variables p = 4 and ρ = 0.9. These variables are standardized such that X′X is in the correlation form and it is used for the generation of Y with β = (2,3,5, 1)′. We have simulated the data with sample sizes n = 20, 50 and 100. The variance of the error terms is taken as σ² = 1, 5, 10 and 25. Ridge estimates are computed using different ridge parameters given in (13)–(27) and (29)–(32). The MSE of such ridge regression parameters are obtained using (12)(12) . This experiment is repeated 2000 times and obtains the AMSE. Firstly, we computed the AMSE ratios (AMSE /AMSE () of OLS estimator over different estimators for various values of triplet (ρ, n, σ²) and reported in Table 1. We consider the method that leads to the maximum AMSE ratio to the best from the MSE point of view.

Table 1 Ratio of AMSE of OLS over various ridge estimators for different ‘k’.

n		20				50				100
		1	5	10	25	1	5	10	25	1	5	10	25
k	k1	1.9591	1.9041	1.8936	1.6576	1.5648	2.5220	1.4035	2.9800	2.2481	1.8036	1.5990	3.1048
	k2	1.6458	0.9895	0.4923	0.9257	0.9901	1.1969	0.7672	1.7184	1.7886	1.1572	0.6954	2.1013
	k3	1.3152	1.3529	0.9294	1.2887	1.0035	1.7400	1.0407	2.4535	1.1916	1.2865	1.1165	2.6206
	k4	1.7382	1.8200	2.1747	1.6185	1.5653	2.2507	1.6252	2.4887	1.9691	1.2809	1.4109	2.3090
	k5	1.8347	1.9279	1.9896	1.6721	1.5275	2.5228	1.4097	2.9830	2.1999	1.8048	1.6031	3.1061
	k6	1.6473	0.9834	0.4908	0.9277	0.9900	1.1914	0.7644	1.6984	1.7886	1.1534	0.6935	2.0706
	k7	0.3247	0.9443	0.4901	0.9241	0.1079	0.9689	0.7559	1.7019	0.0466	0.7116	0.6531	2.0729
	k8	1.6918	1.3932	0.9431	1.3282	1.2879	1.8878	1.0647	2.5851	1.7534	1.4120	1.1524	2.7445
	k9	1.3903	1.2905	1.5517	1.3176	1.1746	1.4637	1.2562	1.5268	1.3655	1.3197	1.2091	1.5733
	k10	1.4950	1.0041	0.5202	1.0275	1.2124	1.6613	0.8165	2.5551	1.3958	1.2047	1.2136	2.2630
	k11	1.6073	1.0439	0.5224	0.9630	1.3523	1.6802	0.8153	2.1401	1.4944	1.2839	0.9872	2.2678
	k12	1.0007	1.7249	2.2101	1.6536	0.8251	1.9723	1.6099	2.5894	0.5697	1.0581	1.3364	2.3380
	k13	1.4461	0.0093	0.2329	0.0221	0.4099	0.6154	0.0489	0.6211	0.0860	0.2930	0.5761	0.0650
	k14	1.8815	1.8245	2.1426	1.7185	1.4737	2.1611	1.5981	2.5000	1.8469	1.7491	1.5616	2.5921
	k15	0.13589	0.7942	0.47573	0.8983	0.05383	0.67948	0.71321	1.5857	0.02639	0.44348	0.56721	1.89147
	k1(AD)	1.2140	1.1574	1.3590	1.2027	1.0938	1.2634	1.1487	1.2918	1.2187	1.1850	1.1156	1.3133
	k2(AD)	1.4810	1.0225	0.5435	1.1078	1.1589	1.7110	0.8607	2.7609	1.3960	1.2103	1.3920	2.3595
	k3(AD)	1.6132	1.1010	0.5511	0.9986	1.4388	1.8322	0.8557	2.3839	1.6500	1.3221	1.1685	2.3874
	k4(AD)	1.9872	2.0282	2.2600	1.8183	1.5990	2.5482	1.6182	2.9882	2.3328	1.8823	1.6926	3.2643

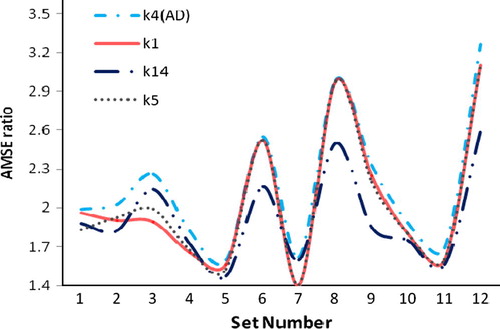
In the following figure (Fig. 1), we represent the same values reported in Table 1 Here we noted that values of AMSE ratios only for k₁,k₅,k₁₄ and k₄(AD) are represented because these values for remaining choice of ‘k’ have less importance for the comparative study. Here input values are n, ρ and σ². These input values are ordered according to the increase of values. For fixed value of ‘ρ’ changes values of ‘n’ and for fixed values of (ρ, n) changes the values of σ². There are 12 sets of (ρ, n, σ²) values. These are arranged as (0.9,20,1), (0.9,20,5), …, (0.9,100,25) and it is numbered as 1, 2, …, 12, respectively.

Figure 1 Ratio of AMSE of OLS over various ridge estimators for different ‘k′ (p = 4, β = (2,3,5,1)′ and ρ = 0.9).

Same procedure for another choice of p = 3 and β = (3,1, 5)′ is done and AMSE ratios are computed and represented in Fig. 2.

Figure 2 Ratio of AMSE of OLS over various ridge estimators for different ‘k’ (p = 3, β = (3,1,5)′ and ρ = 0.9).

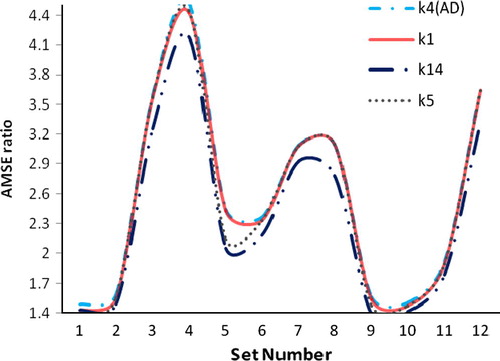
From Table 1, Figs. 1 and 2, we observe that the performance of proposed ridge parameters k₁(AD),k₂(AD),k₃(AD) and k₄(AD) is better than OLS. Particularly k₄(AD) performs equivalently and is little better than ridge parameters proposed by Hoerl et al. (1975) and Dorugade and Kashid (2010)" whereas, it gives better performance than other ridge parameters reviewed in this article for all combinations of correlation between predictors (ρ), sample size (n) and variance of the error term (σ²) used in this simulation study.

4.2 Part B

Here we evaluate the performance of proposed ridge parameters in case of GRR. Here we generate the data which exhibit with multicollinearity using the procedure for the generation of y with β = (2,3,5,1)′ as discussed in part A. We consider predictor variables p = 4 and ρ = 0.9. We have simulated the data with sample sizes n = 20, 50 and 100. The variance of the error term is taken as σ² = 1,5,10 and 25. Generalized ridge estimators are computed using different ridge parameters given in (6)–(10) and (28)(28) . The MSE of such ridge regression parameters are obtained using (5)(5) . This experiment is repeated 2000 times and obtains the AMSE.

We computed the AMSE ratios (AMSE / AMSE ) of OLS estimator over different estimators for various values of triplet (ρ, n, σ²). These ratios are reported in Table 2 and here we noted that values of AMSE ratios only for k_i(HK), k_i(FG) and k_i(AD) are represented in Fig. 3

Figure 3 Ratio of AMSE of OLS over various ridge estimators for different ‘k_i’ (p = 4, β = (2,3,5,1)′ and ρ = 0.9).

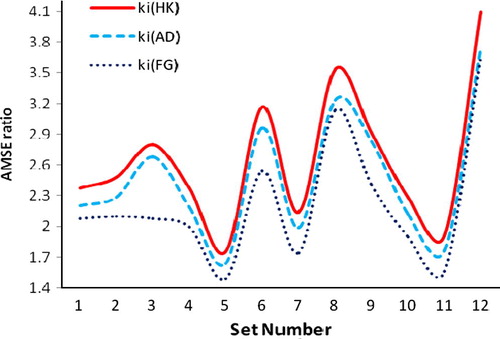
Table 2 Ratio of AMSE of OLS over various ridge estimators for different ‘k_i’.

n		20				50				100
		1	5	10	25	1	5	10	25	1	5	10	25
ki	ki(HK)	2.3771	2.4828	2.7997	2.3730	1.7549	3.1660	2.1404	3.5339	2.9098	2.2880	1.9120	4.1019
	ki(HMO)	1.7969	2.0272	2.0637	1.9364	1.2744	2.4380	1.7089	3.0186	1.8384	1.7823	1.5184	3.5253
	ki(FG)	2.0767	2.0997	2.0756	1.9922	1.4868	2.5389	1.7438	3.1379	2.4047	1.9007	1.5634	3.6587
	ki(TC)	1.9325	1.9963	2.0460	1.9345	1.5955	2.1970	1.8157	2.3773	2.0415	1.8883	1.7068	2.5269
	ki(F)	1.1077	1.1161	1.1112	1.1166	1.0371	1.0419	1.0420	1.0431	1.0178	1.0201	1.0203	1.0208
	ki(AD)	2.2035	2.2866	2.6788	2.1872	1.6402	2.9614	1.9841	3.2328	2.8273	2.1192	1.7657	3.7458

Same procedure for another choice of p = 3 and β = (3,1, 5)′ is done and AMSE ratios are represented in Fig. 4.

Figure 4 Ratio of AMSE of OLS over various ridge estimators for different ‘k_i’ (p = 3, β = (3,1,5)′ and ρ = 0.9).

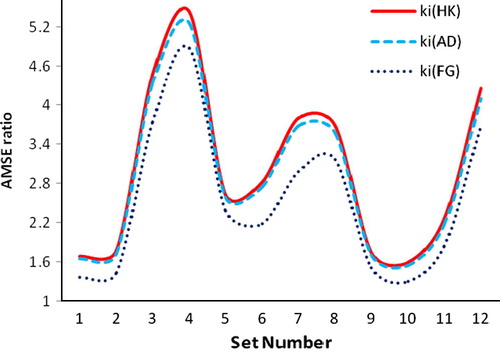
From Table 2, Figs. 3 and 4, we conclude that proposed ridge parameter k_i(AD) and k_i(HK), the ridge parameter proposed by Hoerl and Kennard (1970a) both perform equivalently. Whereas, the performance of k_i (AD) is better than OLS, k_i(HMO), k_i(FG),k_i(TC) and k_i(F) for all combinations of correlation between predictors (ρ), sample size (n) and variance of the error term (σ²) used in this simulation study.

5 Conclusion

In this article we have proposed a new method for estimating the ridge parameter in the presence of multicollinearity. The performance of the proposed ridge parameter is evaluated through the simulation study, for different combinations of correlation between predictors (ρ), the number of explanatory variables (p), sample size (n) and variance of the error variable (σ²). The evaluation of our estimator has been done by comparing the AMSE ratios of OLS estimator over the proposed estimator and the other estimators reviewed in this article. Finally, we found that the performance of the proposed estimator is satisfactory over the other estimators in the presence of multicollinearity.

Acknowledgments

The author is very grateful to the reviewers and the editor for so detailed comments and constructive suggestions which resulted in the present version. The present studies were supported in part by University Grants Commission, India, Project No. F.No.23-1743/10 (WRO), dated 22.9.10.

Notes

Peer review under responsibility of University of Bahrain.