Traveling wave solutions of KdVs using sine–cosine method

Peer review under responsibility of University of Bahrain.

Abstract

Traveling wave solutions are obtained by using the sine–cosine method for KdVs. Solution procedure and the obtained results re-confirm the efficiency of the proposed scheme.

Keywords:

• Nonlinear equations
• Sine–cosine method
• Traveling wave solutions
• Generalized KdV equation

1 Introduction

There has been an unprecedented development in the solutions of nonlinear sciences (see Abbasbandy, 2007; Abdou and Soliman, 2005; Ablowitz and Clarkson, 1991; Al-Muhiameed and Abdel-Salam, 2011; Aslan, 2011; Bekir and Boz, 2008; Bekir and Cevikel, 2011; Deakin and Davison, 2010; Feng et al., 2011; Gepreel, 2011a,b; Gepreel and Shehata, 2012; Gomez and Salas, 2010; Guo et al., 2011; He, 2006; He and Wu, 2006; Hirota, 1971; Liu et al., 2010; Ma and You, 2004; Massabo et al., 2011; Mohyud-din et al., 2010; Malfliet, 1992; Naher et al., 2011a,b; Nofel et al., 2011; Ozis and Aslan, 2010; Rogers and Shadwick, 1982; Salah et al., 2011; Salas, 2008; Salas and Gomez, 2010; Soliman and Abdo, 2009; Wang et al., 2008; Wazwaz, 2004a,b, 2007, 2011; Yildirim and Pinar, 2010; Yun, 2011; Zayed and Al-Joudi, 2010; Zayed and Gepreel, 2011; Zhang et al., 2010; Zhao et al., 2011; Zhu, 2008") during the last two decades. In the similar context, several numerical and analytical techniques including Homotopy Analysis (HAM), Perturbation, Modified Adomian’s Decomposition (MADM), Variational iteration (VIM), Variation of Parameters, Finite difference, Finite volume, Backlund transformation, inverse scattering, Jacobi elliptic function expansion, tanh function have been developed to solve such equations (see Abbasbandy, 2007; Abdou and Soliman, 2005; Ablowitz and Clarkson, 1991; Al-Muhiameed and Abdel-Salam, 2011; Aslan, 2011; Bekir and Boz, 2008; Bekir and Cevikel, 2011; Deakin and Davison, 2010; Feng et al., 2011; Gepreel, 2011a,b; Gepreel and Shehata, 2012; Gomez and Salas, 2010; Guo et al., 2011; He, 2006; He and Wu, 2006; Hirota, 1971; Liu et al., 2010; Ma and You, 2004; Massabo et al., 2011; Mohyud-din et al., 2010; Malfliet, 1992; Naher et al., 2011a,b; Nofel et al., 2011; Ozis and , 2010; Rogers and Shadwick, 1982; Salah et al., 2011; Salas, 2008; Salas and Gomez, 2010; Soliman and Abdo, 2009; Wang et al., 2008; Wazwaz, 2004a,b, 2007, 2011; Yildirim and Pinar, 2010; Yun, 2011; Zayed and Al-Joudi, 2010; Zayed and Gepreel, 2011; Zhang et al., 2010; Zhao et al., 2011; Zhu, 2008") and the references therein. Most of these techniques have their inbuilt deficiencies including the evaluation of the so-called Adomian’s polynomials, divergent results, successive applications of the integral operator, un-realistic assumptions, non-compatibility with the nonlinearity of physical problem and very lengthy calculations. Inspired and motivated by the ongoing research in this area, we apply a relatively new technique which is called sine–cosine method (Wazwaz, 2004a,b") to find traveling wave solutions of Generalized KdVs. It is to be highlighted that such an equation arises frequently in various branches of physics, applied and engineering sciences (see Abbasbandy, 2007; Abdou and Soliman, 2005; Ablowitz and Clarkson, 1991; Al-Muhiameed and Abdel-Salam, 2011; Aslan, 2011; Bekir and Boz, 2008; Bekir and Cevikel, 2011; Deakin and Davison, 2010; Feng et al., 2011; Gepreel, 2011a,b; Gepreel and Shehata, 2012; Gomez and Salas, 2010; Guo et al., 2011; He, 2006; He and Wu, 2006; Hirota, 1971; Liu et al., 2010; Ma and You, 2004; Massabo et al., 2011; Mohyud-din et al., 2010; Malfliet, 1992; Naher et al., 2011a,b; Nofel et al., 2011; Ozis and Aslan, 2010; Rogers and Shadwick,1982; Salah et al., 2011; Salas, 2008; Salas and Gomez, 2010; Soliman and Abdo, 2009; Wang et al., 2008; Wazwaz, 2004a,b, 2007, 2011; Yildirim and Pinar, 2010; Yun, 2011; Zayed and Al-Joudi, 2010; Zayed and Gepreel, 2011; Zhang et al., 2010; Zhao et al., 2011; Zhu, 2008") and the references therein. The proposed scheme is fully compatible with the complexity of such problems and is very user-friendly. It is to be highlighted that the proposed algorithm gives some solutions which are compatible with solutions obtained in the Tanh method and the Tanh–Coth method. The reliability of the method and the reduction in the size of computational domain give this method a wider applicability. Moreover, some modifications can be seen in Nofel et al. (2001).

2 Sine–cosine method

In the proposed scheme, introducing the wave variable ξ = x − ct, we get(1) where u(x, t) is the traveling wave solution. This enables us to use the following changes(2) One can immediately reduce the nonlinear PDE (1) into a nonlinear ODE(3) The ordinary differential Eq. (3)(3) is then integrated as long as all terms contain derivatives, where we neglect integration constants. The solutions of many nonlinear equations can be expressed in the form(4) or in the form(5) where , μ and β are parameters that will be determined, μ and c are the wave number and the wave speed, respectively.

We use(6) and the derivatives of (5) become(7) and so on for the other derivatives. We substitute (6) or (7) into the reduced equation obtained above in (3), balancing the terms of the sine functions when (6) is used to otherwise balance the terms of the cosine functions. The resulting system of algebraic equations is solved by using the computerized symbolic calculations. We next collect all terms with the same power in cos^k(μξ) or sin^k(μξ) and equating their coefficients to zero to get a system of algebraic equations with unknowns , μ and β. All possible values of the parameters , μ and β are obtained.

3 Solution procedure

3.1 Generalized KdV equation

Consider the following gKdV equation(8) We now employ the sine–cosine method. Using the wave variable ξ = x − ct carries (8) into ODE(9) Integrating (9) gives and by considering the constant of integration to be zero for simplicity, we get(10) Substituting (7) into (10) gives(11) Equating the exponents and the coefficients of each pair of the cosine functions, we find the following system of algebraic equations:(12) Solving the system (12) yields(13) The result (13) can be easily obtained if we also use the sine method (6). 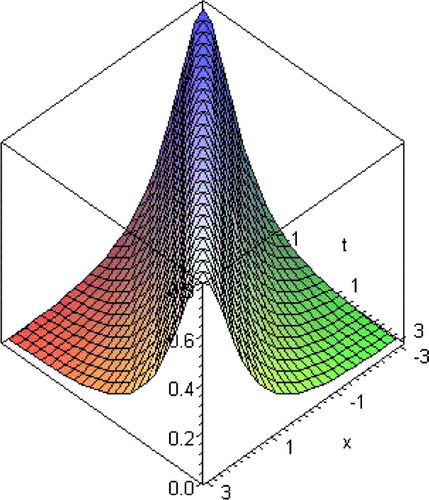We obtain the following periodic solutions for c < 0,(14) and(15) However, for c > 0, we obtain the soliton solutionThe graphical representation of u₃(x, t) is shown in Fig. 1

Figure 1 Soliton solution corresponding to u₃(x,t) for c = 1, n = 3.

Fig. 1 depicts soliton solution corresponding to u(x,t) for c = 1, n = 3.

3.2 mKdV equation

Consider the modified KdV equation(16) We now employ the sine–cosine method. Using the wave variable ξ = x − ct carries (16) into ODE(17) Integrating (17) gives and by considering the constant of integration to be zero, we get(18) Substituting (6) into (18) gives(19) Equating the exponents and the coefficients of each pair of the sine functions we find the following system of algebraic equations:(20) Solving the system (20) yields(21) Consequently, we obtain the following periodic solutions c < 0,(22) and(23) However, for c > 0, we obtain the soliton solutionFig. 2 depicts soliton solution corresponding to u(x,t) for c = 1.

Figure 2 Soliton solution corresponding to u(x,t) for c = 1.

4 Conclusion

The study shows that sine–cosine method is quite efficient and practically well suited for use in calculating traveling wave solutions for KdVs and other differential equations. The proposed algorithm gives some solutions which are compatible with solutions obtained in the Tanh method and the Tanh–Coth method. The reliability of the method and the reduction in the size of computational domain give this method a wider applicability.

Notes

Peer review under responsibility of University of Bahrain.