Chromaticity of a family of 5-partite graphs

Peer review under responsibility of University of Bahrain.

Abstract

Let P(G,λ) be the chromatic polynomial of a graph G. Two graphs G and H are said to be chromatically equivalent, denoted G ∼ H, if P(G,λ) = P(H,λ). We write [G] = {H∣H ∼ G}. If [G] = {G}, then G is said to be chromatically unique. In this paper, we first characterize certain complete 5-partite graphs G with 5n vertices according to the number of 6-independent partitions of G. Using these results, we investigate the chromaticity of G with certain stars or matching deleted parts . As a by-product, two new families of chromatically unique complete 5-partite graphs G with certain stars or matching deleted parts are obtained.

Keywords:

• Chromatic polynomial
• Chromatically closed
• Chromatic uniqueness

1 Introduction

All graphs considered here are simple and finite. For a graph G, let P(G,λ) be the chromatic polynomial of G. Two graphs G and H are said to be chromatically equivalent (or simply χ-equivalent), symbolically G ∼ H, if P(G,λ) = P(H,λ). The equivalence class determined by G under ∼ is denoted by [G]. A graph G is chromatically unique (or simply χ-unique) if H ≅ G whenever H ∼ G, i.e, [G] = {G} up to isomorphism. For a set of graphs, if for every , then is said to be χ-closed. Many families of χ-unique graphs are known (Koh and Teo, 1990, 1997").

For a graph G, let V(G), E(G), t(G) and χ(G) be the vertex set, edge set, number of triangles and chromatic number of G, respectively. Let O_n be an edgeless graph with n vertices. Let Q(G) and K(G) be the number of induced subgraphs isomorphic to C₄ and complete subgraphs K₄ in G. Let S be a set of s edges in G. By G − S (or G − s) we denote the graph obtained from G by deleting all edges in S, and 〈S〉 the graph induced by S. For t ⩾ 2 and 1 ⩽ n₁ ⩽ n₂ ⩽ ⋯ ⩽ n_t, let K(n₁,n₂,…,n_t) be a complete t-partite graph with partition sets V_i such that ∣V_i∣ = n_i for i = 1, 2,…,t. In (Dong et al., 2001; Lau and Peng, 2010a,b, Lau et al., 2010; Roslan et al., 2010, 2011a, 2012a; Zhao et al., 2004; Zhao, 2004, 2005"), the authors proved that certain families of complete t-partite graphs (t = 2, 3, 4, 5) with a matching or a star deleted are χ-unique. The case for the complete 6-partite graphs has been investigated in (2011c; 2012b; 2012c"). In particular, Zhao et al. (2004) and Zhao (2005) investigated the chromaticity of complete 5-partite graphs G of 5n and 5n + 4 vertices with certain stars or matching deleted parts. Roslan et al. (2011b) studied the chromaticity of complete 5-partite graphs G with 5n + i vertices for i = 1, 2, 3 with certain stars or matching deleted parts. As a continuation, in this paper, we characterize certain complete 5-partite graphs G with 5n vertices according to the number of 6-independent partitions of G. Using these results, we investigate the chromaticity of G with certain stars or matching deleted parts. As a by-product, two new families of chromatically unique complete 5-partite graphs with certain stars or matching deleted parts are obtained. These results generalized Theorems 3 and 4 in (Zhao, 2005).

2 Some lemmas and notations

Let be the family {K(n₁,n₂,…,n_t) − S∣ S ⊂ E(K(n₁,n₂,…,n_t)) and ∣S∣ = s}. For n₁ ⩾ s + 1, we denote by (respectively, ) the graph in K^−s(n₁,n₂,…,n_t) where the s edges in S induce a K_1,s with center in V_i and all the end vertices in V_j (respectively, a matching with end vertices in V_i and V_j).

For a graph G and a positive integer r, a partition {A₁,A₂,…,A_r} of V(G), where r is a positive integer, is called an r-independent partition of G if every A_i is independent of G. Let α(G,r) denote the number of r-independent partitions in G. Then, we have , where (λ)_r = λ(λ − 1)(λ − 2) ⋯ (λ − r + 1) and p is the number of vertices of G(see Read and Tutte, 1988). Therefore, α(G,r) = α(H,r) for each r = 1, 2,…, if G ∼ H.

For a graph G with p vertices, the polynomial is called the σ-polynomial of G (see Brenti, 1992). Clearly, P(G,λ) = P(H,λ) implies that σ(G,x) = σ(H,x) for any graphs G and H.

For disjoint graphs G and H, G + H denotes the disjoint union of G and H. The join of G and H denoted by G ∨ H is defined as follows: V(G ∨ H) = V(G) ∪ V(H); E(G ∨ H) = E(G) ∪ E(H) ∪ {xy∣x ∈ V(G),y ∈ V(H)}. For notations and terminology not defined here, we refer to (West, 2001).

Lemma 2.1

(Koh and Teo, 1990) Let G and H be two graphs with H ∼ G, then ∣V(G)∣ = ∣V(H)∣, ∣E(G)∣ = ∣E(H)∣, t(G) = t(H) and χ(G) = χ(H). Moreover, α(G,r) = α(H,r) for r ⩾ 1, and 2K(G) − Q(G) = 2K(H) − Q(H). Note that if χ(G) = 3, then G ∼ H implies that Q(G) = Q(H).

Lemma 2.2

(Brenti, 1992) Let G and H be two disjoint graphs. ThenIn particular,

Lemma 2.3

Zhao et al., 2004

Let G = K(n₁,n₂,n₃,n₄,n₅) and S be a set of some s edges of G. If H ∼ G − S, then there is a complete graph F = K(p₁,p₂,p₃,p₄,p₅) and a subset S′ of E(F) of some s′ edges of F such that H = F − S′ with ∣S′∣ = s′ = e(F) − e(G) + s.

Let n₁ ⩽ n₂ ⩽ n₃ ⩽ n₄ ⩽ n₅ be positive integers and . If there exist two elements and in {n₁,n₂,n₃,n₄,n₅} such that , is called an improvement of H = K(n₁,n₂,n₃,n₄,n₅).

Lemma 2.4

Zhao et al., 2004

Suppose n₁ ⩽ n₂ ⩽ n₃ ⩽ n₄ ⩽ n₅ and is an improvement of H = K(n₁,n₂,n₃,n₄,n₅), then

Let G = K(n₁,n₂,n₃,n₄,n₅). For a graph H = G − S, where S is a set of some s edges of G, define α′(H) = α(H,6) − α(G,6). Clearly, α′(H) ⩾ 0.

Lemma 2.5

Zhao et al., 2004

Let G = K(n₁,n₂,n₃,n₄,n₅). Suppose that min {n_i∣i = 1, 2, 3, 4, 5} ⩾ s + 1 ⩾ 1 and H = G − S, where S is a set of some s edges of G, thenα′(H) = s if and only if the set of end-vertices of any r ⩾ 2 edges in S is not independent in H, and α′(H) = 2^s − 1 if and only if S induces a star K_1,s and all vertices of K_1,s other than its center belong to a same A_i.

Lemma 2.6

Dong et al., 2001

Let n₁,n₂ and s be positive integers with 3 ⩽ n₁ ⩽ n₂, then

(1)

• is χ-unique for 1 ⩽ s ⩽ n₂ − 2,

(2)

• is χ-unique for 1 ⩽ s ⩽ n₁ − 2, and

(3)

• is χ-unique for 1 ⩽ s ⩽ n₁ − 1.

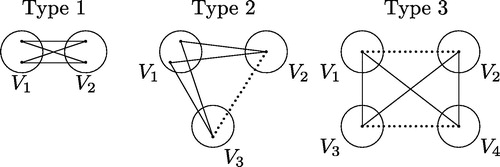
For a graph G ∈ K^−s(n₁,n₂,…,n_t), we say an induced C₄ subgraph of G is of Type 1 (respectively Type 2 and Type 3) if the vertices of the induced C₄ are in exactly two (respectively three and four) partite sets of V(G). An example of induced C₄ of Types 1, 2 and 3 is shown in Fig. 1.

Figure 1 Three types of induced C₄.

Suppose G is a graph in K^−s(n₁,n₂,…,n_t). Let S_ij(1 ⩽ i ⩽ t,1 ⩽ j ⩽ t) be a subset of S such that each edge in S_ij has an end-vertex in V_i and another end-vertex in V_j with ∣S_ij∣ = s_ij ⩾ 0.

Lemma 2.7

Lau and Peng, 2010b

For integer t ⩾ 3, let F = K(n₁,n₂,…,n_t) be a complete t-partite graph and let G = F − S, where S is a set of s edges in F. If S induces a matching in F, thenand

By using Lemma 2.7, we obtain the following.

Lemma 2.8

Let F = K(n₁,n₂,n₃,n₄,n₅) be a complete 5-partite graph and let G = F − S where S is a set of s edges in F. If S induces a matching in F, thenand

3 Characterization

In this section, we shall characterize certain complete 5-partite graphs G = K(n₁,n₂,n₃,n₄,n₅) according to the number of 6-independent partitions of G where n₅ − n₁ ⩽ 4.

Theorem 3.1

Let G = K(n₁,n₂,n₃,n₄,n₅) be a complete 5-partite graph such that n₁ + n₂ + n₃ + n₄ + n₅ = 5n and n₅ − n₁ ⩽ 4. Define θ(G) = [α(G,6) − 2ⁿ⁺¹ − 2ⁿ⁻¹ + 5]/2ⁿ⁻². Then

(i)

• θ(G) = 0 if and only if G = K(n,n,n,n,n);

(ii)

• θ(G) = 1 if and only if G = K(n − 1,n,n,n,n + 1);

(iii)

• θ(G) = 2 if and only if G = K(n − 1,n − 1,n,n + 1,n + 1);

(iv)

• if and only if G = K(n − 2,n,n,n + 1,n + 1);

(v)

• if and only if G = K(n − 2,n − 1,n + 1,n + 1,n + 1);

(vi)

• θ(G) = 4 if and only if G = K(n − 1,n − 1,n,n,n + 2);

(vii)

• if and only if G = K(n − 3,n,n + 1,n + 1,n + 1);

(viii)

• if and only if G = K(n − 2,n,n,n,n + 2);

(ix)

• θ(G) = 5 if and only if G = K(n − 1,n − 1,n − 1,n + 1,n + 2);

(x)

• if and only if G = K(n − 2,n − 1,n,n + 1,n + 2);

(xi)

• θ(G) = 7 if and only if G = K(n − 2,n − 2,n + 1,n + 1,n + 2);

(xii)

• if and only if G = K(n − 2,n − 1,n − 1,n + 2,n + 2);

(xiii)

• θ(G) = 9 if and only if G = K(n − 2,n − 2,n,n + 2,n + 2);

(xiv)

• θ(G) = 11 if and only if G = K(n − 1,n − 1,n − 1,n,n + 3);

Proof

In order to complete the proof of the theorem, we first give a table for the θ-value of various complete 5-partite graphs with 5n vertices as shown in Table 1.

By using Table 1, Lemma 2.4 and the definition of improvement, the proof is complete. □

Table 1 Some complete 5-partite graphs with 5n vertices and their θ-values.

Gi(1 ⩽ i ⩽ 23)	θ(Gi)	Gi(24 ⩽ i ⩽ 46)	θ(Gi)
G1 = K(n,n,n,n,n)	0	G24 = K(n − 4,n,n + 1,n + 1,n + 2)
G2 = K(n − 1,n,n,n,n + 1)	1	G25 = K(n − 4,n,n,n + 2,n + 2)
G3 = K(n − 1,n − 1,n,n + 1,n + 1)	2	G26 = K(n − 4,n,n,n + 1,n + 3)
G4 = K(n − 2,n,n,n + 1,n + 1)		G27 = K(n − 1,n − 1,n − 1,n − 1,n + 4)	26
G5 = K(n − 1,n − 1,n,n,n + 2)	4	G28 = K(n − 2,n − 1,n − 1,n,n + 4)
G6 = K(n − 2,n,n,n,n + 2)		G29 = K(n − 2,n − 2,n − 1,n + 2,n + 3)	16
G7 = K(n − 1,n − 1,n − 1,n + 1,n + 2)	5	G30 = K(n − 3,n − 1,n − 1,n + 2,n + 3)
G8 = K(n − 2,n − 1,n + 1,n + 1,n + 1)		G31 = K(n − 3,n − 2,n + 1,n + 2,n + 2)
G9 = K(n − 2,n − 1,n,n + 1,n + 2)		G32 = K(n − 3,n − 2,n + 1,n + 1,n + 3)
G10 = K(n − 3,n,n + 1,n + 1,n + 1)		G33 = K(n − 4,n − 1,n + 1,n + 2,n + 2)
G11 = K(n − 3,n,n,n + 1,n + 2)		G34 = K(n − 4,n − 1,n + 1,n + 1,n + 3)
G12 = K(n − 1,n − 1,n − 1,n,n + 3)	11	G35 = K(n − 3,n − 2,n,n + 2,n + 3)
G13 = K(n − 2,n − 1,n,n,n + 3)		G36 = K(n − 4,n − 1,n,n + 2,n + 3)
G14 = K(n − 3,n,n,n,n + 3)		G37 = K(n − 5,n + 1,n + 1,n + 1,n + 2)
G15 = K(n − 2,n − 1,n − 1,n + 2,n + 2)		G38 = K(n − 5,n,n + 1,n + 2,n + 2)
G16 = K(n − 2,n − 1,n − 1,n + 1,n + 3)		G39 = K(n − 5,n,n + 1,n + 1,n + 3)
G17 = K(n − 2,n − 2,n + 1,n + 1,n + 2)	7	G40 = K(n − 5,n,n,n + 2,n + 3)
G18 = K(n − 3,n − 1,n + 1,n + 1,n + 2)		G41 = K(n − 3,n − 3,n + 2,n + 2,n + 2)
G19 = K(n − 2,n − 2,n,n + 2,n + 2)	9	G42 = K(n − 3,n − 3,n + 1,n + 2,n + 3)
G20 = K(n − 2,n − 2,n,n + 1,n + 3)	13	G43 = K(n − 4,n − 2,n + 2,n + 2,n + 2)
G21 = K(n − 3,n − 1,n,n + 2,n + 2)		G44 = K(n − 4,n − 2,n + 1,n + 2,n + 3)
G22 = K(n − 3,n − 1,n,n + 1,n + 3)		G45 = K(n − 6,n + 1,n + 1,n + 2,n + 2)
G23 = K(n − 4,n + 1,n + 1,n + 1,n + 1)		G46 = K(n − 6,n + 1,n + 1,n + 1,n + 3)

4 Chromatically closed 5-partite graphs

In this section, we obtain a χ-closed family of graphs from the graphs in Theorem 3.1.

Theorem 4.1

The family of graphs where n₁ + n₂ + n₃ + n₄ + n₅ = 5n, n₅ − n₁ ⩽ 4 and n₁ ⩾ s + 5 is χ-closed.

Proof

By Theorem 3.1, there are 14 cases to consider. Denote each graph in Theorem 3.1 (i),(ii),…,(xiv) by G₁,G₂,…,G₁₄, respectively. Suppose H ∼ G_i − S. It suffices to show that H ∈ {G_i − S}. By Lemma 2.3, we know there exists a complete 5-partite graph F = (p₁,p₂,p₃,p₄,p₅) such that H = F − S′ with ∣ S′∣ = s′ = e(F) − e(G) + s ⩾ 0.

Case (i). Let G = G₁ with n ⩾ s + 2. In this case, . By Lemma 2.5, we haveHence,By the definition, α(F,6) − α(G,6) = 2ⁿ⁻²(θ(F) − θ(G)). By Theorem 3.1, θ(F) ⩾ 0. Suppose θ(F) > 0, thencontradicting α(F − S′,6) = α(G − S,6). Hence, θ(F) = 0 and so F = G and s = s′. Therefore, .

Case (ii). Let G = G₂ with n ⩾ s + 3. In this case, . By Lemma 2.5, we haveHence,By the definition, α(F,6) − α(G,6) = 2ⁿ⁻²(θ(F) − θ(G)). Suppose θ(F) ≠ θ(G). Then, we consider two subcases.

Subcase (a). θ(F) < θ(G). By Theorem 3.1, F = G₁ and H = G₁ − S′ ∈ {G₁ − S′}. However, G − S ∉ {G₁ − S′} since by Case (i) above, {G₁ − S′} is χ-closed, a contradiction.

Subcase (b). θ(F) > θ(G). By Theorem 3.1, α(F,6) − α(G,6) ⩾ 2ⁿ⁻². So,contradicting α(F − S′,6) = α(G − S,6). Hence, θ(F) − θ(G) = 0 and so F = G and s = s′. Therefore, .

Using Table 1, we can prove (iii) to (xiv) in a similar way. This completes the proof.□

5 Chromatically unique 5-partite graphs

The following results give two families of chromatically unique complete 5-partite graphs having 5n vertices with a set S of s edges deleted where the deleted edges induce a star K_1,s and a matching sK₂, respectively.

Theorem 5.1

em The graphs where n₁ + n₂ + n₃ + n₄ + n₅ = 5n, n₅ − n₁ ⩽ 4 and n₁ ⩾ s + 5 are χ-unique for 1 ⩽ i ≠ j ⩽ 5.

Proof

By Theorem 3.1, there are 14 cases to consider. Denote each graph in Theorem 3.1 (i),(ii),…,(xiv) by G₁,G₂,…,G₁₄, respectively. The proof for each graph obtained from G_i (i = 1, 2,…,14) is similar, so we only give the detailed proof for the graphs obtained from G₂ below.

By Lemma 2.5 and Case 2 of Theorem 4.1, we know that is χ-closed for n ⩾ s + 3. Note that

• ,

• ,

• ,

• .

By Lemmas 2.2 and 2.6, we conclude that for each (i,j) ∈ {(1,2),(1,5),(4,5)}. We now show that and are not χ-equivalent for (i,j) ∈ {(1,5),(5,1)}. We havewithsince s_ij = 0 if (i,j) ≠ {(2,3),(1,5),(5,1)}.

We also obtainwithsince s_ij = 0 if (i,j) ≠ {(2,3),(1,5),(5,1)}.

This means that , contradicting Lemma 2.1. Hence, is χ-unique where n ⩾ s + 3 for 1 ⩽ i ≠ j ⩽ 5.

The proof is thus complete.□

Theorem 5.2

The graphs where n₁ + n₂ + n₃ + n₄ + n₅ = 5n, n₅ − n₁ ⩽ 4 and n₁ ⩾ s + 5 are χ-unique.

Proof

By Theorem 3.1, there are 14 cases to consider. Denote each graph in Theorem 3.1 (i),(ii),…,(xiv) by G₁,G₂,…,G₁₄, respectively. For a graph K(p₁,p₂,p₃,p₄,p₅), let S = {e₁,e₂,…,e_s} be the set of s edges in E(K(p₁,p₂,p₃,p₄,p₅)) and let t(e_i) denote the number of triangles containing e_i in K(p₁,p₂,p₃,p₄,p₅). The proofs for each graph obtained from G_i(i = 1, 2,…,14) are similar, so we only give the proof for the graph obtained from G₁ and G₂ as follows.

Suppose for n ⩾ s + 2. By Theorem 4.1 and Lemma 2.1, and α′(H) = α′(G) = s. Let H = F − S where F = K(n,n,n,n,n). Clearly, t(e_i) ⩽ 3n for each e_i ∈ S. So,with equality holds only if t(e_i) = 3n for all e_i ∈ S. Since t(H) = t(G) = t(F) − 3ns, the equality above holds with t(e_i) = 3n for all e_i ∈ S. Therefore each edge in S has an end-vertex in V_i and another end-vertex in V_j(1 ⩽ i < j ⩽ 5). Moreover, S must induce a matching in F. Otherwise, equality does not hold or α′(H) > s. By Lemma 2.8, we obtainwhereasand the equality holds if and only if s = s_ij for 1 ⩽ i < j ⩽ 5, or s = s_ij + s_kl for 1 ⩽ i < j ⩽ 5,1 ⩽ k < l ⩽ 5, {i,j} ∩ {k,l} = ∅. Moreover, K(G) = K(F) − 3sn² whereasand the equality holds if and only if s = s_ij for 1 ⩽ i < j ⩽ 5. Hence,and the equality holds if and only if s = s_ij for 1 ⩽ i < j ⩽ 5. Consequently, 〈S〉 = sK₂ with H ≅ G.

Suppose for n ⩾ s + 3. By Theorem 4.1 and Lemma 2.1, and α′(H) = α′(G) = s. Let H = F − S where F = K(n − 1,n,n,n,n + 1). Clearly, t(e_i) ⩽ 3n + 1 for each e_i ∈ S. So,with equality holds only if t(e_i) = 3n + 1 for all e_i ∈ S. Since t(H) = t(G) = t(F) − s(3n + 1), the equality above holds with t(e_i) = 3n + 1 for all e_i ∈ S. Therefore each edge in S has an end-vertex in V₁ and another end-vertex in V_j(2 ⩽ j ⩽ 4). Moreover, S must induce a matching in F. Otherwise, equality does not hold or α′(H) > s. By Lemma 2.8, we obtainwhereasand the equality holds if and only if s = s_1j(2 ⩽ j ⩽ 4). Moreover, K(G) = K(H) = K(F) − s(3n² + 2n). Hence, 2K(G) − Q(G) = 2K(H) − Q(H) if and only if 〈S〉 ≅ sK₂ with H ≅ G.

Thus the proof is complete.□

Remark: Our results generalized Theorems 3 and 4 in (Zhao, 2005).

Acknowledgement

The authors would like to extend their sincere thanks to the referees for their constructive and valuable comments.

Notes

Peer review under responsibility of University of Bahrain.