Application of the (-expansion method for the generalized Fisher‘s equation and modified equal width equation

Peer review under responsibility of University of Bahrain.

Abstract

In this work, the exact traveling wave solutions of the generalized Fisher’s equation and modified equal width equation are studied by using the -expansion method. As a result, many solitary wave solutions are derived from the solutions via hyperbolic functions, trigonometric functions and rational functions. When the parameters were taken at special values, the results obtained were compared with the solution via the tanh method established earlier. In fact, many general non-traveling wave solutions are obtained. The efficiency of the method is demonstrated by applying it for a variety of selected equations.

Keywords:

• -Expansion method
• Fisher’s equation
• Modified equal width equation
• Tanh method
• Traveling wave solution

1 Introduction

In recent years, the exact solution of non-linear partial differential equations has been investigated by many authors (Krisnangkura et al., 2012; Wazwaz, 2004, 2006; Shi et al., 2012; Jabbari and Kheiri, 2010; Lee and Sakthivel, 2010a,b, 2011a,b, 2012; Parand and Rad, 2012; Elboree, 2012a,b; Abdel Rady et al., 2012; Honga and Lub, 2012; Abbasbandy and Shirzadi, 2010; Taghizadeh et al., 2012; Babolian and Dastani, 2012; Kafash et al., 2013; Mu and Ye, 2011; Ebadi and Biswas, 2010a,b; Kim and Sakthivel, 2010, 2011; Malik et al., 2010, 2012; Kabir et al., 2011; Feng et al., 2011; Jabbari et al., 2011; Ayhan and Bekir, 2012; Naher and Abdullah, 2012; Kraenkel et al., 2013; Taha and Noorani, 2013; Taha et al., 2013; Wang et al., 2008"), who are interested in non-linear physical phenomena in various fields of physics and engineering. Many powerful methods have been presented such as the tanh-method (Krisnangkura et al., 2012; Wazwaz, 2004"), sine–cosine method (Shi et al., 2012; Wazwaz, 2006"), tanh–coth method (Jabbari and Kheiri, 2010; Lee and Sakthivel, 2012, 2011a"), exp-function method (Lee and Sakthivel, 2010a, 2011b; Parand and Rad, 2012"), homogeneous-balance method (Elboree, 2012a; Abdel Rady et al., 2012"), Jacobi-elliptic function method (Honga and Lub, 2012; Lee and Sakthivel, 2010b"), first-integral method (Abbasbandy and Shirzadi, 2010; Taghizadeh et al., 2012"), similarity reduction method (Jie–Fang et al., 2013; Dai et al., 2012, 2010"), also many numerical method applied to solve nonlinear partial differential equations like homotopy perturbation method (Babolian and Dastani, 2012), variational iteration method (Kafash et al., 2013), finite volume method (Mu and Ye, 2011) and so on.

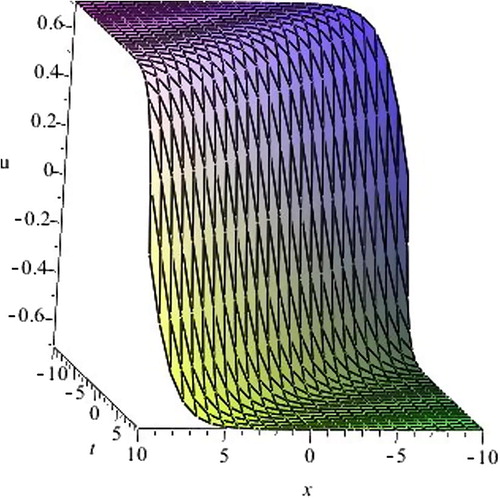
Figure 1 3D Graphs of a kink solution of (a) Eq. (33)(33) when + sign is taken and (b) Eq. (33)(33) when −ve sign is taken.

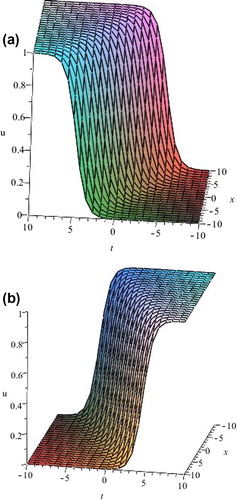
Figure 2 3D plot of Eq. (35)(35) .

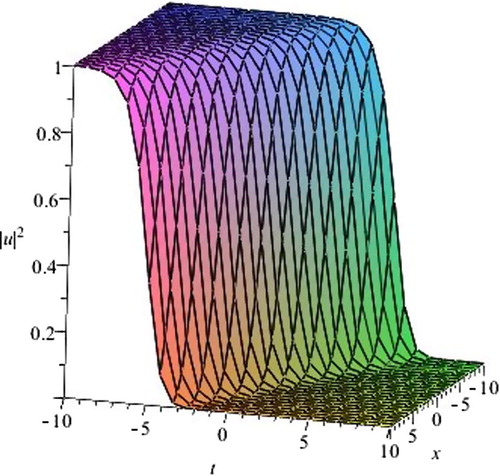
Figure 3 3D plot of Eq. (18)(18) .

The objective of this paper is to use a powerful method which is called the -expansion method (Ebadi and Biswas, 2010a,b; Kim and Sakthivel, 2010, 2011; Malik et al., 2010; Kabir et al., 2011; Feng et al., 2011; Jabbari et al., 2011; Ayhan and Bekir, 2012; Malik et al., 2012; Naher and Abdullah, 2012; Elboree, 2012b; Kraenkel et al., 2013; Taha and Noorani, 2013; Taha et al., 2013"), to obtain traveling wave solutions of such equations. The main ideas are that the traveling wave solutions of a non-linear equation can be expressed by a polynomial in , where G = G(ζ) satisfies the second order linear ordinary differential equation: G″(ζ) + λG′(ζ) + μ G(ζ) = 0 , where ζ = x − ct and λ, μ,c are constants. The degree of this polynomial can be determined by considering the homogeneous balance between the highest order derivative and non-linear terms appearing in the given non-linear equations. The coefficients of the polynomial λ, μ, and c can be obtained by solving a set of algebraic equations resulting from the process of using the proposed method (Wang et al., 2008). Solitary wave solutions have been found to many nonlinear evolution equations and play a very important role in various areas of applied mathematics and theoretical physics (Antonova and Biswas, 2009; Biswas, 2009, 2010, 2011; Girgis et al., 2010; Krishnan et al., 2011; Girgis and Biswas, 2011; Krishnan et al., 2012; Razborova et al., 2013").

In this paper, the traveling wave solutions obtained via this method are expressed by hyperbolic functions, the trigonometric functions and the rational functions. In addition the solitary wave solutions are obtained from the generalized Fisher’s equation and modified equal width equation when the choice of parameters are taken at special values. Fisher’s equation is a partial differential equation introduced by Fisher in 1937. Fisher’s equation describes the process of interaction between diffusion and reaction, and this equation is encountered in chemical kinetics and population dynamics (Wazwaz, 2009). The modified equal width equation (MEW) is a non-linear partial differential equation which was introduced by Morrison and Meiss (Morrison et al., 1984). The wide applicability of these equations is the main reason why many mathematicians have used them (Cheng and Liew, 2012).

2 Summary of the-expansion method

In this section, we describe the -expansion method for finding traveling wave solutions of NLPDE. Suppose that a nonlinear partial differential equation, say in two independent variables x and t, is given by.(1) where u = u(x,t) is an unknown function, P is a polynomial in u = u(x,t) and its various partial derivatives, in which highest order derivatives and nonlinear terms are involved.

The summary of the -expansion method, can be presented in the following six steps:

Step 1:

• To find the traveling wave solutions of Eq. (1)(1) , we introduce the wave variable(2) where the constant c is generally termed the wave velocity. Substituting Eq. (2)(2) into Eq. (1)(1) , we obtain the following ordinary differential equations (ODE) in ζ (which illustrates a principal advantage of a traveling wave solution, i.e., a PDE is reduced to an ODE).(3)

Step 2:

• If necessary we integrate Eq. (3)(3) as many times as possible and set the constants of integration to be zero for simplicity.

Step 3:

• We suppose the solution of nonlinear partial differential equation can be expressed by a polynomial in as(4) where G = G(ζ) satisfies the second-order linear ordinary differential equation(5) where and a_i, λ and μ are real constants with a_m ≠ 0. Here the prime denotes the derivative with respect to ζ. Using the general solutions of Eq. (5)(5) , we have(6) The above results can be written in simplified forms as(7)

Step 4:

• The positive integer m can be accomplished by considering the homogeneous balance between the highest order derivatives and nonlinear terms appearing in Eq. (3)(3) as follows: if we define the degree of u(ζ) as D[u(ζ)] = m, then the degree of other expressions is defined byTherefore, we can get the value of m in Eq. (4)(4) .

Step 5:

• Substituting Eq. (4)(4) into Eq. (3)(3) using general solutions of Eq. (5)(5) and collecting all terms with the same order of together, then setting each coefficient of this polynomial to zero yield a set of algebraic equations for a_i, c, λ and μ.

Step 6:

• Substitute a_i, c, λ and μ obtained in step 5 and the general solutions of Eq. (5)(5) into Eq. (4)(4) . Next, depending on the sign of the discriminant (λ² − 4μ), we can obtain the explicit solutions of Eq. (1)(1) immediately.

The advantages of the approach taken in this paper are as follows:

•

• It will be more important to seek solutions of higher-order nonlinear equations which can be reduced to ODEs of the order greater than 3.

•

• In the -expansion method, there is no need to apply the initial and boundary conditions at the outset. The methods yield a general solution with free parameters which can be identified by the above conditions.

•

• The general solution obtained by -expansion method without approximation.

•

• Finally, the solution procedure can be easily implemented in Mathematica or Maple.

3 Application the -expansion method

3.1 Modified equal width equation

In this section, we apply the -expansion method to solve the modified equal width equation. First, consider the modified equal width equation in the forms (Wazwaz, 2006).(8) Using the wave transformation u(x,t) = u(ζ),ζ = x − ct. The following equation is obtained(9) Integrating the equation and neglecting the constant of integration. (9)(9) becomes(10) Considering the homogeneous balance between the highest order derivative and the non-linear term, then 3m = m + 2 gives m = 1 therefore, the solution of (10)(10) can be written in the form(11) by Eqs. (5)(5) and (11)(11) we drive(12) (13) Substituting (12)(12) and (13)(13) into (10)(10) , collecting all terms with the same powers of and setting each coefficient to zero, we obtain a system of algebraic equations for a₀,a₁,c, λ and μ as follows.solving this system by Maple gives(14) λ, b, c and a are arbitrary constants. Substituting the solution set (14)(14) into (11)(11) , the solution formulae of Eq. (10)(10) can be written as(15)

Substituting the general solutions of second order linear ODE in to (15)(15) gives three types of traveling wave solutions.

Case a. When λ² − 4μ > 0, we obtain the hyperbolic function traveling wave solution(16) (17) c₁ and c₂ are arbitrary constants. On the other hand, assuming c₁ = 0 and c₂ ≠ 0, the traveling wave solution of (17)(17) can be written as.(18) assuming c₂ = 0 and c₁ ≠ 0, then we obtain(19) where ζ = x − ct.

Case b. When λ² − 4μ < 0, we obtain the trigonometric function traveling wave solutions(20) (21) Also, if assume c₁ = 0 and c₂ ≠ 0, then(22) and when c₂ = 0,c₁ ≠ 0, the solution of Eq. (21)(21) will be(23) where ζ = x − ct.

Case c. When λ² − 4μ = 0, we obtain the rational function solutions(24) (25) where ζ = x − ct.

For the comparison between our solution and that of Wazwaz as given in Wazwaz (2006), first we assume and then we get the same as that of Wazwaz (2006) (see Table 1).

Table 1 Comparison of our solutions with Wazwaz solutions.

Wazwaz solutions	Our solutions
If b > 0 then Eq. (38) becomes	If c1 ≠ 0 Eq. (18)(18) becomes
If b > 0 then Eq. (39) becomes	If c2 ≠ 0 Eq. (19)(19) becomes
When b < 0 then Eq. (40) becomes	When c1 ≠ 0 Eq. (22)(22) becomes
When b < 0 then Eq. (41) becomes	When c2 ≠ 0 Eq. (23)(23) becomes

3.2 Generalized Fisher’s equation

In this section, we study generalized Fisher’s equation (Wazwaz, 2004)(26)

To solve the above generalized fisher’s equation by using the -expansion method, we use the transformations u(x,t) = u(ζ) with wave variable ζ = k(x − ct), the system (26)(26) is carried to a system of ODEs(27)

According to the previous steps, using the balancing procedure between u³ and u″ in (27)(27) we get m = 1. The solution of (27)(27) can be expressed by a polynomial in as follows(28)

On substituting (28)(28) into ODEs (27)(27) , collecting all terms with the same powers of and setting each cofficient to zero, we obtain the following system of algebraic equationsby using Maple, we get(29) k and μ are arbitrary constants, substituting (29)(29) into (28)(28) the solution formulae of (26)(26) could be written:(30) where ζ = k(x − ct) = kx.(31) where .(32) where .

Substituting general solution of (5)(5) into (30)–(32) three types of traveling wave solutions of the generalized Fisher’s equations are obtained.

Hyperbolic function solutions

When λ² − 4μ > 0, substituting the general solution of (5)(5) into (30)–(32), we obtain the following traveling wave solution of (26)(26) :where ζ = kx.where .where and c₂ are arbitrary constants.

The various known results can be rediscovered, if c₁ and c₂ are taken as special values. For example:

If c₂ = 0,c₁ ≠ 0 and k = 1(33) On the other hand, if c₁ = 0,c₂ ≠ 0 and k = 1, the traveling wave solution can be written as(34) where (33)(33) and (34)(34) are the same as the result obtained by the tanh method (Wazwaz, 2004).

Trigonometric function solutions

When λ² − 4μ < 0, then we havewhere ζ = kx.where .where .

If c₂ = 0 and k = 1, then u(ζ) becomes(35) If c₁ = 0 and k = 1, the traveling wave solution can be written as(36)

Rational function solution

When λ² − 4 = 0, then(37) This solution is the exact same solution obtained byWazwaz’s (Wazwaz, 2004) see Table 2.

Table 2 Comparison of our solutions with Wazwaz solutions.

Wazwaz solutions	Our solutions
Eq. (16)(16) becomes	If c1 ≠ 0 and k = 1 Eq. (33)(33) becomes
Eq. (17)(17) becomes	If c2 ≠ 0 and k = 1 Eq. (34)(34) becomes

3.3 Graphical representations of the solutions

The graphical illustrations of the solutions are described in Figs. 12–3 with the aid of Maple. All solutions appear as kink wave solution (depending upon the choice of sign).

4 Conclusion

In this paper, we obtain the traveling wave solutions of generalized Fisher’s equation and modified equal width equation by using the -expansion method. We have seen that three types of traveling wave solutions were successfully found, in terms of hyperbolic, trigonometric and rational functions. Also comparison was made between the solution of the -expansion method and the tanh method under special conditions. The solution of the -expansion method is exactly the same as the solution of the tanh method. In our opinion the -expansion method is more efficient from the tanh method. Moreover, the tanh method may give more than one soliton solution. But, the -expansion method gives many-soliton solutions for nonlinear partial differential equations, this means the tanh method does not have this capability. Also, the solutions contain free parameters. These solutions will be very useful in various physical situations where these equations arise. We have noted that the -expansion method changes the given difficult problems into simple problems which can be solved easily. We hope that they will be helpful for further studies in applied sciences.

Notes

Peer review under responsibility of University of Bahrain.