New (G′/G)-expansion method and its application to the Zakharov-Kuznetsov–Benjamin-Bona-Mahony (ZK–BBM) equation

Peer review under responsibility of University of Bahrain.

Abstract

In this article, new (G′/G)-expansion method is used to look for the traveling wave solutions of nonlinear evolution equations and abundant traveling wave solutions to the Zakharov-Kuznetsov–Benjamin-Bona-Mahony equation are constructed. The performance of the method is reliable, useful and gives more new general exact solutions than the existing methods.

Keywords:

• New (G′/G)-expansion method
• Zakharov-Kuznetsov–Benjamin-Bona-Mahony equation
• Solitary wave solutions
• Auxiliary nonlinear ordinary differential equation
• Exact solutions

Introduction

It is well known that nonlinear evolution equations (NLEEs) are widely used to describe complex phenomena in various fields of science, especially in physics, plasma physics, fluid physics, quantum field theory, biophysics, chemical kinematics, geochemistry, electricity, propagation of shallow water waves, high-energy physics, quantum mechanics, optical fibers, elastic media and so on. The analytical solutions of such equations are of fundamental importance. Among the possible solutions to NLEEs, certain special form solutions may depend only on a single combination of variables such as solitons. In mathematics and physics, a soliton is a self-reinforcing solitary wave, a wave packet or pulse that upholds its shape while it travels at constant speed. Due to the availability of symbolic computation software, direct methods to search exact solutions have attracted much more attention. In the past years, many powerful and direct methods have been developed to find special solutions, such as, Weierstrass elliptic function method (Kudryashov, 1990), Jacobi elliptic function expansion method (Chen and Wang, 2005; Liu et al., 2001), tanh-function method (Malfliet, 2004; Malfliet, 1992; Abdou, 2007; Wazwaz, 2008; Fan, 2000), Inverse scattering transform method (Ablowitz and Clarkson, 1991), Hirota method (Hirota, 1971), Backlund transform method (Rogers and Shadwick, 1982), Exp-function method (He and Wu, 2006; Naher et al., 2011, 2012; Mohyud-Din, 2009, 2010; Akbar and Ali, 2012), Truncated Painleve expansion method (Kudryashov, 1991), Extended tanh-method (Abdou and Soliman, 2006; El-Wakil and Abdou, 2007; Lü and Zhang, 2004) and the homogeneous balance method (Zhao et al., 2006; Zhaosheng, 2004; Zhao and Tang, 2002) are used for searching the exact solutions.

Fig. 1 Soliton solution for Eq. (17)(17) .

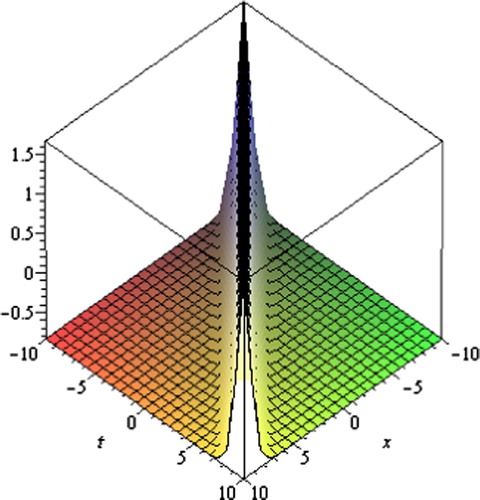
Fig. 2 Soliton solution for Eq. (18)(18) .

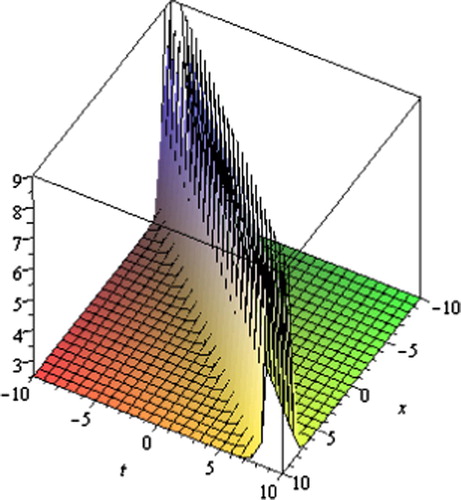
Fig. 3 Soliton solution for Eq. (25)(25) .

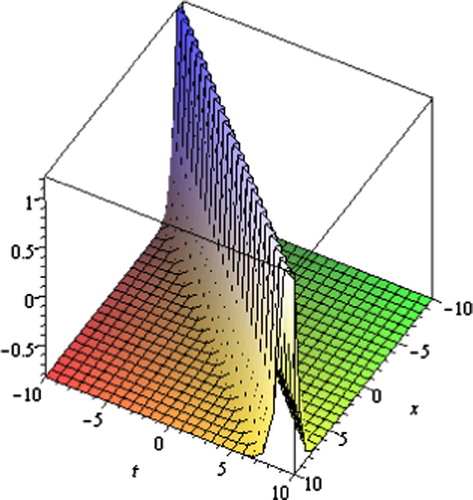
Fig. 4 Singular periodic solution for Eq. (28)(28) .

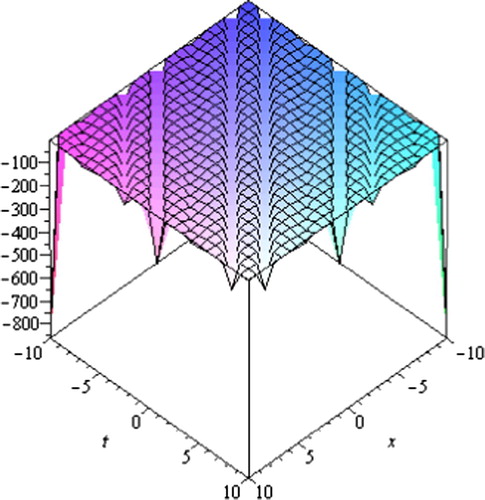
Fig. 5 Singular periodic solution for Eq. (29)(29) .

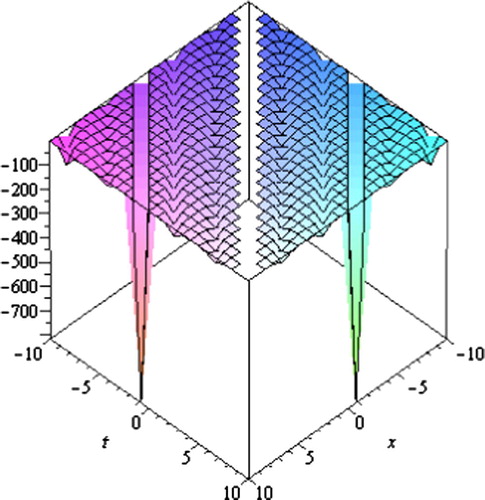
Fig. 6 Soliton solution for Eq. (39)(39) .

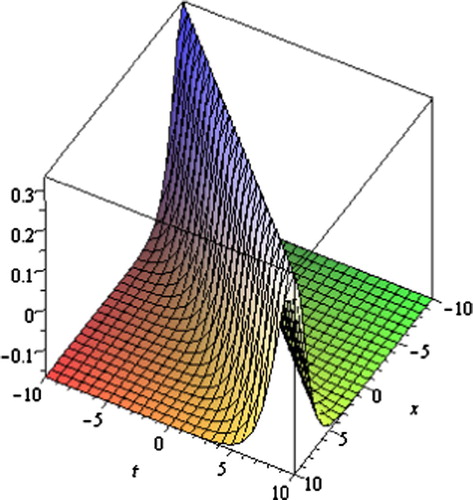
Fig. 7 Periodic solution for Eq. (46)(46) .

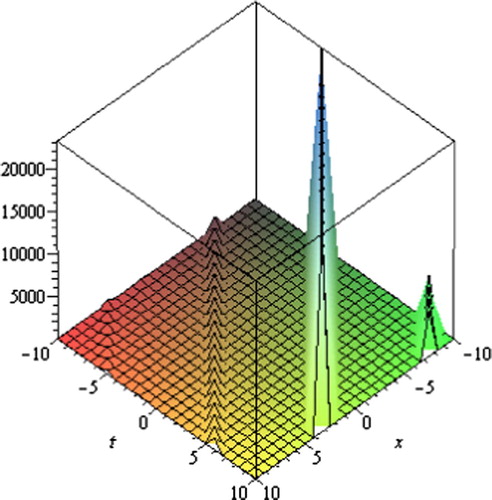
Fig. 8 Singular periodic solution for Eq. (52)(52) .

Table

New approach	Old approach
1. The new about “new (G′/G)-expansion approach” is that, in this technique the highly nonlinear equation (6) is used as an auxiliary equation. This equation has a variety of solutions.	1. In traditional (G′/G)-expansion technique the second order linear ordinary differential equation G^″(ξ) + λ G′(ξ) + μG(ξ) = 0 is used as an auxiliary equation.
2. The Cole-Hopf transformation reduces the Eq. (6)(6) to the Riccati Eq. (7)(7) . The Riccati Eq. (7)(7) has a variety of exact solutions with more free parameters. (see Zhu, 2008 for details). The solution is written in a more general form which gives the number of solution sets for the nonlinear equations. Also, if we set k = 0, A = −λ, B = −μ, C = 0 and negative the exponents of (G′/G) are zero in Eq. (4)(4) , then the proposed new method turns out into the basic (G′/G)-expansion method introduced by (Wang et al., 2008). So our solution is more general than the basic (G′/G)-expansion.	2. Whereas, in traditional (G′/G)-expansion introduced by (Wang et al., 2008), the auxiliary equation G^″(ξ) + λG′(ξ) + μ G(ξ) = 0 has the following three types of the solutions whereas the solution is written in the form which is a special case of our solution (4). All the above mentioned solutions are rediscovered when c1 = 0, c2 ≠ 0 and c1 ≠ 0, c2 = 0.
3. The solutions given by the new (G′/G)-expansion approach are more general with three free parameters. When these free parameters are given particular values, the previous results obtained by the other authors are rediscovered.The additional unknown constant k in the solution will help us to obtain solution of the algebraic equations resulted in step 4 of “The method” section.	3. The solutions obtained by basic (G′/G)-expansion method contain only two free parameters.

Lately, Wang et al. (2008) introduced a direct method, called (G′/G)-expansion method and demonstrated that it is a powerful method for seeking analytic solutions of NLEEs. For additional references see the articles (Akbar et al., 2012a,b,c; El-Wakil et al., 2010; Parkes, 2010; Akbar and Ali, 2011; Zayed, 2009a,b; Zayed and Abdelaziz, 2010, 2012a,b, 2013; Zayed and Al-Joudi, 2009, 2010; Zayed and Gepreel, 2009a,b; Zayed and Gepreel, 2011). In order to establish the efficiency and tenacity of the (G′/G)-expansion method and to extend the range of applicability, further research has been carried out by several researchers. For instance, Zhang et al. (2008) made a generalization of the (G′/G)-expansion method for the evolution equations with variable coefficients. Zhang et al. (2010) also presented an improved (G′/G)-expansion method to seek more general traveling wave solutions. Zayed (2009a,b)" presented a new approach of the (G′/G)-expansion method where G(ξ) satisfies the Jacobi elliptic equation, [G′(ξ)]² = e₂ G⁴(ξ) + e₁ G²(ξ) + e₀, e₂, e₁, e₀ are arbitrary constants, and obtained new exact solutions. Zayed (2011) again presented an alternative approach of this method in which G(ξ) satisfies the Riccati equation G′(ξ) = AG(ξ) + BG²(ξ), where A and B are arbitrary constants.

In this article, we use a new (G′/G)-expansion method introduced by Alam et al. (2013) to solve the NLEEs in mathematical physics and engineering. To illustrate the originality, consistency and advantages of the method, Zakharov-Kuznetsov–Benjamin-Bona-Mahony equation is solved and abundant new families of exact solutions are found.

The method

Suppose the nonlinear evolution equation is of the form(1) where P is a polynomial in u(x,t) and its partial derivatives wherein the highest order partial derivatives and the nonlinear terms are concerned. The main steps of the method are as follows:

• Step 1: Combining the real variables x and t by a compound variable ξ, we suppose that(2) where V is the speed of the traveling wave. Eq. (2)(2) transforms Eq. (1)(1) into an ordinary differential equation (ODE) for u = u(ξ):(3) where Q is a function of u(ξ) and its derivatives in which prime stands for derivative with respect to ξ.

• Step 2: Assume the solution of Eq. (3)(3) can be expressed as:(4) where(5)

  Herein α_−m or α_m may be zero, but both of them can not be zero simultaneously. α_i (i = 0, ±1, ±2,…, ±N) and k are constants to be determined later and G = G(ξ) satisfies the second order nonlinear ordinary differential equation:(6) where prime denotes the derivative with respect to ξ; A, B, and C are real constants.

  The Cole–Hopf transformation reduces the Eq. (6)(6) to the Riccati equation:(7)

  Eq. (7)(7) has 25 individual solutions (see Zhu, 2008 for details).

• Step 3: The value of the positive integer m can be determined by balancing the highest order linear terms with the nonlinear terms of the highest order shown in Eq. (3)(3) .

• Step 4: Substitute Eq. (4)(4) including Eqs. (5)(5) and (6)(6) in Eq. (3)(3) , we obtain polynomials in and . Collect each coefficient of the resulted polynomials to zero, yields an over-determined set of algebraic equations for α_i(i = 0, ±1, ±2,…, ±N), k and V.

• Step 5: Suppose the value of the constants can be obtained by solving the algebraic equations obtained in Step 4. The values of the constants together with the solutions of Eq. (6)(6) yield abundant exact traveling wave solutions of the nonlinear evolution Eq. (1)(1) .

Application

In this section, we will use the new (G′/G)-expansion method to find exact traveling wave solutions of the celebrated Zakharov-Kuznetsov–Benjamin-Bona-Mahony (ZK–BBM) equation.

Let us now, consider the ZK–BBM equation(8)

Using the traveling wave variable u = u(ξ), ξ = x − Vt in Eq. (8)(8) and integrating once, we obtain(9) where C₁ is an integration constant.

Considering the homogeneous balance between u″ and u² in Eq. (9)(9) , we obtain m = 2. Therefore, the trial solution becomes(10)

Using Eq. (10)(10) in Eq. (9)(9) , the left hand side transforms into polynomials in, (i = 0, 1, 2,…,N) and, (i = 0, 1, 2,…, N). Equating the coefficients of same power of the resulted polynomials to zero, we obtain a set of algebraic equations (which are omitted for the sake of simplicity) for α₀, α₁, α₂, α₋₁, α₋₂, k, C₁ and V. Solving the over-determined set of algebraic equations by using the symbolic computation software, such as Maple 13, we obtain

• Set 1:(11) where k, V, A, B and C are arbitrary constants.

• Set.2:(12) where k,V,A,B and C are arbitrary constants.

• Set 3:(13) where V, A, B and C are arbitrary constants.

Substituting Eqs. (11)–(13) in Eq. (10)(10) , we obtain(14) (15) (16) where ξ = x − Vt; V, A, B and C are arbitrary constants.

Substituting the solutions G(ξ) of the Eq. (6)(6) in Eq. (14)(14) and simplifying, we obtain the following solutions:

When Δ = A² − 4BC + 4B > 0 and A(C − 1) ≠ 0 (or B(C − 1) ≠ 0),(17) (18) (19) (20) (21) (22) (23) where F and H are real constants.(24) (25) (26) (27)

When Δ = A² − 4BC + 4B < 0 and A(C − 1) ≠ 0 (or B (C − 1) ≠ 0),(28) (29) (30) (31) (32) (33) (34) where F and H are real constants such that F² − H² > 0.(35) (36) (37) (38)

When B = 0 and A(C − 1) ≠ 0,(39) (40) where c₁ is an arbitrary constant.

When A = B = 0 and (C − 1) ≠ 0, the solution of Eq. (8)(8) is(41) where c₂ is an arbitrary constant.

Substituting the solutions G(ξ) of the Eq. (6)(6) in Eq. (15)(15) and simplifying, we obtain the following solutions:

When Δ = A² − 4BC + 4B > 0 and A(C − 1) ≠ 0 (orB (C − 1) ≠ 0),(42) where ξ = x − Vt; k, A, B and C are arbitrary constants.(43) (44)

The other families of exact solutions of Eq. (8)(8) are omitted for convenience.

When Δ = A² − 4BC + 4B < 0 and A(C − 1) ≠ 0 (or B (C − 1) ≠ 0),(45) (46) (47)

When A = B = 0 and(C − 1) ≠ 0, the solution of Eq. (8)(8) is(48) where c₃ is an arbitrary constant.

We can write down the other families of exact solutions of Eq. (8)(8) which are omitted for practicality.

Finally, substituting the solutions G(ξ) of the Eq. (6)(6) in Eq. (16)(16) and simplifying, we obtain the following solutions:

When Δ = A² − 4BC + 4B > 0 and A(C − 1) ≠ 0 (or B (C − 1) ≠ 0),(49) where ξ = x − Vt; A, B and C are arbitrary constants.(50) (51)

For simplicity others families of exact solutions are omitted.

When Δ = A² − 4BC + 4B < 0 and A(C − 1) ≠ 0 (or B (C − 1) ≠ 0),(52) (53) (54)

When (C − 1) ≠ 0 and A = B = 0, the solution of Eq. (8)(8) is(55) where c₄ is an arbitrary constant.

The other families of exact solutions of Eq. (8)(8) are omitted for convenience.

Graphical presentation

Graph is a powerful tool for communication and describes logically the solutions of the problems. Therefore, some graphs of the solutions for different values of parameters are given (Figs. 1–8). The graphs readily have shown the solitary wave form of the solutions.

Remark 1

We have checked the obtained solutions by putting them back in the original equation and found correct.

Results and discussion

From the above solutions we observe that, if we put A = −λ, B = −μ, C = 0, k = 0, a = a, b = b and V = −V in our solutions , then (Zhang et al., 2010) solutions (14) and (15) are identical to our solutions when C₁ = 0 and C₂ = 0, respectively. Similarly, if we put A = λ, B = −μ, C = 0, k = 0, a = a, b = b and V = −V in our solutions , then (Zhang et al., 2010) solutions (17) and (19) are identical to our solutions when C₁ = 0 and C₂ = 0, respectively. On the other hand (Zhang et al., 2010) solution (20) is identical to our solution for different values of parameters. Zhang et al. (2010) did not find any more solution, but by using the new (G′/G)-expansion method, we have obtained some new and exact solutions. It can be shown that solutions obtained by the improved (G′/G)-expansion method Zhang et al. (2010) are only special cases of the new (G′/G)-expansion method.

Comparison

Comparison of old and new (G′/G)-expansion approaches.

Conclusion

New (G′/G)-expansion method is applied to the Zakharov-Kuznetsov–Benjamin-Bona-Mahony equation and abundant exact traveling wave solutions are constructed for this equation. The obtained solutions are more general, and many known solutions are only a special case of them. Further, this study shows that the method is quite efficient and practically well suited to be used in finding exact solutions of nonlinear evolution equations. It is noteworthy to observe that the basic (G′/G)-expansion method, improved (G′/G)-expansion, generalized and improved (G′/G)-expansion method are only special cases of the new (G′/G)-expansion method. Thus the new (G′/G)-expansion method would be a powerful mathematical tool for solving nonlinear evolution equations.

Notes

Peer review under responsibility of University of Bahrain.