Shape changing nonlocal molecular deformations in a nematic liquid crystal system

Peer review under responsibility of University of Bahrain.

Abstract

The nature of nonlinear molecular deformations in a homeotropically aligned nematic liquid crystal (NLC) is presented. We start from the basic dynamical equation for the director axis of a NLC with elastic deformation and mapped onto a integro-differential perturbed Nonlinear Schrödinger equation which includes the nonlocal term. By invoking the modified extended tangent hyperbolic function method aided with symbolic computation, we obtain a series of solitary wave solutions. Under the influence of the nonlocality induced by the reorientation nonlinearity due to fluctuations in the molecular orientation, the solitary wave exhibits shape changing property for different choices of parameters. This intriguing property as a result of the relation between the coherence of the solitary deformation and the nonlocality reveals a strong need for a deeper understanding in the theory of self-localization in NLC systems.

Keywords:

• Nonlocal nonlinear Schrödinger equation
• Liquid crystal
• Symbolic computation
• Solitons

1 Introduction

Nonlinear dynamics of liquid crystals has been a subject of intensive study for more than two decades (de Gennes and Prost, 1993; Chandrasekhar, 1992; Rodrigueze and Reyes, 1997; Ilichev and Semenov, 1992; Brotherton-Ratcliffe and Smith, 1989; Bassom Andrew and Seddougui Sharon, 1995; Renardy, 1992; Zakharov Vladimir, 2010). Not surprisingly, in both basic and applied research solitons have been found to have important effects in the mechanical, hydrodynamical and thermal properties of these highly nonlinear liquid crystals and play an important role in the switching mechanism of some ferroelectric liquid crystal displays (Lam and Prost, 1992; Conti et al., 2003; Lam et al., 1993) . In a nematic liquid crystal (NLC), the molecules are considered as elongated rods which are positionally disordered but reveal a long-range orientational order. This property is described on a mesocopic level by a unit vector , which is called as the director axis pointing in the direction of the average molecular alignment. Due to the absence of a permanent polarization in the nematic phase the director just indicates the orientation but it has neither head nor tail. However, the director reorientation or molecular excitation in NLC systems takes place due to elastic deformations such as splay, twist and bend (Lin, 1981).

The nonlinearity due to reorientation effect in a nematic phase leads to numerous effects not observed in any other types of nonlinearity. Mostly the nonlinear effects are based on molecular reorientation, and this behavior leads to soliton and under suitable conditions solitary waves can exist in NLC systems which has been investigated extensively both from theoretical and experimental points of view (Zhu, 1982; Helfrich, 1968; Leger, 1972; Migler and Meyer, 1991; Lin et al., 1985; Shu and Lin, 1985; Strinic et al., 2009; Peccianti et al., 2010) . Propagation of solitons in an uniform shearing nematics was first studied by Lin et al. (Lin, 1981) and Zhu experimentally confirmed the existence of solitary like director wave excited by a mechanical method (Zhu, 1982). Magnetically induced solitary waves were found to evolve in a NLC which was first discovered by Helfrich (Helfrich, 1968) and later confirmed by Legar (Leger, 1972). Further Migler and Meyer reported the novel nonlinear dissipative dynamic patterns and observed several types of soliton structures in the case of NLC systems under the influence of a continuously rotating magnetic field (Migler and Meyer, 1991). In addition, the effect of external field on multisolitons and the relation between observed optical-interference patterns and the director reorientation have also been investigated. Using the reorientational nonlinearity (Khoo and Wu, 1997) it is possible to generate spatial solitons called nematicons, at relatively low powers (Assanto et al., 2003; Karpierz, 2001). Mclaughlin et al. (Mclaughlin et al., 1995) have predicted that, owing to the nonlocality of their nonlinearity, liquid crystals can sustain single component higher order mode solitons. The nonlocality of the material can have profound effects on the properties of the optical beams and the soliton formation e.g., leading to collapse arrest of finite size beams (Bang et al., 2002), attraction and formation of bound states of dark solitons (Nikolov et al., 2004). Lately, it has been verified (Conti et al., 2003) that the nematicons are exact accessible solitons for the nematic liquid crystal exhibiting strongly nonlocal nonlinear behavior. Single solitons generated by pressure gradients in long and circular cells of nematics respectively have also been reported recently (Lin et al., 1985). More recently Daniel et al. studied the director dynamics in a quasi-one-dimensional NLC under elastic deformations in the absence of an external field without imposing the one constant approximation (Daniel and Gnanasekaran, 2005; Daniel et al., 2008). The molecular deformation in terms of a rotational director axis field is found to exhibit localized behavior in the form of pulse, hole and shock as well as solitons (Daniel and Gnanasekaran, 2008). Assanto et al. studied, the NLC large optical nonlinearity stems from light-induced molecular reorientation, which can extend well beyond the excitation region owing to elastic intermolecular forces and the nonlocal character of the reorientational nonlinearity has a striking effect on the propagation of light, and its fundamental role has been addressed in terms of both soliton and modulational instability. The soliton formation in the form of molecular reorientation can tune the nonlocality with respect to optical nonlinearity (Peccianti et al., 2005).

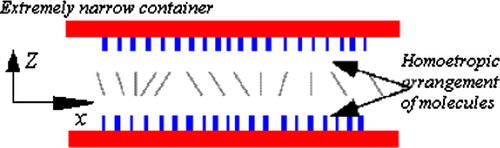
In the present chapter, we assume that our liquid crystal system is contained in an extremely narrow container with homoetropic alignment of molecules with a strong surface anchoring at the boundaries as illustrated in Fig. 1. In this case, the molecular field due to elastic energy is assumed to be perpendicular with the director axis which necessarily involves splay and bend type deformations in addition to twist. We attempt to demonstrate the shape changing director dynamics by employing the modified extended tangent hyperbolic (METF) method to solve the associated dynamical equation and understand the nonlinear dynamics. The plan of the paper is as follows. We construct the dynamical torque equation representing the director dynamics and recast the same to an equivalent perturbed nonlocal nonlinear Schrödinger (NLS) equation using the space–curve mapping procedure. We solve the perturbed integro-differential NLS by means of a computerized symbolic computation using a modified extended tangent-hyperbolic function method and the Jacobi elliptic function method is employed to construct a series of solitary wave solutions. In order to better understand the nonlocality induced by the director reorientations of nematic liquid crystal, we have constructed the component form of director axis using the Darboux vector transformation. Finally we conclude our results.

Figure 1 A sketch of the quasi one-dimensional nematic liquid crystal system contained in an extremely narrow infinite container.

2 Director dynamics

Liquid crystals are anisotropic materials with an anisotropy axis along the molecular orientation. At a given temperature, NLC molecules fluctuate around the mean direction defined by the director n(r). The distortion of the molecular alignment corresponds to the free energy density of NLC (Daniel and Gnanasekaran, 2004; Simoes, 1997; Kelley and Palffy-Muhoray, 1997; Karpierz, 2002) given by(1) where represents elastic constants for the three different basic cannonical deformations such as splay , twist and bend . These constants are phenomenological parameters which can be connected with the intermolecular interaction giving rise to the nematic phase. Usually , but Eq. (1)(1) is simplified by assuming the one-elastic constant approximation . We ignore the spatial variations in the degree of orientational order and describe the NLC in terms of the director rather than the order parameter tensor. We also ignore the effects of flow and work in the one-elastic approximation. Under this approximation, the free energy density given in Eq. (1)(1) takes the simple form(2)

To obtain the equation of motion, it is necessary to describe the generalized thermodynamic force acting on the director. We note that the molecular field corresponding to the pure elastic deformations using the Lagrange equation and satisfies introduced by de Gennes (de Gennes and Prost, 1993). The quantity may be interpreted as the Lagrange multiplier associated with the constraint and the condition for equilibrium is that or . Nematic liquid crystals are charge carrying fluids with long range, uniaxial orientation and molecular alignment giving rise to anisotropic, macroscopic properties. By virtue of the anisotropic properties of nematic liquid crystals, it is advantageous to study the dynamics of director axis n(r) instead of studying the dynamics of all the molecules. In the absence of flow, the director axis n(r) do not remain in the same position but fluctuates about the mean position which is mainly due to the thermodynamical force caused by the elastic deformation in nematics in the form of splay, twist and bend. Away from the equilibrium in the absence of flow, the thermodynamic force is balanced by a viscous force and the dynamics of the director is expressed by(3) where is a viscosity coefficient. In our model, NLC is contained in an extremely narrow container with the two ends along x-axis open and infinite. Under the assumption the equation of motion takes the form(4)

The second term in the right hand side of Eq. (4)(4) determines the Lagrange multipler term which has been introduced to take care of the director to point parallel to the molecular field at equilibrium. When the molecular and viscous fields of the equations of motion do not lie parallel with the director axis they develop a torque given by(5)

It may be noted in Eq. (5)(5) is invariant, when , and so that the rod like molecules in NLC do not have head or tail. Having derived the equation of motion to represent the dynamics now the task ahead is to solve Eq. (5)(5) and to understand the underlying director oscillations. However, Eq. (5)(5) is a highly nontrivial vector nonlinear partial differential equation and it is very difficult to solve it in its natural form. This difficulty can be overcome by rewriting Eq. (5)(5) in a suitable equivalent representation before solving. Experience shows that this can be done by mapping the NLC onto a moving helical space curve (Lakshmanan, 1977; Lamb, 1976; Lamb, 1977; Pereira Nino, 1978) in using a procedure in differential geometry in which Eq. (5)(5) can be mapped to one of the nonlinear Schrödinger family of equations or to its perturbed version. We map the NLC at a given instant of time onto a moving helical space curve in and a local coordinate system is formed on the space curve by identifying the unit director axis with the tangent vector of the space curve and by defining the unit principal and binormal vector and respectively in the usual way. The change in the orientation of the orthogonal trihedral which defines the space curve uniquely within rigid motions is determined by Serret–Frenet (S–F) equations (Kavitha and Daniel, 2003; Kavitha et al., 2010; Lakshmanan, 1978; Lakshmanan, 1979)(6) where and are the curvature and torsion of the space curve. In view of the above identification and upon using the S–F Eq. (6)(6) , can be found and the trihedral evolves as(7) where

and . Here the suffices t and x represent partial derivatives with respect to t and x. The following conditions for the compatibility of S–F Eqs. (6)(6) of the trihedron(8) lead to the following evolution equations for the curvature and torsion of the space curve(9) (10)

In order to identify the set of coupled Eqs. (9)(9) and (10)(10) with a more standard nonlinear partial differential equation, we make the following complex transformation(11) with appropriate rescaling of time and spatial variable as and , and we obtain the following integro-differential nonlinear Schrödinger equation(12)

Eq. (12)(12) is a perturbed nonlinear nonlocal Schrödinger equation that represents the director dynamics of our NLC system. When , Eq. (12)(12) reduces to the well-known completely integrable cubic nonlinear Schrödinger equation which possesses N-soliton solutions (Ablowitz and Clarkson, 1991; Matveev and Salle, 1991). Nematic liquid crystals have a highly nonlocal nonlinearity (Conti et al., 2003) associated with the orientation of the dipole induced on each individual liquid crystal molecule (Peccianti et al., 2005). The nonlinear response of liquid crystals can be highly nonlocal, a phenomenon that dramatically affects the excitation dynamics. The high anisotropy of physical properties as well as the collective behavior of nematic molecules lead to nonlinear oscillations of the director axis n(r) governed by solitons. It might be mentioned that Eq. (12)(12) resembles the damped NLS discussed by Pereira and Stenflo (Pereira and Stenflo, 1977) except for the nonlocal term. In Eq. (12)(12) , represents the strength of nonlocal nonlinearity arises especially due to the molecular deformations and director oscillations. In Eq. (11(11) ), represents the degree of nonlocal nonlinearity and the nonlocality can dramatically modify the soliton property. This nonlocal nature often results from transport processes such as atom diffusion, heat transfer, drift of electric charges (Suter and Blasberg, 1993; Gordon et al., 1965) and in this case it is induced by a long range molecular interactions in a NLC, which exhibit orientational nonlinearity (Peccianti et al., 2000; Pecseli and Rasmussen, 1980; Perez-Garcia et al., 2000). Spatial nonlocality of the nonlinear response is a generic property of a wide range of physical systems, which manifests itself in new and exciting properties of nonlinear waves. This nonlocality implies that the response of the NLC medium at a given point depends not only on the wave function at that point (as in local media), but also on the wave function in its vicinity. In various areas of applied nonlinear science, nonlocality plays a relevant role and radically affects the underlying physics. Some striking evidences are found in plasma physics (Pecseli and Rasmussen, 1980), in Bose–Einstein condensates (BEC) (Perez-Garcia et al., 2000). The nonlocality comes into play when underlying transport processes such as diffusion of atoms in a gas (Suter and Blasberg, 1993), heat conduction in thermal media (Litvak et al., 1975; Dreischuh et al., 1999), charge carrier transfer in photorefractive crystals (Segev et al., 1992; Duree et al., 1993) or long range interactions such as long range electrostatic interaction in nematic liquid crystals (Conti et al., 2003; Assanto and Peccianti, 2003) and many body interaction in Bose–Einstein condensates (Perez-Garcia et al., 2000; Cuevas et al., 2009), where contrary to the prediction of purely local nonlinear models, nonlocality may give rise to or prevent, the collapse of a wave. In nonlinear optics, particularly when dealing with the self-localization and solitary waves, nonlocality is often associated to time-domain phenomena through a retarded response and the spatially nonlocal effects have been associated to photorefractive and thermal or diffusive processes (Abe and Ogura, 1998). In this context, we would like to investigate the effect of nonlocal term on the solitary director oscillations by constructing an exact solution to Eq. (12)(12) using computational algebraic methods. It is a standard feature of nonlinear systems that exact analytic solutions are possible only in exceptional cases. In order to analyze the nature of nonlinear excitations of the system under consideration, we are often forced to attempt approximation methods. More recently, searching for exact solutions of nonlinear problems has attracted a considerable amount of research work and a series of solutions can be found using symbolic computation.

3 Shape changing solitary oscillations

Nonlinear evolution equations are often used as models to describe complex phenomena in various fields of sciences, especially in physics and engineering. One of the basic physical problems for those models is to find their traveling wave solutions. During the past decades, quite a few methods for dealing with traveling wave solutions of those nonlinear equations have been proposed (Mohajer, 2009; Camacho et al., 2011; Matioc, 2012; Matioc and Matioc, 2012; Deconinck, 2012; Raju and Panigrahi, 2011; Andriopoulos et al., 2009; Zhang, 2009; Zhang, 2008; Conde et al., 2012; Sinelshchikov, 2010; Kavitha et al., 2011a, 2013; Darvishi et al., 2012). The various powerful methods for obtaining solitary wave solutions have been proposed such as Hirota’s bilinear method, Painlevé expansions, the Inverse Scattering Transform, homogeneous balance method, F-expansion method, Jacobi-elliptic function method and the first integral method (Wang, 1996; Fan, 2000; Malfliet, 1992; Fan, 2003; El-wakil et al., 2003; Taghizadeh et al., 2011). Recently tanh method (Malfliet, 1992) has been proposed to find the exact solutions to nonlinear evolution equations. Later, Fan (2003) has proposed an extended tanh-function method and obtained new traveling wave solutions that cannot be obtained by the tanh-function method. Most recently, El-Wakil (El-wakil et al., 2003) modified the extended tanh-function method and obtained some new exact solutions. Most recently Soliman (Soliman, 2006) and El-Wakil (El-Wakil et al., 2005) modified the extended tanh-function method and obtained some new exact traveling wave solutions. We employ the modified extended tanh-function (METF) method (Soliman, 2006; El-Wakil et al., 2005; Kavitha et al., 2011b, 2012) to solve the Eq. (12)(12) which governs the dynamics of director oscillations with elastic deformations such as splay, twist and bend. For convenience we substitute , and assume with in Eq. (12)(12) and c is the velocity of the traveling wave. Upon separating the real and imaginary parts of the resultant equation, we obtain the following set of ordinary differential equations(13) (14) (15) (16) where, 4. Substituting Eq. (16)(16) in , it is verified that Eq. (14)(14) is automatically satisfied. Further, Eq. (16)(16) is directly integrated to obtain , where C is the constant of integration. Thus, the solution can be evaluated using Eq. (13)(13) or Eq. (15)(15) with the relation . We have considered Eq. (13)(13) and employed the tanh function method as given below. Let us introduce the following ansatz(17) and(18) where s is the constant to be determined later. The value of i can be found by inserting Eqs. (17)(17) and (18)(18) in Eq. (13)(13) and balancing the higher-order linear term with the nonlinear terms yielding . Upon substituting Eqs. (17)(17) and (18)(18) in the ordinary differential Eqs. (13)(13) , will yield a system of algebraic equations with respect to and s. The system of equations is further solved using Matlab and we obtain

Case: 1(19) (20) and(21)

Upon substituting Eqs. (19)–(21) in Eq. (17)(17) , the solution takes the following form(22) where .

Case: 2(23) (24) (25)

Also upon using Eqs. (23)–(25) in Eq. (17)(17) , we found(26)

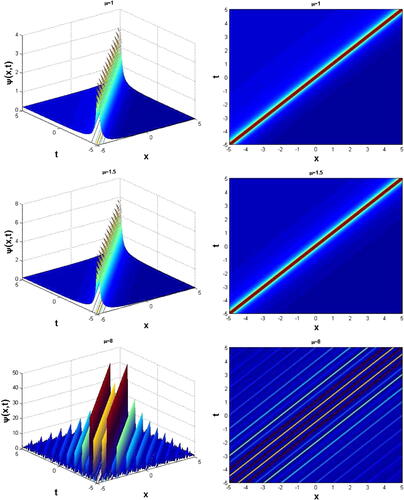
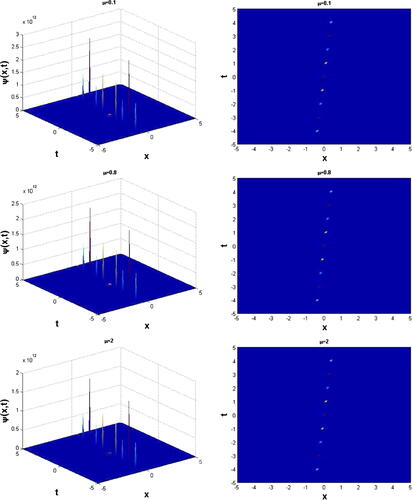
We have plotted the solution Eq. (22)(22) and obtained the effect of nonlocality on the director deformation on the NLC system. It is interesting to note that, when the nonlocality parameter increases from to , the highly localized cusp-like soliton significantly disintegrates to a multiple humped localized soliton pulses as displayed in Fig. 2. We also have plotted the other case of solution Eq. (26)(26) in Fig. 3, which displays the singular soliton solutions with decreasing amplitude when increases from to .

Figure 2 Snapshots of NLC deformation for various values of nonlocal parameters and .

Figure 3 Snapshots of singular deformation in NLC molecules for various values of and .

Set: B

In order to analyze the other possible solutions, we assume(27) (28) and(29) where b is the parameter to be determined later. The parameters and n can be found by inserting Eqs. (27)–(29) in Eqs. (13)–(16) and balancing the higher-order linear term with the nonlinear terms yielding and . Upon substituting Eqs. (27)–(29) in the ordinary differential Eqs. (13)–(16), will yield a system of algebraic equations with respect to and since all the coefficients of and have to vanish. We are interested to solve the system of equations for many choices of parameters in the following two different cases.

3.1 Case – A

In this case we choose the set of parameters and vanish in order to satisfy Eqs. (13)–(16) and with the aid of MAPLE, we get a system of algebraic equations for and as follows(30)  (31) (32) (33)

Further solving the system of equations using symbolic computation, we can distinguish two types of solutions for this case as follows

3.1.1 Solution – (i)

We collect the coefficients at different powers of and again solving the same we obtain(34)

Also upon using Eq. (34)(34) in Eqs. (27)–(29), we elucidate i and (35) and(36)

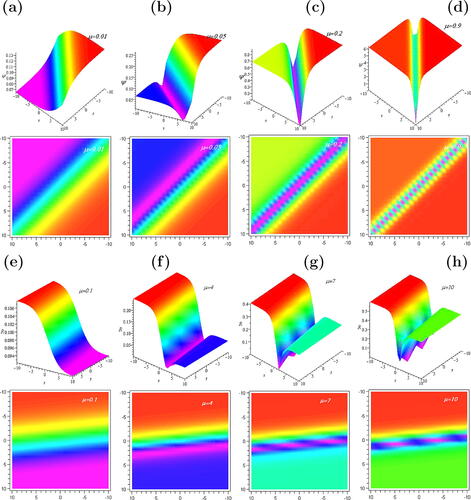
Eqs. (35)(35) and (36)(36) represent the exact solitary wave solutions in the form of kink excitations for the dynamical equation governing the director fluctuations due to molecular reorientation in NLC systems. In Fig. 4, we have plotted the solutions and represented in Eqs. (35)(35) and (36)(36) by choosing and for various values of the parameter which physically signifies the role of nonlinear nonlocal term. From the figures, it is evident that any increment in the degree of nonlocality enables the kink-like excitation to gradually change its shape from kink to anti-soliton as depicted in Fig. 4(a–d) and (e–h) depicts the change from anti-kink to anti-soliton, a more localized coherent soliton exhibiting shape changing property. It should be noted from the corresponding contour plots that the excitations are trapped due to reorientation nonlinearity so that it is highly localized and intact. In the contour plots the brighter regions with red, yellow and green colors represent the maximum amplitude regions and the darker regions with blue and pink colors represent the minimum or zero amplitude of the soliton. A noteworthy characteristic of these solitons is that the degree of coherence varies with the nonlocality parameter . 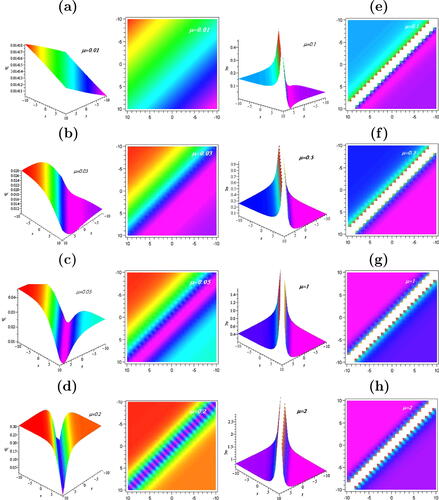The properties of nonlocal spatial incoherent soliton solutions have been investigated in NLC cells and the effect of nonlocality on the coherence properties of this self-trapped states have been studied in detail. In the case of coherent nematicons, the optically induced index profile tends to be broader than the soliton intensity profile depending on the degree of nonlocality thus leading to long range interactions in NLC systems (Peccianti et al., 2002; Conti et al., 2003). The effects of nonlocality on coherent solitons, modulational instability and soliton interactions have also been investigated for several types of nonlocal response functions (Peccianti et al., 2004).

Figure 4 Snapshots of soliton changing shape from kink-anti-soliton and its contour plots (a–d) for Eq. (35)(35) and anti-kink to anti-soliton and its contour plots (e–h) for Eq. (36)(36) .

3.1.2 Solution – (ii)

In a similar way, we compute another set of solutions for as follows(37)

Upon substituting Eq. (37)(37) in Eqs. (27)–(29), the solution takes the following form(38) and(39)

The above solitary solution Eq. (38)(38) also exhibits shape changing property. We have plotted Eq. (38)(38) in Fig. 5(a–d) by choosing the parametric values and and the corresponding contour plots are also depicted. The parameter can be considered as a measure of the nonlocality of this nonlinear medium which is also evident from Fig. 5. As portrayed in Fig. 5(a–d), for , the director fluctuations represented in Eq. (38)(38) are governed by anti-kink soliton and when is increased further the localized excitations continuously changes its shape and when , it takes the form of a coherent profile of anti-soliton. The shape changing property is also evident from the contour plots and when the diagonal blue region with pink periodic strips represents the peak of the coherent profile. Similarly, from Fig. 5(e–h) for Eq. (39)(39) , one can observe how the molecular reorientational nonlinearity balances with the nonlocal parameter and settles up in the cusp-soliton (Kavitha et al., 2009a) singular profile when .

Figure 5 Snapshots of soliton changing shape from anti-kink to anti-soliton and its contour plots (a–d) for Eq. (38)(38) and cusplike-soliton and its contour plots (e–h) for Eq. (39)(39) .

3.2 Case – B

In this case, the parameters and vanishes, on inserting Eqs. (27)–(29) in Eqs. (13)–(16) we get an algebraic set of equations as follows(40) (41) (42) (43)

Solving the system of equations with the aid of MAPLE, we find the two types of solutions for and .

3.2.1 Solution-(i)

We collect the coefficients for different powers of and solving the same we obtain(44)

Also upon using Eq. (44)(44) in Eqs. (27)–(29), we elucidate(45) and(46)

More interestingly again the solution Eq. (45)(45) exhibits shape changing property for the choices of parameters and . From the plots in Fig. 6(a–d), one can infer that when , the solution suffers with multiple-periodic line solitonic oscillations. When the strength of the nonlocal term increases more and more, leading further to the shape of anti-soliton at . A close inspection on the contour plots as presented in Fig. 6(a–d) reveals that the green stripes represent the peaks of the soliton and ultimately leading to a anti-soliton with single pink peak with the higher amplitude red tails. In a similar manner, the solution for from Eq. (46)(46) is also portrayed in Fig. 6(e–h) for the choices of and and it is evident that in this case the shape changing occurs from anti-soliton to anti-soliton via anti-kink like director oscillations. From the contours depicted in Fig. 6(e–h), it is clear that the gradient amplitude distribution at Fig. 6(e) leads gradually to the exact anti-kink with two distinguished maximum red and minimum amplitude pink regions as depicted in Fig. 6(f). From this study, one can conclude that the nonlocality arising from the long-range molecular interaction characteristic of NLC media could favor shape changing molecular deformations. This shape changing molecular deformations have also been reported by Srivasta et al. with a different model of study (Srivasta and Ranganath, 2001). Recently, Conti et al. (Conti et al., 2003) have presented the theory of spatial solitary waves in nonlocal NLC media and reported self-trapping of light. The same has been predicted in nematic media, where the reorientation nonlinearity is saturable and nonlocal, it generally stabilizes self focusing and supports the creation of robust spatial solitons (Synder et al., 1995). In a different context, it has been demonstrated that the spin soliton representing the dynamics of ferromagnetic spin chain admits shape changing during its evolution. This shape changing property can be exploited to reverse the magnetization without loss of energy which may have potential applications in magnetic memory and recording devices (Kavitha et al., 2009b; Daniel and Kavitha, 2002)

Figure 6 Snapshots of soliton changing shape from periodic line solitons to anti-soliton and its contour plots (a–d) for Eq. (45)(45) and anti-soliton to anti-soliton via anti-kink soliton and its contour plots (e–h) for Eq. (46)(46) .

3.2.2 Solution – (ii)

In a similar way, we compute another set of solutions for as follows(47)

Upon substituting Eq. (47)(47) in Eqs. (27)–(29), the solution takes the following form(48) and(49)

In this case, the solution as represented in Eq. (48)(48) , exhibits unusual breather like director oscillations which are both temporally and spatially periodic modes as depicted in Fig. 7(a–c). As the value of increases the preiodicity becomes large leading to the reduction in the number of breathing modes which can be seen more clearly in the corresponding contour plots. Eventually, the solution in Eq. (49)(49) is demonstrating the shape changing from antikink to antisoliton excitations as depicted in Fig. 7(d–f).

Figure 7 Snapshots of breathing soliton and its contour plots (a)–(c) for Eq. (48)(48) and shape changing anti-kink to anti-soliton (d)–(f) solutions for Eq. (49)(49) .

4 Conclusions

The exact solitary wave solutions for the nonlocal nonlinear Schrödinger equations governing the molecular deformations in NLC have been constructed using symbolic computation. As a physical relevance, the effect of nonlocal term on the solitary deformation profile leading to the shape changing property has been studied for different cases. The presented intriguing unifying shape changing character of the molecular deformations in NLC systems shines new light on self-localization in liquid crystals and may be exploited for NLC display devices. We believe that this will stimulate new experiments towards a deeper understanding of self-trapping and self-localization in highly nonlocal nonlinear NLC media and development of novel all-optical and switching devices.

Acknowledgements

L.K gratefully acknowledges the financial support from NBHM, India in the form of major research project, BRNS, India in the form of Young Scientist Research Award, UGC, India in the form of Research Award, and ICTP, Italy in the form of Junior Associateship. M.V acknowledges BSR-Research Fellowship under UGC Non-SAP Scheme, India.

Notes

Peer review under responsibility of University of Bahrain.