Approximate solutions for solving the Klein–Gordon and sine-Gordon equations

Peer review under responsibility of University of Bahrain.

Abstract

In this paper, we practiced relatively new, analytical method known as the variational homotopy perturbation method for solving Klein–Gordon and sine-Gordon equations. To present the present method’s effectiveness many examples are given. In this study, we compare numerical results with the exact solutions, the Adomian decomposition method (ADM), the variational iteration method (VIM), homotopy perturbation method (HPM), modified Adomian decomposition method (MADM), and differential transform method (DTM). The results reveal that the VHPM is very effective.

Keywords:

• Variational homotopy perturbation method
• Klein–Gordon equation
• sine-Gordon equation

1 Introduction

Differential equations can model many physics and engineering problems especially the nonlinear differential equations, but to reach exact solutions is not an easy way. Therefore analytical methods have been used to find approximate solutions. In recent years, many analytical methods such as Variational iteration method (He, 1999b; Muhammad and Syed, 2008; Zayed and Abdel Rahman, 2010b"), and modified variational iteration method (Zayed and Abdel Rahman, 2009, 2010a") and variational homotopy perturbation method (Fadhil et al., 2015; Matinfar et al., 2010; Matinfar and Ghasemi, 2010") have been utilized to solve linear and nonlinear equations. The Klein–Gordon and sine-Gordon equations are a two non-linear hyperbolic partial differential equations, which are model problems in classical and quantum mechanics, solitons, and condensed matter physics.

Let us consider the Klein–Gordon and sine-Gordon equation, respectively,(1) and(2) subject to initial conditions(3) where u is a function of x and is a nonlinear function, f is a known analytic function, and are constants.

In recent years, there has appeared an ever increasing interest of scientist and engineers in analytical techniques for studying Klein–Gordon and sine-Gordon equations. The Klein–Gordon equation was solved by many analytical methods such as variational iteration method (Elcin, 2008; Semary and Hassan, 2015") differential transform method (Ravi Kanth and Aruna, 2009), the decomposition method (El-Sayed, 2003), homotopy perturbation method (Chowdhury and Hashim, 2009), new homotopy perturbation method (Biazar and Mostafa, 2014), Local fractional series expansion method (Yang et al., 2014), and the tanh and the sine-cosine methods (Wazwaz, 2005). Also, the sine-Gordon equation has been solved analytically by modified decomposition method (Kaya, 2003), variational iteration method (Batiha, 2007; Abbasbandy, 2007"), and differential transform method (Biazar and Mohammadi, 2010). Recently many authors studied Klein/sine-Gordon equations (see Fukang et al., 2015; Chen et al., 2014; Dehghan et al., 2015").

The goal of the this paper is to solve Klein–Gordon and sine-Gordon equations by applying another powerful analytical method, called the variational homotopy perturbation method (VHPM), the method is a coupling of homotopy perturbation method (He, 1999a) and variational iteration method (He, 1999b). VHPM was first envisioned by Muhammad and Syed (see Muhammad and Syed, 2008). VHPM used to solve many equations such as Higher Dimensional Initial Boundary Value Problems (Muhammad and Syed, 2008), Benjamin-Bona-Mahony (Fadhil et al., 2015), Zakharove-Kuznetsov equations (Matinfar and Ghasemi, 2010), Fishers equation (Matinfar et al., 2010), the fractional equations (Guo and Mei, 2011), and fractional diffusion equation (Guo et al., 2013).

2 Variational Homotopy perturbation Method (VHPM)

To clarify the basic ideas of VHPM, we consider the following differential equation(4) where L is a linear operator defined by is a nonlinear operator and is a known analytic function. According to VIM, we can write down a correction functional as follows:(5) where is a Lagrange multiplier, which can be identified optimally via a variational iteration method. The subscripts n denote the th approximation, is considered as a restricted variation. That is, ;. Now, we apply the homotopy perturbation method,(6)

As we see, the procedure is formulated by the coupling of variational iteration method and homotopy perturbation method. A comparison of like powers of p gives solutions of various orders.

3 Applications

To illustrate the effectiveness of the present method, several test examples are considered in this section.

3.1 Example 1

We consider the linear Klein–Gordon equation(7) subject to the initial conditions(8)

According Eq. (5)(5) , the correction functional is given by(9)

Making the above correction functional stationary, and noting that , we get(10) which yields the following stationary conditions:(11) (12) (13)

Then, the Lagrange multiplier, can be identified as(14)

As a result and Eq. (9)(9) , we get(15)

Applying the variational homotopy perturbation method, we have(16)

Comparing the coefficient of like powers of p, we have(17) (18)

Thus solving Eqs. (17)(17) and (18)(18) , using initial conditions (8)(8) yields(19) (20) (21)

This shows that the solution is the same as that obtained by ADM El-Sayed (2003), HPM Chowdhury and Hashim (2009), and VIM Elcin (2008).

3.2 Example 2

We consider nonlinear Klein–Gordon equation(22) subject to the initial conditions(23)

According Eq. (5)(5) , the correction functional of Eq. (22)(22) is given by(24) where is considered as a restricted variation, Its stationary conditions can be obtained as follows:(25) (26) (27) Then, we get(28)

Substituting Lagrangian multiplier (28)(28) into functional (24)(24) , we get(29)

Applying the variational homotopy perturbation method, we have(30)

Comparing the coefficient of like powers of p, we have(31) (32) (33) (34)

Thus solving Eqs. (31)(31) and (34)(34) , using initial conditions (23)(23) yields(35) (36) (37) (38)

Then, the 4-term approximate series solution can be written as(39)

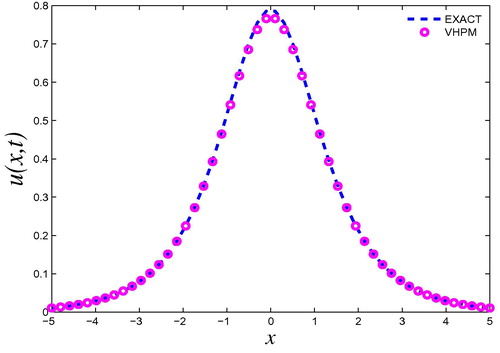
3.3 Example 3

We consider nonlinear Klein–Gordon equation(40) subject to the initial conditions(41)

The exact solution of Eq. (40)(40) is (see Ref. Zhao et al., 2006)(42)

According Eq. (5)(5) , the correction functional of Eq. (40)(40) is given by(43)

Then, the Lagrange multiplier, can be identified as(44)

Substituting Lagrangian multiplier (44)(44) into functional (43)(43) , we get(45)

Applying the variational homotopy perturbation method, we have(46)

Comparing the coefficient of like powers of p, we have(47) (48) (49) (50) (51)

Thus solving Eqs. (47)(47) and (51)(51) , using initial conditions (41)(41) yields(52) (53) (54) (55)

Then, the 4-term approximate series solution can be written as(56)

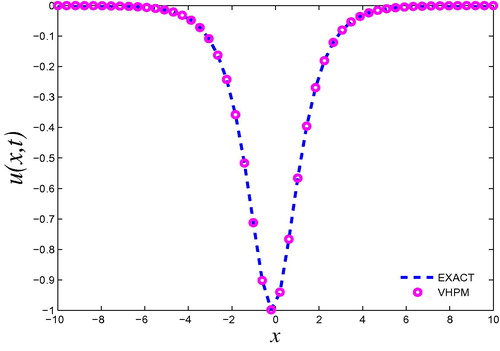
We compare our results obtained by VHPM and exact solution (42)(42) of Eq. (40)(40) in Table 1 and Fig. 1.

Figure 1 VHPM solution at difference time, when .

Table 1 The absolute error between exact solution (42)(42) and 4-term of VHPM for different values of .

x

3.4 Example 4

We consider nonlinear sine-Gordon equation(57) subject to the initial conditions(58)

The exact solution of Eq. (57)(57) is(59)

According Eq. (5)(5) , the correction functional of Eq. (57)(57) and taking is given by(60)

Then, the Lagrange multiplier, can be identified as(61)

Substituting Lagrangian multiplier (61)(61) into functional (60)(60) , we get(62)

Applying the variational homotopy perturbation method, we have(63)

Comparing the coefficient of like powers of p, we have(64) (65) (66)

Thus solving Eqs. (64)(64) and (66)(66) , using initial conditions (58)(58) yields(67) (68) (69) (70)

Hence, the 4-term VHPM solution is(71)

The comparison between absolute errors of exact solution with the 5-terms of modified decomposition method (Kaya, 2003), 2-iteration solution of the variational iteration method (Batiha, 2007), and 4-iteration solution of variational homotopy perturbation method is given in Table 2. Also, we compared between exact solution and approximate solution obtained by variational homotopy perturbation method in Fig. 2.

Figure 2 Exact solution and VHPM, when .

Table 2 The absolute error between exact solution and 5-term MADM (Kaya, 2003), 2-iterate VIM (Batiha, 2007) and 4-term VHPM, when and different values of t.

t

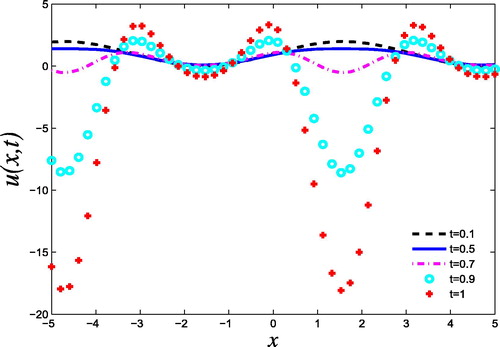
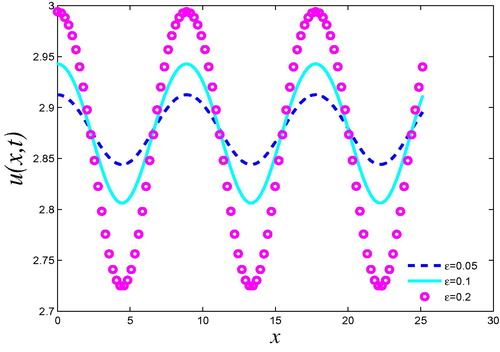
3.5 Example 5

We consider nonlinear sine-Gordon equation(72) subject to the initial conditions(73)

Same as Example 4. by means VHPM 2-term of solution are(74) (75)

Then, the approximate solution via VHPM of Eq. (72)(72) is(76)

We showed the solution obtained by VHPM in Fig. 3. Also, we showed the effectiveness of to the solution.

Figure 3 Exact solution and VHPM, when .

4 Discussion of results

In this section, we discuss the results obtained by the VHPM for Klein–Gordon sine-Gordon equations.

In Example (3.1), the analytical solution obtained by the VHPM is same as that obtained by the ADM, HPM, and VIM (see Eq. (21)(21) ). Example (3.2) observe the solution via VHPM and showed in Fig. 1 at difference time and it is clear that the time effect to the solution. From Example (3.3), we compared the results obtained via VHPM with the exact solution. Also, we found absolute error between exact solution and present work (see Table 1 and Fig. 2). In Example (3.4), the results by the VHPM are more accurate than those obtained by MADM and VIM (see Table 2 and Fig. 3). Also, the application of the VHPM to Example (3.5), showed that, the parameter played an important role in initial conditions (see Fig. 4).

Figure 4 Approximate solution via VHPM, when and different values of .

5 Conclusion

In this work, variational homotopy perturbation method is applied to solve the Klein–Gordon and sine-Gordon equations. The present study has confirmed that the variational homotopy perturbation method is effective and suitable for solving these types of linear and nonlinear equations. Also, we showed that the present method has good agreement with other analytical methods such as ADM, VIM, HPM, and MADM.

Acknowledgement

We thank the editor and the referee for their comments.

Notes

Peer review under responsibility of University of Bahrain.