Nonlocal symmetries and interaction solutions for the KdV-type equation

Peer review under responsibility of University of Bahrain.

Abstract

The nonlocal symmetries for the special equation, which is called KdV-type equation, are obtained by means of the truncated Painlevé method. The nonlocal symmetries can be localized to the Lie point symmetries by introducing auxiliary dependent variables and the corresponding finite symmetry transformations are computed directly. The KdV-type equation is also proved to be consistent tanh expansion solvable. New exact interaction excitations such as soliton–cnoidal wave solutions are given out analytically and graphically.

Keywords:

• Nonlocal symmetries
• Consistent tanh expansion
• Soliton-cnoidal wave solutions

1 Introduction

Rosenau and Hyman introduced and studied the KdV-type equations with nonlinear dispersion(1) to understand the role of nonlinear dispersion in pattern formation in Rosenau and Hyman (1993). The and the models are just the usual KdV and modified KdV equations. The integrability of the models , and was proved by means of an equivalent approach and the Lagrange transformation by Rosenau in Rosenau (1996), and the author also analyzed the interaction of traveling compactons. The authors classified the Painlevé integrability of the Eq. (1)(1) and obtained the single soliton and compacton solutions in Lou and Wu (1999), Marinakis (2015) and Pikovsky and Rosenau (2006)". The explicit solutions and the stability of the compacton solutions are studied extensively by many authors (Biswas, 2008, 2010b; Dey and Khare, 1998; Ebadi and Biswas, 2011; Inc et al., 2013; Rosenau, 1996, 1994; Rosenau et al., 2007; Rosenau, 1998). The traveling wave solutions and source solutions of the Eq. (1)(1) are discussed from the point of view of the theory of symmetry reduction (Bruzon and Gandarias, 2010; Wang and Lou, 2009) and the 1-soliton solution and topological soliton solutions are studied in Biswas (2010a). The solitary solutions, conservation laws, cnoidal waves and snoidal waves for the other types of the nonlinear equations such as equation and equation are discussed in detail in Biswas and Kara (2011), Biswas and Triki (2011), Ebadi et al. (2013), Antonova and Biswas (2009) and Girgis and Biswas (2010)".

Recently, abundant interaction solutions among solitons and other complicated waves including periodic cnoidal waves, Painlevé waves and Boussinesq waves for many integrable systems were obtained by nonlocal symmetries reduction and the consistent tanh expansion method related to the Painlevé analysis (Cheng et al., 2014; Lou et al., 2012; Lou et al., 2014). Hinted at by the results of nonlocal symmetry reduction, Lou found that the symmetry related to the Painlevé truncated expansion is just the residue with respect to the singular manifold in the Painlevé analysis procedure and called residual symmetry (Gao et al., 2013; Hu et al., 2012; Lou, 2013). Furthermore, the author proposed a simple effective method, the consistent tanh expansion (CTE) method in Lou (2015), which is based on the symmetry reductions with nonlocal symmetries. The CTE method can be used to identify CTE solvable systems and it is a more generalized but much simpler method to look for new interaction solutions between a soliton and other types of nonlinear excitations (Chen and Lou, 2013; Chen et al., 2015). The new interaction solutions using the CTE method in the paper are all analytical exact solutions, which are different from those ones in Sheikholeslami et al. (2015, 2012) and Sheikholeslami and Ganji (2015)" using the Adomian decomposition method and semi analytical method. All these analytical and numerical solutions can help us to learn more about the equation.

For the special in the Eq. (1)(1) , we will study the nonlocal symmetries related to the Painlevé analysis and different interaction solutions from the consistent tanh expansion method for the KdV-type equation (Lou and Wu, 1999; Marinakis, 2015; Inc et al., 2013)(2)

The outline of the paper is as follows. In Section 2, the nonlocal symmetries related to the Painlevé truncated expansion are obtained and the corresponding finite transformation is derived by solving the initial value problem of the enlarged system. Section 3 is devoted to the consistent tanh expansion method for the KdV-type Eq. (2)(2) and different interaction solutions among different nonlinear excitations. Summary and discussions are given in the last section.

2 Nonlocal symmetries and its localization for the KdV-type equation

In Ref. Lou and Wu (1999), the KdV-type Eq. (2)(2) is proved to be Painlevé integrable and the truncated Painlevé expansion reads(3) by the usual leading order analysis where are functions to be determined later and is an arbitrary singularity manifold. Substituting the Eq. (3)(3) into the Eq. (2)(2) and collecting the coefficients of different powers of , we have(4) (5) (6) (7)

It is clear that the Eq. (7)(7) is just the Eq. (2)(2) with the solution and the residual is the symmetry corresponding to the solution based on the residual symmetry theorem in Lou (2013). So the truncated Painlevé expansion(8) is an auto-Bäcklund transformation between the solutions u and if the function satisfies the Eqs. (5)(5) and (6)(6) .

For the nonlocal symmetry , the corresponding initial value problem is(9) with being an infinitesimal parameter. In order to localize the nonlocal symmetry , we introduce five new dependent variables by requiring(10)

Then the linearized equations of the prolonged system of (5)–(7) and (10)(10) are listed as follows(11) (12) (13) (14)

It is not difficult to find that the solution of the Eqs. (11)–(14) has the form(15)

Then the corresponding initial value problem becomes

The solution of the initial value problem for the enlarged system (5)–(7) and (10)(10) can be written as

Using the finite symmetry transformation, one can obtain solitary wave solution for the Eq. (2)(2) with the trivial solution by supposing the function as(16) where k and l are arbitrary constants. The function (16)(16) is the solution of (5)(5) and (6)(6) only with the relation(17)

Then substituting the Eq. (16)(16) with (17)(17) into the Eq. (8)(8) , one can obtain the solitary wave solution for the KdV-type Eq. (2)(2) . If selecting the nontrivial seed solution and different types of the function , one can obtain much more exact solutions of the Eq. (2)(2) and the main purpose of the paper is to study the new interaction solutions from the CTE method, which are discussed in detail in the next section.

3 Consistent tanh expansion solvability and interaction solutions

In this section, the consistent tanh expansion method is developed to find the interaction solutions between solitons and other types of nonlinear waves such as cnoidal periodic waves, Airy waves and so on. By the leading order analysis for the KdV-type Eq. (2)(2) , we can take the following truncated tanh function expansion(18) where and w are functions of to be determined later. Substituting (18)(18) into the Eq. (2)(2) and vanishing the coefficients of different powers of , we have(19) (20) (21)

The Eqs. (20)(20) and (21)(21) are the consistent conditions for the equation, which is also called w-equation for simplicity. It is very difficult to solve the nonlinear Eqs. (20)(20) and (21)(21) because of the higher derivatives of the unknown function w. From the Eqs. (18)–(21), we can prove the following nonauto Bäcklund transformation (BT) theorem after direct calculations.

Nonauto-BT theorem. If w is a solution of the Eqs. (20)(20) and (21)(21) , then(22) is a solution of the Eq. (2)(2) . That is to say, once the solution of (20)(20) and (21)(21) is known, the corresponding expression u can be obtained from the nonauto-BT theorem directly, whence the new solution of the Eq. (2)(2) can be obtained. Some interesting examples are listed in the following paper.

A quite trivial solution of (20)(20) and (21)(21) has the form(23) with k being an arbitrary constant. Substituting the trivial solution (23)(23) into Eq. (22)(22) , the soliton solution of the Eq. (2)(2) yields

In order to obtain the interaction solutions between solitons and other nonlinear excitations of the Eq. (2)(2) , we try to find different solutions to the w-equations (20)(20) and (21)(21) . The first type of the soliton–cnoidal wave interaction solution for the Eq. (2)(2) possesses the form(24) then substituting the Eq. (24)(24) into the consistent conditions (20)(20) and (21)(21) , we can find the constant relation(25) where are arbitrary constants. Substituting the Eqs. (24)(24) and (25)(25) into the Eq. 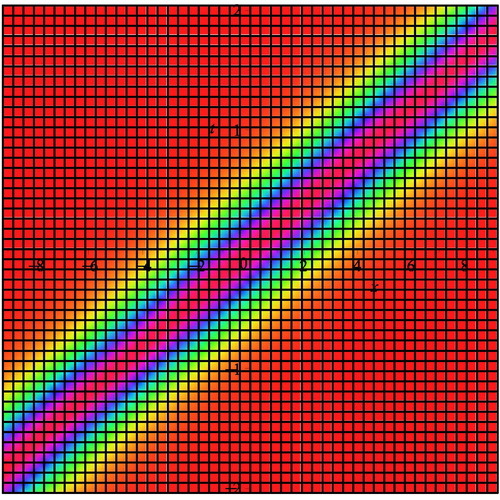(22)(22) , one can arrive at the special solitary wave solution(26) by selecting the proper arbitrary constants(27) and the density plot of the solution (26)(26) with constant selection (27)(27) is shown in Fig. 1. Here we give the simple example to show that we can obtain the same solitary wave solutions of the nonlinear equation from the CTE method, which can also be constructed by means of the other traditional methods such as the function expansion method and the Painlevé truncated expansion method. Because the equation describes the motion of the shallow water waves, this simple solitary solution is just a special solution of the equation.

Fig. 1 A special solitary wave solution for u with the constants selection .

The soliton–cnodial interaction solution for the Eq. (2)(2) is obtained by choosing(28) where is the third type of incomplete elliptic integral and is the usual Jacobi elliptic sine function. Substituting the Eq. (28)(28) into the Eq. (22)(22) , the constants should satisfy the relation(29) where is an arbitrary constant. Then substituting the Eqs. (28)(28) and (29)(29) into the Eq. (22)(22) , one can obtain the soliton–cnoidal interaction solution for the equation with the special parameter selection.

4 Summary and discussions

In summary, the nonlocal symmetries of the KdV-type equation are obtained with the truncated Painlevé expansion method. In order to solve the initial value problem related to the nonlocal symmetries, we prolong the KdV-type equation such that the nonlocal symmetries become the local Lie point symmetries for the enlarged system. The finite symmetry transformations of the enlarged KdV-type equation are derived by using the Lie’s first principle and the corresponding finite symmetry group is given out explicitly. Meanwhile, the KdV-type equation is proved to be consistent tanh expansion solvable and we find abundant interaction solutions between the soliton and cnoidal periodic waves including arbitrary constants. By selecting the proper arbitrary constants, these new interaction solutions are displayed analytically and graphically from the nonauto-Bäcklund transformation theorem. Furthermore, there exist other methods to find the exact solutions of the nonlinear systems such as nonlinearizations, Lie point symmetries and Darboux transformations, etc. More about the consistent tanh expansion method and the Bäcklund transformation related to the nonlocal symmetries of the KdV-type equation and other interesting integrable systems are worthy of further study.

5 Nomenclature

Consistent tanh expansion method: (CTE method)

For a given derivative nonlinear polynomial system,(30) we look for the following possible truncated expansion solution(31) where w is an undetermined function of space x and time should be determined from the leading order analysis of the Eq. (30)(30) and all the expansion coefficient functions should be determined by vanishing the coefficients of different powers of after substituting the Eq. (31)(31) into the Eq. (30)(30) .

Definition: If the system for and w obtained by vanishing all the coefficients of powers after substituting the Eq. (31)(31) into the Eq. (30)(30) is consistent, or, not over-determined, we call that the expansion (31)(31) is a CTE and the nonlinear system (30)(30) is CTE solvable.

Acknowledgements

The work is supported by National Natural Science Foundation of China (Nos. 11071164 and 11201302), Shanghai Natural Science Foundation (No. 10ZR1420800), the Hujiang Foundation of China (B14005).

Notes

Peer review under responsibility of University of Bahrain.