Abstract
In this work, we are concerned with the investigation of the qualitative behaviors of certain systems of non-linear differential equations of second order. We make a comparison between applications of the integral test and Lyapunov’s function approach on some recent stability and boundedness results in the literature. An example is furnished to illustrate the hypotheses and main results in this paper.
1 Introduction and main results
It is well-known that the investigation of stability and boundedness of solutions plays an important role in qualitative theory and applications of differential equations. Besides, the qualitative behaviors of solutions of differential equations of second order, stability, boundedness, etc., play an important role in many real world phenomena related to the sciences and engineering technique fields. However, we would not like to give here the details of applications done in the literature.
In this paper, motivated by the results and method used in (Kroopnick, Citation2013, Citation2014; Tunç, Citation2010, Citation2016; Tunç and Tunç, Citation2015, Citation2016), we obtain some new results on the stability and boundedness problems of certain systems of non-linear differential equations of second order by means of Lyapunov’s direct method. The technique of proofs here involves Lyapunov’s function approach instead of the integral test used in (Kroopnick, Citation2013, Citation2014; Tunç and Tunç, Citation2015, Citation2016). We make a comparison between the applications of these methods on the same problems and their conditions. We also extend and improve some results obtained in these sources from linear case to the non-linear case (see, Kroopnick, Citation2013, Citation2014; Tunç and Tunç, Citation2015, Citation2016). Our aim is to do a contribution to the topic and literature. The results to be established here may be useful for researchers working on the qualitative theory of differential equations. These are the novelty and originality of this paper.
In CitationKroopnick (2013) considered the second order scalar linear differential equation of the form(1)
CitationKroopnick (2013) gave two new and elementary proofs proving the stability of solutions and the boundedness of solutions when for the well-known linear differential equation, Eq. (1), where it is given various constraints on
While the results of (CitationKroopnick, 2013) are not new, the proofs in there are less complex and quite general.
The results of (CitationKroopnick, 2013) are the following two theorems, respectively.
Theorem A
(CitationKroopnick, 2013; Theorem I). Let such that
Then all solutions of Eq. (1) are bounded as and the absolute values of the amplitudes form a non-increasing sequence.
Theorem B
(CitationKroopnick, 2013; Theorem II). Let be a continuous function on
such that
where
and
are some positive constants.
Then all solutions of Eq. (1) are bounded as , stable and the absolute values of the amplitudes form a non-increasing sequence.
Remark 1
Benefited from the integral test, CitationKroopnick (2013) proved both of Theorems A and B.
Later, CitationTunç and Tunç (2015) considered the following vector linear differential equation of the second order(2) where
and
are continuous functions.
It follows that Eq. (2) represents the system of real second order linear differential equations like
This shows that Eq. (1) is a special case of Eq. (2).
Throughout this paper the symbol corresponding to any pair
in
stands for the usual scalar product
and for any
, we define the scalar quantity
and call it the norm of
, the usual Euclidean norm.
CitationTunç and Tunç (2015) proved the following two theorems, respectively.
Theorem C
We assume that the following assumptions hold:
Let such that
and
Then all solutions of Eq. (2) are bounded as . If
in Eq. (2), then all solutions of Eq. (2) are bounded as
and the absolute values of the amplitudes form a non-increasing sequence.
Theorem D
Let and
be continuous functions on
such that
where
and
are some positive constants, and
Then all solutions of Eq. (2) are bounded as . If
in Eq. (2), then all solutions of Eq. (2) are stable and the absolute values of the amplitudes form a non-increasing sequence.
Remark 2
By means of the integral test, CitationTunç and Tunç (2015) proved Theorems C and D.
In this paper, instead of Eqs. (1) and (2), we consider the vector non-linear differential equation of the second order(3) or its equivalent differential system
(4) where
and
are continuous functions.
The continuity of the functions and
is a sufficient condition to guarantee the existence of solutions of Eq. (3). In addition, we assume that the function
satisfies a Lipschitz condition with respect to
. In this case, the uniqueness of solutions of Eq. (3) is guaranteed. In particular, for the existence and uniqueness of solutions and some qualitative properties of solutions, we can refer to (Tunç, Citation2010, Citation2017; Song et al., Citation2011; Wang et al., Citation2010a,Citationb).
It is obvious that Eq. (3) represents the system of real second order non-linear differential equations like
This shows that Eqs. (1) and (2) are special cases of Eq. (3). That is, our equation, Eq. (3), includes the equations discussed by CitationKroopnick (2013) and CitationTunç and Tunç (2015), Eqs. (1) and (2), respectively.
Our first main result is the following theorem.
Theorem 1
We assume that the following assumptions hold:
Let such that
and there exists a non-negative and continuous function
such that
and
where
denotes the space of Lebesgue integrable functions.
Then all solutions of Eq. (3) are bounded as . If
in Eq. (3), then all solutions of Eq. (3) are bounded as
and the zero solution of Eq. (3) is asymptotically stable.
Proof
We define a continuous differentiable function by
It is clear thatand
when
and
.
The time derivative of along any solution
of (4), is given by
By the assumptions of Theorem 1 and the inequality , it follows that
The integration of the last estimate from to
,
, gives that
Let Using the Gronwall inequality, we obtain
In view of the Lyapunov function , it follows that
In addition, since for all
then it is clear for some positive constant
that
Then, we haveso that
where
.
This inequality verifies the boundedness of the solutions as .
In addition, if in Eq. (3), for the time derivative of the function
we have
This inequality guarantees the stability of the zero solution of Eq. (3).
On the other hand, consider the set defined by
When we apply the well-known LaSalle’s invariance principle, we observe that implies that
and hence
is a constant vector). From the last estimate and (4), we have
which necessarily implies that
since
for all
. Therefore,
In fact, this result implies that the largest invariant set contained in is
Hence, we can conclude that the zero solution of system (4) is asymptotically stable when
. Thus, the zero solution of Eq. (3) is the asymptotically stable when
This completes the proof of Theorem 1.
Our second main result is the following theorem concerns the boundedness of solutions when and
, and the asymptotic stability of the zero solution when
in Eq. (3). □
Theorem 2
Let and
be continuous functions on
such that
where
and
are some positive constants, and there exists a non-negative and continuous function
such that
where
denotes the space of Lebesgue integrable functions.
Then all solutions of Eq. (3) and their derivatives are bounded as . If
in Eq. (3), then zero solution of Eq. (3) is asymptotically stable.
Proof
In the proof of this theorem, we will also benefit from the function used in proof of Theorem 1.
In view of the assumptions of Theorem 2, it is obvious thatand
when
and
.
By following the way done in the proof of Theorem 1, it can be concluded that
The assumption implies that
Then, it follows that
Let
Thus, it is obvious thatwhere
This completes the proof of the boundedness of solutions. The remaining of the proof related to the asymptotic stability of the zero solution of Eq. (3) can be easily completed by following the procedure as that in the proof of Theorem 1. We omit here the details of the poof.
The second result proved in (CitationTunç and Tunç, 2015) is the following theorem concernings the boundedness of solutions when and
and the stability of the solutions when
in Eq. (2).
In addition, CitationKroopnick (2014) discussed some qualitative properties of the following scalar linear homogeneous differential equation of second order(5)
He established sufficient conditions under which all solutions of Eq. (5) are bounded, and the solution and its derivative are both elements in .
The result of (CitationKroopnick, 2014) for Eq. (5) is given as the following by Theorem E. □
Theorem E
(CitationKroopnick, 2014; Theorem I). Let such that
, where
and
are some positive constants. Then all solutions of Eq. (5) are bounded. If any solution
is non-oscillatory, then both
and
as
. In addition, the solution and its derivative are both elements of
.
Finally, more recently, in lieu of Eq. (6), CitationTunç and Tunç (2016) considered the more general form of Eq. (5) given by the second order vector linear homogenous differential equation of the form(6) where
are continuous functions and
and
have also lower and upper positive bounds.
It is clear that Eq. (6) represents the vector version for the system of real second order linear homogeneous differential equations of the form(7)
Then, it is apparent that Eq. (5) is a special case of Eq. (6).
The result of (CitationTunç and Tunç, 2016) is given by Theorem F.
Theorem F
(CitationTunç and Tunç, 2016; Theorem I). We assume that and
are positive elements in
such that
where
,
,
and
are some positive constants. Then all solutions of Eq. (6) are bounded. If any solution
of Eq. (6) is non-oscillatory, then both
and
hold as
. Finally, the solution and its derivative are both elements of
.
Remark 3
CitationKroopnick (2014) and CitationTunç and Tunç (2016) proved Theorems E and F by the integral test, respectively.
In this paper, in lieu of Eq. (6), we consider the more general vector non-linear differential equation of the second order(8) or its equivalent differential system
(9) where
and
are continuous functions, and
and
have also lower and upper positive bounds.
Clearly, Eq. (7) includes the differential equations discussed by CitationKroopnick (2014) and CitationTunç and Tunç (2016), Eqs. (5) and (6), respectively.
Our third and last main result is the following theorem.
Theorem 3
Let and
be positive elements in
such that
where
,
,
and
are some positive constants, and there exists a non-negative and continuous function
such that
where
denotes the space of Lebesgue integrable functions.
Then all solutions of Eq. (7) are bounded. In addition, any solution of Eq. (7) and its derivative
satisfies both
and
as
. That is,
and
are asymptotically stable.
Proof
We define a continuous differentiable function by
It is clear thatand
when
and
.
The time derivative of , along any solution
of (8), is given by
By the assumptions of Theorem 3 and the inequality , it can be easily obtained that
The integration of both sides of the last inequality, between to
,
, leads that
Let
Then
By noting the Gronwall inequality, we can get
If we consider last inequality together with thatthen the rest of the proof for regarding the boundedness of the solutions when
can be easily completed. In addition, the asymptotic stability of the zero solution when
can be also easily completed, and hence we omit the details. □
Example 1
Let . Consider non-linear differential system of second order given by
Here,and
Then, we have
That is, .
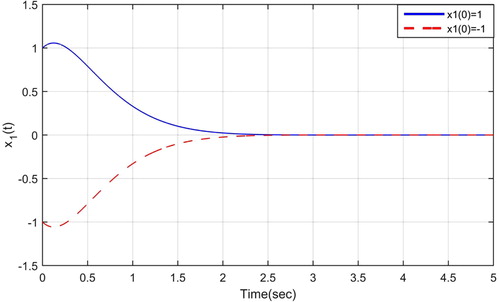
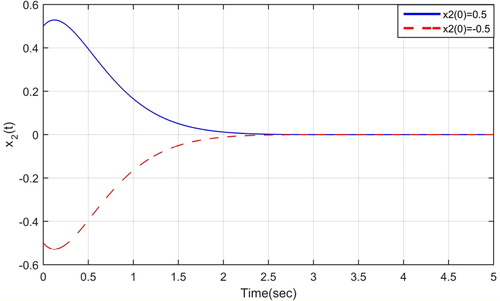
The asymptotic stability of the zero solution and boundedness of all solutions for the considered differential system, when , is shown by the following graphs as
( and ).
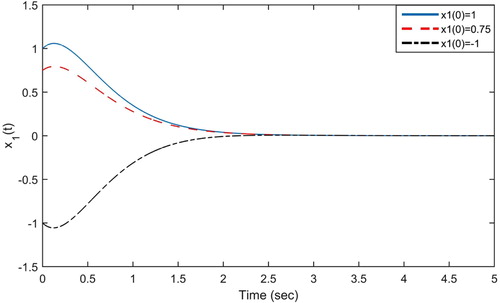
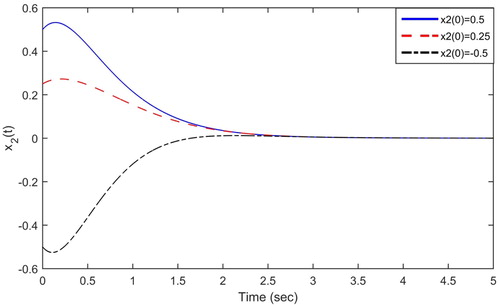
The asymptotic stability of zero solution and boundedness of all solutions for the considered differential system, when , is shown by the following graphs as
(EquationFigs. 3 and Equation4).
Hence, all the conditions of Theorems 1, 2 and 3 can be heldold for Eqs. (3) and (7).
Remark 4
CitationKroopnick (2013) proved Theorems A and B by the integral test to scalar linear homogenous differential equation of second order, . After that, by Theorems C and D, CitationTunç and Tunç (2015) generalized and improved the results of (CitationKroopnick, 2013), Theorems A and B, to the second order vector linear and non-homogenous differential Eq. (3),
, when (3)
and
respectively, by utilizing the integral test.
In this paper, we first considered a more general second order vector non-linear differential equation, . This equation includes and improves the equations considered in (Kroopnick, Citation2013; Tunç and Tunç, Citation2015), respectively.
In this paper, instead of the integral test, we use Lyapunov’s function approach to prove the stability and boundedness results discussed in (Kroopnick, Citation2013; Tunç and Tunç, Citation2015). This case is a new and different approach and has a contribution to the topic, completes the results of (Kroopnick, Citation2013; Tunç and Tunç, Citation2015).
Besides, instead of the stability of the zero solution in (Kroopnick, Citation2013; Tunç and Tunç, Citation2015), we prove the asymptotic stability of the zero solution. This case improves the stability results of (Kroopnick, Citation2013; Tunç and Tunç, Citation2015) to the asymptotic stability of the zero solution of equation , when
. Moreover, it is worth mentioning that our assumptions which are established on the stability and boundedness of solutions reduce to that of (CitationKroopnick, 2013) for the cases
and
and that of (CitationTunç and Tunç, 2015), when
, despite we did a different approach.
Finally, CitationKroopnick (2014) proved Theorem E to the scalar linear homogenous differential equation of second order, ,
and, by Theorem F, CitationTunç and Tunç (2016) generalized the result of (CitationTunç and Tunç, 2016) to the second order vector linear and homogenous differential equation
, respectively. The technique of the proofs in (Kroopnick, Citation2014; Tunç and Tunç, Citation2016) involves the integral test. In this paper, we are concerned with a more general second order vector non-linear differential equation,
. This equation includes and improves the equations discussed in (Kroopnick, Citation2014; Tunç and Tunç, Citation2016), respectively. Here, instead of the integral test, we use Lyapunov’s function approach to extend and improve boundedness results discussed in (Kroopnick, Citation2014; Tunç and Tunç, Citation2016), and we give an additional result like asymptotic stability of the zero solution of Eq. (7), when
. Hence, our result, Theorem 3 includes, improves and completes the boundedness results of (Kroopnick, Citation2014; Tunç and Tunç, Citation2016). The obtained asymptotic stability has an additional contribution to the results of (Kroopnick, Citation2014; Tunç and Tunç, Citation2016) and that in the literature.
2 Conclusion
A class of non-linear differential systems of second order is considered. Certain sufficient conditions are established which guarantee the boundedness and asymptotic stability of solutions. To prove the main results here, we put to use Lyapunov’s function approach instead of the integral test. The results obtained essentially complement, extend and improve some well-known results in the literature from the linear cases to the non-linear cases. An example is furnished to illustrate the hypotheses and main results in this paper.
Acknowledgement
The authors of this paper would like to express their sincere appreciation to the anonymous referees for their valuable comments and suggestions which have led to an improvement in the presentation of the paper.
Notes
Peer review under responsibility of University of Bahrain.
References
- Allan J.KroopnickTwo new proofs for the boundedness of solutions to MissouriJ. Math. Sci.2512013103105
- Allan J.KroopnickOn the integration of L2 - solutions of non-oscillatory solutions to Int. Math Forum9102014475481
- B.SongL.PanJ.CaoPeriodic solutions for a class of n-th order functional differential equationsInt. J. Differ. Equ.201121 Art. ID 916279
- C.TunçBoundedness results for solutions of certain nonlinear differential equations of second orderJ. Indones. Math. Soc.1622010115126
- C.TunçStability and boundedness in delay system of differential equations of third orderJ. Assoc. Arab Univ. Basic Appl. Sci.2220177682
- C.TunçO.TunçA note on certain qualitative properties of a second order linear differential systemAppl. Math. Inf. Sci.922015953956
- C.TunçO.TunçOn the boundedness and integration of non-oscillatory solutions of certain linear differential equations of second orderJ. Adv. Res.712016165168
- Z.WangS.LuJ.CaoExistence of periodic solutions for a p-Laplacian neutral functional differential equation with multiple variable parametersNonlinear Anal.7222010734747
- Z.WangL.QianS.LuJ.CaoThe existence and uniqueness of periodic solutions for a kind of Duffing-type equation with two deviating argumentsNonlinear Anal.739201030343043