Abstract
The purpose of this article is to generate the closed form traveling wave solutions of some nonlinear partial differential equations namely; the KdV equation and the modified KdV equation using the recently established rational (G′/G)-expansion method. By this method, new and further general closed form solutions expressed by three types of functions as for instance hyperbolic, trigonometric and rational function solutions are found. The basic ideas presented in this article and the obtained solutions might be useful to analyze the shallow water waves, ion acoustic waves in plasma, acoustic waves on a crystal lattice and the role of nonlinear dispersion in the formation of structures like liquid drops.
1 Introduction
The nonlinear evolution equations (NLEEs) are extensively used as models to depict the complex physical phenomena. One of the elementary problems for these models is to obtain their closed form traveling wave solutions. The closed form solutions of NLEEs play an ultimate role in nonlinear science and engineering. Therefore, many researchers paid attention to investigate the closed form traveling wave solutions of NLEEs. Their interest on finding traveling wave solutions of NLEEs is increasing day by day and now it becomes an attractive topic of research. In the recent years, the researchers established several powerful and direct methods to comprehend the internal mechanisms of these physical phenomena. Some of the existing methods are: the inverse scattering method (CitationAblowitz and Clarkson, 1991), the Backlund transformation method (Rogers and Shadwick, Citation1982; Jianming and Wenjun, Citation2011"), the Adomian decomposition method (Wazwaz, Citation2002; Helal and Mehana, Citation2006"), the Hirota bilinear transformation method (CitationHirota, 1971), the He homotopy perturbation method (Ganji, Citation2006; Ganji et al., Citation2007"), the Jacobi elliptic function method (Xu, Citation2006; Yusufoglu and Bekir, Citation2008"), the tanh-function method (Malfliet and Hereman, Citation1996; Abdou, Citation2007"), the variational iteration method (CitationMohyud-Din et al., 2009), the sine–cosine method (CitationYusufoglu and Bekir, 2006), the homogeneous balance method (CitationWang, 1995), the F-expansion method (CitationWang and Li, 2005), the Lie group symmetry method (CitationGuo and Lin, 2010), the Exp-function method (He and Wu, Citation2006; Naher et al., Citation2012"), the (G′/G)-expansion method (Wang et al., Citation2008; Zhang et al., Citation2010; Feng et al., Citation2011; Akbar et al., Citation2012; Islam et al., Citation2015"), the ansatz method (CitationHu, 2001), the modified simple equation method (Jawad et al., Citation2010; Zayed and Ibrahim, Citation2012; Khan et al., Citation2013; Khan and Akbar, Citation2013"), the exp(−ϕ(η))-expansion method (CitationHafez et al., 2015), the variational approximation method (Seadawy, Citation2011; Helal and Seadawy, Citation2009"), the reductive perturbation procedure (Seadawy, Citation2016a; Selima et al., Citation2016"), the direct algebraic method (Seadawy and Rashidy, Citation2013; Seadawy, Citation2014"), the extended auxiliary equation method (CitationSeadawy, 2017), the extended modified direct algebraic method (Seadawy, Citation2015, Citation2016b; Arshad et al., Citation2016; Seadawy et al., Citation2016"), the improved Bernoulli sub-equation function method (Baskonus and Bulut, Citation2015a,Citationb, Citation2016a; Boskonus, Citation2017; Baskonus et al., Citation2017a"), the generalized Kudryashov method (Baskonus and Bulut, Citation2015c,Citationd"), the modified exp-function method (CitationBaskonus and Bulut, 2015e), the modified exp (−Ω(ξ)) expansion method (CitationBaskonus and Bulut, 2016a), the sine-Gordon expansion method (Baskonus and Bulut, Citation2016b; Baskonus et al., Citation2017b"), the modified tanh-coth method and the extended Jacobi elliptic function method (CitationLee and Sakthivel, 2014), the homotopy perturbation method (CitationChun and Sakthivel, 2010), the extended tanh method (CitationSakthivel et al., 2010), the differential transform method (CitationLee and Sakthivel, 2013), etc.
Table 1 Comparison between newly obtained solutions of the KdV Eq. (8) and CitationWang et al. (2008) solutions.
Table 2 Comparison between newly obtained solutions of the mKdV Eq. (31) and CitationWang et al. (2008) solutions.
The main objective of this study is to derive closed form traveling wave solutions for some NLEEs arise in applied mathematics, mathematical physics and engineering, namely the KdV equation and the modified KdV equation by the rational (G′/G)-expansion method which is established by CitationIslam et al. (2015). This method gives new and further developed closed form solutions to the KdV equation and the modified KdV equation. The major advantage of this method lies in its ability to solve the nonlinear evolution equations exactly and offers further general wave solutions. The effectiveness and efficiency of this method are shown by comparing the solutions obtained in this work with the existing results.
2 Description of the method
Suppose the general nonlinear evolution equation in two independent variables x and t is as follows:(1) where u = u(x, t) is an unknown function, P is a polynomial in u(x, t) and its partial derivatives in which the highest order partial derivatives and the nonlinear terms are included. In order to examine (1) by means of the recently proposed rational (G′/G)-expansion method, we go through the following steps:
Step 1: Assign a compound variable ξ with the real variables x and t by the following transformation:(2) where v is the celerity of traveling wave. The wave variable assigned in (2) transforms Eq. (1) into an ordinary differential equation (ODE) for u = u(ξ):
(3) where Q is a polynomial of u and its various derivatives. The superscripts stand for ordinary derivatives with respect to ξ.
Step 2: Integrate Eq. (3) one or more as possible. For simplicity, set the constant(s) of integration to zero, as we are seeking for solitary wave solutions.
Step 3: Suppose the solution of Eq. (3) can be expressed as follows:(4) where ai and bi
are arbitrary constants to be determined later, such that an = bn ≠ 0 and G = G(ξ) satisfy the following second order ODE:
(5) where λ and μ are real constants. Eq. (5) can be rearranged into
(6)
Eq. (5) (or equivalent to Eq. (6)) possesses the following general solutions:(7) where A and B are constants of integration.
Step 4: To determine the positive integer n, substitute (4) along with (5) into Eq. (3) and take the homogeneous balance between the highest order derivatives and the highest order nonlinear terms appearing in (3). If the degree of u(ξ) is , then, the degree of the other expressions will be as follows:
Step 5: Substitute Eq. (4) along with Eq. (5) into Eq. (3) with the value of n obtained in step 4. This substitution forms a polynomial of (G′/G). Equate the coefficients of (G′/G) and set to zero. This procedure yields a system of algebraic equations which can be solved for getting ai, bi, λ, μ and v and the value of the other needful parameters.
Step 6: We substitute the values of ai, bi, λ, μ and v together with the solutions given in Eq. (7) into Eq. (4). This completes the determination of the solutions to the nonlinear evolution equation Eq. (1).
3 Application of the method
In this section, the rational (G′/G)-expansion method is applied to investigate some new and further general closed form solitary wave solutions to the KdV equation and the modified KdV equation.
3.1 The KdV equation
Let us consider the nonlinear KdV equation in the following form(8) where the coefficient δ of linear dispersive term can be determined from the properties of the linear long wave mode. The KdV equation models the shallow-water waves with weakly nonlinear restoring forces, ion acoustic waves in a plasma, long internal wave in a density-stratified ocean and acoustic waves on a crystal lattice. This equation is one of the most familiar models for solitons and the foundation which studies other equations.The traveling wave transformation u(x, t) = u(ξ), ξ = x – v t, transforms Eq. (8) into the following ODE:
(9) where the primes in u denote the order of derivative with respect to ξ. Integrating Eq. (9) once, yields
(10) where C is the constant of integration to be determined later. Taking homogeneous balance between u2 and u″ appearing in (10) gives n = 2. Therefore, the solution Eq. (4) becomes:
(11)
Inserting (11) into (10), the left hand side is converted into a polynomial in (G′/G). Equating the coefficients of the same power of (G′/G) to zero, yields a set of simultaneous algebraic equations (for simplicity omitted them in this article) for and v. Solving this set of equations using the computer algebra systems, such as Maple 13, provides the following set of solutions:
Set-1:(12) where a0, b0, λ and μ all are arbitrary constants.
Set-2:(13) where a2, b2, λ and μ all are arbitrary constants.
Set-3:(14) where b2, λ and μ all are arbitrary constants.
Set-4:(15) where a2, b1, b2, λ and μ all are arbitrary constants.
Using the values of the constants from (12) into solution Eq. (11), provides(16) where
.
By means of the solutions arranged in (7), from (16), we obtain the following traveling wave solutions of the KdV Eq. (8):
When , the hyperbolic function solution can be obtained as
(17) where
, A and B are arbitrary constants. If we choose
and
with r1 = 1, then after simplification solution (18) becomes
(18) where
.
When , the trigonometric function solution can be obtained as
(19) where
, A and B are arbitrary constants. If we use
and
with r1 = 1, then after simplification solution (20) becomes
(20) where
.
When , the rational solution is derived as
(21) where
, A and B are arbitrary constants.
Assigning b0 = 1, the solutions (17)–(21) are identical to the solutions obtained by CitationWang et al. (2008).
Using the values of the constants from (13) into solution Eq. (11), provides(22) where
.
Utilizing the general solutions assembled in (7) into (22) provides the following traveling wave solutions of the KdV equation (8).
When , the hyperbolic function solution can be obtained as
(23) where A and B are arbitrary constants. Since A and B are arbitrary constants, one may randomly choose their values. Therefore, we choose
and
,
,
,
,
,
,
and after simplification (taken two significant figure), the solution Eq. (23) becomes
(24) where
and
.
When , the trigonometric function solution can be obtained as,
(25) where A and B are arbitrary constants. Since A and B are arbitrary constants, we choose
,
, also
,
,
,
,
,
and under simplification (taking two significant figure), Eq. (25) implies
(26) where
and
.
When , the rational function solution is derived as
(27) where
; A and B are arbitrary constants.
If , the solutions for solution set-1 are similar to those of CitationWang et al. (2008). But, the solutions for solution set-2 are new and further general which were not obtained by CitationWang et al. (2008).
Putting the values of the constants provided in (14) into solution Eq. (11), give(28) where
.
Employing the general solutions offered in (7) into (28) derives the following closed form traveling wave solutions of the KdV equation.
When , the hyperbolic function solution can be obtained as
(29)
Assign arbitrary values to A and B as done in Eq. (23), then under simplification Eq. (29) possesses(30) where
,
and
.
By the similar procedure as maintained for solution set-2, the trigonometric function solution and the rational function solution can also be obtained under the conditions and
respectively, but for simplicity these solutions are not provided here.
For the solution set-4, we might get further three types of closed form traveling wave solutions, namely the hyperbolic function solution, the trigonometric function solution and the rational function solution under the conditions ,
and
respectively. But for convenience, the detail is omitted.
3.2 The modified KdV equation
In this subsection, we examine the modified KdV equation(31)
Here, δ is the coefficient of linear dispersive term, can be determined from the properties of the linear long wave mode. This equation arises in the process of understanding the role of nonlinear dispersion and in the formation of structures like liquid drops. It exhibits compaction solitons with compact support.Using the traveling wave transformation
Eq. (31) reduces into the following ODE:(32) where the primes in u denote the order of derivative of u with respect to ξ. Integrating (32) once, yields
(33) where the constant of integration is supposed to be zero. Considering the homogeneous balance u3 and u″ appearing in Eq. (33) yields
. Thus, the solution Eq. (4) takes the form
(34)
Substitute Eq. (34) into Eq. (33) and put the coefficients of the same power of (G′/G) to zero, yields a set of algebraic equations (for simplicity, we did not display them) for and v. Solving this set of equations using the computer algebra software, such as Maple 13, possesses the following set of solutions:
Set-1:
(35) where b0, λ and μ all are arbitrary constants.
Set-2:
(36) where b0, b1, λ and μ all are arbitrary constants.
Putting the values of constants obtained in (35) and (36) into solution Eq. (34), we attain(37) where
.
(38) where
.
Solution (37) with the values of (G′/G) possesses the hyperbolic function solution, trigonometric function solution and rational solution similar to those of CitationWang et al. (2008). But, so that nobody is disturbed, these solutions have not been written in this work.
Substituting the general solutions offered in (7) into (38) gives the following traveling wave solutions of Eq. (31).
When ,
(39) where A and B are arbitrary constants. Since, A and B are arbitrary constants, if one chooses
and
, then after simplification, the solution Eq. (39) becomes
(40) where
,
and
.
When ,
(41) where A and B are arbitrary constants. Since A and B are arbitrary constants, one might choose
,
and under simplification, solution (41) implies
(42) where
,
and
.
When ,
(43) where
; A and B are arbitrary constants.
We achieved nine different solutions to the mKdV equation. If and
, the above solutions namely; hyperbolic function solution, trigonometric function solution and rational solution of Eq. (31) are similar to those of CitationWang et al. (2008). Thus, we might assert the solutions obtained in this article are new and further general.
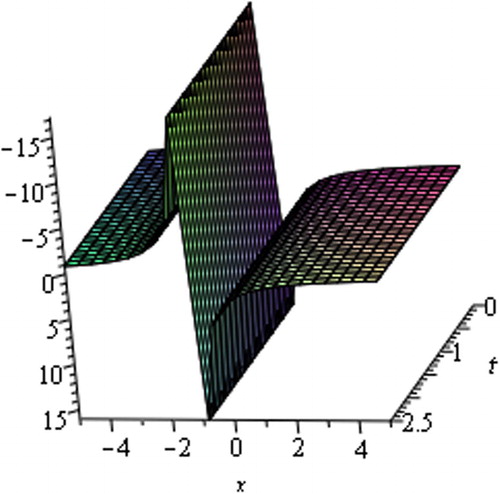
4 Graphical representations
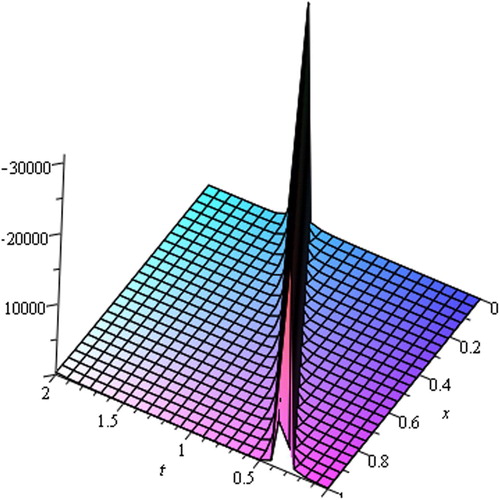
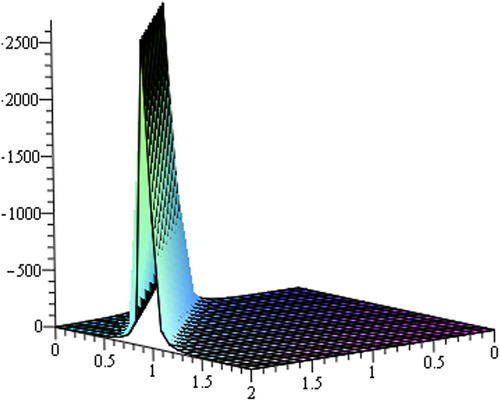
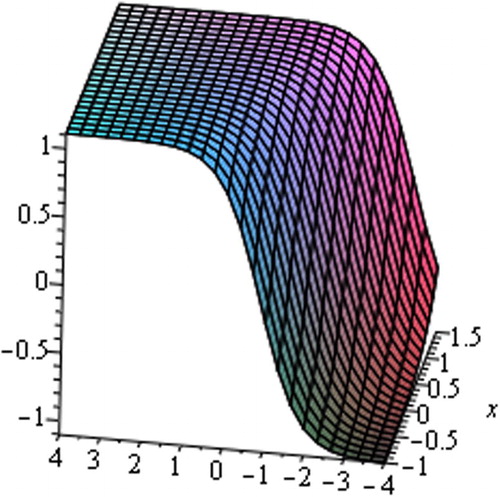
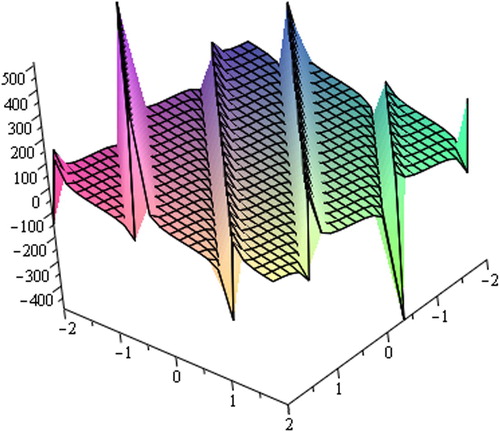
Graph is an important tool to analyze the problems and depicts simply the solutions of the phenomena. For this reason, several graphs of the solutions are provided underneath. The graphs express clearly the solitary wave form of the solutions (–).From figures, we observe that the solutions include kink shape soliton, Cuspon, non-symmetry cuspon, periodic solution, bi-symmetric contracted soliton, etc. shows kink shape soliton for ,
,
,
,
,
drawn within the interval
and
. represents cuspon generated from solution (16) for
,
,
,
,
,
depicted within
,
. illustrates the non-symmetry cuspon propagated from solution (16) for
,
,
,
,
,
,
within
,
. interprets kink shape soliton obtained from solution (32) for
,
,
,
within
,
. demonstrates periodic solution attained from (32) for
,
,
,
within the interval
. exhibits bi-symmetric contracted soliton depicted from solution (32) for
,
,
,
,
,
within
,
.
5 Comparison of the results
In order to compare the results obtained in this article with the others available in the literature, in the following two tables the results are presented:
The other values of b0 and b1, deliver further particular traveling wave solutions of the modified KdV equation. Therefore, we might assert that the solutions of Eq. (31) obtained in this article are new and more general than those of CitationWang et al. (2008) (see and ).
6 Conclusion
In this article, the closed form wave solutions of the NLEEs, namely the KdV equation and the modified KdV equation, are successfully constructed by the recently established rational (G′/G)-expansion method. The obtained solutions will be helpful to analyze shallow-water waves with weakly nonlinear restoring forces, ion acoustic waves in plasma, acoustic waves on a crystal lattice and the role of nonlinear dispersion in the formation of structures like liquid drops. The method gives three types of exact traveling wave solutions, such as, the generalized hyperbolic solutions, the generalized trigonometric solutions and rational function solutions. On comparison to other methods, the results throughout this article are new and further general. The analysis shows that the suggested method is inventive and compatible to find exact solutions to (1+1)-dimensional NLEEs. The procedure is not yet implemented in higher dimensional NLEEs as well as NLEEs with variable coefficients. Thus, the application of this method to the higher dimensional as well as variable coefficients NLEEs deserves further research.
Conflict of interest
The authors have no conflict of interest.
Notes
Peer review under responsibility of University of Bahrain.
References
- M.A.AbdouThe extended tanh method and its applications for solving nonlinear physical modelsAppl. Math. Comput.19012007988996
- M.J.AblowitzP.A.ClarksonSolitons, Nonlinear Evolution Equations and Inverse Scattering Transform1991Cambridge University PressCambridge, UK
- M.A.AkbarN.H.M.AliE.M.E.ZayedAbundant exact traveling wave solutions of the generalized Bretherton equation via (G′/G)-expansion methodCommun. Theor. Phys.572012173178
- M.ArshadA.R.SeadawyD.LuJ.WangTravelling wave solutions of generalized coupled Zakharov-Kuznetsov and dispersive long wave equationsResults Phys.6201611361145
- H.M.BaskonusH.BulutAn effective scheme for solving some nonlinear partial differential equation arising in nonlinear physicsOpen Phys.1312015280289
- H.M.BaskonusH.BulutOn the complex structures of Kundu-Eckhaus equation via improved Bernoulli sub-equation function methodWaves Random Complex Media2542015720728
- H.M.BaskonusH.BulutOn some new analytical solutions for the (2+1)-dimensional Burgers equation and the special type of Dodd-Bullough-Mikhailov equationJ. Appl. Anal. Comput.542015613625
- H.M.BaskonusH.BulutNew hyperbolic function solutions for some nonlinear partial differential equation arising in mathematical physicsEntropy176201542554270
- H.M.BaskonusH.BulutAnalytical studies on the (1+1)-dimensional nonlinear dispersive modified Benjamin-Bona-Mahony equation defined by seismic sea wavesWaves Random Complex Media2542015576586
- H.M.BaskonusH.BulutExponential prototype structures for (2+1)-dimensional Boiti-Leon-Pempinelli systems in Mathematical PhysicsWaves Random Complex Media2622016201208
- H.M.BaskonusH.BulutNew wave behaviors of the system of equations for the ion sound and Langmuir wavesWaves Random Complex Media2642016613625
- H.M.BoskonusNew complex and hyperbolic function solutions to the generalized double combined sinh-cosh-Gordon equationAIP Conf. Proc.17982017020018-1020018-9
- H.M.BaskonusT.A.SulaimanH.BulutNew solitary wave solutions to the (2+1)-dimensional Calogero-Bogoyavlenskii-Schi and the Kadomtsev-Petviashvili hierarchy equationsIndian J. Phys.201710.1007/s12648-017-1033-z
- H.M.BaskonusT.A.SulaimanH.BulutOn the novel wave behaviors to the coupled nonlinear Maccari’s system with complex structureOptik-Int. J. Light Electron Opt.131201710361043
- C.ChunR.SakthivelHomotopy perturbation technique for solving two-point boundary value problems-comparison with other methodsComput. Phys. Commun.1816201010211024
- J.FengW.LiQ.WanUsing (G′/G)-expansion method to seek the traveling wave solution of Kolmogorov-Petrovskii-Piskunov equationAppl. Math. Comput.217201158605865
- D.D.GanjiThe application of He’s homotopy perturbation method to nonlinear equations arising in heat transferPhys. Lett. A3552006137141
- D.D.GanjiG.A.AfrouziR.A.TalarposhtiApplication of variational iteration method and homotopy perturbation method for nonlinear heat diffusion and heat transfer equationsPhys. Lett. A3682007450457
- A.L.GuoJ.LinExact solutions of (2+1)-dimensional HNLS equationCommun. Theor. Phys.542010401406
- M.G.HafezM.N.AlamM.A.AkbarTraveling wave solutions for some important coupled nonlinear physical models via the coupled Higgs equation and the Maccari systemJ. King Saud Univ. Sci.272015105112
- J.H.HeX.H.WuExp-function method for nonlinear wave equationsChaos, Solitons Fract.302006700708
- M.A.HelalM.S.MehanaA comparison between two different methods for solving modified KdV-Burgers equationChaos, Solitons Fract.282006320326
- M.A.HelalA.R.SeadawyVariational method for the derivative nonlinear Schrodinger equation with computational applicationsPhys. Scr.802009350360
- R.HirotaExact solution of the Korteweg-de Vries equation for multiple Collisions of solitonsPhys. Rev. Lett.2718197111921194
- J.L.HuA new method for finding exact traveling wave solutions to nonlinear partial differential equationsPhys. Lett. A2862001175179
- M.T.IslamM.A.AkbarA.K.AzadA rational (G′/G)-expansion method and its application to the modified KdV-Burgers equation and the (2+1)-dimensional Boussinesq equationNonlinear Stud.642015111
- A.J.M.JawadM.D.PetkovicA.BiswasModified simple equation method for nonlinear evolution equationsAppl. Math. Comput.2172010869877
- L.JianmingD.JieY.WenjunBacklund transformation and new exact solutions of the Sharma-Tasso-Olver equationAbstr. Appl. Anal.20112011935710
- K.KhanM.A.AkbarM.N.AlamTraveling wave solutions of the nonlinear Drinfel’d-Sokolov-Wilson equation and modified Benjamin-Bona-Mahony equationsJ. Egypt. Math. Soc.212013233240
- K.KhanM.A.AkbarExact and solitary wave solutions for the Tzitzeica-Dodd-Bullough and the modified KdV-Zakharov-Kuznetsov equations using the modified simple equation methodAin Shams Eng. J.42013903909
- J.LeeR.SakthivelDirect approach for solving nonlinear evolution and two-point boundary value problemsPharmacol. J. Phys.8162013893909
- J.LeeR.SakthivelExact traveling wave solutions of a variety of Boussinesq-like equationsChin. J. Phys.5232014939957
- W.MalflietW.HeremanThe tanh method II: perturbation technique for conservative systemsPhys. Scr.541996563569
- S.T.Mohyud-DinM.A.NoorK.I.NoorModified variational iteration method for solving Sine-Gordon equationsWorld Appl. Sci. J.6720099991004
- H.NaherA.F.AbdullahM.A.AkbarNew traveling wave solutions of the higher dimensional nonlinear partial differential equation by the Exp-function methodJ. Appl. Math.20122012575387
- C.RogersW.F.ShadwickBacklund transformations and their applicationsMathematics in Science and Engineering1611982Academic PressNew York, USA
- R.SakthivelC.ChunJ.LeeNew travelling wave solutions of Burgers equation with finite transport memoryZ. Naturforsch.65a2010633640
- A.R.SeadawyNew exact solutions for the KdV equation with higher order nonlinearity by using the variational methodComput. Math. Appl.62201137413755
- A.R.SeadawyFractional solitary wave solutions of the nonlinear higher-order extended KdV equation in a stratified shear flow: Part IComput. Math. Appl.702015345352
- A.R.SeadawyStability analysis solutions for nonlinear three-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov equation in a magnetized electron-positron plasmaStat. Mech. Appl. Phys. A45520164451
- A.R.SeadawyThree-dimensional nonlinear modified Zakharov-Kuznetsov equation of ion-acoustic waves in a magnetized plasmaComput. Math. Appl.712016201212
- A.R.SeadawyO.H.E.KalaawyR.B.AldenariWater wave solutions of Zufiria’s higher-order Boussinesq type equations and its stabilityAppl. Math. Comput.28020165771
- A.R.SeadawyK.E.RashidyTraveling wave solutions for some coupled nonlinear evolution equationsMath. Comput. Model.57201313711379
- A.R.SeadawyStability analysis for Zakharov-Kuznetsov equation of weakly nonlinear ion-acoustic waves in a plasmaComput. Math. Appl.672014172180
- E.S.SelimaA.R.SeadawyX.YaoThe nonlinear dispersive Davey-Stewartson system for surface waves propagation in shallow water and its stabilityEur. Phys. J. Plus1312016425
- A.R.SeadawyTravelling-wave solutions of a weakly nonlinear two-dimensional higher-order Kadomtsev-Petviashvili dynamical equation for dispersive shallow-water wavesEur. Phys. J. Plus132201729
- M.WangSolitary wave solutions for variant Boussinesq equationsPhys. Lett. A1991995169172
- M.L.WangX.Z.LiExtended F-expansion method and periodic wave solutions for the generalized Zakharov equationsPhys. Lett. A34320054854
- M.WangX.LiJ.ZhangThe (G′/G)-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physicsPhys. Lett. A3722008417423
- A.M.WazwazPartial Differential Equations: Method and Applications2002Taylor and Francis
- G.XuAn elliptic equation method and its applications in nonlinear evolution equationsChaos, Solitons Fract.292006942947
- E.YusufogluA.BekirExact solution of coupled nonlinear evolution equationsChaos, Solitons Fract.372008842848
- E.YusufogluA.BekirSolitons and periodic solutions of coupled nonlinear evolution equations by using sine-cosine methodInt. J. Comput. Math.83122006915924
- E.M.E.ZayedS.A.H.IbrahimExact solutions of nonlinear evolution equations in mathematical physics using the modified simple equation methodChin. Phys. Lett.2962012060201
- J.ZhangF.JiangX.ZhaoAn improved (G′/G)-expansion method for solving nonlinear evolution equationsInt. J. Comput. Math.878201017161725