Compression of nanomaterials under pressure

Peer review under responsibility of Taibah University.

Abstract

A simple equation of state (EOS) model is proposed to predict the high pressure compression behaviour of nanomaterials. The model is based on the fact that the product of the thermal expansion coefficient (α) and the bulk modulus (B_T) (i.e., αB_T) remains constant under pressure. This model is used to study the compression behaviour of a number of nanomaterials, i.e., CuO, TiO₂ (anatase), α-Fe₂O₃, γ-Fe₂O₃, n-ZnO, n-CeO₂, n-PbS, carbon nanotube (individual), Ni-filled multi-wall carbon nanotube (MWCNT), Fe-filled MWCNT, AlN (hexagonal), γ-Al₂O₃ (67 nm), Ni (20 nm) and CdSe (rocksalt phase). The beauty of the model used in the present study is that it needs only one input parameter, the bulk modulus at zero pressure. The results obtained using the present formulation are in agreement with the existing experimental data. This shows the legitimacy of the present approach.

Keywords:

• Nanomaterial
• Equation of state
• Volume compression

1 Introduction

Studies of compressibility and pressure-induced phase transitions for nanocrystalline materials can improve our understanding of the stability of materials at the nanometre scale. Most of the high pressure research on nanocrystalline materials has been on semiconductors, although some work on insulators and metals has been reported recently. While applying high pressure on a nanomaterial, many effects may occur, such as the (i) transformation of the nano-constitutive elements, (ii) transformation of the interaction between nano-objects and (iii) modification of interactions between the nano-objects and the pressure transmitting medium. Due to such applications, the effects of pressure on nanomaterials have attracted the attention of researchers. The EOS of nanocrystalline CuO (24 nm) has been studied by Wang et al. [1] using high energy Synchrotron radiation and Raman spectroscopic techniques. Swamy et al. [2] presented a synchrotron XRD study of pressure-induced changes in nanocrystalline anatase TiO₂ (with a crystallite size of 30–40 nm) at 35 GPa and found that the bulk modulus value obtained for the nanocrystalline anatase is approximately 35% larger than that of the macrocrystalline counterpart. Olsen et al. [3] studied the high pressure behaviour of nanocrystalline rutile TiO₂ at ambient temperature by using X-ray diffraction and found it to be transforming to the monoclinic baddeleyite structure between 20 and 30 GPa. Clark et al. [4] observed a pressure-induced γ-Fe₂O₃ (maghemite) to α-Fe₂O₃ (hematite) structural phase transition in nanocrystals, which was analogous to the findings of Zhao et al. [5]. Using energy dispersive synchrotron XRD produced wiggler radiation, Quadri et al. [6] investigated the effect of size on compressibility and phase transition in PbS nanocrystals.

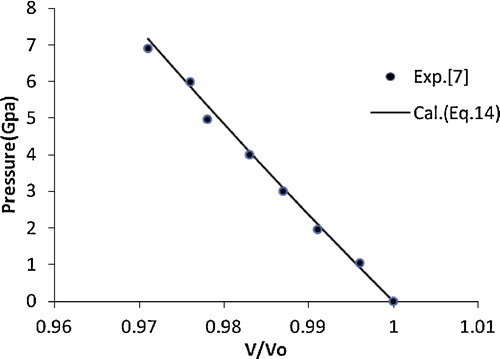
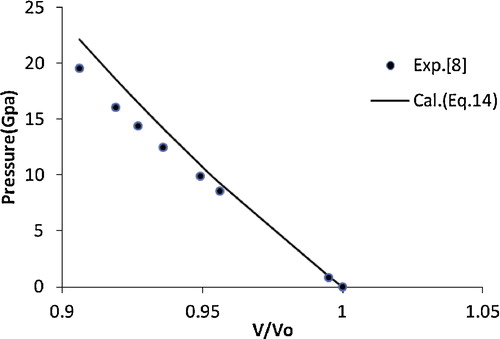
The high pressure compression behaviour of carbon nanotubes was studied experimentally by Tang et al. [7]. With the help of synchrotron-based angle dispersive X-ray diffraction, the high pressure behaviour of Ni and Fe filled multiwalled carbon nanotubes was investigated by Poswal et al. [8] up to pressures of 27 and 19 GPa, respectively. These nanotubes do not show any structural transformation, even at the highest pressures studied.

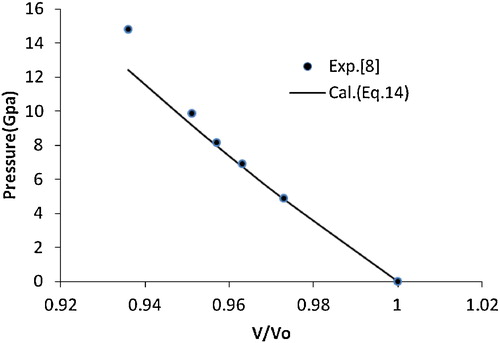
The study of AlN nanocrystals under hydrostatic conditions was performed by Wang et al. [9] up to 36.9 GPa using an energy dispersive synchrotron-radiation technique in a diamond anvil cell (DAC). Shen et al. [10] have investigated the structural transition of AlN nanowires by in situ angle dispersive high-pressure X-ray diffraction using a synchrotron radiation source and found a pressure-induced wurtzite to rocksalt phase transition at 45.4 GPa.

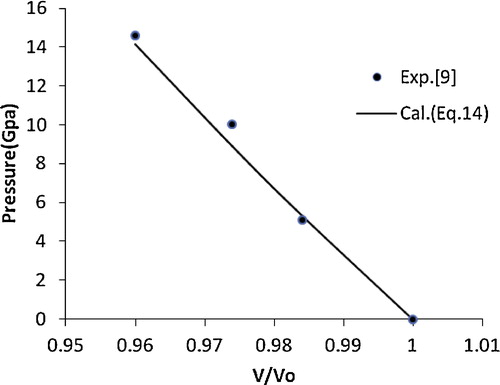
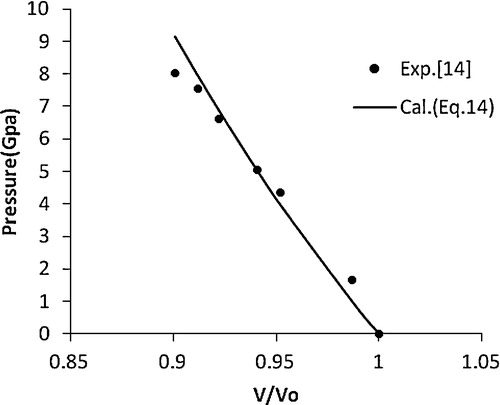
At room temperature, Mao et al. [11] compressed nanocrystalline γ-Al₂O₃(67 nm) quasi-hydrostatically at pressures of up to 60 GPa in a Mao-Bell type DAC, and a X-ray diffraction study was carried out by Chen et al. [12]. The bulk modulus was found to be different during the two processes. To understand the size effect on the bulk modulus and to look for possible new high pressure phases, nanocrystalline Ni (20 nm) was studied under high pressure by Chen et al. [13]. The structural transformation in CdSe nanocrystals was studied [14] using high pressure X-ray diffraction and high pressure optical absorption at room temperature. The nanocrystal undergoes a wurtzite to rocksalt transition analogous to that observed in bulk CdSe. The nanocrystal phase transition pressures vary from 3.6 to 4.9 GPa for crystallite ranging from 21 to 10 Å in radius, respectively, in comparison to the value of 2 GPa for bulk CdSe.

In the present paper, we present a simple theoretical model to study the compression behaviour of nanosystems through several experimental studies to understand the high pressure behaviour of nanomaterials, but the theoretical efforts are deficient. In addition to the available models, the study of the high pressure compression behaviour requires two input parameters, the bulk modulus and the first order pressure derivative of the bulk modulus, and among these experimental values, the first order pressure derivative of the bulk modulus is not always available in the literature, especially for nanomaterials. Thus, it is justifiable and may be useful to present a simple theoretical method, which requires only a zero pressure value of the bulk modulus at zero pressure, to study the high pressure compression behaviour of nanomaterials. The method of analysis is given in Section 2. The results and discussion are given in Section 3 and the conclusion in Section 4.

2 Theory of analysis

Assuming the fact that the product of the thermal expansion coefficient (α) and the bulk modulus (B_T) is constant under the effect of pressure [15], i.e.,(1) $\alpha B_T=\text{constant.}$(1)

The differentiation of Eq. (1)(1) $\alpha B_T=\text{constant.}$(1) with respect to the volume at a constant temperature gives(2) $\alpha {\left(\frac{dB}{dV}\right)}_T+B{\left(\frac{d\alpha }{dV}\right)}_T=0\text{.}$(2)

The Anderson–Grüneisen parameter is defined as(3) ${\delta }_T=\frac{V}{\alpha }{\left(\frac{d\alpha }{dV}\right)}_T\text{,}$(3) where δ_T is Anderson–Grüneisen parameter at constant temperature.

From Eqs. (2)(2) $\alpha {\left(\frac{dB}{dV}\right)}_T+B{\left(\frac{d\alpha }{dV}\right)}_T=0\text{.}$(2) and (3)(3) ${\delta }_T=\frac{V}{\alpha }{\left(\frac{d\alpha }{dV}\right)}_T\text{,}$(3) we obtain(4) ${\delta }_T=\frac{V}{\alpha }{\left(\frac{d\alpha }{dV}\right)}_T=-\frac{V}{B}{\left(\frac{dB}{dV}\right)}_T\text{.}$(4)

Assuming δ_T to be independent of V,(5) ${\delta }_T={\left(\frac{dB}{dP}\right)}_T={B^{\prime }}_0$(5) and the Anderson–Grüneisen parameter δ_T and η = V/V₀ (where V₀ is the initial volume) are related by the following relation [16](6) $\frac{({\delta }_T+1)}{\eta }=A\text{,}$(6) where A is a constant for a given solid. In view of Eq. (6)(6) $\frac{({\delta }_T+1)}{\eta }=A\text{,}$(6) , Eq. (4)(4) ${\delta }_T=\frac{V}{\alpha }{\left(\frac{d\alpha }{dV}\right)}_T=-\frac{V}{B}{\left(\frac{dB}{dV}\right)}_T\text{.}$(4) can be written as(7) $\frac{dB}{B}=\left[-\frac{A}{V_0}+\frac{1}{V}\right]dV\text{.}$(7)

Integrating the above equation, we obtain(8) $\frac{B}{B_0}=\frac{V}{V_0}\exp A\left[1-\frac{V}{V_0}\right]\text{,}$(8) where(9) $B=-V{\left(\frac{dP}{dV}\right)}_T\text{.}$(9)

Using Eq. (9)(9) $B=-V{\left(\frac{dP}{dV}\right)}_T\text{.}$(9) , Eq. (8)(8) $\frac{B}{B_0}=\frac{V}{V_0}\exp A\left[1-\frac{V}{V_0}\right]\text{,}$(8) may be written as(10) $\frac{B}{B_0}\exp A\left[1-\frac{V}{V_0}\right]dV=-dP\text{.}$(10)

The integration of Eq. (10)(10) $\frac{B}{B_0}\exp A\left[1-\frac{V}{V_0}\right]dV=-dP\text{.}$(10) gives(11) $P=\frac{B_0}{A}\left[\exp A\left(1-\frac{V}{V_0}\right)-1\right]\text{.}$(11)

Here, B₀ is the bulk modulus at the zero pressure, and the constant A is determined from the initial conditions, viz. at V = V₀, $A={\delta }_T^0+1$, or ${\delta }_T^0={B^{\prime }}_0$.

Expanding the exponential term, the following relation is found(12) $P=\frac{B_0}{A}\left[\left\{1+A\left(1-\frac{V}{V_0}\right)+\frac{A^2}{2}{\left(1-\frac{V}{V_0}\right)}^2+\cdots +\infty \right\}-1\right]\text{.}$(12)

Neglecting the higher order terms, Eq. (12)(12) $P=\frac{B_0}{A}\left[\left\{1+A\left(1-\frac{V}{V_0}\right)+\frac{A^2}{2}{\left(1-\frac{V}{V_0}\right)}^2+\cdots +\infty \right\}-1\right]\text{.}$(12) gives(13) $P=B_0\left[\left(1-\frac{V}{V_0}\right)+\frac{(K_o^1+1)}{2}{\left(1-\frac{V}{V_0}\right)}^2\right]\text{.}$(13)

Eq. (13)(13) $P=B_0\left[\left(1-\frac{V}{V_0}\right)+\frac{(K_o^1+1)}{2}{\left(1-\frac{V}{V_0}\right)}^2\right]\text{.}$(13) is basically a two-parameter isothermal EOS. To make Eq. (13)(13) $P=B_0\left[\left(1-\frac{V}{V_0}\right)+\frac{(K_o^1+1)}{2}{\left(1-\frac{V}{V_0}\right)}^2\right]\text{.}$(13) a one-parameter EOS, the first order pressure derivative of the bulk modulus is fixed to 4, while keeping in mind that the lower the input parameters, the better the EOS. Thus, Eq. (13)(13) $P=B_0\left[\left(1-\frac{V}{V_0}\right)+\frac{(K_o^1+1)}{2}{\left(1-\frac{V}{V_0}\right)}^2\right]\text{.}$(13) takes the following form(14) $P=B_0\left[\left(1-\frac{V}{V_0}\right)+\frac{5}{2}{\left(1-\frac{V}{V_0}\right)}^2\right]\text{.}$(14)

Other EOSs that we included for comparison purposes are the Murnaghan EOS, Vinet EOS, Birch–Murnaghan EOS and Usual Tait EOS and are given as follows.

The Murnaghan EOS reads as follows [17],(15) $\frac{V}{V_0}={\left[1+\frac{{B^{\prime }}_{0}P}{B_0}\right]}^{-(1/{B^{\prime }}_0)}\text{,}$(15) which can be written as(16) $P=\frac{B_0}{{B^{\prime }}_0}\left[{\left(\frac{V_0}{V}\right)}^{{B^{\prime }}_0}-1\right]\text{.}$(16)

The Vinet EOS reads as follows [18](17) $P=3(1-X)B_0[\exp \eta (1-X)]/X^2$(17) where $X={(V/V_0)}^{1/3},\eta =3({B^{\prime }}_0-1)/2$.

The Birch–Murnaghan EOS reads as [19](18) $P=\frac{3}{2}{B}_0\left\{{\left(\frac{V_0}{V}\right)}^{7/3}-{\left(\frac{V_0}{V}\right)}^{5/3}\right\}\times \left[1+\frac{3}{4}({B^{\prime }}_0-4)\left\{{\left(\frac{V_0}{V}\right)}^{2/3}-1\right\}\right]\text{.}$(18)

The Tait equation of state reads as [20](19) $P=\frac{B_0}{A}\left[\exp A\left(1-\frac{V}{V_0}\right)-1\right]\text{,}$(19) which is same as Eq. (11)(11) $P=\frac{B_0}{A}\left[\exp A\left(1-\frac{V}{V_0}\right)-1\right]\text{.}$(11) , here $A={B^{\prime }}_0+1$.

The bulk modulus is defined as$B=-V{\left(\frac{dP}{dV}\right)}_T\text{.}$

Using the definition of the bulk modulus, Eq. (11)(11) $P=\frac{B_0}{A}\left[\exp A\left(1-\frac{V}{V_0}\right)-1\right]\text{.}$(11) may be written as follows(20) $\frac{B}{B_0}=\frac{V}{V_0}\left[\exp A\left(1-\frac{V}{V_0}\right)\right]\text{.}$(20)

On expanding the exponential term, Eq. (20)(20) $\frac{B}{B_0}=\frac{V}{V_0}\left[\exp A\left(1-\frac{V}{V_0}\right)\right]\text{.}$(20) gives(21) $\frac{B}{B_0}=\frac{V}{V_0}\left[\left\{1+A\left(1-\frac{V}{V_0}\right)+\frac{A^2}{2}{\left(1-\frac{V}{V_0}\right)}^2+\cdots +\infty \right\}-1\right]\text{.}$(21)

Neglecting the higher order terms in Eq. (16)(16) $P=\frac{B_0}{{B^{\prime }}_0}\left[{\left(\frac{V_0}{V}\right)}^{{B^{\prime }}_0}-1\right]\text{.}$(16) , we obtain(22) $\frac{B}{B_0}=\frac{V}{V_0}\left[1+({B^{\prime }}_o+1)\left(1-\frac{V}{V_0}\right)\right]\text{.}$(22)

For ${B^{\prime }}_0=4$, Eq. (22)(22) $\frac{B}{B_0}=\frac{V}{V_0}\left[1+({B^{\prime }}_o+1)\left(1-\frac{V}{V_0}\right)\right]\text{.}$(22) can be written as follows,(23) $\frac{B}{B_0}=\frac{V}{V_0}\left[1+5\left(1-\frac{V}{V_0}\right)\right]\text{.}$(23)

Eq. (23)(23) $\frac{B}{B_0}=\frac{V}{V_0}\left[1+5\left(1-\frac{V}{V_0}\right)\right]\text{.}$(23) can be used to study the variation of bulk modulus with pressure.

3 Results and discussion

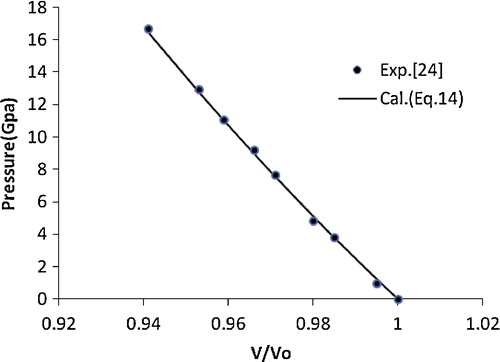
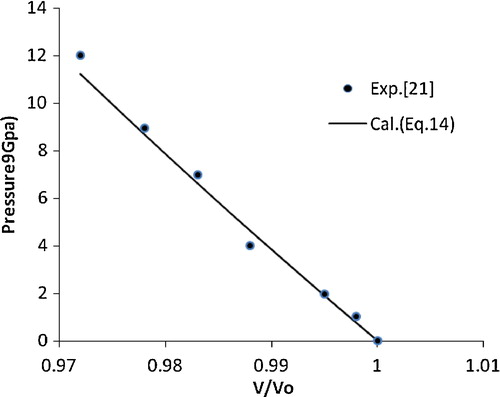
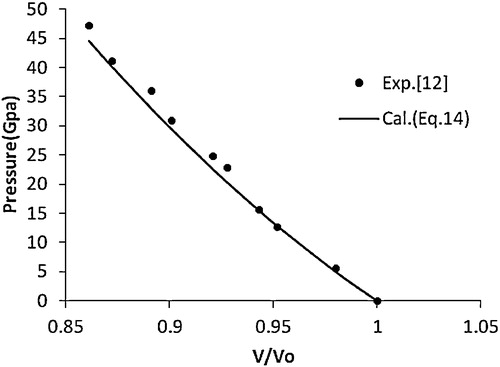
Recently, Kholiya and Chandra [24] showed that the quasi-harmonic approximation, i.e., αB_T = constant, is valid for nanocrystalline forsterite. They also revealed that the bulk modulus decreases while the coefficient of volume thermal expansion increases with a decrease in the grain size of a nanomaterial, which is a consequence of the fact that αB_T is constant for nanomaterials. The present model for studying the effect of pressure on nanomaterials is also based on the same approximation that the product of the thermal expansion coefficient (α) and the bulk modulus (B_T) [αB_T] is constant under pressure. The most attractive feature of the present model is that it requires only one input parameter, the bulk modulus at zero pressure (B₀), to study the compression of nanomaterials under pressure. The value of the input parameter used in the present study is given in Table 1 along with the corresponding reference. Thus the present EOS, i.e., Eq. 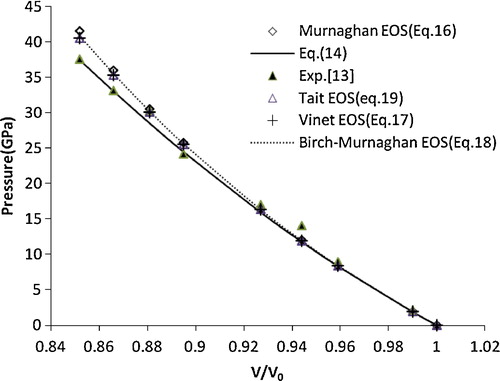(14)(14) $P=B_0\left[\left(1-\frac{V}{V_0}\right)+\frac{5}{2}{\left(1-\frac{V}{V_0}\right)}^2\right]\text{.}$(14) is independent of any fitting parameter. The studies on the compression behaviour of nanocrystalline Ni have attracted much attention in experimental studies [13]. We thus considered this material in the present study to test the validity of Eq. (14)(14) $P=B_0\left[\left(1-\frac{V}{V_0}\right)+\frac{5}{2}{\left(1-\frac{V}{V_0}\right)}^2\right]\text{.}$(14) in with regard to other EOSs, i.e., Murnaghan EOS (Eq. (16)(16) $P=\frac{B_0}{{B^{\prime }}_0}\left[{\left(\frac{V_0}{V}\right)}^{{B^{\prime }}_0}-1\right]\text{.}$(16) ), Vinet EOS (Eq. (17)(17) $P=3(1-X)B_0[\exp \eta (1-X)]/X^2$(17) ), Birch–Murnaghan EOS (Eq. (18)(18) $P=\frac{3}{2}{B}_0\left\{{\left(\frac{V_0}{V}\right)}^{7/3}-{\left(\frac{V_0}{V}\right)}^{5/3}\right\}\times \left[1+\frac{3}{4}({B^{\prime }}_0-4)\left\{{\left(\frac{V_0}{V}\right)}^{2/3}-1\right\}\right]\text{.}$(18) ) and Tait EOS (Eq. (19)(19) $P=\frac{B_0}{A}\left[\exp A\left(1-\frac{V}{V_0}\right)-1\right]\text{,}$(19) ). The compression behaviour of the nanocrystalline Ni is shown in Fig. 1. It is found that Eq. 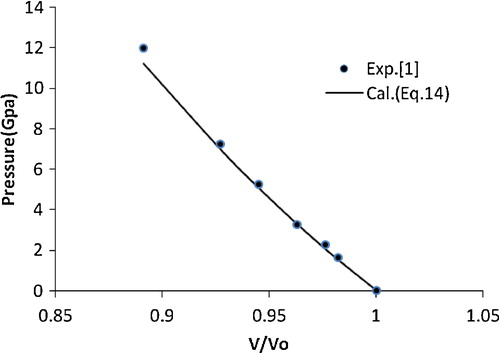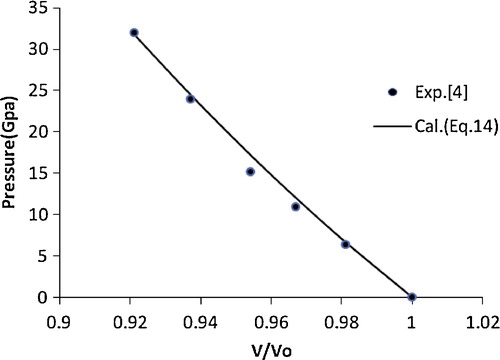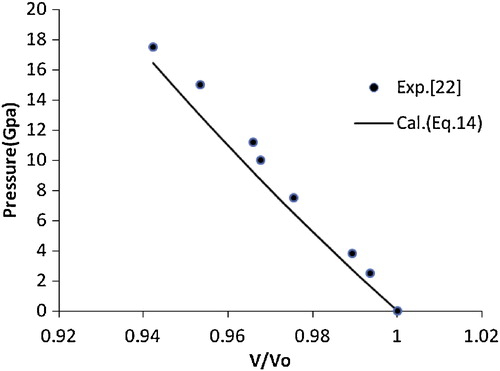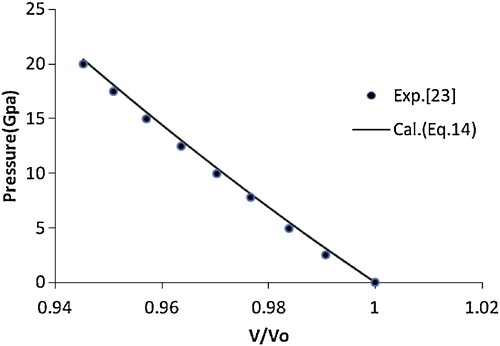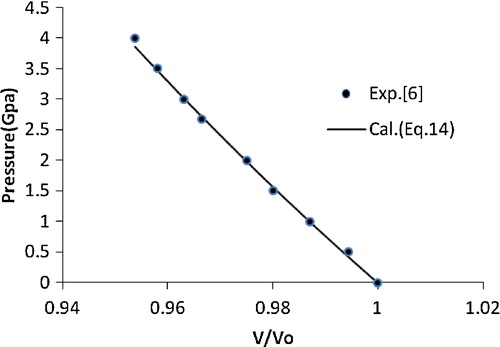(14)(14) $P=B_0\left[\left(1-\frac{V}{V_0}\right)+\frac{5}{2}{\left(1-\frac{V}{V_0}\right)}^2\right]\text{.}$(14) is in better agreement with the experimental data [13] compared with the other EOSs. This encouraged the authors to extend the application of the present approach to various nanomaterials, i.e., CuO, TiO₂ (anatase), α-Fe₂O₃, γ-Fe₂O₃, n-ZnO, n-CeO₂, n-PbS, Ni-filled MWCNT, Fe-filled MWCNT, AlN (hexagonal), γ-Al₂O₃ (67 nm), carbon nanotube (individual) and CdSe (rocksalt phase). The results obtained for these nanomaterials are shown in Figs. 2–14 and are compared with the available experimental data. A good agreement was found between the experimental and calculated values, which demonstrates the validity of the present approach. These results also show that the quasi-harmonic approximation, i.e., the product of the thermal expansion coefficient (α) and the bulk modulus (B_T) [αB_T] remains constant under pressure, is valid for nanomaterials.

Table 1 Values of the input parameter along with the corresponding references.

Sr. no.	Material	B0 (GPa)	References
1	CuO	81	[1]
2	TiO2 (anatase)	243	[2]
3	α-Fe2O3	336	[4]
4	γ-Fe2O3	374	[21]
5	n-ZnO	249	[22]
6	n-CeO2	328	[23]
7	n-PbS	75	[6]
8	Carbon nanotube (individual)	230	[7]
9	Ni-filled MWCNT	190.4	[8]
10	Fe-filled MWCNT	167	[8]
11	AlN (hexagonal)	321	[9]
12	γ-Al2O3 (67 nm)	238	[12]
13	Ni (20 nm)	185	[13]
14	CdSe (rocksalt phase)	74	[14]

Fig. 1 Pressure versus V/V₀ for n-Ni.

Fig. 2 Pressure versus V/V₀ for n-CuO.

Fig. 3 Pressure versus V/V₀ for n-TiO₂.

Fig. 4 Pressure versus V/V₀ for n-α-Fe₂O₃.

Fig. 5 Pressure versus V/V₀ for n-γ-Fe₂O₃.

Fig. 6 Pressure versus V/V₀ for n-ZnO.

Fig. 7 Pressure versus V/V₀ for n-CeO₂.

Fig. 8 Pressure versus V/V₀ for n-PbS.

Fig. 9 Pressure versus V/V₀ for CNT individual.

Fig. 10 Pressure versus V/V₀ for Ni-filled CNT.

Fig. 11 Pressure versus V/V₀ for Fe-filled CNT.

Fig. 12 Pressure versus V/V₀ for n-AlN.

Fig. 13 Pressure versus V/V₀ for n-Ni.

Fig. 14 Pressure versus V/V₀ for n-CdSe.

Through the use of Eq. (23)(23) $\frac{B}{B_0}=\frac{V}{V_0}\left[1+5\left(1-\frac{V}{V_0}\right)\right]\text{.}$(23) , the present study may also be extended to study the variation of bulk modulus with pressure in the case of nanomaterials. A simple calculation may give the pressure dependence of the bulk modulus for the nanomaterials used in the present study, but we have not computed its value, as there is no experimental data to compare to our results. Thus our model may also be used to study the variation of the bulk modulus with pressure for nanomaterials.

Finally, it is pertinent to mention that the present model is derived in such a way that it is independent of structure. For the nanomaterials, the zero pressure bulk modulus (B₀) differs significantly from their counter bulk-sized materials, and the present model requires B₀ as an input parameter. Therefore, taking B₀ corresponding to the bulk material, the present model works for the bulk material, while taking B₀ corresponding to their counter nano-sized material model works for the nanomaterial. In addition, our model, in its present form, is only valid within the phase-pressure stability range of the nanomaterial and therefore cannot be used to determine the phase transition.

4 Conclusion

In the present study, we developed a simple theory to predict the isothermal compression of nanomaterials by developing an EOS, which is a consequence of the fact that αB_T is a constant for nanomaterials. The present state equation requires only one input parameter. The results obtained are in good agreement with the experimental data, which demonstrates the legitimacy of the formulation developed.

Notes

Peer review under responsibility of Taibah University.