Three-dimensional morphological analysis of humeral heads

Abstract

Background Anatomy of the humeral head may be of importance for the kinematics of the shoulder joint. We therefore evaluated the three-dimensional morphology of humeral heads.

Material and methods We performed three-dimensional morphological analysis of the articular surfaces of 14 humeral heads in the proximal humeri of 7 cadavers. The articular surface was divided into 9 portions, which were in turn equally divided into 3 sections by an angle in supero-inferior and antero-posterior directions. Each portion of the articular surface was fitted to a sphere, and we calculated the radius of the curvature of each portion.

Results The mean radius of the superior portion was significantly greater than that of the central portion, and the mean radii of the anterior and posterior portions were significantly less than that of the central portion.

Interpretation Our findings lead us to believe that the morphology of the humeral head is of importance for the kinematics of the shoulder joint.

The morphology of the glenohumeral joint has been described in very few studies, but this information is essential for analysis of kinematics. Some studies (Soslowsky et al. 1992a, Boileau and Walch 1997) have shown the relationship between the humeral head and the glenoid as a pair of mating spherical surfaces. In kinematics studies (Veeger 2000, Kelkar et al. 2001), the glenohumeral joint has been evaluated as a ball and socket joint. In other studies (Sarrafian 1983, Iannotti et al. 1992), the humeral head was approximated as an ellipsoid rather than a sphere. There is no consensus as to whether the shape of the humeral head should be approximated as a sphere or an ellipsoid. Saha (1971) classified the glenohumeral articular surfaces into 3 types according to the contact patterns, but there has been no consensus to date as to the morphology of the glenohumeral surfaces.

In our previous study (Inui et al. 2001), in which we used reconstructed three-dimensional MR images, we found that the bony structure of the glenoid cavity was twisted anteriorly to posteriorly, and most glenoids had a deep concave shape at the caudal area and a flat shape at the cranial area. These findings suggest that precise evaluation of the humeral head has implications for kinematics of the shoulder joint. In the present study, we evaluated the three-dimensional morphology of cadaveric humeral heads using a precise digitized measuring device and a novel analysis method.

Material and methods

Specimen preparation

We obtained 14 proximal humeri from 7 cadavers fixed in formalin. We excluded humeral heads that had apparent abnormalities, deformities or cartilagious degeneration. The cadavers were of 3 women and 4 men, with a mean age of 72 (61–78) years. All specimens were excised at the proximal third of the humerus, and surrounding soft tissues were removed.

Three-dimensional measurement of the proximal humerus

We measured three-dimensional coordinates of the surface of the proximal third of the humerus using a Renishaw Cyclone three-dimensional measuring device (Mitsutoyo Co., Japan). This machine touches the subject with a spherical sensor fixed on the tip of its probe, and measures three-dimensional coordinates of surface points of the subject. In the preliminary study for determination of measurement error, we measured surface points on a sphere with a diameter of 25 mm using this device. The measurement error was less than 23.7 μm, which indicated a high accuracy.

All specimens were fixed on the inclined plane with strong industrial adhesive agent so that the articular surface of the humeral head faced the top and was firmly secured during mapping (Figure 1). The device allowed parallel slices to be measured at intervals of 0.3 mm on the articular surface of the humeral head, and at intervals of 1 mm on the surface of the humeral shaft.

Figure 1. The device used for three-dimensional morphological analysis.This is only a sample picture.This humerus is not a real one for measurement, but a dummy bone.All specimens were fixed so that the articular surfaces faced upwards, and they were measured at intervals of 0.3 mm on the articular surfaces and 1 mm at the shafts.

Morphological analysis of articular surfaces

Using three-dimensional visualization software (the Poly-Editor software program developed by the Division of Interdisciplinary Image Analysis, Osaka University Graduate School of Medicine), we accumulated data from the articular surface of the humeral head and the proximal part of the humeral shaft. The anatomical neck plane was defined as the edge of the articular surface. The data points of the articular surface were extracted (Figure 2).

Figure 2. (A) Definition of three-dimensional coordinate system of the humeral head (diagram shows a right-side specimen). The data points of the articular surface were extracted by the anatomical neck plane. The origin is defined as a center point of the whole articular surface. The x-axis is defined as a line passing through the origin and perpendicular to the anatomical neck plane. The y-axis is defined as a line passing through the origin which was perpendicular to the x-axis and the diaphyseal axis. The z-axis is perpendicular to x- and y-xes.

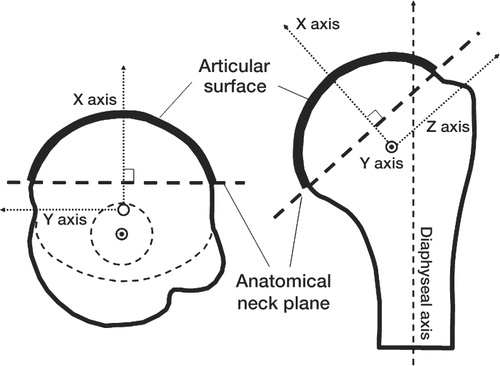
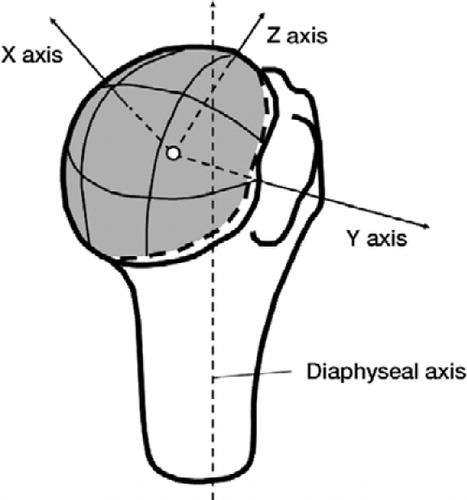
Figure 2. (B) The whole articular surface, which is shown in gray, consists of 9 portions, which have been equally divided into 3 sections by an angle in supero-inferior and antero-posterior directions.

The data points of the whole articular surface were fitted to a sphere, the radius and center of which were calculated using the least-squares method, which was defined from the numerical formula:

where R is the radius, xi, yi and zi are the coordinates of each data point, and C_x, C_y and C_z are the coordinates of the center of the sphere.

The data points of the humeral shaft were fitted to a cylinder, and the longitudinal axis was defined as the diaphyseal axis. We calculated the three-dimensional coordinate system of the articular surface by the position of the origin, the direction of the anatomical neck plane and the direction of the diaphyseal axis. The center was defined as the origin of the axis of coordinates. The x-axis was defined as a line passing through the origin and perpendicular to the anatomical neck plane. The y-axis was defined as a line passing through the origin which was perpendicular to the x-axis and the diaphyseal axis. The z-axis was perpendicular to the x- and y-axes (Figure 2).

The articular surfaces consisted of 9 portions, which were equally divided into 3 sections by an angle in the supero-inferior and antero-posterior directions (Figure 2B). Each portion of the articular surface was fitted to a sphere, and the radii of curvature in each portion were calculated. The ratio of mean radius between each portion and the whole articular surface was calculated to account for differences in physique among the specimens. We statistically compared the ratio in each portion to the ratio in the central portion.

To evaluate the sphericity of the data points of the whole articular surface, a deviation of the data points from a mathematical sphere was calculated as:

where Ri is the distance between the center point and each data point, and Rm is the radius of a mathematical sphere. The average number of data points for each portion of the articular surface was 5,800 (3,300–9,500), and the average number of data points for the whole articular surface was 56,000 (42,000–68,000).

Statistics

We used unpaired t-test to compare the radius of curvature between men and women. We used one-way ANOVA and post-hoc test (Fisher’s LSD) to compare the ratio of mean radial length between each portion and the central portion. All statistical testing was performed using StatView for Windows version 5.0 (SAS Institute Inc., Cary, NC), with the level of significance set at p < 0.05.

Results

The average radius of the whole articular surface was 24.4 (SD 0.8) mm for men and 20.8 (SD 1.4) mm for women. The radius of male humeral heads was greater than that of female humeral heads (p < 0.001 by unpaired t-test). The average radii of the articular surfaces in each portion are shown in Table 1, and the average ratios between the radius of each portion and that of the whole surface are shown in Table 2.

Table 1.  The average radii (mm) of curvature at each portion of the articular surfaces for men (upper row; n = 8) and women (lower row; n = 6)

Anterior	Superior			Posterior
	26.4 ± 2.3	26.7 ± 1.5	22.0 ± 1.4
	22.0 ± 3.4	23.2 ± 3.0	19.6 ± 1.2
	22.6 ± 1.3	24.3 ± 1.3	22.3 ± 1.4
	18.6 ± 1.2	21.1 ± 1.4	18.6 ± 0.6
	23.8 ± 1.0	23.6 ± 1.4	23.6 ± 1.4
	19.8 ± 1.2	21.2 ± 1.8	19.1 ± 1.8
	Inferior

Table 2.  Comparison of ratios of average radii between the central portion and the other portions (n = 14), (SD)

Anterior	Superior			Posterior
	1.08 (0.13)	1.09 (0.06)	0.93 (0.05)
	p = 0.002	p < 0.001	p = 0.003
	0.93 (0.05)	1.00 (0.03)	0.91 (0.05)
	p = 0.02		p < 0.001
	0.97 (0.03)	0.98 (0.05)	0.94 (0.05)
	p = 0.1	p = 0.4	p = 0.01
	Inferior

The ratios of the superior and anterosuperior portions of the articular surfaces were greater than that of the central portion. This indicates that the mid-superior and anterosuperior portions of the articular surface were flatter than the central portion. The mean radii of the midsuperior and anterosuperior portions were greater than that of the central portion, by 2.1 (SD 1.6) mm and 1.6 (SD 2.8) mm.

The ratios of mean radius of the anterior, posterosuperior, posterior and posteroinferior portions of the articular surfaces were less than that of the central portion. The mean radii of the anterior, posterosuperior, posterior and posteroinferior portions were less than that of the central portion, by 1.7 (SD 1.0), 1.7 (SD 1.1), 2.2 (SD 1.6) and 1.4 (SD 1.4) mm.

The average deviation of data points from a mathematical sphere, which is sphericity, was 0.17 (SD 0.05) mm.

Discussion

Iannotti et al. (1992) measured the radii of curvature of humeral heads and glenoid articular surfaces of 96 cadaveric shoulders and 44 normal subjects, in the coronal and axial planes. They reported that the radii of curvature of humeral heads were approximately 2 mm less in the axial plane than in the coronal plane. They also reported that the radii of curvature of the glenoids, measured in the coronal plane, were 2.3 mm greater than those of the humeral heads. In addition, Sarrafian (1983) reported that the average radii in the coronal and axial planes were 25 mm and 22 mm. We found that the average radii in the anterior and posterior portions of the surfaces were 2 mm less than that of the central portion. The average radii of the anterosuperior and midsuperior portions were 2 mm greater than that of the central portion. Thus, our findings are consistent with those of Iannotti et al. (1992) and Sarrafian (1983).

Soslowsky et al. (1992a) and Boileau and Walch (1997) evaluated the three-dimensional morphology of the joint cartilage of humeral heads, and concluded that the surface could be approximated as a sphere. However, in our study it was not approximated as a perfect sphere. This discrepancy appears to be the result of differences in the methods used for analysis. In the 2 previous reports, all three-dimensional data from the joint cartilage were fitted to a single sphere. To verify the sphericity of the cartilage surfaces, Boileau and Walch (1997) calculated the difference between the diameters of the outer and inner mathematical spheres in which all digitized points were contained. They reported that the difference between the 2 extreme diameters was less than 1 mm in 9 out of every 10 specimens. The difference between the 2 extreme radii of our surface data, using the same method, was 1.07 (range 0.60–1.49; SD 0.29) mm. These results are consistent with those of Boileau and Walch (1997). The slight difference may be due to the details of digitizing measurements of the articular surfaces. In the study by Boileau and Walch (1997), the surface of the proximal part of the humerus was measured at intervals of 5 mm on parallel slices perpendicular to the diaphyseal axis. The number of data points they obtained for the whole Inferior humerus was over 1,200, whereas in our study, the number of data points obtained for the articular surface was 56,000 on average. In a computed tomographic study with a method similar to that of Boileau and Walch (1997), Robertson et al. (2000) found that the humeral head was not a perfect sphere; the radius of curvature in the superior portion was less than that of the anterior portion (but they did not provide detailed data).

Soslowsky et al. (1992a) calculated the average radius and standard deviation of a mathematical sphere, which is sphericity. They calculated that the sphericity of their data from humeral heads was 0.17 (SD 0.04) mm, which was less than 1% of the radius of the humeral heads. The sphericity of our data was 0.17 (SD 0.05) mm, however, which is similar to the results of Soslowsky et al. (1992a). This indicates that the difference between their conclusions and ours is not due to difference in data or subjects, but rather to the methods used for analysis. We attempted to clarify the differences in radii in each portion by dividing the surface into 9 portions and analyzing the radius at each portion by fitting spheres to them.

We considered the possibility that the average age of the cadavers (72 years) was too high for evaluation of the surfaces of the joint cartilage. However, Meachim (1971) and Petersson (1983) reported that age had no significant effect on the thickness of the cartilage of humeral heads. Soslowsky et al. (1992b), Warner et al. (1998) and Nobuhara (2001) recently analyzed the articular contact areas of the glenohumeral joint using cadavers. They demonstrated that the inferior portion of humeral head made contact with the glenoid in the hanging position and the superior portion made contact in the maximum abduction, and that the contact area of the glenohumeral joint increased during abduction motion. Although we did not analyze the morphology of the mating glenoid, we speculated on the influence of the morphology of the humeral head on the contact area with the glenoid. Considering our own results and those of others, the greater radius of the superior portion of the humeral head may contribute to increasing the contact area in maximum abduction. On the other hand, the smaller radii of the anterior and posterior portions may contribute to reducing the contact area during the internal and external rotation. The standard shapes of the humeral head and glenoid prosthetic components are spherical. Our findings may contribute to other designs of total shoulder prostheses.

The authors wish to thank Mr. A. Miyata and Mr. Y. Kawai (Nakashima Medical Division of Nakashima Propeller Co. Ltd., Japan) for technical support. We are indebted to Professor Tamura of the Division of Interdisciplinary Image Analysis, Osaka University Graduate School of Medicine, Osaka, for using the Poly-Editor software program.