Encyclopedia of Knot Theory

I came to the area of knot theory through an REU (Research Experience for Undergraduates) program on “The Colorability of Knots” with Professor Thomas Mattman at my undergraduate institution, California State University, Chico. My enjoyment of the visual aspects of mathematics expanded when I was introduced to the area of DNA topology by Mariel Vázquez and Isabel Darcy at San Francisco State University and the University of Iowa, respectively. While much of my recent research has been in the area of network theory applied to social and biological questions, I have always enjoyed learning more about the knots and their applications.

Many books have been written about knot theory that researchers can turn to in order to learn about the field, but The Knot Book, written by Colin Adams [1] has been my preferred text ever since I read it during my REU. Since then, I have been exposed to books such as Knots and Links by Dale Rolfsen [5], Knots and Links by Peter Cromwell [4], Knots by Gerhard Burde, Heiner Zieschang, and Michael Heusener [3], and DNA Topology by Andrew Bates and Anthony Maxwell [2], all of which I recommend to students to introduce them to the beauty of knot theory and show them a wide range of applications. I always hope that these books will become a foundation for my students to dive deeper into different aspects of the field. The book I am reviewing here, Encyclopedia of Knot Theory, is a great addition to the collection of sources that can entice an undergraduate to explore topics in the field. It also repeatedly poses the question, “What can be added to this story?” by including articles with open questions, thus giving students and researchers the opportunity to investigate new connections and make their own contributions to this exciting field.

Published in December 2020 by Chapman and Hall/CRC Press, the Encyclopedia begins with an introduction to the history of knot theory authored by Lewis Ludwig. This chapter provides a mathematical definition of knots along with its historical motivation. The author describes the origins of the field in terms of understanding atoms in ether, which led to a desire to enumerate the different kinds of knots. Of course, in order to count knots we need to be able to distinguish them from each other, and various methods of achieving this are described throughout the text, starting right away with the concept of Reidemeister moves. The second section focuses on different representations of knots, including 2-dimensional diagrams, numerical codes, and artistic representations. We also see that it is sometimes better to study a knot by instead looking at properties of its complement, defined as the object that is left behind when it is removed from space.

There are so many paths that one can take when discovering the richness of the topological objects seen in knot theory. The 953-page Encyclopedia is composed of 15 sections that total 91 chapters written by highly accomplished researchers, providing a great resource for showing these many areas of the field. In this review, I will explore three topics, focusing on parts of this book that lead researchers down these paths. I will first discuss the sections on virtual knots, then the chapters that focus on categorification, and finally end with my area of research, applications of knot theory to biology.

Virtual knots may be the most well-known object in the family of knotlike objects that make up the seventh section of the Encyclopedia. To describe these objects and their invariants requires a little background. In particular, one way of representing knots is through what has become known as the “Gauss code.” A Gauss code is a sequence of numbers obtained by first enumerating the crossings of a knot diagram and then recording the order in which these values are encountered as one traverses the knot. Each value appears twice in a Gauss code – once as an overcrossing strand and once as an undercrossing strand. Not every sequence of pairs of integers, however, can be realized as the Gauss code for a knot. This led Louis Kauffman to define the concept of a “virtual knot” in 1999. By allowing the addition of “virtual crossings” to classical crossings, one can realize any sequence of pairs of integers as the Gauss code for a virtual knot. (See Figure 1 for an example).

Fig. 1 On the left is the trefoil knot drawn using the Gauss code O1U2O3U1O2U3, as you can see by starting at the indicated point and following the knot along, writing down the crossings in the order you encounter them and whether you cross over or under until you return to the starting point. On the right we draw a knot diagram with the Gauss code O1U2U1O2. One must then introduce an extra “virtual crossing” to join the end back up to the starting point.

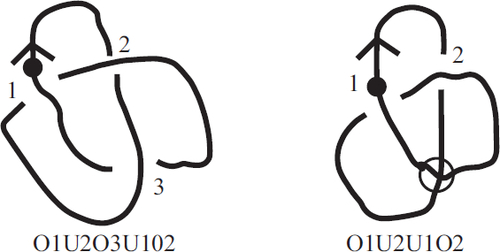
A chapter written by Kauffman himself provides the definition and construction of virtual knots, while also introducing a diagrammatic approach that leads to several interesting questions. Subsequent chapters go on to interpret virtual knot theory as the study of the embeddings of curves in thickened surfaces of arbitrary genus. Together with the classical knot crossings and diagrams, adding virtual crossings allows knot theorists to extend many classical knot ideas to more general ones, specifically by looking at the virtual Reidemeister moves.

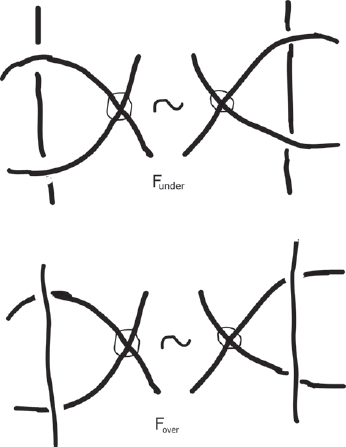
The rest of the section considers the relationship between virtual knots and surfaces and forbidden moves (Figure 2). By including the ability to pass a strand under a virtual crossing, F_under , one can describe a knot quandle of a virtual knot. And if one decides to include the other forbidden move, F_over , one obtains a welded knot. This style of mathematics has always intrigued me! Questions like “What happens if we allow this to happen?” or “What happens if we relax this hypothesis or condition?” are ideas that we start with as children really, taking things apart, seeing how they work, and looking at different ways we can put them back together. Virtual knot theory has allowed topologists to take known results in classical knot theory and ask questions about generalizations. We have obtained some really interesting answers, many of which are included in this section. The authors go on to discuss new topological objects, such as virtual braids, biquandles, pseudoknots, and flat knots. One of those areas leads to my next topic: Categorification.

Fig. 2 Allowing both forbidden moves, F_under or F_over , would render the theory of virtual knots trivial, since every two virtual knot diagrams are equivalent by a sequence of virtual and forbidden moves.

While numerical invariants can be very useful in distinguishing knots, it turns out that one can do even better by defining polynomial invariants. The most studied of these polynomials include the Jones polynomials, Kauffman polynomials, Conway polynomials and the twisted Alexander polynomials. In each case, one defines a polynomial that encodes certain information about a knot by defining how the polynomial changes when one changes certain features at a crossing in the knot diagram. More precisely, one defines skein relations, which are specific ways of smoothing out the crossings of a knot, and looks at the connection between these polynomials and associated “skein modules.” These are all defined and written about in such a way that the reader can learn the history and the applications of each important development. These polynomials are often one of the first “higher structure” invariants learned by budding knot theorists. When I first moved away from learning about numerical invariants, such as the minimum crossing number and the unknotting number, and began looking at polynomial invariants, I was in awe of the idea that an algebraic item could hold so much information about a topological object. I often tell my students that a lot of knot theory can be done with high school algebra skills and a good pencil, thanks to these discoveries and inventions.

The tenth section of the Encyclopedia is entitled “Quantum Link Invariants” and starts with a chapter on the history of these objects, which generalize the idea of polynomial invariants even further. This discussion acts as a nice bridge to a section on homological invariants of knots, which includes well-written expositions on two of the newest knot invariants, Khovanov homology and knot Floer homology, both of which can be viewed as the categorification of polynomial invariants. Radmila Sazdanovic shares with the reader the story of how, in the late 1990s, Mikhail Khovanov introduced the mathematics community to categorification by discovering a way to use skein relations to construct new and powerful knot invariants. He was able to replace a known polynomial invariant with a family of chain complexes so that the coefficients of the original polynomial are the Euler characteristics of these complexes. Similarly, Khovanov homology, denoted $(H(L,R))$, is defined as the categorification of the Jones polynomial. This theory associates a bigraded homology R-module $H(L;R)=\underset{i,j\in \mathbb{Z}}{\oplus }{H}^{i,j}(L;R)$ to the link L. These ideas have led to many new results, including the discovery of Khovanov homology of virtual knots. In his chapter, Alexander Shumakovitch shares the construction of this homology and provides insights into its many properties.

Building on these ideas, knot Floer homology was constructed by Peter Ozsváth and Zoltán Szabó, and independently by Jacob Rasmussen. Often denoted HFK, it is the homology of a bigraded complex $(C,\partial )$ with Maslov grading m and Alexander grading $a:\mathit{HFK}=\underset{m,a\in \mathbb{Z}}{\oplus }HF{K}_m(K,a).$ This new invariant can be viewed as the categorification of the Alexander polynomial. András Stipsicz provides a short but thorough survey of knot Floer homology and its combinatorial version using grid diagrams. When I first started thinking about knot Floer homology, the combinatorial version was my entry point. For me it provided a helpful visualization of the calculation for the homology of various knots. This allowed me to present the theory as well as the calculation to different mathematical audiences.

I was first exposed to these topics in 2009 while at a knot theory graduate summer school hosted by the International Center for Theoretical Physics in Trieste, Italy. One of the lectures was by Peter Ozsváth. The first time I saw this development, I was in awe. The idea of adding more algebraic structure to the area of knot invariants was exciting to me, as I had only been focusing on polynomials at the time. Over the last decade, there has been a lot of growth in this area with discoveries about these homologies and various topological structures. These structures include tangles, braids, quasi-alternating knots, Legendrian knots, graphs, virtual knots, pointed links and many others. There have also been extensions of these categorifications such as bordered Floer homology and sutured Floer homology. Each of these results has brought diverse voices and ideas to the area, many of which are covered throughout the Encyclopedia.

The last two sections of the text concern topics in physical knot theory as well as a number of applications. While many mathematicians view knots as abstract three-dimensional objects without any thickness, physical knot theorists do work that takes into account the geometric and topological characteristics of knots leading to ideas like rope length, rope thickness and knot energies. As one example, in the first chapter of this section author Colin Adams defines the stick number of a knot. Also known as the edge number or polygon number, this value describes the minimum number of sticks, glued end to end, needed to construct the knot diagram in question. The section continues by illustrating random knots and the multiple ways for representing them, including some we have seen earlier in the book, such as Gauss codes, as well as a few new ones, such as Dowker-Thistlewaite codes and petal diagrams. Ideas such as generating random knots through closure techniques, spatial embeddings, and folded ribbons are also included to round out this thoughtful analysis of the physical properties of knots.

After exploring these physical representations of knots, one naturally starts to ponder applications to modeling various physical phenomena, and the final section of the text goes deeper into these ideas. The relationship between knots and biochemistry is a long one, although it was only formalized in the 1980s. It was the discovery by Watson and Crick, using the work of Rosalind Franklin, of the structure of DNA that was essential to the development of this story. Their work established a functional importance of the structure of DNA and motivated the study of this structure through topological objects we have been discussing such as knots, links, and tangles. Later researchers showed the ways that classical knot and tangle operations can be applied to model the interactions between proteins and DNA. (For those readers unfamiliar with tangles, the Encyclopedia contains a wonderful introduction to the topic by Emille Davie Lawrence.) Using knots to model the structure and behavior of DNA further inspired researchers and scientists to apply mathematical methods to study enzymes that may have an impact on their topology and geometry.

This section starts with an article authored by my advisor Isabel Darcy discussing the development of DNA topology, an area of research that focuses on the importance of these shapes to biological processes. There is also information about the use of Topoisomerase, a protein that can efficiently cut and glue DNA strands, changing their topology. A second family of proteins known as Recombinase also change the topology of DNA and sometimes even impact the number of link components present. There are many new developments in this area, and researchers are looking closer at the structure of RNA, the interactions between RNA and DNA, and interactions with proteins that do not change the topology of DNA yet still have interesting binding properties.

In one chapter, Stefan Friedl defines spatial graphs and provides some interesting results about how to use this theory to distinguish both topological isomers and chemical stereoisomers. Another chapter explores connections between intrinsically knotted or linked graphs, chirality in S³, and topological symmetry groups. The section also includes a fascinating exposition of pseudoknots, a concept motivated in the 1980’s by pictures of knots in DNA where some crossing information is unidentifiable.

In the next chapter, Helen Wong takes on the task of describing protein knots and links. Because they are often not as flexible as DNA, the folding of the protein backbones often leads to topologically complex features. This section describes the use of topological nonplanar graphs to support visualization of knotted proteins. In the final chapter of the book, Erica Flapan writes about molecular knots and links that can be created in laboratory experiments. She discusses various strategies that organic chemists have employed for synthesizing these molecules, and some possibilities for what the future holds in this very active area of research. This section is a fitting note that brings us back full circle to the idea that first motivated the study of knots: knotted atoms.

The Encyclopedia of Knot Theory is close to 1000 pages, and every section, article, paragraph, and sentence inspires the reader to want to learn more knot theory. A wonderful attribute of this text is the reference section at the end of each article as opposed to the end of the book. This allows readers to highlight different sources that will allow them to dive deeper into the topic of that section. At the same time, while the text includes an index of terms at the end, I believe that a glossary would have also benefited readers as a reference for reminding them of certain words or ideas. And while it is nearly impossible to include discussions of every branch of the knot theory tree, the editors made a great choice to focus on current topics showing how the area is still a living subject. That said, there are many more topics that are not included. These omissions, along with many new results that are published each year, offer an opportunity for future volumes of this encyclopedia to include other authors or editors.

As a knot theory enthusiast, I truly enjoyed reading about topics I was more familiar with while also exploring topics that were new to me. As an educator, I am excited to share this book with my students and encourage them to read more articles on the topics. Some of the articles in the book include thoughtful open questions for researchers in the field to enjoy, while also providing background for anyone new to knot theory research to use as a foundation. All in all, I loved this text.

Dept of Mathematics & Statistics, Smith College, Burton Hall 115, Northampton MA 01063
[email protected]