What Properties Might Statistical Inferences Reasonably be Expected to Have?—Crisis and Resolution in Statistical Inference

ABSTRACT

There is a crisis in the foundations of statistical inference. I believe that this crisis will eventually be resolved by regarding the subjective Bayesian paradigm as ideal in principle but often using standard procedures which are not subjective Bayesian for well-defined standard circumstances. As a step toward this resolution, this article looks at the question of what properties statistical inferences might reasonably be expected to have and argues that the use of p-values should be restricted to pure significance testing. The value judgments presented are supported by a range of examples.

KEYWORDS:

• Bayesian inference
• Neyman–Pearson hypothesis testing
• Objectivity
• p-Value

1. Introduction

Within the statistical research community, the Bayesian, Frequentist, and Likelihood approaches to statistical inference all have supporters and critics. They have been reviewed by, for instance, Barnett (1962), Cox and Hinkley (1974), and Welsh (1996). The first part of the title of this article is a reaction to Welsh (1996, p. 393), where he writes “We do need to maintain a perspective about what can reasonably be expected to be achieved” but fails to give his personal perspective. This article gives my perspective on the properties that inferences can be expected to have.

For about a hundred years, the foundations of statistical inference have been in what Kuhn (1970) would call a crisis, with supporters of the different paradigms disagreeing about what questions are important. The second part of the title of this article indicates my intention to contribute to resolution of this crisis.

Within the research communities that use applied statistics, the Frequentist approach is dominant. Papers published in areas such as psychology, medicine, epidemiology, pharmacology, agriculture, and environmental science often use p-values as the basis for claims about “statistical significance,” but seldom include the measures of reliability advocated by the Bayesian and Likelihood approaches. Hoenig and Heisey (2001, p. 5) wrote “the real world of data analysis is for the most part solidly frequentist and will remain so into the foreseeable future.”

Concern about p-values and the foundations of statistical inference is widespread. See, for instance, Nuzzo (2014) and Wasserstein and Lazar (2016). Here I concentrate on the questions which I consider to be most relevant to the choice between paradigms. Most of the sections of this article deal with one question each, sometimes with subsections dealing with closely related questions. Mathematical rigor is not a priority.

2. Is Quoted Confidence Consistent With the Rate of Subsequent Contradiction?

The following example discusses a conclusion of great practical importance which was reported to be “statistically significant” but subsequently found not to be “statistically significant.”

Example 1.

The data from Rossouw et al. (2002, Table 2) shown in Table 1

Table 1. Results of HRT trial at the time of its termination (2002 version of data).

	CHD	No CHD	Total
HRT	164	8342	8506
Placebo	122	7980	8102
Total	286	16,322	16,608

arose from a longitudinal study of the effects of hormone replacement therapy (HRT). Fisher’s exact test on this 2 × 2 table gives a two-tailed p-value of 0.0369. This is less than 0.05, so the data were considered to provide “statistically significant” evidence that HRT increases the rate of coronary heart disease (CHD). The finding was worldwide news. There was also concern that HRT increases the risk of invasive breast cancer, but we will ignore this. The study was terminated on the grounds that it would be unethical to further expose participants to the apparently increased risk of CHD.

Table 2. Final results from HRT trial (2003 version of data).

	CHD	No CHD	Total
HRT	188	8318	8506
Placebo	147	7955	8102
Total	335	16,273	16,608

Some additional data arrived after the decision were made to terminate the study, as discussed in Manson et al. (2003). CHD was observed in 24 additional subjects on HRT and 25 additional subjects on placebo. The final (2003) version of the data is shown in Table 2. For this version of the data, the two-tailed p-value is 0.0771, so the evidence that HRT increases the rate of CHD was no longer “statistically significant.” For a review of the medical and study design issues with the benefit of hindsight, see Langer, Manson, and Allison (2012) and Shapiro et al. (2011).

Ioannidis (2005b) reviewed the reproducibility of apparently reliable medical research results. He looked at 115 published articles which all had more than 1000 citations. Of these, 45 articles made efficacy claims. For 14 of these articles (31%), subsequent studies that were either larger or better controlled either contradicted the findings (7 articles) or found that the effects were weaker than claimed (7 articles); for 20 articles (44%), subsequent studies found similar effects and were regarded as having replicated the results; and the claims of 11 articles (24%) remained largely unchallenged. He considered that the overall reproducibility of research findings was poor compared to the reproducibility which he expected based on the p-values.

Motulsky^{Table 1, Table 2}(2014) mentioned two other reviews which found smaller proportions of studies to be reproducible. Young and Karr (2011) also discussed this problem. Collins and Tabak (2014) expressed several concerns about the poor reproducibility of biomedical research. Statistical analysis was not their primary focus, but they did state “Some irreproducible reports are probably the result of coincidental findings that happen to reach statistical significance, coupled with publication bias” and “there remains a troubling frequency of published reports that claim a significant result, but fail to be reproducible.”

In statistical theory, we seldom study the probability that a statistical conclusion will be subsequently contradicted because it varies with the amount of data in the subsequent trials. Instead we make probability statements involving the true values of parameters. This amounts to the case where a subsequent trial is of infinite size.

The next example concerns a single observation on a normal distribution with unit variance. This abstract example is important because many practical situations have test statistics which are approximately normally distributed. For instance, rather than using Fisher’s exact test for Example 1, we could have used the normal approximation to the binomial distribution. Let X₁ denote the number of women with CHD out of n₁ on HRT and X₂ be the number with CHD out of n₂ not on HRT. The observed proportions p₁ = X₁/n₁ and p₂ = X₂/n₂ are independently distributed with approximate variances p(1 − p)/n₁ and p(1 − p)/n₂, respectively, where p = (X₁ + X₂)/(n₁ + n₂). The statistic $$Z=\frac{p_1-p_2}{\sqrt{p(1-p)(1/n_1+1/n_2)}}$$is approximately normally distributed with unit variance. Its mean is zero if the true proportions are equal.

Example 2.

Suppose that a single observation, X, is normally distributed with unknown mean, μ, and unit standard deviation. The null hypothesis, H₀, that μ = 0 can be rejected if |X| > 1.96 with p-value 0.05. The interval (X − 1.96, X + 1.96) is a 95% Neyman confidence interval for μ.

Consider a Bayesian prior distribution which gives probability 0.8 to H₀ and gives the remaining 0.2 prior probability to an $\mathcal{N}(0.5,2^2)$ distribution for μ. Posterior distributions can be readily calculated. For instance, if X = 2 then prior times likelihood is 0.04319 for H₀ and 0.02849 for $\mu \sim \mathcal{N}(1.7,0.{8944}^2)$. Normalizing, the posterior distribution has a component with probability 0.6025 for H₀ and a component with probability 0.3975 that $\mu \sim \mathcal{N}(1.7,0.{8944}^2)$.

The solid line in Figure 1

Figure 1. Posterior probability that a 95% Neyman confidence interval covers the true value of μ for two different prior distributions.

shows the posterior probability given X = x that μ ∈ (x − 1.96, x + 1.96). Using the law of total probability, this may be written as $$\begin{array}{ccc}& & \text{Pr}[X-1.96<\mu <X+1.96|X=x,\mu =0]\hfill \\ & & \times \text{Pr}[\mu =0|X=x]+\hfill \\ & & \text{Pr}[X-1.96<\mu <X+1.96|X=x,\mu \ne 0]\hfill \\ & & \times \text{Pr}[\mu \ne 0|X=x].\hfill \end{array}$$The term  Pr[X − 1.96 < μ < X + 1.96|X = x, μ = 0] is 1 if − 1.96 < x < 1.96 and 0 otherwise, causing the jumps in the posterior visible in Figure 1.

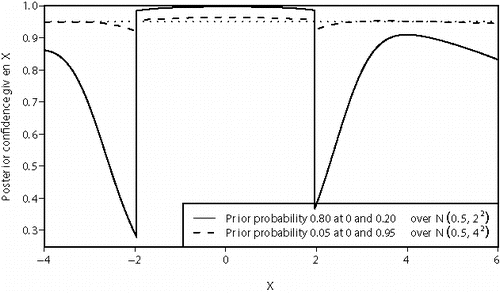
The definition of the p-value tells us that  Pr[μ ∈ (X − 1.96, X + 1.96)|μ = 0] = 0.95. This is a statement about the probability distribution of X under H₀. It is mathematically consistent with Figure 1 in that the posterior probability averaged over the distribution of X given H₀ is 0.95. However, the posterior probabilities that μ ∈ (x − 1.96, x + 1.96) for x values just outside ( − 1.96, 1.96) are less than 50%. The posterior probabilities describe our subjective beliefs after seeing X (a subjective answer to the right question) whereas the p-value provides an objective answer to a question which has only a very tenuous link to what we should believe after seeing X (an objective answer to the wrong question).

The dashed line in Figure 1 shows the posterior probability that μ ∈ (x − 1.96, x + 1.96) for a prior distribution with prior probability 0.05 at μ = 0 and probability 0.95 that $\mu \sim \mathcal{N}(0.5,4^2)$. For this prior, the posterior probability is much closer to the nominal 0.95. In general, if a prior distribution has very small prior probability that μ = 0 and elsewhere has a prior density that is close to uniform then the posterior probability that the 95% Neyman confidence interval covers μ will be close to 0.95.

For the effect of hormone replacement therapy on the rate of coronary heart disease, a Bayesian statistician might have used a prior distribution for the logarithm of the relative risk with a substantial probability at zero and having a nonzero mean, since any effect was more likely to be deleterious than advantageous. Prior distributions with substantial probability that the true effect is precisely zero seem likely to be useful in fields like modern biomedical research where, as Ioannidis (2005a, p. 700) suggested, the prestudy probabilities for individual effects being nonzero are very small.

Personal perspective. The rate of subsequent contradiction of medical trials has been found to be higher than one might be mislead to believe on the basis of the p-values. The rate is broadly consistent with Bayesian prior distributions which give substantial prior probability to the null hypothesis.

3. What Questions Should Statistical Inferences Answer?

An example will help distinguish the three questions of Royall (1997).

1.	What evidence is there?
2.	What should I believe?
3.	What should I do?

Example 3.

Suppose that a positive result for a blood test is 25 times more likely if a person has condition A than otherwise. The strength of evidence provided by a positive result could be summarized by the likelihood ratio, 25. This answers Royall’s first question.

Suppose the proportion of people having condition A is 1 in 10,000. Then the probability that a person testing positive has condition A is, by Bayes’s rule, $$1\times 25/(1\times 25+9999\times 1)=25/10,024\approx 0.0025.$$This answers Royall’s second question. It is unlikely that the person has condition A; though much less unlikely than before the positive test result was observed.

To answer Royall’s third question, expected utilities should be calculated from the point of view of the person being treated and the action of highest expected utility should be chosen. A standard treatment for condition A which is cheap, is very effective, and has no side-effects might be the best action. Additional testing might be the best action given other utilities.

Statistical inference in scientific articles is generally concerned with the first of Royall’s questions. However, it is useful to distinguish between the strength of evidence provided by the results being newly reported and the strength of evidence provided by all available results. Lau et al. (1992) listed many trials of the benefit of giving streptokinase after heart attacks. A meta-analysis after eight trials would have shown that the efficacy of streptokinase was statistically significant, but its efficacy was not regarded as reliably demonstrated until many years later. I believe that researchers should feel some obligation to assess the totality of relevant data, even if only to make some informal remarks.

The second and third of Royall’s questions both include the word “I,” implying that the answers are expected to be subjective; while the first question has no personal pronoun, implying that there is an objective measure of the amount of evidence. The entire likelihood function always summarizes the evidence, so the likelihood ratio is an objective measure of the amount of evidence for testing between two simple hypotheses, but no scalar measure of the strength of evidence is independent of the Bayesian prior for more complicated situations.

3.1. What Questions do p-Values Answer?

Suppose that large values of a statistic S(X) would be rare if a null hypothesis H₀ were true. We observe X = x. The probability  Pr[S(X) > S(x)∣H₀] of getting the observed or a more extreme result is called a p-value. Fisher (1970) argued that if the p-value is very small, say 0.01, then either a rare event has occurred or H₀ is false; and so the hypothesis H₀ may be rejected.

p-Values make no reference to alternative hypotheses. Cox and Hinkley (1974, chap. 3) described situations where null hypotheses are considered without considering explicit alternatives as “pure significance tests.” Cox (2006) used the term “simple significance test.” I prefer the term “pure significance test” because it suggests that the difference from tests where alternative hypotheses are specified is qualitative rather than a difference in complexity. The earliest examples of use of p-values are all pure significance tests. The following three seem to have been the most influential.

Example 4.

Arbuthnott (1711) is often cited as the earliest example of the p-value approach to statistical inference. It showed that numbers of male and female children christened in London from 1629 to 1710 were not consistent with the null hypothesis that the probabilities of male and female children are each 1/2. The aspect of the data which was highlighted as being extremely unlikely under the null hypothesis is that the number of males exceeded the number of females for each of the 82 years. The probability of this event was calculated as ${\left(\frac{1}{2}\right)}^{82}=1/(4.836\times {10}^{24})$, so the null hypothesis was rejected.

Note that Hacking (1965, p. 76) cautioned his readers: “It is conceivable that this dilettante, amateur probabilist, physician to Queen Anne, buffoon, friend and fellow satirist of Swift, had tongue in cheek.”

Example 5.

Another early example of the p-value approach was highlighted by Todhunter (1949, paragraphs 394–397). In a treatise about planetary orbits in 1734, Daniel Bernoulli considered available data on the orbits of the six then-known planets. For each of three measures of the range of the orientations of the orbits, he found that the event of the measure being as small or smaller than the value actually observed had very small probability under the hypothesis of uniform distribution of orbits. He concluded that the hypothesis of uniform distribution of orbits was untenable, and he stated this conclusion without reference to any alternative hypothesis.

Todhunter (1949) suggested that the calculations should have been based on the locations of orbital poles. A modern version of a calculation like that of Daniel Bernoulli is as follows. For a sphere of radius r, the area of the curved surface of a spherical cap (portion of a sphere on one side of a plane) of angular radius θ is $2\pi r^2(1-cos\theta )=4\pi r^2{sin}^2\left(\frac{1}{2}\theta \right)$. This is ${sin}^2\left(\frac{1}{2}\theta \right)$ of the surface of the sphere. Relative to the celestial pole of the sun’s rotation, the largest angle to the orbital poles for the six planets is 7°30’. Hence, the orbital poles are all within a spherical cap which has area 0.004278 of the surface of the sphere. The probability of this for six orbital poles assuming that they are independently randomly distributed over the sphere is 0.004278⁶ = 6.1 × 10^{− 15}. This number can be regarded as a p-value for testing the null hypothesis that orbital poles are uniformly distributed.

Bernouilli used three different measures. p-Values for all three measures were very much smaller than 0.05 (which is nowadays commonly used as a cut-off for statistical significance), so his use of p-values was very conservative compared to modern usage.

Example 6.

Another historically influential use of the p-value approach was by Pearson (1900) for the now-commonly used χ² goodness-of-fit test. One of the examples in that article concerned 26,306 tosses of 12 dice. The number of dice showing “5” or “6” can be from 0 to 12. The observed frequencies of the 13 possible outcomes were compared to the theoretical frequencies, m, calculated assuming that the probability of “5” or “6” was 1/3. Deviations, e, of the observed frequencies from the theoretical frequencies were also computed as shown in Table 3

Table 3. Frequencies of results from 26,306 throws of 12 dice; and calculations associated with a χ² goodness-of-fit test.

Number of dice	Observed	Theoretical	Deviation
with “5” or “6”	frequency	frequency (m)	(e)
0	185	203	− 18
1	1149	1217	− 68
2	3265	3345	− 80
3	5475	5576	− 101
4	6114	6273	− 159
5	5194	5018	+ 176
6	3067	2927	+ 140
7	1331	1254	+ 77
8	403	392	+ 11
9	105	87	+ 18
10	14	13	+ 1
11	4	1	+ 3
12	0	0	0

.

A χ² goodness-of-fit statistic was calculated as the sum of e²/m. The numerical value is 43.87. Pearson (1900) argued that if the null hypothesis were true then the distribution of this number would have approximately a χ² distribution with 13 degrees of freedom. He computed the probability of a value of 43.87 or larger as 0.000016; so he concluded that the data were not consistent with the null hypothesis. His argument that a small p-value justifies rejection of a null hypothesis is essentially the same as is commonly used today, though Fisher (1970, p. 64) and modern practice would combine the last three rows of this table so that theoretical frequencies exceed 5.

p-Values are difficult to criticize for pure significance testing because performance of statistical procedures under alternative hypotheses is necessarily irrelevant and measures of evidence based on likelihood and Bayes factors are not available as alternatives.

The many editions of Fisher (1970) were very influential in popularizing use of p-values for situations where alternative hypotheses are specified (e.g., testing means, differences of means and regression coefficients). However, no argument was given to justify extending use of p-values from pure significance tests to situations where alternative hypotheses are specified. One superficially persuasive argument is that p-values are valid for pure significance tests so they remain valid when situations are specified in greater detail. However, if we replace the word “valid” with “the best available techniques,” then this argument seems less persuasive because the second sets of available techniques are much larger.

For situations where alternative hypotheses are specified, most criticisms of p-values amount to saying that p-values do not answer Royall’s first question. Dempster (1964) introduced the terms “predictive” and “postdictive” to distinguish between probability statements made before data are observed and statements made after the data are observed. He argued that p-value statements are valid and objective as predictive statements, but have no validity as postdictive probability statements about the values of parameters or about whether hypotheses are true, although they might perhaps be interpreted as indicating a measure of surprise. Berkson (1942, p. 327) suggested that assessment of strength of evidence should not be based solely on the probability of an event under the null hypothesis because in his opinion “the definitive question is not ‘Is this an event which would be rare if H₀ is true?’ but ‘Is there an alternative hypothesis under which the event would be relatively frequent?’ ”

Frequentist statisticians have sometimes responded to criticisms of p-values by implying that p-values are not intended as a measure of strength of evidence but are only useful for answering questions of the convoluted form “What was the probability which applied before X was observed to be x that S(X) > S(x) given H₀?” For instance, Goodman (2008), Klein (2004, pp. 63–70), and Lambdin (2012) gave lists of common misconceptions and explanations why p-values should not be interpreted as providing answers to questions like “What is the strength of evidence?” Yet p-values are very often used as if they were a measure of strength of evidence. In particular, the editors of many scientific journals and the referees they rely on often use p-levels as a measure of strength of evidence. This matters because, as Johnson (1999, p. 771) remarked, they are “really the arbiters of scientific practice.”

3.2. What Questions do Neyman–Pearson Hypothesis Tests Answer?

Like p-values, the Neyman–Pearson lemma does not address the question “What is the strength of evidence?” It deals with choosing between two simple hypotheses: H₀ that X has density function f₀(x) and H₁ that X has density function f₁(x). Assuming that a choice must be made after observing X, it shows that the likelihood ratio L = f₁(x)/f₀(x) should be larger in the region where H₀ is rejected than in the region where H₀ is not rejected (and H₁ is rejected). I will refer to this as two-region hypothesis testing.

In my opinion, inference (as opposed to merely choosing) must always allow the additional option of stating that the evidence is not sufficiently strong for a reliable choice to be made between the hypotheses. The most natural three-region hypothesis tests between the two hypotheses are of the form:

• reject H₁ (and accept H₀) if L < a;

• reject H₀ (and accept H₁) if L > b; and

• state that there is insufficient evidence to support a conclusion if a < L < b.

There may be some arbitrariness if L = a or L = b, which can be important if the sample space is discrete.

Example 7.

Suppose that a random variable, X, is normally distributed with unit variance and mean either − 1.645 under H₀ or 1.645 under H₁. Figure 2 illustrates examples of two-region and three-region tests.

Figure 2. The probability density of X under H₀ is shown by a bold line. The density under H₁ is shown with a lighter line. Regions for two-region and three-region tests are shown using arrows.

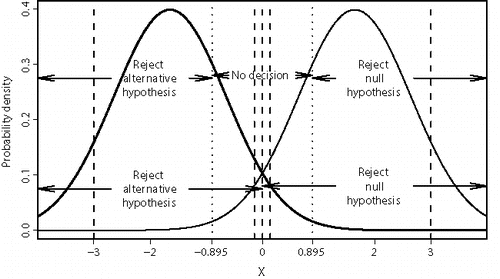
A symmetrical two-region hypothesis test rejects H₀ if X > 0. The Type I and Type II error rates are both 0.05. These error rates are averages over the entire sample space. Errors are more likely for X near to the cut-off value, X = 0. For instance, the error rates conditional on |X| < 0.14 are both 0.4428, whereas the error rates conditional on |X| > 3 are both 0.00002. It seems intuitively unreasonable to quote the same measure of confidence as to which hypothesis is true in these two quite different circumstances.

One symmetrical three-region test accepts H₀ whenever X < −0.8950 (i.e., the likelihood ratio for H₀ relative to H₁ is at least 19:1) and accepts H₁ whenever X > +0.8950 (i.e., the likelihood ratio for H₁ relative to H₀ is at least 19:1). The probability of correctly accepting the true hypothesis is 0.7733, the probability of wrongly accepting the other hypothesis is 0.005544, and the probability of making no conclusion is 0.2211, regardless of which hypothesis is true. There is no obvious event whose probability is equal to 0.05. The likelihood ratio cut-off value, 19, is the natural measure of the reliability of any conclusions reached.

The distinction between the questions being answered by two-region tests and three-region tests seems to have been understood by Barnard (1947a). I believe that he regarded three-region tests as a form of sequential analysis which is terminated after one stage of data collection. He wrote

“[...] sequential analysis poses the question in a more natural manner than the classical theory of testing hypotheses. In the classical approach, the question is put: Which of the two hypotheses, H or H′, should we adopt, on the basis of the data R? As if we were always compelled to choose one or other of these two alternatives. Sequential analysis, on the other hand, poses the question: Are the data R sufficient ground for adopting H, or for adopting H′, [or]are the data insufficient? In other words, we ask, is the likelihood ratio L′/L so large that we can safely accept H′, is it so small that we can safely accept H, or is it so near to 1 that we have no safe grounds for decision? A rule for answering this question will take the form of fixing two numbers, A > 1 and B < 1, and prescribing that we are to accept H′ if the likelihood ratio is greater than A, we are to accept H if the likelihood ratio is less than B, while we consider the data insufficient if the likelihood ratio lies between A and B.”

Hacking (1965, p. 106) wrote

“We have been speaking as if the only possible consequence of a test is that one might reject or fail to reject an hypothesis. ... In reality, if H is being tested against some J, possible results of a test divide into three categories: reject H; accept H and so reject J; and remain agnostic. The third possibility invites future experimentation.”

Similarly, Armitage (1975, p. 10) and Anscombe (1963, p. 366) both discussed three possible trial outcomes: H₀ is preferable to H₁, H₁ is preferable to H₀, and the evidence is inadequate to choose confidently between H₀ and H₁.

The difference between these questions is also illustrated by Example 8.

Table 4. Probabilities for a blood test.

	Probabilities for observations
Hypothesis	X = 0	X = 1	X = 2	X = 3
H0	0.90	0.05	0.04	0.01
H1	0.01	0.04	0.05	0.90

Example 8.

Consider a blood test with four possible discrete outcomes. Their probabilities under two hypotheses are given in Table 4. The test generally gives X = 0 under H₀ that a person does not have some disease and generally gives X = 3 under H₁ that the person does have the disease. The two other possible outcomes X = 1 and X = 2 have fairly small probabilities under both H₀ and H₁, with X = 1 being slightly more likely under H₀ and X = 2 being slightly more likely under H₁.

One two-region Neyman–Pearson hypothesis test rejects H₀ if X is 2 or 3 and rejects H₁ if X is 0 or 1. This test has probability 0.05 of Type I error (falsely rejecting H₀) and probability 0.05 of Type II error (falsely rejecting H₁). An intuitively natural three-region test accepts H₀ if X = 0, accepts H₁ if X = 3, and states that the evidence is not strong enough for a conclusion to be made if X = 1 or X = 2. The three-region test is more satisfactory intuitively.

3.3. What Questions Should Sequential Probability Ratio Tests Answer?

When sequential probability ratio tests (SPRTs) were developed by Wald (1947), the most important measures of performance of hypothesis tests (including SPRTs) were assumed to be the Type I and Type II error rates. Computing these generally requires complicated calculations or approximations. The questions to which these measures of performance provide answers are of the form “What is the probability which applied before all of the possible stages of the sequential test that the alternative/null hypothesis would be accepted/rejected given that the null/alternative hypothesis is true?”

However if likelihood ratios are used to measure strength of evidence, then an SPRT is a direct way answering the question “Is the strength of evidence adequate to choose between the alternative hypothesis and the null hypothesis?” An SPRT is a form of three-region hypothesis test where more data may be acquired if no decision can yet be made.

Personal perspective. As has been said many times in many ways by many people, p-values answer the question “Are the data likely given the specified null hypothesis?” They do not answer the question “How strong is the evidence?” Two-region Neyman–Pearson hypothesis testing also fails to answer any of Royall’s questions. In contrast, a three-region version does tell us whether the evidence is strong enough for a choice to be made between two simple hypotheses; and Wald’s SPRT may be viewed as an extension of three-region Neyman–Pearson hypothesis testing.

4. Should the Likelihood Principle be Satisfied?

Based on Berger and Wolpert (1984, p. 19), the likelihood principle says that all evidence is contained in the likelihood of the data actually observed. One way of justifying this principle is Bayesian. For a given prior distribution, the posterior distribution only depends on the likelihood. Your conclusion depends on the likelihood of the observed data, but not on the stopping rule nor on the likelihoods of unobserved data. Birnbaum (1962) provided a non-Bayesian justification of the likelihood principle. See Berger and Wolpert (1984) for a thorough discussion of the history of the likelihood principle with many examples.

A memorable intuitive justification of the likelihood principle was given by Pratt in the discussion of Birnbaum (1962). An engineer measures some voltages, obtaining data ranging from 75 to 99 volts. After analyzing the data, a statistician notices that the volt-meter reads only as far as 100. Any data exceeding 100 would have been “censored,” so a new analysis appears to be required. The engineer also has a high-range volt-meter, equally accurate and reading to 1000 volts, which he at first says that he would have used if any voltage had been over 100; so new data analysis is not required. He later realizes that it was not working the day the experiment was performed, and admits that he would not have held up the experiment until the meter was fixed. The statistician concludes that the new data analysis will indeed be required. The engineer retorts “But the experiment turned out just the same as if the high-range meter had been working. I obtained the precise voltages of my sample anyway, so I learned exactly what I would have learned if the high-range meter had been available. Next you’ll be asking about my oscilloscope.”

4.1. Should the Stopping Rule Principle be Satisfied?

One logical consequence of the likelihood principle is the stopping rule principle: that the evidence provided by the final data from a sequential experiment does not depend on the stopping rule. See Berger and Wolpert (1984, p. 76). Frequentist methods for sequential analysis do not satisfy the stopping rule principle, as Cornfield (1966) argued by formulating and then denigrating what he called the α-postulate: “All hypotheses rejected at the same critical level have equal amounts of evidence against them.” Frequentist methodology suggests that data analysts ought to take into account whether experimenting stopped because the data appeared to be providing strong evidence for or against some null hypothesis; or because money, suitable subjects, or enthusiasm had run out. They should consider the experimenters’ original intentions and how they would have reacted to all of the possible data that might have arisen. This seems to be a nonobjective and very unfortunate feature of Frequentist methods. It is illustrated by Examples 9 and 10.

Example 9.

Consider Neyman–Pearson testing between the two simple hypotheses H₀ that $X\sim \mathcal{N}(0,1)$ and H₁ that $X\sim \mathcal{N}(1,1)$ on the basis of three possible experiments.

Experiment 1

is that eight independent observations are made and H₀ is rejected if $\bar{X}>0.6$. This Neyman–Pearson test has Type I error rate 0.0448 and Type II error rate 0.1289.

Experiment 2

is that 18 independent observations are made and H₀ is rejected if $\bar{X}>0.6$. This Neyman–Pearson test has Type I error rate 0.0055 and Type II error rate 0.0448.

Experiment 3

is a two-stage sequential test. First, eight independent observations are made. If $\bar{X}>0.8$, H₀ is rejected; and if $\bar{X}<0.3$, H₁ is rejected. If $0.3\le \bar{X}\le 0.8$, then an additional 10 independent observations are made. Then using the mean of all 18 observations, H₀ is rejected if $\bar{X}>0.6$. This two-stage test has Type I error rate 0.0150 and Type II error rate 0.0533.

Consider observing $\bar{X}=0.801$ after eight observations. If this is part of Experiment 1 then the Type I error rate would be quoted as 0.0448, but if it is part of Experiment 3 then the Type I error rate would be quoted as 0.0150. Second, consider $\bar{X}=0.73$ after 8 observations and $\bar{X}=0.601$ after 18 observations. If this is part of Experiment 2 then the Type I error rate would be quoted as 0.0055, but if it is part of Experiment 3 then the Type I error rate would be quoted as 0.0150. Outcomes with the same likelihood ratio from different experiments are reported differently. The likelihood principle and stopping rule principle are violated.

The following illustration of how Type I error rates appear to be affected by stopping rules is from Barnard (1947b), based on a letter from R.A. Fisher.

Example 10.

Suppose that 10 chrysanthemum seeds were planted. The null hypothesis is that half will produce white flowers and half will produce purple flowers. Let p denote the probability that a seed grows to maturity. If 9 seeds grow to maturity and produce purple flowers, then the outcomes which are as likely or less likely than the observed outcome are 9 white & 0 purple, 0 white & 9 purple, 10 white & 0 purple, and 0 white & 10 purple. The total probability of these four outcomes under the null hypothesis is $$10p^9(1-p)(2^{-9}+2^{-9})+p^{10}(2^{-10}+2^{-10})={(p/2)}^9(20-19p)$$which has a maximum value of 0.002401 at p = 18/19. This number might be quoted as a Type I error rate.

On the other hand, if all seeds sprouted but one plant was killed by a statistician while running for a bus, the experiment might be analyzed as if the intention had been to grow nine plants. The outcomes which are as likely or less likely than the observed outcome are 9 white & 0 purple, and 0 white & 9 purple. Their total probability is 2^{− 9} + 2^{− 9} = 0.003906 and this number might be quoted as a Type I error rate. This analysis would also be preferred by statisticians who condition on ancillary statistics, such as the number of seeds growing to maturity in this example.

In Example 1, perhaps the p-level for the 2002 data should have been adjusted to allow for the fact that the steadily-accumulating body of data would be examined on many occasions or to take into account that many possible relationships were investigated and only the ones with the smallest p-value were being highlighted. An adjusted 95% confidence interval for the CHD risk of HRT was given in Rossouw et al. (2002, Table 2) as 0.85–1.97. The reporting of statistical analysis concentrated on the unadjusted confidence intervals on the grounds that the adjusted confidence intervals were “conservative.”

4.2. Is Selective Reporting OK?

Selective reporting is not necessarily relevant to a discussion of the properties that statistical inferences should satisfy; but other people have included it as part of the topic of “P-hacking” while discussing p-values so I feel a need to discuss it also.

Motulsky (2014) used the term “P-hacking” to include a variety of procedures for reanalyzing data which might be tried “until you obtain a statistically significant result or until you run out of money, time, or curiosity.” The cartoon on his page 202 (which was also reproduced in Young and Karr 2011) illustrates the conducting of 20 experiments to investigate possible relationships between eating jelly beans of particular colors and acne. One experiment found a “statistically significant” relationship between green jelly beans and acne when analyzed as if that hypothesis had been the only one of interest.

Simmons, Nelson, and Simonsohn (2011) referred to researchers making decisions about amount of data, exclusion of some data, choice of control variables, and data transformations as “researcher degrees of freedom.” This is a less derogatory term than “P-hacking.”

Insofar as “P-hacking” means looking at the data-to-date on several occasions during data collection and choosing to stop the data collection or experiment if the data-to-date supports some conclusion, I think that “P-hacking” is part of a sequential approach and is not merely acceptable according to the likelihood principle and the stopping rule principle but is a desirable practice.

Insofar as “P-hacking” means conducting many statistical tests and only reporting the ones that make the results look important, I would describe it as “selective reporting” and believe that it is highly undesirable. An example of such selective reporting is that Cacioppo et al. (2013) says

“The percentage of marital break-ups was lower for respondents who met their spouse on-line (5.96%) than off-line (7.67%) [ χ²(1) = 9.95, p < 0.002]. Importantly, after controlling for year of marriage, to account for different follow-up times across respondents, and for sex, age, educational background, ethnicity, household income, religious affiliation, and employment status as covariates, this difference was attenuated but remained significant [χ²(1) = 3.87, p < 0.05].”

In their (observational) study there were substantial differences in the distributions of covariates between respondents who met their spouse online and respondents who met their spouse off-line. In my opinion, the first statistical analysis has essentially no value because it fails to adjust for the covariates. It appears to have been given more emphasis because it has a more extreme p-value. If I had reviewed Cacioppo et al. (2013) then I think that I would have asked that the first analysis be omitted. To have reported only the first analysis would have been grossly misleading.

It is generally accepted that estimated effects should be adjusted for covariates when analyzing observational studies. A classic example was given by Cochran (1968). The unadjusted death rates given in Table 5 suggest that smoking cigars and pipes is much more dangerous than smoking cigarettes. However, death rates are known to increase with age and the cigarette smokers were much younger on average than the cigar and pipe smokers. Adjusted death rates computed using 12, 8, and 11 age categories for the Canadian, British, and U.S. studies, respectively, are also shown in Table 5. They are adjusted to the mean age for nonsmokers. These adjusted rates suggest that cigarette smoking is dangerous but cigar and pipe smoking are not.

Personal perspective. I believe that the likelihood principle should be satisfied. Strength of evidence should not depend on the data which might have been observed but was not. In particular, the evidence provided by a sequential experiment should not depend on the stopping rule.

Table 5. Death rates per 1000 person-years and mean ages for groups of men classified by smoking habit in three studies.

	Study
Smoking group	Canadian	British	U.S.
Nonsmoker
(mean age)	(54.9)	(49.1)	(57.0)
Unadjusted death rate	20.2	11.3	13.5
Adjusted death rate	20.2	11.3	13.5
Cigarettes only
(mean age)	(50.8)	(49.8)	(53.2)
Unadjusted death rate	20.5	14.1	13.5
Adjusted death rate	29.5	14.8	21.2
Cigars, pipes
(mean age)	(65.9)	(55.7)	(59.7)
Unadjusted death rate	35.5	20.7	17.4
Adjusted death rate	19.8	11.0	13.7

5. Do Hypothesis Tests and Interval Estimates Need to be Mutually Consistent?

In the Frequentist paradigm, it is usual for hypothesis tests and interval estimates to be mutually consistent in the sense that a confidence interval includes precisely those parameter values which would not be rejected by a hypothesis test. In the subjective Bayesian paradigm, if you were interested in testing the hypothesis that θ = 0 then your subjective prior distribution would include an atom of probability at θ = 0. For instance for the HRT example, many possible effects might have been of interest. Perhaps HRT affects susceptibility to diabetes or stroke; either by itself or in combination with other drugs or particular features of diet. Many of these effects will be essentially zero. A reasonable person’s prior distribution for any particular effect might ascribe substantial prior probability to the hypothesis that the effect is precisely zero or very nearly zero. In contrast, if you were interested in interval estimation then your prior would generally not include such an atom.

5.1. Does Avoiding Hypothesis Testing Avoid the Problems Endemic to Frequentist Statistical Inference?

Particularly in psychology, many people have advocated avoiding hypothesis testing and encouraging the quoting of effect sizes and interval estimates. See Yates (1951), Carver (1978), Gardner and Altman (1986), Sterne and Smith (2001), Harlow, Muliak, and Steiger (1997), Cumming (2012), and Valentine, Aloe, and Lau (2015).

If hypothesis testing and interval estimation are always mutually consistent then it seems to me that preferring interval estimates to hypothesis tests changes little. For instance, 95% confidence intervals for the relative risk of coronary heart disease from HRT in Example 1 would not have included unity for the 2002 data but would have included unity for the 2003 version of the data. Interpretation of the results by the news media would have been much the same whether researchers reported hypothesis tests or confidence intervals.

Personal perspective. I think that the assumption that hypothesis tests and interval estimates must be mutually consistent should be discarded, allowing hypothesis tests to be more stringent.

6. What Questions do Bayesian and Likelihood Methods Answer?

The subjective Bayesian approach advocated by, for instance, Lindley (1972) and Goldstein (2006) provides all three of Royall’s questions with answers which are coherent in many senses. These answers are often described as “subjective,” emphasizing their sensitivity to choices of prior distributions. They are also sensitive to modeling assumptions, such as independence and the forms of probability distributions, but the term “subjective” is seldom used to describe such sensitivities because other approaches are similarly sensitive. Bayes factors are considered to summarize amounts of evidence. The Bayes factor for some hypothesis, H₁, relative to another hypothesis, H₀, is the posterior odds in favor of H₁ divided by the prior odds in favor of H₁.

The objective Bayesian approach advocated by, for instance, Berger (2006) and Bernardo (1979) aims to be less subjective by using prior distributions variously described as being “objective,” “reference,” “conventional,” “standard,” or “ignorance” priors. These priors are usually improper in that their densities do not integrate to unity. Objective Bayesian methods sometimes have poorer coherence properties than subjective Bayesian methods, particularly when posteriors from improper priors are not well-behaved limits of sequences of posteriors from proper priors.

For testing between two simple hypotheses, the likelihood ratio provides a very satisfactory answer to the first of Royall’s questions: “What evidence is there?” Both Neyman–Pearson and three-region hypothesis tests depend primarily on the likelihood ratio; and the Bayes factor is always equal to the likelihood ratio.

For testing between a simple hypothesis and a compound hypothesis, different approaches do not lead to the same endpoint. Consider Example 2 where $X\sim \mathcal{N}(\mu ,1)$, H₀ is μ = 0 and H₁ is μ ≠ 0. Suppose X = 2.3 is observed.

A simple Likelihood approach suggests that the ratio of maximum likelihoods, 14.08, measures the strength of evidence in favor of H₁. This overstates the strength of evidence in that it is equal to or greater than the Bayes factors for all possible priors.

Using a prior distribution of $\mathcal{N}(0,5^2)$ for μ given H₁, the Bayes factor in favor of H₁ is 2.495. Using a prior distribution given H₁ which is a mixture of $\mathcal{N}(0,5^2)$ and $\mathcal{N}(20,5^2)$ in equal proportions, the Bayes factor in favor of H₁ is 1.251. The difference illustrates the sensitivity of Bayes factors to prior distributions. Following Berger and Pericchi (2001, p. 137), such Bayes factors may be viewed as ratios of prior-weighted likelihoods and therefore answering the question “What it the strength of evidence averaged over the prior distributions given H₀ and H₁?”

Resolution of the crisis in statistical inference may require relinquishing the quest for objectivity. However, as Berger and Delampady (1987, p. 330) wrote, “First and foremost, when testing precise hypotheses, formal use of p-values should be abandoned. Almost anything will give a better indication of the evidence provided by the data against H₀.”

One such “anything” uses the Akaike (1974) information criterion (AIC) which says that the maximum log-likelihood of the compound hypothesis H₁ should be penalized by subtracting 1 (or the maximum likelihood penalized by a multiplicative factor of e). We could regard AIC-penalized ratios of maximum likelihoods as indicative if they exceed 10, reliable if they exceed 100, and very reliable if they exceed 1000. For Example 2, the corresponding cut-offs for standard normal statistics are 2.570, 3.348, and 3.977. These are substantially more stringent than the cut-offs 1.960, 2.576, and 3.291 which correspond to two-tailed p-values of 0.05, 0.01, and 0.001, respectively.

For the 2002 version of the data for Example 1, the most likely relative risk is 1.286 and its likelihood is 8.98 times as large as that of the null hypothesis that the relative risk is 1. For the 2003 version of the data, the most likely relative risk is 1.223 and its likelihood is 5.21 times as large as that of the null hypothesis. The penalized likelihood ratios are 3.30 and 1.92 for the 2002 and 2003 versions of the data. These both indicate weak evidence.

Personal perspective. Penalized likelihood and the subjective and objective Bayesian approaches are all sounder bases for inference than p-values, but I would not describe any of them as “objectively correct.”

7. Discussion

Frequentist procedures based on p-values have been observed in practice to allow an unreasonably high rate of subsequent contradiction. After considering the questions and examples in this article, my attitude toward the Frequentist paradigm is summarized by the statement: “p-values are like a Birmingham screwdriver.” According to Green (2005), the term “Birmingham screwdriver” is slang for a hammer and its use highlights “the supposed oafishness of the Birmingham worker who would rather hammer in a screw than use the correct tool.” p-Values were originally developed as a tool for doing one job (pure significance testing) but are sometimes rather oafishly used for doing different jobs (hypothesis testing or interval estimation when alternative hypotheses are fully specified) thereby appearing to provide objective measures of reliability for a very large number of academic papers in medical, psychological, environmental, and other journals.

Acknowledgments

The author gratefully acknowledges guidance from many visitors and staff while a Ph.D. student at University College London from 1972 to 1974, particularly Allan Birnbaum, A. Philip Dawid, Dennis Lindley, and Mervyn Stone. He also thanks colleagues at CSIRO, particularly Bill Venables, and two reviewers.