Stochastic volatility forecasting of the Finnish housing market

ABSTRACT

The purpose of the article is to assess the in-sample fit and the out-of-sample forecasting performances of four stochastic volatility (SV) models in the Finnish housing market. The competing models are the vanilla SV, the SV model where the latent volatility follows a stationary AR(2) process, the heavy-tailed SV and the SV with leverage effects. The models are estimated using Bayesian technique, and the results reveal that the SV with leverage effects is the best model for modelling the Finnish house price volatility. The heavy-tailed SV model provides accurate out-of-sample volatility forecasts in most of the studied regions. Additionally, the models’ performances are noted to vary across almost all cities and sub-areas, and by apartment types. Moreover, the AR(2) component substantially improves the in-sample fit of the standard SV, but it is unimportant for the out-of-sample forecasting performance. The study outcomes have crucial implications, such as portfolio management and investment decision-making. To establish suitable time-series volatility forecasting models of this housing market, these study outcomes will be compared to the performances of their GARCH models counterparts.

KEYWORDS:

• Stochastic volatility
• Bayesian estimation
• forecasting
• Finland
• house prices

JEL CLASSIFICATION:

• C11
• C22
• C53

I. Introduction

Volatility modelling and forecasting are a vital task in financial markets. As the asset volatility holds critical information; it has been recognized as the most risk measure broadly used in many areas of finance (Bollerslev, Chou, and Kroner 1992). In the housing market, as housing assets have a dual role of consumption and investment; understanding price volatility plays an essential role in the housing investment decision-making and the asset allocation (Milles 2008a). Moreover, housing is a crucial factor for the country’s economy; in particular, in Finland, Statistics Finland (2016) reported that housing made up to 50.3% of the Finnish households’ total wealth. Thus, housing affects the country’s economy through wealth effects (Case, Quigley, and Shiller 2013) as well as through influences on many parties exposed to housing and mortgage activity. Therefore, better housing modelling and forecasting would be beneficial for consumers, mortgage market, mortgage insurance and mortgage-backed securities (Segnon et al. 2020). Furthermore, as pointed out by Zhou and Haurin (2010), insights into house price volatility are the key input in designing housing policies. In the light of the abovementioned points, understanding the dynamics of the house price volatility is crucial for portfolio management, risk assessment and investment decision-making.

An increasing amount of studies have attempted to model and/or forecast the house price volatility of individual markets. However, the literature has mainly focussed on the use of different Generalized Autoregressive Conditional Heteroscedasticity (GARCH)-type models. Under this approach, the volatility evolution is modelled deterministically; a framework which has its roots from the Engle’s (1982) and Bollerslev’s (1986) groundbreaking works. Taylor (1982), on the other hand, provided an alternative way; to model volatility probabilistically, meaning that volatility is treated as an unobserved component that follows a stochastic process. The specification is known as the Stochastic Volatility (SV) models. Even though SV models are theoretically attractive and there is some empirical evidence in their favour over GARCH models (Jaquier, Polson, and Rossi 1994; Gysels, Harvey, and Renault 1996; Kim et al., 1998; Nakajima and Omori 2012); they have drawn little attention among practitioners. The challenges pointed out by Bos (2012) are highly non-linear estimations and lack of standard software packages implementing these methods. In response to these challenges, Chan and Grant (2016b) provided the means for the Bayesian estimation of not only the vanilla SV model but also the heavy-tailed SV model and the SV model with leverage effects. Specifically, this study uses Chan and Grant (2016b) approach to model and forecast the studied housing market. To the best of the author’ knowledge, in the housing markets, there has yet to be empirical modelling and forecasting using the SV framework. Hence, this is the first study that models and forecasts the Finnish housing market volatility using the SV framework in general, and incorporating both non-Gaussianity and asymmetry effects in particular.

Moreover, the emphasis of the housing market volatility modelling and/or forecasting has been on a limited number of countries such as the United States, United Kingdom, Australia and Canada. Regarding housing market volatility modelling without the forecasting aspect, the authors (to cite few) who have employed GARCH-type models to study US house prices include Dolde and Tirtiroglu (1997, 2002), Miller and Peng (2006), Milles (2008b), and more recently, Apergis and Payne (2020). The UK house price volatility investigation consists of the work of Willcocks (2010), Tsai, Chen, and Ma (2010), Milles (2011b), and more recently, Begiazi and Katsiampa (2019). The Australian house price volatility has been examined by Lee (2009) and Lee and Reed (2014b); while Hossain and Latif (2009) and Lin and Fuerst (2014) studied the Canadian house price volatility. For Finland, Dufitinema (2020) has recently explored different aspects of the Finnish housing market volatility. Regarding the housing market volatility forecasting, the US housing market is the widely studied housing market. Beginning with the work of Crawford and Fratantoni (2003), followed by Milles (2008a), Li (2012), more recently, Segnon et al. (2020). For Finland, there has yet to be an empirical forecasting of the Finnish housing market, even though Statistics Finland (2016) reported that housing made up to 50.3% of the Finnish households’ total wealth. Therefore, this article aims to fill that gap by being the first study that forecasts the Finnish housing market volatility and further extends the ongoing literature on the countries’ house price volatility forecasting.

Furthermore, in contrast to previous studies which employed the data sets of the family–home property type; the studied type of dwellings in the article at hand is apartments (block of flats) categorize by the number of rooms. That is one-room, two-room and more than three rooms apartment types. One reason is that, according to Statistics Finland Overview, at the end of 2018, among all occupied dwellings, 46% were in apartments; which reflects how living in flats is growing in popularity in Finland, compared to other house types. Detached and semi-detached houses occupied 39%, terraced 14%, while 1% were in other buildings. The other reason is that apartments property type has not only increased its attractiveness in consumers but also in the Finnish residential property investors. Currently, foreign investors own some 15,000 rental flats, and between 2015 and 2018, in the Finnish housing development which has been very active in apartment buildings (Statistics Finland 2019); the share of foreign investors was up to 38%, and domestic and individual investors together hold some 40% (KTI, Autumn, 2019). Additionally, in the same standpoint of housing investment, this study uses data on both metropolitan and geographical level, to analysis and cross-compare housing investment in different cities and sub-areas, and portfolio allocation across Finland.

The purpose of the study is to assess the in-sample fit and the out-of-sample forecasting performance of four stochastic volatility models in the Finnish housing market. The competing models are the vanilla SV, the SV model where the latent volatility follows a stationary AR(2) process, the heavy-tailed SV and the SV with leverage effects. In other words, the goal of this model comparison exercise is to examine, in the SV framework, which volatility model tends to fit better the dynamics of the Finnish house prices and which one provides superior out-of-sample forecasts. Additionally, these models are used to answer the following questions: Are leverage effects and heavy-tailed distributions crucial in modelling and forecasting the Finnish house price volatility? Is the AR(2) component a useful addition to the vanilla SV model? The study assesses the Finnish housing market by apartment types categorize by the number of rooms. That is, single-room, two-room and apartments with more than three rooms. These apartment type prices are for 15 main regions divided geographically, according to their postcode numbers, into 45 cities and sub-areas. Each model is estimated for each city and sub-area with significant clustering effects. For the assessment of the out-of-sample forecasting performance of the four models, the data is split into two parts: the training set used for the estimation and prediction, and the test set used for the evaluation of the forecast built by the fitted model. Results reveal that, for the in-sample fit analysis, in all three apartment types, the stochastic volatility model with leverage effect ranks as the best model for modelling the Finnish house price volatility. For the out-of-sample forecasting assessment, in most of the regions, the heavy-tailed stochastic volatility model excels in forecasting the house price volatility of the studied types of apartments. Additionally, the models’ performances are noted to vary across almost all cities and sub-areas, and by apartment types – no geographical pattern is observed. Moreover, for the in-sample fit analysis, the AR(2) component is found to be a valuable addition to the vanilla SV, whereas, for the out-of-sample forecasting assessment, the vanilla SV model outperforms the SV-2 in most of the regions.

The remainder of the article is as follows. Section 2 describes the data and outlines the methodology to be employed. Section 3 presents and discusses the results. Section 4 concludes the article.

II. Data and methodology

Data

The study uses quarterly house price indices of 15 main regions in Finland estimated by Statistics Finland using the so-called hedonic method. The studied period is from 1988:Q1 to 2018:Q4, and the type of dwellings is apartments categorize by the number of rooms, that is, one-room, two-room and more than three rooms apartment types. The studied regions are Helsinki, Tampere, Turku, Oulu, Lahti, Jyväskylä, Kuopio, Pori, Seinäjoki, Joensuu, Vaasa, Lappeenranta, Kouvola, Hämeenlina and Kotka. Additionally, these regions are divided geographically, according to their postcode numbers, into 45 cities and sub-areas. The data regions’ ranking according to their number of inhabitants and regional division by postcode numbers is described in detailed in Dufitinema (2020).

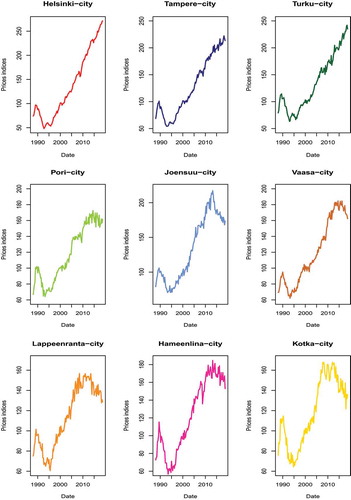
For a sample of three cities in each of the apartments categories, a house price movement is graphed in Figure 1. Those are Helsinki, Tampere, Turku in the one-room flats group; Pori, Joensuu, Vaasa in the two-room flats group; Lappeenranta, Hämeenlina, Kotka in the more than three rooms flats group. A similar pattern is observed in all sample graphs from the end of 1980s to mid-1993. During this period, house prices in Finland experienced a structural break due to the financial market deregulation (Oikarinen 2009a, 2009b). Moreover, as it can be noted since the bursting of the bubble, one-room apartment prices have been increasing. Two-room apartments experienced downturns in the 2010s, same as large apartments; however, large apartments prices continue to decrease especially in less densely populated regions such as Kotka-city.

Figure 1. The house price movement – Sample cities

Methodology

The methodology used in this study is as follows: For each city and sub-area in each apartment type, we transform house price indices into continuous compound returns. Next, by employing the Akaike and Bayesian information criteria, we determine the ARMA model of appropriate order that filters out the first autocorrelations from the returns. Then, we test the clustering effects or Autoregressive Conditional Heteroscedasticity (ARCH) effects from the ARMA filtered returns. Lastly, for cities and sub-areas exhibiting ARCH effects, the four SV models’ in-sample estimations are performed, and the out-of-sample volatility forecasting performances are evaluated using the stochastic volatility framework.

Testing for ARCH effects

Two tests are employed to test clustering effects; those are Ljung-Box (LB) and Lagrange Multiplier (LM). An extensive discussion is given in Dufitinema (2020) and results are outlined in Table 1. In summary, both tests found significant clustering effects in over half of the cities/sub-areas in all three studied types of apartments. Plus precisely, in the one–room flats category, ARCH effects were found in 28 out of 38 cities/sub-areas. In two-room flats category, they were significant in 27 out of 42;, and in the more than three rooms flats category, they were found in 31 out of 39.

Table 1. ARCH effects tests results

		One room flats		Two rooms flats		Three rooms flats
Regions	Cities/sub-areas	ARMA	ARCH?	ARMA	ARCH?	ARMA	ARCH?
Helsinki	hki	ARMA(2,1)	Yes	ARMA(2,1)	Yes	AR(1)	Yes
	hki1	MA(2)	Yes	ARMA(2,1)	Yes	AR(2)	Yes
	hki2	ARMA(2,1)	Yes	AR(1)	Yes	AR(1)	No
	hki3	ARMA(2,1)	No	AR(2)	Yes	AR(2)	Yes
	hki4	AR(2)	Yes	ARMA(1,1)	Yes	AR(2)	Yes
Tampere	tre	ARMA(1,1)	No	ARMA(2,1)	No	ARMA(2,2)	Yes
	tre1	ARMA(2,2)	Yes	AR(2)	Yes	ARMA(2,2)	Yes
	tre2	ARMA(1,1)	No	ARMA(0,0)	Yes	ARMA(2,2)	Yes
	tre3	AR(2)	Yes	ARMA(2,2)	No	ARMA(1,1)	Yes
Turku	tku	ARMA(2,2)	Yes	ARMA(2,2)	Yes	ARMA(2,2)	Yes
	tku1	ARMA(1,1)	Yes	AR(2)	No	AR(1)	Yes
	tku2	AR(1)	Yes	ARMA(0,0)	Yes	ARMA(2,2)	Yes
	tku3	AR(1)	Yes	MA(3)	No	ARMA(0,0)	Yes
Oulu	oulu	ARMA(1,1)	Yes	AR(2)	No	ARMA(1, 2)	Yes
	oulu1	AR(1)	Yes	ARMA(1,2)	No	ARMA(1,2)	Yes
	oulu2	AR(1)	No	ARMA(0,0)	No	MA(3)	No
Lahti	lti	AR(2)	Yes	AR(2)	Yes	ARMA(2,2)	Yes
	lti1	AR(1)	Yes	AR(2)	No	MA(3)	Yes
	lti2	AR(1)	No	ARMA(1,2)	No	ARMA(2,2)	No
Jyväskylä	jkla	ARMA(1,1)	Yes	ARMA(2,2)	Yes	ARMA(1,2)	Yes
	jkla1	ARMA(1,1)	Yes	MA(3)	Yes	ARMA(2,2)	Yes
	jkla2	ARMA(0,0)	Yes	ARMA(1,2)	Yes	ARMA(1,2)	Yes
Pori	pori	MA(1)	Yes	MA(3)	Yes	ARMA(2,2)	No
	pori1	AR(2)	Yes	MA(3)	Yes	MA(1)	Yes
	pori2	–	–	ARMA(2,2)	Yes	–	–
Kuopio	kuo	ARMA(0,0)	Yes	AR(2)	Yes	ARMA(0,0)	Yes
	kuo1	MA(2)	Yes	ARMA(0,0)	Yes	MA(1)	Yes
	kuo2	ARMA(0,0)	Yes	AR(2)	No	ARMA(1,2)	Yes
Joensuu	jnsu	MA(3)	No	AR(3)	No	AR(1)	No
	jnsu1	MA(3)	Yes	AR(3)	Yes	AR(1)	No
Seinäjoki	seoki	–	–	AR(1)	Yes	MA(3)	Yes
Vaasa	vaasa	MA(1)	No	ARMA(1,2)	Yes	ARMA(1,2)	Yes
	vaasa1	MA(1)	No	MA(2)	No	MA(1)	Yes
	vaasa2	–	–	–	–	ARMA(0,0)	Yes
Kouvola	kou	AR(1)	Yes	ARMA(1,2)	Yes	MA(3)	No
Lappeenranta	lrta	AR(1)	Yes	MA(3)	Yes	MA(3)	Yes
	lrta1	MA(1)	Yes	ARMA(2,2)	Yes	–	–
	lrta2	–	–	AR(1)	No	ARMA(0,0)	Yes
Hämeenlinna	hnlina	MA(3)	Yes	ARMA(0,0)	Yes	MA(3)	No
	hnlina1	MA(3)	No	ARMA(1,2)	Yes	AR(1)	Yes
Kotka	kotka	MA(1)	Yes	MA(3)	No	ARMA(2,2)	Yes
	kotka1	MA(3)	No	MA(2)	Yes	–	–
	kotka2	–	–	MA(2)	No	–	–

Notes: This table reports, for each city and sub-area, the ARMA model and the outcomes of the two tests of ARCH effects. ”Yes” indicates that a city/sub-area exhibits ARCH effects, ”No” means that a city/sub-area does not.

In-sample fit analysis

For cities and sub-areas exhibiting clustering effects, the in-sample fit is performed using the stochastic volatility approach. That is, in contrast to the GARCH-type framework where the conditional variance is assumed to follow a deterministic process; a stochastic volatility (SV) model treats the time-varying volatility as an unobserved component that mimics a stochastic process. The most popular SV model is the vanilla SV model with normal distribution errors proposed and developed by Taylor (1982, 1986). However, several authors have pointed out that a normal distribution assumption is not plausible when analysing asset returns with SV framework as well as GARCH-type models (Tsay 2013; Harvey and Shephard 1996; Omari et al. 2007; Nakajima and Omori 2012). A suitable distribution requires to accommodate the characteristics of asset returns such as skewness and fat tails. Therefore, for each city and sub-area in each apartment type, the in-sample estimations of the vanilla SV model and the SV model with additional AR(2) component are compared to the SV model with Student’s t errors (heavy-tailed SV) and SV model with leverage effects. The models are estimated on the whole sample data from 1988:Q1 to 2018:Q4.

Vanilla SV model

Let $y_t$ denotes the demeaned return process $y_t=log(S_t/S_{t-1})-{\mu }_t.$ A basic stochastic volatility model is of the following form:

$y_t={\sigma }_t{ϵ}_t,t=1,2,\dots .T,$

where the $log{\sigma }_t^2$ follows an AR(1) process. To adopt the convention often used in literature, we write for $h_t=log{\sigma }_t^2,$

(1) $\begin{array}{rl}& y_t={\sigma }_t{ϵ}_t,t=1,2,\dots .n\\ & {\sigma }_t^2=exp(h_t)\\ & h_t=\mu +\varphi h_{t-1}+{\sigma }_{\eta }{\eta }_t,\end{array}$(1)

where $h_t$ is the latent stochastic process (more precisely, the log-variance process), $\mu$ is a constant or the level of the log-variance process, $\varphi$ is a parameter representing persistence in the log-variance process, ${\sigma }_{\eta }$ is the volatility or the standard deviation of the log-variance process (also called volvol), and ${\eta }_t$ is the random shocks in the log-variance process; a white noise uncorrelated with ${ϵ}_t$. $\theta =(\mu ,\varphi ,{\sigma }_{\eta }{)}^T$ is referred to as the SV parameter vector.

Equation (1)(1) $\begin{array}{rl}& y_t={\sigma }_t{ϵ}_t,t=1,2,\dots .n\\ & {\sigma }_t^2=exp(h_t)\\ & h_t=\mu +\varphi h_{t-1}+{\sigma }_{\eta }{\eta }_t,\end{array}$(1) can be expressed in hierarchical form. In its centred parameterization form, it is written as:

$\begin{array}{rl}& y_t|h_t\sim \mathcal{N}(0,exp(h_t)),\\ & h_t|h_{t-1},\theta \sim \mathcal{N}(\mu +\varphi (h_{t-1}-\mu ),{\sigma }_{\eta }^2),\end{array}$

where $\mathcal{N}(\mu ,{\sigma }_{\eta }^2)$ denotes the normal distribution with mean $\mu$ and variance ${\sigma }_{\eta }^2$.

The SV model with additional AR(2) component, which is referred to as the SV-2, is the model where the observation is the same as in Equation (1)(1) $\begin{array}{rl}& y_t={\sigma }_t{ϵ}_t,t=1,2,\dots .n\\ & {\sigma }_t^2=exp(h_t)\\ & h_t=\mu +\varphi h_{t-1}+{\sigma }_{\eta }{\eta }_t,\end{array}$(1) ; however, the log-variance $h_t$ mimics a stationary AR(2) process.

SV with student’s t errors (SVt)

As discussed above, the non-normal conditional residual distributions are recommended when analysing asset returns. The proposed distributions include, for instance, the Student’s t distribution by Harvey, Ruiz, and Shephard (1994); the (semi-)parametric residuals by Jensen and Maheu (2010) and Delatola and Griffin (2011); the extended generalized Inverse Gaussian by (Silva, Lopes, and Migon 2006); and the generalized hyperbolic skew Student’s t errors by Nakajima and Omori (2012).

The SV model with Student’s t errors is described as:

(2) $\begin{array}{cc}\hspace{0.17em}& y_t|h_t,\nu \sim t_{\nu }(0,exp(h_t/2)),\\ \hspace{0.17em}& h_t|h_{t-1},\theta \sim \mathcal{N}(\mu +\varphi (h_{t-1}-\mu ),{\sigma }_{\eta }^2).\end{array}$(2)

The observations now follow a conditionally Student’s t distribution $t_{\nu }(a,b)$ with $\nu$ degrees of freedom, mean $a$ and scale $b$. The parameter vector of the SVt model is $\theta =(\mu ,\varphi ,{\sigma }_{\eta },\nu {)}^T$.

SV with leverage effects (SVl)

It has been argued that the returns of financial variables have three major distribution characteristics. Those are heavy-tailedness, skewness and volatility clustering with leverage effects. The leverage effect emerged from Black’s (1976) and Christie’s (1982) studies outcome that a drop in return (a negative chock) has more impact on asset price volatility increase than a rise in return (a positive chock). Various extensions of the vanilla SV model with normal errors have been proposed to model this effect. The proposed asymmetric innovations include, for instance, the distributions featuring correlation and variance by Harvey and Shephard (1996), and Jaquier, Polson, and Rossi (2004); the skewed distributions by Nakajima and Omori (2012) and the non-parametric distributions by Jensen and Maheu (2014).

The SV model with leverage effects is described as:

(3) $\begin{array}{cc}\hspace{0.17em}& y_t|h_t,\theta \sim \mathcal{N}(0,\mathrm{\Sigma }),\\ \hspace{0.17em}& h_t|h_{t-1},\theta \sim \mathcal{N}(\mu +\varphi (h_{t-1}-\mu ),\mathrm{\Sigma }),\\ \hspace{0.17em}& \mathrm{\Sigma }=\left(\begin{array}{cc}exp(h_t)& \rho {\sigma }_{\eta }exp(h_t/2)\\ \rho {\sigma }_{\eta }exp(h_t/2)& {\sigma }_{\eta }^2\end{array}\right).\end{array}$(3)

The vector $\theta =(\mu ,\varphi ,{\sigma }_{\eta },\rho {)}^T$ collects the SVl parameters. The parameter $\rho$ measures the correlation between the residuals of the observations (${ϵ}_t$) and the innovations of the log-variance process (${\eta }_t$). Leverage effects exist when $\rho <0$.

Model comparison

As the latent volatility process ($h_t$) enters the models in a non-linear fashion, the maximum likelihood estimation framework is not a straightforward task as in the GARCH-type models’ case. The reason being that for the SV models, the likelihood function does not have a closed form (Gysels, Harvey, and Renault 1996). Hence, the estimation of the SV models is done through Bayesian parameter estimation technique via Markov Chain Monte Carlo (MCMC) methods (Kim et al., 1998). The estimation of the four SV models was performed by following Chan and Grant’s approach, which is outlined in Chan and Grant (2016b, Appendix A). In estimating the SV models, the vital step is the joint sampling of the log volatilities. The novelty of Chan and Grant’s approach is that instead of using the conventional Kalman Filter to achieve this key step; the algorithm employs the fast band matrix routines (Chan and Jeliazkov 2009; Chan 2013).

The four models performances are compared using two popular Bayesian model comparison criteria, namely, deviance information criterion (DIC) and Bayes factor. The deviance information criterion (DIC) proposed by Spiegelhalter et al. (2002) is a trade-off between the model’s goodness of fit and its corresponding complexity. The fit is measured by the deviance, defined as

$D(\theta )=-2log\mathcal{L}(y|\theta ),$

where $\mathcal{L}(y|\theta )$ is the likelihood function. The complexity is measured by an estimate of the effective number of parameters $p_{\mathrm{D}}$, defined as

$p_{\mathrm{D}}=\bar{D}-D(\bar{\theta }).$

That is, the difference between the posterior mean deviance and the deviance evaluated at the posterior mean of parameters. Thus, the DIC is the sum between the Monte Carlo estimated posterior mean deviance and the effective number of parameters:

$\mathrm{D}\mathrm{I}\mathrm{C}=\bar{D}+p_{\mathrm{D}}.$

The smaller the DIC, the better the model supports the data. The widely used version of DIC is the one obtained by conditioning on the latent variables, that is, the DIC based on conditional likelihood. However, studies such as Li, Zeng, and Yu (2012) have warned against using this DIC version on the grounds of being non-regular and thus invalidates the needed justification of DIC – the standard asymptotic arguments. Moreover, Millar (2009) and Chan and Grant (2016a) provided Monte Carlo evidence that this DIC version always favours the most complex and overfitted model. To overcome this issue, Chan and Grant (2016a) proposed importance sampling algorithms to compute DIC by integrating out the latent variables; that is, the DIC based on the observed data likelihood. The authors showed in a Monte Carlo study that indeed the observed data DIC was able to select the correct model. Following Chan and Grant (2016a) approach, this article carries out the four models comparison exercise using the observed data DICs.

Another popular metric for Bayesian model comparison is the Bayes factor; it is defined as a ratio of marginal likelihoods. That is, given the likelihood function $\mathcal{L}(y|{\theta }_k,M_k)$ of a model $M_k$ and its prior density $\mathcal{L}({\theta }_k|M_k)$, the Bayes factor in favour of Model $M_i$ against $M_j$ is

$\mathrm{B}{\mathrm{F}}_{ij}=\frac{\mathcal{L}(y|M_i)}{\mathcal{L}(y|M_j)}>1,\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}$

(4) $\mathcal{L}(y|M_k)=\int \mathcal{L}(y|{\theta }_k,M_k)\mathcal{L}({\theta }_k|M_k)d{\theta }_k$(4)

is the marginal likelihood under model $M_k$, $k=i,j$.

The interpretation of the marginal likelihood is that of the density forecast of the data under model $M_k$ evaluated at the actual observed data $y$. Therefore, the more likely the observed data are to be under the model, the ‘larger’ the corresponding marginal likelihood would be. Furthermore, the Bayes factor is a consistent model selection creation (Kass and Raftery 1995). However, one potential drawback of the marginal likelihoods is that they are relatively sensitive to the prior distribution. In addition, their computation is non-trivial; the integral in Equation (4)(4) $\mathcal{L}(y|M_k)=\int \mathcal{L}(y|{\theta }_k,M_k)\mathcal{L}({\theta }_k|M_k)d{\theta }_k$(4) does not have an analytical solution as it is often high-dimensional. Chan and Grant (2016b) provided an improved approach to compute the marginal likelihoods using an adaptive importance sampling method called the cross-entropy method. It is an importance sampling estimator based on independent draws from convenient distributions. This article employs Chan and Grant (2016b) approach; the model selection criterion results are available from the author upon request.

Out-of-sample volatility forecasting

For the out-of-sample forecasting performance comparison of the four used models, the data is split into two parts: the training set which includes 25-year sample data (estimation sample: 1988:Q1–2013:Q4) and 5-year sample data for the test set or validation test (5-year forecast: 2014:Q1–2018:Q4). The prediction procedure starts with the estimation of each model using the training data set. Next, the estimated models are used to build the one-step-ahead (quarter) volatility forecasts. Finally, the predicted volatility (${\hat{\sigma }}^2$) is compared to the proxy of the true volatility (${\sigma }^2$).

By nature, true volatility is unobserved, and its appropriate proxy to use in the evaluation of the forecasting performance of different models remains the centre of active ongoing debate. Although most studies such as Brailsford and Faff (1996), Brooks and Persands (2002), and Sadorsky (2006) have employed the squared return as a proxy of ${\sigma }^2$, the realized volatility (RV) has been recognized as the natural benchmark against which to quantify volatility forecasts since it provides a consistent non-parametric estimate of the variability of the asset price over a given discrete period. The point which was first pointed out by Andersen and Bollerslev, in their (1998a)’s work which was further developed by Andersen, Bollerslev, and Lange (1999); (2003); 2004) and Patton (2007). Recently, in the stock market, the use of available intraday data and realized daily volatility had been praised for providing better forecast accuracy (Xingyi and Zakamulin 2018). In the housing market, ${\sigma }^2$ is also proxied by realized volatility calculated from the asset returns, as employed by Zhou and Kang (2011). Following this study, a proxy of the true volatility used in this article is the released volatility constructed as a rolling sample. Moreover, following other studies on conditional volatility forecasting, the forecasting accuracy of the studied models is measured using two popular measures; the Root Mean Squared Error (RMSE) and the Mean Absolute Error (MAE). The two criteria are defined as follows:

$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{N}\sum _{i=1}^N{({\hat{\sigma }}_i^2-{\sigma }_i^2)}^2}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{N}\sum _{i=1}^N\left|{\hat{\sigma }}_i^2-{\sigma }_i^2\right|,$

where $N$ is the number of forecasts, ${\hat{\sigma }}^2$ is the forecast volatility, and ${\sigma }^2$ is the true volatility.

III. Results and discussions

In-sample fit analysis

For cities and sub-areas with significant clustering effects in each apartment category, all four stochastic models are estimated using the Bayesian approach. The estimated observed data DICs and their standard errors are reported in Table 2–4. Various conclusions can be drawn from this model comparison exercise.

Table 2. Estimated DICs – One room flats

		One room flats
Regions	Cities/Sub-areas	SV	SV-2	SVt	SVl	The best model
Helsinki	hki	602.6 (0.94)	603.9 (0.57)	601.6 (0.16)	600.6 (0.19)	SVl
	hki1	687.5 (0.09)	686.0 (0.49)	688.0 (0.30)	685.3 (0.25)	SVl
	hki2	627.7 (0.73)	628.5 (0.53)	627.1 (0.12)	626.0 (0.32)	SVl
	hki4	697.7 (0.23)	700.8 (0.59)	697.9 (0.16)	693.7 (0.27)	SVl
Tampere	tre1	735.6 (0.39)	736.0 (0.75)	734.9 (0.13)	728.3 (0.29)	SVl
	tre3	726.1 (0.82)	718.8 (1.16)	725.7 (0.30)	722.5 (1.27)	SV-2
Turku	tku	711.5 (0.25)	705.3 (1.05)	711.7 (0.12)	708.1 (0.38)	SV-2
	tku1	764.7 (0.29)	764.8 (1.59)	764.9 (0.23)	757.1 (0.44)	SVl
	tku2	728.1 (0.32)	717.6 (2.42)	727.6 (0.21)	724.2 (0.43)	SV-2
	tku3	749.5 (0.38)	742.3 (1.35)	749.3 (0.71)	741.1 (0.52)	SVl
Oulu	oulu	699.8 (0.57)	705.2 (0.19)	702.5 (0.46)	698.4 (0.69)	SVl
	oulu1	748.9 (0.37)	749.2 (0.10)	747.1 (0.86)	759.2 (11.19)	SVt
Lahti	lti	757.9 (0.64)	760.4 (0.26)	757.0 (0.36)	750.0 (0.76)	SVl
	lti1	720.2 (0.20)	717.4 (1.47)	719.8 (0.19)	719.9 (0.37)	SV-2
Jyväskylä	jkla	730.1 (0.24)	729.4 (1.77)	731.9 (0.91)	724.7 (0.17)	SVl
	jkla1	753.6 (0.70)	748.5 (0.71)	753.0 (0.20)	750.4 (0.51)	SV-2
	jkla2	614.9 (0.40)	599.5 (1.02)	614.6 (0.44)	607.5 (0.41)	SV-2
Pori	pori	853.9 (0.39)	851.9 (0.16)	852.8 (0.71)	845.2 (0.54)	SVl
	pori1	717.8 (1.74)	711.2 (0.21)	716.1 (0.72)	710.3 (0.49)	SVl
Kuopio	kuo	695.3 (0.20)	691.7 (0.79)	695.5 (0.09)	687.7 (0.55)	SVl
	kuo1	689.0 (0.07)	682.7 (0.71)	689.3 (0.32)	686.2 (0.25)	SV-2
	kuo2	573.7 (0.25)	570.2 (0.86)	573.6 (0.10)	571.1 (0.54)	SV-2
Joensuu	jnsu1	724.4 (0.94)	722.5 (0.27)	723.7 (0.27)	719.3 (0.73)	SVl
Kouvola	kou	777.3 (0.44)	774.3 (0.52)	778.7 (0.72)	764.4 (0.49)	SVl
Lappeenranta	lrta	725.0 (0.30)	722.0 (0.89)	724.2 (0.41)	718.8 (0.31)	SVl
	lrta1	635.5 (0.59)	632.0 (1.43)	635.8 (0.30)	631.1 (0.27)	SVl
Hämeenlinna	hnlina	787.1 (0.21)	786.4 (0.40)	788.0 (0.64)	780.1 (0.52)	SVl
Kotka	kotka	756.7 (1.29)	755.3 (1.54)	755.8 (0.83)	748.6 (0.60)	SVl

Notes: This table reports, for each city and sub-area, the estimated observed data DICs – the information criterion for model comparison. The preferred model is the one with the minimum DIC value. The standard errors are in parentheses.

Table 3. Estimated DICs – Two-room flats

		Two rooms flats
Regions	Cities/Sub-areas	SV	SV-2	SVt	SVl	The best model
Helsinki	hki	583.5 (0.47)	585.7 (1.06)	583.4 (0.42)	581.8 (0.45)	SVl
	hki1	698.8 (0.35)	697.4 (1.05)	698.5 (0.10)	697.9 (0.28)	SV-2
	hki2	601.1 (0.07)	604.3 (1.12)	602.3 (0.13)	599.9 (0.36)	SVl
	hki3	645.7 (0.23)	644.3 (0.43)	646.0 (0.12)	638.1 (0.28)	SVl
	hki4	643.7 (0.27)	645.4 (1.48)	643.9 (0.17)	636.0 (0.36)	SVl
Tampere	tre1	637.0 (0.21)	635.8 (0.70)	637.2 (0.43)	631.2 (0.30)	SVl
	tre2	712.1 (0.58)	710.7 (1.98)	711.0 (0.37)	708.5 (0.30)	SVl
Turku	tku	629.3 (0.43)	630.8 (1.69)	628.6 (0.24)	627.0 (0.18)	SVl
	tku2	713.9 (0.29)	714.7 (1.53)	714.6 (0.30)	710.8 (0.35)	SVl
Lahti	lti	638.8 (0.29)	640.4 (1.36)	639.5 (0.23)	631.4 (0.44)	SVl
Jyväskylä	jkla	630.5 (0.72)	631.4 (1.01)	629.2 (0.30)	622.3 (0.42)	SVl
	jkla1	661.7 (0.25)	661.5 (1.71)	662.7 (0.32)	655.2 (0.30)	SVl
	jkla2	704.6 (0.41)	701.7 (0.42)	703.3 (0.28)	693.5 (0.50)	SVl
Pori	pori	743.2 (0.57)	739.2 (2.03)	743.0 (0.19)	733.8 (0.50)	SVl
	pori1	802.4 (0.43)	801.2 (2.28)	802.8 (0.43)	789.1 (0.35)	SVl
	pori2	787.1 (0.45)	785.8 (0.24)	786.9 (0.31)	780.2 (0.75)	SVl
Kuopio	kuo	640.1 (0.23)	641.4 (1.98)	640.3 (0.40)	638.0 (0.60)	SVl
	kuo1	722.4 (0.14)	719.1 (0.92)	722.4 (0.12)	716.6 (0.46)	SVl
Joensuu	jnsu1	761.2 (0.16)	758.5 (2.15)	761.5 (0.27)	757.7 (0.10)	SVl
Seinäjoki	seoki	750.8 (0.39)	743.0 (1.22)	751.0 (0.40)	746.9 (0.54)	SV-2
Vaasa	vaasa	689.0 (0.34)	689.7 (0.52)	690.5 (0.57)	685.4 (0.25)	SVl
Kouvola	kou	767.6 (0.29)	761.7 (1.93)	765.7 (0.36)	759.8 (0.57)	SVl
Lappeenranta	lrta	680.1 (0.43)	680.6 (0.22)	679.4 (0.59)	677.1 (0.20)	SVl
	lrta1	756.4 (0.33)	753.5 (0.15)	756.2 (1.05)	750.9 (0.34)	SVl
Hämeenlinna	hnlina	714.3 (0.26)	709.1 (1.07)	715.1 (0.22)	709.2 (0.39)	SV-2
	hnlina1	745.2 (0.91)	741.1 (1.32)	744.1 (0.35)	739.1 (0.36)	SVl
Kotka	kotka1	786.6 (0.88)	784.0 (2.77)	786.9 (0.35)	778.1 (0.16)	SVl

Notes: This table reports, for each city and sub-area, the estimated observed data DICs – the information criterion for model comparison. The preferred model is the one with the minimum DIC value. The standard errors are in parentheses.

Table 4. Estimated DICs – More than three rooms flats

		Three rooms flats
Regions	Cities/Sub-areas	SV	SV-2	SVt	SVl	The best model
Helsinki	hki	627.4 (0.15)	631.2 (0.84)	628.0 (0.28)	628.2 (0.79)	SV
	hki1	728.5 (0.14)	728.9 (0.73)	729.2 (0.19)	727.7 (0.55)	SVl
	hki3	649.8 (0.14)	648.3 (0.63)	649.9 (0.12)	646.9 (0.50)	SVl
	hki4	665.4 (0.43)	661.6 (1.81)	664.6 (0.11)	661.2 (0.38)	SVl
Tampere	tre	629.9 (0.65)	631.7 (0.81)	630.1 (0.22)	628.2 (0.20)	SVl
	tre1	713.2 (0.15)	713.2 (1.25)	713.4 (0.17)	710.5 (0.44)	SVl
	tre2	721.9 (0.60)	714.8 (1.93)	722.8 (0.49)	717.5 (0.52)	SV-2
	tre3	617.4 (0.18)	619.4 (1.09)	617.3 (0.42)	614.2 (0.26)	SVl
Turku	tku	676.3 (0.12)	673.7 (1.12)	676.6 (0.34)	671.0 (0.34)	SVl
	tku1	757.3 (0.15)	756.1 (2.07)	757.7 (0.23)	753.3 (0.52)	SVl
	tku2	725.3 (0.40)	725.9 (2.41)	724.3 (0.39)	722.2 (0.43)	SVl
	tku3	706.1 (0.25)	706.6 (0.90)	706.9 (0.21)	702.3 (0.74)	SVl
Oulu	oulu	658.7 (0.17)	658.0 (1.00)	659.8 (0.15)	656.0 (0.31)	SVl
	oulu1	716.9 (0.20)	715.0 (1.18)	717.7 (0.23)	713.8 (0.62)	SVl
Lahti	lti	710.3 (0.16)	711.7 (0.16)	710.6 (0.72)	701.8 (0.51)	SVl
	lti1	769.6 (0.40)	767.7 (0.12)	770.8 (0.23)	762.2 (0.58)	SVl
Jyväskylä	jkla	709.5 (0.59)	703.8 (0.25)	710.5 (0.20)	706.2 (0.26)	SV-2
	jkla1	730.1 (0.40)	725.4 (2.05)	730.7 (0.45)	725.0 (0.63)	SVl
	jkla2	787.1 (0.44)	785.2 (0.11)	787.2 (0.35)	781.6 (0.28)	SVl
Pori	pori1	768.6 (0.94)	762.1 (2.18)	769.9 (0.64)	761.1 (0.41)	SVl
Kuopio	kuo	703.2 (0.08)	700.0 (0.42)	703.4 (0.16)	701.1 (0.34)	SV-2
	kuo1	754.2 (0.22)	746.2 (0.83)	754.9 (0.39)	751.1 (0.49)	SV-2
	kuo2	719.2 (0.33)	714.7 (1.32)	717.8 (0.17)	716.5 (0.22)	SV-2
Seinäjoki	seoki	697.2 (0.31)	686.6 (0.19)	697.1 (0.52)	691.0 (0.48)	SV-2
Vaasa	vaasa	744.2 (0.55)	743.5 (0.20)	744.9 (0.39)	737.9 (0.30)	SVl
	vaasa1	737.3 (1.04)	737.6 (0.13)	737.2 (0.90)	740.2 (0.41)	SVt
	vaasa2	544.1 (0.26)	536.9 (1.88)	544.7 (0.25)	542.8 (0.25)	SV-2
Lappeenranta	lrta	749.5 (0.38)	747.8 (0.10)	749.7 (0.33)	743.3 (0.29)	SVl
	lrta2	511.7 (0.19)	500.1 (1.20)	511.0 (0.10)	510.8 (0.12)	SV-2
Hämeenlinna	hnlina1	727.9 (0.51)	718.5 (0.15)	727.7 (0.20)	720.8 (0.49)	SV-2
Kotka	kotka	778.1 (0.14)	773.0 (1.03)	778.9 (0.33)	770.9 (0.38)	SVl

Notes: This table reports, for each city and sub-area, the estimated observed data DICs – the information criterion for model comparison. The preferred model is the one with the minimum DIC value. The standard errors are in parentheses.

Overall, in all three apartment types, the SVl model ranks as the best model for modelling the Finnish house price volatility. In the one–room flats category, out of 28 cities/sub-areas exhibiting ARCH effects, SVl model comes on top in 19. In two–room flats category, SVl model leads in 24 cities/sub–areas out of 27;, and in the more than three rooms flats category, SVl comes on top in 20 cities/sub–areas out of 31. These results are in line with the general finding that asymmetric volatility (leverage effect and volatility feedback effect) is a crucial component in modelling assets returns. The results are also consistent with the findings of Dufitinema (2020) who documented, using the GARCH-type framework, the evidence of leverage effects in the price volatility of the studied types of apartment.

Next, the SV-2 model interchanges with the SVl and takes the first place. This pattern is observed in eight cities/sub-areas in the one-room flats category, in three cities/sub-areas in the two-room flats category, and in nine cities/sub-areas in the more than three rooms flats category. The exceptions of this general pattern are Oulu-area1 in the one-room apartments, Helsinki-city and Vassa-area1 in the more than three rooms apartments. In both sub–areas (Oulu and Vassa), the heavy-tailed model (SVt) performs better, followed by the Vanilla SV; whereas in the Helsinki–city the model performance rank is the other way around.

Finally, to further investigate the features that are vital in modelling the Finnish house price volatility dynamics; the vanilla SV and SV-2 model are compared. In doing so, the question of whether the AR(2) component is a useful addition to the vanilla SV model is also answered. As it can be observed in the one–room flats category where the SV-2 model outperforms the vanilla SV in 20 out 28 cities/sub–areas; the richer AR(2) volatility process provides significant benefits. In the two–room flats category, the SV-2 performs better than SV in 17 cities/sub-areas out of 27, and in 22 out of 31 in the more than three rooms flats category. Although the SV-2 general excel in comparison to the vanilla SV, cautions should be taken when modelling house prices volatility of individual regions. As it can be noted, the performance of the two models differs across cities and sub-areas, and by apartment types – no geographical pattern is observed. Therefore, retaining the standard specification of an AR(1) volatility process or adding a component depends on the house price dataset under study.

In summary, the stochastic volatility model with leverage effect is the best model for modelling the house prices volatility of most of the Finnish cities and sub-areas. In the rest of the regions, the SVl swaps places with the SV model where the latent volatility follows a stationary AR(2) process. In a few cases, the second place is less clear-cut; the vanilla and the heavy-tailed SV models share the ranking. However, again as above, the model performance differs from region to region. Therefore, when modelling house price, even by employing the SV framework, one has to enable different house price dynamics across cities and sub-areas; rather than imposing one SV model on the whole dataset. As it has been stressed in various studies, such as Milles (2011b) and Begiazi and Katsiampa (2019) that house prices present a heterogeneous dynamics across different areas and property types.

Out-of-sample volatility forecasting

Since the model that performs better in-sample does not necessarily imply that it will provide accurate forecasts, the out-of-sample forecast performance of the four competing models is investigated. The procedure starts by estimating the models using the training dataset, build 5-year volatility forecasts in terms of one step ahead, and validate the constructed predictions using the test dataset. For each city and sub-area in each apartment category, Tables 5–7 report the Root Mean Squared Error (RMSE) and the Mean Absolute Error (MAE); the measures used in assessing the forecasting accuracy for each model. The lower the value of the two criteria, the better the model’s forecasting performance.

Table 5. The results of RMSE and MAE – One room flats

		One room flats
Regions	Cities/Sub-areas	SV	SV-2	SVt	SVl
		RMSE MAE	RMSE MAE	RMSE MAE	RMSE MAE	The best model
Helsinki	hki	0.0152 0.0142	0.0167 0.0156	0.0148 0.0138	0.0157 0.0147	SVt
	hki1	0.0228 0.0195	0.0232 0.0198	0.0218 0.0187	0.0227 0.0194	SVt
	hki2	0.0169 0.0153	0.0178 0.0161	0.0166 0.0149	0.0173 0.0156	SVt
	hki4	0.0186 0.0152	0.0189 0.0154	0.0182 0.0148	0.0191 0.0155	SVt
Tampere	tre1	0.0351 0.0304	0.0351 0.0302	0.0352 0.0304	0.0350 0.0300	SVl
	tre3	0.0580 0.0435	0.0570 0.0420	0.0583 0.0435	0.0572 0.0441	SV-2
Turku	tku	0.0277 0.0249	0.0256 0.0231	0.0264 0.0238	0.0278 0.0249	SV-2
	tku1	0.0384 0.0332	0.0385 0.0334	0.0381 0.0324	0.0384 0.0333	SVt
	tku2	0.0338 0.0253	0.0335 0.0252	0.0333 0.0254	0.0332 0.0252	SVl
	tku3	0.0412 0.0362	0.0418 0.0367	0.0411 0.0359	0.0417 0.0367	SVt
Oulu	oulu	0.0357 0.0242	0.0360 0.0241	0.0359 0.0240	0.0357 0.0239	SVl
	oulu1	0.0494 0.0359	0.0497 0.0360	0.0501 0.0362	0.0495 0.0359	SV
Lahti	lti	0.0550 0.0394	0.0554 0.0394	0.0555 0.0394	0.0548 0.0393	SVl
	lti1	0.1657 0.1277	0.1664 0.1281	0.1674 0.1288	0.1655 0.1275	SVl
Jyväskylä	jkla	0.0337 0.0281	0.0332 0.0280	0.0339 0.0282	0.0337 0.0281	SV-2
	jkla1	0.0372 0.0336	0.0372 0.0338	0.0369 0.0332	0.0373 0.0337	SVt
	jkla2	0.0739 0.0579	0.0740 0.0580	0.0744 0.0581	0.0739 0.0578	SVl
Pori	pori	0.0619 0.0527	0.0615 0.0524	0.0624 0.0529	0.0617 0.0526	SV-2
	pori1	0.0484 0.0388	0.0483 0.0388	0.0497 0.0388	0.0481 0.0386	SVl
Kuopio	kuo	0.0271 0.0201	0.0272 0.0203	0.0271 0.0198	0.0272 0.0198	SVt
	kuo1	0.0672 0.0423	0.0691 0.0429	0.0693 0.0430	0.0673 0.0424	SV
	kuo2	0.0927 0.0739	0.0929 0.0740	0.0943 0.0751	0.0924 0.0738	SVl
Joensuu	jnsu1	0.0616 0.0372	0.0619 0.0373	0.0623 0.0374	0.0626 0.0379	SV
Kouvola	kou	0.0549 0.0411	0.0549 0.0411	0.0549 0.0407	0.0552 0.0412	SVt
Lappeenranta	lrta	0.0388 0.0316	0.0387 0.0314	0.0390 0.0315	0.0389 0.0319	SV-2
	lrta1	0.0459 0.0397	0.0461 0.0398	0.0464 0.0398	0.0461 0.0399	SV
Hämeenlinna	hnlina	0.0422 0.0311	0.0424 0.0312	0.0428 0.0313	0.0421 0.0310	SVl
Kotka	kotka	0.0289 0.0240	0.0290 0.0241	0.0292 0.0243	0.0288 0.0240	SVl

Notes: This table reports the performance of the four competing models in forecasting the house price volatility. The training set is 1988:Q1–2013:Q4, while the test set is 2014:Q1–2018:Q4.

RMSE is Root Mean Squared Error and MAE is the Mean Absolute Error.

Table 6. The results of RMSE and MAE – Two-room flats

		Two rooms flats
Regions	Cities/Sub-areas	SV	SV-2	SVt	SVl
		RMSE MAE	RMSE MAE	RMSE MAE	RMSE MAE	The best model
Helsinki	hki	0.0107 0.0091	0.0109 0.0093	0.0106 0.0090	0.0112 0.0096	SVt
	hki1	0.0182 0.0144	0.0183 0.0145	0.0179 0.0142	0.0191 0.0151	SVt
	hki2	0.0106 0.0093	0.0105 0.0092	0.0103 0.0090	0.0106 0.0092	SVt
	hki3	0.0182 0.0156	0.0176 0.0153	0.0179 0.0155	0.0183 0.0156	SV-2
	hki4	0.0227 0.0204	0.0222 0.0200	0.0220 0.0198	0.0223 0.0201	SVt
Tampere	tre1	0.0227 0.0213	0.0233 0.0219	0.0224 0.0210	0.0219 0.0204	SVl
	tre2	0.0247 0.0216	0.0241 0.0209	0.0239 0.0207	0.0252 0.0221	SVt
Turku	tku	0.0144 0.0126	0.0145 0.0127	0.0136 0.0118	0.0147 0.0129	SVt
	tku2	0.0309 0.0284	0.0308 0.0283	0.0302 0.0276	0.0306 0.0281	SVt
Lahti	lti	0.0176 0.0153	0.0178 0.0153	0.0179 0.0153	0.0177 0.0153	SV
Jyväskylä	jkla	0.0219 0.0146	0.0218 0.0146	0.0222 0.0148	0.0215 0.0143	SVl
	jkla1	0.0210 0.0158	0.0208 0.0158	0.0209 0.0157	0.0211 0.0160	SV-2
	jkla2	0.0648 0.0400	0.0653 0.0398	0.0652 0.0397	0.0647 0.0401	SVl
Pori	pori	0.0443 0.0339	0.0444 0.0340	0.0444 0.0340	0.0442 0.0339	SVl
	pori1	0.0572 0.0432	0.0574 0.0433	0.0578 0.0435	0.0569 0.0429	SVl
	pori2	0.0396 0.0356	0.0398 0.0358	0.0383 0.0345	0.0399 0.0358	SVt
Kuopio	kuo	0.0176 0.0151	0.0179 0.0154	0.0175 0.0151	0.0181 0.0155	SVt
	kuo1	0.0224 0.0197	0.0226 0.0198	0.0222 0.0196	0.0225 0.0198	SVt
Joensuu	jnsu1	0.0288 0.0256	0.0285 0.0253	0.0270 0.0239	0.0286 0.0255	SVt
Seinäjoki	seoki	0.0376 0.0321	0.0374 0.0319	0.0373 0.0318	0.0375 0.0320	SVt
Vaasa	vaasa	0.0192 0.0159	0.0199 0.0168	0.0188 0.0156	0.0194 0.0162	SVt
Kouvola	kou	0.0802 0.0474	0.0802 0.0474	0.0807 0.0474	0.0801 0.0474	SVl
Lappeenranta	lrta	0.0255 0.0223	0.0251 0.0220	0.0245 0.0214	0.0256 0.0224	SVt
	lrta1	0.0301 0.0270	0.0300 0.0269	0.0295 0.0260	0.0302 0.0272	SVt
Hämeenlinna	hnlina	0.0278 0.0246	0.0279 0.0247	0.0274 0.0237	0.0277 0.0244	SVt
	hnlina1	0.0328 0.0284	0.0330 0.0288	0.0324 0.0277	0.0329 0.0285	SVt
Kotka	kotka1	0.0698 0.0579	0.0699 0.0581	0.0705 0.0584	0.0702 0.0583	SV

Notes: This table reports the performance of the four competing models in forecasting the house price volatility. The training set is 1988:Q1–2013:Q4, while the test set is 2014:Q1–2018:Q4.

RMSE is Root Mean Squared Error and MAE is the Mean Absolute Error.

Table 7. The results of RMSE and MAE – More than three rooms flats

		Three rooms flats
Regions	Cities/Sub-areas	SV	SV-2	SVt	SVl
		RMSE MAE	RMSE MAE	RMSE MAE	RMSE MAE	The best model
Helsinki	hki	0.0205 0.0185	0.0206 0.0186	0.0199 0.0180	0.0207 0.0187	SVt
	hki1	0.0243 0.0197	0.0241 0.0194	0.0237 0.0191	0.0247 0.0199	SVt
	hki3	0.0178 0.0153	0.0181 0.0157	0.0176 0.0151	0.0183 0.0159	SVt
	hki4	0.0201 0.0174	0.0194 0.0166	0.0196 0.0168	0.0204 0.0176	SV-2
Tampere	tre	0.0216 0.0198	0.0213 0.0194	0.0208 0.0189	0.0217 0.0199	SVt
	tre1	0.0251 0.0224	0.0255 0.0228	0.0241 0.0212	0.0253 0.0226	SVt
	tre2	0.0506 0.0426	0.0504 0.0423	0.0503 0.0421	0.0505 0.0425	SVt
	tre3	0.0186 0.0152	0.0182 0.0146	0.0181 0.0145	0.0191 0.0161	SVt
Turku	tku	0.0194 0.0148	0.0195 0.0150	0.0195 0.0152	0.0196 0.0150	SV
	tku1	0.0290 0.0257	0.0291 0.0258	0.0289 0.0256	0.0291 0.0259	SVt
	tku2	0.0311 0.0263	0.0312 0.0263	0.0310 0.0261	0.0311 0.0264	SVt
	tku3	0.0358 0.0279	0.0359 0.0282	0.0357 0.0277	0.0358 0.0279	SVt
Oulu	oulu	0.0179 0.0157	0.0177 0.0155	0.0173 0.0152	0.0181 0.0159	SVt
	oulu1	0.0255 0.0228	0.0255 0.0229	0.0247 0.0220	0.0262 0.0235	SVt
Lahti	lti	0.0277 0.0237	0.0276 0.0236	0.0275 0.0234	0.0278 0.0238	SVt
	lti1	0.0317 0.0270	0.0311 0.0263	0.0309 0.0261	0.0320 0.0273	SVt
Jyväskylä	jkla	0.0212 0.0183	0.0218 0.0189	0.0210 0.0181	0.0213 0.0184	SVt
	jkla1	0.0281 0.0238	0.0278 0.0235	0.0268 0.0227	0.0282 0.0238	SVt
	jkla2	0.0526 0.0389	0.0522 0.0387	0.0536 0.0397	0.0524 0.0388	SV-2
Pori	pori1	0.0766 0.0536	0.0767 0.0536	0.0772 0.0538	0.0765 0.0535	SVl
Kuopio	kuo	0.0278 0.0246	0.0277 0.0246	0.0271 0.0237	0.0279 0.0247	SVt
	kuo1	0.0358 0.0329	0.0353 0.0322	0.0354 0.0323	0.0355 0.0324	SV-2
	kuo2	0.0514 0.0400	0.0512 0.0400	0.0521 0.0405	0.0513 0.0400	SV-2
Seinäjoki	seoki	0.0425 0.0350	0.0435 0.0361	0.0438 0.0366	0.0423 0.0346	SVl
Vaasa	vaasa	0.0341 0.0275	0.0339 0.0271	0.0340 0.0271	0.0341 0.0276	SV-2
	vaasa1	0.0392 0.0299	0.0396 0.0300	0.0398 0.0301	0.0395 0.0301	SV
	vaasa2	0.0300 0.0279	0.0301 0.0277	0.0301 0.0281	0.0299 0.0275	SVl
Lappeenranta	lrta	0.0348 0.0296	0.0350 0.0297	0.0349 0.0297	0.0349 0.0297	SV
	lrta2	0.0178 0.0157	0.0185 0.0164	0.0206 0.0189	0.0171 0.0150	SVl
Hämeenlinna	hnlina1	0.0424 0.0370	0.0423 0.0370	0.0422 0.0368	0.0424 0.0371	SVt
Kotka	kotka	0.0573 0.0387	0.0572 0.0386	0.0578 0.0391	0.0574 0.0386	SV-2

Notes: This table reports the performance of the four competing models in forecasting the house price volatility. The training set is 1988:Q1–2013:Q4, while the test set is 2014:Q1–2018:Q4.

RMSE is Root Mean Squared Error and MAE is the Mean Absolute Error.

Overall, in all three apartment types, both evaluation criteria rank the heavy-tailed stochastic volatility model (SVt) as the best model. Especially in the two rooms and more than three rooms flats categories, where the SVt model provides the best forecasts in, respectively, 17 out on 27 and 18 out of 31 cities/sub-areas. In the one-room flats category, the SVt and SVl models are neck and neck; they forecast best in, respectively, 9 and 10 out of 28 cities/sub-areas. These results confirm again, the importance of the heavy-tailed distributions not only in modelling but also in forecasting assets volatility. Moreover, as it has been found in other assets such as stocks (Nakajima and Omori 2009; Chan and Grant 2016a), even in the SV framework, when the heavy-tailed distribution is employed, it provides the model with extra flexibility against misspecification and outlier. The same conclusion can also be drawn in the case of house prices, where the SVt outperforms the SV model with standard errors.

A geographical pattern is observed in some regions where, in all three apartment types, the same model performs well in producing accurate forecasts. In Helsinki-city, Helsinki-area1 and Kuopio-city, the SVt is the first–ranked model across all apartment types, whereas the SVl comes on top in Pori-area1. These results imply that, in addition to the volatility clustering, the returns distributions of the former regions in all three apartments types are characterized by skewness and heavy-tailedness. While in the latter area, the returns’ major characteristic is leverage effect; a drop in apartment price causes an increase in house price volatility.

Regarding, the forecasting performance of the vanilla SV in comparison to the SV-2 model, unlike in the in-sample fit analysis where the SV-2 general excel; for the out-of-sample forecasting assessment, the vanilla SV model outperforms the SV-2 in most of the regions. Plus precisely, the vanilla SV does better in approximately 64% (18 out of 28) in the one-room apartments category; in 59% (16 out of 27) in the two-room apartments category; and in 52% (16 out of 31) in the more than three rooms apartments category. Thus, for forecasting the house prices at least, one can feel comfortable retaining the standard specification of an AR(1) volatility process. However, as there is no geographical pattern observed, the same as discussed above, cautions should be taken when forecasting house prices volatility of individual regions.

In summary, indeed, a model that performs well in the in-sample analysis may not provide accurate out-of-sample forecasts. The heavy-tailed stochastic volatility model is the best model for forecasting the house prices volatility of most of the Finnish cities and sub-areas. On the second place comes the stochastic volatility model with leverage effect, while the vanilla SV and SV-2 models share the last two rankings. Moreover, apart from a few areas (two cities and two sub–areas), no geographical pattern is observed in all three apartment types; the models’ forecasting performances vary across cities and sub-areas, and by apartment types.

IV. Conclusions, implications and further research

Volatility forecasting is one of the most fundamental methodologies in financial economics as it is a vital tool for asset allocation in general, and specifically for investors who implement volatility targeting. This article assesses the in-sample fit and the out-of-sample forecasting performance of four stochastic volatility models in the Finnish housing market. The competing models are the vanilla SV, the SV model where the latent volatility follows a stationary AR(2) process, the heavy-tailed SV and the SV with leverage effects. The study uses quarterly house price indices from 1988:Q1 to 2018:Q4, for 15 main regions in Finland.

The study has various findings. First, in all three apartment types, the stochastic volatility model with leverage effect ranks as the best model for modelling the Finnish house price volatility; indicating that leverage effect is a crucial component in modelling house price returns. Second, in most of the regions, the heavy-tailed stochastic volatility model excels in forecasting the house price volatility of the studied types of apartments, indicating that the skewness and the heavy-tailedness characteristics are vital components in forecasting house price volatility. Moreover, results suggest that the t innovations component is a useful addition to the vanilla SV model. Third, for the in-sample fit analysis, the AR(2) component is found to be a valuable addition to the vanilla SV, whereas, for the out-of-sample forecasting assessment, the vanilla SV model outperforms the SV-2 in most of the regions. Last, except for two cities and two sub-areas, no geographical pattern is observed for the models’ out-of-sample forecasting performances in all three apartment types. Their performances vary across cities and sub-areas, and by apartment types.

The findings have some housing investment implications. As housing investors, policy-makers and consumers are recommended to monitor the asset volatility; accurate forecasts help to improve portfolio diversifications across Finland and by apartment type. In addition, in the viewpoint of volatility as a measure of risk, precise predictions are the key to assessing investment risks; an essential decision-making factor for foreign as well as domestic investors who dominate the Finnish housing market.

In the standpoint of establishing suitable time-series volatility forecasting models of this housing market; these study findings – the performance of the four stochastic models – will be weighed up to their GARCH models counterparts. One reason is that Dufitinema and Pynnönen (2020) have found, in all three apartment types, evidence of long-range dependence in the returns and volatility for the majority of cities and sub-areas. The long memory present in the housing market returns suggests that the asset is forecastable on a long horizon, whereas the evidence of long-range dependence in the housing market volatility is the key to establish suitable time-series volatility forecasting models for the market. The other reason is that Dufitinema (2020) employed the Exponential GARCH (EGARCH) model to investigate whether the asymmetric effects of shocks are noted in the Finnish house price volatility. The author found that, indeed, these asymmetric impacts of shocks are observed in all three studied apartment types. Therefore, to assess whether the deterministic conditional variance under GARCH or the unobserved time-varying volatility under SV is more favoured by the house price data; these study outcomes will be compared to the performance of the short memory and long memory GARCH-type models. Namely, the EGARCH model, the Component GARCH (CGARCH) model and the Fractionally Integrated GARCH (FIGARCH) model. The aim is to provide to the investors, risk managers and consumers enlightenments with regards to which forecasting approach delivers accurate and superior volatility forecasts of the apartment types under study.

Moreover, it would also be of interest to incorporate, in a multivariate analysis, macroeconomic factors such as interest rates and unemployment rates; as the interaction between these variables and house prices is often of interest. Additionally, several studies have referred to the importance of spatial dependence in regional housing markets known as ‘the ripple effect’. The phenomenon refers to the house prices’ tendency to rise first in the part of the country during an upswing and to gradually spread out or ‘ripple out’ across the country. Meen, 1999 was the fisrt to provide convincing economic explanations for the ripple effect, and by utilizing different approaches, many studies have contributed to the discussions of the spatial interaction of regional house prices. Among the methods used to detect the ripple effect includes tests of cointegration (Alexander and Barrow 1994), the concept of absolute and conditional convergence (Chow, Fung, and Cheng 2016), a measure of the regional–national return spillover indices through Vector Autoregressive (VAR) model (Tsai 2015), and use of time-series volatility models (Morley and Thomas 2011; Lin and Fuerst 2014). Therefore, following Morley and Thomas and Lin and Fuerst, and using the current study outcomes, the analysis of the spatial spillover in the Finnish housing market is also subjected to future research. That is, as the stochastic volatility model with leverage effect (SVl) has been ranked as the best model for modelling the Finnish house price volatility of most of the regions. The ripple effects will be allowed in the model by incorporating house prices of the most populated area – the Helsinki region – as highlighted by the above-cited studies that the most populated area in a country may be a leading factor to influence the rest of the housing markets.

Furthermore, it would be worth investigating the structural breaks in the studied housing market. For instance, as discussed earlier, during the period of the end of 1980s to mid-1993, house prices in Finland experienced a structural break due to the financial market deregulation. By examining the occurrence of structural breakpoints, the full sample data can be divided into subsamples based on the estimated break dates, and hence improve forecast accuracy.

Disclosure statement

No potential conflict of interest was reported by the author.

Additional information

Funding

This work was supported by the Foundation for Economic Education (Liikesivistyrahasto) [16-8653].