Spatial Random Slope Multilevel Modeling Using Multivariate Conditional Autoregressive Models: A Case Study of Subjective Travel Satisfaction in Beijing

Abstract

This article explores how to incorporate a spatial dependence effect into the standard multilevel modeling (MLM). The proposed method is particularly well suited to the analysis of geographically clustered survey data where individuals are nested in geographical areas. Drawing on multivariate conditional autoregressive models, we develop a spatial random slope MLM approach to account for the within-group dependence among individuals in the same area and the spatial dependence between areas simultaneously. Our approach improves on recent methodological advances in the integrated spatial and MLM literature, offering greater flexibility in terms of model specification by allowing regression coefficients to be spatially varied. Bayesian Markov chain Monte Carlo (MCMC) algorithms are derived to implement the proposed model. Using two-level travel satisfaction data in Beijing, we apply the proposed approach as well as the standard nonspatial random slope MLM to investigate subjective travel satisfaction of residents and its determinants. Model comparison results show strong evidence that the proposed method produces a significant improvement against a nonspatial random slope MLM. A fairly large spatial correlation parameter suggests strong spatial dependence in district-level random effects. Moreover, spatial patterns of district-level random effects of locational variables have been identified, with high and low values clustering together.

本文探讨如何将空间依赖效应纳入标准多层级模式化（MLM）。本文所提出的方法, 特别适合在地理上聚集的调研数据分析, 其中个人在地理区域中套叠。我们运用多变量条件式自迴归模型, 发展空间随机斜率 MLM 方法, 以解释在同一区域内的个人对群体内部的依赖, 以及同时在区域之间的空间依赖。我们的方法, 改善晚近整合式的空间与MLM文献中的方法学进展, 并透过让迴归係数在空间上具有差异, 提供模型特殊化方面更大的弹性。该方法衍生出贝叶斯的马可夫链蒙地卡罗（MCMC）演算法, 以执行提出的模型。我们运用在北京的二层旅行满意度数据, 并应用提出的方法以及标准非空间随机斜率 MLM, 探讨居民的主观旅行满意度及其决定因素。模式比较的后果, 显示出强健的证据, 支持提出的方法对非空间随机斜率 MLM 而言产生显着的改进。相当大的空间相关参数, 显示出在行政区层级随机影响的大幅空间依赖。此外, 本研究指认区位变数中的行政区层级随机影响的空间模型, 其中高数值与低数值聚共同聚集。

En este artículo se explora el modo de incorporar un efecto de dependencia espacial en un procedimiento de modelado estándar a nivel múltiple (MLM). El método propuesto es particularmente adecuado para el análisis de datos de estudios aglomerados geográficamente, donde los elementos individuales están anidados en áreas geográficas. Basándonos en modelos de auto-regresión condicionales multivariados, desarrollamos un enfoque espacial MLM de inclinación aleatoria con el cual explicar simultáneamente la dependencia al interior del grupo entre individuos de la misma área y la dependencia entre áreas. Se destacan las mejoras de nuestro enfoque en el contexto de avances metodológicos recientes en la literatura espacial integrada y del MLM, ofreciendo una mayor flexibilidad en términos de la especificación del modelo al permitir que los coeficientes de regresión varíen espacialmente. Se derivan algoritmos bayesianos de la cadena de Markov Monte Carlo (MCMC) para implementar el modelo propuesto. Usando datos de satisfacción de viaje a dos niveles para Beijing, aplicamos el enfoque propuesto lo mismo que el MLM de inclinación aleatoria estándar no-espacial para investigar la satisfacción subjetiva de viaje de los residentes y sus determinadores. Los resultados de la comparación de los modelos muestran una fuerte evidencia de que el método propuesto produce una mejora significativa frente al enfoque MLM de inclinación aleatoria no-espacial. Un parámetro de correlación espacial bastante grande sugiere una fuerte dependencia espacial de los efectos aleatorios a nivel de distrito. Aún más, los patrones espaciales de los efectos aleatorios a nivel de distrito de las variables locacionales han sido identificados, con los valores altos y bajos agrupándose entre sí.

Key Words:

• Bayesian estimation
• Beijing
• conditional autoregressive model
• multilevel modeling
• subjective travel satisfaction

关键词：:

• 贝叶斯评估法
• 北京
• 条件式自迴归模型
• 多层级模式化
• 主观旅行满意度。

Palabras clave:

• estimación bayesiana
• Beijing
• modelo de auto-regresión condicional
• modelado a nivel múltiple
• satisfacción subjetiva de viaje

Suppose we want to understand what determines perceived travel satisfaction of commuters. We might be interested, for example, in the extent to which travel satisfaction is determined by travel-related variables (commuting time and mode choices) and locational variables (proximity to public amenities) versus the extent to which it is determined by individual life circumstance characteristics such as age, income, and gender. From our data on individuals i grouped into areal units j, we know that there are likely to be unobserved similarities and connections between individuals in the same area (Browne and Goldstein 2010). A modeling framework that explicitly acknowledges the multilevel structure of the data in terms of lower (individual i) and higher levels (areal unit j) will be required. An obvious solution would be to adopt a standard multilevel modelling (MLM) framework of the kind proposed by Goldstein (2003). MLM not only naturally captures the dependence effect within each group but offers a flexible framework for modeling heterogeneity of covariate effects whereby the slopes of covariates are allowed to vary across groups.

There is a potential problem, however, when applying MLM to hierarchical data where the study area is made up of groups defined by geographical areas such as districts or regions. In this context, although the vertical or hierarchical group dependence is modeled in an MLM, the horizontal dependence among areas is not (Dong and Harris 2015). More specifically, random effects including regression intercepts and slopes of one area are assumed to be uncorrelated with those of areas nearby even when they are geographically adjacent. That is, MLM conceptualizes geography simply as “place” through which group membership structure is defined, ignoring the dimension of “space”—the interplay and interactions between areas and the people who live in them (Arcaya et al. 2012; Owen, Harris, and Jones 2015).

Some arguments for the inclusion of spatial dependence in the area-level random effect have been put forward. For example, Morenoff (2003) and Savitz and Raudenbush (2009) argued that individuals' outcomes in one area could be affected by what happens in nearby areas because boundaries of spatial units might not be strictly impermeable. In other words, individuals might be living in different areas but in close proximity if they are located on either side of a geographical boundary and so might experience broadly the same events in the local area (Haining 2003). Second, geographical outcomes might be varying continuously across areas because they simply do not follow geographical boundaries (Fotheringham, Brunsdon, and Charlton 2002; Haining 2003). Third, the geographical boundaries used to designate areas at the various levels of a multilevel model are often arbitrary or determined by data availability. If, as is likely, there is a mismatch between the chosen spatial units and the spatial scales at which certain social processes under exploration operate, spatial dependence tends to occur (Anselin 1988; Fotheringham, Brunsdon, and Charlton 2002). Failing to account for spatial dependence will lead to unreliable estimates for both variance parameters and regression coefficients in MLM (Dong et al. 2015).

With increasing awareness of the problems associated with applying MLM to geographically hierarchical data, there is emerging interest in the development of hybrid methodologies to incorporate spatial dependence effect into MLM (Owen, Harris, and Jones 2015). Notably, in the spatial econometrics literature, efforts have recently been made to develop integrated spatial econometric and MLM frameworks (Corrado and Fingleton 2012; Baltagi, Fingleton, and Pirotte 2014; Dong and Harris 2015). Regarding these methodological advances, spatial dependence is conceptualized as a simultaneous autoregressive (SAR) model following the spatial econometrics convention (e.g., Cliff and Ord 1981; Anselin 1988; LeSage and Pace 2009). In another type of hybrid model, spatial dependence (at the lower level) is represented by a conditional autoregressive (CAR; e.g., Besag, York, and Mollie 1991; Banerjee, Carlin, and Gelfand 2004) model in addition to another set of independent random effects at the higher level (Arcaya et al. 2012). Similarly, Browne, Goldstein, and Rasbash (2001) employed a spatial multiple membership model to tackle spatial dependence effects in the sense that individuals are allowed to be influenced by both their immediate and neighboring contexts. Other conceptualizations of spatial dependence such as spatial Gaussian processes (e.g., Cressie 1993; Haining 2003; Banerjee, Carlin, and Gelfand 2004) have been included in MLM by Chaix, Merlo, and Chauvin (2005) and Chaix, Merlo, Subramanian, et al. (2005). A brief summary on differences between these methodologies is provided in Dong et al. (2015).

The baseline model on which the aforementioned extensions build is the standard random intercept MLM, which means that neither varying covariate effects nor spatial dependence in covariate effects is considered. This represents a serious limitation. Research questions of how covariate effects are heterogeneous across areas might be of great interest to researchers and policymakers. Although the standard random slope MLM is suitable for this type of research with multilevel data structures if higher level units are independent of each other (Raudenbush and Bryk 2002; Goldstein 2003), how to incorporate spatial dependence into the standard random slope MLM for investigating spatially varying covariate effects has rarely been studied.

This article fills the gap by proposing a spatial random slope MLM in which the higher level random effects are conceptualized as a multivariate CAR (MCAR) model. With a complex MCAR model (e.g., Besag, York, and Mollie 1991; Banerjee, Carlin, and Gelfand 2004), both the spatial dependence across areas and the within-area correlations between different sets of random covariate effects can be simultaneously accommodated. There are several important advantages associated with the proposed model. Generally, it will provide more efficient and accurate estimation for regression coefficients when compared to the standard nonspatial random slope MLM. In addition, MCAR models can introduce spatial smoothing and the borrowing of strength across neighboring areal units, leading to estimates of random covariate effects that are robust and have higher precision, which is of particular importance for areas with small sample sizes (Neelon, Anthopolos, and Miranda 2014). Furthermore, as correlations between different sets of random covariate effects are considered in the developed approach, the derivation of one set of random effects can benefit from the estimation of other sets of random effects (Congdon 2014). Finally, we contribute to the ongoing integrated spatial and MLM literature by proposing a flexible approach that simultaneously considers spatially varying intercepts and covariate effects.

In a simpler single-level modeling setting, MCAR models have been employed to examine spatially heterogeneous covariate effects across a study region in the so-called spatially varying coefficient models (e.g., Assuncao 2003; Congdon 2014). A close counterpart of our model is the one developed by Gelfand et al. (2007), which is motivated by a very specific set of house price data where residential apartments nest into spatially referenced building projects. Their higher level units are represented by spatial point objects and a multivariate spatial Gaussian process is employed to model the project-level random effects. In contrast, the higher level units in our case study are areal units (census districts in Beijing, China), as in many other geographically clustered survey data, and random effects at the area level are represented by the MCAR model, which is more suitable than the spatial Gaussian processes (Banerjee, Carlin, and Gelfand 2004; Wall 2004).

Using Beijing as a case study, we use the proposed method to investigate spatial variations of individuals' subjective travel satisfaction and its determinants. The data are derived from a large satisfaction survey of Beijing in 2005, which has a two-level structure with individuals nested into districts. We first comprehensively investigate how sociodemographic attributes, travel-related characteristics, and locational variables influence individuals' subjective travel satisfaction. Our main interest, however, is in whether and how the effects of locational factors (e.g., proximity to green parks and subway accessibility) vary across districts. The case study shows strong evidence that the proposed model provides a significant improvement against the nonspatial random slope MLM. Moreover, it also presents the spatial patterns of district-level random effects of locational variables with high and low values clustering together, which has rarely been researched before.

The remainder of the article is organized as follows. First, we introduce the technical foundations for our model, including the basics of the standard random slope MLM, followed by the CAR and MCAR models. We then specify the spatial random slope MLM and derive Bayesian Markov chain Monte Carlo (MCMC) algorithms for model implementation. Next, we apply the proposed approach to investigate the determinants of subjective travel satisfaction in Beijing, China. Finally, we conclude with a brief summary of research findings and suggestions for future work.

Model Foundations: Random Slope MLM, CAR, and MCAR

The Standard Nonspatial Random Slope MLM

Consider two-level clustered survey data where individuals nest into areas, at some more aggregate scale. Following Goldstein (2003), the standard nonspatial random slope MLM is specified as (1) (2) (3) (4) where i and j indicate individual and higher levels, respectively; y_ij is the outcome value for the ith individual within the jth higher level unit; x_ij is an individual-level covariate and β_1j are the associated regression slopes that vary across higher level units; β_0j are the random intercepts; and ϵ_ij is the individual-level residuals that are assumed to follow an independent normal distribution, N (0, σ_e²).

Equations 2 and 3 relate the random effects to a higher level covariate (x_j). In other words, higher level covariates can be included to explain the heterogeneity in the two sets of random effects (β_0j and β_1j). The term γ₀ measures the effect of x_j in explaining the random intercepts, and γ₁ quantifies the effect of x_j in explaining the random slopes of x_ij. The unexplained heterogeneity is denoted by u_0j and u_1j, respectively. The parameters σ_u0² and σ_u1² measure the amount of variation in the intercept and regression slope, and σ_u01² is the covariance of these two sets of random effects.

The resultant marginal distribution for u_0j is an independent normal distribution N (0, σ_u0²) and that for u_1j is N (0, σ_u1²). The covariance parameter σ_u01² is interpreted as the within-area association between u_0j and u_1j with the correlation coefficient measured by σ_u10²/sqrt(σ_u0²×σ_u1²). As previously mentioned, when the groups are areal units, we also anticipate the existence of between-area associations in each set of higher level random effects, which occur because of the geographical proximity-based spatial dependence effect.

CAR Models

Following Banerjee, Carlin, and Gelfand (2004), a J by J spatial weights matrix or neighborhood structure for higher level spatial units, W = (w_jk) is usually defined by geographical contiguity: w_jk = 1 if the jth and the kth areas share boundaries (denoted by j ~ k) and 0 otherwise. The intrinsic CAR (ICAR) is defined by the following full conditional distributions (Besag, York, and Mollie 1991; Congdon 2014):(5) where w_j+ is the number of neighbors of the jth area; u_j = (u₁, … , u_j-1, u_j+1, … , u_J) indicates random effects other than the jth area; the scalar τ² is the conditional precision parameter and so the variance of random effects u is 1/τ²; the conditional expectation of u_j, E(u_j | u_-j) is the mean of random effects from surrounding areas; and the conditional precision prec(u_j | u_-j) is proportional to the number of neighbors w_j+.

It is well known that the full conditional distributions for each observation together give rise to a unique intrinsic Gaussian Markov random field (GMRF), u ~ MVN (0, Ω_ICAR) (Besag, York, and Mollie 1991; Rue and Held 2005). The J by J precision matrix Ω_ICAR is(6) where D_W = diag (w₁₊, w₂₊, . . . , w_J+). Therefore, the density distribution of u is given by(7)

The precision matrix Ω_ICAR is improper because the row sums of (D_W – W) are equal to a vector of zeros. |Ω_ICAR|* denotes the generalized determinant calculated by the product of the (n – 1) nonzero eigenvalues of Ω_ICAR (Rue and Held 2005). In implementation, a sum-to-zero constraint on random effects should be enforced in each of the MCMC iterations (Banerjee, Carlin, and Gelfand 2004).

As an alternative, Leroux, Lei, and Breslow (1999) proposed a new CAR formulation (LCAR), specified as(8)

The resultant precision matrix for the LCAR specification is Ω_LCAR = τ²(L_W – λW), where L_W = diag (1 – λ + λw_j+). The LCAR model corresponds to an ICAR model when λ equals 1, reducing to an independent normal distribution when λ equals 0. At its heart, LCAR conceptualizes two sources of variability in area effects, the first being spatially structured and characterized by an ICAR process and the other being randomly distributed, characterized by an independent normal distribution (MacNab 2011). The parameter λ serves as a weight parameter measuring the relative importance between the two sources and as an indicator of the intensity of spatial dependence (Congdon 2014).

Other types of GMRF models such as proper CAR and convolution CAR (or the BYM model; Besag, York, and Mollie 1991) have also been extensively used to model spatial dependence (for a comprehensive technical review, see Banerjee, Carlin, and Gelfand [2004] and Congdon [2014]). One of the appealing theoretical properties of LCAR is that it can properly represent various levels of spatial dependence with a single set of random effects (Lee 2011). In contrast, ICAR models are only appropriate in situations when spatial dependence is very strong, which is self-evident as the spatial correlation parameter is set to one. The BYM model, on the other hand, uses the sum of two independent sets of random effects (one being ICAR and the other being independent normal) to represent spatial dependence. This complex conceptualization of spatial dependence makes BYM suffer from a lack of model identifiability, normally leading to large uncertainty in estimated model parameters (MacNab 2011). Technically, simulation studies have found that the LCAR model outperforms other CAR models including ICAR, proper CAR, and BYM in terms of both retrieving predefined spatial parameters and covariate effects across a wide range of spatial dependence scenarios (Lee 2011). Similar arguments and suggestions of using LCAR and its multivariate version to model spatial dependence have been made in MacNab (2011). As such, this article focuses on the LCAR model and its multivariate version for incorporating spatial dependence into the standard nonspatial random slope MLM. For the purpose of an easy exposition of complex MCAR models, ICAR and its multivariate version are also discussed in the article.

MCAR Models

In this section, multivariate ICAR (MICAR) and multivariate LCAR (MLCAR) models are briefly reviewed. For a general discussion on MCAR, see Gelfand and Vounatsou (2003), Banerjee, Carlin, and Gelfand (2004), Martinez-Beneito (2013), and Congdon (2014), among others.

Suppose there are P random effects for each area j (here we have P random covariate slopes) and denote u = (u₁, u₂, … , u_J) with u_j = (u_j1, u_j2, … , u_jP), j = 1, 2, …, J, p = 1, 2, …, P. Following Congdon (2014), the conditional distribution for u_j in MICAR is(9) where I_P is a P-dimensional identity matrix, Г is a P by P positive definite precision matrix, and its inverse, Σ, is the familiar covariance matrix. The diagonal entries of Σ are variances of each set of random effects and the off-diagonal entries measure the within-area correlations between different sets of random effects. As in ICAR, full conditionals specified in Equation 9(9) together result in a unique intrinsic multivariate GMRF, u ∼ MVN (0, Ω_MICAR) with a JP by JP precision matrix defined as(10) where the symbol ⊗ denotes the Kronecker product (Banerjee, Carlin, and Gelfand 2004). Similarly, the conditional distribution of u_j in MLCAR is (Congdon 2014)(11)

The precision matrix for the MLCAR is Ω_MLCAR = (L_W − λW) ⊗ Г. In contrast, the precision matrix for the nonspatial random slope MLM is simply I_n ⊗ V_u⁻¹, where I_n is an identity matrix of order n. In the subsequent analyses, MLCAR will be incorporated into nonspatial random slope MLM to model the spatial dependence among higher level random effects.

Proposing a Spatial Random Slope MLM Approach

Model Specification

Proceeding with the notation in the standard nonspatial random slope MLM, a spatial random slope MLM is specified as(12)

Note that the MLCAR model for the two sets of area-level random effects u₀ and u₁ is used in Equation 12(12) given the MICAR model is a just special case of the MLCAR with λ equal to one. For the purpose of the simplicity, a spatial random slope MLM with the MLCAR model is labeled as MLM-MLCAR, and a spatial random slope MLM with the MICAR model is labeled as MLM-MICAR. Under MLM-MLCAR, arranging the two sets of random effects by areas, as in Equation 9(9) , the distribution of random effects u is MVN (0, Ω_MLCAR), where Ω_MLCAR = (L_W – λW) ⊗ Г. The covariance of u is Ω_MLCAR⁻¹ = [(L_W – λW) ⊗ Г]⁻¹ = [(L_W – λW)]⁻¹ ⊗ Г⁻¹. The inverse of the precision matrix Г, Г⁻¹, is similar to V_u in the nonspatial random slope MLM in Equation 4. Spatial dependence effects in regression slopes are not modeled because of the missing spatial component [(L_W – λW)]⁻¹ in the covariance matrix from the nonspatial random slope MLM. It is useful to note that higher level residuals are assumed to be uncorrelated with residuals at the individual level in the proposed model to avoid the problem of identifiability.

Model Implementation

The proposed MLM-MLCAR is implemented within the Bayesian framework, using a Gibbs sampler with Metropolis updates when required (Banerjee, Carlin, and Gelfand 2004; Gelman et al. 2004). The choice of a Bayesian approach over a frequentist one for model implementation lies in that the model fits nicely into the Bayesian hierarchical spatial modeling framework (Banerjee, Carlin, and Gelfand 2004). Although frequentist approaches are possible for the proposed model, Bayesian estimation enables exact inference on model parameters and appropriate model uncertainty assessment (Gelfand 2012). To derive the full conditional posterior distributions of each model parameter, we rewrite the model in a compact matrix format:(13) where y is an N by 1 outcome vector, X is a covariate design matrix, which can consist of lower covariates, higher level covariates, and potential interaction terms between them. For example, if there are p low-level covariates and q higher level ones, then X will be an N by pq matrix. The pq by 1 vector β are fixed regression coefficients to estimate. Z is an N by Jp random effect design matrix, which is a block diagonal matrix with each block containing the lower level covariate values of individuals within one area. The Jp by 1 vector θ stores the random effects arranged by area.

Prior Distributions

For Bayesian inference, the basic principle is that the posterior distribution of θ* (unknown model parameters) is proportional to the product of the data likelihood and prior distributions (Gelman et al. 2004), as denoted by(14)

For the proposed approach here, the unknown model parameter vector is θ* = {β, θ, λ, σ_e², Г}. For prior distributions, a k-dimensional multivariate normal prior is set for β, with mean M₀ and covariance T₀. Therefore, P (β) ∼ MVN(M₀, T₀). The individual-level variance σ_e² is assigned an inverse gamma distribution, P (σ_e²) ∼ IG (c₀, d₀), and the area-level precision matrix Г is assigned a Wishart distribution, P (Г) ∼ dwish (R₀, v₀). These priors are conjugate priors so that the posterior distributions of parameters are in the same family as the prior probability distributions and are employed mainly for computational convenience. A uniform prior distribution is assigned for λ over (0, 1). Following Gelman et al. (2004), the inverse gamma distribution with c₀ and d₀ being the shape parameter and scale parameter is parameterized as(15) and a Wishart distribution with a scale matrix R₀ and a degree of freedom parameter v₀ is specified as(16)

The likelihood function for a spatial random slope MLM is(17) Therefore, the full posterior distribution for θ* = {β, θ, λ, σ_e², Г} is(18)

The Full Conditional Posterior Distribution of β

Let the posterior distribution for β be P (β | Y, θ, λ, σ_e², Г) ∼ MVN (M_β, ∑_β). According to Equation 18(18) , the posterior distribution for β is(19) where con is a constant value regardless of β. Comparing this with a standard multivariate normal density, we obtain(20)

The Conditional Posterior Distributions for {θ, σ_e², Г}

Following procedures similar to those used in deriving the full posterior distribution for β, we show the full posterior distribution for θ is also MVN (M_θ, ∑_θ), where(21)

The full conditions for σ_e² is IG (c_e, d_e), where(22)

The full conditional distribution for the within-area precision matrix Г is dwish (R*, v*) where(23) in which θ* is a J by p matrix with each column being the random effects that pertain to each individual-level covariate.

The Conditional Posterior Distribution for λ

The posterior condition distribution for λ, P (λ | Y, β, θ, σ_e², Г) P (θ | λ, Г) × P (λ) is(24)

Unlike {β, θ, σ_e², Г}, the spatial correlation parameter λ does not have a standard density distribution from which samples can be easily drawn. Therefore, an adaptive Metropolis approach with an acceptance rate of about 50 percent is used to update λ (Chib and Greenberg 1995; Gelman et al. 2004).

Application of MLM-MLCAR to Subjective Travel Satisfaction

In this section, the proposed MLM-MLCAR is employed to examine social and spatial variations in individuals' subjective travel satisfaction in urban Beijing, China. Based on a large-scale satisfaction survey conducted in 2005, we comprehensively investigate the impacts of sociodemographic attributes, travel-related characteristics, and locational variables on individuals' subjective travel satisfaction. Furthermore, we seek to understand how geographical context might influence covariate effects on travel satisfaction, which is an underresearched area.

Data and Variables

Our data are derived from a large-scale household satisfaction survey conducted in Beijing that collects residents' sociodemographics, travel-related characteristics, and evaluation of general living environment. The purpose was to evaluate Beijing's general livability, including life convenience, travel satisfaction, human and physical environment suitability, and health and safety conditions. The target population were residents living in urban Beijing (including 134 districts or Jiedao in total) for at least six months who are presumed to be familiar enough with their living environment to provide a good assessment. The survey had a stratified random sampling process, with the sample size in each district approximately proportional to its total population. In total, 11,000 questionnaires were issued and 7,647 of them were returned, of which 6,544 were valid. Further details of the survey and sample profiles are provided in Zhang, Yin, and Zhang (2006). It has been reported that this survey is quite representative of the overall characteristics of Beijing's population, when compared to the population census data (Zhang, Yin, and Zhang 2006; Meng, Zheng, and Yu 2011).

In this study, the overall travel satisfaction of each individual is modeled as the outcome of interest. Daily travel satisfaction is an important component of emotional well-being, and it might have a significant influence on overall life satisfaction (Ettema et al. 2012). Moreover, subjective travel satisfaction seems to be a more comprehensive and welfare-related indicator of effectiveness of urban planning and transport policy, when compared to objective evaluation measures such as average commuting time or traffic congestion (Meng, Zheng, and Yu 2011). As Beijing is experiencing rapid urban expansion, growing car use, increasing transport carbon emission, and serious air pollution, a better investigation and understanding of what factors influence subjective travel satisfaction and how geographical context shapes its spatial variation is of great value to urban planning, transport development, and relevant public policy evaluation in urban China (Ma et al. 2014).

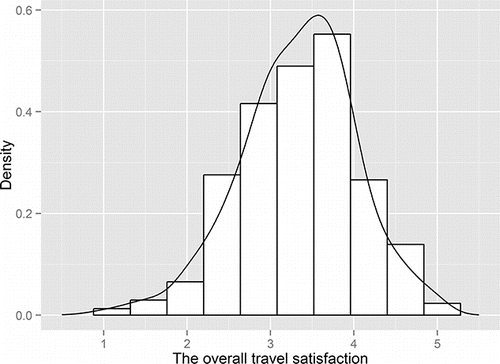
Table 1 presents the specific survey questions on travel satisfaction, including how people rate their satisfaction with public transport convenience, commuting convenience, and non-work-related travel convenience. For each of the survey questions, residents' responses are measured on a five-category Likert scale ranging from very unsatisfied to very satisfied. The overall travel satisfaction of each individual, defined as the outcome variable in the model, is calculated by averaging scores on each specific survey question listed in Table 1. The mean travel satisfaction scores approximate well to a continuous normal distribution (Figure 1) and thus are modeled as a continuous variable in this study.

Figure 1. The histogram plot of the overall travel satisfaction superimposed with a density curve.

Table 1. Survey questions on overall travel satisfaction

Survey questions			Measurement
The overall degree of travel satisfaction	How well do you satisfy with …	1. Public transport convenience 2. Traffic congestion conditions 3. Commuting convenience 4. Recreation-related travel convenience 5. Convenience to the city center	1 = very unsatisfied 2 = unsatisfied 3 = normal 4 = satisfied 5 = very satisfied

Much research has attempted to examine how subjectively experienced satisfaction correlates with various factors, such as sociodemographic attributes, density and diversity variables, accessibility to services, and social context. Conclusions remain equivocal (e.g., Ettema et al. 2012; Schwanen and Wang 2014). In our travel satisfaction model, the covariates are broadly divided into three categories. The first category includes a series of life circumstance variables or individual sociodemographic attributes, such as age, gender, and monthly income (Table 2). These variables are widely believed to have influence on overall life satisfaction, well-being, or happiness (e.g., Easterlin 2001; Ballas and Tranmer 2012). Second, a couple of travel-related variables, such as commuting time and transportation modes, are included in the travel satisfaction model. As the commute to and from work accounts for a significant part of daily travel, it might play an important role in overall travel satisfaction (Ettema et al. 2012). Moreover, we also take into account the interaction effects between commuting time and transportation modes on travel satisfaction.

Table 2. Summarizing the travel satisfaction data used in the analysis

Variable names	Definition	Mean/proportions	SD
Dependent variable
Travel	The overall travel satisfaction	3.333	0.698
Individual-level covariates
Sociodemographic variables
Income_1	Below 3,000 RMB	25.9%
Income_2	3,000–4,999 RMB	38.7%
Income_3	5,000–9,999 RMB	27.1%
Income_4	Above 10,000 RMB	8.3%
Age_below30	Age below 30	43.4%
Age_30–39	Age between 30 and 39	23.8%
Age_40–49	Age between 40 and 49	22.3%
Age_above50	Age above 50	10.6%
Female	Male as base category	50.2%
Commute-related characteristics
Commuting time	Log of resident's commuting time (minutes)	3.423	0.719
Commuting mode
Public	Public transport such as bus and subway	46.8%
Car	Private car	12.5%
Others	Walk, cycling, and other modes	40.8%
Locational variables
Dist_subway	Log of distance to the nearest subway stations	7.087	0.977
Dist_recreation	Log of distance to the nearest recreational facilities (e.g., sport centers)	6.628	0.938
Dist_park	Log of distance to the nearest green parks	7.667	0.851
Dist_CBD	Log of distance to city center (central business district)	9.162	0.679
District-level variables
Population density	Population density of each district (1,000 persons/km^2)	29.204	43.306

Note: RMB = Chinese Yuan Renminbi.

Finally, a set of locational variables is included in the model to measure multiple dimensions of urban form, including population density, accessibility to public transit, proximity to green space, availability of various recreational facilities, and accessibility to the city center (Table 2). Drawing on these diversified locational variables can help us extend the understanding of how geographical factors affect individuals' subjective travel satisfaction. Furthermore, we investigate whether and how the effects of locational variables vary across districts in urban Beijing, with particular interest in the proximity effects of green parks and subway stations, which are allowed to be different in each geographical area. This is partly because spatial heterogeneity in the capitalization of access to green parks and subway stations into land values in the study area has been recently acknowledged (Harris, Dong, and Zhang 2013; Wu and Dong 2014). Moreover, although subway service expansion is currently the focus of municipal policies for encouraging public transport in Beijing, a further exploration of spatially varying effects of proximity to subway stations could be beneficial to public transit development (e.g., identifying particular districts with transport infrastructure priority) and transport policy evaluation (Ma, Mitchell, and Heppenstall 2015).

Travel Satisfaction Model Specification

The empirical travel satisfaction equation to estimate is as follows:Travel_i,j = αX′ _i,j + γL′_i,j + δP′_i,j + β_jA′ _i,j + ϵ_i,j (25) where Travel represents travel satisfaction; i and j are individual and district indexes as in Equation 1(1) ; X represents sociodemographic variables including age, gender, and income (Table 2); L refers to locational variables of proximity to center city and recreational facilities whose effects are assumed to be fixed across districts; and P represents the urban form indicator (i.e., population density) at the district level. Parameters a, γ, and δ are fixed regression coefficients that we seek to estimate. A refers to proximity to green parks and subway stations and β_j are the associated regression coefficients that are assumed to be varied across districts. The fixed part (mean) of β_j is [β₁, β₂] and the random part is specified by [u₁, u₂], which follows a multivariate normal distribution with mean 0 and precision matrix Ω. Different formations of the precision matrix Ω from nonspatial random slope MLM, MLM-MLCAR, and MLM-MICAR were discussed earlier.

Model Comparisons

Comparing the performance of nonspatial random slope MLM, MLM-MLCAR, and MLM-MICAR, we adopt two commonly used Bayesian procedures: the deviance information criterion (DIC; Spiegelhalter et al. 2002) and the pseudo-Bayes factor (PsBF) calculated by an approximation to marginal likelihoods of two competing models (Neelon, O'Malley, and Normand 2010; Congdon 2014). The DIC is calculated as the sum of the posterior mean of the deviance (twice the negative log-likelihood of a model) and the number of effective model parameters. As a rule of thumb, if two competing models differ in DIC by more than three, the model with smaller DIC is regarded as a better fitting (Spiegelhalter et al. 2002). The Bayes factor (BF), obtained as the ratio of marginal likelihoods for two models, is another popular way to compare two competing models, which provides the evidence in the data that favors one model relative to another (Kass and Raftery 1995).

Following Neelon, O'Malley, and Normand (2010), to overcome the great computational difficulties of BF (calculation of marginal likelihoods of a model), we use the PsBF—an approximation of the BF through a cross-validation estimate of the marginal likelihood of a model (Gelfand and Dey 1994) to compare the performance of different models. The cross-validation predictive density for observation i is expressed as (Neelon, O'Malley, and Normand 2010)(26) where y_[-(i,j)] denotes the vector of outcome with the y_i,j deleted and θ represents the model parameters to estimate. The quantity f(y_i,j | y_[-(i,j)]) is called the conditional predictive ordinate (CPO) for the ith observation in district j, of which the Monte Carlo estimate is given by(27) where θ^(r) refers to the parameter vector sampled at the lth iteration l = 1, …, R (following a burn-in period) and f(y_i,j | θ^(r)) is the likelihood of observation [i, j] evaluated at iteration l. The product of CPOs for each observation is called the pseudo-marginal likelihood (PsML; Gelfand and Dey 1994), and the ratio of PsMLs of two competing models gives a PsBF (Congdon 2014).

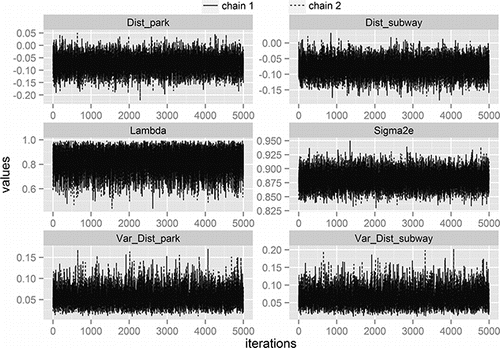
All competing models are coded using the R language. Diffuse or quite noninformative priors were placed on model parameters: fixed regression coefficients β ∼ MVN (0, 1000*I₁₈), the precision matrix Г ∼ dwish (I₂, 2), and the individual level variance σ_e² ∼ IG (0.01, 0.01). Initial values for each model parameter were drawn from their corresponding probability distribution. For each of these models, statistical inferences were based on two MCMC chains, each of which consisted of 60,000 iterations with a burn-in period of 10,000. We further retained every tenth sample to reduce autocorrelation in each MCMC chain. MCMC diagnostics including trace plots and Brooks–Gelman–Rubin scale reduction statistics (Brooks and Gelman 1998) indicated rapid convergence of our samplers and efficient mixing of chains for each model under study. Figure 2 provides post-burn-in trace plots for several representative model parameters from MLM-MLCAR: fixed regression coefficients including the proximity to nearest green park (Dist_park) and also the proximity to nearest subway station (Dist_subway), the individual-level variance parameter Sigma2e, the spatial correlation parameter λ, and variance parameters of two sets of random effects (Var_Dist_park and Var_Dist_subway). The two much overlapped trajectory lines show convergence and efficient mixing of chains (Figure 2). The mean of the lag-5 autocorrelations for parameters in MLM-MLCAR was 0.003, ranging from –0.026 to 0.063, and the 97.5 percent quantiles of the Brooks–Gelman–Rubin statistics were all less than 1.01, indicating good convergence of each chain (Neelon, O'Malley, and Normand 2010).

Figure 2. Trace plots based on two Markov chain Monte Carlo chains for six representative parameters from multilevel modeling-multivariate Leroux conditional autoregressive (MLM-MLCAR) model.

Model comparison results for the three models are provided in Table 3. All of the quantities are calculated based on the 10,000 post-burn-in samples from two MCMC chains. As shown in Table 3, the MLM-MLCAR produces the best model fit according to both the DIC and PsML statistics, compared to MLM-MICAR and nonspatial random slope MLM. Using the PsBF statistic, we find that the data strongly favor the MLM-MLCAR against nonspatial random slope MLM and MLM-MICAR with odds of 15.8 and 20.6, respectively (Kass and Raftery 1995). A better model fit of MLM-MLCAR against MLM-MICAR indicates the benefit of allowing the spatial correlation parameter to be estimated through data rather than defined a priori (equal to one in MLM-MICAR). The comparison between nonspatial random slope MLM and MLM-MICAR also supports this argument.

Table 3. Model fit comparisons using metrics of DIC, PsML, and PsBF

	DIC	PsML	PsBF (in favor of MLM-MLCAR)
MLM_MLCAR	17,602.0	–8,806.2
MLM_MICAR	17,608.7	–8,809.2
Nonspatial MLM	17,608.7	–8,809.0
MLM_MLCAR/MLM_MICAR	–6.7	3.0	20.6 (strong)
MLM_MICAR/nonspatial MLM	–6.7	2.8	15.8 (strong)

Note: DIC = deviance information criterion; PsML = pseudo-marginal likelihood; PsBF = pseudo-Bayes factor; MLM = multilevel modeling; MLCAR = multivariate Leroux conditional autoregressive; MICAR = multivariate intrinsic conditional autoregressive.

Results

Table 4 presents estimation results from MLM-MLCAR and nonspatial random slope MLM for a comparison. As shown later, posterior median and 95 percent credible intervals of each model parameter are produced. The estimate of the spatial correlation parameter in MLM-MLCAR is about 0.84 with a 95 percent credible interval [0.62, 0.97], indicating a fairly strong spatial dependence in each set of district-level random effects. We also investigate whether the district-level random effects of Dist_subway and Dist_park are spatially independent (as assumed to be so in nonspatial random slope MLM) by using the Moran's I statistic based on the same spatial weights matrix W used in MLM-MLCAR. The resultant Moran coefficient for random effects of Dist_subway is 0.144 with a p value equal to <0.001, and the Moran coefficient for random effects of Dist_park is 0.127 with a p value equal to <0.01. This demonstrates the existence of positive spatial dependence in the estimated random effects from nonspatial random slope MLM, which is in contradiction with the core model assumption of independence of random effects. Although there are no qualitative differences in fixed effect estimation between two models, MLM-MLCAR seems to be more efficient than nonspatial random slope MLM, as most of the 95 percent credible intervals of covariates are narrower than those from nonspatial random slope MLM.

Table 4. Summarizing the estimation results from the MLM-MICAR and MLM

	MLM-MLCAR			Nonspatial MLM
	Posterior median	2.5%	97.5%	Posterior median	2.5%	97.5%
Fixed effect estimates
Intercept	1.546	0.848	2.250	1.479	0.712	2.268
Income_1	−0.117	−0.176	−0.057	−0.115	−0.177	−0.055
Income_3	0.066	0.009	0.124	0.068	0.009	0.126
Income_4	0.187	0.096	0.274	0.186	0.094	0.276
Age_below30	0.055	−0.003	0.115	0.056	−0.003	0.114
Age_40-49	−0.095	−0.161	−0.027	−0.095	−0.162	−0.026
Age_above50	−0.176	−0.271	−0.088	−0.172	−0.263	−0.079
Female	0.004	−0.043	0.052	0.005	−0.040	0.051
Commuting time	−0.046	−0.096	0.003	−0.047	−0.098	0.004
Car	0.492	0.044	0.917	0.489	0.041	0.929
Public	0.791	0.508	1.085	0.787	0.494	1.094
Commuting time × Car	−0.158	−0.285	−0.027	−0.158	−0.287	−0.029
Commuting time × Public	−0.218	−0.298	−0.138	−0.217	−0.301	−0.134
Dist_subway	−0.078	−0.133	−0.023	−0.079	−0.132	−0.024
Dist_recreation	−0.009	−0.051	0.033	−0.010	−0.055	0.034
Dist_park	−0.076	−0.141	−0.008	−0.069	−0.137	−0.001
Dist_CBD	−0.110	−0.250	0.029	−0.093	−0.216	0.024
Population density	0.015	−0.065	0.094	0.017	−0.081	0.105
Lambda	0.840	0.620	0.970	N/A	N/A	N/A
Random effect estimates
Sigma2e	0.881	0.852	0.913	0.879	0.850	0.909
Var_Dist_subway	0.059	0.025	0.117	0.028	0.015	0.052
Var_Dist_park	0.050	0.022	0.099	0.024	0.013	0.044
Cov_ Dist_park/Dist_park	−0.050	−0.103	−0.020	−0.023	−0.045	−0.012
Corr_ Dist_park/Dist_park	−0.926	−0.965	-0.822	−0.901	−0.947	−0.814

Note: MLM = multilevel modeling; MLCAR = multivariate Leroux conditional autoregressive; CBD = central business district.

^a Although the main effect of commuting time is not statistically significant at the 95 percent credible level, it is significant at the 90 percent credible level with an interval of [–0.087, –0.005].

Travel Satisfaction and Life Circumstance

The estimates from MLM-MLCAR demonstrate that most of these life circumstance variables are significantly correlated with individuals' travel satisfaction (Table 4). For example, monthly income is significantly and positively associated with travel satisfaction. People with low-level income tend to have lower travel satisfaction, whereas high-level income tends to increase subjective travel satisfaction of residents. This broadly supports previous studies that have reported a significant impact of household income on life satisfaction or well-being, although the correlation is not linear (Easterlin 2001; Clark et al. 2008).

Distinctness is also found between different age cohorts. Older people are significantly associated with lower level of travel satisfaction, whereas young people (aged thirty and below) tend to score highest in satisfaction with travel. This is possibly because people aged forty and older are more likely to be involved in housework (e.g., child care and family errands) and recreational activities and thus they are more likely to be exposed to poor travel conditions in urban Beijing (Ma et al. 2014). Regarding the gender effect, there is no significant difference between men and women's travel satisfaction, which is in line with prior studies reporting similar satisfaction for gender (e.g., Ettema et al. 2012).

Travel Satisfaction and Commuting Behavior

Commute to and from work accounts for an important part of daily life, and it has a significant and negative effect on travel satisfaction. The MLM-MLCAR results show that with commuting time increasing, people's satisfaction with travel decreases while everything else equal, and this association is significant at the 90 percent credible level (Table 4). Commuting mode is also very significantly correlated with overall travel satisfaction. Compared to other travel modes such as walking or cycling, people commuting by car or public transport (i.e., bus and subway) tend to have higher travel satisfaction. The relationship between commuting behavior and travel satisfaction is complicated, however, by the inclusion of interaction effects between commuting time and modes, which are all statistically significant in the model.

As shown in Table 4, the negative regression coefficients of the interaction terms (Commuting time × Car and Commuting time × Public) suggest that with commuting time increasing, people's subjective satisfaction with travel by car and public transit tends to decrease. When commuting times for car or public transport surpass twenty-three or fifty-eight minutes, respectively, people's travel satisfaction with car or public transport is lower than that with other commuting modes, such as walking or cycling. From our survey data, we find that the average commuting time for the base category (e.g., walking and cycling) is approximately twenty minutes, which indicates that people are more likely to have higher satisfaction when they travel by car or public transport, rather than other commuting modes.

Travel Satisfaction and Geographical Context

The modeling results show that, of the locational variables, proximity to green parks and accessibility to subway stations are significantly associated with travel satisfaction. For instance, with close proximity to green parks at their residence, people tend to visit parks more often and they have higher travel satisfaction than their counterparts. Similarly, higher subway accessibility significantly increases residents' travel satisfaction, possibly due to the fact that the subway is fast, inexpensive, and uncongested in Beijing. People living in neighborhoods with higher population density or proximity to various recreational facilities also have higher travel satisfaction, although their correlations are not significant at the 95 percent credible level. Although proximity to city center is usually considered a proxy of employment accessibility, its correlation with travel satisfaction is insignificant. This is possibly because Beijing has undergone rapid urbanization, industrial decentralization, and residential suburbanization since the 1990s. High-tech industry zones and housing were established mainly in the suburbs, whereas employment opportunities for tertiary industries remained in the inner city (Ma et al. 2014). The emerging subcenters and coexistence of diversified land use configuration cause a complicated urban spatial structure in Beijing and also make it necessary to examine travel satisfaction under various geographical contexts.

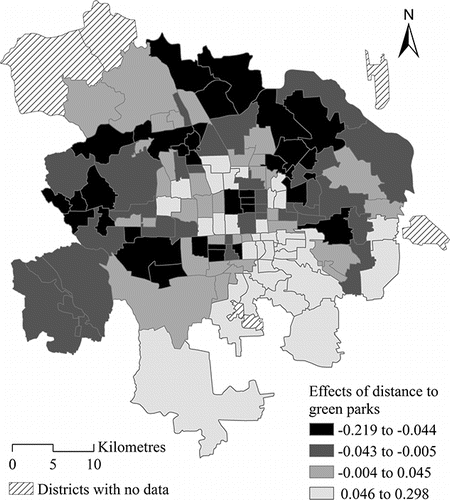
Regarding the random effect estimates of locational variables, Figure 3 illustrates the spatially varying effects of proximity to subway stations in urban Beijing. The break points in Figure 3 correspond to the lower quartile, median, and upper quartile of estimated posterior means of the district-level effect of proximity to subway stations. Clusters with large effects of being close to subway stations (large negatives) are identified, including areas to the southeast of the central business district (CBD), areas near Zhongguancun (a subcenter in Beijing), and areas in the northwest suburb of Beijing. It suggests that increasing the subway accessibility, particularly for the districts around employment centers (e.g., the CBD and Zhongguancun) and large “bedroom” communities (e.g., Hui Long Guan in the northwest suburbs), will increase travel satisfaction of residents in these areas substantially. This is possibly because higher subway accessibility significantly increases commuting satisfaction on a typical workday, as a job–housing spatial mismatch exists in Beijing (Ma et al. 2014). This analysis, for the first time, investigates spatially varying effects of subway accessibility on travel satisfaction, identifies the particular districts with subway development priorities, and suggests useful solutions to improving people's well-being in Beijing.

Figure 3. District-level effects of proximity to subway stations using estimates from multilevel modeling-multivariate Leroux conditional autoregressive (MLM-MLCAR) model.

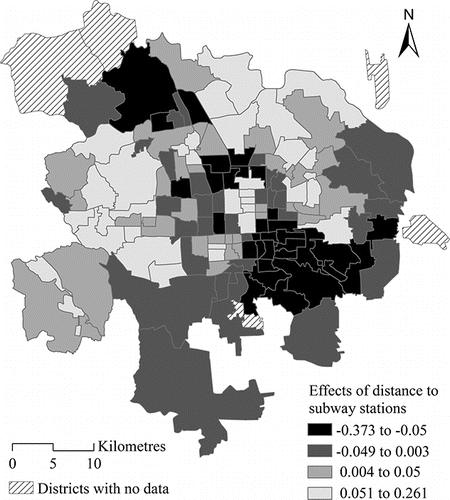
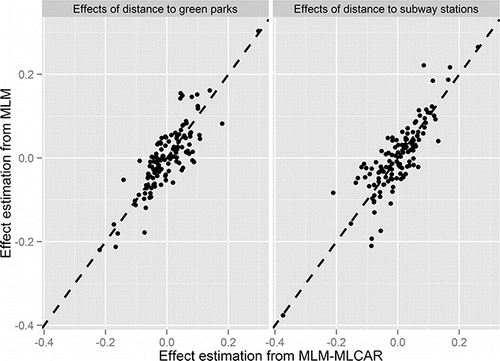
Figure 4 illustrates the spatially varying effects of proximity to green parks, with break points at the lower quartile, median, and upper quartile of estimated posterior means at the district level. It also shows that the marginal effect of proximity to green parks on travel satisfaction varies across districts, with the high effect of proximity to green parks predominately distributed in the northern area of Beijing. Although the employment subcenters are mostly located in northern Beijing, better access to green space substantially increases travel satisfaction of residents in northern districts, possibly due to the higher satisfaction with recreational travels. In addition, the random effect estimates of proximity to green parks and subway stations from nonspatial random slope MLM and MLM-MLCAR are illustrated and compared in Figure 5, with a scatter plot superimposed by a 45-degree dashed line. By and large, it presents a good correspondence in estimates between these two models, with simple Pearson correlation coefficients for estimated effects of proximity to green parks and subway stations being 0.835 and 0.839, respectively. It also shows that the large positive effects of these two locational variables are reduced in MLM-MLCAR, whereas the small negative values are raised.

Figure 4. District-level effects of proximity to green parks using estimates from multilevel modeling-multivariate Leroux conditional autoregressive (MLM-MLCAR) model.

Figure 5. Comparing effect estimates of proximity to green parks and subway stations from multilevel modeling-multivariate Leroux conditional autoregressive (MLM-MLCAR) and nonspatial multilevel modeling (MLM).

Conclusion

This study presents a new modeling approach through the development of a spatial random slope MLM that incorporates the spatial dependence effects into standard nonspatial MLM. The motivation is that for many geographically clustered survey data, the crucial assumption of independence among the higher level spatial units underlying the standard nonspatial random slope MLM is challengeable. The geographical closeness of areal units is likely to induce spatial dependence in geographical-level random effects, which means that the contextual effects at higher level in random slope MLM might be dependent across space.

Building on an MCAR model, we define the area-level random effects as a complex and correlated spatial process, and propose a complex MLM-MLCAR approach. The proposed approach can simultaneously model the spatial dependence effect across space and the within-area correlations between different sets of random effects. Given the proliferation of geographically grouped data on individuals and their extensive use in social, health, and environmental research, we anticipate that the developed approach could be useful in a wide range of applications.

Using Beijing as a case study, we use the new method to investigate the spatial variations of people's subjective travel satisfaction and its determinants. Model results show that life circumstance variables including income and age and commute-related characteristics such as commuting time and travel mode choices are significantly associated with travel satisfaction. Regarding the locational variables, better access to subway stations and green parks is significantly correlated with higher levels of travel satisfaction. Furthermore, the effects of proximity to subway stations and green parks exhibit a fairly strong spatial pattern in Beijing, with high and low values clustering together, respectively. This could be due to the relatively large spatial correlation parameter identified in the model.

One potential issue not addressed here regards the sensitivity of the identified district-level effect, due to the notable issue of uncertain geographic context (Kwan 2012). The problem might exist in our case study, as districts might not be the true geographical context that influences individuals' subjective travel satisfaction. We hope, however, that using the developed hybrid spatial MLM that allows the outcomes to be not only influenced by their immediate geographical context but also by neighboring contexts, random effect estimates at the higher level can be more robust.

Although spatial dependence is considered globally in our model, we find that some districts that are geographical neighbors can have different random effect estimates (Figures 3 and 4). Our next step is to further incorporate a localized perspective of spatial dependence into the model using the approach developed by Lee and Mitchell (2013). A further extension of our method would allow for nonspatial dependence between aerial units. Pryce (2013), for example, argued that Euclidean distance or contiguity might not be the only way that dependence occurs between aerial units—perceived substitutability; social networks or communication and transport links might lead to some units being “close” even if they are spatially distant. In such circumstances, the conditional autoregressive component of the model could be constructed in substitutability or network space rather than Cartesian space (Łaszkiewicz, Dong, and Harris 2014).

Acknowledgments

The authors are grateful for the comments of three reviewers and the editor, which have greatly improved the content of this article. They also would like to thank Professor Bill Browne and Dr. George Leckie from the Centre for Multilevel Modeling (CMM), University of Bristol for providing valuable comments on the previous draft of the article. Thanks are also due to Professor Wenzhong Zhang and Dr. Jianhui Yu from the Institute of Geographical Sciences and Natural Resources Research, Chinese Academy of Sciences for providing the data used in the study.

Funding

This work was funded by the Economic and Social Research Council (ESRC) through the Applied Quantitative Methods Network: Phase II, grant number ES/K006460/1. The first author also gratefully acknowledges the ESRC for funding his doctoral research during 2011 and 2014 and support from the National Natural Science Foundation of China (Project No. 41201169).

Additional information

Notes on contributors

Guanpeng Dong

GUANPENG DONG is a Postdoctoral Research Associate of Quantitative Methods in Sheffield Methods Institute, the University of Sheffield, Sheffield S1 4DP, UK. E-mail: [email protected]. His core research interests include developing integrated spatial statistical and multilevel modeling methodologies for properly analyzing geographically hierarchical data and the application of a wide range of spatial statistical and econometric approaches in housing markets, environmental evaluation, housing behavior analysis, and urban economics.

Jing Ma

JING MA is an Assistant Professor of Human Geography in the School of Geography, Beijing Normal University, Beijing, 100875, P.R. China. E-mail: [email protected]. Her main research interests include spatial microsimulation, activity-travel behavior, urban geography, environmental pollution, and sustainable development.

Richard Harris

RICHARD HARRIS is a Professor of Quantitative Social Geography in the School of Geographical Sciences, University of Bristol, Bristol BS8 1SS, UK. E-mail: [email protected]. His core research interests include spatial statistics and geodemographics in marketing, education, public policy, and urban geography.

Gwilym Pryce

GWILYM PRYCE is a Professor of Urban Economics and Social Statistics and the Director of Sheffield Methods Institute, University of Sheffield, Sheffield S1 4DP, UK. E-mail: [email protected]. His core research interests are largely in the broad field of urban economics, including housing and mortgage markets analysis, urban segregation, economic valuation of environmental amenities, and neighborhood effect inference.

Notes

1. For each of the spatial multilevel models implemented, the convergence of the MCMC sampler is diagnosed using the CODA package (Plummer et al. 2006) in R. In terms of efficient computation, a crucial part is updating the spatially random effect, a JP by 1 (384 by 1 in this case) vector based on its full posterior conditional distribution. We take advantage of a desirable characteristic of the GMRFs, the sparsity of their precision matrix, and therefore some fast sparse matrix Cholesky factorization can be carried out. More specifically, a canonical parameterization of the posterior distribution of the spatial random effect is used to draw samples of them via a very useful and computationally efficient function in an R package, SPAM, created by Furrer and Sain (2010). Details on fast sampling algorithms for GMRFs are provided in Rue and Held (2005) and Furrer and Sain (2010). It takes about four minutes for the MCMC sampler of the MLM-MLCAR model to produce 10,000 samples on a laptop with an Intel Core 2.5 GHz processor. Before applying the code to the travel satisfaction data, we conducted a series of simulation studies with known data generating processes and using the geography (data structure) of the travel data to test the code. The results show that spatial multilevel models can accurately retrieve the true model parameters. The R code for implementing the spatial multilevel models and the simulation study results are available on request.

2. Based on estimates from MLM-MLCAR in Table 4, the marginal effects of commuting by car and public transports (with other transport modes as baseline category) are 0.492 + (–0.158) × Commuting time and 0.791 + (–0.218) × Commuting time, respectively. Equating the two marginal effects to zero (and exponentiating the solutions) gives the commuting time thresholds in the main text.