Implementation of FOPID controller with modified harmony search optimization for precise modelling and auto-tuning of nonlinear systems

Abstract

This research aims to optimize the fractional order proportional integral derivative (FOPID) controller for nonlinear process tests. Instead of relying on the traditional trial-and error method for dynamic parameter selection, this proposes a modified harmony search optimization method to compute the optimal dynamic parameters. Based on the physical parameters, using mathematical modelling techniques system transfer function is determined. Additionally, the delay of the control scheme is determined using the Open Loop Transfer Function (OLTF) response. The dynamic parameters of the FOPID controller are evaluated using the Harmonic Search Algorithm – Fractional Order Proportional Integral Derivative (HAS_FOPID) optimization technique, which aims to minimize the system's Integral Square Error (ISE). Time responses, including rise time, peak time, and peak overshoot, are obtained and optimized through the HAS_FOPID algorithm. To verify systems stability, the output response is analysed using various techniques such as bode plots, pole placement, and Nyquist plots. Furthermore, the HAS_FOPID optimization technique is compared with other natural optimization techniques to assess its effectiveness. The research also evaluates the system's robustness by supply/ load disturbances. The objective is to demonstrate that, the optimized HAS_FOPID technique, has significantly enhanced control performance, stability, and robustness of nonlinear systems compared to natural and alternative optimization approaches.

KEYWORDS:

• FOPID
• PID
• optimization
• model
• HAS

1. Introduction

Nonlinear-based modelling is a phenomenon of concern in many industries, namely slurry, liquid feeds and liquid fertilizer storage, chemical retention & blend barrels, biodiesel processing, reactor tanks, and leaching extractions in pharmaceutical and chemical industries, food processing industries, and petroleum industries. Conventional system modelling techniques used for nonlinear-based modelling such as direct relapse and essential measurable strategies are prone to errors and are highly inaccurate, nonlinear methods, modern approaches incorporate non-parametric methods, such as feed-forward which makes them tedious for usage in real-time applications.

Flow & level control in conical tank-based systems are the key industrial areas requiring modelling of non-linearity with high accuracy for precision control. Narrowed Tank is a non-linear scheme with a lot of moving parts. As a result, the output may be impaired from time to time. Because of its form, the conical tank is prone to non-linearity. In some process industries, a conical-bottomed cylindrical tank is employed for complete fluid drainage, where the nonlinearity is only at the bottom. However, because the tank system is always changing, it is very nonlinear, making liquid-level management challenging in such systems.

The nonlinear system performances are controlled based on the conventional method like the Integer Order PID controller (IOPID). The controller dynamic constraints can be computed based on the controller tuning formulas. One of the drawbacks of conventional controller design is that the power value of the IOPID should be always an integer value and fractional inputs are not possible. So, the response of the system is inadequate and not accurate.

FOPID controllers are used to overcome this issue. This controller's dynamic parameters can be optimized using various optimization techniques, such as the Artificial Bee Colony technique, Butterfly Optimization, Biogeography-based optimization, etc. A Harmonic Search Optimization algorithm is proposed to be used in the FOPID controller.

The objective of the research is to optimize the fractional order proportional integral derivative (FOPID) controller for nonlinear process tests. The traditional method of parameter selection using trial and error is replaced with the harmony search optimization method to compute the optimum dynamic parameters.

The specific contribution of the research includes:

• Computation of Nonlinear System Transfer Function: Determine the transfer function of the nonlinear system based on the physical features such as length, diameter, inflow, and outflow of the conical tank. Mathematical modelling techniques are used to derive the transfer function.

• Calculation of Delay: Compute the delay of the control scheme using the Open Loop Transfer Function (OLTF) of the system.

• Dynamic Parameters Evaluation: Evaluate the dynamic parameters of the FOPID controller using the Harmonic Search Algorithm – Fractional Order Proportional Integral Derivative (HAS_FOPID) optimization technique. The dynamic parameters are optimized based on the system's Integral Square Error (ISE).

• Optimization of System Responses: Optimize system responses such as rise time (tr), peak time (tp), peak overshoot (Mp), and other relevant performance metrics. The HAS_FOPID optimization technique is used to find the optimal values for these parameters.

• Verification of System Stability: Verify the stability of the system by analysing the output response using techniques such as the bode plot, pole placement, and Nyquist plot.

• Comparison with Natural Optimization Techniques: Compare the performance of the HAS_FOPID optimization technique with various other natural optimization techniques to assess its effectiveness and superiority.

• Analysis of System Robustness: Analyse the robustness of the system by evaluating its response to supply disturbances and set point changes. The optimized FOPID controller's ability to maintain stability and performance under varying conditions is assessed.

• The overall objective is to demonstrate the effectiveness of the HAS_FOPID optimization technique in achieving improved control performance, stability, and robustness for nonlinear systems, compared to traditional trial-and-error methods and other optimization techniques.

The paper is planned as follows, the first section clarifies why this project is needed and introduces the topic. The second section contains the literature review. Third section explains the system design of proposed work. Section 4 contains the results of simulation studies as well as a discussion of the findings. Finally, Section 5 has the conclusion.

2. Literature review

Mary et al. study an optimized FOPID controller for a nonlinear conical tank process. Integral Absolute Error (IAE), Integral Time Absolute Error (ITAE), and Integral Time Square Error (ITSE), the performance indices of the tuned FOPID controller, are discovered to be superior to those of the traditional PID and other FOPID controllers. They recommended creating a conical liquid-level process controller using an adaptive FOPID controller. [1].

In a different investigation, the controller gains, delay time, and dead time were determined using an open loop step test approach by Sudharsana et al. Because Taylor series approximation has better accuracy than other non-linear approximation approaches, the authors chose it for the non-linear approximation [2]. Fuzzy controllers and PI controllers for conical tank systems were compared by Sitanshu et al. The performance of a typical Proportional–Integral (PI) fuzzy controller and MISO (multiple input single output) fuzzy controllers were examined. It has been demonstrated through experimentation that the fuzzy controller performs better than the PI controller. The PI has a relatively sluggish reaction, but the fuzzy controller provides a steady state error and has a better settling time [3].

To regulate the temperature of the Small Scale Industry Steam Distillation Pilot Plant, Marzaki et al. researched the Model Predictive Controller (MPC) approach and contrasted it with the PID controller Small Scale Industry Steam Distillation Pilot Plant (SSISD). It is observed that MPC performs better than PID-based betting-based controllers. Even though the offered analysis is surely not exhaustive [4].

G. Saravanakumar et al. [5] investigated the conical tank's nonlinearity. Cohen and Coon, IMC, and conventional PID controllers were used and a comparison of these results was determined. Introducing a model-reference adaptive controller to avoid the minimal rise time will be the forthcoming plan for the evolution of the system.

D. Mercy et al. [6] proposed a technique built on Particle Swarm Optimization, toward implementing Particle Swarm Optimization (PSO) with PID tuning of a practical scheme provided used in sewage handling using an algorithmic approach. Dongdong Zhao et al. [7,8] a “FOPID” controller for the fuel cell air supply system based on an indeterminate feedback nonlinear spectator. The Proton-exchange membrane fuel cells (PEMFC) cathode pressure was estimated by the suggested non-linear observer.

Xi Zhou et al. [9] propounded a technique that concentrates on Fractional-order systems, PID control, nonlinear optimization, robust control implementation robust PID controller of fractional order design, and parameter tuning. Sudharsana Vijayan et al. [2] proposed an Adaptive PID controller technique to implement Conical Tank Level Monitoring with Soft Computation it uses a Taylor series approximation for non-linear approximation since it is more precise than other non-linear approximation methods.

D. Mercy et al. [6] proposed an algorithmic method to treat wastewater by employing particle swarm optimization for a real-time conical tank by PSO-PID tuning. Alok K. Mishra et al. [10] achieved the minimal harmonics cooperating PSO-Grey Wolf Optimization (GWO) process by which the parameter of FOPID was tuned. The designed system is convincing in terms of budget whereas the former has a drawback cumbersome in its size.

Deep Mukherjee et al. [11] deal with the idea of reducing the objective function which is correlated with the Nelder-Mead optimization technique holding the performance measures such as ISE, ITSE, and IAE producing the output of PID controllers in integral and fractional order. Gandikota Gurumurthy et al. [12] estimated the fractional integral terms of the controller using Recursive Approximation for the stable frequency bands.

Murad Yaghi et al. [13] introduced the tuning technique that allows the controller to be more optimized to track the target near the region of impact and consequently reach the target with more accuracy and less missed distance. Abhijeet Lanjewar et al. [14] illustrated that the FOPID and Linear–quadratic regulator (LQR) controller overcomes the shortcomings of both the LQR and PID and LQR controllers. The FOPID and LQR control strategy is an example of this. The control efforts needed are reduced over two other control strategies that point to the controller’s energy-efficient design.

Debasish Biswas et al. [15] describe the importance of solving the dynamics of the fractional order method by using the NSOF matrix method. Several modelling simulations such as NSOF-based FOPID and NSOF-based adaptive FOPID controllers were derived and their results proved their appropriateness.

Himanshu Kumar R. Patel et al. [16] propound that ISE index and integer order PID controller specifications were evaluated based on Zigler Nichols for FOPID parameters. Simulation experiments are carried out for a “fractional-order PID” (FOPID) controller in the nonlinear coupled conical tank level control system that produces sudden and incipient presence of actuator faults.

Baran Hekimoğlu et al. [17] is possible to avoid local minimal stagnation from the original algorithm and increase its convergence rate and subsequent accuracy. Initially, the suggested Chaos Decision Tree Algorithm uses a surrogate-based approach to test for stochasticity (ChASO) algorithm was implemented on six Unimodal and multimodal benchmark optimization problems. S. S. Mohamed et al. [15] designed the FOPID controller and the dynamic specification Kp, Ki, Kd as the powers of integral and derivative actions, viz. λ and µ respectively.

Abdullah Mughees et al. [17] developed tuning parameters for the FOPID controller, in conjunction with two fractional order parameters (λ and µ). According to the first modelling and laboratory model, the Maglev plant's mathematical model was achieved.

The existing works mainly focus on the dynamic calculation of parameters which can be more effective when a powerful search algorithm is integrated. The current work proposes precise modelling and auto-tuning with Harmony Search optimization techniques implementation using FOPID and PID controller for nonlinear systems.

Xu et al. [18] propose a novel fractional order PID (FOPID) controller based on a modified harmony search (MHA) algorithm for the control of nonlinear systems. The MHA algorithm is used to optimize the controller parameters, and the simulation results show that the proposed controller can effectively improve the control performance of the nonlinear system.

Kumar et al. [19] describe the implementation of a fractional order PID (FOPID) controller using a modified harmony search (MHA) algorithm for a DC motor drive system. The MHA algorithm is used to optimize the controller parameters, and the simulation results show that the proposed controller can effectively improve the performance of the DC motor drive system.

Singh et al. [20] present the design of a fractional order PID (FOPID) controller for a permanent magnet synchronous motor (PMSM) drive system using a modified harmony search (MHA) algorithm. The MHA algorithm is used to optimize the controller parameters, and the simulation results show that the proposed controller can effectively improve the performance of the PMSM drive system.

Md. Ariful Islam et al. [21] propose a modified harmony search algorithm for the design of fractional order PID controllers for a class of nonlinear systems. The proposed algorithm is compared to a conventional harmony search and genetic algorithms. The results show that the proposed algorithm outperforms the other two algorithms in terms of tracking error, overshoot, and settling time.

Md. Ariful Islam et al. [22] propose a hybrid harmony search algorithm for the design of fractional order PID controllers. The proposed algorithm is compared to a conventional harmony search and genetic algorithms. The results show that the proposed algorithm outperforms the other two algorithms in terms of tracking error, overshoot, and settling time.

3. System design

The flow outlet of the conical tank is nonlinear and the controller’s output given to the tank is linear. The tank outlet is made to approximate its nonlinear parameter to linear parameters from the survey of literature several existing algorithms were studied which are used for linear controllers. In the existing algorithms, auto-tuning is not applicable and has only one dynamic parameter throughout the process. Hence modelling and auto-tuning through harmonic search optimization algorithms were performed in this study.

The container is finished with stainless steel vertically balanced on a spot. Liquid arrives at the container after the roof and flows out of the storage tank from the bottom. The nonlinear setup's requirements have specified in Table 1 as follows:

Table 1. System physical specifications.

Equipment	Details
Conical tank	Built of Stainless casing with 70 cm height, Top to the bottom radius of 17.5 and 1.25 cm respectively.
Differential Pressure Transmitter (DPT)	The level is measured using DPT with one end open to the air.
Centrifugal Pump	Capacity of 800LPH
Final Control Actuator/ Element (FCA)	Air to release, input 3-15 PSI, pneumatically actuated
Flow meter	Rota meter capacity of 0-600 LPH

3.1. Technical specification

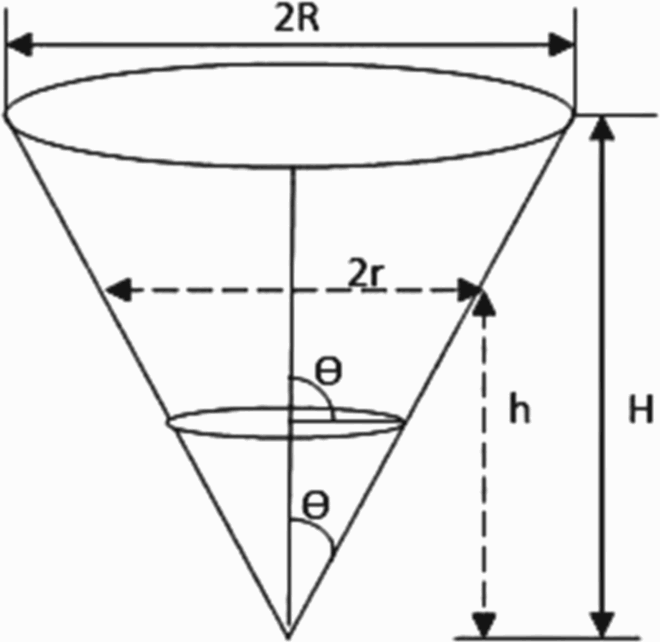
The conical tank-based system radius increases from bottom to top. So, the volume of the tank changes at each moment passing of stature of the container. Considering the height of the tank as the control variable and the flow rate of liquid into the container by way of the manipulated variable are taken for the mathematical modelling.

where h = Liquid in the tank Height [changing value], r = Liquid radius in the tank [fixed value], R = tank Radius [fixed value], H = whole height [fixed value].

Let the angle between theta $\theta$ $\tan \theta =\frac{\text{opp}.}{\text{adj}.}=\frac{\text{r}}{\text{h}}=\frac{\text{R}}{\text{H}}$Here the ratio r/h is equal to R/H. So, (1) $r=\left(R{}^{\ast }h\right)/H$(1) As we know the formula for the conical tank, cross-section is given by, (2) $\mathrm{Area}\left(A\right)=\pi r^2$(2) Substitute Equation (1) with Equation (2) to differentiate concerning time, (3) $\frac{\text{da}}{\text{ dt}}=\pi {\left[\frac{\text{R}}{\text{H}}\right]}^{2}2\text{h}\frac{\text{dh}}{\text{dt}}$(3)

The Cone Volume is calculated as follows: (4) $\text{V}=\left[\frac{1}{3}\right]\pi {\text{r}}^2\text{h}$(4) Differentiate Equation (4) concerning time, (5) $\frac{\text{dV}}{\text{dt}}=\frac{1}{3}\left[\text{A}\frac{\text{dh}}{\text{dt}}+\frac{\text{da}}{\text{dt}}\right]$(5) Substitute Equation (3) with Equation (5) (6) $\frac{\text{dV}}{\text{dt}}=\frac{1}{3}\frac{\text{dh}}{\text{dt}}\left[\text{A}+\pi {\left[\frac{\text{R}}{\text{H}}\right]}^{2}2\text{h}\right]$(6) According to Newton's Laws of Motion, Flow inlet $\left(\mathrm{Fin}\right)$ and Flow outlet $\left(\mathrm{Fout}\right)$ are equal, when there are no restrictions/disturbances. (7) $F_{\mathrm{in}}-F_{\mathrm{out}}=\frac{1}{3}{}^{\ast }\frac{\text{dh}}{\text{dt}}{}^{\ast }[\text{A}+2{\text{h}}^2\pi {\left[\frac{\text{R}}{\text{H}}\right]}^2$(7) Then F_out can be taken as, F_out= K$\sqrt{h}$, Here K is constant. (8) $F_{\mathrm{in}}-K\sqrt{h}=\frac{1}{3}\frac{\text{dh}}{\text{dt}}[\text{A}+2{\text{h}}^2\pi {\left[\frac{\text{R}}{\text{H}}\right]}^2$(8) where rate of change of height can be represented as, $\frac{\text{dh}}{\text{dt}}=\frac{3{}^{\ast }\left[\text{F}\mathrm{in}-\text{K}\sqrt{\text{h}}\right]}{\text{A}+2{\text{h}}^2\pi {\left[\frac{\text{R}}{\text{H}}\right]}^2}$Substitute the area value into the rate of change of height equation, which will get the Rate of change of height as, $\frac{\text{dh}}{\text{dt}}=\frac{3{}^{\ast }\left[\text{Fin}-\mathrm{K}{}^{\ast }\sqrt{\text{h}}\right]}{\pi {}^{\ast }{\left[\frac{\text{R}}{\text{H}}\right]}^2+2{}^{\ast }{\text{h}}^2\pi {}^{\ast }{\left[\frac{\text{R}}{\text{H}}\right]}^2}$Let, $\alpha =\frac{1}{{\text{h}}^2\pi {\left[\frac{\text{R}}{\text{H}}\right]}^2}$ & β = kα (9) $\begin{array}{rl}\frac{\text{dh}}{\text{dt}}& =\frac{\alpha {}^{\ast }\mathrm{Fin}}{{\text{h}}^2}-\text{β}{}^{\ast }\frac{{\text{h}}^{1/2}}{{\text{h}}^2}\\ \frac{\text{dh}}{\text{dt}}& =\alpha {}^{\ast }\mathrm{Fin}{}^{\ast }{\text{h}}^{-2}-\text{β}{}^{\ast }{\text{h}}^{-\frac{3}{2}}\end{array}$(9) According to Taylor’s expansion: Linearizing the rate of change of height equation ends $F{h}^2$ superscript can be rewritten as, (10) $\begin{array}{rl}& \text{F}\left({\text{h}}_1\text{Fin}\right)\\ & =\text{F}\left({\text{h}}_{\text{s}},\text{Fi}{\text{n}}_{\text{s}}\right)-2\text{Fin }{{\text{h}}_{\text{s}}}^{-3}\left(\text{h}-{\text{h}}_s\right)\\ & +{{\text{h}}_{\text{s}}}^{-2}\left(\text{F}-\text{Fi}{\text{n}}_{\text{s}}\right)\\ & \text{At the begining, Rate of change of height }\frac{\text{dh}}{\text{dt}}={\text{h}}^{-\frac{3}{2}}\end{array}$(10) (11) $\begin{array}{rl}& {\text{h}}^{-\frac{3}{2}}=\text{h}{\text{s}}^{-\frac{3}{2}}-{{\text{h}}_{\text{s}}}^{-\frac{5}{2}}\left(\text{h }-\text{ hs}\right)\end{array}$(11) Substitute Equations (11), (10) into Equation (9) (12) $\begin{array}{rl}\frac{\text{dh}}{\text{dt}}& =\alpha {}^{\ast }\left[\text{F }\right(\text{hs},\text{ Fi}{\text{n}}_{\text{s}})-2{}^{\ast }\text{Fin}{}^{\ast }{{\text{h}}_{\text{s}}}^{-3}(\text{h}-{\text{h}}_{\text{s}})\\ & +{{\text{h}}_{\text{s}}}^{-2}{}^{\ast }\left(\text{F}-\text{Fins}\right)]\\ & -\text{β}{}^{\ast }[\text{h}{\text{s}}^{-3/2}-\frac{3}{2}{}^{\ast }{{\text{h}}_{\text{s}}}^{-5/2}{}^{\ast }(\text{h}-{\text{h}}_{\text{s}}\left)\right]\end{array}$(12) At the beginning of settling state, (13) $\begin{array}{rl}\frac{\text{d}\left(\text{h}-\text{hs}\right)}{\text{dt}}& =\alpha {}^{\ast }[\phantom{\frac{3}{2}}-2{}^{\ast }\text{Fins}{}^{\ast }\text{ h}{\text{s}}^{-3}(\text{h }-\text{ hs})\\ & +\text{h}{\text{s}}^{-2}{}^{\ast }\left(\text{F }-\text{Fins}\right)\\ & +\frac{3}{2}{}^{\ast }\text{β}\mathrm{h}{\text{s}}^{-5/2}{}^{\ast }\left(\text{h}-\text{hs}\right)]\end{array}$(13)

Consider, $\text{y}=\left(\text{h}-\text{hs}\right)\text{ and u}=\text{F}-\text{Fins}$Substitute, y and u values in the Equation (13) and obtain the value of $\frac{\text{d}y}{\text{d}t}$ as, (14) $\begin{array}{rl}& \frac{\text{dy}}{\text{dt}}=-2\alpha \mathrm{Fi}{{\text{n}}_{\text{s}}}^{-3}\text{y}+\alpha {}^{\ast }{{\text{h}}_{\text{s}}}^{-2}{}^{\ast }\text{ U}+\frac{3}{2}{}^{\ast }\text{β}{}^{\ast }{{\text{h}}_{\text{s}}}^{-5/2}\text{y}\left)\right]\end{array}$(14) (15) $\begin{array}{rl}& \frac{\text{dy}}{\text{dt}}=-2\text{β}{}^{\ast }{{\text{h}}_{\text{s}}}^{1/2}{}^{\ast }{{\text{h}}_{\text{s}}}^{-3}\text{y}+\alpha {}^{\ast }\text{ h}{\text{s}}^{-2}{}^{\ast }\text{U}\\ & +\frac{3}{2}\text{β}{}^{\ast }\text{h}{\text{s}}^{-5/2}\text{y}\left)\right]\end{array}$(15) (16) $\begin{array}{rl}& \frac{\text{dy}}{\text{dt}}=-\left(\frac{1}{2}\right)\text{β}{}^{\ast }{{\text{h}}_{\text{s}}}^{-5/2}\text{y }+\alpha {}^{\ast }{{\text{h}}_{\text{s}}}^{-2}{}^{\ast }\text{ U}\end{array}$(16) (17) $\begin{array}{rl}& \left[\frac{2}{\text{β}}{}^{\ast }\mathrm{h}{\text{s}}^{-2}\right]\frac{\text{dy}}{\text{dt}}+\text{y}=\alpha {}^{\ast }\mathrm{h}{\text{s}}^{-2}{}^{\ast }\text{U}\left[\frac{2}{\text{β}}{}^{\ast }\mathrm{h}{\text{s}}^{5/2}\right]\end{array}$(17) (18) $\begin{array}{rl}& \tau \frac{\text{dy}}{\text{dt}}+\text{y}=\text{ cU }\end{array}$(18)

Comparing (17) and (18)  (19) $\tau =\frac{2}{\text{β}}{\text{h}}_{\text{s}}^{5/2}\text{and}\text{C}=2\frac{\alpha }{\text{β}}{h_s}^{1/2}$(19) Applying the Laplace transform the Equation (18) (20) $\begin{array}{rl}\tau \mathrm{sy}\left(\text{s}\right)+\text{y}\left(\text{s}\right)& =\text{ CU}\left(\text{s}\right)\\ \frac{\text{y}\left(\text{s}\right)}{\text{U}\left(\text{s}\right)}& =\frac{\text{C}}{\tau \mathrm{s}+1}\end{array}$(20) The various height of the tank transfer function is illustrated in Table 2. The optimum model is expressed as, $\text{G}\left(\text{s}\right)=\text{exp}\left(-1.05{}^{\ast }\mathrm{s}\right){}^{\ast }\frac{8.414}{0.06608\text{ s }+1}$The transfer function of the unity feedback system is represented by $\text{H}\left(\text{s}\right)=\frac{1}{\text{s}+1}$.

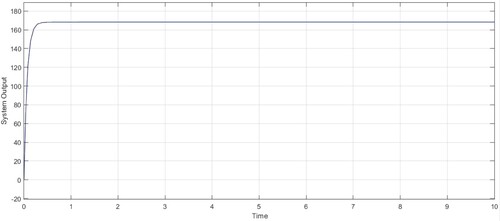
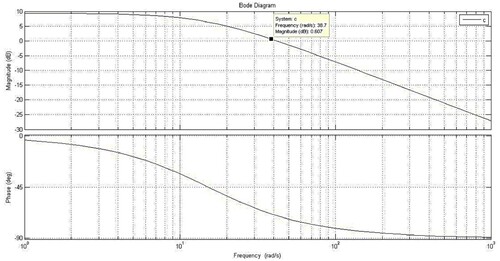
The open loop reaction of the derived plant transfer function is shown in Figure 1.

Figure 1. Reaction of the open-loop plant/system.

Table 2. The transfer function of the system based on the height of the tank.

Model No.	Range in cm	Height of the tank	The transfer function of the process
1	0–5	5	Drain
2	6–25	20	${\displaystyle \frac{8.414}{0.06608\text{ s}+1}}{}^{\ast }\mathrm{e}\left(-1.05\text{s}\right)$
3	26–45	40	${\displaystyle \frac{14.57}{1.03\text{ s}+1}}{}^{\ast }\mathrm{e}\left(-1.05\text{s}\right)$
4	46–65	60	${\displaystyle \frac{18.81}{3.684\text{ s}+1}}{}^{\ast }\mathrm{e}\left(-1.05{}^{\ast }\mathrm{s}\right)$
5	66–70	5	Vent

The dynamic parameters of the “FOPID” controller with various transfer function related to height are tabulated as follows. Here the tank height, on the top 5 cm is considered for the vent limit, and the bottom 5 cm is considered as the drain limit. The tank’s remaining range is divided into three parts with equal heights of 20 cm.

3.2. Maintaining transfer function of the plant

3.2.1. Open loop system

The system response can be determined by the open loop method. Give the known step input to the system and collect its response. From this, can able to formulate the system transfer function using process reaction curve method.

The plant or system transfer function can be represented as, $\frac{\text{H}\left(\text{s}\right)}{{\text{F}}_{\text{i}{\text{n}}^{\left(\text{s}\right)}}}=\frac{\text{k}}{\tau \mathrm{S}+1}$where

The gain constant $K=\frac{2\sqrt{{\text{h}}_1}}{\text{K}}$ and $\tau =\pi {\left(\frac{\text{R}}{\text{H}}\right)}^{2}K{h}_1^2$.

3.2.2. Input setting

The step input value is set by the amplitude of 10. The sample time has been set to 0.01 as shown in Figure 2.

Figure 2. Settings of the system.

The step input is given to the system and observes the response in scope. The system block elements including the source sink, and transfer functions are organized in a systematic way to attain the system function. For the open-loop system, step input is given, and the performance of variation related to the transient and steady-state are observed using the scope of the display shown in Figure 3.

Figure 3. Response of the open loop with input.

3.3. Feedback system

Established settings of the reference value, the plant produces an output that replica of its performance in an open-loop manner. The plant model is derived from the transient parameters. This model-based equation is being used for system control in a closed-loop manner.

3.3.1. PID controller

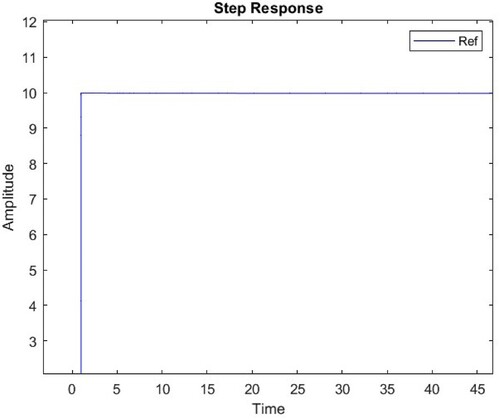
From the open loop system response, compute the dynamic parameters according to the tuning rules. Once the values are fed to the system, then the system is allowed to the closed-loop PID control operation. Here the set point taken as 10 cm and the figure shows the variation of amplitude. The closed-loop set point change performances is shown in Figure 4. According to the set point changes the system response can be viewed from the graph shown in Figure 5. The time domain parameters or data’s of the corresponding graphical details are viewed from the command window of MATLAB.

Figure 4. Step input to system.

Figure 5. Response of the PID controller.

3.3.2. FOPID-based controller

To improve the PID controller recital in a closed loop system, preferring the fractional order PID-based controller (FOPID).

As the computing parameters of FOPID are Kp, Ki, Kd, mu (µ), and lambda (λ). Here the FOPID controller is taken as the controller for the specified transfer function. The step input is given to the error detector for error calculation. The entire performance of the system is monitored using the scope.

3.4. Harmony search algorithm (HSA) response

One of the harmonic search algorithms commonly used is the swarm intelligent optimization algorithm [1,2]. When developing the harmonious melody, the musical orchestra enhances the musical harmony which resembles the same. The process of optimization assignment is usually correlated with each harmony to k decision variables for each harmony. The harmony memory consists of harmony memory with a size (HMS) identical to the genetic algorithm (GA) population, where HMS is referred to as the HM size. For the genome-wide association study, here k-way interaction model is considered a harmony. The main aim of this study is to get better harmony which will also have a substantial association with the phenotype.

4. Results and discussion

From there, we are going to compute the parameter (Kp, Kd, Ki, mu, lambda) values for the FOPID controller. The fitness function of the Harmonic Search Optimization can be derived from the following,

Min. (or) Max. f $\left(x_1,x_2,x_3,\dots \dots x_d\right)$

where

f = Fitness function

Here $x_i$ (i = 1, 2, … , d)

i = Decision variable

d = Problem dimension

$x_{i,j}=l_j+\mathrm{rand}{}^{\ast }\left(u_i-l_j\right)$

Here, i = 1, 2, 3, … N

j = 1, 2, 3, … .d

where

$l_j$ = Lower bounds decision variable of j

$u_j$ = Upper bounds decision variable of j

rand = Uniform distribution random number from 0–1.

Mathematical model of harmony memory is represented in matrix format as, $\begin{array}{rl}& \text{Harmony Memory }\left(\text{HM}\right)\\ & =\left|\begin{array}{c}\text{Harmony }1\\ \dots \\ \text{Harmony }1\end{array}\right|=\left[\begin{array}{ccc}{x}_{1,1}& \cdots & x_{1,d}\\ ⋮& \ddots & ⋮\\ x_{N,1}& \cdots & x_{N,d}\end{array}\right]\left|\begin{array}{c}{f}_1\\ ⋮\\ f_N\end{array}\right|\end{array}$From the matrix format, New Harmony memory model elements are derived as, $x_{\mathrm{new},j}=x_{\mathrm{new},j}+\mathrm{BW}{}^{\ast }\left(\mathrm{rand}-0.5\right){}^{\ast }|u_i-l_j|$where

BW = Generation of Bandwidth

(rand - 0.5) = Generate random number in the range from −0.5 to +0.5

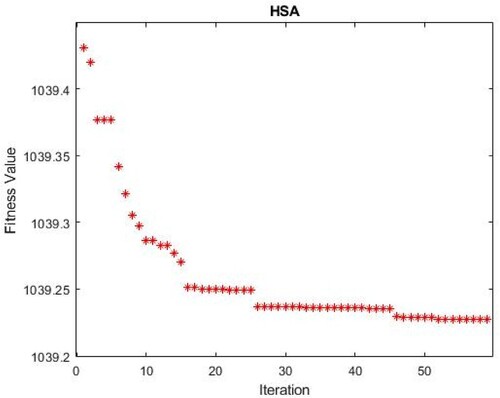
Based on this, the fitness value computed using FOPID-HAS.

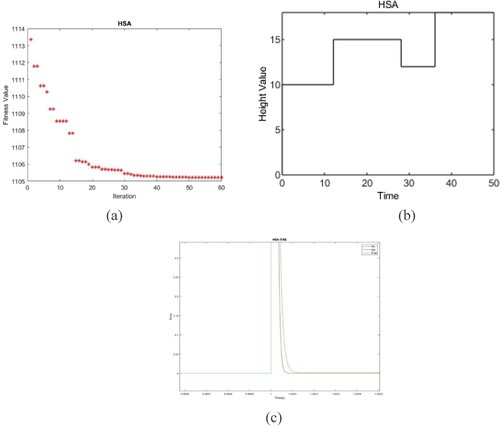
As shown in Figure 6, a fitness function is a fundamental type of objective function that is employed to sum up, how close a certain design strategy is to fulfill the predetermined goals as a single figure of merit. Fitness functions are employed in genetic algorithms and genetic programming to guide simulations toward the best architectural solutions.

Figure 6. Fitness function of HSA with iteration.

4.1. Optimal error value

If the facades are complex, there is no guarantee that the optimal parameters for the fitness function can necessarily be identified by the mechanism employed. The process will also converge to a surface position that it assumed is ideal, but is just a local optimum, not the global minimum. These parameters as an entry into another aspect of the phase of this portfolio. Optimal parameters are sought by restricting optimization to a classification of functions.

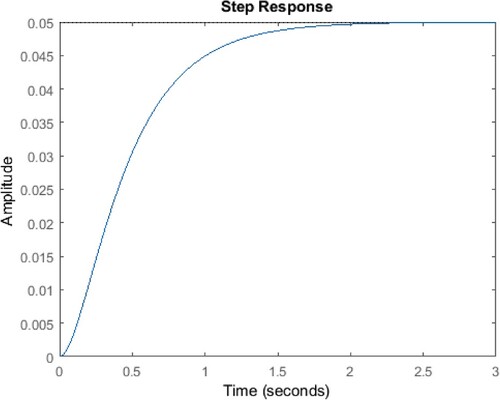
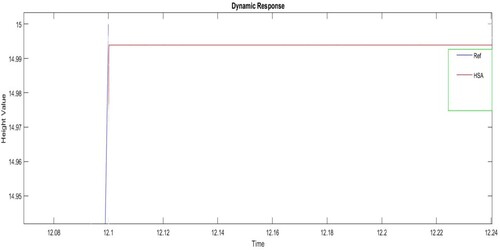
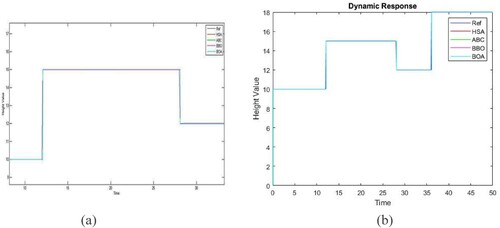
Here the required value is considered as 10 and the plant output received from the feedback element is 9.997. From this, concluded that, the steady state optimum error deviation is 0.003. The optimum value responses are shown in Figure 7(a,b). The error based on the HAS optimization is shown in Figure 7(c).

Figure 7. (a) Optimal response of HSA (b) Response of HSA with various set points (c) Error performance of the system.

4.2. Fopid output responses

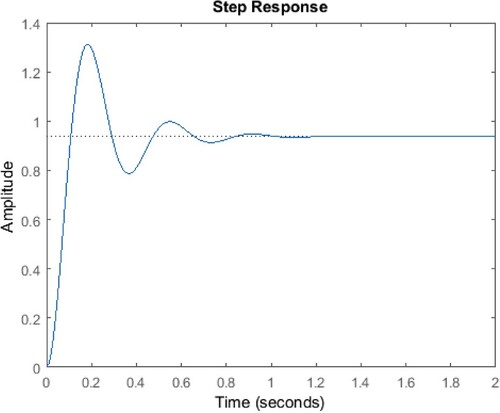
The HAS-tuned FOPID controller overtakes the typical PID controller in terms of unit recital, stoutness, and prime energy consumption for the operating range of 20–40 cm, according to simulation and real-time experimentation.

FOPID controllers are best apt to non-linear schemes; it can be noted in Figure 8. Figure 9 demonstrates that the suggested optimization strategy achieves an outstanding convergence rate and solution quality.

Figure 8. Output response of FOPID with system.

Figure 9. HSA convergence curve.

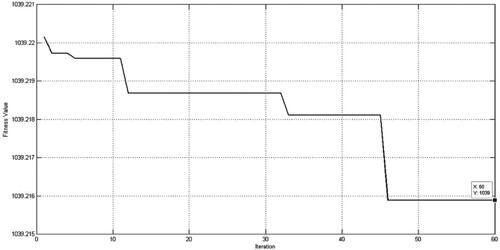
4.3. Has convergence behaviortions

In just 60 simulation iterations, the suggested approach effectively got the minimized value, 1039.2159, demonstrating its usefulness in tackling the current optimization issue.

4.4. Dynamic response evaluation HSA

The FOPID controller’s dynamic parameters are shown in Table 3. According to some of the most significant dynamic response measures, such as percentage overshoot, settling time, and peak time, Table 4 gives a quantitative assessment of the dynamic response.

Table 3. Optimized gain for FOPID.

Sl. No.	Constraint	Value
1	KP	24.904799659226462
2	KI	0.047159861740317
3	KD	6.531214849178121
4	Μ	0.054520288198813
5	Λ	0.059107294824940

Table 4. Evaluation of the envisioned HAS-based system's dynamic responsiveness.

Time domain Parameters/ Optimization method	HAS- FOPID	ABC (Artificial Bee Colony)- FOPID	BBO (Biogeography-based optimization)- FOPID	BOA (butterfly optimization algorithm)- FOPID	FF (Fire Fly)- FOPID	PSO (Particle swarm Optimization)- FOPID
Rise Time (tr)	6.2416e^−04	4.0025	2.2301e^−04	6.3660e^−04	8.2126e^−04	4.2640e^−04
Settling Time (ts)	1.2001	1.3061	1.4062	1.3071	1.4901	1.3001
Overshoot (%Mp)	5.4627e^−05	2.2377e^−06	3.2091e^−05	8.0278e^−05	3.2088e^−07	1.5994e^−04
Peak Value	9.9981	12.9943	10.9969	14.9961	11.9973	14.9955
Peak Time (tp)	1.0002	1.9236	1.7132	1.4235	1.6002	1.1403

However, modern conical tank design provides the minimum Rise time (tr) and percentage overshoot among all the studied conical tank optimization designs; thus, proving its efficacy and significance.

4.5. Stability assessment

Based on the system input or disturbance changes, system response may or may not be stable. Therefore, need to analyse/identify the system stability. Here, a bode diagram is used for identifying the stability of the system performances as shown in Figure 10.

Figure 10. Bode diagram of conical tank between phase, magnitude, and frequency.

The transfer function of tank level from 6 to 25 cm is given by (8.414)/(0.06608 s + 1)*e^∧ ((−1.05s)).

The transfer function of various tank heights performance is provided in Table 5. Here the Phase margin (PM), Gain margin (GM), Phase cross-over frequency (ωpc) in rad/sec, and gain cross-over frequency (ωgc) in rad/sec are considered for the analysis.

Table 5. Tank Transfer function.

Model No.	The transfer function of the Tank	PM	GM	ωpc	ωgc
1	${\displaystyle \frac{8.414}{0.06608\text{ s}+1}}{}^{\ast }\mathrm{e}(-1.05{}^{\ast }\mathrm{s})$	109.8544	Inf	NaN (Not a Number)	41.9092
2	${\displaystyle \frac{8.414}{0.06608\text{ s}+1}}{}^{\ast }\mathrm{e}(-1.05{}^{\ast }\mathrm{s})$	Inf	101.3109	NaN	4.8539
3	${\displaystyle \frac{8.414}{0.06608\text{ s}+1}}{}^{\ast }\mathrm{e}(-1.05{}^{\ast }\mathrm{s})$	Inf	98.7383	NaN	1.7660

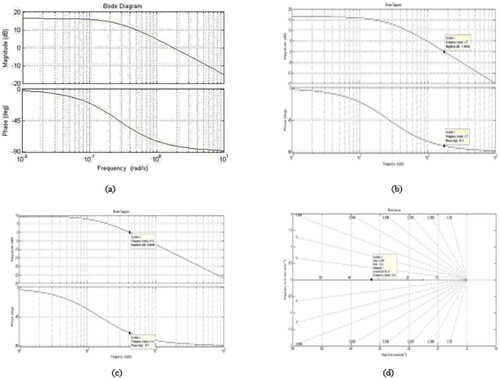
Based on a few significant illustrations of stability indicators phase Margin (PM), Delay Margin (DM), Bandwidth (BW), and Phase Gain (PG) system is considered to be stable. The proposed system design logic is represented as a Nyquist diagram. The real and imaginary axis details representation are shown in Figure 11(a,b).

Figure 11. (a,b) Effect of supply disturbance in conical tank system.

If the Bode plot's phase and gain margins are both greater than zero, all of the poles are positioned in the leftmost direction according to the pole-zero map, and the phase crossover frequency is higher than the gain crossover frequency, the tank level is regarded as stable. Figures 12(a–c) show the Bode plots of the conical tank system's different model transfer functions, and Figure 12(d) shows the suggested conical tank design's Pole-Zero Map.

Figure 12. (a) Bode plot of model no.1 transfer function conical tank system (b) Bode plot of model no.2 transfer function conical tank system (c) Bode plot of model no.3 transfer function conical tank system (d) Pole-Zero Map of the conical tank design.

4.6. File for robust scrutiny mats for graphics

When designing a control system, robustness analysis is done to determine how well the system will operate steadily under various parametric changes. In this experimental study, the robustness of the scheme is evaluated by altering the intrinsic conical tank transfer function gains, set point, and introducing noise or disturbance.

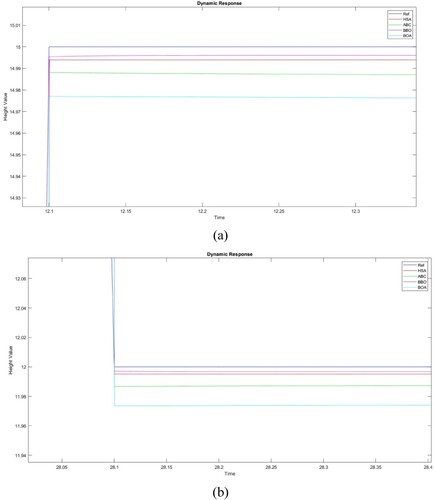
In Figure 13(a), the system's reaction is depicted together with a fair comparison to other met heuristic optimization algorithms.

Figure 13. (a) Robust analysis plot (b) Robust analysis plot disturbance point.

This subsection examines the proposed conical tank system’s robustness over set point changes. An additional input of magnitude 5 is inserted and reduced for testing purposes at 12 and 28 s into the simulation run, respectively. Figure 13(b) shows that the predicted HAS_FOPID controls the value at its set point and offers the best dynamic response among all the HAS_FOPIDs taken into consideration under the given input circumstances.

5. Conclusion

The dynamic constraints of “FOPID controller for nonlinear systems” remained optimized by HSA-FOPID optimization technique. The dynamic response parameters of the conical tank system were obtained by simulation was compared with various existing optimization techniques applied to a similar system. This present HSA Optimization is found to be an efficient and significant one with the least Rise time (tr) and minimum percentage overshoot among existing optimization techniques. The system stability was validated successfully with a bode plot, pole placement, and Nyquist plot analysis. Our future Scope is to model and analyse the SISO scheme, in order to prolong toward a MIMO-based complex scheme for improving their dynamic performance.

Disclosure statement

No potential conflict of interest was reported by the author(s).