Advancing Equitable and Responsible Research Involving Gender and Sexuality within Mathematics Education

Abstract

Mathematics education research has been slow to adopt inclusive practices concerning Queer students. In this study, two doctoral dissertations highlight responsible research approaches to advance inclusivity. Ambiguous use of the terms “sex” and “gender” and using only binary statistical methods can lead to erroneous assumptions about factors that might be biological, psychological, or social. Queer-related discussions in classrooms and research, both now largely non-existent, could support students in feeling visible and valued.

Keywords:

• Mathematics education
• gender
• sexuality
• teaching of mathematics for social justice
• inclusive statistics
• queer education

Mathematics education has been slower than other fields to adopt inclusive practices around gender and sexuality. Ambiguous use of sex and gender terms not only presents challenges in creating inclusive spaces for Queer students but also affects the ways research is interpreted and shared. Often, in mathematics education literature the terms “male” and “female” are used to connote biological sex assigned at birth, or the terms “gender” and “sex” are used interchangeably without recognizing their differences in meaning. This conflation has been criticized for well over a decade for its potentially harming effects (e.g. Ataide Pinheiro, 2021; Cox, 2022; Damarin & Erchick, 2010; Leyva, 2017; Lubienski & Ataide Pinheiro, 2020; Neto & Ataide Pinheiro, 2021); readers might assume biological factors are at play, when instead, gender and sexuality are socially or culturally formed. Glasser and Smith (2008) critiqued mathematics education researchers’ ambiguous use of the terms “gender” and “sex,” saying that this trend “slowed progress in understanding how gender influences students’ educational experiences” (p. 343). Likewise, Damarin and Erchick (2010) asked researchers to “elucidate their own meanings” and argued for “more careful and accountable uses” of the terms (p. 310). With that said, in an attempt to be accountable for the terms we use, in this article, we will use the term “Queer” as an umbrella term for LGBTQ+ people, unless interviewed students use specific terms. The term “Queer” is widely accepted in gender and sexuality research in an attempt to reclaim and reappropriate the term.

Regardless of whether research uses the term “gender” or the term “sex,” mathematics education research has predominantly approached gender in a binary “boys vs. girls” way, instead of addressing the complex and fluid ways in which their research subjects might identify (e.g. Damarin & Erchick, 2010; Glasser & Smith, 2008; Leyva, 2017). Some researchers in other disciplines have discarded this binary view of gender, often referring to three different variables: sex assigned at birth, gender identity, and gender expression (e.g. Lindqvist et al., 2021; Spencer et al., 2021). Damarin and Erchick (2010) stated, “The absence of attention to the complexity of gender, and to situating studies of gender and mathematics in theories of gender, effectively denies the richness and power that mathematics education might gain from this work” (p. 319). Using this more inclusive approach might give more nuanced understandings of the social and cultural complexities underlying gender research.

As a further consequence of these poor practices, some groups of people have been left out of mathematics education literature completely (see discussions of equity in Darwin & Ataide Pinheiro, 2023; Goldberg et al., 2023; Willey & Ataide Pinheiro, 2019). In an article about the importance of gender inclusivity in large-scale datasets, Forgasz (2021) provided a refreshingly honest example of her own past binary approach to gender research, as she admitted to listwise deleting students who failed to respond to the “Are you male or female?” survey item in her early 1990s doctoral study. Recently, American Educational Research Association president Shaun Harper and executive director Harper and Levine (2021) issued a statement that urged a “responsibility to extend the reach of our research expertise on gender, trans people’s experiences and outcomes, public policy, and related topics” (para. 3). Likewise, Lev (2007) has urged lesbian, gay, and bisexual groups to support research including transgender persons, saying, “Why have we abandoned transgender people and their concerns in our rush for equality?” (p. 147). In recent years, gender constructs and societal views of gender have changed remarkably fast. With this in mind, it is not uncommon to run into dated views of gender when reviewing literature, even within the last few years. For these reasons, it is important to acknowledge the contributions of prior research—which often raised awareness of gender disparities in mathematics—while continuing to leverage new gender-related ideas and frameworks within mathematics education.

Additionally, gender has garnered significant attention in mathematics education research; however, comparatively, little emphasis has been placed on studying sexuality (Rubel, 2016; Waid, 2020). Nonetheless, a limited number of studies exploring Queer-Related discussions in mathematics education have shed light on the prevalence of heteronormativity within mathematics teaching and curricula (Moore, 2021; Rubel, 2016; Waid, 2020). These researchers argued that there has been a dearth of research concerning sexuality in mathematics education. In 2022, Ataide Pinheiro proposed that gender, sex, and sexuality are distinct constructs with varying natures, suggesting that our classifications of sexuality is as socially constructed as gender, as posited in the work of Gillis and Jacobs (2017).

This article advances inclusive inquiry practices used in two doctoral dissertations, which are referred to as S1 and S2. The first study, S1, titled Compliance, Competitiveness, and Confidence: Investigating Patterns in Mathematics Anxiety Using a Nuanced View of Gender (Cox, 2022) was a mixed-methods study examining mathematics anxiety that used an inclusive approach to statistics. The second study, S2, titled At the Intersections: Queer High School Students’ Experiences with the Teaching of Mathematics for Social Justice (Ataide Pinheiro, 2022) was a qualitative study examining Queer students’ experiences in mathematics, schools, communities, and ways of teaching mathematics for social justice that combatted the oppression Queer high school students experience in society. In S2, this approach to teaching was called Teaching of Mathematics for Social Justice Gender and Sexuality (TMSJGS). The findings from both research projects are included in this article in hopes that these two works might guide researchers in best practices in working with students from a multitude of genders and sexualities.

Literature Review: Sex and Gender Research in Mathematics Education

A Psychobiosocial Model: Sex Assigned at Birth, Gender Identity, and Gender Expression

The American Psychological Association (APA, 2015) stated, “Psychologists understand that gender is a nonbinary construct that allows for a range of gender identities and that a person’s gender identity may not align with sex assigned at birth” (p. 832). Bergvall (1996) described gender as “psychological features and role attributes that society has assigned to the biological category of sex” (p. 3) and gives examples of cross-cultural differences. For example, in the United States, women are said to be more “caring and helpful” but in China, this is a desired quality in both men and women; as for gender expression, wearing skirts is feminine in the United States but wearing kilts is masculine in Scotland (Bergvall, 1996). Therefore, it is important for researchers to understand that one person’s view of gender identity and gender expression might differ from others, especially when including participants from different countries and even different regions within the United States.

In the following paragraphs, we describe the three different sex- and gender-related variables. Halpern et al. (2005) encouraged the use of a “psychobiosocial model” in research, which shows “the way biological and psychosocial variables exert mutual influences on each other” (p. 52). In S1, sex assigned at birth, or “sex,” represents a biological variable, while “gender” is a psychosocial variable, with gender identity as psychological (an inherent sense) and gender expression as social (externally expressed); all three of these sex- and gender-related variables influence one another.

Sex assigned at birth, or biological sex, is historically defined by the presence or absence of a male sex organ in infancy. Lines were blurred when a non-developed organ was present, and historically these infants were surgically altered and assigned a label of “female” (Money et al., 1957). This was often confusing and harmful for the child in later years, especially if secondary sex characteristics developed in adolescence. Today, if an infant’s sex cannot be determined with external genitalia, indicators such as internal genitalia, chromosomes, and hormones are used (APA, 2015). For instance, blood tests could be used to determine the presence of XX or XY chromosomes and to measure hormone levels or an ultrasound could be used to check for undescended testes (Mayo Clinic, 2018).

Gender identity is a term first coined by Robert Stoller (1964), and is now commonly described as

A person’s deeply felt, inherent sense of being a boy, a man, or male; a girl, a woman, or female; or an alternative gender (e.g. genderqueer, gender nonconforming, gender neutral) that may or may not correspond to a person’s sex assigned at birth or to a person’s primary or secondary sex characteristics. (APA, 2015, p. 862)

Gender identity is internal and is not necessarily visible to others (APA, 2015). Some people view their gender identity as fluid (Lev, 2007; Monro, 2005). If a person’s gender assigned at birth conflicts with their gender identity, the person is said to be transgender or gender nonconforming (TGNC).

The third aspect of gender is related to how a person externally expresses their gender and is called gender expression. APA (2015) defined gender expression as “the presentation of an individual, including physical appearance, clothing choice and accessories, and behaviors that express aspects of gender identity or role” (p. 861). Echoing a social, externally viewed concept of gender, West and Zimmerman (1987) and Butler (1990) described gender as a performative act that actively surfaces in everyday social interactions, and they referred to this process as “doing gender.” Using Butler’s work as a base, Damarin and Erchick (2010) mentioned research concerned with “masculinities”—ways that men choose to perform their masculine gender in the world—and posited that work focused on attracting women to STEM careers might be moving toward a new definition of “femininities,” where math is “savvy and defiant of the social construction of women as generally less able and interested in mathematics than their male peers” (p. 319). They argued that women performing their gender in these nonnormative ways simultaneously change norms, creating a new context for future women.

Gender identity, gender expression, and sex assigned at birth have been carefully defined and researched within other fields. These three sex- and gender-related variables likely influence one another, but refusing to elucidate specific meanings leaves us with research that is “ill defined” and “atheoretical” (Damarin & Erchick, 2010, p. 319). It is important to use sex- and gender-related survey items that have been validated with adults and adolescents in a variety of studies. For example, a 2017 Child Trends report (Temkin et al., 2017) found that middle- and high-school-aged youth understood sex- and gender-related measurement items and encouraged the use of a two-step approach of asking both sex assigned at birth and current gender identity, and expert panel members suggested that the use of only binary choices such as “Are you male or female?” could dissuade Transgender and Gender Nonconforming (TGNC) students from completing survey research. Therefore, in S1, a 2017 Child Trends Report (Temkin et al., 2017) and a brief by Research Triangle Institute International (RTI International) (Colaço & Watson-Grant, 2021) were used for the survey questions, which asked for both gender identity and sex assigned at birth. Students were first asked, “What sex were you assigned at birth, such as on an original birth certificate?” and were given only two options: male and female. Gender identity comes from the question “How would you describe yourself?” and had three choices: boy/man, girl/woman, and gender nonconforming or non-binary. Participants could not leave the question unanswered, but they could self-describe if they wished. Similarly, S1 used a study by Journal of the American Medical Association (JAMA) Pediatrics (Lowry et al., 2018) for gender expression survey items. It asked respondents, “A person’s appearance, style, dress, or the way they walk, or talk may affect how people describe them. How do you think people at school would describe you?” Response options ranged from very masculine to very feminine. The inclusion of gender identity, sex assigned at birth, and gender expression allows researchers to investigate the interplay between these assumed “independent” variables.

An Overview of Sexuality Research Used in Mathematics Education

Sexuality discussions in mathematics education have been exclusively explored in studies focusing on Queer-Related discussions (Ataide Pinheiro, 2023; Ataide Pinheiro & Chávez, 2023). Existing research consistently demonstrates that mathematics reflects and propagates gender and sexual normativity (Leyva, 2017; Moore, 2021; Rubel, 2016; Waid, 2020). Rands (2009) conducted a study on the inclusivity of Queer students in mathematics teaching and curriculum and highlighted the misconceptions surrounding discussions of sexuality, especially by conflating sexuality with discussions of sex. Later, Rands (2016) referred to this research as “mathematical inqueery.” Rands emphasized the significance of recognizing sexuality as a social identity, comparable to gender, which significantly influences social interactions, including those within the mathematics classroom. In another study, Rubel (2016) made a compelling contribution to the field by addressing the discursive nature of mathematics, wherein assumptions of heterosexuality persist even when efforts are made to promote inclusivity. For instance, Rubel discussed a series of books by McKellar (2007, 2009, 2012), which challenge the perception of mathematics as a masculine domain with taglines such as “Girls get curves” and “Smart is sexy,” as well as questions like “Do you hide your smarts, especially around guys?” (2016, p. 436). While acknowledging McKellar’s attempts to expand girls’ interests in mathematics, Rubel highlighted that their work predominantly portrayed heterosexual girls, revealing a heteronormative slant rather than a gender-complex approach. In a similar work, Waid (2020) highlighted the neglect of Queer student identities in mathematical research, explicitly critiquing the disproportionate focus on gender while disregarding sexuality. This disparity inadvertently perpetuated the notion that issues related to sexuality are inconsequential to heteronormativity in mathematics.

Context for Two Studies

The overall aim of this article is to provide researchers with best practices for inclusive inquiry. Full details on the methods, data analysis, and results are not included. Instead, an introduction and overall context are provided for both studies.

Dissertation Study 1: Introduction

The first study presented in this paper, S1, investigated factors of compliance, competitiveness, and confidence, which had all previously shown gendered patterns in the literature. The author of S1, Cox, was concerned that the public often makes biological claims about differences on tests such as the SAT; for instance, a University of Michigan Flint Campus professor, Mark Perry (2016), said that gaps on the SAT would never be closed because of “inherent gender differences [in] mathematical ability” (para. 12) and journalist Welton (2019) said, “You don’t get many women geniuses because their IQ range is more bunched towards the mean” (para. 11). Cox was interested in seeing if socially constructed factors such as encouraging “teacher-pleasing” and “good girl” behaviors in girls contributed to the slightly greater percentage of girls suffering from mathematics anxiety. S1 consisted of four research questions:

1. To what extent does gender, as indicated by three related variables of sex assigned at birth, gender expression, and gender identity, relate to students’ level of mathematics anxiety?

2. In what ways could compliance, competitiveness, and confidence mediate the relationships between gender and mathematics anxiety?

3. In the focus student interviews, how do students describe compliance, competitiveness, confidence, or other factors as related to mathematics anxiety?

4. How do students talk about gender in relationship to compliance, competitiveness, and confidence in mathematics?

To achieve more nuanced results, Cox used an inclusive view of gender, reporting results for sex assigned at birth, gender identity, and gender expression, and recognizing that psychological, social, and biological variables might influence a person’s experiences. The viewpoints of people who identify as transgender and gender nonconforming were included throughout the study.

Dissertation Study 1: Context

In this paper, S1 was used to answer the research question “How can inclusive inquiry approaches provide nuanced understandings of data?” For the quantitative portion of S1, 84 high-school aged students in a Midwestern state filled out a survey that included items about mathematics anxiety from Richardson and Suinn’s Abbreviated Mathematics Anxiety Scale (1972), teacher-pleasing behaviors, bold problem solving, and mathematical confidence from Lubienski et al. (2021), interpersonal competitiveness and goal competitiveness from Griffin-Pierson (1990), and enjoyment of competition and contentiousness from Houston et al. (2002). The final portion of the survey focused on the sex- and gender-related variables. Students were also asked if they felt safe with regards to their gender and had the option to be connected with resources in their area.

The quantitative portion of S1 used inclusive statistics, avoiding binary-only methods such as t-tests, and instead running three separate linear regression models. Each regression model included the dependent variable of mathematics anxiety and the eight possible predictor variables of the sex/gender variable (sex assigned at birth, gender identity, or gender expression), bold problem solving, teacher pleasing, goal competitiveness, interpersonal competitiveness, enjoyment of competition, contentiousness, and, lastly, confidence. This approach proved to be more tedious, as three sets of regression models were analyzed instead of one, but it gave nuanced results that not only support TGNC persons, but also gave stronger evidence that social factors—not biological factors—might contribute to any gender-related differences in mathematics anxiety.

For the qualitative portion, 10 students were selected for one-on-one interviews. To form this group of 10, the researcher first selected four boys whose sex assigned at birth was male and four girls whose sex assigned at birth was female. They were chosen in a strategic way to provide for a greater spread of mathematics anxiety scores. Lastly, two students were selected who identified in ways other than their sex assigned at birth: one student identified as non-­binary, while the other student identified as a transgender woman.

Dissertation Study 2: Introduction

The second study (S2) presented in this paper was conducted by Ataide Pinheiro. In S2, Ataide Pinheiro introduced 10 Queer high school students from a midwestern state to the Teaching of Mathematics for Social Justice (TMSJ). Specifically, Ataide Pinheiro wanted to foreground Queer students’ voices in the TMSJ that combats and challenges the injustices Queer students have gone through in society in the United States. It is important to do so, because recently mathematics education researchers have found that the field of mathematics propagates heteronormativity and cisnormativity (Leyva, 2017; Moore, 2021; Rubel, 2016; Waid, 2020). As a consequence, scholars have emphasized the need for research that specifically challenges gender and sexual normativities through the teaching of mathematics. However, in current research that encourages us to include Queer-Related discussions and queerize mathematics teaching and curricula (Dubbs, 2016; Rands, 2009, 2016), very little is known in terms of how Queer students would respond to Queer mathematics. And since students are part of the consumers of education, their voices, together with those of researchers, teachers, and community members, also matter to a sophisticated TMSJ.

Again, the aim of this paper is not to provide evidence for why TMSJ is important and how the lessons used impacted students’ learning. On the contrary, we are using the TMSJ study as an example of how inclusive approaches to inquiry, such as TMSJ, can benefit the research community and teachers in better understanding Queer students’ experiences in school and mathematics. Therefore, not much background information will be provided on the lessons conducted and the TMSJ review of literature.

Dissertation Study 2: Context

For this article, S2 is used to answer the research questions: What are the perspectives of Queer high school students in the Midwest regarding their high school experience? How could a more inclusive approach to teaching mathematics empower these Queer students to reflect on their high school experience critically? S2 consisted of a case study, in which survey, classroom study, and interview data were collected by Ataide Pinheiro in Fall 2021 (July through November). Primarily, Gender and Sexuality Alliances (GSA) supervisors were contacted by an organization that supervises all GSAs in the Midwestern state and asked them to forward the survey to their GSA students. The survey asked if students would consider participating in further studies that investigated Queer students’ identities. A total of 10 students who answered to the survey demonstrated interest in participation in further studies and were contacted via email. The second phase of S2 consisted of a classroom study with the 10 Queer students who demonstrated interest in participating in further studies. In this phase of the study, Queer students were taught three Teaching of Mathematics for Social Justice Gender and Sexuality lessons by Ataide Pinheiro. The three lessons came from the textbook Mathematics Lessons to Explore, Understand, and Respond to Social Injustices by Berry et al. (2020). Closely following the TMSJ framework, these lessons have the objectives to (a) introduce students to a social injustice pertinent to the experiences of Queer high school students (bullying and harassment); (b) model the social injustice using mathematics; and (c) support students to become agents of change and think of ways their schools’ initiatives have or have not combatted bullying and harassment that Queer students go through daily. The mathematical exploration that took place in this study involved a discussion on matrix and matrix multiplication. Queer students were provided data that represented bullying and harassment that Queer students have experienced in the United States, and created matrices that represented this data. The major goal of the mathematical lesson was to find the number of students in each grade in their schools who had gone through victimization due to their gender and sexual orientation. To do so, students needed to engage with matrix multiplication, with no previous knowledge of matrices. This exploration provided an inquiry based approach to contextualizing the matrix multiplication algorithm, centering on a relatable social injustice.

Each lesson lasted around 60 min and was video recorded. The lessons occurred in person with four students who attended the same school (Rob, Lacy, Lin, and Beth) and via Zoom with the other six students (DW, Tom, Eric, Olive, Mackenzie, and Cameron), who came from all around the state. Both in-person and Zoom lessons followed the same lesson plans available in the textbook mentioned previously.

After the lessons were completed, all 10 students returned for a follow-up interview to share further about their experiences as Queer students in schools, in mathematics, and in their communities. The follow-up interviews also asked Queer students’ perspectives on the three lessons they took for TMSJGS, whether they thought these lessons could take place at their schools, and if not, what they thought might be alternatives for TMSJGS in regular classrooms. Finally, five returning participants came back for focus group interviews. The focus group interviews presented the five participants with preliminary findings from the follow-up interviews and asked their collective opinion on the findings. Queer students commented on why they liked TMSJGS, why they thought TMSJGS might or might not occur in the regular classroom, and why there is a disconnect between mathematics and Queer-Related discussions. To fulfill the goals of this paper, findings on four Queer students’ perspectives of Queer-Related discussions in schools and the impact of the TMSJGS on the 10 Queer students who participated in S2 are presented, analyzed, and discussed. Theoretically, S2 used Queer theory and social justice theory underpinnings to make sense of the data discussed in the article. On the one hand, Queer theory guided the analysis of the data by providing Ataide Pinheiro with the understanding of how inclusive curriculum challenges normalcy toward the reproduction of cisnormativity and heteronormativity (see Queer theory discussions in Schmidt, 2010; Shlasko, 2005). On the other hand, social justice teaching allows students to understand oppression and develop agency to disrupt current oppressive injustice practices and mechanisms (Alsup & Miller, 2014).

Results

In this section, we share the results of both dissertation studies, highlighting moments that Queer participants provided more nuanced and richer findings. We also share ways that Queer participants felt visible and valued.

Dissertation Study 1: Quantitative Portion

The three sets of hierarchical linear regression models were parallel in their use of independent variables, differing only in terms of the sex- and gender-related variable included. The three linear regression models first included sex assigned at birth, gender identity, or gender expression, and then bold problem solving, teacher-pleasing behaviors, enjoyment of competition, contentiousness, and mathematical confidence were added, one at a time. Initial explorations such as the box plot shown in Figure 1 revealed that each predictor variable did go in the direction indicated by the literature. In other words, boys were more likely to enjoy competition, to solve problems in a “bold” way, and to be more confident and “contentious” (e.g. argue for their answer, vocally disagree with group members), while girls had higher scores for teacher pleasing. The series of regression models using sex assigned at birth (female = 1) is shown in Table 1. Table 2 shows the models using gender identity, for which two dummy variables were used: “identify as girl” (1 if identifies as a girl and 0 if not) and “non-binary” (1 if “non-binary,” “bigender,” or “questioning” and 0 if not). Lastly, Table 3 shows similar models using gender expression.

Figure 1. Box plots with outliers for all variables, grouped by gender identity.

Note. This figure shows several gender-related differences for the variables of interest. Girls in the sample had higher levels of mathematics anxiety and teacher-pleasing behaviors than boys. Boys in the sample had higher levels for bold problem solving, enjoyment of competition, and contentiousness than girls. Students who self-identified as “non-binary,” “bigender,” and “questioning” showed higher levels of mathematics anxiety and lower levels of teacher pleasing, bold problem solving, interpersonal competitiveness, enjoyment of competition, and contentiousness than both boys and girls in the sample. Several students were considered outliers (open circles) and extreme outliers (stars).

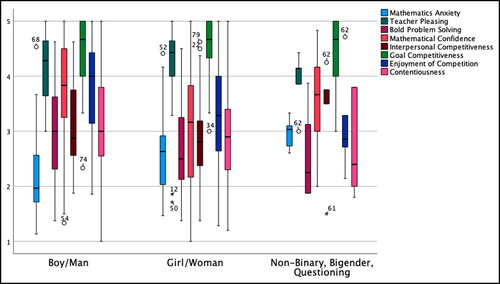
Table 1. Mathematics anxiety predicted by sex assigned at birth.

	Model 1 β (SE)	Model 2 β (SE)	Model 3 β (SE)	Model 4 β (SE)	Model 5 β (SE)	Model 6 β (SE)
(Constant)	2.19 (.12)	2.74 (.28)	1.53 (.52)	2.11 (.58)	2.77 (.62)	2.98 (.60)
Sex Assigned at Birth (SAB) (Female = 1)	.45 (.15)**	.40 (.15)**	.37 (.14)**	.33 (.14)*	.35 (.14)*	.23 (.12)^
Compliance
Bold Prob. Solving		−.18 (.08)*	−.16 (.08)^	−.16 (.08)^	−.14 (.08)^	−.05 (.07)
Teacher Pleasing			.28 (.10)**	.27 (.10)**	.17 (.11)	.24 (.09)*
Competitiveness
Enjoyment of Comp.				−.15 (.07)*	−.07 (.08)	−.03 (.07)
Contentiousness					−.21 (.08)*	−.18 (.07)*
Confidence
Confidence						−.27 (.06)***
	R^2 = .10	R^2 = .15	R^2 = .22	R^2 = .27	R^2 = .32	R^2 = .48

^{^} p<.10, *p<.05, **p<.01, ***p<.001.

Note. Predictor variables for compliance, competitiveness, and confidence were added, one-by-one, into successive models. In Model 1, with no additional predictors, sex assigned at birth significantly predicts mathematics anxiety (p<.01). However, as additional variables are added, this significance is reduced to the .10 level, with teacher pleasing, contentiousness, and mathematical confidence contributing to the final model with much greater significance. Overall, the six predictor variables explain 48% of the variance in mathematics anxiety levels.

Table 2. Mathematics anxiety predicted by gender identity.

	Model 1 β (SE)	Model 2 β (SE)	Model 3 β (SE)	Model 4 β (SE)	Model 5 β (SE)	Model 6 β (SE)
Constant	2.134 (.12)	2.66 (.27)	1.38 (.51)	1.89 (.58)	2.55 (.68)	2.71 (.53)
GI: Identifies as Girl	.50 (.15)***	.45 (.15)**	.42 (.14)**	.37 (.14)*	.40 (.16)**	.28 (.12)*
GI: Identifies as Non-Binary	.83 (.31)**	.76 (.31)*	.82 (.29)**	.75 (.29)*	.74 (.32)**	.80 (.24)***
Compliance
Bold Problem Solving		−.17 (.08)*	−.15 (.08)^	−.15 (.08)^	−.13 (.08)^	−.03 (.07)
Teacher Pleasing			.30 (.10)**	.29 (.10)**	.19 (.12)^	.26 (.09)**
Competitiveness
Enjoyment of Comp.				−.13 (.07)^	−.05 (.09)	.001 (.07)
Contentiousness					−.21 (.09)*	−.18 (.07)*
Confidence
Confidence						−.28 (.05)***
	R^2 = .15	R^2 = .20	R^2 = .27	R^2 = .30	R^2 = .36	R^2 = .54

^{^} p<.10, *p<.05, **p<.01, ***p<.001.

Note. Predictor variables for compliance, competitiveness, and confidence were added, one-by-one, into successive models. In Model 1, with no additional predictors, gender significantly predicts mathematics anxiety (p<.001). However, as additional variables are added, this significance is reduced to the .05 level, with teacher pleasing, contentiousness, and mathematical confidence contributing to the final model with much greater significance. Overall, the six predictor variables explain 54% of the variance in mathematics anxiety levels. Notably, students who self-identified as “non-binary,” “bigender,” and “questioning” still had gender significantly predicting mathematics anxiety throughout all six models. Results such as these warrant future mathematics anxiety research with this subset of students.

Table 3. Mathematics anxiety predicted by gender expression.

	Model 1 β (SE)	Model 2 β (SE)	Model 3 β (SE)	Model 4 β (SE)	Model 5 β (SE)	Model 6 β (SE)
Constant	1.80 (.20)	2.39 (.31)	1.33 (.52)	1.88 (.59)	2.53 (.62)	2.84 (.56)
Gender Exp. (GE)	.15 (.04)***	.14 (.04)***	.12 (.04)**	.11 (.04)**	.12 (.04)**	.07 (.04)*
Compliance
Bold Prob. Solving		−.19 (.08)*	−.17 (.08)*	−.17 (.08)*	−.15 (.08)*	−.06 (.07)
Teacher Pleasing			.25 (.10)*	.25 (.10)*	.15 (.10)*	.22 (.10)*
Competitiveness
Enjoyment of Comp.				−.14 (.07)^	−.06 (.08)	−.02 (.07)
Contentiousness					−.21 (.08)*	−.18 (.07)*
Confidence
Confidence						−.26 (.06)***
	R^2 = .14	R^2 = .20	R^2 = .26	R^2 = .29	R^2 = .35	R^2 = .48

^{^} p<.10, *p<.05, **p<.01, ***p<.001.

Note. Predictor variables for compliance, competitiveness, and confidence were added, one-by-one, into successive models. In Model 1, with no additional predictors, gender expression significantly predicts mathematics anxiety (p<.001). However, as additional variables are added, this significance is reduced to the .05 level, with teacher pleasing, contentiousness, and mathematical confidence contributing to the final model with much greater significance. Overall, the six predictor variables explain 48% of the variance in mathematics anxiety levels.

It is important to note that for each regression model (Tables 1–3), the sex and gender-related variable had strong significance in predicting mathematics anxiety in the first model, when it was the only predictor variable included. As successive predictors were added, the significance of sex assigned at birth, gender identity, and gender expression in predicting mathematics anxiety decreases in strength. However, in Table 2, one can see that the six students who identified as non-binary, bigender, or questioning are still flagged as strongly significant (p < .001). This was a substantial finding of S1. To have significance here, even with a small sample size, shows evidence that this set of students has greater levels of mathematics anxiety than their peers. Instead of listwise removing this group of students because they could not make a “binary” choice for a traditional statistical test, such as a t-test, S1 provides evidence that this group of students deserves to be researched.

Lastly, another important takeaway from these quantitative results can be found in the very first model, Model 1. When designing the linear regression, Cox did not put all predictor variables in together. Instead, she carefully added each predictor, one at a time. The design of this model was intentional. When looking at Model 1 in each table, we see only the sex- or gender-related variable and its effect on levels of mathematics anxiety. This approach gives us nuanced information about the age-old “nature vs. nurture” debate. While it can, at times, to understand the effects of each and research shows socialization begins at birth, we can see that Model 1 with gender identity explains 15% of the variance in mathematics anxiety (Table 2), while Model 1 with sex assigned at birth (Table 1) explains only 10% of the variance in mathematics anxiety. While gender expression would not be a typical variable researchers have used in the past, it does provide more of a continuous metric than gender identity and sex assigned at birth. Additionally, it also explains more of the variance in mathematics anxiety than sex assigned at birth in Model 1. The three regression results, therefore, give slight evidence that mathematics anxiety is more related to “social” variables than “biological” variables, and with a large-scale dataset, we would likely see even more nuance here. The inclusion of compliance, competitiveness, and confidence variables increases the gender identity model to explain 54% of the variance, indicating that these additional, socially constructed variables are quite important to explaining mathematics anxiety.

Dissertation Study 1: Qualitative Portion

The 10 focus students, in general, reported that girls tended to be quiet in class and rarely asked questions; girls were more likely to memorize teacher-given procedures; and girls often did all of the homework, even when the number of problems was excessive. The girls interviewed also often admitted to not correcting classmates, even when they knew their group members’ answers were incorrect. Of boys, they said that boys tended to be more competitive both in classroom games and on tests; and boys would often loudly brag about high scores, despite little studying. This section gives the results of two students: Emmaline, a 18-year-old student who identifies as a transgender White woman and Cameron, an 18-year-old student who identifies as Black and non-binary. These two students, like the other eight focus students, provided much insight on gender-related views of mathematics students, but for the purposes of this paper, we address how the inclusion of these students—instead of listwise deleting them—further supported the findings.

Emmaline

At the time of the interview, Emmaline was a senior at a rural Midwestern school with nearly 1,300 students. Emmaline enjoyed building robots and wanted to pursue engineering in college. During the interview, Emmaline said that she had grappled with her gender identity since 2020, about a year before the quantitative data collection, and had briefly changed her gender identity to girl/woman at that time. However, she quickly decided this would be too difficult, and Emmaline openly identified as a boy/man again. At the time of the interview, Emmaline said she preferred to identify as a girl/woman and used this identity with close friends, but in school, Emmaline still identified as a boy/man. For this article, we refer to Emmaline as “she/her,” since she planned to use these pronouns exclusively in college.

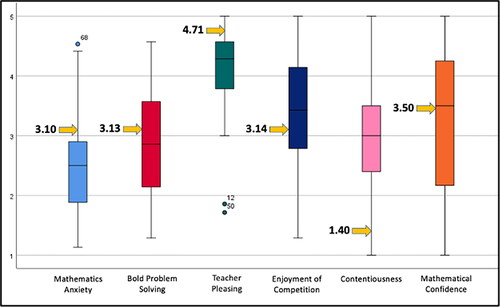
When it came to the predictor variables shown in the literature to be gender-related, Emmaline’s quantitative data, found in Figure 2, had more “feminine” results: high in mathematics anxiety, high in teacher pleasing, and very low in contentiousness. She also had a lower than average enjoyment of competition. On the other hand, her bold problem solving was slightly higher than average, which contradicted more “feminine” patterns. Her qualitative data seemed at odds with this score, though, as Emmaline solved three computation problems in the interview in very predictable, teacher-given ways; every problem was aligned vertically and solved using a traditional standard algorithm written on a piece of paper.

Figure 2. Emmaline’s quantitative results, in yellow, compared to box plots for full sample.

Note. Emmaline’s results, shown with yellow arrows, more closely mirror the results of girls/women, with higher levels of mathematics anxiety and teacher-pleasing behaviors, and lower levels of enjoyment of competition and contentiousness. Students 12 and 50 were outliers with low teacher-pleasing levels. Both are female students who identify as girls.

Emmaline described several moments of mathematics anxiety. On tests, Emmaline said:

I won’t see. Everything gets dark for me. It’s just kind of … like, if I look at the first page, and I see nothing that I actually know. I just kind of look down and time kind of freezes, and I’m like, “Well, better start thinking!”

Emmaline said she had also felt “basically, like a weird feeling in my stomach, like butterflies in my stomach, and also just sometimes shaking a bit,” and she would sometimes develop a “1,000-yard stare,” where she sat looking into space with no ideas. Emmaline said:

Sometimes I’m working with numbers, and like I’m very focused, and I’m doing addition [but] sometimes I’d either do multiplication or just pick a random number and put it there. I do that. So I remember there being one time I got a simple addition problem wrong because I was too hyper-focused, and I actually picked a number from somewhere else.

Her reflection was related to mathematics anxiety literature on “working memory disruption” (Ramirez et al., 2013), as students often lose track of numbers in the middle of problems.

Emmaline described her better qualities as being a “good friend” and a consistent theme in her interview was her relationships with teachers; she wanted her teachers to be proud of her. She described an unwillingness to ask questions:

I would say I’m just too worried about, like, “Oh, this was very easy,” like, “This was a very easy question to answer, and I should have been paying attention.” I’m afraid they won’t be of any help, and they’ll just say, “Oh. Well, you should have been paying attention!” or “This was easy, why are you asking about this?” but the teacher would never do that.

Emmaline said her teachers were all quite kind, but only one teacher knew about her choice to change her gender identity. Her Spanish teacher had a strong relationship with her, even proudly sharing an image robot Emmaline constructed on her Instagram page. Emmaline’s descriptions of this particular teacher showed that she felt accepted by her and would likely do anything to please her. Emmaline said her teacher recently told her, “I will only call you [dead name] in class if it’s okay with you.” When discussing why she did not volunteer answers in class, Emmaline mentioned being concerned about peers’ perceptions of her, which could have also been related to this critical time in her life, as she did not openly identify in school as a woman. Emmaline described that she did not like to be the center of attention or have others “stare” at her. When it came to other aspects of being a good student, she said that this teacher recently told her, “You have to start believing in yourself more” and encouraged her to speak up in class. Emmaline’s shy, teacher-pleasing personality aligned with more “feminine” mathematics characteristics and might have contributed to her higher levels of mathematics anxiety (3.10) than that of other students whose sex assigned at birth was male (2.16).

Cameron

At the time of the interview, Cameron was a senior at a Midwestern metropolitan arts-based charter school with nearly 1,000 students. Cameron identified as non-binary. Their sex assigned at birth was male, but they said others would view their gender expression as “somewhat feminine” while they felt like they expressed their gender in an “equally masculine and feminine” way. They further stated:

I feel as if the intonation of my voice along with my particular way of speaking would make some perceive me as feminine. It’s not uncommon for someone to mistake me for a woman over the phone or even occasionally in person.

Cameron enjoyed mathematics and wanted to pursue a career in STEM, possibly biomedical engineering. Cameron’s quantitative data, shown in Figure 3, showed that they had a high level of mathematics anxiety. They also had higher levels for the more “masculine” variables of bold problem solving and mathematical confidence, while they had lower values for enjoyment of competition and contentiousness, which aligned with more “feminine” patterns in the literature.

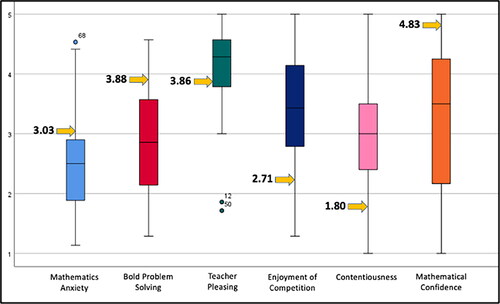
Figure 3. Cameron’s quantitative results, in yellow, compared to box plots for full sample.

Note. Cameron’s results, shown with yellow arrows, show a mix of “masculine” and “feminine” characteristics. While they show lower values for contentiousness and enjoyment of competition and higher values for mathematics anxiety, like girls/women, they show higher values for mathematical confidence and bold problem solving, like boys/men. Students 12 and 50 were outliers with low teacher-pleasing levels. Both are female students who identify as girls.

Cameron had the same teacher for four of their high school mathematics courses. They credited this teacher and her warm and welcoming classroom with positively influencing them in mathematics. Even though Cameron took challenging courses and had high mathematics anxiety, they said:

My perceptions of the course are partially dictated by the social experience, but then also my experience with the teacher and obviously the rigor of the course. But if the first two are positive, I’ve noticed that the latter factor isn’t as much of a negative thing. Like the other two cancel out like the rigor of the course and allow me to not be as weighed down by it, if that makes any sense.

In contrast, negative experiences chipped away at Cameron’s trust in teachers. Cameron described a very early experience in first grade in which they misunderstood a mathematics coloring assignment, and the teacher announced loudly in front of the whole class, “You get a BIG FAT ZERO!” Cameron went on to describe this experience as upsetting for them as such a young child, saying, “At that age, it’s a pretty big thing for a teacher to be that disapproving of you for something you did in class.”

Later on in the interview, this social experience in the classroom was discussed again, as I asked what might happen if a teacher did not use their pronouns correctly or called them by their birth name. They said:

I feel like [some] don’t understand the impact of that or maybe don’t agree with that, [they] would say, “Well that’s such a minor thing, I don’t understand why that would affect your academic performance,” and to their credit, in a way, they do technically have a point. As much as I really don’t want to give it to them, because it can come down to how much power you allow someone to have over you sort of thing, but at the same time, I feel as if no matter how strong you are mentally that still will take a toll, and it’s ultimately going to be easier to perform in a safe environment than it will be [in] an environment where you don’t feel safe. I mean they’re both possible to do, and you could probably get similar results if you push yourself in either environment, but at the end of the day, what’s the purpose of putting that kind of difficulty on yourself if you don’t have to.

While some might assume that mathematics anxiety and mathematical confidence have a natural reciprocal relationship, Cameron’s data did not reflect this. In the literature, Ramirez et al. (2018) said, “As much as the field would benefit from studying math-anxious students who do not identify strongly with math, the opposite side of the spectrum is also an important population of study—students who are math anxious but also have strong math identity and math motivation” (p. 159). Unlike most students, Cameron showed this conflicting relationship with high mathematical confidence and high mathematics anxiety. Cameron said, “If I’m casually doing [mathematics], or doing it in a setting where I’m not pressed for time, I generally don’t feel anxiety about numbers at all.” Cameron also described natural abilities in mathematics, rarely feeling like they needed to study for mathematics tests. When describing preparedness for tests, they said:

I may need to go over this again but generally after doing a math problem once or twice, or a particular type of problem, I’m able to catch on [and see] how to do that particular kind of problem pretty easily. I’m generally able to do it.

However, Cameron repeatedly mentioned grade-based anxiety triggers, like course grades and scores on high-stakes tests, like the AP exams and the SAT. For tests that occurred in the classroom, Cameron said:

There are more chances to correct [my grade], and I feel like it’s a more accurate indicator of … not that a class grade is an indicator of your complex understanding of the subject, but I feel like it’s a better indicator of my understanding of the subject than the SAT or the AP exam because that’s a “one-off” thing, it’s a stimulus-based test, which I find that I generally don’t tend to do well on in the first place, because I have to be quick about it, and I’m not used to working in that particular way.

In the interview, I asked Cameron if they would call themselves a good student, and they said “No.” When I asked more, they said, “I don’t think I’m a good student but that’s because I’m a perfectionist, and I’m working on that. I feel like most people would say I’m a good student. I mean, I have a 4.3 GPA, so that’s good, but it’s not where I want it.” They continued by saying that they often participated in class—“Sometimes too much! I try not to!”

Overall, Cameron reported more mathematics anxiety when involved in activities that might be barriers to their success. They did not claim to be a “teacher pleaser,” but they mentioned having a high grade point average, actively participating in class, and taking multiple classes with a beloved teacher. Cameron also repeatedly mentioned the social aspect of the classroom. If they were in a safe environment with positive interactions with their classmates and teachers, they were not as anxious and felt comfortable participating. A “safe” and “positive” classroom may be even more important to TGNC students. In the quantitative portion, students who reported gender identities of “non-binary,” “questioning,” and “bigender” reported more mathematics anxiety, and Table 3 showed that these students’ gender identity still was a significant predictor of mathematics anxiety, even when additional predictor variables were included.

Taken together, Cameron and Emmaline’s data showed more complex relationships between variables. Cameron’s data showed a combination of both masculine and feminine characteristics, while Emmaline’s data was mostly feminine. Cameron was one of the few students who showed both high mathematics anxiety and high mathematical confidence. However, their high mathematics anxiety did not seem to be related to casual settings; instead, it was more focused on how a poor score might reflect their grade—similar to “goal competitiveness,” often more strongly linked to girls (Griffin-Pierson, 1990), who are more likely to attend college and have higher grade point averages than boys (Carnevale et al., 2018). Additionally, the inclusion of Cameron and Emmaline and other transgender and non-binary students provided more nuance statistically. Results were stronger for the psychological and social variables of gender identity and gender expression than the biological variable of sex assigned at birth. Therefore, an inclusive approach in both qualitative and quantitative inquiry has the potential to provide more nuanced understandings of data.

Dissertation Study 2

One of the significant contributions of including Queer people and their experiences in mathematics is the increased opportunity for these students to be visible, valued, respected, and accepted in terms of their identities. Queer students in S2 have demonstrated a lack of exposure to discussions on Queer-related topics in school, directly and negatively impacting their educational experiences. These students have also actively reflected on the benefits of the TMSJGS in supporting their journey toward positive changes. The following section presents and discusses these findings in detail.

Lack of Learning about Queer Issues through Formal Schooling

A commonly shared experience for Queer high school students in S2 emerged from the fact that Queer high school students did not learn anything about Queer people and Queer history in schools. The lack of these learnings affected Queer students’ experiences throughout their schooling. Queer students in S2 discussed that a possible consequence of adding the TMSJGS in school would be less discrimination from their non-Queer counterparts due to their gender and sexuality. Queer students also felt confused about why people did not understand their existence, and they usually wanted people to realize that being Queer is just something normal. Since the TMSJGS was in the context of bullying and harassment, Queer students discussed the benefit the TMSJGS would have in the lives of Queer students because it could be a source to help end discrimination. This theme came from data across questions that concerned Queer students’ general experiences in school and experiences with gender and sexuality in high school and is discussed below.

Queer high school students know the hurdles of being Queer in high school, and it showed throughout the interviews how unsatisfied Queer students in S2 are with the current situations in schools regarding discussions related to gender and sexuality. From the data, it seemed that many of the experiences of Queer students, in S2, throughout schooling were marked by this lack of understanding from others concerning gender and sexuality. This, as is argued later in this section, might be due to the lack of formal exposure students have to Queer-related discussion in schools. When asked if there was one thing that Eric would change in his high school experience, he said:

Eric: That is a tough question. I think it would be how me and the LGBT crowd were seen. Because I think that if we were seen as just regular people, just trying to be happy, just like everybody else, so much would be changed.

Weverton: Can you talk to me a little bit more about, like, what are the things that you think would change?

Eric: Well, I think there would be less discrimination. People would realize that we were just like them, just trying to be happy. They would kind of start to realize that there was nothing to make fun of us for, I mean. There’s nothing to really even hate us for because some people hate us and whatnot for just being who we are, but I think if they realized that we were just like them, they would not hate us anymore, because they would relate to us, “They just want to be happy and we just want to be happy.”

Eric’s experiences in high school have been marked by discrimination, hatred, and harassment. When thinking about the things he would change in his high school experiences, the most relevant thing for him is related to the fact that he would like people to accept Queer people for who they are and understand that Queer people are just regular people.

When Queer students were asked about their experiences with gender and sexuality discussions in formal schooling, surprisingly or not, none of the 10 Queer high school students ever experienced any such discussions. These students’ experiences with discussions about gender and sexuality happened in informal settings in and outside of schools. Tom brought out in his interview issues of the non-normalization of Queer-related discussions in his school spaces, then, I asked him why identifying as Queer was not normalized, and he said:

I think it goes back to just where I live. I’m from southern [Midwest state]. There’s a lot of not great people here. Very, for lack of a better word, “redneck,” very country, which of course, isn’t always bad. I like cornbread too [laughs]. You know, it tends to skew more—I know being Queer isn’t political—but it does tend to skew more republican, um, let’s just be honest, it is. [Midwest state] overall is a very republican state, but especially southern [Midwest state] leans very heavily into that quote unquote “southern heritage” thing that isn’t even really a thing. But you know, that’s a whole other discussion. Basically, people just tend to be bigots. There are a lot of bigots, there are a lot of discriminatory people, a lot of people I hate, honestly. So, whenever you have your school council board or you know all of your school’s, like, CEOs, they’re all like cis straight able bodied middle aged White men. Like, they don’t care. They don’t care. No CisHet White man is like, “How do I make this a good space for Queer kids?” That’s not what they’re thinking about. We’re not the focus, we’re not really thought of, in general, especially with these policies, they don’t really care about Queer kids. We’re just not thought of or included in the discussion. So, whenever it comes to my school environment, I just find that I’m not represented at all, because they don’t even think to.

For Tom, the non-normalization of Queer-identifying students in schools is given because he is from southern [Midwest state]. Although being Queer is not political, in the political arena of the republicans, identifying as Queer became a political discourse that has prevented essential conversations from happening. Tom suggested that in southern [Midwest state] there are a lot of bigots, and these same people are the ones sitting on the school boards to make the necessary decisions that affect discourses in schools. Since the people who sat on the board were the bigots, who in many cases even created feelings of hatred in Tom, these people were not worried about Queer students’ experiences. In particular, Tom called out CisHet White abled-body middle-aged men who, he felt, completely ignored the relevance of Queer people’s issues and experiences. Therefore, there is no representation regarding Queer identities since Queer students’ existence is “ignored.”

Olive helped us to understand the feelings of Queer students when thinking of the benefits of discussing social justice in schools related to gender and sexuality. She said:

I think [Queer-related discussions] will be more normalized and accepted, you know. Since we don’t have that education in school, right now, I think, talking about it in schools will lead to more acceptance and more rates of LGBTQ people being happy and doing better in school, you know because they’re not being bullied or belittled or hearing people belittle or talk about them, you know.

In the quote above, Olive brought out that there were no discussions about social justice in schools that particularly challenged the social injustices Queer students faced in school. She suggested that by bringing social justice discussions to schools related to gender and sexuality, Queer students would become more accepted in the school community, resulting in Queer students doing better in school and being happier. Later in the interview, Ataide Pinheiro continued to push Olive to discuss her understanding of the current mathematics curriculum in her school and how the TMSJGS could be brought into the curriculum. Although she was not sure changes would be made, she discussed the possible benefits if Queer history was brought into the curriculum, such as in the case of the TMSJGS. When asked her how she thought having Queer history in the school curriculum would help in any way, she said:

I think it would help a lot. You know, we don’t learn anything about LGBTQ people right now, and if there was the history about them, that would be great because people would be getting something in schools about LGBTQ people—other than the things that they’re exposed to online, which can either be really good or really awful. And you know, half the people at school are exposed to really awful things about the LGBTQ people and half of them are exposed to good things, so if there was this school thing that was a middle ground, it would make schools safer, because more people would realize that LGBTQ people are not insane or bad or crazy.

Olive expressed how people would be able to get a middle ground in terms of their understanding of Queer students. Such a middle ground would be fundamental to making Queer people seem not insane or bad or crazy, which in turn would lead to a safer school. The lack of discussion of Queer history in schools left schools such as Olive’s school as spaces that did not provide students with support to accept Queer students. As Olive mentioned, students learned about Queer identifications online; half of it could be harmful and the other half good. If schools taught Queer history, the Queer community would be understood as normal and not “insane, bad, or crazy,” as described by Olive.

Lin described similar experiences. When Lin was asked about her experiences discussing gender and sexuality, she said:

I think that it is [discussed] most out of time in school. The most I learn about the community and stuff is on social media. We don’t really talk about it in school so much, at least not in the classes I am taking. I know we have a sociology class [where] we talk about that a bit, but still.

Ataide Pinheiro then probed Lin, asking why she felt people did not talk much about gender and sexuality in schools.

Lin: I feel like they are maybe trying to bring it into the curriculum more, but like, for instance, there are these classes, there is a certain amount of things you need to know. They go through really fast, there are certain things that they need to talk about in the curriculum, but they don’t talk much about the civil rights, well, they talk about the civil rights, but they don’t talk about like (the) gay movement or anything, they just kind of skim over them.

Weverton: And how does that make you feel?

Lin: I feel, like, just like excluded from the history. It is not something we ever talk about or aim really to talk about honestly.

Lin’s experiences with discussions of gender and sexuality were an evident frustration. She had the understanding that there might be an effort to bring more of these discussions into the classroom, yet it was unclear why she thought that such an attempt had been made. She did clarify that while there were some discussions of the civil rights movements, the gay movement was just skimmed over in school—the gay movement was not discussed. Consequently, Lin felt she, as a Queer person, was not even part of history.

From the discussion above, we can conclude that it is essential to push for the inclusion of discussions of gender and sexuality in schools, so Queer-Related discussions and identifying as Queer can be normalized, and people (Queer and non-Queer people) can learn about Queer identities, that being Queer is completely normal, and that Queer-related discussions could benefit the whole school community. Consequently, Queer students would possibly be more respected and understand their identities, and cis people would learn that being Queer is normal. Queer people must be treated with fairness and justice in society, and it is crucial that they are not, as Lin suggested, “excluded from history.” To accomplish this, Queer people’s experiences should be included in both mathematics curriculum and research.

“These Numbers Could Actually Do Something and Help People at My School”

During S2 classroom study, Queer high school students had the opportunity to find out, through matrix multiplication, how many students in their school were experiencing harassment and assault due to having historically marginalized gender and/or sexual identities. Therefore, the Queer students discussed the needs they saw to move toward actions that tackle the injustices Queer students face in schools. Queer participants expressed willingness to be more engaged to help change the experience of their Queer counterparts in schools. They also discussed the possibilities of engaging in supporting the necessary healing in the lives of their Queer friends. Finally, they expressed hope for the change and the creation of awareness of a problem that is still persistent in the Queer school community–harassment and assault.

To understand the importance Queer students saw in the TMSJGS concerning the applicability of these lessons to real-world issues, we analyze Tom’s quote below. When Ataide Pinheiro asked what Tom liked the most about the lessons, he said:

If I’m honest, looking at what I did like the most was the discussions. I liked how we were able to reflect on the data, and I liked how when you guys would ask specifically: what did this data mean to you? And, what is this data trying to say? I liked how the lessons were about more than just getting the numbers, but actually understanding what they meant and understanding what they reflected in the real world.

Above, Tom expressed the power of discussions during the TMSJGS. He appreciated being given the opportunity to reflect on what the data meant. Being engaged in this activity helped Tom shift his perspectives on the doing of mathematics. The TMSJGS went beyond “just getting the numbers,” it was an opportunity to understand what the numbers meant and the impact the data has in the real world. This was so important to Tom that later in the interview, when trying to understand his mathematical identity and experiences with the TMSJGS, Tom said, “I don’t care about you know finding x, but I do care about the social issues.” This statement shows that the social issues being discussed, bullying and harassment, are more important than doing “procedural mathematics.” Therefore, by implementing the TMSJGS in the classroom, we might be able to help Queer students develop more powerful mathematical identities since this type of teaching can shift the perspectives of what mathematics is and why it is crucial to learn it (mathematics can be used to combat social injustices).

Queer students who had experienced bullying and harassment at their schools because of their Queer identity also expressed how change could be accounted for through the TMSJGS. Below, we analyze Olive’s quote. Olive is one of the students who came from schools where experiences with discrimination occur daily. When asked what stood out the most about the lessons, she said:

Olive: It was just really how calm and just collected everyone was. There was no, like, craziness and we actually felt like we were doing something at the end. It wasn’t just like useless numbers, I felt like these numbers could actually do something and help people at my school.

Weverton: Nice, you said like we felt like we’re doing something, can you tell me more about that?

Olive: So, finding out these potential numbers could help us identify people at, like, my school. And then identifying people that can help bring them together, have a community, and then ultimately try to heal and learn from everyone’s experiences and make it better.

The numbers that Olive was referring to are the ones she found using matrix multiplication that expressed the number of students at her school who were going through bullying and harassment because of their Queer identities. Olive also saw the possibility of using these numbers to help students in her school going through these experiences. She continued to discuss how the numbers could be used to find people going through bullying and harassment and create a school community that supports Queer people. She argued for the possibility of helping students heal; in other words, she recognized the traumas Queer students go through as they experience bullying and harassment. She also advocated for the possibility of giving back to the Queer community and moving forward to improve Queer students’ experiences in her school. As she stated last:

Olive: So, I thought it was important [to find the numbers] in my own school because, you know, I could relate to them [number of students going through discrimination]. And also, maybe find that would be a better way to start helping the school, since we have the numbers, now we can help like start changing things.

Weverton: Nice and you mentioned that you can relate to them. Would you expand a little bit on what you mean by that?

Olive: Well, I’m also LGBT and have experienced a lot of discrimination, so I can relate to these numbers and it’s interesting to know about how many people might have had the same experiences, and then, how we might be able to help those people.

After asking a similar question to Eric, (“What stood out the most for you about the lessons?”), he expressed that the number of Queer students being discriminated against shocked him. When Ataide Pinheiro asked him what he thought as he read/discussed all those high numbers. He said:

I just wish I could help other people. That people could accept each other because that is all that we need is for people to accept each other for who they are, and some people just can’t see that, and some people hate to think that, and it’s horrible that they have to go through people thinking that.

Eric reaffirmed how much he wished he could help people. The number of Queer students who are being discriminated against is so high that Eric, as reflected, demonstrated his frustration with those who discriminate against Queer identities and that he wished people could accept Queer students for who they are. It is unfair that some Queer students have to go through discrimination just because they are themselves.

Agency/Power/Authority to Make Change

It was common for Queer students in S2 to discuss who had authority and who could bring changes to the current situation Queer students face in high schools. One way these discussions arose was in the interviews. We analyzed Tom’s statement to demonstrate students’ sense of agency in making changes at school. In the follow-up interview, Tom expressed that there would be a possibility for the TMSJGS to happen in his school, but not in every classroom. Therefore, Ataide Pinheiro probed Tom to know in what type of classroom the TMSJGS would not work out. Tom said:

Well, of course there’s always going to be people in schools you don’t agree with, or you don’t get along with, but for lack of a better word the like, “yee ha!” mullet boys in my school make up a very large demographic and a very loud demographic. Very loud. Even if there’s only one or two people like that in the class, they tend to overshadow everyone else because of how loud and how bold they are about their political statements that it tends to make everyone uncomfortable. I’ve been in classroom settings where maybe there’s one or two people who you know, are very anti-Queer and it just makes the entire space unsafe, even if the rest of the class is majority Queer students. So, I feel like the struggle comes with whenever you have such outspoken people like that in those classrooms that is just like we do at [my] high school. Especially people who have, like, parents on the school board or parents who donate to the school, it could cause trouble, because one thing my school really cares about is getting funding and they’re not getting their funding from the Queer students, so let me tell you that.

In the above statement, Tom expressed that Queer people would feel unsafe and shut off, even in places where they were the majority, if some very vocal anti-Queer students were in the classroom. Tom recognized those “loud” students could impact the possibility of the TMSJGS happening because if they spoke up, they would cause trouble, which implied these classes would not happen.

Similar to Tom, Olive opined about the possibilities of the TMSJGS being implemented in her school. She said:

Right now, if they [her school] just got it [the TMSJGS lessons] they probably wouldn’t do anything about it because there’s not that student or parent support and my school is such a big school, I go to South Corner High School (pseudonym), that they woudn’t want to lose on funding or, like, students from those parents who don’t want their kids to learn about it [TMSJGS].

Olive expressed how vital funding is to her school, and most likely, if her school was introduced to the TMSJGS, they would not do anything about it [implement it in the classroom]; noting that if her school did implent TMSJGS they could lose funding and lose students which means losing more funding. The primary reason she attributed her school losing students was that parents would not be happy about their kids learning the TMSJGS in school. After all, she made it clear that there is not much support available from students and parents to implement these types of teaching in the school.

In sum, Queer high school students in S2 saw through the TMSJGS an opportunity to reflect on the consequences that bullying and harassment have on Queer high school students’ lives. Using mathematics to model discrimination and understand how discrimination looks in their schools, Queer students showed sentiments toward the community and argued the importance of advocating for changes. The TMSJGS helped Queer students in S2 to increase their sense of belonging in the Queer community and also their sense of agency.

Discussion and Implications

While these two dissertations differed in their overall contexts and aims, both provided ways researchers can incorporate inclusive inquiry practices. First and foremost, both studies included students who had previously been overlooked. S1 showed statistical approaches that expanded beyond binary methods, such as t-tests that forced students into two categories, and included previously vetted items to conscientiously collect students’ sex assigned at birth, gender identity, and gender expression. This approach provided nuanced statistical results, which could support researchers in differentiating between biological, psychological, and social factors. Students who identified in a variety of ways were interviewed to further examine these factors. Additionally, if research utilizes these previously-vetted survey items about sex, gender, and sexuality and allows students to self-identify, researchers should also provide students with resources if students request. This might include information about community youth groups or safe websites. S2 utilized a social justice lesson to shed light on ways Queer students have been bullied and harassed in their schools. The students who participated in these lessons noted the importance of activities such as this, which normalized their identities and made their experiences visible in the curriculum. As they noted, they felt that they were no longer “excluded from history” and their peers could see that they were “just regular people, just trying to be happy, just like everybody else.”

S2’s use of gender and sexuality within the curriculum allowed students to better understand complex forms of identity in a safe and monitored environment. As Olive, a participant in the study, explicitly stated, most students are accessing information about gender and sexuality online, information that may present negative and harmful idea about the LBGTQ community. While some students may access “really good” information, such as information provided by community you groups, schools could step in and provide somewhat neutral information that would potentially allow Queer students to feel safer and possibly reduce the higher suicide rates of suicide of queer students (e.g. Gnan et al., 2019). Queer inclusive schools could also help educators make their teaching practices more LGBTQ+ inclusive. Further, the US students in S2 said that discussions of gender and sexuality are usually restricted to coursework such as Sociology or not discussed at all.

Professional development centered on teachers moderating discussions in other courses, such as mathematics, could go a long way toward inclusion. After all, one student in S2 mentioned that “loud” and “bold” voices are comfortable saying hurtful things, even if the majority of the class might be accepting of Queer people. Another simple suggestion might be to give students more choice in their activities and projects. For instance, in a recent statistics course, Cox had her students group by interests first, picking a topic within larger categories such as Sports and Entertainment, Health and Wellness, and Diversity, Equity, and Inclusion (DEI). Under each category, the teacher could provide examples of previous projects or ideas students might want to pursue. For instance, the teacher could suggest DEI projects might involve discrepancies in salaries for various groups of people or limited access to healthcare for Queer people. Within smaller groups that have self-selected a DEI category, students might have more agency to discuss complicated issues and investigate common interests, and these smaller projects might open the door for the full class to express interest in investigating a topic further. A final suggestion would be for teachers to be aware of classic textbook problems that can be harmful to Queer-Identifying people. For instance, Rubel (2016) discussed heteronormative “married couple” problems, which assumed man and woman pairs were the only spousal pairs allowed. As an additional example related to gender, when discussing Bernoulli Trials, a classic question is “What is the probability that a family of 4 children has 3 girls?” To solve the problem, we assume 50% of babies are “boys” and 50% of babies are “girls,” but, as we know, gender is much more complex and fluid. This problem conflates gender and sex, and could be slightly improved by phrasing it as, “In a certain hospital, there are approximately 10 babies born each day. If we know 49.7% of babies are assigned “female,” what is the probability that at least 6 are assigned female?” Additionally, a teacher could put a footnote or mention that even this phrasing tends to oversimplify, as it is suggested that 1–2% of people have “intersex” characteristics (Cleveland Clinic, 2022).

Recent literature and these two doctoral studies underscore the urgency of addressing gender and sexuality within mathematics education research (e.g. Ataide Pinheiro, 2021; Cox, 2022; Damarin & Erchick, 2010; Glasser & Smith, 2008; Leyva, 2017; Lubienski & Ataide Pinheiro, 2020; Neto & Ataide Pinheiro, 2021). Our work highlights the role of mathematics in propagating normativities, the need for inclusivity, and the limitations present in current efforts to foster diversity. By examining and understanding these dynamics, educators and curriculum developers can create more inclusive mathematics learning environments that embrace all students’ diverse identities and experiences. Additionally, being cognizant of conflations in “sex” and “gender” terms and using these terms responsibly, researchers can better convey their work and provide nuanced understandings of possible factors, which could be psychological, biological, or socially or culturally formed (Cox, 2022; Halpern et al., 2005). With inclusive inquiry practices such as these, we will make great strides at supporting Queer students to feel visible and valued, both within the classroom and within research.

Disclosure statement

No potential conflict of interest was reported by the author(s).