A randomized trapezoidal quadrature

Abstract

A randomized trapezoidal quadrature rule is proposed for continuous functions which enjoy less regularity than commonly required. Indeed, we consider functions in some fractional Sobolev space. Various error bounds for the randomized rule are established while an error bound for classical trapezoidal quadrature is obtained for comparison. The randomized trapezoidal quadrature rule is shown to improve the order of convergence by half.

Keywords:

• Randomized trapezoidal quadrature
• fractional Sobolev space
• almost sure convergence
• $L^p$ convergence

2010 Mathematics Subject Classifications:

• 65C05
• 65D30

1. Introduction

It is well known that the trapezoidal quadrature in classical numerical analysis is a technique for approximating ${\mathbb{R}}^d$-valued definite integral when the integrand is at least twice differentiable. It has been well-studied by Goodwin [7], Schwartz [9] and Stenger [10]. The case of a rough integrand was investigated in [3]. More recently, a stochastic version of the trapezoidal quadrature was proposed for approximating the Itô integral where the integrator is a Brownian motion [5].

Without loss of generality, we consider the time interval $[0,T]$ and let $g\in C^2([0,T])$ to be the integrand of interest, where $C^2([0,T]):=C^2([0,T];{\mathbb{R}}^d)$ is the space of ${\mathbb{R}}^d$-valued continuous functions that have continuous first two derivatives, endowed with the uniform norm topology. The trapezoidal quadrature is proven to achieve a order of convergence as high as 2 for evaluating the integral $I[g]:={\int }_0^{T}g(t)\mathrm{d}t$ with finite many point evaluations [4]. To implement this, we first partition the interval $[0,T]$ into N equidistant intervals with stepsize $h_N=\frac{T}{N}$, i.e. (1) ${\mathrm{\Pi }}_h:=\{t_j:=jh{\}}_{j=0}^N\subset [0,T],$(1) where the subscription N is suppressed in h for the sake of notational simplicity but assumed implicitly in all of the quantities introduced involving h. Define (2) $Q_h[g]:=\frac{h}{2}\sum _{i=0}^{N-1}(g(t_i)+g(t_{i+1})).$(2) When g has less regularity, the trapezoidal quadrature shows a slower convergence with a sharp bound [3]. To accelerate the convergence when g is ‘rougher’, we consider a randomized trapezoidal quadrature, which is inspired by the randomized version of mid-point Runge–Kutta quadrature rule [8] and stochastic version of trapezoidal quadrature for Itô integral [5]. In this paper, the ${\mathbb{R}}^d$-valued integrand g is assumed to be in fractional Sobolev space $W^{\sigma ,p}(0,T)$ under Sobolev–Slobodeckij norm: (3) $\Vert g{\Vert }_{W^{\sigma ,p}(0,T)}={({\int }_0^T|g(t){|}^p\mathrm{d}t+{\int }_0^T|\dot{g}(t){|}^p\mathrm{d}t+{\int }_0^T{\int }_0^T\frac{|\dot{g}(t)-\dot{g}(s){|}^p}{|t-s{|}^{1+(\sigma -1)p}}\mathrm{d}t\mathrm{d}s)}^{\frac{1}{p}},$(3) for $\sigma \in (1,2)$ and $p\in [2,\mathrm{\infty })$. We may write $\Vert g{\Vert }_{W^{\sigma ,p}(0,T)}$ as $\Vert g{\Vert }_{W^{\sigma ,p}}$ for short. Let us define a randomized trapezoidal quadrature as follows: (4) $R{Q}_h^{\tau ,n}[g]:=\frac{h}{2}\sum _{i=0}^{n-1}(g(t_i+{\tau }_{i}h)+g(t_i+{\overline{\tau }}_{i}h))\mathrm{for}n\in [N],$(4) where $\{{\tau }_i{\}}_{i=0}^{N-1}$ is a sequence of independent and identically (i.i.d.) uniformly distributed random variables on a probability space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$, ${\overline{\tau }}_i:=1-{\tau }_i$ and $[N]:=\{1,\dots ,N\}$. The main result, Theorem 3.2, shows that the convergence rate can be improved to $\mathcal{O}(N^{-\sigma -\frac{1}{2}})$ compared to $\mathcal{O}(N^{-\sigma })$ achieved by the classical trapezoidal quadrature (Theorem 3.1) when $g\in W^{\sigma ,p}$.

The paper is organized as follows. In Section 2, we present some prerequisites from probability theory. In Section 3, we give the error estimates for both the classical trapezoidal quadrature and the randomized trapezoidal quadrature. In addition, we also investigate the error estimate in almost sure sense for the randomized trapezoidal quadrature in Theorem 3.3, which is proven still superior to the classical one. In the last section, we verify the results through several numerical experiments.

2. Preliminaries

This section is devoted to a brief review of essential probability results for audience who are not familiar with probability theory. Most of the contents are repeated material from Section 2 in [8]. One may refer to [2] for a more detailed introduction.

Recall that a probability space $(\mathrm{\Omega },\mathcal{F},\mathbb{P})$ consists of a measurable space $(\mathrm{\Omega },\mathcal{F})$ endowed with a finite measure $\mathbb{P}$ satisfying $\mathbb{P}(\mathrm{\Omega })=1$. A random variable $X:\mathrm{\Omega }\to {\mathbb{R}}^d$ is called integrable if ${\int }_{\mathrm{\Omega }}|X(\omega )|\mathrm{d}\mathbb{P}(\omega )<\mathrm{\infty }$. Then, the expectation of X is defined as $\mathbb{E}[X]:={\int }_{\mathrm{\Omega }}X(\omega )\mathrm{d}\mathbb{P}(\omega )={\int }_{{\mathbb{R}}^d}x\mathrm{d}{\mu }_X(x),$where ${\mu }_X$ is distribution of X on its image space. We write $X\in L^p(\mathrm{\Omega };{\mathbb{R}}^d)$ with $p\in [1,\mathrm{\infty })$ if ${\int }_{\mathrm{\Omega }}|X(\omega ){|}^p\mathrm{d}\mathbb{P}(\omega )<\mathrm{\infty }$, where $L^p(\mathrm{\Omega };{\mathbb{R}}^d)$ is a Banach space endowed with the norm $\Vert X{\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}={\left(\mathbb{E}[|X{|}^p]\right)}^{\frac{1}{p}}={({\int }_{\mathrm{\Omega }}|X(\omega ){|}^p\mathrm{d}\mathbb{P}(\omega ))}^{\frac{1}{p}}.$We will write $\Vert X{\Vert }_{L^p(\mathrm{\Omega };\mathbb{R})}$ as $\Vert X{\Vert }_{L^p(\mathrm{\Omega })}$ for short.

We say that a family of ${\mathbb{R}}^d$-valued random variables $(X_m{)}_{m\in \mathbb{N}}$ is a discrete-time stochastic process if we interpret the index m as a time parameter. A crucial concept in our main proof is martingales, which is a special case of the discrete-time stochastic process with many nice properties. If $(X_m{)}_{m\in \mathbb{N}}$ is an independent family of integrable random variables satisfying $\mathbb{E}[X_m]=0$ for each $m\in \mathbb{N}$, then the stochastic process defined by the partial sums $S_n:=\sum _{m=1}^n{X}_m,n\in \mathbb{N},$is a discrete-time martingale. One of the most important inequalities for martingales is the Burkholder–Davis–Gundy inequality. In this paper, we need its discrete-time version.

Theorem 2.1

Burkholder–Davis–Gundy

For each $p\in (1,\mathrm{\infty })$ there exist positive constants $c_p$ and $C_p$ such that for every discrete time martingale $(X_n{)}_{n\in \mathbb{N}}$ and for every $n\in \mathbb{N}$ we have $c_p\Vert [X{]}_n^{1/2}{\Vert }_{L^p(\mathrm{\Omega })}\le {\Vert \underset{j\in \{1,\dots ,n\}}{max}|X_j|\Vert }_{L^p(\mathrm{\Omega })}\le C_p\Vert [X{]}_n^{1/2}{\Vert }_{L^p(\mathrm{\Omega })},$where $[X{]}_n=|X_1{|}^2+\sum _{k=2}^n|X_k-X_{k-1}{|}^2$ denotes the quadratic variation of $(X_n{)}_{n\in \mathbb{N}}$ up to n.

3. Trapezoidal quadratures for a rougher integrand

This section investigates the errors from trapezoidal rules for approximating integral of $g\in W^{\sigma ,p}$. The error bound from the classical trapezoidal rule is obtained in Section 3.1 and the ones from the randomized trapezoidal rule is in Section 3.2.

3.1. Classical trapezoidal quadrature for $g\in W^{\sigma ,p}$

Theorem 3.1

If $g\in W^{\sigma ,p}(0,T)$ for $\sigma \in [1,2)$, then we have (5) $|I[g]-Q_h[g]|\le C{T}^{1-\frac{1}{p}}{h}^{\sigma }\Vert g{\Vert }_{W^{\sigma ,p}(0,T)},$(5) where C is a constant that only depends on p.

Proof.

To show Equation (5(5) $|I[g]-Q_h[g]|\le C{T}^{1-\frac{1}{p}}{h}^{\sigma }\Vert g{\Vert }_{W^{\sigma ,p}(0,T)},$(5) ), we follow [5] to rewrite (6) $g(t_i)+g(t_{i+1})=2g(t_{i+\frac{1}{2}})+{\int }_{t_{i+\frac{1}{2}}}^{t_i}\dot{g}(s)\mathrm{d}s+{\int }_{t_{i+\frac{1}{2}}}^{t_{i+1}}\dot{g}(s)\mathrm{d}s,$(6) where $t_{i+\frac{1}{2}}:=\frac{1}{2}(t_i+t_{i+1})$. Then, the LHS of Equation (5(5) $|I[g]-Q_h[g]|\le C{T}^{1-\frac{1}{p}}{h}^{\sigma }\Vert g{\Vert }_{W^{\sigma ,p}(0,T)},$(5) ) can be rewritten as $I[g]-Q_h[g]=\sum _{i=0}^{N-1}{E}_1^{i,i+1}+\sum _{i=0}^{N-1}{E}_2^{i,i+1},$where (7) $E_1^{i,i+1}:={\int }_{t_i}^{t_{i+1}}(g(t)-g(t_{i+\frac{1}{2}}))\mathrm{d}t=\frac{1}{2}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\dot{g}(r)\mathrm{d}r\mathrm{d}t$(7) and (8) $E_2^{i,i+1}:=\frac{1}{2}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i}\dot{g}(s)\mathrm{d}s+{\int }_{t_{i+\frac{1}{2}}}^{t_{i+1}}\dot{g}(s)\mathrm{d}s)\mathrm{d}t.$(8) Regarding $E_1^{i,i+1}$, first note that $V_i:=\frac{1}{h}(g(t_{i+1})-g(t_i)){\int }_{t_i}^{t_{i+1}}(t-t_{i+\frac{1}{2}})\mathrm{d}t=\frac{1}{h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t{\int }_{t_i}^{t_{i+1}}\dot{g}(s)\mathrm{d}s\mathrm{d}r\mathrm{d}t=0.$Then, we can rewrite $E_1^{i,i+1}$ as (9) $\begin{array}{rl}{E}_1^{i,i+1}& =E_1^{i,i+1}-V_i=\frac{1}{h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\dot{g}(r)\mathrm{d}r\mathrm{d}s\mathrm{d}t-V_i\\ & =\frac{1}{h}\sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t(\dot{g}(r)-\dot{g}(s))\mathrm{d}r\mathrm{d}s\mathrm{d}t.\end{array}$(9) Thus evaluating $\sum _{i=0}^{N-1}{E}_1^{i,i+1}$ under $L^p$ norm gives (10) $\begin{array}{rl}\left|\sum _{i=0}^{N-1}{E}_1^{i,i+1}\right|& \le \sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}|\dot{g}(r)-\dot{g}(s)|\mathrm{d}r\mathrm{d}s\\ & \le \sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{({\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}|\dot{g}(r)-\dot{g}(s){|}^p\mathrm{d}r\mathrm{d}s)}^{\frac{1}{p}},\end{array}$(10) where the second line is deduced by applying Hölder's inequality twice, and $\frac{1}{q}:=1-\frac{1}{p}$. For the case $\sigma =1$ and any $p\ge 2$, we may directly apply the discrete Hölder's inequality to the last term above: $\begin{array}{rl}& \sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{({\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}|\dot{g}(r)-\dot{g}(s){|}^p\mathrm{d}r\mathrm{d}s)}^{\frac{1}{p}}\le C\sum _{i=0}^{N-1}{h}^{\frac{2}{q}+\frac{1}{p}}{({\int }_{t_i}^{t_{i+1}}|\dot{g}(r){|}^p\mathrm{d}r)}^{\frac{1}{p}}\\ & \le Ch{\left(\sum _{i=0}^{N-1}h\right)}^{\frac{1}{q}}{(\sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}|\dot{g}(r){|}^p\mathrm{d}r)}^{\frac{1}{p}}=Ch{T}^{1-\frac{1}{p}}\Vert g{\Vert }_{W^{1,p}}.\end{array}$For the case $\sigma \in (1,2)$ and any $p\ge 2$, we may first make use of the definition of $W^{\sigma ,p}$ and then apply the discrete Hölder's inequality: $\begin{array}{rl}& \sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{({\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}|\dot{g}(r)-\dot{g}(s){|}^p\mathrm{d}r\mathrm{d}s)}^{\frac{1}{p}}\\ & \le \sum _{i=0}^{N-1}{h}^{\frac{2}{q}+\frac{1}{p}+\sigma -1}{\left({\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}\frac{|\dot{g}(r)-\dot{g}(s){|}^p}{|r-s{|}^{1+(\sigma -1)p}}\mathrm{d}r\mathrm{d}s\right)}^{\frac{1}{p}}\\ & =h^{\sigma }\sum _{i=0}^{N-1}{h}^{\frac{1}{q}}{\left({\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}\frac{|\dot{g}(r)-\dot{g}(s){|}^p}{|r-s{|}^{1+(\sigma -1)p}}\mathrm{d}r\mathrm{d}s\right)}^{\frac{1}{p}}\le h^{\sigma }{T}^{1-\frac{1}{p}}\Vert g{\Vert }_{W^{1,p}}.\end{array}$For term $E_2^{i,i+1}$, we can follow a similar argument in [5] to show that (11) $E_2^{i,i+1}=\frac{1}{2h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r+{\int }_{t_{i+\frac{1}{2}}}^{t_{i+1}}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r)\mathrm{d}s\mathrm{d}t.$(11) Indeed, note that $(t_i-t_{i+\frac{1}{2}})+(t_{i+1}-t_{i+\frac{1}{2}})=0,$If defining a new process $P_i:=\frac{t_i-t_{i+\frac{1}{2}}}{2h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}\dot{g}(r)\mathrm{d}r\mathrm{d}t+\frac{t_{i+1}-t_{i+\frac{1}{2}}}{2h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}\dot{g}(r)\mathrm{d}r\mathrm{d}t,$then Equation (11(11) $E_2^{i,i+1}=\frac{1}{2h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r+{\int }_{t_{i+\frac{1}{2}}}^{t_{i+1}}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r)\mathrm{d}s\mathrm{d}t.$(11) ) can be obtained through the fact that $E_2^{i,i+1}=E_2^{i,i+1}-P_i.$Thus applying a similar argument as for $\sum _{i=0}^{N-1}{E}_1^{i,i+1}$, we can show that (12) $\left|\sum _{i=0}^{N-1}{E}_2^{i,i+1}\right|\le C{T}^{1-\frac{1}{p}}{h}^{\sigma }\Vert g{\Vert }_{W^{\sigma ,p}[0,T]}.$(12) Finally, we can conclude that $|I[g]-Q_h[g]|\le \left|\sum _{i=0}^{N-1}{E}_1^{i,i+1}\right|+\left|\sum _{i=0}^{N-1}{E}_2^{i,i+1}\right|\le C{T}^{1-\frac{1}{p}}{h}^{\sigma }\Vert g{\Vert }_{W^{\sigma ,p}[0,T]}.$

For the classical trapezoidal quadrature (CTQ), Theorem 3.1 claims that its order of convergence would be the same as the regularity of the integrand. For the boundary case, when $g\in W^{1,p}$, the order is 1.

3.2. Randomized trapezoidal rules for $g\in W^{\sigma ,p}$

For the randomized trapezoidal quadrature (4(4) $R{Q}_h^{\tau ,n}[g]:=\frac{h}{2}\sum _{i=0}^{n-1}(g(t_i+{\tau }_{i}h)+g(t_i+{\overline{\tau }}_{i}h))\mathrm{for}n\in [N],$(4) ), the proof follows a similar argument as in Theorem 4.2 [8].

Theorem 3.2

Define $I^n:={\int }_0^{t_n}g(t)\mathrm{d}t$ for $n\in [N]$ for $g\in W^{\sigma ,p}$ with $\sigma \in [1,2)$ and $p\ge 2$. Then $R{Q}_h^{\tau ,n}[g]\in L^p(\mathrm{\Omega };{\mathbb{R}}^d)$ and is an unbiased estimator of $I^n[g]$, i.e. $\mathbb{E}[R{Q}_h^{\tau ,n}[g]]=I^n[g]$. Moreover, it holds true that (13) $\Vert I[g]-R{Q}_h^{\tau ,N}[g]{\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}\le C_p|T{|}^{\frac{p-2}{2p}}{h}^{\frac{1}{2}+\sigma }\Vert g{\Vert }_{W^{\sigma ,p}(0,T)},$(13) where $C_p$ is a constant that depends only on p.

Proof.

First, due to $g\in W^{\sigma ,p}$ we have $\Vert g{\Vert }_{L^p([0,T];{\mathbb{R}}^d)}<\mathrm{\infty }$. Recall that ${\tau }_i\in \mathcal{U}(0,1)$ for each $i\in [N-1]\cup \{0\}$. Then, it follows that $\frac{h}{2}(\Vert g(t_i+{\tau }_{i}h){\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}^p+\Vert g(t_i+{\overline{\tau }}_{i}h){\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}^p)={\int }_{t_i}^{t_{i+1}}|g(t){|}^p\mathrm{d}t<\mathrm{\infty }.$Hence $R{Q}_h^{\tau ,n}[g]\in L^p(\mathrm{\Omega })$ for $n\in [N]$. To show $R{Q}_h^{\tau ,n}[g]$ is unbiased, we need to examine each term in RHS of Equation (4(4) $R{Q}_h^{\tau ,n}[g]:=\frac{h}{2}\sum _{i=0}^{n-1}(g(t_i+{\tau }_{i}h)+g(t_i+{\overline{\tau }}_{i}h))\mathrm{for}n\in [N],$(4) ) through spelling out the expectation and changing variable, i.e. $\frac{h}{2}\mathbb{E}[g(t_i+{\tau }_{i}h)]=\frac{h}{2}{\int }_0^{1}g(t_i+rh)\mathrm{d}r=\frac{1}{2}{\int }_{t_i}^{t_{i+1}}g(t)\mathrm{d}t$and $\frac{h}{2}\mathbb{E}[g(t_i+{\overline{\tau }}_{i}h)]=\frac{h}{2}{\int }_0^{1}g(t_i+(1-r)h)\mathrm{d}r=\frac{1}{2}{\int }_{t_i}^{t_{i+1}}g(t)\mathrm{d}t.$Summing these terms up gives that $R{Q}_h^{\tau ,n}[g]$ is unbiased for $I^n[g]$. Furthermore, if define the error term like (14) $E^n:=I^n[g]-R{Q}_h^{\tau ,n}[g]=\frac{1}{2}\sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}(2g(t)-g(t_i+{\tau }_{i}h)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t,$(14) then each summand is a mean-zero random variable, i.e. $\mathbb{E}[{\int }_{t_i}^{t_{i+1}}(2g(t)-g(t_i+{\tau }_{i}h)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t]=0.$Note that the summands are mutually independent due to the independence of $\{{\tau }_i{\}}_{i=0}^{N-1}$. In addition, it is easy to show $E^n\in L^p(\mathrm{\Omega };{\mathbb{R}}^d)$. Therefore, $E^n$ is a $L^p$-martingale. Then applying the discrete version of the Burkholder–Davis–Gundy inequality leads to (15) $\begin{array}{rl}& {\Vert \underset{n}{max}|E^n|\Vert }_{L^p(\mathrm{\Omega })}\le C_p\Vert [E^n{]}_N^{\frac{1}{2}}{\Vert }_{L^p(\mathrm{\Omega })}\\ & =\frac{C_p}{2}{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(2g(t)-g(t_i+{\tau }_{i}h)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & \le C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & +C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })},\end{array}$(15) where in the second line we substitute the quadratic variation $[E^n{]}_N$. Due to symmetric property, it is easy to see we only need to handle the first term on the RHS of Equation (15(15) $\begin{array}{rl}& {\Vert \underset{n}{max}|E^n|\Vert }_{L^p(\mathrm{\Omega })}\le C_p\Vert [E^n{]}_N^{\frac{1}{2}}{\Vert }_{L^p(\mathrm{\Omega })}\\ & =\frac{C_p}{2}{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(2g(t)-g(t_i+{\tau }_{i}h)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & \le C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & +C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })},\end{array}$(15) ). Note that (16) $\begin{array}{rl}& C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & =C_p{\Vert \sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t|}^2\Vert }_{L^{\frac{p}{2}}(\mathrm{\Omega })}^{\frac{1}{2}}\\ & \le C_p{\left(\sum _{i=0}^{N-1}{\Vert {\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}^2\right)}^{\frac{1}{2}}.\end{array}$(16) Then we have that $\begin{array}{rl}& C_p{\left(\sum _{i=0}^{N-1}{\Vert {\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}^2\right)}^{\frac{1}{2}}\\ & =C_p{\left(\sum _{i=0}^{N-1}{\Vert {\int }_{t_i}^{t_{i+1}}{\int }_{t_i+{\tau }_{i}h}^t\dot{g}(s)\mathrm{d}s\mathrm{d}t\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}^2\right)}^{\frac{1}{2}}\\ & \le C_p{\left(\sum _{i=0}^{N-1}{\Vert {\int }_{t_i}^{t_{i+1}}{\int }_{t_i+{\tau }_{i}h}^t|\dot{g}(s)|\mathrm{d}s\mathrm{d}t\Vert }_{L^p(\mathrm{\Omega })}^2\right)}^{\frac{1}{2}}\\ & \le C_{p}h{\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}|\dot{g}(s)|\mathrm{d}s|}^2\right)}^{\frac{1}{2}}\le C_{p}h{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{|{\int }_{t_i}^{t_{i+1}}|\dot{g}(s){|}^p\mathrm{d}s|}^{\frac{2}{p}}\right)}^{\frac{1}{2}}.\end{array}$When p = 2, the term on the right-hand side above can be directly bounded by (17) $C_{p}h{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{|{\int }_{t_i}^{t_{i+1}}|\dot{g}(s){|}^p\mathrm{d}s|}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\le C_p{h}^{\frac{3}{2}}\Vert g{\Vert }_{W^{1,p}},$(17) where $\frac{1}{q}+\frac{1}{p}=1$. For p>2, we may apply discrete Hölder inequality and get (18) $\begin{array}{rl}& C_{p}h{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{|{\int }_{t_i}^{t_{i+1}}|\dot{g}(s){|}^p\mathrm{d}s|}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\le C_{p}h{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}\frac{p}{p-2}}\right)}^{\frac{p-2}{2p}}{(\sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}|\dot{g}(s){|}^p\mathrm{d}s)}^{\frac{1}{p}}\\ & \le C_p{h}^{1+(\frac{2p}{q(p-2)}-1)\frac{p-2}{2p}}|T{|}^{\frac{p-2}{2p}}\Vert g{\Vert }_{W^{1,p}}=C_p{h}^{\frac{3}{2}}|T{|}^{\frac{p-2}{2p}}\Vert g{\Vert }_{W^{1,p}}.\end{array}$(18) Now, we have shown Bound (13(13) $\Vert I[g]-R{Q}_h^{\tau ,N}[g]{\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}\le C_p|T{|}^{\frac{p-2}{2p}}{h}^{\frac{1}{2}+\sigma }\Vert g{\Vert }_{W^{\sigma ,p}(0,T)},$(13) ) when $\sigma =1$. For Bound (13(13) $\Vert I[g]-R{Q}_h^{\tau ,N}[g]{\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}\le C_p|T{|}^{\frac{p-2}{2p}}{h}^{\frac{1}{2}+\sigma }\Vert g{\Vert }_{W^{\sigma ,p}(0,T)},$(13) ) under $\sigma >1$, we first note that Equation (6(6) $g(t_i)+g(t_{i+1})=2g(t_{i+\frac{1}{2}})+{\int }_{t_{i+\frac{1}{2}}}^{t_i}\dot{g}(s)\mathrm{d}s+{\int }_{t_{i+\frac{1}{2}}}^{t_{i+1}}\dot{g}(s)\mathrm{d}s,$(6) ) remains true if replacing $t_i$ by $t_i+{\tau }_{i}h$ and $t_{i+1}$ by $t_i+{\overline{\tau }}_{i}h$, i.e. (19) $g(t_i+{\tau }_{i}h)+g(t_i+{\overline{\tau }}_{i}h)=2g(t_{i+\frac{1}{2}})+{\int }_{t_{i+\frac{1}{2}}}^{t_i+{\tau }_{i}h}\dot{g}(s)\mathrm{d}s+{\int }_{t_{i+\frac{1}{2}}}^{t_i+{\overline{\tau }}_{i}h}\dot{g}(s)\mathrm{d}s.$(19) Thus, the second line of Equation (15(15) $\begin{array}{rl}& {\Vert \underset{n}{max}|E^n|\Vert }_{L^p(\mathrm{\Omega })}\le C_p\Vert [E^n{]}_N^{\frac{1}{2}}{\Vert }_{L^p(\mathrm{\Omega })}\\ & =\frac{C_p}{2}{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(2g(t)-g(t_i+{\tau }_{i}h)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & \le C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & +C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })},\end{array}$(15) ) can be further split as the follows: $\begin{array}{rl}& \frac{C_p}{2}{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(2g(t)-g(t_i+{\tau }_{i}h)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & \le C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_{i+\frac{1}{2}}))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & +C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^{t_i+{\tau }_{i}h}\dot{g}(s)\mathrm{d}s\mathrm{d}t+{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^{t_i+{\overline{\tau }}_{i}h}\dot{g}(s)\mathrm{d}s\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}.\end{array}$Similar as in the proof of Theorem 3.1, we introduce $E_1^{i,i+1}$ defined in Equation (7(7) $E_1^{i,i+1}:={\int }_{t_i}^{t_{i+1}}(g(t)-g(t_{i+\frac{1}{2}}))\mathrm{d}t=\frac{1}{2}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\dot{g}(r)\mathrm{d}r\mathrm{d}t$(7) ) and (20) $E_2^{i,i+1}(\tau ):=\frac{1}{2}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i+\tau h}\dot{g}(s)\mathrm{d}s+{\int }_{t_{i+\frac{1}{2}}}^{t_i+\overline{\tau }h}\dot{g}(s)\mathrm{d}s)\mathrm{d}t.$(20) As in the proof of Theorem 3.1, $E_1^{i,i+1}$ can be handled through the equivalent form Equation (9(9) $\begin{array}{rl}{E}_1^{i,i+1}& =E_1^{i,i+1}-V_i=\frac{1}{h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\dot{g}(r)\mathrm{d}r\mathrm{d}s\mathrm{d}t-V_i\\ & =\frac{1}{h}\sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t(\dot{g}(r)-\dot{g}(s))\mathrm{d}r\mathrm{d}s\mathrm{d}t.\end{array}$(9) ) and $E_2^{i,i+1}(\tau )$ can be treated in a similar way as Equation (11(11) $E_2^{i,i+1}=\frac{1}{2h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r+{\int }_{t_{i+\frac{1}{2}}}^{t_{i+1}}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r)\mathrm{d}s\mathrm{d}t.$(11) ) by replacing $t_i$ by $t_i+{\tau }_{i}h$ and $t_{i+1}$ by $t_i+{\overline{\tau }}_{i}h$ in the inner integral of Equation (11(11) $E_2^{i,i+1}=\frac{1}{2h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r+{\int }_{t_{i+\frac{1}{2}}}^{t_{i+1}}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r)\mathrm{d}s\mathrm{d}t.$(11) ), i.e. (21) $E_2^{i,i+1}=\frac{1}{2h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i+{\tau }_{i}h}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r+{\int }_{t_{i+\frac{1}{2}}}^{t_i+{\overline{\tau }}_{i}h}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r)\mathrm{d}s\mathrm{d}t.$(21) Thus $\begin{array}{rl}& \frac{C_p}{2}{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(2g(t)-g(t_i+{\tau }_{i}h)-g(t_i+{\overline{\tau }}_{i}h))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & \le C_p{\Vert {\left(\sum _i^{N-1}|E_1^{i,i+1}{|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}+C_p{\Vert {\left(\sum _i^{N-1}|E_2^{i,i+1}{|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & =\frac{C_p}{h}{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t(\dot{g}(r)-\dot{g}(s))\mathrm{d}r\mathrm{d}s\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & +\frac{C_p}{2h}\Vert (\sum _{i=0}^{N-1}|{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i+{\tau }_{i}h}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r\\ & {{{+{\int }_{t_{i+\frac{1}{2}}}^{t_i+{\overline{\tau }}_{i}h}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r)\mathrm{d}s\mathrm{d}t|}^2)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })},\end{array}$where the first term on the right-hand side from Equation (9(9) $\begin{array}{rl}{E}_1^{i,i+1}& =E_1^{i,i+1}-V_i=\frac{1}{h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\dot{g}(r)\mathrm{d}r\mathrm{d}s\mathrm{d}t-V_i\\ & =\frac{1}{h}\sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t(\dot{g}(r)-\dot{g}(s))\mathrm{d}r\mathrm{d}s\mathrm{d}t.\end{array}$(9) ) and the second term is due to Equation (21(21) $E_2^{i,i+1}=\frac{1}{2h}{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}({\int }_{t_{i+\frac{1}{2}}}^{t_i+{\tau }_{i}h}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r+{\int }_{t_{i+\frac{1}{2}}}^{t_i+{\overline{\tau }}_{i}h}(\dot{g}(s)-\dot{g}(r))\mathrm{d}r)\mathrm{d}s\mathrm{d}t.$(21) ). Let us now deal with the first term, the second term can be handled in the same way. Following a similar argument in (16(16) $\begin{array}{rl}& C_p{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & =C_p{\Vert \sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t|}^2\Vert }_{L^{\frac{p}{2}}(\mathrm{\Omega })}^{\frac{1}{2}}\\ & \le C_p{\left(\sum _{i=0}^{N-1}{\Vert {\int }_{t_i}^{t_{i+1}}(g(t)-g(t_i+{\tau }_{i}h)))\mathrm{d}t\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}^2\right)}^{\frac{1}{2}}.\end{array}$(16) ), we have that $\begin{array}{rl}& \frac{C_p}{h}{\Vert {\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t(\dot{g}(r)-\dot{g}(s))\mathrm{d}r\mathrm{d}s\mathrm{d}t|}^2\right)}^{\frac{1}{2}}\Vert }_{L^p(\mathrm{\Omega })}\\ & \le \frac{C_p}{h}{\left(\sum _{i=0}^{N-1}{\Vert {\int }_{t_i}^{t_{i+1}}{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t(\dot{g}(r)-\dot{g}(s))\mathrm{d}r\mathrm{d}s\mathrm{d}t\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}^2\right)}^{\frac{1}{2}}\\ & \le C_p{\left(\sum _{i=0}^{N-1}{|{\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t|\dot{g}(r)-\dot{g}(s)|\mathrm{d}r\mathrm{d}s|}^2\right)}^{\frac{1}{2}}\\ & \le C_p{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{\left({\int }_{t_i}^{t_{i+1}}{({\int }_{t_{i+\frac{1}{2}}}^t|\dot{g}(r)-\dot{g}(s)|\mathrm{d}r)}^p\mathrm{d}s\right)}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\\ & \le C_p{\left(\sum _{i=0}^{N-1}{h}^{\frac{4}{q}}{({\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t|\dot{g}(r)-\dot{g}(s){|}^p\mathrm{d}r\mathrm{d}s)}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\\ & \le C_p{\left(\sum _{i=0}^{N-1}{h}^{\frac{4}{q}+\frac{2}{p}+2(\sigma -1)}{\left({\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\frac{|\dot{g}(r)-\dot{g}(s){|}^p}{|r-s{|}^{1+(\sigma -1)p}}\mathrm{d}r\mathrm{d}s\right)}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\\ & =C_p{h}^{\sigma }{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{\left({\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\frac{|\dot{g}(r)-\dot{g}(s){|}^p}{|r-s{|}^{1+(\sigma -1)p}}\mathrm{d}r\mathrm{d}s\right)}^{\frac{2}{p}}\right)}^{\frac{1}{2}},\end{array}$where we apply Hölder's inequality in Line 4 and 5. Similarly as in (17(17) $C_{p}h{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{|{\int }_{t_i}^{t_{i+1}}|\dot{g}(s){|}^p\mathrm{d}s|}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\le C_p{h}^{\frac{3}{2}}\Vert g{\Vert }_{W^{1,p}},$(17) ), for p = 2 we have that $C_p{h}^{\sigma }{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{\left({\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\frac{|\dot{g}(r)-\dot{g}(s){|}^p}{|r-s{|}^{1+(\sigma -1)p}}\mathrm{d}r\mathrm{d}s\right)}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\le C_p{h}^{\sigma +\frac{1}{2}}\Vert g{\Vert }_{W^{\sigma ,p}}.$Applying discrete Hölder inequality for p>2 as in (18(18) $\begin{array}{rl}& C_{p}h{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{|{\int }_{t_i}^{t_{i+1}}|\dot{g}(s){|}^p\mathrm{d}s|}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\le C_{p}h{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}\frac{p}{p-2}}\right)}^{\frac{p-2}{2p}}{(\sum _{i=0}^{N-1}{\int }_{t_i}^{t_{i+1}}|\dot{g}(s){|}^p\mathrm{d}s)}^{\frac{1}{p}}\\ & \le C_p{h}^{1+(\frac{2p}{q(p-2)}-1)\frac{p-2}{2p}}|T{|}^{\frac{p-2}{2p}}\Vert g{\Vert }_{W^{1,p}}=C_p{h}^{\frac{3}{2}}|T{|}^{\frac{p-2}{2p}}\Vert g{\Vert }_{W^{1,p}}.\end{array}$(18) ), we have that $C_p{h}^{\sigma }{\left(\sum _{i=0}^{N-1}{h}^{\frac{2}{q}}{\left({\int }_{t_i}^{t_{i+1}}{\int }_{t_{i+\frac{1}{2}}}^t\frac{|\dot{g}(r)-\dot{g}(s){|}^p}{|r-s{|}^{1+(\sigma -1)p}}\mathrm{d}r\mathrm{d}s\right)}^{\frac{2}{p}}\right)}^{\frac{1}{2}}\le C_p{h}^{\sigma +\frac{1}{2}}{T}^{\frac{p-2}{2p}}\Vert g{\Vert }_{W^{\sigma ,p}}.$Altogether we have achieved Bound (13(13) $\Vert I[g]-R{Q}_h^{\tau ,N}[g]{\Vert }_{L^p(\mathrm{\Omega };{\mathbb{R}}^d)}\le C_p|T{|}^{\frac{p-2}{2p}}{h}^{\frac{1}{2}+\sigma }\Vert g{\Vert }_{W^{\sigma ,p}(0,T)},$(13) ).

For a fixed integrand, the randomized quadrature rule (RTQ) improves the order of convergence by $\frac{1}{2}$ through incorporating randomness compared to Theorem 3.1. One may also be interested in the almost sure convergence of RTQ. Indeed, the argument from [8, Theorem 3.2] can be directly adapted here:

Theorem 3.3

Almost sure convergence

Assume that conditions from Theorem 3.2 are satisfied. Let $(h_m{)}_{m\in \mathbb{N}}\subset (0,1)$ be an arbitrary sequence of step sizes with $\sum _{m=1}^{\mathrm{\infty }}{h}_m<\mathrm{\infty }$. Then, there exists a nonnegative random variable $m_0:\mathrm{\Omega }\to \mathbb{N}\cup \{0\}$ and a measurable set $A\in \mathcal{F}$ with $\mathbb{P}(A)=1$ such that for all $\omega \in A$ and $m\ge m_0(\omega )$, then for every $ϵ\in (0,\frac{1}{2})$ there exist a nonnegative random variable $m_0^{ϵ}:\mathrm{\Omega }\to {\mathbb{N}}_0$ and a measurable set $A_{ϵ}\in \mathcal{F}$ with $\mathbb{P}(A_{ϵ})=1$ such that such that for all $\omega \in A$ and $m\ge m_0(\omega )$ we have (22) $\underset{n\in \{0,1,\dots ,N_{h_m}\}}{max}|I^n[g]-R{Q}_{h_m}^{\tau ,n}[g](\omega )|\le h_m^{\frac{1}{2}+\gamma -ϵ},$(22) where $N_{h_m}:=\lfloor \frac{T}{h_m}\rfloor$, i.e. the integer part of $\frac{T}{h_m}$.

Theorem 3.3 ensures that RTQ can achieve a slightly better order of pathwise convergence in the almost sure sense compared to CTQ when stepsize is adequately small.

4. Numerical experiments

In this section, we assessed the proposed method via different experiments. For simplicity, we fix T = 1.

4.1. Example 1

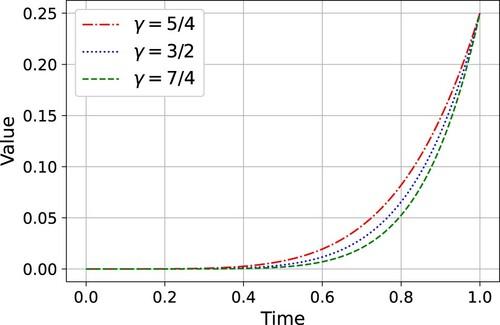
Consider the function: (23) $g_{\gamma }(t):=t^{\gamma },$(23) where $\gamma \in \{\frac{5}{4},\frac{3}{2},\frac{7}{4}\}$, $g_{\gamma }\in W^{\sigma ,2}(0,T)$, for all $ϵ\in (1,\frac{1}{2}+\gamma )$ (Sobolev's inequality in [1]). The curves of $g_{\gamma }$ with different values in γ can be found in Figure 1. The true solution was easily obtained as $\frac{1}{\gamma +1}$. The numerical approximations were calculated for both kinds of trapezoidal quadrature with step sizes $h\in \{2^{-i}:i=5,\dots ,10\}$ and then compared to the true solution for errors. For RTQ, we computed errors in $L^2$ norm via Monte Carlo method and also computed pathwise error, i.e.error from one realization.

Figure 1. Function values for $g_{\gamma }$ under different choices for γ.

The results of our simulations are shown in Figure 2 and Table 1. Across all different values of γ, RTQ gave the higher order of convergence compared to CTQ. When γ increased from $\frac{5}{4}$ to $\frac{7}{4}$, the order of convergence for RTQ increased eventually to a number very close to 2.5. Note that the order of convergence for CTQ are not beyond 2 for all γ values. All the performances were superior to theoretical order of convergences shown in Theorems 3.1 and 3.2. We also examined the computational efficiency of both methods (lower right in Figure 2). Though incorporating randomness increased computational expense, RTQ quickly offsetted its cost with its higher accuracy.

Figure 2. Error plots for approximating $I[g_{\gamma }]$ via variants of trapezoidal rule under different choices for γ (upper left: $\gamma =\frac{5}{4}$; upper right: $\gamma =\frac{3}{2}$; lower left: $\gamma =\frac{7}{4}$) and time cost plot for $\gamma =\frac{3}{2}$ (lower right).

Table 1. Order of convergences for simulating $I[g_{\gamma }]$.

γ	CTQ	RTQ ($L^2$)	RTQ (pathwise)
${\displaystyle \frac{5}{4}}$	1.96	2.24	2.13
${\displaystyle \frac{3}{2}}$	1.99	2.44	2.17
${\displaystyle \frac{7}{4}}$	1.99	2.50	2.43

4.2. Example 2

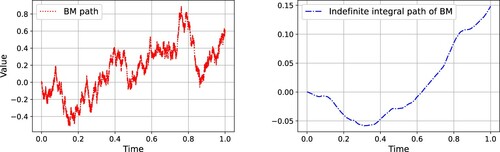
Consider the function: (24) $g_B(t):={\int }_0^{t}B(s)\mathrm{d}s,\mathrm{for}t\in [0,T],$(24) where $B(s)$ is a realization of standard Brownian motion (BM) (cf. Section 3.1 in [6]). It is well known that $B\in C^{\frac{1}{2}-ϵ}$ for arbitrary small $ϵ>0$, therefore $g_B\in W^{\frac{3}{2}-ϵ,p}$ for p>1. Figure 3 illustrates how one BM path looks like and the curve of its $g_B$.We are interested in approximating $I[g_B]$.

Figure 3. One realization of standard Brownian motion and function values for the corresponding $g_B$.

Due to the nature of BM, it is not easy to obtain the exact value of $g_B$. To approximating terms $g_B(t_n)$, one simply applies the Euler method, i.e. $g_B(t_n)={\int }_0^{t_n}B(s)\mathrm{d}s=\sum _{i=0}^{n-1}{\int }_{t_i}^{t_{i+1}}B(s)\mathrm{d}s\approx h\sum _{i=0}^{n-1}B(t_i).$For CTQ, for a fixed stepsize $h\in [0,1],$ we have that $\begin{array}{rl}{Q}_h[g_B]& =\frac{h}{2}\sum _{n=0}^{N-1}(g_B(t_n)+g_B(t_{n+1}))=h\sum _{n=0}^{N-1}{g}_B(t_n)+\frac{h}{2}\sum _{n=0}^{N-1}(g_B(t_{n+1})-g_B(t_n))\\ & =h\sum _{n=0}^{N-1}{g}_B(t_n)+\frac{h}{2}{g}_B(t_N)=h\sum _{n=1}^N{g}_B(t_n)-\frac{h}{2}{g}_B(t_N)\approx h^2\sum _{n=0}^{N-1}\sum _{i=0}^{n}B(t_i)-\frac{h^2}{2}\sum _{i=0}^{N-1}B(t_i).\end{array}$For RTQ, define the corresponding i.i.d. uniform distributed sequence is $\{{\tau }_j^h{\}}_{j\in \mathbb{N}}$, we have a similar expression: (25) $\begin{array}{rl}& R{Q}_h^{\tau ,N}[g_B]=\frac{h}{2}\sum _{n=0}^{N-1}(g_B(t_n+{\tau }_n^{h}h)+g_B(t_n+{\overline{\tau }}_n^{h}h))\\ & =h\sum _{n=0}^{N-1}{g}_B(t_n)+\frac{h}{2}\sum _{n=0}^{N-1}({\int }_{t_n}^{t_n+{\tau }_n^{h}h}B(s)\mathrm{d}s+{\int }_{t_n}^{t_n+{\overline{\tau }}_n^{h}h}B(s)\mathrm{d}s)\\ & \approx h\sum _{n=0}^{N-1}{g}_B(t_n)+\frac{h}{2}\sum _{n=0}^{N-1}(\frac{{\tau }_n^{h}h}{2}(B(t_n)+B(t_n+{\tau }_n^{h}h))+\frac{{\overline{\tau }}_n^{h}h}{2}(B(t_n)+B(t_n+{\overline{\tau }}_n^{h}h))),\end{array}$(25) where the last term can be further expanded as $\begin{array}{rl}& \frac{h}{2}\sum _{n=0}^{N-1}(\frac{{\tau }_n^{h}h}{2}(B(t_n)+B(t_n+{\tau }_n^{h}h))+\frac{{\overline{\tau }}_n^{h}h}{2}(B(t_n)+B(t_n+{\overline{\tau }}_n^{h}h)))\\ & =\frac{h^2}{4}\sum _{n=0}^{N-1}B(t_n)+\frac{h^2}{4}\sum _{n=0}^{N-1}({\tau }_n^{h}B(t_n+{\tau }_n^{h}h)+{\overline{\tau }}_n^{h}B(t_n+{\overline{\tau }}_n^{h}h)).\end{array}$Note that to deduce the third line of Equation (25(25) $\begin{array}{rl}& R{Q}_h^{\tau ,N}[g_B]=\frac{h}{2}\sum _{n=0}^{N-1}(g_B(t_n+{\tau }_n^{h}h)+g_B(t_n+{\overline{\tau }}_n^{h}h))\\ & =h\sum _{n=0}^{N-1}{g}_B(t_n)+\frac{h}{2}\sum _{n=0}^{N-1}({\int }_{t_n}^{t_n+{\tau }_n^{h}h}B(s)\mathrm{d}s+{\int }_{t_n}^{t_n+{\overline{\tau }}_n^{h}h}B(s)\mathrm{d}s)\\ & \approx h\sum _{n=0}^{N-1}{g}_B(t_n)+\frac{h}{2}\sum _{n=0}^{N-1}(\frac{{\tau }_n^{h}h}{2}(B(t_n)+B(t_n+{\tau }_n^{h}h))+\frac{{\overline{\tau }}_n^{h}h}{2}(B(t_n)+B(t_n+{\overline{\tau }}_n^{h}h))),\end{array}$(25) ), we make use of CTQ rather than the Euler method. The reason for this is that using the Euler method will result in the same expression as $Q_h[g_B]$. It is easy to see the difference between expressions for CTQ and RTQ lies in the last two terms of the equation above.

To compute the reference solution, we first sampled a BM path with a small stepsize $h_{\mathrm{ref}}=2^{-14}$. Then, we generated an i.i.d. standard uniformly distributed sequence $\{{\tau }_j{\}}_{j\in \mathbb{N}}$, and sampled $B((j+{\tau }_j)h_{\mathrm{ref}})$, which is determined by property of Brownian bridge (cf. Section 3.1 in [6]), i.e. $B((j+{\tau }_j)h_{\mathrm{ref}})\sim \mathcal{N}({\overline{\tau }}_{j}B((j+1)h_{\mathrm{ref}})+{\tau }_{j}B(j{h}_{\mathrm{ref}}),{\tau }_j{\overline{\tau }}_j{h}_{\mathrm{ref}}),$where $\mathcal{N}(\mu ,{\sigma }^2)$ is normal distribution with mean μ and variance ${\sigma }^2$, and ${\overline{\tau }}_j:=1-{\tau }_j$ for all j. The reference solution was thus computed via CTQ on grid points consisting of $\{j{h}_{\mathrm{ref}}{\}}_{j\in \mathbb{N}}$ as well as these intermediate $\{(j+{\tau }_j)h_{\mathrm{ref}}{\}}_{j\in \mathbb{N}}$.

The reason for including randomness at this early stage is that this allows an easier sampling procedure for $\{{\tau }_j^h{\}}_{j\in \mathbb{N}}$ on coarser grids of stepsize h. For instance, if $h=2h_{\mathrm{ref}}$ and consider interval $[t_0,t_0+h]$, then $t_0+{\tau }_0{h}_{\mathrm{ref}}$ and $t_0+h_{\mathrm{ref}}+{\tau }_1{h}_{\mathrm{ref}}$ are in the same interval. Thus ${\tau }_0^h$ can be determined from $t_0+{\tau }_0^{h}h={\mathbf{1}}_{U_0}(0)(t_0+{\tau }_0{h}_{\mathrm{ref}})+{\mathbf{1}}_{U_0}(1)(t_0+h_{\mathrm{ref}}+{\tau }_1{h}_{\mathrm{ref}}),$where ${\mathbf{1}}_{\cdot }(\cdot )$ is the indicator function, $U_0\sim \mathcal{U}\{0,1\}$, i.e. a discrete uniform distribution on the integers 0 and 1.

The numerical approximations were calculated for both trapezoidal quadratures with larger step sizes $h\in \{2^{-i}:i=5,\dots ,10\}$ and then compared to the reference solution for errors. The results of our simulations are shown in Figure 4. RTQ gave the higher order of pathwise convergence compared to CTQ and gained a minor advantage in absolute error. Both the performances are consistent with the theoretical order of convergences shown in Theorems 3.1 and 3.3. We, in the meantime, examined the computational efficiency of both methods. Due to additional terms involved for RTQ in Equation (25(25) $\begin{array}{rl}& R{Q}_h^{\tau ,N}[g_B]=\frac{h}{2}\sum _{n=0}^{N-1}(g_B(t_n+{\tau }_n^{h}h)+g_B(t_n+{\overline{\tau }}_n^{h}h))\\ & =h\sum _{n=0}^{N-1}{g}_B(t_n)+\frac{h}{2}\sum _{n=0}^{N-1}({\int }_{t_n}^{t_n+{\tau }_n^{h}h}B(s)\mathrm{d}s+{\int }_{t_n}^{t_n+{\overline{\tau }}_n^{h}h}B(s)\mathrm{d}s)\\ & \approx h\sum _{n=0}^{N-1}{g}_B(t_n)+\frac{h}{2}\sum _{n=0}^{N-1}(\frac{{\tau }_n^{h}h}{2}(B(t_n)+B(t_n+{\tau }_n^{h}h))+\frac{{\overline{\tau }}_n^{h}h}{2}(B(t_n)+B(t_n+{\overline{\tau }}_n^{h}h))),\end{array}$(25) ), its time cost roughly doubled that of CTQ at the same stepsize. In this case, unfortunately, the slight odds of RTQ in accuracy did not offset its cost.

Figure 4. Error plot (left) and time cost plot (right) for approximating $I[g_B]$ using CTQ and RTQ.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Alan Turing Institute under the Engineering and Physical Sciences Research Council (EPSRC) grant EP/N510129/1 and by EPSRC though the project EP/S026347/1, titled ‘Unparameterized multi-modal data, high order signatures, and the mathematics of data science’.