State estimation for linear and non-linear equality-constrained systems

Abstract

This article addresses the state-estimation problem for linear and non-linear systems for the case in which prior knowledge is available in the form of an equality constraint. The equality-constrained Kalman filter (KF) is derived as the maximum-a-posteriori solution to the equality-constrained state-estimation problem for linear and Gaussian systems and is compared to alternative algorithms. Then, four novel algorithms for non-linear equality-constrained state estimation based on the unscented KF are presented, namely, the equality-constrained unscented KF, the projected unscented KF, the measurement-augmentation unscented KF, and the constrained unscented KF. Finally, these methods are compared on linear and non-linear examples.

Keywords:

• equality constraints
• state estimation
• Kalman filtering
• unscented Kalman filter

1. Introduction

The classical Kalman filter (KF) for linear systems provides optimal state estimates under standard noise and model assumptions (Jazwinski 1970). In practice, however, additional information about the system may be available, and this information may be useful for improving state estimates. A scenario we have in mind is the case in which the dynamics and the disturbances are such that the states of the system satisfy an equality or inequality constraint (Robertson and Lee 2002; Goodwin, Seron, and de Doná 2005). For example, in a chemical reaction, the species concentrations are non-negative (Massicotte, Morawski, and Barwicz 1995; Chaves and Sontag 2002), whereas in a compartmental model with zero net inflow (Bernstein and Hyland 1993), mass is conserved. Likewise, in undamped mechanical systems, such as a system with Hamiltonian dynamics, conservation laws hold, while, in the quaternion-based attitude estimation problem, the attitude vector must have unit norm (Crassidis and Markley 2003; Choukroun, Bar-Itzhack, and Oshman 2006). Additional examples arise in optimal control (Maciejowski 2002; Goodwin et al. 2005), parameter estimation (Chia, Chow, and Chizeck 1991; Aguirre, Barroso, Saldanha, and Mendes 2004; Nepomuceno, Takahashi, Aguirre, Neto, and Mendes 2004; Walker 2006; Aguirre, Alves, and Corrêa 2007), tracking and navigation (Wen and Durrant-Whyte 1992; Alouani and Blair 1993; Dissanayake, Sukkarieh, and Nebot 2001; Shen, Honga, and Cong 2006) and aeronautics (Rotea and Lana 2005; Simon and Simon 2006). In such cases, we wish to obtain state estimates that take advantage of prior knowledge of the states and use this information to obtain better estimates than those provided by the Kalman filter in the absence of such information.

Various algorithms have been developed for equality-constrained state estimation. One of the most popular techniques is the measurement-augmentation Kalman filter (MAKF), in which a perfect ‘measurement’ of the constrained quantity is appended to the physical measurements (Porrill 1988; Tahk and Speyer 1990; Wen and Durrant-Whyte 1992; Alouani and Blair 1993; Chen and Chiang 1993; De Geeter, van Brussel, and De Schutter 1997; Walker 2006). In addition, estimate-projection (Simon and Chia 2002), system-projection (Ko and Bitmead 2007) and gain-projection (Gupta and Hauser 2007; Teixeira et al. 2008b) methods have been considered. A two-step projection algorithm for handling non-linear equality constraints has also been presented (Julier and LaViola 2007).

For state estimation with inequality constraints, moving horizon estimators (MHE) (Rao, Rawlings, and Lee 2001; Rao, Rawlings, and Mayne 2003), unscented filtering algorithms (Vachhani, Narasimhan, and Rengaswamy 2006; Teixeira 2008; Teixeira, Tôrres, Aguirre, and Bernstein 2008d) and probabilistic methods (Rotea and Lana 2005) have been developed. However, inequality constraints are outside the scope of the present article. Finally, a general framework for state estimation with an equality constraint on the estimator gain (aiming at enforcing special properties on the state estimates) is presented in Teixeira et al. (2008b).

The contributions of the present article are as follows. First, we investigate how a linear equality state constraint arises in a linear dynamic system and present necessary conditions on both the dynamics and process noise for the state to be equality constrained. In Ko and Bitmead (2007), this problem is stated in the opposite way, that is, given that a system satisfies an equality constraint, the goal is to characterise the process noise. In these cases, we show that an equality-constrained linear system is controllable from the process noise only in the subspace defined by the equality constraint and that additional information regarding the initial condition provided by the equality constraint is useful for improving the classical Kalman filter estimates.

Second, we derive the equality-constrained Kalman filter (ECKF) as the maximum-a-posteriori analytical solution to the equality-constrained state-estimation problem for linear and Gaussian systems. We also prove the equivalence of ECKF and MAKF and discuss connections with the estimate-projection and system-projection approaches. We compare these four algorithms by means of a compartmental system example in which the disturbances are constrained so that mass is conserved.

Next, our main contribution in this article is to develop and compare four suboptimal algorithms for equality-constrained state estimation for non-linear systems, namely, the equality-constrained unscented Kalman filter (ECUKF) the projected unscented Kalman filter (PUKF), the measurement-augmentation unscented Kalman filter (MAUKF) and the constrained unscented Kalman filter (CUKF). These methods, which extend algorithms for constrained state estimation developed for linear systems, are based on the unscented Kalman filter (UKF) (Julier and Uhlmann 2004), which is an example of sigma-point Kalman filters (SPKF) (van der Merwe, Wan, and Julier 2004). In addition, CUKF is based on MHE with unitary horizon. Recent work (Julier, Uhlmann, and Durrant-Whyte 2000; Haykin 2001; Lefebvre, Bruyninckx, and De Schutter 2002; Lefebvre, Bruyninckx, and De Schutter 2004; Romanenko and Castro 2004; van der Merue et al. 2004; Hovland et al. 2005; Choi, Yeap, and Bouchard 2005; Crassidis 2006; Chandrasekar, Ridley, and Bernstein 2007; Teixeira, Santillo, Erwin, and Bernstein 2008e) illustrates the improved performance of SPKF compared to the extended Kalman filter (EKF) (Jazwinski 1970), which is prone to numerical problems such as initialisation sensitivity, divergence, and instability for strongly non-linear systems (Reif, Günther, Yaz, and Unbehauen 1999). A quaternion-based attitude estimation problem (Crassidis and Markley 2003) is used to illustrate UKF, ECUKF PUKF, MAUKF and CUKF. Although the state of the process model satisfies the unit norm constraint, this constraint is violated by the state estimates obtained from unconstrained Kalman filtering.

Finally, we use equality-constrained Kalman filtering techniques to improve estimation when an approximate discretised model is used to represent a continuous-time process. The problem of using UKF with a discrete-time model obtained from black-box identification to perform state estimation for a continuous-time non-linear system is treated in Aguirre, Teixeira, and Tôrres (2005). According to Rao et al. (2003), constraints can also be used to correct model error. We illustrate the application of equality-constrained unscented Kalman filter techniques to this problem through an example of a discretised model of an undamped single-degree-of-freedom pendulum without external disturbances. Although energy is conserved in the original, continuous-time system, the discretised model is approximate, and the energy constraint is intended to improve estimates of the discretised states. Additionally, an application of equality-constrained Kalman filtering to magnetohydrodynamics data assimilation (Chandrasekar, Barrero, Ridley, Bernstein, and De Moor 2004; Chandrasekar, Ridley, and Bernstein 2007), in which the zero-divergence constraint is enforced on the magnetic field using finite-volume discretised models, is discussed in Teixeira, Ridley, Tôrres, Aguirre, and Bernstein (2008c). The present article is based on research in Teixeira (2008), while preliminary versions of it appear as Teixeira, Chandrasekar, Tôrres, Aguirre, and Bernstein (2007, 2008a).

2. State estimation for linear systems

For the linear stochastic discrete-time dynamic system

where A _k−1 ∈ ℝ ^n×n , B _k−1 ∈ ℝ ^n×p , G _k−1 ∈ ℝ ^n×q , and C _k ∈ ℝ ^m×n are known matrices, the state-estimation problem can be described as follows. Assume that, for all k ≥ 1, the known data are the measurements y _k ∈ ℝ ^m , the inputs u _k−1 ∈ ℝ ^p , and the statistical properties of x ₀, w _k−1 and v _k . The initial state vector x ₀ ∈ ℝ ⁿ is assumed to be Gaussian with mean and error-covariance . The process noise w _k−1 ∈ ℝ ^q , which represents unknown input disturbances, and the measurement noise v _k ∈ ℝ ^m , concerning inaccuracies in the measurements, are assumed white, Gaussian, zero mean and mutually independent with known covariance matrices Q _k−1 and R _k , respectively. Next, define the profit function

which is the conditional probability density function of the state vector x _k ∈ ℝ ⁿ given the past and present measured data y ₁, …, y _k . Under the stated assumptions, the maximisation of (3) is the state-estimation problem, while the maximiser of J is the optimal state estimate.

The optimal state estimate is given by KF (Jazwinski 1970), whose forecast step is given by

where , , and , and whose data-assimilation step is given by

where is the error-covariance matrix and K _k is the Kalman gain matrix. The notation indicates an estimate of z _k at time k based on information available up to and including time k − 1. Likewise, indicates an estimate of z at time k using information available up to and including time k. Model information is used during the forecast step, while measurement data are injected into the estimates during the data-assimilation step, specifically (10).

3. State estimation for equality-constrained linear systems

In (1), assume that rank(G _k−1) = q < n, and define r ≜ n − q, where 1 ≤ r ≤ n. The case r = n indicates that G _k−1 w _k−1 is absent. Therefore, there exists E _k−1 ∈ ℝ ^r×n such that rank(E _k−1) = r and

Let T _1,k−1 ∈ ℝ^(n−r)×n be such that

is invertible. For example, we can choose . Multiplying (1) by T _k−1 yields

Hence, for all k ≥ 1,

where e _k−1 ≜ E _k−1(A _k−1 x _k−1 + B _k−1 u _k−1). Note that e _k−1 is not necessarily constant even if system (1) and (2) is time invariant. Since rank(G _k−1) < n, G _k−1 w _k−1 has singular covariance (Goodwin et al. 2005; Ko and Bitmead 2007).

Let s be an integer satisfying 1 ≤ s ≤ r, and partition , where

It thus follows from (12) that

Proposition 3.1

Assume that

and

Then, for all k ≥ 1,

where

Proof

It follows from (13) that D _k−1 x _k = D _k−1 × (A _k−1 x _k−1 + B _k−1 u _k−1) = D _k−1 x _k−1 = d _k−1.□

Corollary 3.1

If the system given by (1) and (2) is time invariant and (14–16) hold, then, for all k ≥ 1,

where D ≜ D _k−1 and

Note that, if s = r = n, then x _k = D ⁻¹ d. Hence, this case is not of practical interest.

The next result shows that, if (1) is equality constrained, then it is not controllable in ℝ ⁿ from the process noise, but it is rather controllable in the subspace defined by (17).

Proposition 3.2

If (14) and (15) hold, then (A _k−1, G _k−1) is not controllable in ℝ ⁿ .

Proof

Multiplying the controllability matrix

by D _k−1 yields

implying that the columns of 𝒦 lie on the null space of D _k−1 such that rank(𝒦) < n.□

Assuming that, for all k ≥ 1, D _k−1 ∈ ℝ ^s×n satisfying (14–16) and d _k−1 defined by (18) are known, the objective of the equality-constrained state-estimation problem is to maximise (3) subject to (17).

4. Equality-constrained Kalman filter

In this section, we solve the equality-constrained state-estimation problem to obtain ECKF. Let denote the solution of the equality-constrained state-estimation problem.

Lemma 4.1

Assume that given by (5) and R _k are positive definite. maximises J given by (3) subject to (17) if and only if minimises

subject to (17), where is given by (4).

Proof

The proof is similar to the unconstrained counterpart investigated in Maybeck (1979, pp. 234–235) or Jazwinski (1970, pp. 207–208) and is omitted for brevity. For completeness, the proof to the constrained case is presented in Teixeira (2008, Lemma 5.2.1).□

Define the projected error covariance , where 0 < δ ≪ 1 is a very small number compared to the entries of that guarantees that is positive definite. From our experience, we set 10⁻¹⁵ ≤ δ ≤ 10⁻⁹ for computational implementation.

Proposition 4.1

Let and be given by

Define

where is given by (10) and is given by (11). Then and are given by

Proof

Using Lemma 4.1, let λ ∈ ℝ ^s and define the Lagrangian

The necessary conditions for a minimiser are given by

It follows from (30) that

From (11), using (7–9) and the matrix inversion lemma (Bernstein 2005), we have

Furthermore, from (9), using (7) and (8), we have

Substituting (33) and (34) into (32) and multiplying by yields

Substituting (35) into (31) yields

which implies

Likewise, substituting (36) into (35) yields

Now using (24–27), (9–11), we obtain

which proves (28).

Given the symmetry between (28) and (10) and recalling that is given by (11), it follows that is given by (29).□

Remark 4.1

Note that ECKF is expressed in three steps, namely, the forecast step (22) and (23), (6–8), the data-assimilation step (9–11) and the projection step (24–29), where the updated estimates are projected onto the hyperplane defined by the equality constraint (17).

Lemma 4.2

Let 𝒩(D _k−1) denote the null space of D _k−1, let W ∈ ℝ ^n×n be positive definite, and define

Then is an oblique projector whose range is 𝒩(D _k−1), that is, but it is not necessarily symmetric.

For the following two results, let given by (10) and given by (11) denote the updated estimate and updated error covariance provided by ECKF. Also, let given by (28) and given by (29) denote the projected estimate and projected error covariance of ECKF.

Proposition 4.2

Set in (37). Then, the projection step (24–29) is equivalent to

where .

Proof

Using Lemma 4.2 and substituting (24–27) into (28) and (29) yields (38) and (39).□

Proposition 4.3

Assume that (1) and (2) is time invariant. Also, assume that D in (19) satisfies (14–16). Furthermore, assume that, for a given k − 1, and and set δ = 0. Then , , , and .

Proof

Multiplying (22) and (23) by D yields

With (8) and (41), multiplying (9) by D yields

With (40) and (42), multiplying (10) and (11) by D yields

Given (43) and (44) and δ = 0, from (38) and (39), we have and .□

Corollary 4.1

Assume that and . Then, for all k ≥ 2, and .

Remark 4.2

Therefore, for time-invariant systems, whenever (14–16) hold, the projection step of ECKF given by (24–29) is required only at k = 1, so that, for all k ≥ 2, the updated estimate given by (10) satisfies .

5. Connections between ECKF and alternative approaches

We now compare ECKF to three Kalman filtering algorithms that yield state estimates satisfying an equality constraint.

First we consider MAKF (Porrill 1988; Tahk and Speyer 1990; Wen and Durrant-Whyte 1992), which treats (17) as perfect measurements. In Appendix I, we present the MAKF equations and prove that the MAKF and ECKF estimates are equal.

In Appendix II, we show that the projected Kalman filter by system projection (PKF-SP) (Ko and Bitmead 2007), which, assuming that (14–16) hold, incorporates the information provided by (17) only in filter initialisation, that is, k = 0, is a special case of ECKF for time-invariant systems.

In Appendix III, we briefly review the projected Kalman filter by estimate projection (PKF-EP) (Simon and Chia 2002; Simon 2006), which projects onto the hyperplane (17) for all k ≥ 1. Unlike ECKF, the projected estimate of PKF-EP is not recursively fed back in the next iteration.

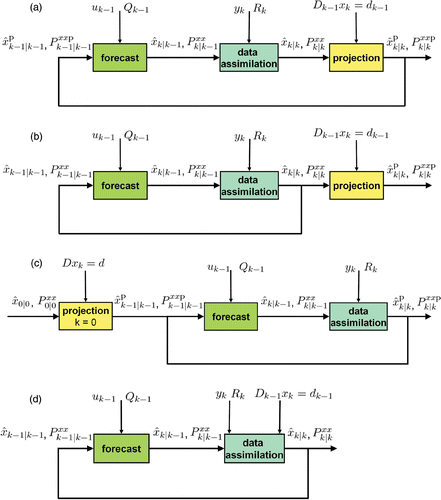
Figure 1 illustrates how the forecast, data-assimilation and projection steps are connected for ECKF, PKF-SP, PKF-EP and MAKF.

Figure 1. Comparative diagram of (a) ECKF, (b) PKF-EP, (c) PKF-SP and (d) MAKF. Unlike PKF-EP, the projection step of ECKF is connected by feedback recursion. In PKF-SP, in the context of time-invariant dynamics, the initial state estimate and the associated error covariance carry the information provided by the equality constraint. Note that, since (14) holds such that GQ _k−1 G ^T is a ‘constrained’ covariance, Q _k−1 need not to be modified in the PKF-SP implementation. Otherwise, we can replace GQ _k−1 G ^T by 𝒫_𝒩(D) GQ _k−1 G ^T in (5), where 𝒫_𝒩(D) is given by (A.25). In MAKF, the equality constraint is enforced at the data-assimilation step.

Also, for the special case of unitary horizon, ECKF and MHE (Rao et al. 2001) minimise the same cost function, specifically (21). However, ECKF provides the analytical solution to the equality-constrained optimisation problem. Moreover, unlike MHE, ECKF enforces the constraint information on the error covariance in addition to the state estimate.

We also remark that, if m = 0, then the problem solved by ECKF in Proposition 4.1 is similar to the case in which Kalman filter is used as an iterative solver for systems of linear algebraic equations such as Dx = d, where D ∈ ℝ ^s×n , d ∈ ℝ ^s , and rank(D) = s (Pinto and Rios Neto 1990, Theorem 2).

Note that, if d _k−1 is uncertain, then (17) can be replaced by the noisy equality constraint (De Geeter et al. 1997; Walker 2006; Ko and Bitmead 2007)

where is a white, Gaussian, zero-mean noise with covariance , and it is treated as an extra noisy measurement by MAKF (Appendix I) but with

replacing .

6. State estimation for equality-constrained non-linear systems

For the non-linear stochastic discrete-time dynamic system

where f : ℝ ⁿ × ℝ ^p × ℝ ^q × ℕ → ℝ ⁿ and h : ℝ ⁿ × ℕ → ℝ ^m are, respectively, the process and observation models, and whose state vector x _k is known to satisfy the equality constraint

where g : ℝ ⁿ × ℕ → ℝ ^s and d _k−1 is known, the objective of the equality-constrained state-estimation problem is, for all k ≥ 1, to maximise (3) subject to (48). However, the solution to this problem is complicated (Daum 2005) by the fact that, for non-linear systems, ρ(x _k |(y ₁, …, y _k )) is not completely characterised by its first-order and second-order moments. We thus use an approximation based on the classical Kalman filter to provide a suboptimal solution to the non-linear case.

6.1 Unscented Kalman filter

First, to address the unconstrained case, we consider UKF (Julier and Uhlmann 2004) to provide a suboptimal solution to the state-estimation problem. Instead of analytically or numerically linearising (46) and (47) and using (4–11), UKF employs the unscented transform (UT) (Julier et al. 2000), which approximates the posterior mean ŷ ∈ ℝ ^m and covariance P ^yy ∈ ℝ ^m×m of a random vector y obtained from the non-linear transformation y = h(x), where x is a prior random vector whose mean and covariance P ^xx ∈ ℝ ^n×n are assumed to be known. UT yields the true mean and the true covariance P ^yy if h = h ₁ + h ₂, where h ₁ is linear and h ₂ is quadratic (Julier et al. 2000). Otherwise, ŷ _k is a pseudo mean and P ^yy is a pseudo covariance.

UT is based on a set of deterministically chosen vectors known as sigma points. To capture the mean of the augmented prior state vector

where and n _a ≜ n + q, as well as the augmented prior error covariance

the sigma-point matrix is chosen as

with weights

where (·)^1/2 is the Cholesky square root, 0 < α ≤ 1, β ≥ 0, κ ≥ 0, and λ ≜ α²(κ+n _a)−n _a > −n _a. We set α = 1 and κ = 0 (Haykin 2001) such that λ = 0 (Julier and Uhlmann 2004) and set β = 2 (Haykin 2001). Alternative schemes for choosing sigma points are given in Julier and Uhlmann (2004) and references therein.

The UKF forecast equations are given by (51) and (52) together with

where

and

The UKF data-assimilation equations are given by (9–11).

7. Equality-constrained unscented Kalman filters

In this section, by using UT, we extend the algorithms PKF-EP, ECKF and MAKF to the non-linear case. These unscented-based approaches provide suboptimal solutions to the equality-constrained state-estimation problem for non-linear systems. Unlike the linear case (§ 4), these approaches do not guarantee that the non-linear equality constraint (48) is exactly satisfied, but they provide approximate solutions.

Furthermore, to obtain state estimates satisfying (48) at a given tolerance by solving an optimisation problem online, we also present an unscented extension of the constrained Kalman filter (CKF) for linear systems, which is a special case of MHE with unitary horizon (Rao et al. 2001).

7.1 Projected unscented Kalman filter

The projection step of ECKF given by (24–29) is now extended to the non-linear case by means of UT. Choosing sigma points and associated weights as indicated in (51) and (52), we have

where and are given by (10) and (11), respectively. Then the sigma points , i = 0, …, 2n, are propagated through (48), yielding

such that , , and are given by

and , , and are given by (27), (28) and (29), respectively.

Appending the projection step (60–64), (27–29) to UKF (51–59), (9–11) without feedback recursion (Figure 1(b)) yields PUKF, which extends PKF-EP to non-linear systems.

7.2 Equality-constrained unscented Kalman filter

Define

, and

such that the sigma points

are chosen based on given by (28). Then, by appending the projection step (60–64), (27–29) to Equations (65), (52–59), (9–11), we obtain ECUKF. Note that, unlike PUKF, ECUKF connects the projection step to UKF by feedback recursion; see Figure 1(a).

7.3 Measurement-augmentation unscented Kalman filter

To extend the MAKF algorithm to the non-linear case, we replace (47) by the augmented observation

where

and

With (66), MAUKF combines (51–55) with the augmented forecast equations

where

and the KF data-assimilation equations

Recall that, unlike the linear case, the ECUKF and MAUKF estimates are not necessarily equivalent.

In practice, to circumvent ill-conditioning problems in the inversion of in (69), we replace by , where we set , 10⁻¹⁵ ≤ δ ≤ 10⁻⁹.

7.4 Constrained unscented Kalman filter

We now extend CKF to the non-linear case by combining the forecast step of UKF with the data-assimilation step of CKF. Then we obtain CUKF, whose forecast equations are given by (51–59) and whose data-assimilation equations are given by

together with (9) and (11), where 𝒥₁(x _k ) is given by

where is given by (54) and is given by (55). Various optimisation methods can be used to solve online the constrained optimisation problem (75) (Fletcher 2000). Note that (76) is the non-linear counterpart of (21).

Note that, unlike ECUKF and MAUKF, the equality-constraint information is not assimilated by the error-covariance in (11). Also, CUKF allows the enforcement of inequality constraints in addition to (48) in (75).

8. Numerical examples

In this section, a linear example is investigated using KF, ECKF, MAKF, PKF-EP and PKF-SP, and two non-linear examples are discussed using UKF, ECUKF, MAUKF, PUKF and CUKF.

To compare the performance of these algorithms, we use two metrics over a c-run Monte Carlo simulation. First, the accuracy of the state estimate given by (10), i = 1, …, n and j = 1, …, c, from time k = k ₀ to k _f is quantified by the root mean square error (RMSE) index given by

where x _i,k is the true value. For ECKF and PKF-EP, as well as for ECUKF and PUKF, is replaced by given by (28) and (A.27), respectively. Note that, to calculate RMSE _i , x _i,k must be known, and thus this index is restricted to simulation.

Next, we assess how informative (Lefebvre et al. 2004) the state estimate is by evaluating the mean trace (MT) of given by (11) from time k = k ₀ to k _f, that is,

MT measures the uncertainty in the estimate . For ECKF and PKF-EP, as well as for their non-linear counterparts, is replaced by given by (29) and (39), respectively.

8.1 Compartmental system

Consider the linear discrete-time compartmental model (1) and (2) (Bernstein and Hyland 1993) whose matrices are given by

with initial condition x ₀ = [1 1 1]^T and process noise and observation noise covariance matrices and . The data-free simulation of this system is shown in Figure 2 for σ _w = 1.0. Note that (14–16) hold for (79) such that the trajectory of x _k ∈ ℝ³ lies on the plane (19), whose parameters are assumed to be known and are given by

that is, conservation of mass is verified.

Figure 2. Data-free simulation of the compartmental model. In (a), the state components are shown evolving with time and, in (b), in state space.

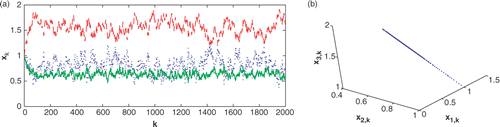
For state estimation, the KF algorithm is initialised with

Figure 3 shows that the KF estimates do not lie on the plane (19). Even if or σ _w = 0, KF does not produce estimates satisfying (19).

Figure 3. Estimate of the total mass (constraint) Dx _k in the conservative compartmental system (79) using KF (—–) in comparison with the true value (− −).

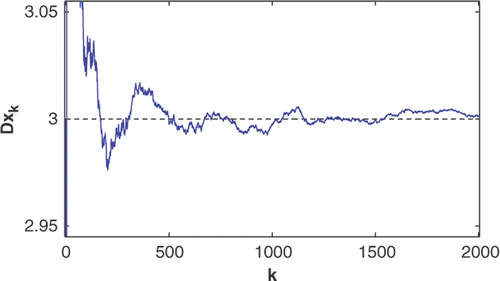
Next, we implement the ECKF algorithm. From a 100-run Monte Carlo simulation for each one of these process noise levels, namely, σ _w = 0, 0.1, 0.5, 1.0, and σ _v = 0.01, Table 1 shows that the ECKF estimates satisfy the equality constraint. In addition, these estimates are both more accurate and more informative than the KF estimates.

Table 1. Percent RMS constraint error, RMSE (77), and MT (78), from k = 1500 to 2000, for 100-run Monte Carlo simulation for compartmental system, concerning process noise levels σ _w = 0, 0.1, 0.5 and 1.0, and KF, ECKF, MAKF, PKF-EP and PKF-SP algorithms.

σ w	KF	ECKF	MAKF	PKF-EP	PKF-SP
Percent RMS constraint error
0	0.12	4.52×10^−15	4.24×10^−11	4.53×10^−15	8.19×10^−12
0.1	0.22	4.52×10^−15	2.01×10^−11	4.52×10^−15	4.05×10^−12
0.5	0.40	4.50×10^−15	0.88×10^−11	4.51×10^−15	3.92×10^−12
1.0	0.62	4.53×10^−15	0.50×10^−11	4.51×10^−15	3.98×10^−12
RMSE i , i = 1, 2, 3 (×10^−3)
0	0.57, 0.36, 2.93	0.10, 0.16, 0.21
0.1	6.26, 2.60, 7.34	6.25, 2.54, 4.19
0.5	9.01, 4.58, 13.2	9.01, 4.55, 6.75
1.0	9.35, 5.58, 19.7	9.35, 5.56, 8.07
MT (×10^−4)
0	0.0996	0.0012
0.1	1.0515	0.6352
0.5	2.8057	1.4722
1.0	5.4646	1.8387

For MAKF, PKF-EP and PKF-SP, initialisation is defined as in (81), except for PKF-SP (see (A.23) in Appendix II). Table 1 summarises the results. ECKF, MAKF, PKF-SP and PKF-EP guarantee that (19) is satisfied at machine precision and yield improved estimates compared to KF. All equality-constrained methods produce similar results concerning RMSE and MT for this time-invariant system, which is in accordance with Ko and Bitmead (2007, Theorem 2) regarding PKF-SP and PKF-EP. Recall that the numerical differences in Table 1 regarding the RMS constraint error for the equality-constrained algorithms are neglegible. However, though not shown in Table 1, it is relevant to mention that PKF-EP produces less accurate and less informative forecast estimates compared to the other constrained algorithms. This is expected because PKF-EP do not use to calculate ; see Figure 1(b).

In addition, a land-based vehicle linear example with kinematic constraints (Simon and Chia 2002; Ko and Bitmead 2007) is investigated using KF, ECKF, MAKF, PKF-SP and PKF-EP in Teixeira (2008, Chapter 5).

8.2 Attitude estimation

Consider an attitude estimation problem (Crassidis and Markley 2003; Choukroun et al. 2006), whose kinematics are modelled as

where the state vector is the quaternion vector e(t) = [e ₀(t) e ₁(t) e ₂(t) e ₃(t)]^T, the matrix Ω(t) is given by

and the angular velocity vector u(t) = [p(t) q(t) r(t)]^T is a known input. Since ‖e(0)‖₂ = 1 and Ω(t) is skew symmetric, it follows that, for all t > 0,

We set e(0) = [0.9603 0.1387 0.1981 0.1387]^T and

To perform attitude estimation, we assume that

is measured by rate gyros, where T is the discretisation step, is zero-mean Gaussian noise and β _k−1 ∈ ℝ³ is drift error. The discrete-time equivalent of (82) augmented by the gyro drift random-walk model (Crassidis and Markley 2003) is given by

where e _k ≜ e(kT), is process noise associated with the drift-error model,

is the state vector,

is the process noise, and

The constraint (84) also holds for (87), that is,

We set T = 0.1 s, β _k−1 = [0.001 −0.001 0.0005]^T rad s⁻¹, and Q _k−1 = diag(10⁻⁵ I _3×3, 10⁻¹⁰ I _3×3). Attitude observations for a direction sensor are given by (Crassidis and Markley 2003)

where r ^[i] ∈ ℝ³ is a reference direction vector to a known point, and C _k is the rotation matrix from the reference to the body-fixed frame

We assume that two directions are available (Crassidis and Markley 2003; Lee, Leok, McClamroch, and Sanyal 2007), which can be obtained using either a star tracker or a combined three-axis accelerometer/three-axis magnetometer. We set r ^[1] = [1 0 0]^T, r ^[2] = [0 1 0]^T, and R _k = 10⁻⁴ I _6×6. These direction measurements are assumed to be provided at a lower rate, specifically, at 1 Hz, which corresponds to a sample interval of 10T s.

We implement Kalman filtering using UKF, ECUKF, PUKF, MAUKF and CUKF with (87), (92) and constraint (91). We initialise these algorithms with and . We use the fmincon algorithm of Matlab in the CUKF implementation.

Table 2 shows the results obtained from a 100-run Monte Carlo simulation. Note that, for the non-linear case, MT given by (78) is obtained from the pseudo-error covariance, and thus, smaller values of MT do not guarantee a smaller spread about the mean. Nevertheless, with the usage of prior knowledge by ECUKF and MAUKF, the values of MT show that more informative estimates are produced compared to the unconstrained estimates given by UKF. However, a slight increase in the RMS error is observed for algorithms ECUKF and MAUKF implying loss of accuracy around 5% compared to UKF. On the other hand, PUKF and CUKF yield estimates as accurate as UKF does. The equality constraint is more closely tracked whenever a constrained filter is employed; see Figure 4. RMS errors around 0.0007% are obtained for PUKF, MAUKF and ECUKF, which exhibits the smallest constraint error among these three algorithms. Compared to PUKF, MAUKF and ECUKF, note that our implementation of CUKF using the fmincon algorithm provides a 11 times smaller constraint error for the quaternion norm, but at a two times larger processing time.

Table 2. Percent RMS constraint error, RMSE (77), and MT (78), from k = 5000 to 10 000, for 100-run Monte Carlo simulation for attitude estimation using UKF, MAUKF, PUKF, ECUKF and CUKF.

UKF	MAUKF	PUKF	ECUKF	CUKF
Percent RMS constraint error (×10^−4)
254.1	6.50	8.31	6.49	0.58
RMSE i for e 0, e 1, e 2, e 3, β1, β2, β3 (×10^−3)
1.331	1.398	1.334	1.398	1.332
1.366	1.434	1.365	1.433	1.365
1.320	1.377	1.320	1.376	1.318
1.319	1.374	1.315	1.374	1.313
0.124	0.130	0.124	0.130	0.124
0.119	0.125	0.119	0.125	0.119
0.120	0.126	0.120	0.125	0.120
MT for attitude (×10^−6)
8.18	5.42	8.16	5.42	8.18
MT for drift (×10^−7)
1.17	1.09	1.17	1.09	1.17

Figure 4. Estimation error of the quaternion vector norm using UKF (····), ECUKF (thick —–), PUKF (−−−), MAUKF (− · −) and CUKF (thin —–) algorithms. The ECUKF and MAUKF estimates almost coincide, while the constraint error for PUKF is slightly larger than the constraint error for ECUKF and MAUKF. CUKF estimates satisfy the equality constraint at machine precision at most times.

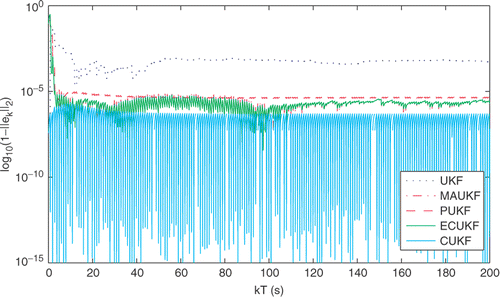
Also, for comparison, we implement the EKF- counterparts of ECUKF, PUKF and MAUKF, namely, ECEKF, PEKF (Simon and Chia 2002) and MAEKF (Alouani and Blair 1993). The results (not shown) indicate that the unscented approaches yield improved results.

8.3 Simple pendulum

We consider the continuous-time undamped and unforced pendulum

where θ(t) is the angular position such that θ = 0 rad corresponds to the stable equilibrium position, g is the gravity acceleration and L is the length. Given noisy measurements of the angular velocity of the pendulum, we want to obtain states that satisfy the energy conservation property.

Using Euler discretisation with time step T, such that t = kT, and defining x _1,k = θ(kT) and , we obtain the approximate discretised model

with noisy measurements of the true (continuous-time model) values of angular velocity given by

By conservation of energy in (94) we have

where E(0) is the total mechanical energy and m is the pendulum mass. Next, we define the approximate energy E _k of the discrete-time model by

We use the fourth-order Runge–Kutta integration scheme to obtain x(kT) for L = 1 m, T = 10 ms, and initial conditions , . We assume that E(0) is known and we implement equality-constrained state estimation by constraining E _k = E(0) for all k ≥ 1. The state estimation is initialised with , , , and , where three values of observation noise are tested, namely, σ _v = 0.1, 0.25 and 0.5, and process noise with σ _w = 0.007 is set to help convergence of estimates (Xiong, Zhang, and Chan 2007). A 100-run Monte Carlo simulation is performed for each σ _v .

Table 3 shows the percent RMS errors related to the equality constraint (98). Figure 5 compares the accuracy of the algorithms with relation to (97). It can be noticed, in this example, that the data-free simulation of the discretised model results in an unrealistic increasing energy E _k . Note that UKF is not able to closely track the constraint. For higher observation noise levels, that is, σ _v = 0.5, RMS constraint errors between 4% and 7% are observed. Nonetheless, whenever PUKF, MAUKF and ECUKF are employed, these indices are reduced by two orders of magnitude, while, by using CUKF, we observe a reduction of seven orders of magnitude. In addition to the improvement in the accuracy of constraint satisfaction, the usage of prior knowledge also results in more accurate and more informative estimates.

Figure 5. Estimation error of the total energy E(0) for the discretised pendulum (95–96) for UKF (····), MAUKF (thick − · −), PUKF (− − −), ECUKF (thick ––) and CUKF (thin ––) with σ _v = 0.25. For comparison, the thin dot-dashed line, which is above the remaining lines, refers to the energy E _k calculated from data-free simulation of the discretised model (95). ECUKF and MAUKF estimates almost coincide, while CUKF estimates satisfy the equality constraint at machine precision at most times.

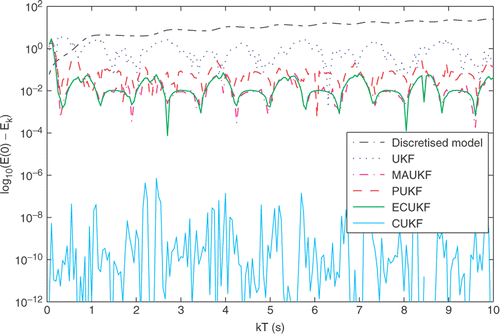
According to the indices in italics in Table 3, the same comparative analysis is applicable when the true continuous-time model (94) is used replacing (95). The use of a fourth Runge–Kutta integration with UKF yields 30% smaller RMSE indices and two times smaller MT index compared to Euler discretisation with ECUKF, but with approximately seven times larger RMS constraint error and with approximately four times larger processing time. Similar to § 8.2, note that the use of a process model whose state vector satisfies an equality constraint does not guarantee that the state estimates satisfy this constraint because such information is not taken into account during data assimilation.

Table 3. Percent RMS constraint error, RMSE (77), and MT (78), from k = 3000 to 4000, for 100-run Monte Carlo simulation for the discretised pendulum (95), concerning different levels of observation noise σ _v = 0.1, 0.25 and 0.5, and algorithms, namely, UKF, ECUKF, PUKF, MAUKF and CUKF. We show in italics results for the case in which the true continuous-time model (94) is used with σ _w = 0.0003 to help convergence.

σ v	UKF	MAUKF	PUKF	ECUKF	CUKF
Percent RMS constraint error (×10^−2)
0.1	356.30	1.95	5.65	1.95	0.000066
	21.81	0.06	0.27	0.06	0.000151
0.25	459.40	3.50	9.11	3.51	0.000050
	25.68	0.14	1.09	0.14	0.000134
0.5	594.61	5.98	15.93	5.97	0.000040
	29.80	0.32	3.16	0.31	0.000119
RMSE i , i = 1, 2 (×10^−2)
0.1	2.95, 2.88	0.91, 1.92	1.15, 2.12	0.91, 1.92	1.20, 2.07
	0.59, 1.16	0.17, 0.36	0.39, 0.82	0.17, 0.36	0.32, 0.67
0.25	3.93, 5.59	1.32, 3.05	1.76, 3.84	1.32, 3.04	1.84, 3.75
	0.98, 2.15	0.30, 0.68	0.70, 1.55	0.29, 0.68	0.59, 1.32
0.5	5.56, 9.61	1.80, 4.00	2.76, 5.93	1.80, 3.99	2.86, 6.03
	1.60, 3.55	0.62, 1.35	1.15, 2.54	0.60, 1.30	0.98, 2.14
MT (×10^−4)
0.1	26.79	8.09	9.08	8.09	26.89
	2.18	0.37	1.09	0.37	0.37
0.25	61.66	20.67	26.63	20.66	61.54
	8.31	0.94	4.18	0.94	0.94
0.5	139.94	42.13	66.86	42.11	138.60
	23.17	2.10	11.73	2.10	2.10

For this numerical example, ECUKF and MAUKF yield more accurate and more informative estimates than PUKF and CUKF. Moreover, the performance of ECUKF and MAUKF almost coincide for this non-linear example. When it comes to constraint satisfaction, CUKF yields the most accurate results.

In addition, we implement the EKF-counterparts of ECUKF, PUKF and MAUKF. The results (not shown) indicate that the unscented approaches yield competitive results compared to the extended approaches.

9. Concluding remarks

We have shown that the problem of equality-constrained state estimation for linear and Gaussian systems arises from the definition of both process noise and dynamic equations with special properties, specifically, (14–16), such that the system is not controllable in ℝ ⁿ from the process noise. In this case, the classical Kalman filter does not guarantee that its estimates satisfy the equality constraint.

Then we have solved the equality-constrained state-estimation problem for linear and Gaussian systems using the maximum-a-posteriori approach, yielding ECKF. Moreover, we have proved the equivalence of ECKF to MAKF and have presented its connections to PKF-SP and PKF-EP. We have compared these four methods by means of a compartmental system example with mass conservation.

For the non-linear case, where it is the main contribution of the present article, four suboptimal algorithms based on UKF were presented, namely, ECUKF, PUKF, MAUKF, CUKF. CUKF, which is an optimisation-based approach, allows the enforcement of both equality and inequality constraints at a given tolerance. These methods were compared on two examples, including a quaternion-based attitude estimation problem, as well as a mechanical system with conserved energy.

Numerical results suggest that, in addition to exactly, that is, at machine precision, (in the linear case and for CUKF in the non-linear case) or very closely (for ECUKF, MAUKF and PUKF in the non-linear case) satisfying a known equality constraint of the system, the proposed methods can yield more accurate and more informative estimates than KF (in the linear case) or UKF (in non-linear case). For the linear scenario, ECKF, MAKF, PKF-SP and PKF-EP have produced similar results. However, for the non-linear case, considering the examples investigated, we recommend the user to test ECUKF, MAUKF and PUKF in this order for a given equality-constrained state-estimation application. If the constraint satisfaction accuracy has priority over processing time and ease of implementation, we suggest CUKF. Recall that, since these non-linear methods are approximate, their performance depends on the application. Moreover, except for CUKF, all equality-constrained approaches have required similar processing time, which was competitive to KF (for linear algorithms) and UKF (for non-linear cases) processing time. In this case, CUKF has a larger processing time because it solves online a constrained optimisation problem. The performance of CUKF depends on the optimisation algorithm and problem. For the two non-linear examples investigated, the CUKF processing time was 2–15 times larger than the UKF processing time.

Finally, we have also addressed the case where an approximate discretised model is used to represent a continuous-time process in state estimation. Improved estimates were obtained when equality-constrained Kalman filtering algorithms were employed to enforce a conserved quantity of the original continuous-time model, but without the higher computational burden required by more accurate integration schemes.

We believe that comparisons of MHE for non-linear systems (Rao et al. 2003) against ECUKF and MAUKF would be valuable in a deeper analysis of the algorithms and that this should be pursued in the near future.

Acknowledgements

We wish to thank Prof. Harris McClamroch for assistance in the attitude estimation example.

This research was supported by the National Council for Scientific and Technological Development (CNPq), Brazil, and by the National Science Foundation Information Technology Research Initiative, through Grants ATM-0325332 and CNS-0539053 to the University of Michigan, Ann Arbor, USA.

Appendix I: Equivalence between ECKF and MAKF

Define the augmented observation

where

With (A.1), MAKF uses (4) and (5) together with the augmented forecast equations

where is given by (71), and the augmented data-assimilation equations given by (72–74).

For convenience, let (4) denote the forecast estimate provided by MAKF. Furthermore, let (5) be the associated forecast error covariance of MAKF. Also let (22) and (23) denote the forecast estimate and the associated error covariance of ECKF. Assume that δ in (29) is sufficiently small and can be neglected.

Proposition 9.1

Assume that and . Then and .

Proof

(A.4) is equivalent to

It follows from Bernstein (2005) that has entries

where

Furthermore, it can be shown that

It follows from (9) that

Furthermore, substituting (A.9) into (11) yields

Hence,

Substituting (A.9) into (10) yields (28). Substituting (24) into (28) yields

It follows from (25), (A.6), (A.8) and (A.10) that

Substituting (A.8) into (A.12) and substituting the resulting expression into yields

Hence, (A.7) and (A.8) imply that

Therefore, it follows from (A.12) and (A.13) that

Since the estimate of MAKF is given by

where

it follows from (A.14) that

Therefore, (A.11) and (A.15) imply that and (4) and (22) imply that .

Note that (11) and (29) can be expressed as

Substituting (A.17) into (A.18) yields

Substituting (A.2) and (A.16) into (A.19) yields

Since, (11) implies that

it follows from (A.20) and (A.21) that . Hence, (4) and (23) imply that .□

Appendix II: Connection between ECKF and PKF-SP

Assume that system given by (1), (2) and (19) is time invariant. Also, assume that (14–16) hold for D in (19). In Ko and Bitmead (2007), using a descriptor system representation (Nikoukhah, Campbell, and Delebecque 1999), the system given by (1) and (2), (19) is written in a projected representation. Then, consider PKF-SP which uses KF equations (4–11), but initialised with satisfying

and the singular initial error covariance

where the projector 𝒫_𝒩(D) ∈ ℝ ^n×n is obtained by the singular value decomposition

where U ₂ ∈ ℝ ^n×(n−s) such that

Also, note that, since (14) holds, Gw _k−1 is constrained in 𝒫_𝒩(D) and GQ _k−1 G ^T is a ‘constrained’ covariance as used in Ko and Bitmead (2007).

With Corollary 4.1 and comparing (A.22) and (A.23) to (38) and (39), we see that, similar to ECKF, which performs projection only at k = 1 to guarantee constraint satisfaction for all k ≥ 1, PKF-SP performs projection in initialisation, that is, only at k = 0, providing that (14–16) hold; see Figure 1(c).

Appendix III: Connection between ECKF and PKF-EP

PKF-EP projects the updated estimate (10) onto the hyperplane defined by (17) by minimising the cost function

subject to (17), where W ∈ ℝ ^n×n is positive definite. The solution to (A.26) is given by

where

The projected error covariance associated with is given by (39) with δ = 0.

PKF-EP is formed by forecast ((4–8)), data-assimilation ((9–11)) and projection ((A.27–A.28), (37), (39)) steps.

We set in (A.28), where is given by (11), such that (A.27) is optimal according to the maximum-a-posteriori and minimum-variance criteria (Simon and Chia 2002). In this case, note that the projection Equations (A.27), (A.28), (37), (39) of PKF-EP are equal to the projection Equations (24–29) of ECKF. However, unlike ECKF, PKF-EP does not recursively feed the projected estimate (A.27) and the error covariance given by (39) back in forecasts (4) and (5); see Figure 1(b). Therefore, the PKF-EP forecast estimate (4) is different from its ECKF counterpart (22).