A nonlinear robust PI controller for an uncertain system

Abstract

This paper presents a smooth control strategy for the regulation problem of an uncertain system, which assures uniform ultimate boundedness of the closed-loop system inside of the zero-state neighbourhood. This neighbourhood can be made arbitrarily small. To this end, a class of nonlinear proportional integral controllers or PI controllers was designed. The behaviour of this controller emulates very close a sliding mode controller. To accomplish this behaviour saturation functions were combined with traditional PI controller. The controller did not need a high-gain controller or a sliding mode controller to accomplish robustness against unmodelled persistent perturbations. The obtained closed-solution has a finite time of convergence in a small vicinity. The corresponding stability convergence analysis was done applying the traditional Lyapunov method. Numerical simulations were carried out to assess the effectiveness of the obtained controller.

Keywords:

• uncertain system
• sliding modes control
• robust control
• adaptive control
• PI controller

1. Introduction

Many of the nonlinear systems used in actual applications are uncertain or partially known (Abdallah, Dawson, Dorato, & Jamshidi, 1991; Bernhard, 2002; Grimble, 2006; Lee & Cheng, 1996; Siqueira, Terra, & Bergerman, 2011; Sira-Ramirez & Spong, 1988). Usually, these systems are subject, both to external unknown or unmodelled sustained perturbations and to the uncertainties produced by the mismatches and discrepancies between the system mathematical model and the actual plants (Fulwani, Bandyopadhyay, & Fridman, 2012). The control approaches known as adaptive and as robust are frequently used to overcome these obstacles. Essentially, the adaptive control approach consists of design a controller able to figure out the actual values of the uncertain terms (Krstic, Kokotovic, & Kanellakopoulos, 1995). On the other hand, a robust controller has a fixed structure, which provides a decent performance for a family of uncertain systems (Qu & Dawson, 1995; Spong & Sira-Ramirez, 1986). These control approaches have their own advantages; for instance, an adaptive controller can be applied to a wider range of uncertainties than a robust controller can (Pérez-Cruz, Ruiz-Velázquez, Rubio, & de Alba-Padilla, 2012; Rubio, 2012; Wen & Moreno-Armendariz, 2005), though its implementation is much more difficult. In addition, a robust controller does not need to be tuned while an adaptive one does. A third strategy combines both approaches to attempt a higher degree of robustness (Abdallah et al., 1991; Bartolini, Ferrara, & Usai, 1997). In Abdallah et al. (1991), an excellent motivation using the robust control approach can be found. In that study, the robust control approach is divided into five categories: linear multi-variable control, passivity, variable structure, saturation, and robust and adaptive. Among these categories, the variable structure or sliding modes approach may well be one of the most used nowadays. This approach ensures robustness against disturbances and parameter variations, though having the inconvenience of produce high-frequency violent control signals, known as chattering. In fact, the presence of chattering may excite unmodelled high-frequency dynamics, resulting in unforeseen instability and damage to the actuators (Bondarev, Bondarev, Kostylyeva, & Utking, 1985; Levant & Fridman, 2002; Rafimanzelat & Yadanpanah, 2004). In recent years, emphasis has been placed on developing a technique to avoid this undesirable effect. Basically, there are three well-established types of approaches to eliminate the chattering effects. Continuous approximations, as the saturation function, of the sign function appearing in the sliding mode controllers are used in the first approach (Burton & Zinober, 1986; Eker, 2006; Slotine & Li, 1991). Approaches based on observers design are another way of overcoming the chattering; here, the idea consists of by passing the plant dynamics by a chattering loop, reducing the robust control problem to an exact robust estimation problem (Rubio & Soriano, 2010; Wen & Li, 2006). Unfortunately, the robustness with respect to the plant uncertainties and disturbances is reduced (Bondarev et al., 1985; Resendiz, Yu, & Fridman, 2008; Sira-Ramirez, 1993). The third type of approach, based on the high-order sliding-mode method, guaranties convergence to the origin of the sliding variable and its corresponding derivatives. Here, the high-order sliding-mode algorithms translate the discontinuity produced by the sign function to the higher order derivatives, producing continuous control signals; however, these algorithms require an onerous computing effort (Davila, Fridman, & Poznyak, 2006; Levant, 1993, 2001; Polyakov & Poznyak, 2009; Santiesteban, Fridman, & Moreno, 2010). In addition to these three approach types, the neural network-based techniques are efficient to identify and control uncertain models. A full review of these topic is beyond the scope of this introduction, but we refer the interested reader to the following references (Wen & Poznyak, 1999; Wen, Poznyak, & Li, 2001).

The present work presents a smooth control strategy for the regulation problem of an uncertain system where the origin is not an equilibrium point. Hence, asymptotic stability of the closed-loop system cannot be expected in a single point (Benabdallah, 2009). Instead, in the present study, attention is focused on assuring uniform ultimate boundedness within an arbitrarily small neighbourhood of the zero state, which can be made as small as needed (there exist other alternative known as uniform stability, see Rubio & Pérez-Cruz, 2013; Rubio, Plamen, & Pacheco, 2011; Rubio & Wen, 2007). The idea behind this consists of shaping a class of nonlinear PI-controllers, which approximately emulate a sliding mode controller. This approach was accomplished using a combination of saturation functions and a traditional PI controller. The stability convergence analysis was carried out using the traditional Lyapunov method. The obtained continuous controller is quite robust against the unmodelled and persistent perturbation without needing to dominate it by a high-gain controller or by a sliding mode controller. In addition, the obtained closed-solution has a finite time of convergence in a small vicinity. As pointed out in Fulwani et al. (2012), Santiesteban et al. (2010), this property is very important. Examples of it can be found in many electro-mechanical, robotics, and power converter systems, which require a quick response without any overshoot. In this context, it is important to mention that the obtained results were based on the works of Santibanez, Kelly, Zavala-Rio, and Parada (2008), Parra-Vega (2001) and Ortega, Astolfi, and Barabanov (2002) and were designed to control generalised uncertain systems of first or second orders.

The remainder of this work is organised as follows. In Section 2, the robust PI controller motivation is introduced. Some generalisations of this controller are developed in Section 3, while Section 4 is devoted to the conclusions. Convincing numerical simulations to assess the effectiveness of the obtained results can be found throughout the, where appropriated.

Notation: Let, x ∈ R, k ∈ (0, ∞), and sign() be the standard sign function. The linear saturation function will be refereed, as In a similar way, the symbol α(x) ∈ R indicates a sigmoidal function; that is, α(x) is any smooth function with the property of α(0) = 0, xα(x) ≥ 0 and, for all x ∈ R, and sign(x), as long as L → ∞. On the other hand, α⁻¹(s) indicates the inverse function of the corresponding sigmoidal function.

2. Robust PI controller motivation

Consider the following control system: (1) where y ∈ R and u ∈ R are the system single state and the system single input, respectively; ρ(*) ∈ R is an unknown continuous function, which satisfies for all t ≥ 0. It is well know that if we select u as (2) then the state y globally converges on the origin in a finite time. However, discontinuities presented in the proposed controller lead to chattering. To overcome this drawback, the following controller is introduced, which can be seen as a generalisation of a PI -controller with variable gains or a smooth approximated version of the twisting algorithm.

Let us introduce the following smooth bounded controller: (3) where L, k_p, k_d, M₁ and M₂ are the positive gains to be designed; γ(y) is defined as (4) Hence, the closed-loop system, defined in (3(3) ) and (1(1) ), is given by (5) In the following subsection, it is demonstrated that the above system is globally ultimately stable.

2.1 Boundedness of the closed-loop system

Proposing V_y = y²/2 and differentiating V_y around the trajectories of (5(5) ), we obtain where k_p, M₁, and M₂ must satisfy with δ > 0. Obviously, if α(L|y|)β(y) > M₁, then . Hence, there exists a finite time, T₀ > 0, after which, (6) implying that (7) Note that in the case when , holds. That is, after some finite T₀ > 0, |y| ≤ y_M where y_M can be as small as desired. Having shown that y is ultimately bounded, we proceed to show that z is also ultimately bounded. To this end, the following auxiliary variable, w = y − k_pz/k_d, with its time derivative is given by (8) with k = k_d/k_p > 0 is used. Therefore, to compute the confined region of w the following function V_w = w²/2 is used where its time derivative, around the trajectories of (8(8) ), produces the following relation: (9) Remembering that |y(t)| ≤ y_M for all t ≥ T₀ (see the previous discussion), it is enough to select with δ > 0 for assuring that , if . This implies that, after some finite time, T₁ ≥ T₀, the following inequality holds Hence, substituting the inequality, |z/k| − |y| ≤ |w|, into the above expression, we have Then, it can be concluded that both states, y and z, are ultimately bounded.

It is noted here that the obtained bounds for y and z are quite conservative, as the present paper is concerned with showing that the whole state is bounded. However, the following subsection is focused on finding a better bound for the state variable, y.

2.2 Improving the estimation of the confined region of the variable, y

In order to determine a good-estimation for the bound, , such that for all t > T_* ≥ T₂, we propose the following Lyapunov function: (10) It must be stressed that the proposed function, V, is a strictly positive and radially unbounded function, with a local minimum at the origin (see Ortega, Loria, & Kelly, 1995). Thus, its time derivative, around (5(5) ), satisfies the following inequality: (11) where the set of control parameters M₁ and M₂ must be selected according to the previous discussion. Therefore, from the last inequality, as long as α(L|y|)β(y) > M₁. Once again, inequality (6(6) ) is satisfied, implying that there exists a finite time, T₁ ≥ T₀ such that works in the lineal region. Consequently, inequality (11(11) ) converts to and, evidently, , while (12) Thus, there exists a time, t > T_* ≥ T₁ such that g(y(t)) ≤ 0∀t > T_*. In other words, y is confined to moving inside of the compact set, , where It should be stressed that the confined region can be shrunk by selecting the values of the control parameters, k_p, k_d, L, β₀ and β₁, as conveniently large.

Remark 1:

Evidently, can be numerically computed by plotting, y > 0, versus, g(y), and detecting the sign change of g(y).

Henceforth, is used to denote the set of positive control gains parameters.

Proposition 1:

Consider the scalar uncertain system (1(1) ), with the uncertain , in closed-loop with (13) where the set control parameters, Q, satisfies the restrictions (14) with (15) Then, the closed-loop system is uniformly ultimately bounded. Besides, for some finite time, T > 0, for all, t > T > 0, where is the single root of (16)

The following properties help to stress some facts about the proposed controller:

(P1)	If ρ(y, t) = r, where r is a constant and, under the same consideration in Proposition 1, we have that y → 0 and z → −r, as long as t → ∞.
(P2)	Suppose that for all y ∈ R with ρb(0) = 0 , and selecting α(Ly), β(y), and the set of control parameters, Q, such that (17) with, , it can be assured that y → 0 and z → 0, as long as t → ∞.

The proofs of these facts are in the Appendix.

Based on the previous facts, Lemma 1 is established as follows.

Lemma 1:

Consider the closed-loop system (1(1) ) and (13(13) ), and suppose that the uncertain term can be written as where r₀ is any fixed constant and ρ_b(y) satisfies P2. Tacking = and restricting the set of control parameters Q, according to (14(14) ), then we have y → 0 and z → −r₀, as long as t → ∞.

The above Lemma is a straightforward consequence of properties P1 and P2.

Comment 1:

The inequality (17(17) ) is quite easy to fulfil by adequately fixing the set of parameters, Q. For instance, suppose that Hence, ρ_b(y) = |sin (y)|ⁱ with i ∈ N. Then, using the following setup inequality (17(17) ) converts to which always holds. In addition, note that the parameter L does not needs to be too large.

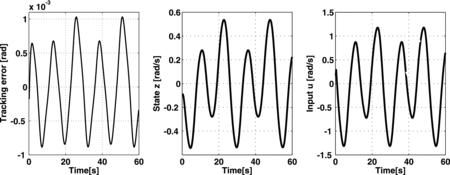
Numerical example: In order to test the effectiveness of the proposed control law strategy (13(13) ), for the uncertain system (1(1) ), we run a numerical simulation for the unknown term, ρ(y, t) = 0.5sin (t/4) + sin (y). The control objective was to follow the reference signal, sin (t/2). The system was initialised at 0.2 rads; the control function was , with L = 50, k_p = 3, k_d = 1, M₁ = 3 and M₂ = 2. The corresponding results can be seen in Figure 1. From this figure it can be seen that the proposed control law effectively makes the uncertain system to follow the selected reference in a very short period of time.

Figure 1. Close-loop response of the uncertain first-order system.

3. Some generalisations of the proposed control scheme

The proposed scheme can be also extended for the case where the uncertain term is unbounded. Suppose that the uncertain term can be upper-bounded by some nonlinear strictly positive function, as (18) where and ρ_u(y) is any strictly positive non-bounded function (for instance, ). Then, the following proposition is fulfilled:

Proposition 2:

Consider the scalar uncertain system (1(1) ), where the uncertainty fulfils the inequity (18(18) ), in closed-loop with (19) where control parameters are selected according to (14(14) ) and (15(15) ). Then, the closed-loop system is uniformly ultimately bounded. That is, , for t > T > 0, where is the single root of (16(16) ).

Proof:

First of all, we must recall that the closed-loop system, defined by (1(1) ) and (19(19) ), is (20) where . Following the same steps as in Proposition 1 is easy to see that this closed-loop system is stable. Now, to estimate a convenient bound for , we use the proposed function, V, given in (10(10) ). Hence, the time derivative of, V, around the trajectories of (20(20) ) can be upperbounded by Now from the restriction that for some finite time, Once again, as long as , implying that for a finite time.

3.1 Controlling a second-order uncertain system

Suppose that we have the following uncertain second-order nonlinear system: (21) where x = (x₁, x₂) ∈ R² is the vector state, u ∈ R is the control action, and ρ(*) is a scalar uncertain nonlinear function, provided that (22) with . The control objective is to render the states x₁ and x₂ to the origin by using a continuous controller. To accomplish this, the auxiliary variable, σ(x) = λx₁ + x₂, with λ > 0, is forced to move very close to the origin in a finite time. Roughly speaking, it is attempted to make variables σ(.) and almost zero in a finite time. Now, this control problem is solved, taking advantage of the previously proposed robust control scheme, leading to the following controller: (23) where ρ_l(x) = (k_b + λ|x₂| + k_a‖x‖), and for simplicity, (24) From the above relation, after some simple algebra, , may be written as (25) where p(x, t) lumped all the uncertain terms, defined by Then, the parameter is redefined as (26) and selecting the control parameters M₁and M₂ according to (14(14) ) and (15(15) ), respectively. It is easy to check whether σ and z are bounded (see the previous section). In fact, from the first equation of (25(25) ), there is T₀ > 0, such that (27) Now in order to determine a good-estimation for the bound, , such that, , from the above restriction, we have that works in the linear region, after t ≥ T₀. Therefore, the following Lyapunov function can be proposed: (28) where the time derivative around of the trajectories of (25(25) ) leads to (29) After some simple algebra, it is easy to show that can be upperbounded by In addition, evidently, , as long as Consequently, there exists a finite time T₁ ≥ T₀ > 0, after which , where is the single root of g(y). This section is ended by introducing the following proposition, which summarises the above developments.

Proposition 3:

The second-order nonlinear system (21(21) ) in closed-loop with (23(23) ), where the saturation function level parameters were selected according to (14(14) ) and (15(15) ), is uniformly ultimately bounded. That is, for all t > T > 0, where is the single root of (16(16) ).

3.2 Stabilisation of a class of nonlinear systems

It is well known that many mechanical systems admit the following cascade form: (30) where x = [x₁, x₂, x₃, x₄] is the state, u ∈ R is the controller, f: R⁴ → R and b: R⁴ → R are nonlinear smooth functions, d₁ and d₂ are bounded perturbations, and, f and d_i satisfy the following: The control objective is to render the state x to one small vicinity at the origin by using a continuous controller. Similarly to before, the variable σ is selected as where the set of constants λ_i > 0 will be selected below. Therefore, its corresponding time derivative is where d₀ = d₁ + λ₂d₁ and Kx = λ₁x₂ + λ₂x₃ + λ₃x₄. Now, using simple algebra, the last equation can be rewritten as (31) where ρ_l(x) and p(x, t) are defined by with k > 1. Again, using simple algebra, .

Based on Proposition 3, u is introduced as (32) Note that the proposed controller (32(32) ) in closed-loop with (31(31) ) corresponds to the previously obtained system (25(25) ). Therefore, following similar steps as before, after some finite time, t ≥ T₀, Even more, there exists some time, T₁ ≥ T₀, such that for all t ≥ T₁, where is the single root of g(y) (e.g. (16(16) )). Hence, , where can be forced to be very close to zero. This means that (33) where for all t ≥ T₁. Observe that the first three differential equation of system ( 30(30) ) are globally Lipschitz. That is, the states {x₁, x₂, x₃} cannot have a finite time of scape (Khalil, 2002). Therefore, after some finite period of time, T₁ > t, these last three equations of (30(30) ) can be rewritten as (34) where where with . Now, to ensure the ultimate boundedness of system (34(34) ), matrix A_λ has to be Hurwitz, and the system has to be asymptotically and exponentially stable if and . It can be easily solved invoking Khalil’s vanishing perturbation theorem (see Khalil, 2002). To achieve this, it is enough to satisfy the following inequity: (35) where Q and P satisfy the following Lyapunov equation: (36) where Q > 0 and P > 0. That is to say, if A_λ is selected such that the expressions (35(35) ) and (36(36) ) are fulfilled, the state q exponentially decayed to zero. However, considering the perturbations d₁ ≠ 0 and δ₁ ≠ 0, it is easy to see that the state q is ultimately bounded. This means that , where the constant can be as small as needed.¹ According to the above discussion, the following proposition gives sufficient conditions to ensure the ultimately boundedness of system (30(30) ) in closed-loop with (32(32) ).

Proposition 4:

Let us consider the nonlinear system (30(30) ) in closed-loop with (32(32) ), under the assumptions that A_λ is selected according to (35(35) ) and (36(36) ), and the saturation function level parameters were selected according to (14(14) ) and (15(15) ). Then, there exists a finite time T > 0 where the state x is ultimately bounded, with , where can be as small as needed, selecting adequately and L.

3.3 Numerical example

To show the effectiveness of the proposed controller (23(23) ), it was applied it to the well-known inverted pendulum attached to a DC-motor, whose state model is given by where x₁ and x₂ are the pendular angle position and the pendular angle velocity, respectively; the control signal u corresponds to the motor torque. The parameters M, L, g and J are the pendulum mass, the pendulum arm length, the gravity constant and the arm inertia, respectively, while ρ is a bounded perturbation. Assuming that physical parameters are partially known and ρ given by The objective is to drive the tracking errors e₁ = x₁ − x_r and close enough to the origin. That is, e₁ ≅ 0 and e₂ ≅ 0. Thus, defining σ = e₁ + e₂ and repeating similar steps as before, the following controller assures that both errors can be as small as desired if the set of control parameters satisfies the conditions (14(14) ) and (15(15) ). In order to achieve a good performance, the control parameters were fixed as where and σ_M = 68 × 10⁻⁴ (see (26(26) ) and (27(27) ), respectively). By numerical computation, it is easy to see that the steady-state error of ‘σ’ is given by , implying that .

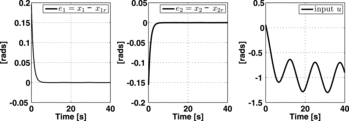
Figure 2 shows the closed-loop response of both tracking errors and the corresponding controller. From this figure, it is clear that the proposed controller effectively renders the errors close enough to the origin in about 2.25 s.

Figure 2. Close-loop response of the uncertain inverted pendulum attached to a DC-motor.

4. Conclusions

A smooth control strategy for the regulation problem of an uncertain system was obtained. This strategy assures uniform ultimate boundedness of the closed-loop system inside of the zero-state neighbourhood, which can be made arbitrarily small. To accomplish this, a class of nonlinear PI controllers was designed. This controller behaves as if it were a sliding mode controller. This behaviour approximation was in turn achieved using a combination of saturation functions and a traditional PI controller. The controller robustness against unmodelled and persistent perturbations did not need a high-gain controller or a sliding mode controller to dominate it. In addition, the obtained closed-solution has a finite time of convergence in a small vicinity. To perform the corresponding stability converge analysis the traditional Lyapunov method was used. Finally, the effectiveness of the obtained controller was validated by numerical simulations, which demonstrated clearly the controller is able to render the system to a small vicinity of the origin. It is worth mentioning that the obtained controller was designed for a generalisation of uncertain systems of first or second order. However, a generalisation for systems of higher order can be obtained.

Acknowledgements

This research was supported by the Centro de Investigación en Computación of the Instituto Politecnico Nacional (CIC-IPN), and by the Secretaría de Investigación y Posgrado of the Instituto Politecnico Nacional (SIP-IPN), under Research Grants 20131342 and 20131304. Julio A. Mendoza is a doctoral student at the Centro en Investigación en Computación and a scholarship holder of the CONACYT and he wants to thanks both institutions.

Notes

1. To avoid unnecessarily extending this report, the computing of is ommited.

Appendix A

Proof of property in P1

If ρ(y, t) = r with r being constant, then the single equilibrium point given by is asymptotically and globally stable for the system (5(5) ). Under the assumption in Proposition 1, y and z are globally stable in a Lyapunovian sense. However, to assure convergence at , we must use the following function: (1) where V(x) > 0 was previously defined in (10(10) ). Evidently, its time derivative of around (5(5) ) leads to (2) Since, V₁(x), is bounded from below and, , is semi-definite negative, then global stability of x = (y, z) is once again assured. However, remarking that , if and only if y = 0, straightforwardly proves global asymptotic stability of the equilibrium point, (y = 0, z = −r), via LaSalle’s theorem (see Khalil, 2002).□

Proof of property in P2

From the previously-defined Lyapunov function, V(x) > 0, defined in (10(10) ), its corresponding time derivative is around the trajectories of (5(5) ) (for more detail, review the first expression of (11(11) )), and after substituting, |ρ(y, t)| ≤ ρ_b(y), the following expression holds: Now, from the assumption (17(17) ), it can be assured that , for all y ∈ R − {0}. After using LaSalle’s theorem, it is easy to show that both variables, y and z, asymptotically converge on the origin.□