Student enrichment in mathematics: a case study with first year university students

ABSTRACT

This paper presents an enrichment case study to showcase a possible avenue for attending to the needs of academically strong mathematics students. We report on a group of university students who were presented with the opportunity of exploring a specific first year mathematics topic deeper, using an inquiry-based learning approach as part of an enrichment programme. Following the intervention, students completed a questionnaire and a few were interviewed to establish their experiences of the enrichment programme. We discuss the successes and pitfalls of the intervention and report on the impact it had on the participants.

KEYWORDS:

• Academically strong students
• inquiry-based learning
• student enrichment

1. Background

Large classes for undergraduate mathematics courses are becoming the norm at many universities [1]. In these courses, lecturers are faced with a large group of students with a broad spectrum of abilities and levels of interest in mathematics. In the classroom, the lecturer has the complex task of creating a learning environment suited to every student in the classroom and also to cater for the needs of every student, in particular also for the academically stronger students in class.

Academically strong students face a higher level of boredom than their peers [2–4]. Studies also indicate that too little challenge in the classroom is largely responsible for the boredom of these academically strong students [5,6].

Student enrichment is a way of nurturing academically stronger students to keep them enthusiastic and to help them discover their potential [7]. In this study, we investigate the experiences in a student enrichment intervention on a selected group of undergraduate mathematics students.

2. Literature

2.1. Student enrichment

There have been several attempts to define student enrichment within an educational setting. Correll [8] defines enrichment as any experience that substitutes, supplements or extends instruction beyond that normally offered by schools. Another definition is given by Stanley [7] who sees enrichment as any educational procedure beyond the usual ones for the subject or grade or age of the student that does not accelerate or retard the student's placement in the subject or grade. Clendening and Davies [9] define enrichment as:

… any learning experience that replaces, supplements, or extends instruction beyond the restrictive boundaries of course content, textbook and classroom and that includes depth of understanding, breadth of understanding and relevance to the student and to the world in which he or she lives. (p.4)

This definition is clearly adapted from Correll's definition. His emphasis on depth, breadth and relevance illuminates the essence of student enrichment that is supported by other scholars [10].

Academically strong students learn differently from their fellow classmates. They are typically not challenged enough and their learning needs are not being met sufficiently [11]. Mathematics and science curricula that are taught in the traditional manner are often inappropriate, because they are repetitive and provide little depth [6,12,13].

According to Caine and Caine [14], learning takes place when students’ abilities and interests are stimulated by appropriate levels of challenge. Stepanek [15] explains this phenomenon physiologically:

When tasks are not sufficiently challenging, the brain does not release enough of the chemicals needed for learning: dopamine, noradrenalin, serotonin and other neurochemicals. [15,p.9]

It has also been reported that student enrichment in mathematics is a way to meet student needs for self-activity and to stimulate their interest in the subject further [16]. Jones and Simons [17] note that this newly gained appreciation of mathematics will raise the profile of mathematics and will demonstrate to students that mathematics is worthwhile pursuing beyond school. This was also noted in a Dutch enrichment programme where the positive effect was carried over to university, and where the participants chose to study more challenging fields on average [18].

In summary, from the literature reviewed, the following goals for an enrichment programme can be listed:

• Keep students enthusiastic and alleviate boredom [2–4,7]

• Offer a challenge to students [11]

• Provide an opportunity for self-activity [16]

• Provide deeper mathematical understanding [6,12,13]

• Help students discover their potential and stimulate personal growth [7]

• Raise appreciation of mathematics [17]

The premise of the paper is that in a successful enrichment programme the goals as envisaged by the instructor should translate into gains for the participants. In reporting on the success of the intervention, achievement of these goals will be evaluated as gains under the headings Enthusiasm, Challenge, Self-activity, Depth of understanding, Self-growth and Appreciation of mathematics.

2.2. Inquiry-based learning

Inquiry-based learning (or enquiry-based learning or problem-based learning) is primarily a pedagogical methodology, developed during the discovery learning movement of the 1960s, in response to the traditional methods of instruction. The philosophy of inquiry-based learning finds its roots in constructivist learning theories, such as in the work of Bruner [19], Dewey [20], Freire [21] and Vygotsky [22] among others.

Inquiry-based teaching is an approach to instruction that begins with students exploring curriculum content rather than lecturers teaching the content. It provides a framework for students to experiment, ask their own questions and be active participants in the learning process. Evidence from literature shows that an inquiry-related teaching approach promotes critical thinking [23], positive attitudes toward science [24] and improved procedural skills [25], but we should also recognise potential disadvantages. One problem is that inquiry-based learning makes little distinction between the methods of a researcher who is an expert and the students who are new to the discipline and can be considered as novices [26]. Another problem is the danger of students losing focus on their goals and the consequent need for guidance and direction from the teacher.

When designing learning activities, it can be useful to consider the information processing approach to learning [27]. Anderson [27] highlights three principles that play a big role in acquiring new information: activation of prior knowledge, encoding specificity and elaboration of knowledge. Education should help students in activating relevant prior knowledge, creating context that resembles the future contexts as closely as possible and to stimulate students to elaborate on their knowledge. It is in stimulating students to elaborate their knowledge that enrichment through inquiry-based learning can be achieved.

Using the principles of inquiry-based learning, we developed an enrichment programme to open up the world of complex numbers to students as explained in the next section. This case study gave students first-hand experience of exploring mathematics by means of inquiry-based activities creating the opportunity to broaden their knowledge and to sharpen their problem-solving skills.

2.3. Sibling curves

Complex numbers are an essential part of any undergraduate mathematics syllabus. In the study of complex functions, visualizing these functions is problematic because of the four-dimensional graphs. Representing the zeros of complex functions graphically is also a problem. Sibling curves is a novel and useful way of visualizing the zeros of any complex function in three dimensions, introduced by Harding and Engelbrecht [28] and further developed in [29] and [30]. It provides a richer representation and visual explanation of the fundamental theorem of algebra.

Given any complex function that maps complex numbers onto complex numbers, we restrict the domain of the function to those complex numbers that map onto real values. On this domain, the function has real values and can be represented in three dimensions with the domain in the horizontal plane and the range along the vertical axis. The resulting set of curves is coined as the sibling curves for the complex valued function. The curves are in three dimensions and contain the zeros of the function.

3. Methodology

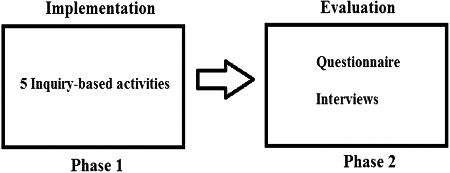
The research methodology followed is that of evaluation research [31,32] with elements of action research [33] embedded within. The student enrichment programme (see Figure 1) went through a planning and implementation phase and was followed by an evaluation phase, the two phases typical of evaluation research. With the implementation, action research principles were followed when we reflected, planned and issued an assignment, then observed student experiences before embarking on the next assignment, once again following the steps of a cycle of action research.

Figure 1. Phases of the enrichment case study.

The purpose of the first phase was to create opportunities for student enrichment. The programme coordinator designed mathematical activities that were assigned for completion by a selected group of students. The participants also had an opportunity to interact with each other as well as with the designer personally and on Facebook.

The purpose of the second phase was to capture students’ experiences regarding the programme, both qualitatively and quantitatively. A survey was conducted at the end of the first phase to capture their immediate perspectives of the programme. During the second semester, the entire class wrote a test on complex numbers. The results of the project group were compared to those of the entire class as well as to those of a control group of students who qualified for entering the project but did not participate. After evaluating the data, a small group of participants were selected for short interviews to get a deeper understanding of experiences of the enrichment programme.

3.1. Phase 1: implementation

Phase 1 was designed to form the backbone of the enrichment programme in which we created an environment where students were exposed to enrichment. They had the opportunity to do mathematics outside of the classroom and curriculum, aimed at benefiting them mathematically. In this phase, the participants investigated the problem in complex numbers on how to visually represent the zeroes of real and complex polynomials by means of sibling curves [28–30] by doing five assignments. This topic is new in mathematics, and students (even most academics) are not familiar with it.

At the university where the programme was conducted, the mainstream first year Calculus 1A course has an enrolment number of approximately 1000 students. This course is presented in the first semester of the year and is a prerequisite for the two follow-up courses Calculus 1B and Linear Algebra 1 in the second semester. The topic of complex numbers is presented in the Linear Algebra 1 course, eight weeks into the second semester.

From the Calculus 1A course, a group of 30 students were selected to take part in the enrichment programme. These students were selected from a larger group of students who all volunteered to participate, without any additional incentive. Students were selected in the first semester on grounds of performance in two semester tests, obtaining 70% or more in these tests and then randomly keeping diversity in mind. All of these students were planning to enrol for the follow-up Calculus 1B course and Linear Algebra 1 course where the topic of complex numbers would be formally taught.

Participation in this programme was voluntary. Students were informed that this would be an enrichment programme involving the topic of complex numbers. They were told that participation was not for marks or extra credit but that they would benefit mathematically from it. The students were also informed that the programme would be time consuming and that it would involve extra work outside their normal university course load. Students were told about the benefits of the programme in terms of general academic skills that would be developed, such as research skills and independent learning.

The students were invited via email and were requested to meet the designer in his office for further information on participation. Out of the 30 that were invited, 22 students accepted the invitation to participate. A few students never replied to the email and others replied explaining that they were too busy with their studies and with other extra-mural activities.

The first phase of the case study was designed to have five activities for the participants to learn about complex numbers in general and sibling curves specifically in an inquiry-based learning environment. Most of the questions posed to students were non-routine and open-ended. In Figure 2, we show some examples of questions used in the assignments.

Figure 2. Sample questions from the activities.

Students’ participation in Phase 1 consisted of the five worksheets to be completed, labelled activities. The activities had no hard deadline, but students were encouraged to complete them as soon as possible as the main goal was to complete all five activities before the topic of complex numbers was taught in the second semester.

Each activity consisted of a worksheet of problems for the student to investigate, explore and to solve with blank spaces to fill in their final answers. Once the student had answered all the questions or completed as many as she/he could, she/he had to return the completed activity to the designer in his office. When the student returned her/his activity, the designer had a brief look at the completed activity. Occasionally some relevant concepts or student concerns were discussed, after which a hard copy of the next activity was handed to the student. So students dictated their own pace. However, on a few occasions, the designer did send out email reminders to caution some students that they were taking too much time on a specific activity.

Each activity focused on a particular topic. Activity 1 was the warm-up activity and took place towards the end of the first semester. In Activity 1, the students were given a Geogebra routine that could sketch polynomials and students got to experiment with graphing polynomials and their roots. Activity 2 took place during the break between the first and the second semester and in this activity they were given introductory notes on complex numbers which they had to read by themselves and then answer some basic related questions. Activity 3 was also based on complex numbers and the concept of polynomials with real or complex roots was explored. Some of the questions in Activity 3 also hinted at the idea of sibling curves. The purpose of this activity was to get students thinking about roots while subtly introducing the idea of sibling curves during the first two weeks of the second semester.

In Activity 4, the concept of sibling curves was introduced and students had to find sibling curves of two specific polynomial examples by themselves and sketch them. Finally, in Activity 5 (in weeks 3–5 of the second semester), students came to explore sibling curves using technology. They were provided with two Geogebra routines, one that could plot sibling curves of real quadratic polynomials and the other for sibling curves of complex quadratic polynomials. The purpose of this activity was first to get students to experiment with sibling curves and to see the connection between roots and sibling curves of a polynomial, and second for students to make their own observations and ask their own questions.

The designer created a Facebook group to connect all the participants in the study mentioned earlier. The purpose of this group was to have a platform for general feedback and to create a network for the participants in the project throughout which they could communicate and ask questions for clarity and sharing remarks.

3.2. Phase 2: evaluation

The aim of the second phase of the study was to capture students’ perspectives on the project. The first phase ended shortly before the participants were going to be taught complex numbers in class. Student perspectives were captured in two ways, first by means of a questionnaire and second by interviewing four of the participants.

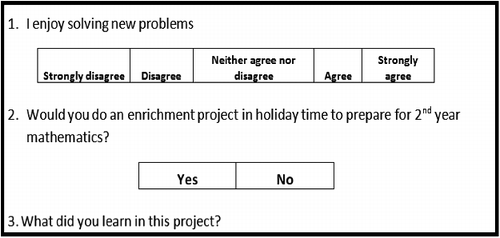
The objective of the questionnaire was to ascertain students’ impressions of enrichment. The questionnaire consisted of three types of questions: Likert scale questions, questions with two options and open-ended questions. In Figure 3, we give a small sample of the questionnaire, showing one example of each of the three types of questions.

Figure 3. Sample questions from the questionnaire.

Question 1 is an example of a Likert scale question; Question 2 is an example of a question with two options; Question 3 is an example of an open-ended question. The questionnaire was emailed to all 22 participants, labelled A to V for reporting purposes. Students had the option of collecting a hard copy of the survey from the designer's office if they wanted to complete it in writing. Participants were requested to complete it either online and email it back or print it out, complete it and return it. Nineteen of the participants completed the survey.

After the completion of the questionnaire, we conducted individual interviews with some of the participants. The purpose of the interviews was to get individual detail on students’ experiences and attitudes towards the mathematics enrichment programme qualitatively. For the sake of diversity, the selection was made to get a representative input on the survey results, on gender and on the degree programmes students were enrolled for. The students were interviewed individually after they had completed the Linear Algebra 1 course examinations. The duration of each recorded interview was approximately 30 min. The interviews were semi-structured and consisted of a set of benchmark questions that each participant was requested to answer but the interviewer had the freedom to ask more questions and/or probe participants on the responses or clarity of answers.

4. Phase 2 results

We report in this section thematically by quoting results from the questionnaire and comments from the interview interchangeably. In reporting the results, we evidence whether the enrichment programme succeeded in translating the goals listed in the summary of the literature review into corresponding gains.

4.1. Enthusiasm

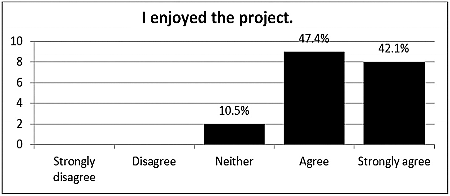
In Figure 4, we present the frequencies of student responses to the statement ‘I enjoyed the project’ as a measure of their enthusiasm.

Figure 4. Student responses about enjoyment of the project.

Responses to the question show that 17 (89.4%) students agreed or strongly agreed that they enjoyed the programme, compared to only 2 (10.5%) students who felt neutral about the programme.

These results indicate that the vast majority of students had appreciation for the enrichment programme and enjoyed participating and thus stimulating enthusiasm. No students disagreed with the statement, a meaningful result in itself. These results are testimony to the deserved place of enrichment in an already full timetable.

The participants were quite eager to hand in their activities and to discuss possible ideas and discoveries they made themselves. This mathematical engagement/stimulation could be another reason for their enjoyment.

The general enjoyment of the project was further confirmed by all four participants during the interviews. Student T experienced the project as well-designed and it felt that it was a fun experience to do mathematics without formally being taught mathematics. Student P commented that it was nice to learn a new number system all by herself. Student G commented that he enjoyed the project, because ‘I learnt new and cool things.’

A certain amount of enjoyment and enthusiasm was also experienced by the developer.

4.2. Challenge

Notable comments during the interviews were:

I enjoyed the project because it was challenging and I got to know how hard research is. (Student O)

Even when you are thinking nonsense, you are thinking. (Student T)

From the questionnaires and interviews it became clear that the majority of the participants enjoyed being challenged and learning new material in an exploring/experimenting manner using the principles of inquiry-based learning. Student O, who is planning to become an applied mathematician, liked the fact that he was given a taste of what research is during this project. Overall, it appears that students appreciated the challenge it offered, use of technology and also the activities that were designed for exploration and not ‘work for marks’ paradigm.

When probed in the questionnaire, several students mentioned as a reason for them enjoying the programme the fact that the programme tapped into their problem-solving skills and hence the challenge it offered. This challenge was also mentioned by all four of the interviewees. Student O said he enjoys being faced with difficult problems, because ‘it opens your mind to think a little bit outside the box like when you are given a difficult problem.’ Student T gets quite excited and proud when she solves a challenging problem by herself. Student P commented that some of the problems in the programme were not easy but also said: ‘I don't see the point of you coming to study if you don't want to challenge yourself to become better.’ Student L expressed appreciation for the programme and commented that ‘New problems expose me to different knowledge.’

4.3. Self-activity and independence

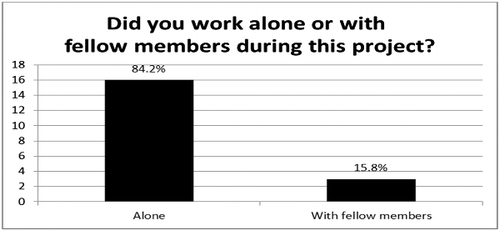
Students had the option of working individually or collaborating with friends in the project. In Figure 5, we present the frequencies of student responses on whether they completed the assignments by themselves.

Figure 5. Student responses on self-activity.

Responses show that 16 students (84.2%) worked alone in this project compared with the 3 students (15.8%) who worked with fellow members of this project. These results strongly indicate that these students prefer to work by themselves than in a group setting even if the material is new and possibly difficult.

Student P explained in her interview: ‘I like working by myself a lot. I am not a team player.’ Student O made the following statement in his interview: ‘You don't always rely on a lecturer, just do your own stuff and so that you see other problems outside the box.’ The project also gave students the freedom to ask their own questions and tap into their own ideas which is not often the case in a normal classroom setting.

A Facebook group was created to connect the participants in the study. The purpose of the Facebook group was to have a platform for general feedback and to create a network for all the participants through which they could communicate, allowing members to share ideas or to direct questions to me or to fellow students, especially over weekends or when the designer was not available.

Of the group of students who participated in this study, only 18 students joined the Facebook group. Although most of the posts were viewed, only 9 different students posted comments during the study on the Facebook page. Nine of the posts related to the study and two posts were of a comical nature. During participation in Activity 4, the first activity on sibling curves when students were first confronted with the concept of a sibling curve, a sense of insecurity was picked up. One student asked to clarify the concept of sibling curves which the designer could step in and help the entire group.

Although the Facebook group proved to be a good idea for connecting participants in the study, it is regrettable that not everybody joined the group. A few students did not have a Facebook profile and others were not interested in joining as they preferred to work alone or would rather visit the designer for consultation or clarification. It was a great platform to clear up misconceptions as the students benefited from the posts.

4.4. Depth of understanding

In his interview, Student L confessed that the work on sibling curves was hard for him, but he gained a better understanding of complex numbers as he came to see ‘a bigger picture’ in the programme. During the interview, student O also commented that he obtained a deeper appreciation of complex numbers due to the programme, compared to the way the topic was introduced in class.

Students gained from the project in that they developed deeper understanding of the mathematics and also realized that perseverance is important in developing better understanding. When asked what they learned, the following noteworthy responses were found:

It expanded my knowledge of complex numbers, by also learning about sibling curves and other things related to this field. (Student D)

Besides learning about complex numbers, I learned that sitting down and struggling with a problem and eventually solving it is key in mastering a topic. (Student L)

To compare the depth of understanding of the group of participants in the project, a control group of students were selected, using the marks criteria for selection to the programme. A further 141 students in the class met these criteria, but did not participate in the project due to various reasons. All students in the class wrote a test on complex numbers. The results of this test appear in Table 1.

Table 1. Results of groups on complex numbers test.

Group	No. of students	Average %	Standard deviation
Project group	21	65.3	2.62
Control group	141	60.1	2.69
Entire class	677	56.5	2.58

In Table 1, we see that the class average was 56.5% for the test compared to the average of the project group, which was 65.3% and the control group with an average of 60.1%. Although the difference is not statistically significant (p = 0.193), the project group performed better than the control group.

4.5. Personal growth

Personal growth was experienced as a gain by all four interviewees. Student O commented that he could immediately share the knowledge and confidence he gained in the programme. Student T said the programme boosted her confidence in mathematics. Student L felt that the programme made him braver to struggle with difficult and previously unseen problems.

From the interviews, it appears that the personal growth of participants can be ascribed to the experiences that came from stepping outside their comfort zone and having to experiment and explore mathematics in a guided fashion but by themselves. This confidence boost could be due to actualization of their own problem solving potential as they had minimal assistance from the designer of the programme.

4.6. Appreciation for mathematics

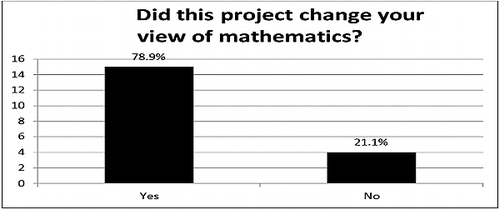
In Figure 6, we present the frequencies of student responses on whether their view of mathematics was changed by the programme.

Figure 6. Student responses on whether their view of mathematics was changed.

Responses show that 15 students (78.9%) felt that the programme had changed their view of mathematics while 4 students (21.0%) did not experience a change. In light of other findings, the conclusion is made that their views were changed positively. This result then bodes well as the programme seems to have favourably swayed most students’ predisposition towards mathematics.

Student P commented ‘I didn't know what type of maths this was’ as the programme topic is quite different from the typical classroom mathematics she had been exposed to, but she gained a new appreciation of mathematics. Student R commented that he enjoyed using the Geogebra routines and it was amazing to see mathematics visually. During his interview, student T said ‘I feel very honoured if lecturers share their passion with students. It makes me enjoy the subject and classes more.’

5. Discussion and conclusions

This enrichment programme was an eye-opening experience for the instructor on how to interact with a small group of academically strong students closer than in the classroom setting. The programme succeeded in translating each of the six identified goals into gains by participants. The programme was an opportunity to keep students enthusiastic [7] and to provide an outlet for self-activity [16]. It was a pleasant task to collaborate with students instead of being a formal teacher. Students enjoyed this form of engagement and it is clear from the questionnaire that the programme stimulated students’ interest in mathematics at the onset of their university studies. Students were also more than prepared to ask questions and to engage with the material but mostly preferred working alone.

When teaching large classes, the lecturer rarely gets time to explore a certain topic or problem in more depth with students. In this study, we could explore the idea of representing the zeroes of functions using sibling curves, with a selected group of students, which offered a challenge to academically strong students [11] and helped students to discover their potential and stimulate personal growth [7]. The participants enjoyed not only being challenged but also getting an opportunity to sharpen their problem solving skills. From the data, it is evident that the programme changed the student's view of mathematics, in that mathematics is not just a set of formulas and algorithms to learn, but it is also about developing problem-solving skills and being exposed to new and different ideas.

This enrichment programme also allowed us to avoid the trap that Freudenthal [34] calls the anti-didactical inversion that is only teaching the final polished mathematical approach without showing its discovery or evolution over time. This clean ‘approach’ hides the adventure of doing mathematics from students, which was unhidden in this enrichment programme, because of the use of inquiry-based learning techniques. As noted, the programme succeeded in providing a deeper understanding [12] of complex numbers to the participants.

From the questionnaire and interviews it was clear that there is a need for academically strong students and/or those planning to become researchers to do non-routine or high-order thinking problems.

This study demonstrated the willingness and enjoyment of academically strong students to participate in an enrichment programme. It highlights the fact that there are educational gains in stimulating keen and interested students, in spite of their busy academic schedules. Enrichment has the potential to raise appreciation of mathematics [17] as showcased in this enrichment programme.

In conclusion, we found limited reports in literature of case studies of enrichment at university level; most enrichment research is done at primary and high-school level. We envisage that this case study could put the spotlight on enrichment at university level, because enrichment at undergraduate level is a perfect vehicle to sharpen problem-solving skills and for alerting students to their potential for research in mathematics.

6. Limitations and recommendations

This enrichment programme was conducted on a small group of academically strong first year students at one South African university. Due to the workload involved, it would require more resources to extend it to more students, possibly to not only top students but also to the whole class.

Research in complex numbers that is accessible on undergraduate level enabled us to enrich the syllabus of complex numbers. This in turn allowed us to develop an enrichment programme on complex numbers to broaden academically strong student's knowledge and interest in mathematics. Not all subject matter can readily be enhanced in this way and so the enrichment topic will have to be chosen carefully. An option is to base enrichment on existing content that is not covered in class. This material can be transformed into an enrichment activity by creating appropriate inquiry-based activities guiding students in their investigation.

Arranging group meetings with the involved participants to discuss material or even explain their results to each other is another possibility. This will create better opportunity for collaboration, meeting like-minded students and improving confidence in mathematics. These group meetings can be conducted with or without the programme designer, depending on the need of the participants.

One of the pitfalls that we experienced in this programme was that we did lose five of the students along the way due to the extensive time required for doing five activities. A possible solution is to have fewer activities or to conduct enrichment activities during the holidays when there is less academic pressure on students. Another possible extension is to create similar programmes for second and third year mathematics students or possibly replicate this case study at other tertiary institutions.

As witnessed from this study, the implementation for an enrichment programme will require three elements: a dedicated lecturer, suitable content and keen students to participate in an enrichment case study. Such a combination is not always readily available.

Disclosure statement

No potential conflict of interest was reported by the authors.