Using students’ selection of significant events in mathematics lessons to deduce their underlying predispositions

Abstract

Learners’ perspectives on classroom teaching have been explored in various ways. Within the context of past research, the student voice approach has shown the potential of making teaching and learning more effective. This article reports on students’ perceptions with the aim of revealing their predispositions in the sense of Bruner’s perceptual set theory concerning mathematics lessons. By asking students about significant events in specific mathematics lessons they attended and their associated justifications, insights into students’ predispositions (beliefs) about teaching and learning mathematics are gained. We were able to reconstruct a wide range of predispositions, which indicate both a view on mathematics education that is quite positive and as well a willingness to learn comprehensively. As a further result, we obtained information about which kinds of scenes are perceived as significant by students, which was then linked to their decisive predispositions. With our results in mind, teachers could react appropriately to the expectations of students related to these predispositions and thus avoid dissatisfaction and barriers to learning.

KEYWORDS:

• Significant events
• student voice
• predispositions
• beliefs
• perceptions

1. Introduction

Different groups of people, depending on which aspects of classroom teaching they focus on, perceive mathematics education in rather different ways. Of course, this influences the way they see mathematics lessons and what kinds of events that take place during mathematics lessons they attach importance to. Taking into account various perspectives, and particularly those of students, is a way of gaining an in-depth insight into classroom practice and a requisite for further developing and improving mathematics lessons (Clarke, 2006). Listening to the voices of students and revealing their predispositions about mathematics lessons is the main focus of our study. It can lead to a more thorough understanding of students’ needs and has the potential to influence educators and policy makers (Mok et al., 2013). In the literature section, we discuss several studies that show in which ways the students’ perspectives can contribute to understanding teaching-learning processes. According to Hattie, ‘[t]he visibility of learning from the students’ perspective needs to be known by teachers so that they can have a better understanding of what learning looks and feels like for the students.’ (Hattie, 2009, p. 116). Exploring which events of mathematics lessons students consider significant and how they perceive their classroom learning can widen the view on mathematics education and has the potential to influence classroom teaching sustainably (Huang & Barlow, 2013; Lee & Johnston-Wilder, 2013). Ultimately, the events that can have an influence on the learning process are especially those which students remember and consider important for their learning.

In this regard, it is of interest during which kind of class organization students typically perceive significant events, which approaches and activities are comprised in these scenes and, above all, how students justify their selections. Certain predispositions about mathematics lessons facilitate, induce and even influence particular perceptions. Therefore, the aim of capturing and understanding students’ specific perspectives can be achieved in a more enriched and substantiated manner by revealing the underlying predispositions (beliefs) that guide their selections and accompanying justifications. This is where our project comes in. Because these predispositions influence students’ actions subconsciously and therefore are not directly accessible, we use the method of objective hermeneutics to reconstruct students’ predispositions from interviews that were conducted right after mathematics lessons.

2. Theoretical framework

Several studies have shown that beliefs play an important role in learning mathematics (e.g. Philipp, 2007; Richardson, 1996; Roesken, Pepin, et al., 2011). However, up until now, there is no generally accepted definition of the concept of beliefs (Beeli-Zimmermann, 2018; Pajares, 1992), even though many researchers have expended a lot of effort trying to propose one (Harvey, 1986; Nisbett & Ross, 1980; Rokeach, 1968; Törner, 2002). Following Abelson (1979), we characterize our concept of beliefs by a number of features, rather than give a specific definition. For this purpose, we use the five dimensions stated by Fives and Buehl (2012) to describe our understanding of beliefs: (i) They are not directly observable and must be inferred from individuals’ statements or actions (Goodman, 1988; Rokeach, 1968; Tabachnick & Zeicher, 1984). (ii) While beliefs may change, studies have shown that beliefs are stable in the sense that they persist even when contradicting experiences are made (Nisbett & Ross, 1980). (iii) In our study, we focus on global educational beliefs concerning the learning of mathematics (Törner, 2002). (iv) Beliefs are organized in a semantic network, which represents the interrelation of several beliefs. Therefore, it is not fruitful to consider a single belief, instead, one must take into account its interplay with other beliefs. (v) In his often-cited three-component approach, Rokeach (1968) considered three aspects of beliefs: a cognitive, an affective and a behavioural component out of which the latter is activated when action is required. In addition, beliefs act as filters or lenses that affect what one perceives (Pajares, 1992; Philipp, 2007).

In our study, we qualitatively investigate the impact of students’ beliefs on their perception of specific mathematics lessons they attended. Influenced by their belief systems, students perceive mathematics lessons and what might be significant about them in a specific way. Our research focuses on students’ choices of important events and the underlying reasons for their selections. In order to link students’ beliefs to their perception, we use the terminology of Bruner’s perceptual set theory. According to Bruner and Postman (1951), perception is influenced by expectations one has about his or her environment. In this sense, a student’s predispositions influence his or her expectations about what he or she is going to perceive in a certain situation (Lilli & Frey, 1993). Considered thus, predispositions are beliefs that take effect on the students’ perception. Each act of perception is induced by the perceptual set that the person has accumulated in the past (Bruner, 1957). Figure 1 shows the relations of the discussed theoretical concepts and their relevance for our study at a glance.

Figure 1. Relationships of theoretical concepts.

Conversely, one can reconstruct underlying predispositions from the specific perceptions and the interpretations and justifications associated with these perceptions. This mechanism is employed in our analysis of the students’ justifications concerning their selections of significant events of mathematics lessons.

In the context of mathematics classes, a possible predisposition might be A good introduction of a new topic is essential for the mathematics lesson as a whole. A student with this predisposition might attend a productive lesson that featured a good introduction of a topic, in the beginning, the experience of which will confirm her predisposition. In fact, it will even reinforce her predisposition. If the student experiences a mathematics lesson with a bad introduction of the topic that leads to a bad subsequent lesson, this will confirm and therefore reinforce her predisposition as well. Only in cases in which the student experiences a bad introduction of the topic with a good subsequent lesson (and in which the student becomes aware of this experience), would this contradict her predisposition and could (if the predisposition is sufficiently weak) lead to its refusal. However, such contradictory experiences are unlikely to be perceived by the student at all (Lilli & Frey, 1993).

As predispositions influence perception, this framework provides us with the opportunity to reveal students’ predispositions from their selection of significant events. This leads us to the following research questions:

• What kinds of events of mathematics lessons do students select as significant?

• What are the underlying predispositions that guide the students’ perceptions and, subsequently, their selections of significant events?

3. Literature review

As we want to gain insights into students’ predispositions in the context of mathematics classes, we need to give them the opportunity to share their views about specific mathematics classes they attended. Such an approach is called ‘student voice’. Early work that was conducted on the voice of students revealed the potential of listening to students in order to understand teaching and learning and make it more effective (e.g. Cook-Sather, 2002; Fielding, 2001; Hancock & Mansfield, 2002; McCallum et al., 2000; Pollard & Triggs, 2000; Rudduck & Flutter, 2000). Student voice initiatives hold potential for improving learning, as the participation of students might have a positive impact on their metacognitive development, as well as on teaching, providing teachers and researchers with valuable insights (Flutter & Rudduck, 2004). Several studies have (also) proved this potential for the teaching and learning of mathematics in particular (e.g. Grootenboer & Marshman, 2016; Hannula, 2006; Harkness & Stallworth, 2013; Hine, 2019; McDonough & Sullivan, 2014; Roesken, Hannula, et al., 2011; Sullivan et al., 2006). Even younger students seem to have a constructive focus on learning and clear perceptions about what helps them in learning mathematics, showing a high consensus across different classes and teachers about what is helpful, though at the same time, showing differences in how they articulate what they find helpful (McIntyre et al., 2005). Students seem to be aware of their own role in learning and of what they need to do in order to be successful (Lee & Johnston-Wilder, 2013). Students begin to develop expectations about their teacher’s role once they start school and as these perceptions influence their view of how mathematics is learned, talking to them about their teacher’s role and their expectations provides important insights (Taylor et al., 2005).

The question of what students attach importance to concerning mathematics lessons has been dealt with in several studies (Huang & Barlow, 2013; Kaur, 1997; Kaur, 2008; Kaur, 2009; Kaur et al., 1999; Kaur & Yap, 1998; Mok et al., 2013; Shimizu, 2006; Wilkie & Sullivan, 2018). Using a paper and pencil survey, Kaur (1997), Kaur and Yap (1998) and Kaur et al. (1999) asked students about good qualities of mathematics teachers in general. Patience, caring/understanding, mathematical expertise and the ability to explain clearly were among the most often mentioned qualities. Kaur (2009) – as part of the Learner’s Perspective Study (LPS) (Clarke et al., 2006) – asked a similar, general question: ‘What has to happen for you to feel that a lesson was a “good” lesson?’, during video-stimulated post-lesson interviews. Again, clear explanations were one main characteristics of a good lesson (Kaur, 2009, p. 343).

In another study that uses the LPS design (Clarke, 2006), Kaur (2008) and Mok et al. (2013) analyzed Singaporean mathematics classes through video-stimulated post-lesson interviews in which students were asked to comment on lesson events they attached importance to. Students could mention as many important events as they wanted. Among the most commonly chosen events were clear teacher explanations and demonstrations of how to solve a problem (Kaur, 2008, p. 955; Mok et al., 2013, p. 201). Important events perceived by Chinese students include the introduction of new concepts/procedures, the solving of exercises as well as comments/explanations regarding students’ solutions (Huang & Barlow, 2013). However, those studies did not focus on the reasons why students perceived events as important.

Rather, they investigated which kinds of events are important to the students and whether the students’ perceptions are in line with the teachers’ intentions for the mathematics lesson. Furthermore, they asked quite explicitly whether the students would describe the experienced lesson as a good one for them (Huang & Barlow, 2013). Lee and Johnston-Wilder (2013) used a questionnaire where the students had to tick sentences for certain beliefs that reflected their stances towards the teaching and learning of mathematics. In contrast, we try to be true to the notion, that beliefs are not directly observable and therefore have to be inferred from students’ statements or actions. For this purpose, we use the students’ justifications for their selections of significant events of mathematics lessons. Specifically, we want to determine beliefs, which influence students’ perceptions in concrete classroom situations. In this regard, the filter function of beliefs is a main issue in our understanding of perception of significance and the theoretical framework we use.

Another study showed that students seem to hold ‘overwhelmingly positive aspirations for their learning’ (Wilkie & Sullivan, 2018, p. 250). The authors analyzed answers to a free-format prompt at the end of an online-survey, in which students were asked what they wish for in their mathematics learning. Students formulated their wishes in highly positive terms, revealing a positive attitude towards the subject, but this does not necessarily lead to positive learning actions in class. The word ‘wish’ might have influenced the students to think about positive aspects. Furthermore, if students are asked directly, social desirability bias cannot be eliminated. To avoid this problem, we try to gain insights into students’ predispositions concerning the teaching and learning of mathematics indirectly by asking for significant events and associated justifications.

4. Method

4.1. Data collection

The data collection took place in the context of the seminar ‘Lesson Planning’ at the University of Vienna in the winter term 2018/19. The 15 pre-service teachers who attended this seminar prepared 90-minute mathematics lessons in pairs. Four participating Austrian school classes amounted to 77 students in total. The students were taught in the following topics:

• 7th grade: Algebra

• 9th grade: Trigonometry

• 11th grade: Differential Calculus; Probability Theory

Each pair of pre-service teachers conducted their planned lesson with one half of a class (approx. 10 students). Each of the eight lessons was fragmented into short scenes. The criteria for a cut were decided upon by examining a video of a previous study, which was then fragmented and double coded to maximize the accuracy. The results of this trial showed high accordance between independent coders, which in turn legitimates the subsequent fragmentation of the eight lessons by only one person. The following criteria for determining where to cut the scenes resulted from this process and were used for the lessons in this study (each lesson was observed by an assistant who generated the fragmentation):

• Change of teaching method

• Change of subject

• Change/beginning of a new didactic strategy

• Discussion of a new task or subtask

• Presenting or discussing a new example

• (Forced) interruption of the lesson

• Beginning or end of a break

The participating students of each lesson were divided into three groups (two to four students each) for post-lesson interviews. Due to authenticity issues, the three interviews belonging to one certain lesson (one half of the 7th-grade class) could not be considered for further analysis. We thus obtained 21 interviews (linked to the remaining seven lessons). All interviews were recorded.

The interviews were semi-structured, following a tripartite interview protocol (Galletta, 2013). They began with an open-ended question aiming at inducing narrative. The students were invited to retell the mathematics lesson and how they experienced it. In the second part, students were asked more specific questions that covered a wide range of what could be understood as significant (significant concerning the learning process, understanding, interest and/or motivation). In the last part, students in each interview group had to come to an agreement about the five events they deemed most important. The chosen events were supposed to be short sequences of approximately two to five minutes and the students were told that they needed to select sequences of such length. In contrast to LPS, we determined the number of events to be chosen for reasons of prioritization and comparability. Furthermore, we did not use video-stimulated recalls, because we solely wanted to register events that were remembered by the students. After the students had chosen their significant events, they were asked to locate them in the lesson fragmentation. The interviewers had not attended the lessons so they could not influence the students’ choice.

The aim of the interviews was to ascertain events that seemed significant to them. We chose the German word ‘wichtig’ out of a group of words with a similar meaning (such as ‘wesentlich’, ‘markant’ or ‘maßgeblich’, which all translate to significant or important, respectively) for its easy comprehensibility and its openness to all kinds of aspects that could be meaningful to the students. ‘Wichtig’ expresses that some aspect is of essential relevance (Duden, 2019). We do not predetermine the term ‘wichtig’ as a survey construct, because we do not aspire to infer causal relationships to other constructs. Actually, we seek to learn more about what is important to students when reflecting their attended mathematics lessons.

In the course of the selection of significant events, students were asked for justifications for their selections. We chose the setting of group discussion as an approach to gain diverse insights about and an in-depth understanding of the students’ selections and associated justifications (Nyumba et al., 2018). The justifications given in the interviews were transcribed. Following Bruner’s perceptual set theory, the collection of these justifications was our data set for reconstructing the students’ predispositions that led to their specific perception.

4.2. Data analysis

In order to investigate the first research question, we coded each scene regarding two coding systems with respect to Mok and Lopez-Real (2006). The first coding system is about the class organization and includes three codes: Classwork, Seatwork Individual and Seatwork Small Group. We assigned only one code per scene. The definition of the codes reads as follows:

• Class Work (CW) refers to teacher activities in a whole-class setting. These include teacher talk only and teacher-led discussions. For example, the teacher gives instructions about an exercise, explains a procedure or asks questions, which are answered by one or more students including follow-up questions.

• Seatwork Individual (SI): Students work on their own, without talking to other students.

• Seatwork Small Group (SG): Students work in pairs or in small groups.

The second coding system concerns the teacher’s approach and the teacher activities and includes seven codes, expanded from an original list of five categories: Exploratory, Directive, Summary, Collection, Comparison, Exercise & Practice and Assigning Work. In its original wording, the system lists five categories, however, during the analysis, we were faced with a huge amount of summary and directive scenes. Hence, we decided to differentiate the code Summary in greater detail and compiled a coding manual. These seven codes form mutually exclusive segments and are defined as follows:

• Exploratory (E): Students tackle relatively open or difficult problems. A growth of knowledge for the students is necessary for assigning this code.

• Directive (D): Again, a growth of knowledge for the students is a necessary condition for assigning this code. In such scenes, students are narrowly guided by the teacher.

• Summary (Sa): is about summaries as teaching results assurance. For example, the teacher writes down a take-home message or repeats something that has already been learned.

• Collection (Sb): The teacher collects students’ results of an exploratory phase.

• Comparison (Sc): Such a scene typically occurs after an Exercise & Practice phase, where the teacher compares the solutions of various exercises with the results of the students.

• Exercise & Practice (EP): A necessary condition for this code is that no new knowledge is developed. Characteristically, the students practise a procedure, which they have already learned.

• Assigning Work (A): The teacher gives instruction for a worksheet or group work.

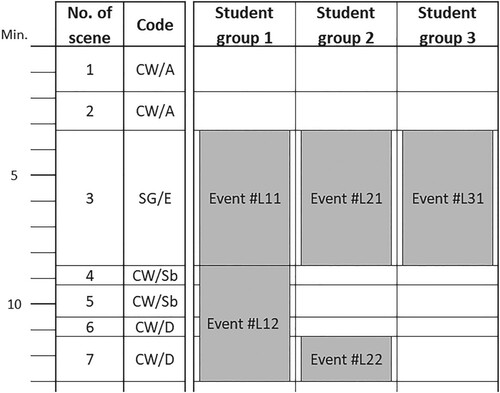
Due to sufficient interrater reliability, one-third of the data was coded by all three researchers (Cohens κ: 0.76), while the rest of the data was then coded by one researcher. We combined the scene fragmentation with the assigned codes with the students’ selection of significant events into a timetable for each lesson. An extract of the timetable of lesson L can be seen in Figure 2.

Figure 2. Timetable of lesson L: Algebra (7th grade).

For the purpose of responding to the second research question, we used the method of objective hermeneutics (Oevermann et al., 1987; Wernet, 2014), which is suitable for revealing objective structures that underlie the subjective meaning of a text. In this sense, it deconstructs the latent, implied and inferred structures behind a given text that determine the text itself (Wodak, 2011). The data set was analyzed sequentially. During group discussions among the authors, the most probable interpretations were selected and elaborated (Oevermann et al., 1987).

At this point, we want to give a brief example of how the students’ predispositions concerning mathematics education can be found by interpreting their justifications for the selection of significant events, using the method of objective hermeneutics. The three researchers went through each transcript that belonged to a justification of a selected event. Line by line, potential underlying predispositions were revealed separately by each researcher and subsequently discussed in a group setting.

Example: One group of students chose the very first scene of the lesson. In the presented part of the transcript of the associated justification, students discuss the relevance of the beginning of this lesson:

Table

S1	I believe that in general the beginning and the ending of a lesson are	1
	important as well.	2
I	And if you have to choose, for this specific mathematics lesson?	3
S1, S2	The beginning.	4
I	The beginning, okay. In addition, can you – just briefly in your own	5
	words – explain why you chose for the beginning or why you	6
	perceived it as important?	7
S1	I believe […] we started with a new topic and they should have	8
	explained that we were going to discuss – what is it called? – the	9
	differential quotient. After that, they could have started just the same	10
	way as they actually did. The example with the bungee jumper was	11
	good, but they should have told us, what we were going to do instead	12
	of directly starting to calculate. (11th grade, two girls, #I11)	13

The statement of student 1 in line 1 led us to the predispositions A good introduction is important and A good ending is important. In this study, we are interested in predispositions that are decisive for choosing certain experienced classroom events, therefore the interviewer immediately prompted her to refer to the mathematics lesson she had attended. Considering the students’ specification in line 4, we rejected the predisposition about the good ending for this event. In the very beginning of her justification in lines 8 and 9, the student complained about a missing explanation by the teacher. At first sight, three predispositions appear to be appropriate: Good and detailed explanations are important, It is important for the topic (of the current lesson) to be clear and It is important that it is clear what is going on at the moment. Through a closer examination of the next sentence and the subordinate clause in lines 12 and 13, it becomes clear that the source of her dissatisfaction stems from the missing mention of the topic of today’s lesson – the differential quotient. Finally, student 1’s statement about the example with the bungee jumper yields two predispositions: It is important to create references to life outside of school and It is important to choose suitable tasks and examples. Summarising, this analysis reveals the following predispositions:

• A good introduction is important.

• It is important for the topic (of the current lesson) to be clear.

• It is important to create references to life outside of school.

• It is important to choose suitable tasks and examples.

Certain expectations accompany these predispositions. The student’s perceptual set can be activated whether or not a certain experience is in line with the associated expectation. In both cases, the perceptual set can be confirmed by this experience. In the transcript, one can see that the expectation of clarity about the topic of the lesson is not met: In lines 8–10, students complained that the teachers did not explain the topic of the lesson (differential quotient) appropriately. That is also why the expectation of a good beginning is only partly met, in spite of the appreciated chosen example that, in addition, fully meets the expectation concerning suitable tasks/examples (line 11–12).

For the predispositions obtained in this manner, the research team employed an interpretative categorial-content analysis inductively referencing the students’ justifications (Mayring, 2015). For quantitative analysis, we recorded the frequencies of all predispositions arising from our data set.

5. Results

5.1. Categorization of significant events

In this section, we focus on the findings with respect to the first research question. Figure 3 shows the distribution of scenes over all videotaped mathematics classes regarding the two above-mentioned coding systems. The combination of the two coding systems reveals many scenes with the codes CW/D, meaning there was a lot of teacher talk and there were many teacher-led discussion scenes carried out in a whole-class setting. In addition to many Exercise & Practice scenes (EP) in different forms of class organization, the number of scenes of comparison (CW/Sc) stands out. However, we are interested in the kinds of significant events from the students’ points of view. For this reason, we consider the absolute and relative frequencies of scenes, which occurred/happened during significant events selected by the students, as can be seen in Figure 4 and 5.

Figure 3. Distribution of the absolute frequencies of all scenes with respect to the two types of coding Class Organisation and Teacher’s Approach.

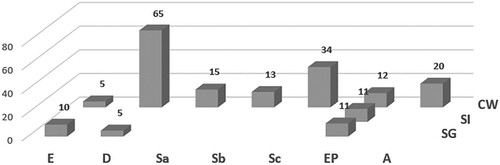
Figure 4. Distribution of the absolute frequencies of scenes which were chosen by at least one group of students.

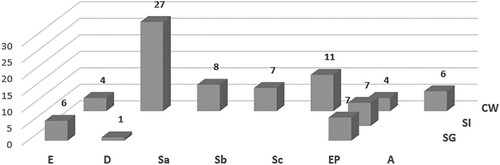
Figure 5. Distribution of the relative frequencies of scenes which were chosen by at least one group of students in relation to all scenes in the respective category.

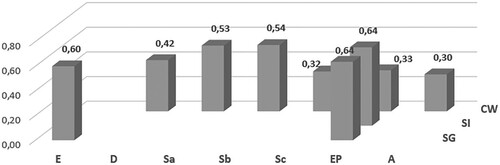
In Figure 4, the value 27 stands out. For each of these 27 scenes, at least one group of students mentioned a significant event that occurred during that scene. The numbers in Figure 4 depend heavily on the distribution of scenes. Therefore, it is not surprising that the largest figure can be found in CW/D. Hence, we took into account relative frequencies, as shown in Figure 5. The value 0.60 means that six out of 10 scenes with the code SG/E were included in at least one group’s mention of significant events. In Figure 5, we neglected all codes which occurred less than six times in Figure 3 because relative frequencies are not meaningful in cases with small denominators. We can deduce that students experienced exercise and practice during individual and group work phases as significant. Moreover, the tackling of difficult or open tasks in groups was significant to the students. Students mentioned significant events which happened during eight of 14 scenes in which the teacher summarized what they had learned. It must be noted that the explanatory power of the relative frequencies in Figure 5 is limited due to the restriction of the students having to choose exactly five significant events. For this reason, a large relative frequency in the category CW/D is impossible to attain. The combination of both figures shows that students perceive CW/D, SG/E, SG/EP, SI/EP and CW/Sa to be important. Now we take a closer look at why the students perceive such events as important.

5.2. Underlying predispositions

Regarding the second research question, the results of the corresponding data analysis are shown in Table 1 (for validity reasons we neglected all predispositions that could only be reconstructed less than three times). The first group includes predispositions about teacher explanations, understanding and connections of different mathematical objects. The ten predispositions of this group could be reconstructed 122 times. The code Good and detailed explanations are important is the most frequent of all. In 30% of a total of 105 justifications, the mentioned predisposition was decisive for the students when perceiving the respective event. This predisposition could become effective in two different ways even for the same group of students. On the one hand, students praised the teacher for her explicit explanation about the meaning of the average rate of change of the distance covered by a bungee jumper:

Table

S1	Then we talked about it and she explained it in detail, yes, we calculate how fast he
	was in the interval four six, and that was pretty good in my opinion, in that moment
	I thought, ah, that is what we have calculated, ah, ok, I understand.
S2	That she gave us understanding of this task. (11th grade, two girls, #I12)

Table 1. Categorization of predispositions about mathematics lessons and their absolute frequencies.

About content and understanding		122
	Good and detailed explanations are important.	32
	Conceptual understanding is important.	20
	It is important to make connections.	13
	Being able to imagine or visualize things is important.	12
	It is important to be able to execute routines.	10
	It is important that the teacher has a high degree of content knowledge.	10
	It is important to explain why something is done or what good it does.	9
	Correctness is important in mathematics lessons.	7
	Simple, suitable approaches should be chosen.	5
	It is important to create references to life outside of school.	4
About clarity, tools, methods and teaching materials		71
	It is important that it is clear what is going on at the moment.	21
	It is important to use suitable visual representations.	20
	It is important to choose suitable tasks and examples.	15
	It is important to use enactive material.	5
	It is important to use appropriate teaching methods.	4
	Technical aids are useful.	3
	It is important that different sensory channels are appealed.	3
About students and their learning process		55
	It is important that students are supported in their learning process.	23
	It is important that teachers appreciate and react to students’ statements.	8
	It is important that students are able to work individually/in groups.	8
	An appropriate tempo is important.	7
	It is important that students are able to experience a feeling of competence.	6
	Mutual assistance between students in mathematics lessons is important.	3
About lesson framing		23
	A good ending is important.	7
	A good introduction is important.	6
	It is important that lessons are structured time-efficiently.	4
	It is important to revise prior knowledge.	3
	It is important for the topic (of the current lesson) to be clear.	3
About motivation		20
	It is important that students get motivated.	9
	It is important that lessons are exciting/interesting.	8
	It is important that lessons are also fun.	3

On the other hand, while justifying the choice of a different significant event they complained about her incomplete explanations of the graphical representation of the derivative of a certain function with GeoGebra:

Table

S1	However, in my opinion, it was explained too little.
S2	I think so too.
S1	[…] Well, in my opinion, that could have been explained in more detail. (11th grade,
	two girls, #I13)

The predisposition Conceptual understanding is important could be revealed from the justifications 20 times. In one case, students lamented about lack of explanations for the limit, stating that because of this, they were not able to imagine anything and, in further consequence, did not understand anything. The same transcript allowed us to reconstruct the aforementioned predisposition about explanations, as well as the predisposition Being able to imagine or visualize things is important. The predisposition It is important to make connections is worth referring to as well. For instance, one group of students reflected on a situation of a teacher showing a secant of a graph on the computer and continuously changing its locus. The students could connect the vanishing of the secant with the necessity of the difference quotient having a non-zero denominator.

The second-largest category About clarity, tools, methods and teaching materials comes to 71 mentions. In this division, we consider teaching methods, all kinds of teaching materials and representations like tables, graphs, sketches, etc. The predisposition It is important that it is clear what is going on at the moment is the most common in this category. Students perceived those events as important, in which they were not sure about the topic of a mathematics lesson. Appropriate representations are also important in mathematics lessons. For example, one group of students said that they understood the random experiment better because of a suitable table:

Table

S1	What I liked about him was that he drew a table.
S2	Exactly, in my opinion he illustrated the table in a good way.
S1	[…] We made a table where one could see – uhm – the number of possibilities and
	that was illustrated in a good way, I think, that helped me a lot. (11th grade, two
	girls, #P32)

Students appreciate an adequate choice of examples and tasks for mathematics lessons. This predisposition could be revealed from the following negative example. There was a worksheet about body heights and weights of the students, but they did not need to calculate anything. Hence, the students considered it pointless.

Six predispositions with a total frequency of 55 could be reconstructed, which belong to the third category About students and their learning process. Among these, the predisposition It is important that students are supported in their learning process stands out. We were able to reveal this predisposition from 23 justifications. For example, one group of students missed the support of the teacher during seatwork. Even though the class became noisier, the teacher did not intervene.

The remaining two categories About lesson framing and About motivation are about a good beginning or ending, time-efficiency, motivation, excitement, interest and fun. The predisposition It is important that students get motivated could be reconstructed in nine justifications, e.g. one group of students was motivated because they could work on their own:

Table

S1	Yes, it was significant, that we tried it out for ourselves.
I	For what reason?
S1	Because one is more motivated, if one can try it out for himself and does not always
	have a teacher talk about it. (9th grade, a boy, #M14)

The perception of one event can depend on more than one predisposition. In our study, the minimum number of predispositions within one justification turned out to be two, the maximum seven and the average number was 2.82. Hence, a typical set of predispositions includes three predispositions that are decisive for the perception of a significant event.

As mentioned in the theoretical framework, a predisposition can be effective in two different ways. On the one hand, if a student with the predisposition Conceptual understanding is important understands a certain approach deeply, which enables her to easily follow the subsequent lesson, this student will see her predisposition confirmed and she will be aware of the event of understanding (fulfilled expectation). On the other hand, if she does not understand the approach, which hinders her in following the subsequent lesson, she will see her predisposition confirmed as well (unfulfilled expectation). During data analysis, we discovered that there are certain predispositions, which predominantly go along with fulfilled, or unfulfilled expectations, respectively. We counted the number of unfulfilled expectations of each predisposition and compared it to the predisposition’s absolute number of occurrences. The top five with respect to this ratio are: It is important that the teacher has a high degree of content knowledge, It is important that it is clear what is going on at the moment, An appropriate tempo is important, It is important that lessons are structured time-efficiently and It is important to use appropriate teaching methods. If one calculates the analogous ratio of fulfilled expectations per number of absolute occurrences of a certain predisposition, the list of the top five includes It is important that lessons are also fun, Technical aids are useful, It is important to create references to life outside of school, It is important to use enactive material and A good introduction is important. Roughly speaking, the students generally perceive fun, use of technology, references to life outside of school, enactive materials and good beginnings if they occur during the lesson and not if they are missing.

5.3. Analyzing predispositions associated with certain classroom events

For three of the five categories – CW/D, SG/EP and SG/E – that were considered most important by students, we compared the relative frequencies of the predispositions underlying the justifications given for that scenes with the relative frequencies of the predispositions in all scenes. For example, we reconstructed the predisposition Conceptual understanding is important in 20 of the 105 justifications. 38 selected events occurred during CW/D phases, of which 10 showed this predisposition. Hence the relative frequencies are 0.19 and 0.26, respectively. In Table 2, predispositions with great differences in their relative frequencies are listed for each category. This analysis of relative frequencies shows that certain predispositions are over- or underrepresented in certain categories. Unsurprisingly, there is a focus on Conceptual understanding is important, Being able to imagine or visualize things is important and It is important to make connections in CW/D, but it is interesting that It is important to be able to execute routines does not seem to play a more important role in those scenes. We conclude that when a teacher introduces new knowledge, students attach more importance to a deeper understanding than to simply ‘getting how it works’. For SG/EP, the high relative frequencies of It is important that students are able to work individually/in groups, It is important that students are supported in their learning process and It is important that teachers appreciate and react to student’s statements are comprehensible, at the same time, students never showed the predisposition It is important to make connections in those scenes. From these results, we can infer that students want to practise individually and in groups, but have the opportunity to consult a teacher in case they need help. Furthermore, students seem to think that phases where they can exercise and practice newly gained knowledge are not primarily about making connections. For the third category SG/E, we conclude that exploring something new (in groups) has indeed the potential to motivate students as well as awaken their interest and keep them entertained (compared to other phases).

Table 2. Relative frequencies (RF) of underlying predispositions.

Category: Classwork/Directive		Number of events: 38
Predisposition	RF related to CW/D	RF related to all scenes
It is important to be able to execute routines	0.03	0.10
Conceptual understanding is important	0.26	0.19
Being able to imagine or visualize things is important	0.21	0.11
It is important to make connections	0.24	0.12
Category: Seatwork Group/Exercise & Practice		Number of events: 13
Predisposition	RF related to SG/EP	RF related to all scenes
It is important to make connections	0.00	0.12
It is important that teachers appreciate and react to student’s statements	0.23	0.08
It is important that students are able to work individually/in groups	0.31	0.08
It is important that students are supported in their learning process	0.62	0.22
Category: Seatwork Group/ Exploratory		Number of events: 11
Predisposition	RF related to SG/E	RF related to all scenes
It is important that lessons are also fun	0.18	0.03
It is important that students are able to work individually/in groups	0.27	0.08
It is important that students get motivated	0.36	0.09
It is important to use enactive material	0.36	0.05

6. Discussion and conclusion

From a theoretical point of view, our article brings together Bruners’ perceptual set theory with a concept of beliefs, that focuses on their implicit nature and their function as filters for perception. This perspective on beliefs gives us the opportunity to investigate our research questions and contribute to the scientific knowledge in two ways: Firstly, by categorizing which kinds of events of specific mathematics lessons students keep in mind and consider significant and, secondly, by revealing the students’ underlying predispositions about mathematics education that led to their selections implicitly. In the section below, we contrast our results with findings in the literature and discuss limitations of our study.

In their selection of significant events, students often mentioned student-centred learning phases (seatwork individual and small group), which is in line with the results of Huang and Barlow (2013) and Mok et al. (2013). The study of Wilkie and Sullivan (2018) showed that students wish (among other things) for more such phases in their mathematics lessons. Phases of activity are more meaningful to students and thus, more likely to be perceived and remembered. The emotional involvement (e.g. discover connections, find solutions to certain problems and so on) might be the reason for selecting events during such scenes. To a certain extent, students highlighted different kinds of summaries. This supports the results of Huang and Barlow (2013) and Mok et al. (2013). Students from Shanghai, Hong Kong and Singapore appreciated bridging past knowledge with the present, hence they valued review and feedback parts, which is in line with our study.

The students’ choices of events and the categorization provided suggest the inclusion of more student-centred and methodically varied learning phases into mathematics lessons (because they have the potential to motivate students and to enhance their activity as well as their attention).

However, asking students directly about what they expect from or wish for in mathematics lessons is only one side of the coin. Revealing the underlying belief system that students hold can give a deeper insight into what is efficacious for perceiving in mathematics lessons. This is the main subject of our study and a specific contribution to scientific knowledge. In order to examine this issue, an underlying theory about beliefs and perceptions is needed. For this purpose, we merged the perceptual set theory with a specific concept of beliefs. Following this amalgamation, the data shows that there are several subconscious predispositions influencing and even determining perception, which one cannot find by asking students directly. In addition, the methods, which we used, minimize the problem of social desirability.

Table 1 shows various predispositions that students possess concerning mathematics lessons. It appears that these predispositions relate to different aspects of mathematics lessons (e.g. content and understanding, methods, tools, learning process, motivation). One can conclude that students look at mathematics lessons with a differentiated perspective and that they obviously have adequate expectations for mathematics lessons. Overall, they show a rather positive attitude towards mathematics education and are eager to learn comprehensibly. In this context, it should be stressed that the predispositions concerning good explanations and conceptual understanding could be reconstructed far more often than those concerning procedural understanding and executing routines. Furthermore, the former appears both when the accompanied expectation (‘conceptual understanding should be fostered’) is met and when it is not (fully) met. This shows that students are sensitive about conceptual understanding. There are quite similar results for the predisposition relating to appropriate support in the learning process and appropriate representations, both of which we could reconstruct in plenty of cases as well.

It is striking that some predispositions are effective almost exclusively when the accompanying expectation is met (e.g. the predispositions related to fun, the use of technology, enactive material, references to life outside of school), while others activate almost exclusively when the expectation is not met (e.g. content knowledge of the teacher, clearness of instructions, time-efficiency). It seems as if the former are considered as ‘goodies’ that are only recognized when they do occur in a mathematics lesson and the latter are considered as requisites that are only recognized when they are not fulfilled.

Of course, our list of predispositions has no claims to completeness. Students may possess predispositions that did not appear in our analyses, such as Mathematics lessons should show how mathematics as a discipline works, Mathematics lessons should respect differentiated learning or Reasoning and proving are important in mathematics lessons. We cannot say anything about whether

• the students do not possess these or other not mentioned predispositions,

• they possess them, but the predispositions are not strong enough to be effective,

• they possess them, but there were no triggers for activating these predispositions in the mathematics lessons they attended.

Nevertheless, according to perceptual set theory, new predispositions can only be included in the belief systems held by students if there are appropriate incentives and enough experiences that make them plausible.

There are no indications in our data that students’ predispositions were rejected. This does not necessarily mean that there were no contradicting perceptions in the mathematics lessons. If there were contradicting perceptions, however, the students did not recognize or mention them due to the filter of their perceptual set.

The absolute frequencies in Table 1 give hints about which predispositions might be particularly effective. Nevertheless, these frequencies depend to a certain extent on the specific mathematics lessons the students attended and are therefore not generalizable. Conversely, the reconstructed predispositions provide hardly any information about the lessons themselves but only about the way the students perceived them.

A practical implication of our study might be that teachers, having our results in mind, could gain some insight into typical predispositions of students that become effective in a certain situation. With that information, they could react appropriately to the accompanying expectations of the students and avoid dissatisfaction and barriers to learning. In addition, aspects that are perceived as ‘goodies’ by the students can be used to enhance motivation and interest.

Although we attached importance to a diverse selection of classes and lesson topics, we are aware of the fact that our results are tied to the specific lessons taught in this project. Thus, further studies are necessary for answering the questions whether the belief system and subsequently the perceptual set of a certain student can change over time, how the belief system and the perceptual set depend on certain teaching practices and what kinds of interventions or experiences are effective in changing certain predispositions.

Acknowledgements

This paper is part of the larger project AmadEUs that was carried out as part of the funding programme Sparkling Science which is supported by the Austrian Federal Ministry of Education, Science and Research.

Disclosure statement

No potential conflict of interest was reported by the authors.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Additional information

Funding

This work was supported by the Austrian Federal Ministry of Education, Science and Research (Bundesministerium für Bildung, Wissenschaft und Forschung) [grant number SPA 06/048].