Programming, mathematical reasoning and sense-making

ABSTRACT

This article explores the features of students’ reasoning and sense-making when computer programming and mathematics interact, specifically, using the exterior angle concept to make different regular polygons with Scratch as a programming tool. At the end of the 2019 spring term in a public elementary school, data were obtained from a pretest, a posttest, programming tasks, surveys, audio recordings, and research field notes. Fifty-six students aged 13–14 years participated in the study. Concepts from variation theory in combination with a post-structuralist philosophical perspective were used to analyse what features of tasks allow students to experience reasoning and sense-making and what features are discerned in students’ reasoning and sense-making. The results illustrate the features of tasks as well as how connections are created during task construction between different concepts from mathematics and programming to promote sense-making and reasoning. The results also indicate that the features discerned in students’ reasoning and sense-making consist of a flow of lines that are diverse in form and are distributed across the task assemblage. The use of repetition as difference at the level of idea is powerful in order to create a close connection between reasoning and sense-making and to support differences and heterogeneities.

KEYWORDS:

• Mathematics
• programming
• reasoning
• sense-making
• variation
• patterns of variation
• Scratch

1. Introduction

Teaching computer programming in schools in Sweden became a mandatory part of the curriculum in autumn 2018. In the Swedish curriculum for grades 7–9, programming is introduced mainly as part of algebra, with a focus on programming in different programming environments and on how algorithms can be created and used for programming (Swedish National Agency for Education, 2018). Using programming as a didactic tool in mathematics is critical because teachers should be aware of students’ prior knowledge of both mathematics and programming and of how these types of knowledge should be coupled. This coupling should give students the opportunity to use sense-making and reasoning in both programming and mathematics.

An abundance of mathematics education research examines students’ ways of reasoning (e.g. Battista, 2012; Hiebert & Carpenter, 1992; Lester, 1994; Steffe & Kieren, 1994). For instance, Bruner (1957) specified that a primary goal of mathematics teaching and learning is to develop students’ reasoning ability. Mathematical reasoning, as a particular form of meaning-making, is defined as the process of making conjectures and drawing conclusions from mathematical information (Bruner, 1957; Fox & Farmer, 2011). Previous studies have concluded that reasoning and sense-making refer to students’ abilities to think about and use mathematics in meaningful ways. Although previous researchers (e.g. Nunes et al., 2007) have demonstrated the importance of sense-making and reasoning for mathematical understanding, the same importance has not been demonstrated when programming and mathematics interact.

This article explores the features of students’ reasoning and sense-making when programming and mathematics interact, specifically, using the exterior angle concept to make different regular polygons with Scratch as a programming tool. The key is to determine how classroom tasks provide mathematical opportunities centred on reasoning and sense-making. What features of tasks allow students to experience reasoning and sense-making? What features are discerned in students’ reasoning and sense-making?

2. Background

In the field of mathematics education, sense-making is used with different meanings. For example, Van Velzen (2016) used sense-making to refer to deepening one’s understanding by applying mathematical concepts. Weick et al. (2005) used sense-making to refer to understanding through retrospective reflection on the decisions and actions of individuals, while Klein et al. (2006) argued that sense-making is a continuous effort to understand connections in order to anticipate their trajectories and act effectively. Researchers have demonstrated that sense-making is supported in the classroom environment by: interaction, negotiation, and discussion, which create meaningfulness and understanding (Boaler, 2014; Schoenfeld, 2006); using student thinking through involving verbal interactions (Leatham et al., 2015); and using tasks that elicit and extend students’ ideas and encourage explanations and justifications of mathematical concepts (Mueller et al., 2014). Many researchers in mathematics education have emphasized the importance of task features, specifying that tasks open to multiple representations and multiple solution strategies promote reasoning and understanding (e.g. Doerr & English, 2006; Maher, 2009). To provide mathematical opportunities centred on reasoning and sense-making, the tasks used in classroom instruction should allow students to discern certain critical aspects of the object of learning (e.g. Marton, 2015; Olteanu & Olteanu, 2018; Vale et al., 2017).

Olteanu (2016) considered an object of learning to be part of an event that is formed through teacher–student communication. The object of learning is the content that the teacher intends to teach as well as how the students are expected to make sense and use of the content (Marton & Booth, 1997). In this article, the object of learning is to develop students’ ability to create and use computer programming as a pedagogical tool to improve their sense-making and reasoning regarding the concept of the exterior of an angle in order to make different regular polygons. Mitchelmore and White (2000, 2004) found that the angle concept is difficult for students to learn because of the multifaceted nature of the concept. For instance, the concept of angle comprises: the vertex (the point at which the two lines or rays join), the sides (the two lines constituting the angle), the interior of the angle (the space or area between the rays that constitute the angle), and the exterior of the angle (all the space on the plane that is not the interior of the angle).

Students should be able to reason about and make sense of the exterior of an angle if they can discern the differences between the interior and exterior angles. If these differences are not discerned, the exterior angle becomes a critical aspect for the students (Marton, 2015; Olteanu, 2016). ‘Critical’ refers to a critical difference in the learners’ ways of grasping and becoming acquainted with the object of learning (Olteanu & Olteanu, 2012). The critical aspects consist of three components that interpenetrate one another: the intended, enacted, and lived aspects (Olteanu, 2014, 2016). Intended aspects refer to the aspects of the content that teachers intend to present in the classroom, whereas the enacted aspects refer to the aspects of the content that teachers actually focus on during the lesson. The lived critical aspects are the aspects of the object of learning that the students distinguish during or after a lesson.

Previous research (Marton & Tsui, 2004; Olteanu, 2014) has identified five patterns of variation that facilitate students’ discernment of critical aspects of the object of learning. These patterns are: (a) contrast (to experience something, a person must experience something else that can be compared with it); (b) generalization (seeing variations in the use of the object to fully comprehend it); (c) separation (varying one aspect while other aspects remain invariant); (d) fusion (taking several critical aspects together); and (e) similarity (seeing that two or more expressions have the same meaning).

Most researchers have striven to find models for introducing programming to novices (Mendelson et al., 1990). For instance, Papert (1980) introduced the Logo programming language with turtle graphics to stimulate the development of the mini-language approach to helping students learn mathematical concepts through programming. Through experimenting with turtle graphics, students can develop a better feel for geometry and discover that 360° makes a full turn (Papert, 1980). Efforts to improve student access to programming have been made in order to move from the programming language used in Logo to the code blocks used, for example, in Scratch. Scratch is a visual block-based programming language that allows students to create a program (project) by dragging, dropping, and snapping graphical blocks of code into different sequences and combinations (e.g. Honey & Kanter, 2013; Marji, 2014; Vlieg, 2016). Resnick et al. (2009) noted that, unlike Logo, Scratch is more ‘tinkerable’, meaningful, and social.

A number of studies found that Logo could make mathematics more concrete for students, simultaneously supporting algebraic formalization and building connections between spatial and numeric/algebraic thinking (Jones, 2005). Working with Logo, and implicitly with Scratch, affords students opportunities to make and test conjectures, thereby promoting mathematical reasoning (e.g. Resnick et al., 2009). Pirolli (2009, p. 1) defined sense-making, in the programming context, as ‘a natural kind of human activity in which large amounts of information about a situation or topic are collected and deliberated upon to form an understanding that becomes the basis for problem solving and actions’. In this article, sense-making is seen as complementary to reasoning because reasoning must build on the understanding provided by making sense of a situation, and because seeking to justify why something is true will enhance one’s understanding of a situation (NCTM, 2009).

3. Theoretical framework

Applying the principles of variation theory to sense-making and reasoning when programming and mathematics interact in the classroom means trying to expose the critical aspects (e.g. Marton, 2015) of the reasoning and sense-making. In this article, the unit of analysis has four dimensions: concepts in geometry, concepts in Scratch programming, intended critical aspects, and lived critical aspects. Reasoning and sense-making are closely related to each other and to these dimensions in the manner of a ‘rhizome’. From a post-structuralist philosophical perspective, the rhizome (Deleuze & Guattari, 1987) enables a constant interplay between materials and theory that gives rise to a dynamic model for understanding what features of tasks allow students to experience reasoning and sense-making and what features are discerned by students. The rhizome concept is used to perceive the intended and lived critical aspects (in both mathematics and programming) as assemblages of words, ideas, concepts, and countless other things that are related to one another but are also distinct. Each assemblage is a constellation of heterogeneous elements and is understood as comprising processes or connections (Freitas, 2012). According to Deleuze and Guattari (1987), the characteristics of a rhizome, among other things, are:

• connection (new connections are created at every point);

• heterogeneity (associating and linking elements of quite different types);

• multiplicity (creating a whole with specific properties that cannot be explained by adding the separate properties of individual parts);

• rupture (the ability of growth to start again along an old line or along a new line if an old line is broken at any place); and

• cartography (no beginning or end, but all points may serve as points of departure).

To study sense-making and reasoning as rhizomatic assemblages is to study the various lines that form them. There are two types of line: lines of segmentarity and lines of flight (flight in the sense of fleeing, or escape, and not in the sense of a controlled movement through air) (Freitas, 2012). The lines of segmentarity are the lines that outline classification and the lines of flight are those parts of the assemblage that escape the structure of that of which they are part, serving to connect such an assemblage to that which is outside itself (Freitas, 2012). In addition to these two types of lines, there are also lines of rupture ‘as if something carried us away, across our segments, but also across our thresholds, towards a destination which is unknown, not foreseeable, not pre-existent’ (Deleuze & Parnet, 2002, p. 125). The lines of flight are associated with the new, with change and reconstruction. Understanding the connectivity between sense-making, reasoning, and critical aspects is useful when capturing different types of lines and the conditions of their specific exposures.

From a variation theory perspective (e.g. Marton, 2015), the moment of rupture corresponds to the way of understanding a phenomenon, and this in turn is directly connected to which critical aspects are discerned. Also, the qualitative differences between ways of experiencing give the opportunity to identify the lines of flight, segmentarity, and rupture that organize the critical aspects through constant decomposition and reconstruction. Variation theory claims that to develop a particular capability (e.g. reasoning), one must focus simultaneously on all critical aspects of the object of learning. This perspective also claims that one can only focus on what is discerned, discern what is experienced as varying, and experience variation if one has previously experienced instances of variation (e.g. Marton, 2015).

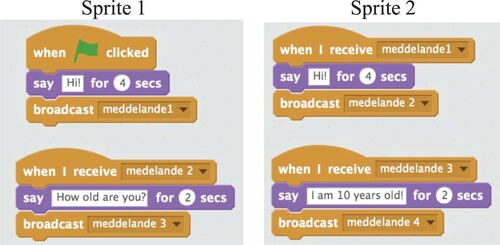
Programming using Scratch (with a focus on mathematical content) is not just about creating blocks; rather, it is a process of operating and analysing objects, representations, diagrams, symbols, or statements to draw conclusions based on evidence or assumptions – namely, a way of reasoning (e.g. Resnick et al., 2009). An important point for this article is that the differences between ways of reasoning and sense-making result from what one can discern or distinguish by experiencing variation. For example, in Figure 1, the reasoning is about the synchronization between Sprite 1 and Sprite 2.

Figure 1. Passing messages between sprites as an event.

In this context, the acts of dragging, dropping, and snapping graphical blocks of code into different sequences and combinations exemplify an event. In this event, the sense-making is a process of discerning ideas and concepts in both mathematics and programming in order to correctly identify, describe, explain, and apply them. This process differs from computational thinking, whose focus is the thought processes used to formulate a problem and express its solution or solutions in terms a computer can apply effectively (Wing, 2017). One important difference is that the classroom problems or tasks are already formulated and accessible to the students. Another difference is that the problems/tasks are intended to allow students to discern and make sense of key aspects of both mathematics and programming as well as to reason about those aspects to arrive at a solution.

Henningsen and Stein (1997) specified that the features of a task are necessary but not sufficient to enhance student reasoning. For this reason, in this article, reasoning and sense-making are regarded as closely interrelated to what students discern and experience when working on tasks in the classroom, and to what varies (difference) and what is invariant (repetition) in these tasks.

By combining variation theory with a philosophical rhizomatic perspective, this article explores how classroom tasks provide important mathematical opportunities centred on reasoning and sense-making when programming and mathematics interact, which allows a better understanding of experience and its dimensions. This philosophical perspective aligns well with the variation theory approach, because both focus on the concepts of repetition (invariant) and difference (variance) from a non-dualistic perspective. Difference is a singularity (turning points and points of inflection in a topological way) at the level of ideas, and repetition is always affected by an order of difference (Olteanu & Olteanu, 2018). Deleuze (1994) specified that the concepts of repetition and difference will intersect, ‘one concerning the essence of repetition, the other the idea of difference’ (p. 31). Repetition is never the reproduction of the same, but the repetition of the different (Deleuze, 1994).

4. Setting of the study

In this study, the research approach used was that of educational design, which is characterized as pragmatic, rooted in praxis, interventionistic, iterative, collaborative, flexible in design, and theory oriented. Educational design research involves understanding the link between teaching and learning through cycles of intervention, with a view to improving the next intervention (e.g. McKenney & Reeves, 2012; Plomp & Nieveen, 2009). In conducting an educational design study, the attributes of a rhizome are connected to different cycles of intervention and the aim is to produce useful and sustainable results for regular use in a school.

Over a year, two teachers and 56 students (aged 13–14 years) participated in the study. For approximately two hours every two weeks, the teachers worked with programming tasks in the classroom. The analysis was grounded in a pretest, a posttest, 30 tasks, 25 h of audio recordings, surveys, and research field notes. During the study, the students worked on their computer programming projects in groups of two.

The data were collected in seven steps. The teachers examined the course module and curriculum to identify the intended object of learning concerning the mathematical content (Step 1). The teachers identified the critical aspects of the mathematical concepts (Step 2). One of the study’s goals was to help teachers understand how programming in the classroom can help students learn mathematics, and vice versa. For most of the teachers, programming was a new experience, so the study started by demonstrating the basics of the Scratch programming environment and language. The researchers then introduced programming concepts (e.g. variables, conditional statements, loops, functions, and arrays) through Scratch. The researchers explained to the teachers the patterns of variation used in variation theory with reference to concepts from both mathematics and programming (Steps 3 and 4). The researchers and the teachers created programming tasks focusing on the identified critical aspects (Step 5). The teachers implemented the tasks in the classrooms. Programming was a new experience for most of the students, so at the beginning of the project, the teachers demonstrated the basics of the Scratch programming environment and language (Step 6). The teachers conducted different tests with the students (Step 7).

An important aspect of the theoretical approach was how to interpret the data collected. In this process, it was necessary to develop an appropriate classification system for sense-making and reasoning. Developing an appropriate classification system is challenging. In this study, a bottom–up approach was used to identify the most obvious features of two events, also inspired by the nature of a rhizome. In the process of analysing the intended and lived critical aspects, various questions arose, such as: What relations and connections (assemblages) are dominant in the tasks and in students’ sense-making and reasoning? What are the lines of segmentarity or rupture and where are they more present? What lines of flight can be identified? These questions were taken into consideration and guided the analysis.

Additional details of the situations are sparingly provided. The word instruction is used to point out a physical object, for instance, one drawn on a piece of paper or blocks on a computer screen. An instruction becomes an illustration if the intention behind the instruction is recognized, i.e. if an instruction makes conjectures and gives an opportunity to extract information and to create new lines of information. An illustration is a dynamic representation on which one can perform movement using inferential procedures and make sense of aspects connected to mathematics and programming.

5. Results

The following sections explore two events in which Scratch was used as the programming environment. These events focus on two tasks and on how the classroom tasks provide mathematical opportunities centred on reasoning and sense-making.

5.1. Event 1 (E1): make a regular polygon

In Scratch, the programmer works in a graphical window where the coordinate system implicitly plays an important role. The object of learning is to develop the students’ ability to draw shapes and to create a simple program to do so. The task consists of five subtasks.

1. Change the sprite ‘cat’ in ‘pencil’.

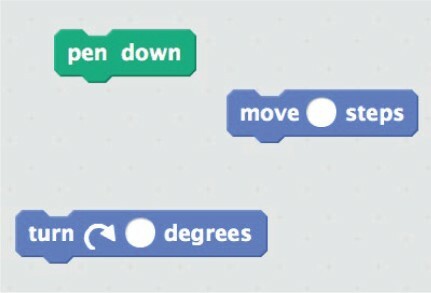
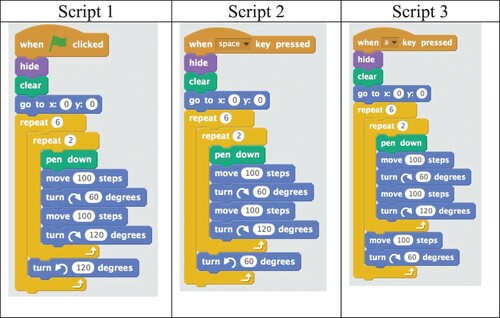
2. Use the following instructions to make a square (Figure 2).

3. Use the following structure to improve the previous programs (Figure 3).

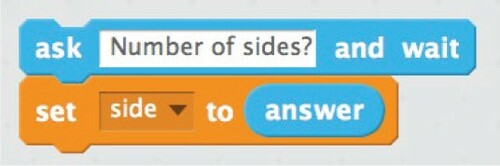
4. Improvement: create a variable ‘side’ using the instructions below. Enter its value using the following code and draw a regular polygon that has the number of sides indicated (Figure 4).

5. Modify the program to obtain an equilateral triangle, then a regular pentagon.

Figure 2. A set of instructions.

Figure 3. Instruction repeat.

Figure 4. The use of a variable.

5.1.1. The intended critical aspect: sense-making and reasoning

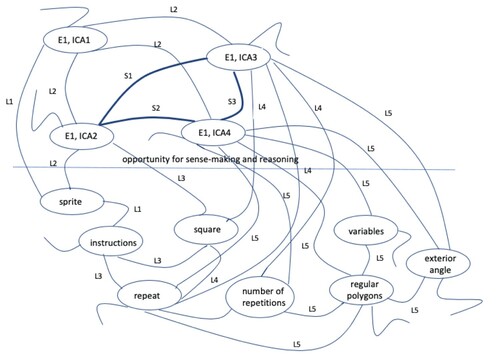
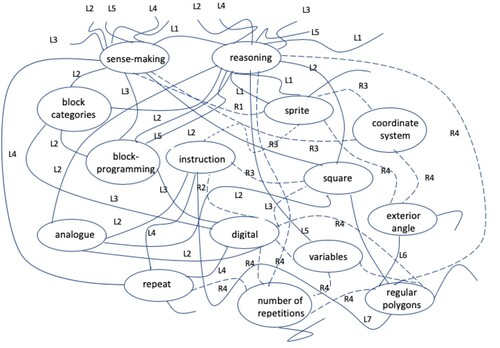
Figure 5 maps the connections that constitute the task assemblage. The assemblage is a gathering and grouping of two planes that describe the relations and connectivity of the intended critical aspects, as well as the associated sense-making and reasoning. The normal lines indicate the lines of flight and the thick lines indicate the lines of segmentarity.

Figure 5. Make a regular polygon – task assemblage.

The first intended critical aspect (E1, ICA1) was to make sense of and reason about a sprite’s ability to change its appearance, but the instructions that control the sprite have the same meaning (subtask a). Here the students used the cartography of a rhizome and similarity as a pattern of variation to create lines of flight (L1) in the students’ sense-making and reasoning concerning the role of a sprite when using Scratch.

The second intended critical aspect (E1, ICA2) was to make sense of and reason about the selection of instructions, the number of steps, and the degree of turning needed to draw a square (subtask b). This critical aspect was connected to the first, since the instructions were coupled to the sprite (lines of flight L2). Fusion was used as a pattern of variation and the multiplicity and heterogeneity of the rhizome gave the students an opportunity to make sense of and reason about the attributes of a square, the instructions used in programming, and how mathematics and programming are interlinked. In this way, several lines of flight were bridged (L3).

The third intended critical aspect (E1, ICA3) was to make sense of and reason about the control block ‘repeat’ and the number of repetitions used to draw a square (subtask c). At this moment, connection, multiplicity, and heterogeneity as characteristics of a rhizome were used to give students the opportunity to reason about and make sense of the depiction of a square and the instruction ‘repeat’ used in programming (lines of flight L4). Similarity as a pattern of variation can be identified in relation to the previous subtask (b), creating segmentarity between the second and the third critical aspects (S1). The fourth intended critical aspect (E1, ICA4) was to make sense of and reason about the use of a variable to control the number of repetitions as well as the number of steps, degree of turning, and exterior angle in order to draw several regular polygons (subtasks d and e). All the characteristics of a rhizome are used in these subtasks (lines of flight L5) and similarity as pattern of variation can be identified in relation to previous subtasks (c and d), creating segmentarity (S2).

5.1.2. The lived critical aspects: sense-making and reasoning

The intended critical aspects that students discern in working on the task ‘Make a regular polygon’ are presented in Figure 6. The points of departure in mapping the assemblage based on students’ sense-making and reasoning are the lines of flight created by the formulation of the task.

Figure 6. Make a regular polygon – students’ sense-making and reasoning.

To make sense of a sprite’s ability to change its appearance, some students’ reasoning was characterized by distinguishing between how to paint a new sprite and how to use ‘delete’ from the menu to delete the cat sprite and then add the pencil sprite. The difference between students’ ways of reasoning was based on the exploration of different blocks or selections from the menu bar (lines of flight L1). However, the students did not reason about the connection between the different appearances of sprites or about the instructions controlling the sprite, namely, whether the instructions have the same meaning in the construction of block-programming (subtask a). This is a moment of rhizomatic rupture in students’ sense-making (lines of rupture R1).

To demonstrate the idea of movement (e.g. move – turn – move – turn) in subtask b, the teacher printed out ‘blocks’ that the students used to make a little program (analogue programming using pen and paper) before going onto the computers. At this moment, the students reasoned about the selection of instructions (lines of flight L2), the order in which the instructions followed one another, and the attributes of a square (lines of flight L2), namely, that the number of steps and the degrees of turning are invariant. Then the students moved from analogue to digital programming (using the computer) by reasoning about choosing corresponding blocks in Scratch. This movement created an opportunity for new rhizomatic lines of flight (lines of flight L3). Discernment of the instructions to be used was difficult for the students (rhizomatic rupture R2) because of the large scale of the blocks as well as the multiple opportunities to move the sprite. One difference in the students’ ways of reasoning concerned the basis of the sense-making about the different block categories (i.e. recognition, lines of flight L3) and how to connect them to one another to construct the required block-programming (i.e. relationships, lines of flight L3). This difference generated reasoning based on sorting and rearranging blocks (reconfiguring) when running the script (lines of flight L3). Another difference was related to the sense-making about the coordinate system for specifying the position of the sprite and the measurement of the number of degrees in order to specify the direction in which the sprite is facing (rhizomatic rupture R3). The students’ reasoning at this moment was about the connection between mathematics and programming, namely, recognizing which procedures to choose and for what purpose. Because of the students’ difficulties discerning this connection, the teacher demonstrated the idea of the coordinate system in Scratch by using the block ‘go to x: … y: … ’ to set the starting points for the sprite at different points on the screen and in this way to contrast the different starting position of the sprite (lines of flight L3).

The next subtask (c) was a repetition of the previous one except that this time the programming could be done more quickly using the block repeat function. Most students made sense of the ‘repeat’ block (profiling) and often reasoned about what was repeated and how in the set of blocks constructed in subtask b, and then about how this change of blocks was implemented in block-programming (filter). The implementation created an opportunity for new rhizomatic lines of flight (L4).

Subtask (d) was similar to the previous one except that this time it used a variable to control the number of repetitions. This required that the students make sense of the use of the variables ‘side’ and ‘answer’, namely, the straightforward comparison of variables used in the construction of block-programming (i.e. comparing, lines of flight L5). Most students’ reasoning was characterized by examination of the use of variables (i.e. explore, lines of flight L5). The following student–student dialogue exemplifies such reasoning.

S3:

Insert side.

S4:

It is a variable?

S3:

No, it’s not.

S4:

They have changed the name … 

S3:

Yes, go to create a variable, a new variable.

S4:

What is this?

S3:

Test to create list.

S4:

No, here it is [points to the screen]. What name should we give it?

S3:

Side.

Analysis of student work in the classroom shows that most students already had some understanding of the translation and rotation of objects in a plane, but that the flipping operation seemed new to them (rhizomatic rupture R4). This is because most students could not discern the relationship between the number of sides and the turns angle.

S6:

We’ll change ‘What’s your name?’ to ‘How many sides?’, by what … 

S5:

Drag ‘answer’ to ‘side’.

S6:

It does not work.

S5:

We have to find out the angle.

S6:

We’ll try it with a different angle.

S5:

No, this will be difficult.

The teachers interrupted the students and emphasized that the angle of a regular polygon with n sides is 360°/n (lines of flight L6). The teacher illustrated different shapes and contrasted the interior and exterior angles to clarify that turning a sprite a given number of degrees refers to the exterior angles.

In subtask (e) the students’ reasoning was characterized by selection of the blocks of interest with which to draw an equilateral triangle, and then a regular pentagon (lines of flight L7). This way of reasoning allows the students to extend their sense-making about flipping by laddering one piece of information to the next one.

5.2. Event 2 (E2): pairing programs and figures

For this task the teacher printed the scripts and the shapes separately (Figure 7) and gave them to the students. The students worked first in analogue and then in digital programming to identify which script belonged to which figure.

Figure 7. Connecting figure and script.

Table

Illustration 1	Illustration 2	Illustration 3

and scripts:

Task 2 differed from task 1. In task 2 the focus was on using repetition at the level of idea, in that the instructions inside the second repeat blocks were the same, but the illustrations and the number of degrees the sprite was to be turned inside the first repeat block were different (Figure 7). This repetition was created by using contrast twice: at the level of the blocks used and at the level of the placement of the blocks. The differences between script 3 and scripts 1 and 2 were in the direction of turning and the placement of the instruction ‘move’ inside the first repeat block (Figure 5).

5.2.1. The intended critical aspect: sense-making and reasoning

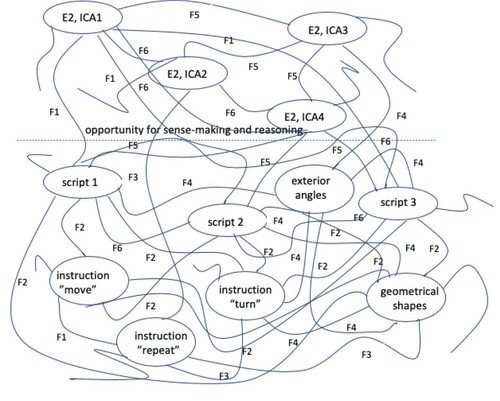
Figure 8 shows the mapping connections that constitute the task assemblage. The assemblage gathers and groups two planes that describe the relations and connectivity between the intended critical aspects, as well as the sense-making and reasoning.

Figure 8. Pairing programs and figures – task assemblage.

The first intended critical aspect (E2, ICA1) was to make sense of and reason about the blocks used in scripts 1, 2, and 3. Within the same script, similarity and contrast were used as patterns of variation to create lines of flight (F1) in the students’ sense-making as well as the heterogeneity and connections of a rhizome to allow the students to reason about the role of the instructions ‘turn’ and ‘move’ in making geometrical shapes (lines of flight F2).

The second intended critical aspect (E2, ICA2) was to make sense of and reason about the structure used in block-programming, namely, the use of the instruction ‘repeat’ twice and the differences between this instruction and the depiction of the geometric shapes. The patterns of variation, similarity, contrast, and generalization created between the scripts allowed the students to experience the rhizomatic multiplicity and connections, in order to make sense of and reason about the characteristics of each geometric shape. In this way, new lines of flight (F3) were associated with the new geometric shape, with change and reconstruction.

The third intended critical aspect (E2, ICA3) was to make sense of and reason about the exterior angles in the three scripts. Here similarity, contrast, and generalization were also used as patterns of variation and rhizomatic multiplicity and connection for sense-making and reasoning, to allow the students to experience the exterior angles (lines of flight F4).

The fourth intended critical aspect (E2, ICA4) concerned the start of each script. The contrast between the instructions indicating the starts of the scripts allowed the students to make sense of and reason about how different instructions can be used as starting points of a program (i.e. rhizomatic cartography). In this way, new lines of flight (F5) were associated with the new ways of starting a script and also with critical aspects ICA1, 2, and 3. The four intended critical aspects and the three scripts were strongly connected to one another and to the illustrations of the geometrical shapes (F6).

5.2.2. The lived critical aspects: sense-making and reasoning

The intended critical aspects that students discerned when working on the task ‘Pairing programs and figures’ are presented in Figure 9. The points of departure in mapping the assemblage of students’ sense-making and reasoning are the lines of flight created by the task formulation.

Figure 9. Pairing programs and figures – students’ sense-making and reasoning.

To discern the first intended critical aspect and to make sense of the blocks ‘turn’, ‘move’, and ‘repeat’ (in the second repeat block), the students’ reasoning focused on encoding the script inside the second block ‘repeat’ by drawing the geometrical shape on the paper (lines of flight F2 and F3). The students made sense of the fact that the repetition used in the three scripts generated a rhombus as the basic geometric figure (lines of flight F4). To link the scripts with the illustration, the students made sense of the ‘turn’ instruction inside the first repeat block. Several students found it difficult to reason using paper and pen, so they used Scratch in their reasoning. The students inputted the instructions to see which shape would be drawn (lines of flight F5). In other words, the students used programming to verify the connection between script and illustration.

S11:

Everything is the same.

S10:

No, the last instruction is different.

S11:

Turn 120 degrees.

S10:

But what does that mean?

S11:

I don’t know. We write the instructions … 

In the process of verifying the block-programming in Scratch, the students’ reasoning was characterized by adapting or changing their experience from event 1 concerning the importance of the exterior angle in constructing geometrical shapes. In this way, the students adjusted the level of abstraction by using more or less detail when constructing a script.

6. Discussion

The analysis of the empirical material presented here shows that the features of the tasks used in events 1 and 2 are: allowing students to make sense of and reason about the exterior angle concept to make different regular polygons using Scratch as a computer programming tool (Figure 5, L4 and 5; Figure 8, F1–5); allowing all students to begin the task (Figures 5 and 8) and then extending the connectivity of the concepts used in both mathematics and programming; allowing students to make connections between the concepts they are supposed to experience (Figure 5 and 8, connections between intended critical aspects); connecting various elements that have their own dimensions and retaining their differences (Figures 5 and 8); bringing together elements of mathematics and programming (Figures 5, L4 and 5; Figure 8, L2-–5); creating movement that forms and expands multiple connections (Figures 5 and 8); outlining the new mathematical information to change and reconstruct the script that generates geometrical shapes (Figures 5 and 8); and using repetition at the idea level to generate different geometrical shapes (Figure 7).

Prior research has demonstrated the importance of task features for encouraging explanations and justifications of mathematical concepts and for promoting reasoning and understanding (e.g. Doerr & English, 2006; Maher, 2009; Mueller et al., 2014). However, as shown here, it is important to consider how connections are created in the task construction (e.g. the lines of segmentarity, the lines of rupture, and the lines of flight) between different concepts from mathematics and programming to promote sense-making and reasoning. Variation theory (e.g. Marton, 2015; Olteanu, 2016) in combination with the post-structuralist philosophical perspective (e.g. Deleuze & Guattari, 1987, Freitas, 2012) shows that understanding the features of tasks as lines of flight that erupt, twist, and fold their way into new dimensions due to the use of different patterns of variation provides a new framework for theorizing about the relationships between tasks, sense-making, and reasoning.

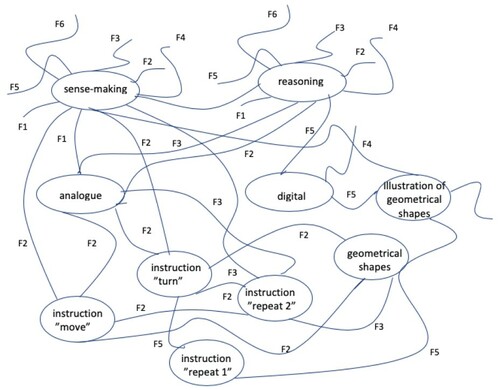
The features discerned in students’ reasoning and sense-making consist of a flow of lines diverse in form and distributed across a task assemblage (Figures 6 and 9). These lines are almost always recaptured and tied back to aspects of the content of both mathematics and programming, looping back to infuse new energy into the students’ reasoning and sense-making. The triggers for rupture (Figure 6) can be minor and seemingly inconsequential, since teachers explain concepts and instructions in ways that allow students to reason about what they are doing. Reasoning and sense-making are closely interrelated and are the foundation for supporting differences and heterogeneities. In line with Klein et al. (2006), in this study sense-making is a continuous effort to understand connections in order to anticipate their trajectories and act effectively. Additionally, the results indicate that these connections are generated by: recognition of similar attributes between mathematics and programming; relationships between concepts used in mathematics and programming; profiling the characterization of blocks to construct geometrical shapes; comparing variables, blocks, angles, and different geometrical shapes; explaining the link between concepts in mathematics and in block-programming; laddering one piece of information to the next one; and verifying by inputting the instructions used in block-programming to see which geometrical shape is drawn in Scratch.

Resnick et al. (2009) specified that Scratch allows students to make and test conjectures, thereby promoting mathematical reasoning. The results presented here indicate which features help promote students’ mathematical reasoning. These features are: selecting blocks of interest with which to construct geometrical shapes; exploring the meaning of different blocks used to construct geometrical shapes; reconfiguring different blocks based on the properties of geometrical shapes; filtering by changing a set of blocks based on specific conditions of geometrical shapes; encoding by changing how the blocks are represented in a script and their significance for constructing geometrical shapes; abstracting, i.e. adjusting the level of abstraction by using more or less detail; and connecting to highlight associations and relationships between different blocks in order to construct geometrical shapes. These features of students’ reasoning created multiple lines of flight that interacted with the lines of flight of students’ sense-making (Figures 6 and 9).

An additional result of the present study is that several lines of rupture in students’ reasoning and sense-making in programming create new and alternative approaches, for example, the use of analogue programming by utilizing instructions in block-programming in new, practical forms (Figure 6). However, if the program consists of several instructions in which repetition is used to create difference at the level of idea (Figure 7), the students will construct new lines of flight connected to digital programming to make sense of and reason about geometrical shapes and the use of the exterior angle in drawing these shapes (Figure 9).

7. Conclusions

This section summarizes the results to highlight some of the most important points and practical implications for teachers. The present results indicate that particular conditions need to be in place to promote mathematical reasoning and sense-making using Scratch as a pedagogical tool: (a) thoughtful teacher interventions if lines of rupture are created when experiencing intended critical aspects; (b) creating rhizomatic tasks; (c) identifying critical aspects; and (d) using patterns of variation. The dynamic of tasks as forming a rhizomatic assemblage contributes to closely interrelated reasoning and sense-making in mathematics and programming. Applying the concept of the rhizome when creating the tasks necessarily entails understanding the different lines that form the rhizome as an entanglement of lines in constant interaction. Lines of rupture expose the limitations imposed by the students’ experience, revealing new ways of thinking and acting.

Simply exposing students to mathematical topics by using tasks is not enough to improve their sense-making and reasoning, because the students need to develop their own mathematical reasoning and sense-making through collaboration and communication. For the teachers to communicate programming connected to mathematics, it is necessary to know how to create programs in Scratch to be able to teach this to the students and identify critical aspects that can form the basis for developing students’ reasoning and sense-making in mathematics and programming. Consequently, the teachers need to develop their own reasoning and sense-making about core computational concepts such as iteration and conditionals, and they need to use important mathematical concepts such as coordinates, variables, and random numbers.

A fundamental implication of the rhizomatic research perspective is to encourage the mathematics education community to create an increasing number of opportunities for dialogue that facilitates new ways of thinking about reasoning and sense-making in mathematics. While existing research in the area of variation theory often focuses on variation, we highlight repetition as a difference at the level of idea. This provides a way to overcome the limits of what can be discerned. In other words, a rhizomatic perspective, with its lines (of segmentarity, rupture, and flight) and assemblages, reveals a dynamic reality in the classroom that needs to be open to repetition, to the unexpected, and, consequently, to reworking the critical aspects to which students should be exposed.

Acknowledgements

We would like to thank the teachers who participated in this study – thank you for sharing your experiences and thoughts with us.

Disclosure statement

No potential conflict of interest was reported by the author.