Clash of cultures? Exploring students’ perceptions of differences between secondary and tertiary mathematics education

Abstract

Research has identified several aspects that influence students’ transition to mathematics studies at university, but these aspects have often been studied separately. Our study contributes to the field's understanding of the transition between upper secondary and university mathematics by taking a multifaceted perspective not previously explored. We analyse experiences and attainment in mathematics of 154 engineering students with respect to known aspects of this transition, and our results show that it is important to consider several aspects together in order to understand the full complexity of the transition. It is revealed that students with previous experiences of university studies, when compared with new first year undergraduates, perceive a larger difference between studying mathematics at the upper secondary level and university. Our results also show that the engineering students enrolled in distance programmes experience larger differences between secondary and tertiary levels than engineering students enrolled in campus programmes. Furthermore, our analyses show that students’ success in mathematics is related to their perceptions of the rift experienced in the transition. In all, our results highlight the importance of taking a student perspective in the development of explanatory and useful models of students’ transition between upper secondary and university mathematics.

KEYWORDS:

• Campus and distance education
• student attainment
• student perspective
• transition

1. Introduction

The transition from secondary to tertiary mathematics education is widely recognized as being connected with various inherent obstacles for students. These obstacles can be seen as caused by different cultures at the two educational stages (Jablonka et al., 2017), and may thus result in ‘culture clashes’ for the students. That is, a culture clash in the context of our study refers to any type of conflict or incompatibility between secondary and tertiary levels concerning values or practices in mathematics education. The differences between secondary and tertiary mathematics education making up a potential culture clash can concern mathematical aspects (e.g. Rach & Heinze, 2017), didactical aspects (e.g. Thomas & Klymchuk, 2012), and social aspects (e.g. Pampaka et al., 2012). Although previous studies have identified all these aspects, they have largely been examined separately (Jablonka et al., 2017), and research that studies the transition from a more comprehensive student perspective is scarce (cf. Jablonka et al., 2017; Pampaka et al., 2012). Therefore, this study includes a broad set of aspects previously identified in research, and investigates for which (if any) of these aspects students perceive a greater contribution to the culture clash.

Even though students perceive a culture clash, this does not automatically imply negative consequences of the transition. On the contrary, many students regard the big change ‘as a positive part of growing up’ (Pampaka et al., 2012, p. 1067). Whether a culture clash becomes a problem or not depends a lot on student attitude and approach to learning, as well as on previous knowledge (Bengmark et al., 2017; Maciejewski & Merchant, 2016; Pampaka et al., 2012; Thomas & Klymchuk, 2012). Therefore, it is important to examine which aspects of the culture clash, and how they are perceived, influence students’ transition more, but such studies are very rare. Our study addresses this issue by investigating relations between students’ perceptions of the culture clash and their results in first year undergraduate mathematics courses.

By adopting a multifaceted perspective on students’ perceptions of the culture clash related to the transition between upper secondary and tertiary mathematics studies and comparing perceptions with course results, our study may contribute to a deeper understanding of potential causes and effects of student perceptions of the transition.

2. Background

In relation to the focus of our study, there are three lines of previous research that we here describe as a background and starting point. Firstly, we present research concerning the transition between secondary and tertiary mathematics education. Secondly, we describe research about potential effects on students’ academic attainment at the beginning of their university studies. Finally, we include research on distance education, as it stands to reason that there could be major differences in the experiences of the transition by students that are enrolled in the distance as opposed to campus education (e.g. due to variances in teaching formats or modes of interaction).

2.1. Transition to university mathematics

The transition problem was identified as early as the 1960s. Now, half a century later, with widening participation in tertiary education seeing about half the yearly cohort of leavers from secondary education entering university, the nature of the problem has not become less complex (e.g. Jablonka et al., 2017). Various aspects of the transition problem, mathematical as well as social and didactical/pedagogical in their nature, have been studied, and the methods have been diverse, ranging from theoretical analyses to empirical studies of student experiences and observational studies of classroom teaching.

From a social/personal point of view, starting as a new first year undergraduate at university can be a tumultuous period (e.g. due to leaving home, family, and friends to move to a new city). Personal responsibilities are increased, including for financial obligations as well as for establishing new social connections. Particularly the anonymity that may be experienced in university environments can be daunting, and building a sense of belonging has been shown important for the transition to pass smoothly (Clark & Lovric, 2008; de Guzmán et al., 1998).

Personal responsibility also differs with respect to the organization of learning, from more controlled and monitored at upper secondary to independently planning and evaluating own learning at university (de Guzmán et al., 1998; Thomas & Klymchuk, 2012; Wingate, 2007), and this is a difference that students easily identify in the transition (Pampaka et al., 2012). University studies not only include a higher autonomy, but also require different learning strategies, which are subject dependent (Kajander & Lovric, 2005; Rach & Heinze, 2017; Wingate, 2007). Many of the issues identified in literature are general in nature, and in all university subjects a higher degree of autonomy is expected from the student. For example, students experience time management issues and a need to improve reading skills, note taking and source criticism skills.

Other pedagogical/didactical aspects of the transition relate to differences in teaching, for example, de Guzmán et al. (1998) highlight a common belief among university teachers that it is enough to know the subject to teach it. Furthermore, they show that the most frequently practised teaching method at university level is the lecture, where students are expected to take notes while the teacher talks. At the same time, Pampaka et al. (2012) show that students’ experiences of the transition become less positive the more teacher-centred the pedagogy is.

By grouping existing research findings regarding the transition using the scale of levels of didactic codetermination (e.g. Artigue & Winsløw, 2010), Gueudet et al. (2016) are aiming at making phenomena and blind spots visible. One of their findings was that even though much research points to phenomena at the more general level, it is also necessary to study the transition at a more subject-specific level.

Others have also found that major aspects of the transition are related to the subject in focus, and to students’ encounter with various mathematical discourses. Several studies have shown a mismatch between university teachers’ expectation of prerequisites and the actual prior knowledge of first year undergraduates. One issue that is addressed in previous research is students’ lack of experience of proofs, mathematical rigour, and deductive reasoning (e.g. Brandell et al., 2008; Leviatan, 2008; Rach & Heinze, 2017; Thomas & Klymchuk, 2012). This addressed expectance of emphasis on proof and rigour at universities, instead of procedures and informal reasoning common at the upper secondary level, also implies differences in the mathematical discourse. That is, what counts as mathematics at the two levels can vary (e.g. Gueudet, 2008; Jablonka et al., 2017).

The different aspects are intertwined, and the transition is a complex phenomenon, as discussed in previous reviews by de Guzmán et al. (1998) and Gueudet (2008), and more recently by Bergsten et al. (2015) and Gueudet et al. (2016). However, few studies have considered this complexity, opting instead to focus on one or two aspects (Jablonka et al., 2017). Addressing this limitation, Bergsten et al. (2015) contributed with a structural analysis of previous research and literature reviews in the area, and they suggested a classification into eight categories of aspects. Within these categories, aspects are both general and more mathematical in nature, that is, some aspects are experienced by all students in the transition to university, independent of their subject of study, while others are specific to mathematics. Bergsten et al. (2015) referred to their categories as dimensions of the transition between upper secondary and university, and labelled them:

1. Completion and recruitment

2. Curriculum misalignment

3. Changes in level of formalization and abstraction

4. Importance of mathematics for various career paths

5. Different teaching formats and modes of assessment

6. Differences in pedagogical awareness of teachers

7. Change in expected learning habits and study organisation

8. Differences in ‘atmosphere’ and sense of belonging

Five of these dimensions (2, 3, 5, 6 and 7) were elaborated further upon by Jablonka et al. (2017) and were later used by Anastasakis et al. (2020). These five dimensions are concerned with discrepancies in the criteria for what is considered as mathematics at upper secondary and tertiary levels. Jablonka et al. (2017) analysed students’ awareness of actual changes with respect to these five dimensions. Their results show that students focus on a wide range of aspects of mathematical texts when they both recognize and mis-recognise what is specific to the mathematics discourse. In Anastasakis et al. (2020), the five dimensions were used to categorize types of difficulties students encounter during a mathematics course. Their findings were that a majority of student difficulties were related to formalisation and curriculum. They suggest that difficulties encountered by students can be seen as being derived from the actual structural traits of upper secondary school and the university respectively.

Another study that does consider several aspects when exploring students’ perception of the transition is Pampaka et al. (2012). Their paper includes a thorough review of relevant previous research, from which they note an absence of a robust instrument for quantitative measures of student experiences of the transition. Thus, a main focus in their study was to develop and validate an instrument to measure the perception. However, their focus was on more general aspects of the transition, such as pedagogy together with social and personal aspects, and so they did not include subject-specific differences such as curriculum mismatches.

As mentioned above, general aspects of the transition refer to differences between upper secondary and university that are not subject dependent, such as completion and recruitment, and differences in ‘atmosphere’ and sense of belonging (dimensions 1 and 8, above), whereas mathematical aspects refer to subject dependent aspects, such as curriculum misalignment and changes in level of formalisation and abstraction (dimensions 2 and 3, above). We agree with Jablonka et al. (2017) and Pampaka et al. (2012) who argue that there is a need for studies taking a holistic approach, particularly through more quantitative analyses of student experiences. For such comprehensive studies, it is particularly relevant to include both the more general aspects as well as the mathematical aspects of the dimensions.

In our study, we take all the eight dimensions identified by Bergsten et al. (2015) as our analytical framework for investigating the student perceptions of the transition and the relation between general and mathematical aspects. Using all these dimensions together in empirical analyses is a type of multifaceted approach previously unseen in this research area, where focus has been on either mathematical aspects (Anastasakis et al., 2020; Jablonka et al., 2017) or on more general aspects (Pampaka et al., 2012). Though robust and validated, the instrument of Pampaka et al. (2012) does not cover all dimensions, and it is thus not used in this study. Instead, we developed a survey based on all eight dimensions in order to cover all the various characteristics of the transition.

2.2. Effects on students’ academic success in first year university mathematics

Many researchers have found that a student’s level of attainment in their prior studies in mathematics is one of the strongest predictors of how well they will succeed in their mathematical studies at university (e.g. Bengmark et al., 2017; Laging & Voßkamp, 2017; Liston & O’Donoghue, 2009). Furthermore, results in aptitude tests, such as the American ACT/SAT scores, are among the strongest predictors for students’ success at university (Robbins et al., 2004). Another strong predictor is the socio-economic background of students (e.g. OECD, 2003).

Other aspects important for how well students will carry through their university studies in mathematics may include the type of learning strategies they adopt, how motivated they are, and their attitude towards, or beliefs about, mathematics as a subject. However, research results differ regarding the significance of the various aspects to the degree of success. According to students and teachers themselves, motivation is the most important success factor (e.g. Anthony, 2000). This is in line with empirical results showing that achievement motivation, optimism and academic self-efficacy are strong predictors for students’ success (Chemers et al., 2001; Robbins et al., 2004; Tossavainen et al., 2019). Also, Code et al. (2016) stress the importance of beliefs and attitudes towards mathematics in their introduction of an instrument for measuring expert-like views and dispositions among undergraduate mathematics students. Kizito et al. (2016) note that students’ perceptions of their workload appeared to be the factor with greatest impact on students’ success. At the same time, Robbins et al. (2004) stress that academic self-efficacy and achievement motivation are not as strong predictors as grades previously obtained. Furthermore, both Liston and O’Donoghue (2009) and Bengmark et al. (2017) show that beliefs about mathematics on their own have a low correlation with student results at university. However, according to Bengmark et al. (2017), although self-efficacy, motivation type, study habits, and beliefs about mathematics do not function as individual predictors, these aspects, when considered together, constitute a strong predictor of student success. Furthermore, Bengmark et al. (2017) emphasize that although self-efficacy and a productive motivation cannot be used as an initial predictor of success, it is important for students to develop these qualities during their first year at university, as these characteristics were found to be closely linked to students’ course results after one year.

Different types of study habits have been examined in previous research. According to Bengmark et al. (2017), study habits relate weakly to results, but seem to be more important for weaker students. One specific aspect of study habits to take into account is surface versus deep learning. Neither Liston and O’Donoghue (2009), nor Kizito et al. (2016) found any significant correlations between study approach and attainment in mathematics courses. Similar results were presented by Laging and Voßkamp (2017), who found no significant correlations between students’ mathematical performance and their self-regulated strategies, which included memorizing and elaboration strategies. On the other hand, Maciejewski and Merchant (2016) found significant correlations between performance and self-regulated strategies. However, the type of correlation was dependent on which year students were in. For first year undergraduate mathematics students, a deep approach resulted in slightly better results, while a surficial approach did not correlate negatively with the results. For students in third/fourth year mathematics courses, the result was reversed. At this level, there was a significant and strong negative correlation between a surficial approach and students’ achievements, while a deep approach did not have a significant effect on students’ results. The nature of mathematics and how it was presented to the students was discussed as a reason for these results: First-year mathematics courses focused on calculations and procedures, while advanced mathematics courses emphasized theorems, proofs, and rigour. This can be compared with other studies discussed above, that university mathematics in general is assumed to be more rigorous and based on proofs and proving than upper secondary mathematics.

To overcome the problem with low pass rates, many universities offer a variety of preparatory courses in order to help students in the transition to university mathematics. However, the effectiveness of such courses has been shown to vary. Engelbrecht (1997) showed that the performance of students who had participated in a preparatory course was significantly better than the performance of the control group. Contrary to this finding, Lagerlöf and Seltzer (2009) found relatively little evidence of positive effects on students’ results following a preparatory course. Sierpinska et al. (2008) point out that often the students are not satisfied with the courses. The fast pace and inadequate assistance from the lecturers are some of the things they quote as sources of student frustration. Also, Maciejewski et al. (2021) emphasise the lack of success with this type of courses when they examine affective and dispositional factors of the students and where the results indicate, among other things, that self-confidence is an important indicator of whether the student will succeed or not in mathematics studies. Based on the notion of rite of passage, Clark and Lovric (2008) have the aim to sort out research results concerning the transition. They conclude, from this point of view, that some of the preparatory courses do not help the students, actually quite the opposite – the way the courses are given lowers student motivation and self-confidence. As emphasized by Greefrath et al. (2017), it is difficult to draw any general conclusions about the benefits of this type of arrangement.

Few studies have focused on pinpointing a connection between how students experience their upper secondary school to university transition and their level of success in first year university mathematics. Pampaka et al. (2012) studied mathematics students’ perceptions of the transitional experience and followed the students during their first year. Their results did not show any clear results concerning a connection between the transitional experience and the study results, while Jablonka et al. (2017) identified such a connection. These two papers examined the transition between upper secondary school and university from two different perspectives, which is one possible reason for their different results. The former studied the transition on a more general level, such as social aspects, and the latter from a more mathematics-specific perspective concerning what is considered mathematics. The contribution of our paper is a study of both general and mathematical aspects of the transition in relation to the students’ learning outcomes.

2.3. Distance education in mathematics

Distance education, in particular online education, is an area that has grown rapidly and intensively in the last decades. There can be many advantages of this form of education, an obvious example being the opportunity for more flexible modes of study. Obvious disadvantages also exist. One of the difficulties, which is often highlighted, is the lack of face-to-face meetings between teacher-student and student-student (e.g. Engelbrecht & Harding, 2009). As teaching online to some extent presents different challenges compared to teaching on-site, it is of interest to investigate which success factors exist for online education, not least concerning the teaching of mathematics.

Much research on online mathematics education compares student results on courses given as a regular campus course as opposed to being given as a pure distance course or one in blended form (a hybrid but still with students at distance). Vilardi and Rice (2014) found that campus students performed better than students attending the pure distance or blended form of the course when comparing the distribution of grades for around 14,500 students, who attended or had taken a course in Precalculus Algebra. Thompson and McDowell (2019) could not identify any significant differences in the final grades when they examined the results from a preparatory course given at an undergraduate university college in the three different formats. Jones and Long (2013) compared grades between students participating in a post-secondary mathematics course given in an on-site format and in an online format. The course was given on ten different occasions. The first three times the course was given, there was a difference in grades in favour of the campus students, but on the seven subsequent occasions, no difference could be detected. A possible explanation offered for the initial difference in grades when the course was new, was that the teachers involved in the course did not coordinate their way of grading. Ashby et al. (2011) compared students’ results on a Development Mathematics course, and they discovered that students on the blended form of the course had significantly lower results than students on both the campus version and the pure distance version of the course. However, further analyses were carried out in which attrition rates were considered. When including only students that completed the course, the analyses showed instead that it was the campus students who had the poorer performance. These examples of studies exhibit a complex variety of results, possibly stemming from different ways of handling attrition rates or differences in the definitions of the different course formats.

There are other aspects of online mathematics education worth examining. The goal of the study conducted by Thompson and McDowell (2019) was, in addition to investigating if there were differences in the course results, to get answers about how students experienced the course in terms of, among other things, level of satisfaction, existing obstacles and engagement. The results showed that students were generally satisfied with both the blended and the pure distance variant of the course. However, the difficulty of getting distance collaboration in groups to function properly was raised. The students also missed not having real-life meetings with the teachers and the other students. This absence of face-to-face meetings is stressed in several studies. Reju and Jita (2018) examined students’ experiences of instructional delivery of distance and online learning of undergraduate mathematics and how they can be explained. A shortcoming they identified was that the students experienced a lack of access to direct contact with the teachers. This lack was also considered to have contributed to a failure in students to understand the abstract nature of mathematics; the course material had not been simplified enough for the students to be able to understand it fully on their own. As a result of the study, high quality of course material and access to support from teachers are emphasised and deemed crucial for online distance courses to work well. The importance of how course material is presented was also noticed by Lee (2014). This study is about an online course in mathematics for preparatory teachers. The level of satisfaction in online learning was examined with respect to the human factor (the teacher), course structure, and technology. Important aspects, contributing in a positive way to the students’ satisfaction with the course, were that the course was presented with clear instructions and that the teacher had good up to date knowledge about the course content.

Regarding the level of engagement of distance students, Galligan et al. (2012) conclude from their study in conjunction with a previous on-campus study of theirs (Loch et al., 2011), that level of engagement is lower among students participating from a distance than among campus students, and the reason for this reduced level of engagement may be that the campus and distance student groups have disparate demographic characteristics, and the distance students could therefore have additional commitments taking their time. It is also noted that when it comes to courses online, while the teacher is still central, student engagement is of increased importance as they need to take a greater responsibility for their own learning in order to succeed. Interaction with the teacher and with other students is also highlighted as key ingredients for a successful result. The aims of Galligan et al. (2012) were to investigate if there is technology available that can facilitate bidirectional communication for distance students and if so, how it would affect student interaction and engagement. More precisely, they provided their online students with a netbook tablet PC for use during the studies. It turned out that the students appreciated the technology and considered it valuable for work on assignments and in the interaction with the teacher.

This summary of previous research illustrates the difficulty in drawing conclusions concerning clear, direct effects on course results in distance as opposed to campus education. There are somewhat more consistent results on how students experience their education, in particular regarding the perception of human contact as a major distinction between distance and campus education. These differences in students’ experiences due to teaching format could thus affect how students experience the transition to tertiary education, and distance students have not been addressed explicitly in previous ‘transition-studies’. We examine if there are differences between distance and campus students concerning their experience of the transition, including how they experience aspects of mathematics, to see if there are discernible effects beyond the more general aspects of the education format discussed above.

3. A research framework

The transition to tertiary mathematics education is a complex phenomenon, which has been made clear through the research background. In particular, previous research has highlighted the breadth of this phenomenon through the eight dimensions of the transition (Bergsten et al., 2015). In this study, we examine all these dimensions concerning how students perceive them when they have transitioned to tertiary mathematics education. For this purpose, we rely on a conceptual framework (cf. Lester, 2005) to provide a structure for conceptualizing and designing this study, while at the same time allowing for future analyses from more specific perspectives, such as more in-depth analyses of the social dimensions of the transition, or the cognitive or mathematical dimensions.

At the core of our study is how students perceive a potential culture clash in the transition to university mathematics. Therefore, we here address perspectives on the core concepts of the study: culture, culture clash, and students’ perceptions of a culture clash. In addition, we discuss issues of cause and effect concerning student perceptions, since we are interested in possible relations between how students perceive a potential culture clash and their learning outcomes.

A general definition of the concept of culture is ‘the set of values, conventions, or social practices associated with a particular field, activity, or societal characteristic’ (Merriam-Webster online dictionary). Based on this definition, mathematics education at university level can be seen as one type of culture. Thus, the many differences between secondary and tertiary mathematics education, as described in the background, can be said to create two different cultures. Some of these differences concern more general aspects of social practices, such as different degrees of autonomy and personal responsibility. Other differences concern aspects of values or conventions specific to mathematics, such as what counts as mathematics.

Several researchers have described a common phenomenon concerning relations between the different cultures in the transition from secondary to tertiary mathematics education. Leviatan (2008) describes this as a ‘cultural gap’, Jablonka et al. (2017) describes a ‘discontinuity’ in the transition, and Gueudet (2008) describes that shifts from secondary to tertiary levels can create ‘ruptures’ (p. 245). Common for these descriptions of the transition is that they describe something that is not smooth or gradual, but more sudden or abrupt. From the perspective of a student, such an experience could be described as a potential culture clash, in the sense of a conflict or incompatibility between cultures. This potential clash thus addresses the situation when students perceive that their existing values or practices from secondary mathematics education are (very) unlike the values or practices in university mathematics education. The range of differences perceived determines the severity of the clash. Thus, students’ perceptions of differences between secondary and tertiary mathematics education can be used to describe if, how, and to what extent they have experienced a culture clash.

What can cause this type of culture clash? Since the clash concerns conflicts between cultures, it is distinct properties of student backgrounds and aspects of the present situation that cause a culture clash. A variety of such properties and differences between them exist, as described in the research background of this paper. They can be placed at different levels in the scale of levels of didactic codetermination (Artigue & Winsløw, 2010, p. 52 as quoted in Gueudet et al., 2016, p. 17):

1. Subject, e.g. Quadratics

2. Theme, e.g. ‘Polynomial equations’

3. Sector, e.g. ‘Polynomials’

4. Domain, e.g. Algebra

5. Discipline, e.g. Mathematics

6. Pedagogy, e.g. Local teaching principles

7. School, e.g. Teaching institution

8. Society, e.g. State, ministry, region

9. Civilization, e.g. ‘Western culture’

The different dimensions of the transition that are our centre of attention can be placed primarily on levels 5–7. Moreover, we examine different aspects of students’ background, in particular such aspects that are more general in the university culture (levels 6 and 7) and such aspects that are more specific for mathematics (level 5).

What effects can a culture clash have on students’ academic success? More generally, this question can be related to perspectives in person-environment fit theories. Such theories have also been used in earlier research on the transition between secondary and tertiary mathematics education, where a starting point is that ‘unsuccessful learning processes indicate an inappropriate fit between variables of the involved learner and the learning environment’ (Rach & Heinze, 2017, p. 1345). A culture clash can be seen as an example of such an ‘inappropriate fit’. Which aspects of a culture clash that are most important for learning processes is an empirical question we address in the present study.

4. Purpose and research questions

As shown in the background section, the ‘transition problem’ is well known and has been studied extensively, but the various aspects of the transition have mostly been addressed separately in empirical studies, concentrating on either mathematical aspects (Anastasakis et al., 2020; Jablonka et al., 2017) or more general aspects (Pampaka et al., 2012), but not both. Practically no previous research has examined students’ perceptions of the transition from a more holistic perspective, including all known obstacles in the transition that could lead to potential problems. Nor has previous research examined students’ perceptions of the transition with respect to various teaching formats, particularly regarding distance education. In addition to our comprehensive study of all known obstacles in the transition, we also examine the transition in relation to several other issues that further add to the holistic perspective. In particular, we analyse the backgrounds of students before they enter university, properties of the study organisation at university (campus or distance education), and students’ success in their first university mathematics course. The background section above showed that only few studies have examined specifically the relation between students’ perception of the transition and their success in tertiary education, both generally and mathematically. Furthermore, there are no previous studies considering both general and mathematical aspects of the transition in conjunction with student attainment. By taking this holistic approach and relating to students’ attainment in mathematics courses at university, our study is a novel contribution to the research field.

The purpose of our study is to gain a deeper understanding of reasons for, and effects of, various perceptions of the transition from upper secondary to university mathematics studies. Within this purpose, the study has an exploratory character since no previous empirical study has included the many dimensions of the transition from a student perspective. The exploratory nature allows for the creation of more elaborate bases for future research, for example concerning what needs to be clarified through more empirical research. The purpose is realized by analysing empirically within which dimensions there is a greater sense of a culture clash, as well as, if, and in what ways, the culture clashes experienced relate to general aspects of the transition or to specific mathematical aspects. Moreover, it is analysed how experiences differ between students studying on campus and at distance, revealing potential effects of a social and organizational aspect in the transition. Finally, the relation between a perceived culture clash and attainment in mathematics at university is analysed. More specifically, the following research questions are addressed:

RQ1: How is student background related to differences in the perceived culture clash?

RQ2: Which distinctions exist in the perceived culture clash between students studying on campus and at distance?

RQ3: What are the relations between the perceived culture clash and success in mathematics at university?

5. Method

The focus of the study is to analyse the overall picture of students’ perceptions of the upper secondary school to university transition with respect to different dimensions of the transition as defined by Bergsten et al. (2015). A questionnaire was used to capture students’ perceptions of the different dimensions. The use of a questionnaire makes it possible to collect data from many students, which in turn allows for quantitative analyses of patterns in perceptions within each dimension. What follows is a description of the construction of the questionnaire and how it is used for data collection, together with a subsequent presentation of the analyses and how these relate to the research questions.

5.1. The questionnaire

In addition to the eight dimensions of the transition between upper secondary school and university defined in Bergsten et al. (2015) and Jablonka et al. (2017), a dimension concerning the transition in general was added. This ninth dimension was used to capture students’ overall and unspecified experience of a potential gap between studying mathematics at upper secondary level and at university. Thus, the questionnaire takes into account nine dimensions.

In total, the questionnaire consisted of 56 items representing the nine dimensions. See Table 1 for examples of questionnaire items for the different dimensions and see Appendix A for a full list of questions on the questionnaire. Four to nine questionnaire items were created for dimensions 1-8, based on various representative aspects of the dimensions. In order to identify aspects of each of these dimensions, the research referred to in Bergsten et al. (2015) and Jablonka et al. (2017) when defining the dimensions was reviewed. In some previous research, specific examples were given of questions used for students. Versions of these questions were used as items in our questionnaire, for example, the item ‘The university mathematics courses cover more in a shorter period of time than do the mathematics courses at upper secondary school’ (dimension 5, different teaching formats and modes of assessment) is a version of the student question ‘The pace of the course is faster/slower/same at the university’ in Pampaka et al. (2012, p. 1071). In other studies, examples of student opinions or specific critical aspects were identified, which we used as a basis for constructing items. For example, Kajander and Lovric (2005) found that students’ experiences of their high school mathematics correlated with their success in university mathematics (dimension 1, completion and recruitment). This is reformulated into the following statement for students to consider ‘Those who are happy with the mathematics teaching in upper secondary school are more successful in university mathematics’. Another example is the item ‘Strict mathematical proofs are required in mathematics courses’ (dimension 3, changes of level of formalisation and abstraction), that is grounded in students’ perception that they are expected to handle proof and proving from the beginning of their university studies (Brandell et al., 2008). When specific aspects of students’ perceptions were not covered with a explicit examples by any study, items were designed based on the discussions in the papers concerning these aspects of the dimensions. For example, regarding formalisation and proof (dimension 3) it is discussed that there is a jump from empirical to abstract mathematics between upper secondary and university mathematics, including requirements of rigour and to make connections and abstractions (Nardi, 1996). This is formulated into the item ‘In mathematics it is acceptable to use trial and error to obtain solutions, there is no requirement to give complete justification’. Answers to the items were given either on a five-point Likert scale (L) (from strongly disagree to strongly agree) or a five-point scale capturing the difference between upper secondary and university (us-u) (much more at upper secondary/ … /equal/ … /much more at university). ‘Don’t know’ was always a response option.

Table 1. Examples of items capturing the dimensions, including answer format (L for Likert-scale and us-u for scale of differences between upper secondary and university).

Dimension	Example of questionnaire item (answer format)
1. Completion and recruitment	Those that are happy with mathematics teaching in upper secondary school are more successful in university mathematics (L)
2. Curriculum misalignment	I lack the arithmetic skills (calculations involving numbers) needed in the first mathematics courses at university (L)
3. Changes in level of formalisation and abstraction	In mathematics it is acceptable to use trial and error to obtain solutions, there is no requirement to give complete justification (us-u)
4. Importance of mathematics for various career paths	For some mathematics courses it is not clear how they are/were related to other courses or the study programme that I am/was doing (us-u)
5. Different teaching formats and modes of assessment	There is/was enough time in class for me to ask questions and discuss problems (us-u)
6. Differences in pedagogical awareness of teachers	Mathematics teachers use a variety of methods to explain when there is something a student does not understand (us-u)
7. Change in expected learning habits and study organisation	I need/needed to take the responsibility for my own learning in mathematics (us-u)
8. Differences in ‘atmosphere’ and sense of belonging	Mathematics teachers engage with each student individually (us-u)
9. General aspects of the transition	The transition to university mathematics was hard for me (L)

In addition to student responses with respect to the dimensions, background data on the participants was collected. Data included previous experiences of university studies in general and mathematics studies in particular, as well as grades on mathematics courses from upper secondary school and on the first mathematics course at university.

5.2. Participants

The participants were first year undergraduate engineering students and foundation year students from one Swedish university. The foundation year at the university is one year of supplementary pre-university mathematics courses giving students access to the engineering degree programmes the following year. Both groups of students start their programme of study in September, and their first mathematics examination is at the end of the first term in late October or early November. The academic year at the university is divided into four terms September–November, November–January, January–March, and March–June. Each term has ten weeks of which the final week is the exam week, and the penultimate week is generally set aside for revision. The content of each course is thus being presented over merely 8 weeks after which the students have the first summative assessment. Each course is being examined three times a year: at the end of the term in which it is given, at the end of the following term, and in a final resit examination in August. There are no resit penalties applied to grades, and there is no limit to how many times a student may attempt any given exam, but once an exam is passed, students are not allowed to resit in order to obtain a higher grade.

The questionnaire was distributed online to all 562 first year engineering students and foundation year students at the end of February, a few months after they had taken the exam in the first mathematics course of the study programme in which they were enrolled. This selection guaranteed a range in students’ background data. Considering the group of all students, it was on average around 6 years since they had studied mathematics at upper secondary school. All engineering students had taken mathematics courses 1–4 of the nationally governed mathematics curriculum at upper secondary level (cf. Swedish National Agency for Education, 2012). These courses cover topics in arithmetic, geometry, algebra, relationships and change, probability and statistics, and problem solving. Around 40% of the students had also taken mathematics course 5, which covers topics in relationships and change, discrete mathematics, and problem solving.

The various engineering programmes lead to either a Master of Science degree in engineering (5 years of study) or a Bachelor of Science degree in engineering (3 years of study). Because programmes differ, the contents and the length of the first mathematics courses also differ slightly. About 70% of the engineering students took a course in algebra during their first term, of either 3 credits or 7.5 credits (where 1 credit corresponds to 26.5 h of full-time study). The rest of the engineering students took a 7.5 credits course in single variable calculus.

Concerning the sizes of groups to which the questionnaire was distributed, the smallest group on campus had 33 students and the largest 162. Moreover, some of the programmes towards a bachelor’s degree are given both as a campus programme and as a distance programme. For the distance groups, the student numbers were between 32 and 116 students. An array of teaching methods was in use, ranging from traditionally lectured campus courses with tutorials or workshops to courses taught by ‘flipped’ classroom methods with recorded lectures and follow-up workshops. Most courses have some form of formative assessment, the forms ranging from online quizzes to traditional, tutor-marked hand-in exercises or in-class tests. Some courses use one of these methods of formative assessment while others use two or even all of them. Further, doing the formative assessment may on some courses result in bonus credit being awarded for the summative assessment, either in the form of extra points or exemption from doing an exercise on the exam.

To maximize the number of respondents, all student groups participating in a campus programme had a visit during class from one of the researchers in connection with the distribution of the questionnaire. Students were informed about the purpose of the study, and they also were allowed some time during the class to complete the questionnaire online. The response rate for the different programmes varied between 11% and 44%. In total, 154 students answered the questionnaire with a total response rate of 27%.

5.3. Analyses of data

First, the two scales in the questionnaire were quantified in order to create a measure of the severity of the perceived transition gap. The Likert scale was transformed to integers from 0 to 4, with 0 for strong disagreement and 4 for strong agreement; and the direction scale was transformed to an integer from −2 to 2, with −2 for much more at upper secondary and 2 for much more at university. Then, a measure of the severity of the transition gap perceived was constructed by normalizing the two scales in a linear manner. For the transformed Likert scale, integers were divided by four, and for the transformed direction scale, absolute value of the integers were divided by two. In this way, 0 represents no gap (0 on both scales) and 1 represents maximum gap (4 on the first scale and −2 and 2 on the second scale). As focus is on the existence of gaps, that is if students perceive any gaps, and in that case how ‘large’ a gap they perceive, the direction of the gap is not relevant in this study. In order to be able to say anything about students’ perception of the transition, an average, based on the normalized scale, was calculated for each dimension (except dimension 1 as explained below). That is, each student had a value for each of the dimensions, concerning how severe the student had perceived the transition to be regarding the content of that dimension. The scale can only be used in relative analyses, for example, to compare values between different groups or to analyse variations. That is, we cannot make any qualitative interpretations of the values in the scale, for example, concerning at what level a clash could be seen as negligible or severe. Future studies might allow for such interpretations, by connecting certain levels in the scale with other types of observations.

To decide if the questionnaire items really captured specific dimensions, Cronbach’s alpha was used for item analysis of each dimension. Values of the coefficient give estimates of internal consistency of each dimension scale. The output from the analysis also gives alternative values of Cronbach’s alpha if an item is deleted from the scale. A commonly accepted general principle is that an alpha of 0.7 or above is acceptable, but the value of alpha is a function of the number of items in a scale and tends to increase with the size of the instrument (Cortina, 1993). Cortina also shows that the more items that are included, the lower the value of the inter-item correlation. This implies that lower values of Cronbach’s alpha, such as alpha greater than 0.6, can be acceptable for a scale with a small number of items.

The results from the analysis suggest that the questionnaire is a reliable instrument for capturing students’ perceptions of each dimension, except for dimension 1 (cf. Table 2). Therefore, this dimension (completion and recruitment) was discarded in the analyses. Furthermore, one item has been deleted for a dimension when it has been possible thereby to increase the internal consistency, in particular to obtain alphas equal to 0.6 or above. Specifically, as seen in Table 2, one questionnaire item has been deleted for each of the dimensions 2, 6, 7, and 9 (see Appendix for specification of deleted items).

Table 2. Cronbach’s alpha with respect to the different dimensions.

Dimension (number of items)	Cronbach’s alpha, using all items	Increased Cronbach’s alpha, after deleting an item
1. Completion and recruitment (5)	0.44	0.55
2. Curriculum misalignment (9)	0.53	0.66
3. Changes in level of formalisation and abstraction (7)	0.68	–
4. Importance of mathematics for various career paths (5)	0.66	–
5. Different teaching formats and modes of assessment (7)	0.60	–
6. Differences in pedagogical awareness of teachers (8)	0.63	0.73
7. Change in expected learning habits and study organisation (6)	0.63	0.70
8. Differences in ‘atmosphere’ and sense of belonging (4)	0.65	–
9. General aspects of the transition (3)	0.58	0.60

To answer our research questions, we used statistical methods in the analyses of data. For RQ1 and RQ2 we compared different groups of students, where a t-test was used to find any statistically significant differences. For RQ3 we examined whether there was a relation between two variables through a partial correlation. Methods for each research question are described in more detail below.

In order to use parametric tests, such as the two-sample t-test and Pearson's correlation coefficient, data should be normally distributed. However, these statistical tests are known for being robust with respect to violations of normality. From the Central Limit Theorem, the t-distribution tends to a normal distribution for large sample sizes, thus the normality condition could be neglected if the sample size is at least 30 (Sokal & Rohlf, 1987). All our analyses do not fulfil this demand, but are not far from it, with a smallest sample of 24. However, de Winter (2013) shows that there are no objections to using a t-test with even very small samples, and that type I error rates (false positives) are relatively independent of degree of skewness. Type II error rates (false negatives) on the other hand, increase with increasing skewness (de Winter, 2013), which can affect our results in such a way that there might be significant perceptions of a gap between upper secondary and university mathematics that is not shown in the results. Pearson's correlation coefficient is also very robust with respect to violations of normality, where only the very small sample size of 5 gives some deviations from expected results (Edgell & Noon, 1984).

5.3.1. RQ1 – effects of student background

Two types of comparisons were done to answer the first research question, where we are able to distinguish effects of general experiences of university studies in the first comparison and effects of the different types of mathematics they meet in the second comparison. That is, we can separate more general issues from issues that are more directly connected to aspects of mathematics.

Firstly, two subgroups of the undergraduate students were considered, more precisely, two groups depending on whether it was their first time at university altogether (New Year 1, number of respondents N = 58) or if they had studied at university before but not mathematics (university experience, N = 27). We then expect any differences in their perception of the different dimensions would be primarily due to general experiences of university studies (both groups were new to university mathematics).

Secondly, the group New Year 1 (N = 58) and the group consisting of foundation year students without previous experience of university studies (Foundation Year, N = 24) were taken into consideration. In this case, both groups were new to university in general, but foundation year students studied upper secondary mathematics rather than university mathematics. Thus, we expect any differences in perceptions of a culture clash would be primarily due to the different types of mathematics they met.

For both these types of comparisons between subgroups, there can be other confounding factors concerning differences between the groups. As always, there can be unknown confounding factors and we do not have information from all participating students on possible confounding variables. However, we do know that there is some variation within each subgroup concerning factors such as previous experiences and achievement in mathematics and also which type of mathematics course they are enrolled in at university, including if it is on campus or distance. Therefore, it is likely that any observed effects stem primarily from the main difference between the groups, based on how the groups have been constructed.

5.3.2. RQ2 – differences between campus and distance education

To answer if there are any differences in students’ perceptions depending on whether they are enrolled in a campus version of a programme or a distance version, students were grouped according to mode of enrolment, and the groups’ perceptions were compared for each dimension. In this analysis, students were included from only three study programmes for which there exist parallel campus and distance groups within the same programme (Campus group, N = 34 and Distance group, N = 26). This selection was done to create maximum comparability between the groups.

As for RQ1, there can still be confounding factors, but also for the subgroups concerning campus or distance education, we do know that there is variation within each subgroup concerning students’ background. Therefore, it is likely that any observed effects stem primarily from the difference between campus and distance education.

5.3.3. RQ3 – relation to success in mathematics at university

To answer the last research question, we considered the group where information about the grades were available (not a compulsory information for the respondents to provide), N = 131. To conclude whether perception of the transition is related to results on the first mathematics courses at university, we calculated partial correlations. Because we know that attainment in previous studies is always a strong predictor of attainment in the first year of university mathematics (cf. the background section above), we control for prior study results when calculating the partial correlations. We use two variables to capture prior study results. One variable is created by taking an average of the course grades from the two last upper secondary mathematics courses taken by all participating students (i.e. courses 3–4 in the Swedish system). We also create a dichotomous variable that signals if a student has taken the highest course from upper secondary school or not (i.e. course 5 in the Swedish system).

The participating students have taken different mathematics courses as their first course at university. This type of data has its pros and cons. The benefit is that we will be able to determine if there is a more robust connection between a perceived culture clash and the success in a first mathematics course at university. However, we will not be able to detect any more nuanced results, for example, if the connection is only present for a certain type of mathematics course.

5.4. Validity and reliability

As described in the background, the dimensions are theoretical categorisations based on a review of empirical studies (Bergsten et al., 2015). Our study is based on the assumption that these dimensions capture essential aspects students face during the transition to tertiary education. The intention in our study is not to test the validity of the existence of these dimensions, but to use them as an analytical framework. As accounted for above, each item in our survey is a construct based on the studies referred to in Bergsten et al. (2015), and construct validity is based on face validity (i.e. the items composing our scale are logically relating to the underlying construct), guaranteed by full transparency through the entire questionnaire being provided in Appendix A.

To guarantee reliability (i.e. that our scales give precise measurements without large random errors), internal consistency is estimated by Cronbach’s alpha as described above. A high value of alpha for one dimension implies that every item in the specific scale for that dimension is measuring something similar to some of the other items in the same scale (Taber, 2018). The value of alpha is dependent on the number of items in such a way that it increases with the number of items. For example, a scale with 10 items with low inter-item correlation will give an acceptable value of alpha (DeCoster, 2005). A reliable way to increase the value of alpha is to remove items that show low inter-item correlation with other items in a particular scale. This is the procedure we adopted for some of the scales used to capture the different dimensions. Removing one item thus increases the accuracy of the calculated means for the particular dimensions. A high (or low) value of alpha for one scale in a survey does not affect the values of alphas for the other scales. Thus, omitting one of the scales (corresponding to one dimension) that was a part of the survey from our analysis does not affect the results concerning the other dimension.

6. Results

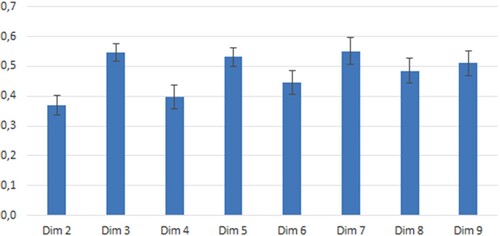
Figure 1 gives some basic descriptive statistics for the group of all students for each dimension. There is variation between the dimensions concerning the average level of a perceived culture clash. Those dimensions that show the highest levels of a culture clash are of mixed type, addressing mathematical issues (dimension 3), pedagogical issues (dimension 5) and social issues (dimension 7). Such variation also exists for the dimensions that show the lowest levels of a culture clash, and we cannot identify any clear pattern as to certain types of dimensions contributing more to a culture clash experienced.

Figure 1. Mean value for the level of a perceived culture clash in the group of all students (N = 154) for each dimension of a culture clash (95% confidence intervals marked).

6.1. Students’ background and their perceptions of a culture clash (RQ1)

When comparing students who had not studied at university before (New Year 1) and students who had studied at university before but not mathematics (Experienced students), differences exist in three of the dimensions (cf. Table 3). For all of them, the Experienced students perceived a higher level of a culture clash. The three dimensions are of mixed type concerning aspects of the mathematics content (dimension 2), aspects of usefulness (dimension 4), and organisational aspects (dimension 7).

Table 3. Difference in the level of a perceived culture clash between students who had not studied at the university before (New Year 1) and students who had studied at university before but not mathematics (Experienced students), for different dimensions of a culture clash.

	New Year 1			Experienced students
Dim	N	Mean	SD	N	Mean	SD	Diff
2. Curriculum misalignment	58	0.31	0.21	27	0.43	0.20	0.12*
3. Changes in level of formalisation and abstraction	58	0.52	0.19	27	0.55	0.17	0.03
4. Importance of mathematics for various career paths	58	0.30	0.24	26	0.44	0.25	0.14*
5. Different teaching formats and modes of assessment	58	0.50	0.18	27	0.53	0.21	0.03
6. Differences in pedagogical awareness of teachers	58	0.38	0.22	27	0.48	0.25	0.10
7. Change in expected learning habits and study organisation	58	0.49	0.27	27	0.68	0.26	0.19**
8. Differences in ‘atmosphere’ and sense of belonging	57	0.52	0.24	27	0.53	0.32	0.01
9. General aspects of the transition	58	0.49	0.26	27	0.58	0.25	0.09

*Statistically significant at level p < .050 .

**Statistically significant at level p < .010.

A variety of dimensions exhibiting significant differences between student groups is also evident (cf. Table 4) when comparing students who were studying university mathematics for the first time (New Year 1) and students who were studying upper secondary mathematics within the foundation year (Foundation Year). The foundation year students perceived a higher level of culture clash concerning mathematical aspects (dimension 2), aspects of usefulness (dimension 4), and aspects of teaching (dimension 6). At the same time, these students perceived a lower level of culture clash concerning atmosphere (dimension 8).

Table 4. Difference in the level of a perceived culture clash between students who were studying university mathematics for the first time (New Year 1) and students who were studying upper secondary mathematics within the foundation year (Foundation Year).

	New Year 1			Foundation Year
Dim	N	Mean	SD	N	Mean	SD	Diff
2. Curriculum misalignment	58	0.31	0.21	24	0.43	0.17	0.12*
3. Changes in level of formalisation and abstraction	58	0.52	0.19	24	0.55	0.21	0.03
4. Importance of mathematics for various career paths	58	0.30	0.24	24	0.45	0.25	0.15*
5. Different teaching formats and modes of assessment	58	0.50	0.18	24	0.58	0.23	0.08
6. Differences in pedagogical awareness of teachers	58	0.38	0.22	24	0.54	0.26	0.16**
7. Change in expected learning habits and study organisation	58	0.49	0.27	24	0.51	0.26	0.02
8. Differences in ‘atmosphere’ and sense of belonging	57	0.52	0.24	24	0.39	0.28	−0.13*
9. General aspects of the transition	58	0.49	0.26	24	0.47	0.26	−0.02

* Statistically significant at level p < .050.

** Statistically significant at level p < .010.

6.2. Perceptions of a culture clash among students studying on campus and at distance (RQ2)

When comparing students who were enrolled in a campus programme with students who were enrolled in a distance programme (see Table 5), there is no significant difference in the more specific dimensions, but a significant difference concerning the more general and unspecified aspects of the transition (dimension 9). The students enrolled in a distance programme experienced a higher level of culture clash.

Table 5. Difference in the level of a perceived culture clash between students who were enrolled in a campus programme or a distance programme.

	Campus students			Distance students
Dim	N	Mean	SD	N	Mean	SD	Diff
2. Curriculum misalignment	34	0.32	0.19	26	0.39	0.19	0.07
3. Changes in level of formalisation and abstraction	34	0.50	0.18	26	0.55	0.17	0.05
4. Importance of mathematics for various career paths	33	0.39	0.25	26	0.32	0.18	−0.07
5. Different teaching formats and modes of assessment	34	0.53	0.16	26	0.48	0.20	−0.05
6. Differences in pedagogical awareness of teachers	34	0.43	0.24	26	0.35	0.17	−0.08
7. Change in expected learning habits and study organisation	34	0.52	0.28	26	0.48	0.26	−0.04
8. Differences in ‘atmosphere’ and sense of belonging	34	0.48	0.24	25	0.51	0.21	0.03
9. General aspects of the transition	34	0.49	0.22	26	0.63	0.30	0.14*

*Statistically significant at level p < .050.

**Statistically significant at level p < .010.

6.3. Relations between a perceived culture clash and success in mathematics at university (RQ3)

In general, correlations between the level of a perceived culture clash and the grade from the first university mathematics course are weak (see Table 6). However, for two of the dimensions of a culture clash, the correlation is statistically significant and negative, with students perceiving a lower level of culture clash tending to have a higher grade in the first university mathematics course. These dimensions address more general and unspecified aspects of the transition (dimension 9) and a difference concerning the curriculum (dimension 2), which focuses primarily on a perception that prior knowledge from upper secondary school is insufficient to succeed at university mathematics.

Table 6. Partial correlation between the level of a perceived culture clash and the grade from the first university mathematics course, when controlling for the mathematics grade from upper secondary school. (Information about grades was not available for all respondents.)

Dimension	N	Correlation coefficient
2. Curriculum misalignment	131	−0.21*
3. Changes in level of formalisation and abstraction	131	−0.11
4. Importance of mathematics for various career paths	130	0.05
5. Different teaching formats and modes of assessment	131	−0.03
6. Differences in pedagogical awareness of teachers	131	−0.08
7. Change in expected learning habits and study organisation	131	−0.04
8. Differences in ‘atmosphere’ and sense of belonging	130	−0.02
9. General aspects of the transition	131	−0.23*

*Statistically significant at level p < .050.

**Statistically significant at level p < .010.

6.4. Summary of results

An overview of the results from all statistical analyses is given in Table 7. Based on these results, we can answer our research questions as follows.

Table 7. Summary of all statistically significant results concerning the degree of a perceived culture clash. Empty cells correspond to no statistically significant result.

	Comparing student groups (t-test)			Correlation
Dimension of culture clash	New Year 1 & Experienced students (RQ1)	New Year 1 & Foundation Year (RQ1)	Campus & distance (RQ2)	University grade (RQ3)
1. Completion and recruitment	Not included in analyses.
2. Curriculum misalignment	More clash for Experienced students	More clash for Foundation Year students		Negative correlation
3. Changes in level of formalisation and abstraction
4. Importance of mathematics for various career paths	More clash for Experienced students	More clash for Foundation Year
5. Different teaching formats and modes of assessment
6. Differences in pedagogical awareness of teachers		More clash for Foundation Year
7. Change in expected learning habits and study organisation	More clash for Experienced students
8. Differences in ‘atmosphere’ and sense of belonging		More clash for New Year 1
9. General aspects of the transition			More clash for distance students	Negative correlation

Concerning relations between student background and the perceived culture clash (RQ1), there is a variety of types of dimensions exhibiting significant differences between student groups. Overall, when compared with year 1 students, both experienced students and foundation year students show a larger perceived clash in their transition to mathematics at university.

Concerning differences in the perceived culture clash between campus and distance students (RQ2), there is a difference only concerning the more general aspects of the transition, for which distance students experience a larger clash.

Concerning relations between the perceived culture clash and success in mathematics at university (RQ3), there are significant correlations for two of the dimensions. The correlation is negative, with students perceiving a lower level of culture clash tending to have a higher grade in the first university mathematics course.

7. Discussion

A main idea in this study was to cover a broad range of aspects of potential differences between studying mathematics at upper secondary level and at university level. This has been done through analyses of student perceptions of the transition between these levels, based on nine different dimensions of potential differences between the levels.

In general, our results show that there are no particular aspects of the differences between studying mathematics at upper secondary level and at university that students perceive as being more major than others. These results highlight the importance of considering research results concerning a variety of aspects when trying to understand what happens in the transition. For example, it is not enough to focus only on differences in mathematics per se, but also pedagogical and social aspects are important to consider. Thus, among the levels of didactic codetermination (Gueudet et al., 2016) that have been examined in this study (primarily levels 5-7), there is no specific level that is clearly more important than the other levels. Without the more holistic approach of our study, which has been absent in previous research (Jablonka et al., 2017), this type of conclusion would not have been possible. Still, our current study primarily focused on levels 5-7, and it would have been relevant also to include questionnaire items focussing on the other levels, even if these have not been included in previous reviews of research literature (Bergsten et al., 2015). For example, questions could be asked about how students experience differences around more specific content in mathematics (levels 1–4), and furthermore, the same type of study could be carried out at other universities in order to capture more aspects of level 7 and also levels 8–9.

Besides these more overarching results, we also have more in-depth results concerning potential effects from students’ backgrounds on how they perceived the transition (RQ1), concerning potential effects from how the university studies are organized, as campus or distance-based studies (RQ2), and concerning effects students’ perceptions of the transition might have on the results in their mathematics studies at university (RQ3). These results are discussed below, where we focus on exploring potential explanations of the empirical results, which will be partly speculative, but based on analytical reasoning around the results. The purpose of these discussions is to create more elaborate bases for future research, for example concerning what needs to be clarified through more empirical research, which also highlights the limitations of this study.

7.1. Effects from students’ backgrounds (RQ1)

A maybe surprising result is that it is not new first year undergraduate students, but the students with former experience of university studies who perceive a larger difference between studying mathematics at upper secondary level and at university level. It would not be unreasonable to think that students with prior experience of university studies, albeit in other subjects than mathematics, would be more accustomed to some aspects of university studies and thereby perceive the start of their mathematics studies at university as less of a clash. However, our results show the opposite. The general experiences of university studies seem to constitute a larger perceived clash in the transition between upper secondary and university mathematics. The larger clash for this group of students includes a variety of aspects, such as differences in curriculum, in the importance of mathematics for coming careers and in learning habits.

One reason for perceiving a larger clash could be that a longer time has passed since these students studied mathematics at upper secondary level, when compared to first year undergraduate students. This may influence their memory, recollection, or perception of mathematics education at upper secondary level. Thus, time elapsed can contribute to the perception of a larger culture clash with respect to mathematics education, which may or may not reflect a ‘true’ difference between the upper secondary and university levels. Furthermore, a longer period of absence from mathematics studies may also yield a decrease in mathematical knowledge, which in turn could affect the perception of the mathematics curriculum at university. However, a connection between prior knowledge in mathematics and perception of the transition has been difficult to establish in previous studies (e.g. Pampaka et al., 2012). In addition, our results show that foundation year students, when compared to first year undergraduate students, perceive a larger curriculum misalignment, even though the foundation year students are studying mathematics from upper secondary level. It may be that also foundation year students have had a sabbatical from mathematics studies, in the same way as the students who have done other studies at university level, or maybe they have been out working for a few years, before they, through a foundation year, have decided to change direction in their studies. The hypothesis that the time between upper secondary school and university is an important factor can be tested empirically, but suitable data for this was not available for the students participating in this study. Suitable data for such an analysis might also not be available in all countries. When compared with many other countries, university students are older in Sweden (OECD, 2019). Therefore, there is more variation in Sweden concerning the time between upper secondary and university studies, which can produce results specific for the Swedish context.

By focusing on the foundation year students, it is possible to disentangle some relations between perceptions of content and of context. The foundation year students do not change from upper secondary to university mathematics concerning mathematical content but change the context in which mathematics is studied. Although the content is familiar, there could be changes in the ‘criteria for what counts as a legitimate mathematical activity’ (Jablonka et al., 2017, p. 69), which in turn could be perceived as a larger clash than a change of content. That is, first year undergraduates may be prepared for differences, in particular concerning content, and thus will not perceive these as large as foundation year students. Therefore, these results highlight the potential importance of student expectations when analysing their perceptions of the transition.

Furthermore, compared to new first year undergraduates, foundation year students perceive a larger difference in teachers’ pedagogical awareness, which can also relate to aspects of expectations. The difference concerning pedagogical awareness could be due to the fact that in the foundation year, it is university teachers that teach the upper secondary mathematics, and they might treat the mathematics in a different way than do the upper secondary teachers (e.g. it is known that university teachers sometimes think it is enough to know the subject without considering pedagogical aspects (de Guzmán et al., 1998)). First year undergraduates on the other hand, know that they will study new mathematics in a new context, and thus might not perceive a clash that deviates from their expectations.

Concerning a more social aspect of the context of mathematics studies, an interesting result is that previous experience of university studies does not seem to influence how students perceive their sense of belonging. At the same time, just as learning is subject dependent (Wingate, 2007), developing a ‘feeling that you belong’ and how the ‘atmosphere’ is perceived is likely also highly dependent on the subject and the context. This conclusion is strengthened by other parts of our results, as first year undergraduates in our study perceive a larger clash with respect to these aspects compared to foundation year students. The organisation of foundation year courses differs somewhat from how the courses on the engineering programmes are organised, although both are organised by the university. Foundation year students study several subjects as a cohesive group during the whole year, whereas the engineering students study some mathematics courses together and other specializing courses separately. In this way, it is reasonable that foundation year students see more similarities with their studies at upper secondary level concerning the atmosphere and sense of belonging in their group of peers.

7.2. Campus or distance-based studies (RQ2)

It is only with respect to more general aspects of the transition where any significant difference exists between campus students and distance students. In particular, there are no differences concerning the more social aspects, such as study organisation or sense of belonging, where it would not be unreasonable to expect to see a difference between these groups. The difference in a general perception could be due to people enrolling in distance studies having other circumstances in life (e.g. they have a family to consider, or they are working to support themselves). Thus, university studies might require more from them than expected, but this is not captured in a clear manner through the other more specific aspects in the questionnaire. For example, it is known that distance students are timewise less engaged in their studies (Galligan et al., 2012) and that studying at distance requires students to take a large amount of individual responsibility for their studies (Reju & Jita, 2018), while campus students might be more prepared to study full time.

7.3. Success in mathematics at university (RQ3)

The correlations in our study between perceptions of a clash and course grades are in the anticipated direction: the perception of a larger clash is associated with lower grades. This can indicate that students who perceive a larger clash in the transition between upper secondary and university mathematics will have more difficulties in performing well in their first mathematics course. However, the causal relationship could also be reversed. After taking a mathematics course, a student who has failed might then experience a clash between tertiary and secondary mathematics. Concerning the correlations, the most important aspects of the transition are the more general perceptions of the transition and aspects of curriculum misalignment.

The importance of the general perception strengthens that there is a causal relationship from the level of success to experiences of the transition. It is reasonable that for students who do not perform well in the university mathematics course attribute this to an experience of differences between secondary and university mathematics. But since this attribution is not directly connected to specific properties of the different educational levels, the connection to the general perception becomes evident.

The curriculum misalignment includes that students perceive that their prior knowledge from upper secondary school is insufficient for them to succeed in their university studies. Note that the correlation is a partial correlation, where the effects of prior knowledge (through their grades from upper secondary level) has been accounted for. That is, the students’ perceptions of curriculum misalignment are still a relevant factor in relation to their course grades, even when the effect of prior knowledge is accounted for. This highlights the general importance of taking students’ perceptions and experiences into account when analysing the transition between upper secondary and university mathematics.

Finally, it should be noted that student results from different university mathematics courses have been used in the analyses. Therefore, the existing correlations show a robust result concerning relationships between perceptions of a clash and course grades.

8. Conclusions

This study has focused on students’ perceptions of the potential clash in the transition from upper secondary to university mathematics, through a multifaceted approach, where we included a variety of aspects of this potential clash. We have shown the importance of taking a student perspective when it comes to the transition, because our results show connections between their perceptions and course grades, even when controlling for the effects of prior knowledge. We have also shown the importance of including a variety of different aspects, as our results demonstrate the relevance of considering mathematical aspects as well as pedagogical and social aspects when trying to understand what happens in the transition.

Furthermore, our study has revealed some counter-intuitive findings, highlighting the complexity of the transition and the exploratory nature of our study. In particular, our analyses of different student groups have shown that we need to take other issues into consideration, such as the time elapsed from the end of secondary school to the start of their mathematics studies at university and also the students’ expectations when starting university, which could be tightly interconnected with (some aspects of) their perceptions and prior experiences.

In particular, relationships between expectations and perceptions of a culture clash could be worth examining in more depth, through longitudinal studies for example, where expectations could be gauged before entering university. Such analyses could clarify if the expectations of large differences between upper secondary and tertiary levels perhaps create a lower-level culture clash, and it would also be possible to disentangle effects of expectations and of experiences in the transition on study results, including any causal effects between experiences of the transition and level of success in the university mathematics courses. Results from such analyses could shed light on different aspects of a poor fit between the learner and the learning environment (cf. Rach & Heinze, 2017).

We thus see a need for further research, both qualitative and quantitative, that takes the complexity of the transition into account, both regarding a focus on student perspectives, on the variety of aspects of their perceptions of the transition, and also regarding other issues, such as time and student expectations. This type of research, to which we have contributed with this paper, is needed in order to create more explanatory and useful models of students’ transition between upper secondary and university mathematics. Such models could be used to adapt the first courses in university mathematics in general, but perhaps also in relation to catering better for specific student groups.

Disclosure statement

No potential conflict of interest was reported by the authors.

Appendix

Appendix A: Student questionnaire items

In the questionnaire given to students, the items were mixed (i.e. not sorted by dimension).

Dimension 1 was not included in the analyses.

Table

Dim	Student questionnaire item (English)	Student questionnaire item (Swedish)
1	Those that are happy with mathematics teaching in upper secondary school are more successful in university mathematics	De som är nöjda med matematikundervisningen på gymnasiet lyckas bättre med matematiken på universitetet
	The first university mathematics courses reveal who is able to study university mathematics	Första matematikkurserna på universitetet visar vilka som klarar av att läsa universitetsmatematik
	It is important to get more girls to choose to study mathematics	Det är viktigt att få fler tjejer att välja att läsa matematik
	Students who have someone in the family or other close relatives who have studied at university do better in university mathematics	Det går bättre i matematik på universitetet för de studenter som har någon i familjen eller nära släkten som studerat på universitet
	All kinds of people can learn mathematics	Alla typer av personer kan lära sig matematik
2	When I started university, I was expected to know things in mathematics that I did not learn in upper secondary school	När jag började på universitetet förväntades jag kunna saker i matematik som jag inte fått lära mig på gymnasiet
	Calculators or other technical tools are/were used in the teaching of mathematics	Miniräknare eller andra tekniska verktyg används/användes i matematikundervisningen
	* My grades from upper secondary school correspond to the mathematical prerequisites I am expected to fulfil	* Mina betyg från gymnasiet motsvarar de förkunskaper jag förväntas ha med mig i matematik
	I have not learnt all the algebra (calculations with numbers replaced by letters) needed in the first university mathematics courses	Jag har inte lärt mig all den algebra (bokstavsräkning) som behövs i de första matematikkurserna på universitetet
	A formula collection is used in the teaching of mathematics	Formelsamling används i matematikundervisningen
	In mathematics I need/needed to master paper and pencil procedures/algorithms to be able to solve tasks	I matematik behöver/behövde jag behärska procedurer/algoritmer för hand, för att kunna lösa uppgifter
	I lack the arithmetic skills (calculations involving numbers) needed in the first mathematics courses at university	Jag saknar de räknefärdigheter i aritmetik (räkning med siffror) som behövs i de första matematikkurserna på universitetet
	In mathematics you need to learn by rote formulas covered by the course	I matematik behöver man lära sig formler som ingår i kursen utantill
	Most mathematics exercises can be solved by ready-made procedures presented by the teacher or the book	De flesta matematikuppgifter kan lösas med färdiga metoder, som presenterats av läraren eller i boken
3	The first mathematics courses at university use several concepts (e.g. function), that I learnt previously, but with new meaning	I de första matematikkurserna på universitetet används flera begrepp som jag lärt mig tidigare (t.ex. funktion), fast med nya innebörder
	Mathematics uses a very formal kind of language	Matematiken använder ett mycket formellt typ av språk
	Mathematical argumentation is based on logical connections	Argumentationen i matematik baseras på logiska samband
	In the first mathematics courses at university, I need to justify my answers mathematically differently from what I have learnt before	I de första matematikkurserna på universitetet behöver jag motivera mina svar matematiskt på ett annat sätt än hur jag har lärt mig förut
	Mathematics is not based on concrete situations but is more abstract	Matematiken utgår inte från konkreta situationer utan är mer abstrakt
	In mathematics it is acceptable to use trial and error to obtain solutions, there is no requirement to give complete justification	I matematik kan man pröva sig fram till olika lösningar utan fullständig argumentation
	Mathematics studies at university require more in-depth learning than at upper secondary school	Matematikstudier på universitetet kräver mer djupinlärning än på gymnasiet
	Strict mathematical proofs are required in mathematics courses	I matematikkurser ställs krav på strikta matematiska bevis
4	Mathematical knowledge is important to be able to learn other subjects	Kunskaper i matematik är viktigt för att kunna lära sig andra ämnen
	For some mathematics courses it is not clear how they are/were related to other courses or the study programme that I am/was doing	Det är oklart hur vissa matematikkurser hör/hörde ihop med övriga kurser eller utbildningsprogram som jag läser/läste
	The contents and knowledge from a mathematics course may be relevant to everyday life	Innehållet och kunskaper från en matematikkurs kan ha relevans för vardagen
	The contents and knowledge from a mathematics course may be relevant for a variety of professions	Innehållet och kunskaper från en matematikkurs kan ha relevans för olika yrken
	Mathematics is a subject in its own right and not just as a ‘tool’ for other subjects	Matematik fungerar som ett eget ämne och inte bara ett "verktyg" för andra ämnen
5	The university mathematics courses cover more in a shorter period of time than do the mathematics courses at upper secondary school	Matematikkurserna på universitetet täcker in mer innehåll på kortare tid än matematikkurserna på gymnasiet
	I get/got all the extra help with mathematics that I need and want	Jag får/fick den extra hjälp med matematiken som jag behöver och vill ha
	Grading in mathematics is done in a very different way at university compared to upper secondary school	Betygsättning i matematik sker mycket annorlunda på universitetet jämfört med på gymnasiet
	There is/was enough time in class for me to ask questions and discuss problems	Det finns/fanns tillräckligt med tid i undervisningen för mig att ställa frågor och diskutera problem
	Mathematics teachers teach towards students doing well on final tests/written exams	Matematiklärare undervisar mot att studenter/elever ska lyckas bra på slutprov/tentor
	I focus more on mathematics exams at university than I did in upper secondary school	Jag fokuserar mer på matematiktentorna på universitetet än vad jag fokuserade på matematikproven på gymnasiet
	I only practice for what I know will be on the exam/test	Jag övar bara på det jag vet kommer på tentan/provet
6	Mathematics teachers have good knowledge of the mathematics that is being taught	Matematiklärare har bra kunskap i den matematik som undervisas om
	Mathematics teachers have good structure in their teaching	Matematiklärare har bra upplägg i sin undervisning
	University teachers know what is included in the upper secondary mathematics syllabus	Universitetslärare känner till vad som ingår i kursplanen för matematik för gymnasiet
	Mathematics teachers adjust their teaching to match our needs and the requests from us students	Matematiklärare anpassar sin undervisning utifrån behov och önskemål från oss studenter/elever
	I am/was happy with the mathematics teaching	Jag är/var nöjd med undervisningen i matematik
	* Upper secondary school teachers know the demands for mathematics studies at university level	* Gymnasielärare känner till vad som krävs för att studera matematik på universitetet
	Mathematics teachers adjust their teaching to match the level of our (student) knowledge	Matematiklärare anpassar sin undervisning utifrån nivån på våra (studenters/elevers) kunskaper
	Mathematics teachers use a variety of methods to explain when there is something a student does not understand	Matematiklärare använder olika förklaringsmodeller när någon student/elev inte förstår
7	* In upper secondary school it was my own responsibility to prepare myself for mathematics studies at university level	* På gymnasiet behövde jag ta eget ansvar i att förbereda mig för matematikstudier på universitetet
	I need/needed to take the responsibility for my own learning in mathematics	Jag behöver/behövde ta ansvar för mitt eget lärande i matematik
	I perceive/perceived the studies of mathematics as being stressful	Jag upplever/upplevde matematikstudierna stressande
	I need/needed to be able to decide by myself if what I have learnt in mathematics is sufficient	Jag behöver/behövde själv kunna avgöra om jag har lärt mig det jag behöver i matematiken
	I am personally responsible for my studies in mathematics	Jag behöver ta eget ansvar för mina studier i matematik
	It is important that I make a time schedule myself when I am studying mathematics	Det är viktigt att jag själv skapar en tidsplanering när jag studerar matematik
8	I interact/interacted with my mathematics teachers	Jag interagerar/interagerade med mina lärare i matematik
	I am/was bonding well with my classmates/ fellow students	Jag har/hade en bra sammanhållning med mina klasskompisar/medstudenter
	Teachers of mathematics have knowledge of most of their students	Lärare i matematik känner till de flesta av sina studenter/elever
	Mathematics teachers engage with each student individually	Lärare i matematik har personlig kontakt med sina studenter/elever
	I feel/felt lonely	Jag känner/kände mig ensam
9	The transition to university mathematics was hard for me	Övergången till universitetsmatematik var svår för mig
	Studying mathematics at university meant something different from what I had expected	Matematikstudierna på universitetet innebar något annat än vad hade jag förväntat mig
	* There is a difference between what is considered mathematics at university and in upper secondary school	* Det är skillnad på vad som räknas som matematik på universitetet och på gymnasiet

* denotes items deleted to increase Cronbach’s alpha.