Improving mathematics diagnostic tests using item analysis

Abstract

Many universities use diagnostic tests to assess incoming students' preparedness for mathematics courses. Diagnostic test results can help students to identify topics where they need more practice and give lecturers a summary of strengths and weaknesses in their class. We demonstrate a process that can be used to make improvements to a mathematics diagnostic test, so that it provides better information about students' abilities. To identify questions that could be improved, our process uses item response theory to analyse student data. We provide an accessible introduction to the key ideas of item response theory, and we describe how we applied the process of improvement of diagnostic tests at two universities. Our method provides a model for others wishing to make improvements to mathematics diagnostic tests.

Keywords:

• Diagnostic testing
• item response theory
• procedural and conceptual knowledge

1. Introduction

Many university mathematics departments administer short diagnostic tests to incoming students; their use was found to be widespread in the UK (Lawson, 2003) and there are many examples internationally (e.g. Carr et al., 2015; Heck & Van Gastel, 2006; Rach & Ufer, 2020). The two main aims of such tests are normally to inform staff about the level of students' basic mathematical skills and to inform individual students of any gaps in the level of assumed mathematical knowledge. Based on the results, staff may highlight and revise particular topics in class, while students can take action to remedy any gaps identified in their assumed knowledge and skills.

Given their widespread use, it should be important to make any diagnostic test as effective as possible. A potential model for improving a test is given by the process of developing a concept inventory, such as the Precalculus Concept Assessment (Carlson, Oehrtman & et al., 2010) or tests of proof comprehension (Mejia-Ramos et al., 2017). However, these processes are typically very rigorous and require substantial effort, which may not be feasible as part of practical teaching rather than research. Another tool which could be used is a taxonomy of question types, to ensure the test contains a balance of items; for instance, the ‘Mathematical Assessment Task Hierarchy’, also known as the MATH taxonomy (Smith et al., 1996), was introduced to help instructors write more balanced assessments.

Here, we describe an approach which integrates these two models, combining the use of the MATH taxonomy with statistical analysis of students' responses. The aim is to provide a practical process which can be used more routinely to improve the effectiveness of tests. We illustrate this process in practice by applying it to the Mathematics Diagnostic Test in use at the University of Edinburgh, and the ‘Selbsteinschätzungstest’ (abbreviated as s21t, because there are 21 letters between the ‘s’ at the start and the final ‘t’) at ETH Zurich. We note that despite the fact that Scotland and Switzerland have very different educational systems, the tests are similar in content as well as in purposes. In particular, they aim to provide students with information about their level of preparedness for first-year mathematics courses.

For each of the diagnostic tests, we address two research questions:

1. how well does the test perform its function?

2. can the test be improved based on insight gained from statistical analysis?

Our main contribution is to describe and exemplify a practical process for improving diagnostic tests, in three stages: analysis (Section 4), refinement (Section 5) and re-analysis (Section 6). In describing the analysis, we provide an accessible introduction to the key ideas of item response theory. As a further contribution, we have developed a set of R scripts to support the analyses. These are openly available at https://github.com/georgekinnear/diagnostic-test-irt so that they can be re-used in the analysis and refinement of other tests.

2. Literature review

2.1. Diagnostic testing

A diagnostic test is a short quiz or exam that is administered to students ‘to determine their mathematical strengths and weaknesses as they begin their courses’ (Hodds et al., 2022, p. 1859). They are widely used, for instance in the UK (Lawson, 2003), Ireland (Hyland & O'Shea, 2022) and the USA (Hsu & Bressoud, 2015).

Scores for individual students can be used to identify students at particular risk of failing; for example, Wakefield et al. (2018) found that performance on a 12 question test of precalculus skills was a good early indicator of students at risk of failing their first university mathematics course. Beyond simply identifying at-risk students, diagnostic test results can be used to intervene with further support. In some cases, support comes from conversations with academic advisors or from providing opportunities for further practice and help from tutors (e.g. Chongchitnan, 2019; Heck & Van Gastel, 2006). In other cases, students may be directed to a bridging course (e.g. Barbas & Schramm, 2018) or an additional credit-bearing course to help them develop the necessary skills (e.g. Kinnear et al., 2022). Individual diagnostic test results can also be used to inform ‘placement’ decisions; for instance, in the USA it is common to use the results from such tests to ‘prevent or discourage students from entering [Calculus I] when they are inadequately prepared or unlikely to succeed’ (Hsu & Bressoud, 2015, p. 59).

Results from a diagnostic test can also be aggregated to give information about a cohort of students, indicating areas of particular strength or weakness. Such aggregate results can provide information to teachers about topics where students may need more support. Aggregated results for cohorts can also be used to track changes over time (e.g. Hodds et al., 2022; Todd, 2003) or to enable comparisons between institutions (Carr et al., 2015).

The statistical analysis of results can be quite sophisticated. For instance, Rach and Ufer (2020) analysed students' scores on an entrance test, and its use as a predictor of success on a first analysis course. Their analysis was based on the Rasch model, which is one of a family of models in item response theory (DeMars, 2010). These models aim to establish a single scale on which to estimate both the difficulty of items on the test and the ability of individual students. This approach can help to reveal issues in a test: for example, Xie et al. (2019) used an item response theory model to evaluate a diagnostic test in computer science, and their analysis highlighted several questions that were too difficult for the group of students taking the test. We make use of item response theory in our analysis and give a detailed explanation in Section 4.5.

2.2. Concept inventory development

Concept inventories are another commonly used tool in education; these are tests that aim to measure students' understanding of particular concepts. A prominent early example, from physics education, is the Force Concept Inventory (FCI) written by Hestenes et al. (1992), that is designed to test understanding of concepts in Newtonian mechanics. The FCI has now been used with tens of thousands of students worldwide (Von Korff et al., 2016), often as a tool to measure the impact of teaching innovations (e.g. Mazur, 1997).

The development of concept inventories or assessments is typically a rigorous process involving careful development of items to target the range of desired concepts, often informed by prior research on students' understandings of particular concepts. While the finalized tests are in multiple-choice form, early versions may be open-ended so that incorrect student responses can inform the design of distractors. Pilot versions of the test often involve interviews with students to check that questions are properly addressing the intended concepts.

There are now several examples of concept inventories in mathematics education. For instance, the Calculus Concept Inventory (Epstein, 2007, 2013) was designed to assess conceptual understanding of basic ideas in differential calculus; however, recent work has cast doubt on the reliability of this test (Gleason et al., 2019). Other examples relevant to introductory courses in calculus include the Precalculus Concept Assessment (Carlson, Oehrtman & et al., 2010), the Calculus Concept Readiness instrument (Carlson, Madison & et al., 2010) and the Function Concept Inventory (O'Shea et al., 2016). The recent development of the Group Theory Concept Assessment (Melhuish, 2019) provides a model for designing and validating new tests for more advanced topics.

The rigorous processes used to develop concept inventories are similar to those used for other types of tests and inventories. For instance, Mejia-Ramos et al. (2017) describe a multi-stage process for developing and validating tests of students' comprehension of particular proofs that involves interviews with students as well as statistical analysis. Similar processes have also been used to develop inventories about students' attitudes, for instance in physics (Adams et al., 2006) and in mathematics (Code et al., 2016). These rigorous processes inform the approach that we outline here, for analysing and improving diagnostic tests.

2.3. Procedural and conceptual knowledge

In the previous sections, we considered diagnostic tests and concept inventories separately. The distinction between these two types of tests broadly parallels the distinction made between procedural and conceptual knowledge in the mathematics education literature. Rittle-Johnson et al. (2015, p. 583) note that tests of conceptual understanding generally require tasks that are ‘relatively unfamiliar to participants, so that participants have to derive an answer from their conceptual knowledge’, while measures of procedural knowledge tend to be based on familiar tasks for which students should know a solution procedure (or on ‘near transfer problems – problems with an unfamiliar feature that require either recognition that a known procedure is relevant or small adaptations of a known procedure to accommodate the unfamiliar problem feature’). Based on this account, the tests that we analyse here (and indeed most of the diagnostic tests discussed in Section 2.1) are clearly focused on procedural knowledge.

Given the emphasis placed on conceptual understanding by mathematics educators (e.g. Skemp, 1976), why should tests of procedural knowledge be of interest? Rach & Ufer (2020, p. 386) noted that the procedural focus of diagnostic testing showed that procedural knowledge was ‘perceived as relevant in research and practice’. An argument for this focus on procedural knowledge is that it can help to lay the groundwork for subsequent development of conceptual knowledge. Indeed, the two types of knowledge can develop hand-in-hand (Rittle-Johnson et al., 2015), and fluency with procedures can enhance students' ability to tackle more complicated, conceptual mathematics (Foster, 2018). Similarly, Maciejewski & Star (2016, p. 302) propose that ‘a pathway to developing deep conceptual understanding of undergraduate mathematics may be in developing corresponding deep procedural knowledge’, where deep procedural knowledge is indicated by an ability to ‘apply procedures flexibly and innovatively to problem situations’ (p. 301).

2.4. Categorizing mathematics tasks

Beyond the procedural/conceptual dichotomy, there are many suggested ways to classify different types of tasks. Perhaps the most famous is Bloom's taxonomy (Bloom et al., 1956), which was developed to support ‘exchange of test items among faculty at various universities’ (Krathwohl, 2002, p. 212), by providing a shared language for describing the educational objective of tasks. However, Bloom's taxonomy is not specific to mathematics; various more specific taxonomies have been developed to better capture distinctions between mathematics tasks (e.g. Lithner, 2008; Pointon & Sangwin, 2003; Tallman et al., 2016).

The Mathematical Assessment Task Hierarchy, also known as the ‘MATH taxonomy’, was developed specifically for the context of undergraduate mathematics (Smith et al., 1996). It was intended to be a tool that lecturers could use to ‘broaden the skills tested’ (p. 66) in their assessments. The MATH taxonomy identifies eight categories of skills needed to solve mathematics tasks, arranged into three groups. Group A tasks are based on factual recall or routine procedures; Group B tasks require the use of mathematical knowledge in new ways; Group C tasks involve application of conceptual knowledge and construction of mathematical arguments. Comparisons of UK school and university assessments using the MATH taxonomy have identified differences in the balance of skills being assessed, with school examinations dominated by Group A tasks (Darlington, 2014; Kinnear et al., 2020). This is relevant to the purpose of a diagnostic test, which should aim to bridge the types of assessment familiar to incoming students from school, with the types of tasks they will face in their course.

3. Test development

One way to develop a new test would be to follow the rigorous approach used to create concept inventories, as discussed in Section 2.2. The approach often involves rounds of consultation with experts to determine the important topics to assess, developing a large pool of items and trialling them with students to select only those items that work as intended (e.g. Melhuish, 2019, pp. 368–373). The approach we took to developing our tests was less stringent, but was informed by our experience as teachers. In particular, we drew on our knowledge of the topics and skills that are important for incoming undergraduates, and our understanding of the background that our students come from. Since these are different at the two institutions, we give some further detail on each case.

3.1. The university of Edinburgh: mathematics diagnostic test

The diagnostic test was designed to test the core high school pure mathematics topics that should be familiar to incoming undergraduates, and that are important for first-year courses. Consequently, the mathematical content fits closely with the syllabus of the Scottish Qualification Authority's ‘Higher Mathematics’ course (SQA, 2018) since this is the minimum qualification required for entry. The topics covered by the test are thus largely in algebra, trigonometry and basic calculus.

The current version of our diagnostic test has 20 items, with a mix of multiple choice and constructed response (numerical answers). A copy is available at https://doi.org/10.5281/zenodo.4772436. While the e-assessment system is capable of handling more complex algebraic inputs (Sangwin, 2013), we used only the simplest input types so these would be readily accessible to incoming students. Students take the test online in a single sitting with a time limit of 90 minutes, although time does not appear to be a limiting factor for most students. Scores on the test are used by students and their advisors to inform course choice, with students who score below 50% strongly recommended to take a credit-bearing course on high school mathematics as one of their options in Year 1 (Kinnear et al., 2022).

3.2. ETH zurich: selbsteinschätzungstest (s21t)

In contrast to the UK, there are no central exams at the end of secondary education in Switzerland. There is substantial regional variation in both the curriculum and the number of lessons dedicated to mathematics (which can vary by a factor of 2 across the country). To enter the ETH (Federal Institute of Technology), there is no entrance exam. The only entry requirement is to have passed the Matura exams, which are not standardized between schools. This results in a rather heterogeneous population in first-year mathematics classes, which is challenging for both the students and the lecturers. To help both groups, an optional diagnostic test, the s21t, was introduced in 2009.

The s21t diagnostic test focuses on the high school mathematics topics required to follow the first-year lectures with mathematical content (e.g. mathematics, physics, mechanics and computer science). The choice of the test items is based on the curriculum and Bloom's taxonomy was used to make sure different types of skills were tested. For each item, the student is given a choice of 5 (sometimes 4 or 6) possible answers of which only one is correct. An ‘I don't know’ option is also provided, and students are encouraged to use this when applicable. This option was included because the curriculum is not standard, so there may well be topics that students do not know about. By providing the ‘I don't know option’, we hoped to gain more insight into the actual knowledge of the students and thereby to eliminate, or at least reduce, the prevalence of guessing.

Over the years, the participation in the test was rather stable with about $60\mathrm{\%}$ of the first-year population. Analysis of results from the 2011/12 academic year found a weak correlation between the s21t test result and the success in the first year (0.27 with 95% CI $[0.20,0.33]$), Caspar et al., 2013). The question of ‘what to do next?’ after a bad result in the test became more and more pressing. In response the department of mathematics developed a so-called ‘bridging course’ which first went online in 2017. In this course, students can develop their mathematics knowledge by watching videos, reading texts and practicing with randomized questions that offer hints. Participation in the s21t is now anonymous, but students must complete it to gain access to the bridging course, and to see suggestions about their strengths and weaknesses.

4. Analysing a test

In this section, we outline an approach to analysing the performance of a test once it has been administered to students. We illustrate using this approach to address RQ1 (how well does the test function) for each test.

The analysis was carried out using R scripts that we developed, available at https://github.com/georgekinnear/diagnostic-test-irt. In particular, full details of the analysis can be seen for the Edinburgh MDT (with items named e1-e20) at https://osf.io/pr3m7/ and for the ETH s21t (with items named z1–z36) at https://osf.io/ez2sx/.

4.1. Mathematical content

Even before any students have taken the test, it is possible to analyse its mathematical content. One approach is to consider the mathematical topics addressed by the test; as noted in Section 3, the development of both tests took account of the topics covered at both school and university level.

Another approach is based on analysing the types of mathematical skills that are likely to be used in answering the items, as discussed in Section 2.4. For instance, the design of the ETH s21t was informed by Bloom's taxonomy to make sure different levels were covered across all topics. For the Edinburgh MDT, the initial design was not based on a specific taxonomy, but there was a definite aim to include items that required the use of standard procedures in non-standard situations. Subsequent analysis of the Edinburgh MDT using the MATH taxonomy confirmed that 6 of the 20 items were Group B, requiring either ‘information transfer’ or ‘application in new situations’, while the remaining 14 items were Group A, being based on ‘routine use of procedures’ (Kinnear et al., 2020).

4.2. Gathering and cleaning data

Both tests were administered online using systems that record all student responses. Following the ethics procedures at our institutions, we obtained approval to analyse the anonymized response data for this research.

The Edinburgh MDT was administered in the same way across four academic years, beginning in 2013/14. The full set of responses includes data from 3472 students; however, we identified that many of these appeared to be abandoned attempts, where students had given only a few responses (and typically only to items near the start). This reflects the fact that participation was optional and took place in students' own time. To avoid these abandoned attempts skewing the analysis, we took steps to remove them from the data set before proceeding. Since our data files only include the score on each item (not the content of the response), we classified an attempt as abandoned if the student scored under 30% overall, with three or more zeros in the five items with the highest mean scores in the second-half of the test. We manually checked the responses entered into the online assessment system from a selection of these students, and this confirmed that the classification had a high level of accuracy (in that these students had in fact responded to few, if any, items). We removed 251 students' abandoned attempts in this way, leaving a total sample of 3221 responses. A summary of the students' total scores is shown in Figure 1; this shows the distribution of scores has a similar shape each year, though the mean score is shifting up over the years (perhaps due to admissions becoming increasingly competitive).

Figure 1. Distribution of total scores for each test cohort, together with summary statistics (number of students, standard deviation, mean and median). The maximum possible scores are 100 for the Edinburgh MDT and 36 for the ETH s21t.

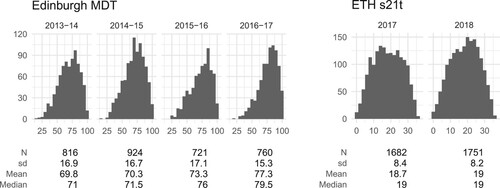
For the ETH s21t, we used data from a total of 3433 students from the 2017 and 2018 cohorts. The summary of students' scores in Figure 1 shows that the pattern of results in 2 years is quite similar. We have complete results for each student, since the test can only be submitted after a response has been provided to every item. Each item offers an ‘I don't know’ response option, so that students are not forced to guess an answer. We assign the ‘I don't know’ responses a score of 0, so that in our analyses, a score of 1 reflects a correct response, while a score of 0 reflects either a mistake or a lack of knowledge of the topic.

4.3. Classical test theory

A simple approach to analysing the response data comes from classical test theory (see, e.g. Embretson & Reise, 2000, Chapter 2). The mean score for each item gives a measure of its facility (i.e. difficulty), and this can highlight items that students found extremely easy or difficult. Classical test theory does also suggest a measure of discrimination for each item that indicates the difference in performance on that item between the highest-scoring and lowest-scoring students on the whole test. These measures are simple to compute, however, they are heavily dependent on the sample of students (Xie et al., 2019).

Instead, we make use of item response theory (IRT). A necessary first step is to check that the assumptions of the IRT model are satisfied, which includes using factor analysis.

4.4. Factor analysis

Exploratory factor analysis is a statistical technique which seeks to reduce the dimensions of observed data by finding a smaller number of factors that explain them. Our primary aim is to check whether the scores appear to be explained by a single factor (which is presumably ‘mathematical ability’), as this allows for the use of a particularly simple (unidimensional) IRT model.

However, we were also interested to see if there were multi-factor solutions. In this case, students' scores would appear to be explained by a small number of underlying factors, with each item associated to the various factors to different degrees. This would highlight groups of items that associate particularly strongly with certain factors. The aim in that case is to find groupings which can be given a meaningful description, e.g. ‘algebra’ versus ‘calculus’, or ‘procedural skills’ versus ‘reasoning’. This process is commonly used when developing survey instruments (e.g. Adams et al., 2006). For our purposes, if such groupings are apparent they would potentially help to give information about students' relative strengths and weaknesses.

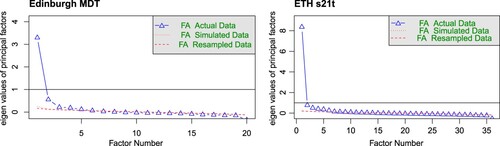
There are many approaches to determining a suitable number of factors (e.g. see DeMars, 2010, p. 40). One approach that is widely used is to analyse a scree plot; this shows the eigenvalues of the inter-item correlation matrix associated to successive factors, and ideally will display a large drop in value after the appropriate number of factors to extract. For both the Edinburgh and ETH tests, the scree plots suggest a 1-factor solution is appropriate (see Figure 2). Our scripts also check the consensus among different approaches, using the n_factors function from the parameters package (Ludecke et al., 2020); as well as examining the 1-factor solution, we also consider other plausible solutions.

Figure 2. Scree plots for both tests, showing a dominant single factor.

4.4.1. Edinburgh MDT

For the Edinburgh MDT, the 1-factor solution explains 16% of the variance in the data (see section 2.2.3 of https://osf.io/pr3m7/). Strikingly, this factor is dominated by MATH Group B items, i.e. those that are somehow ‘non-standard’ – either requiring students to recognize that a particular rule/procedure is applicable before applying it or to apply it in an unusual way. All six of the Group B items on the test appear within the top eight items loading onto this factor.

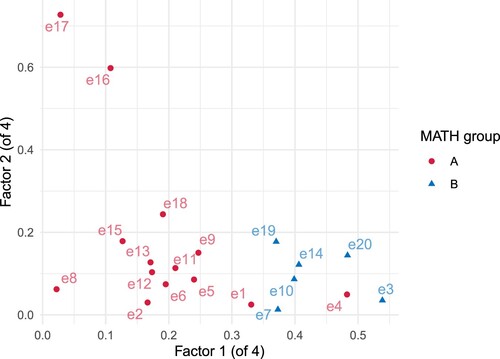
A 4-factor solution is also plausible, explaining 24% of the variance. Again, the first factor is dominated by the MATH Group B items (see Figure 3, and section 2.2.4 of https://osf.io/pr3m7/). The second factor is dominated by the two chain rule items (e16 and e17), along with e18 which is a routine definite integral, suggesting this factor is related to routine calculus computations. The third factor seems to be based on applying calculus techniques to cubic and quadratic curves, e.g. to find tangent lines or stationary points. The fourth factor is dominated by the only two items that require the use of a calculator (to compute trigonometric functions), but more generally seems to be based on non-calculus skills (vectors, trigonometry, and sequences).

Figure 3. Factor loadings for items on the Edinburgh MDT, showing the first two factors from the 4-factor solution. Items are labelled according to their grouping in the MATH taxonomy.

4.4.2. ETH s21t

For the ETH s21t, the 1-factor solution explains 23% of the variance in the data. The items that load most strongly onto this factor (see section 2.2.2 of https://osf.io/ez2sx/) are all standard calculations using calculus tools, suggesting that is the main underlying ability that is being assessed by this test.

For the ETH s21t, a 6-factor solution was also plausible, explaining 32% of the variance (see section 2.2.3 of https://osf.io/ez2sx/). The first factor included both items on abstract understanding and some on calculations using calculus tools while the second clearly addresses the graphical understanding of calculus. The third factor seems to solely consist of computational skill in calculus whereas the first factor is more dominated by understanding the basic concepts. The remaining three factors are the quotient and product rule, vector geometry and 3D skills. This grouping of items gave an interesting insight into the structure of the test, with the later factors reflecting topics that may not be systematically covered in schools (as discussed in Section 3).

4.5. Item response theory analysis

We begin with a brief overview of item response theory; for further details we recommend the introductory text by DeMars (2010).

In a unidimensional IRT model, it is assumed that each student taking the test has a certain ‘ability’, measured on a continuous scale, which is being assessed by the items on the test. A further assumption is that each item on the test has an ‘item characteristic curve’ (ICC) which models the probability that a student with a given ability will answer correctly; the shape of the ICC is specified by certain parameters, which can be interpreted as properties of the item (e.g. difficulty). Data from student attempts at the test can be used to estimate these parameters, and the resulting ICCs can be interpreted to judge how well each item is functioning.

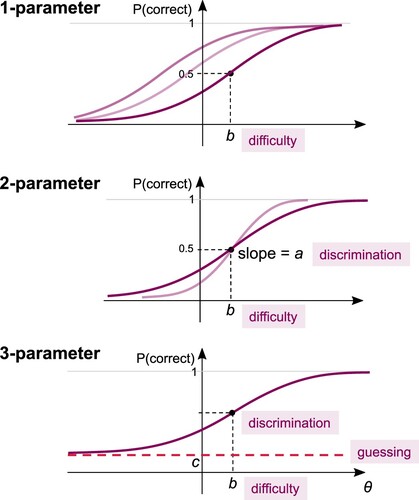
In the three-parameter IRT model, the ICC for an item is given as a function of the ability θ, by $P(\theta ,a,b,c)=c+(1-c)\frac{\exp (a(\theta -b))}{1+\exp (a(\theta -b))},$ where a is the item's discrimination, b is its difficulty and c is the rate of guessing. In the two-parameter model, the guessing parameter is omitted (c = 0), and in the one-parameter model, the discrimination is fixed across all items (a = 1).

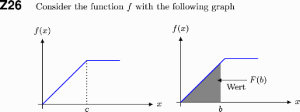
The parameters of the ICC can be interpreted graphically, as shown in Figure 4. The item's difficulty is easily read off by finding the θ value corresponding to a probability of 0.5, and the discrimination is simply the slope of the curve at this point. A highly discriminating item will have a steep slope at this point, meaning that for students with abilities close to the item difficulty, the probability that they will answer this particular item correctly is highly sensitive to their ability.

Figure 4. Illustration of the role of the various parameters in the one-, two- and three-parameter IRT models.

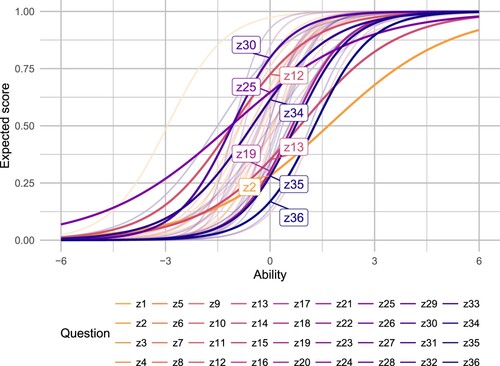
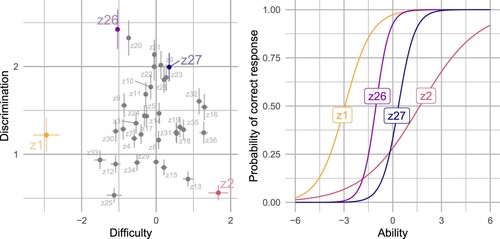
For the ETH s21t, our main analysis is based on a two-parameter model. The parameter estimates for each item are shown in Figure 5. The goal is to have a spread of item difficulties, with a preference for items with high discrimination. The results in Figure 5 show that there is indeed a spread of difficulties, though there are several items with relatively low discrimination (e.g. item z2 which is highlighted in the figure). We return to this in Section 5 when discussing the process of refining the test.

Figure 5. Results of the two-parameter IRT model for the ETH s21t. The left panel shows the estimated difficulty and discrimination parameters for all 36 items (together with the 95% confidence intervals for those parameters). The right panel shows the corresponding ICCs for a selection of items.

While the two-parameter model was used for our main analysis of the ETH s21t, we carried out a further analysis using the three-parameter model, which adds a ‘guessing’ parameter for each item. The items on the ETH s21t are all multiple-choice, with ‘I don't know’ offered as an option; our expectation was that with this option, students would be less likely to resort to guessing. The results of fitting the three-parameter model (see section 4 of https://osf.io/ez2sx/) confirmed this, with the guessing parameters generally well below the level that would indicate that the lowest ability students are simply choosing a response at random. Several items in the first half of the test did have guessing parameters of around 0.1. Interestingly, two of the items with relatively high guessing parameters were those where ‘none of the above’ was given as an option and was in fact the correct answer. This could perhaps indicate that in these cases, students lacked confidence to declare all other answers are wrong (which seems a more demanding task than being able to spot the correct answer).

For the Edinburgh MDT, some of the items award partial credit; this meant that we could not use the IRT models described above, since they assume dichotomous (correct or incorrect) responses. Instead, we made use of a generalized partial credit model, which involves estimating parameters for each different level of partial credit (for full details, see DeMars, 2010, pp. 22–29). The result is that ICCs give the expected score for each ability level, rather than simply the probability of correctness. In practice, these ICCs tend to look quite similar to those of the two-parameter model, allowing for similar observations (e.g. of a suitable spread of difficulties, or of items with relatively low discrimination). We return to discuss the results in detail in Section 5.

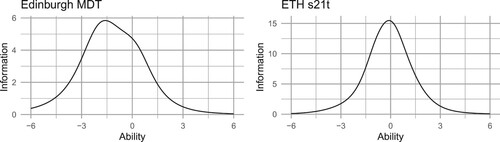
For each item, we can also analyse the item information curve. This formalizes the intuitive idea that items are most informative about a student's ability when they are closely matched to the student's level. The item information curve shows, for each ability level, how informative the item will be in determining the ability of a student at that level. For the two-parameter model¹, an item's information is maximized around $\theta =b$, and the value of a determines the height of the peak: more discriminating items provide a higher level of information. Summing the information curves for each item gives the test information curve, which shows how reliably the test as a whole provides information about students at each ability level. When estimating a student's ability level, the standard error in the estimate will be lower when the test information is high around that ability level. Thus our goal is to have a test information curve that provides a high level of information across a wide range of ability levels.

The test information curves for both tests are shown in Figure 6. For the Edinburgh MDT, the test information curve is skewed toward abilities below 0 on the scale (where the scale is built on the assumption that abilities follow a standard normal distribution). This means that the test is most reliable at determining the ability level of students of below average ability. This does fit with the intended aim of the test, which is to help identify students who would benefit from further support during the first semester, although more information about students of mean ability would be welcome. For the ETH s21t, the test information curve is centred around 0, with only a very small tendency towards lower abilities. This is reflected in the content of the items: some are aimed at distinguishing students of low ability from the rest, but some are also aimed at distinguishing students who are above average.

Figure 6. Test information curves for both tests.

4.6. Predictive validity

As mentioned earlier, previous analysis of the ETH s21t found a moderate correlation between results in the test and performance in first-year exams (Caspar et al., 2013). However, since the test is now administered anonymously, we have no way of linking results in our sample to exam results to repeat this analysis.

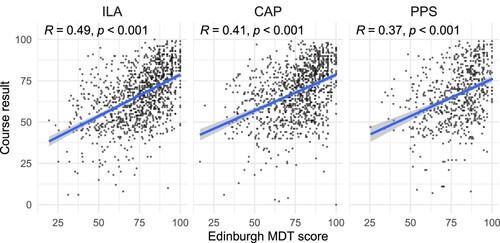
For the Edinburgh MDT, we had access to first-year course results for 2504 of the 3221 students with diagnostic test scores. There are two different streams: specialist mathematics, aimed at students on a programme involving mathematics, and non-specialist mathematics, aimed at engineering and chemistry students. Here we focus on the specialist mathematics stream², where students study linear algebra (course code ILA) in semester 1, then calculus (CAP) and an introductory proof-based course (PPS) in semester 2. The diagnostic test scores have a moderately high correlation with students' results in these courses, as shown in Figure 7. The highest correlation is found with the results in ILA in semester 1 (R = 0.49). Lower correlations with semester 2 results are perhaps to be expected, since the diagnostic test results become less relevant over time as students progress with their studies.

Figure 7. Scatterplots of Edinburgh MDT scores against results in the three first-year mathematics courses: ILA (linear algebra), CAP (calculus) and PPS (proofs and problem solving), for the 2013–14 to 2016–17 cohorts. Regression lines are shown in each panel, and the text at the top of each panel shows the Pearson correlation coefficient.

5. Refinement

For the next step of the process, we consider how to make improvements to the test using the results of the IRT analysis. First, we identify items with relatively poor performance, then outline the process that we used to replace them. This begins to address RQ2 (on whether the test can be improved). We return to addressing RQ2 in the following section, where we analyse results from the new version of the test to check whether the refinement process had the desired effect.

We refer to the original version of the test as Version 1 (with items named e1–e20 for the Edinburgh MDT and z1–z36 for the ETH s21t), and the new version of the test as Version 2 (with items E1–E20 and Z1–Z30).

5.1. Identifying items to remove

When reviewing the IRT results, one of the main criteria to consider is the proportion of total information provided by each item. Items that contribute a low proportion of the total information should be considered for removal. The parameters for each item can also be considered: for instance, items with very low discrimination parameters may be good candidates for refinement. Similarly, an item's difficulty parameter can show if it is too easy or too hard for the intended audience.

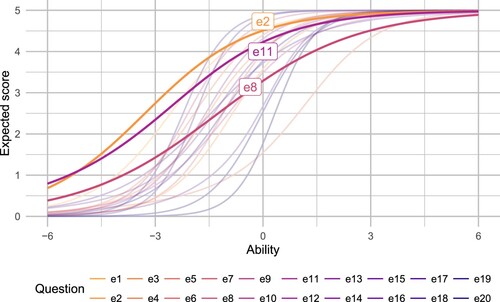
For the Edinburgh MDT, the main criterion we considered was the proportion of total information provided by each item. We identified three items that provided a relatively low proportion of the total information; moreover, the bulk of their information was below 0 on the ability scale which contributed to skewing the overall test information function in this direction. Figure 8 shows the expected score curves for each item on the test, with the three low-information items highlighted. The fact that these items provided low information is visually apparent, by their curves' relatively shallow slopes (i.e. low discrimination). The items were all based on routine skills: e2 asked for the point of intersection of lines with given equations, e8 asked for the angle between two vectors in ${\mathbb{R}}^3$ and e11 asked for the sum of an arithmetic progression.

Figure 8. Expected score for each item in the Edinburgh MDT as a function of ability, based on fitting a generalized partial credit IRT model. The three items providing the lowest information are highlighted.

For the ETH s21t, we used the IRT results to identify a total of five items to remove or replace. First, we considered items that had very low discrimination (and hence information). We removed z2, z12, z13 and z25 for this reason; however, we decided to retain z1 (which stood out for having both low discrimination and difficulty) as we had always intended this to be a straightforward item to ease students into the test. Second, we decided to remove z19, as the IRT analysis had identified that its performance was very similar to z18; indeed, they were one of only two pairs of items showing signs of local dependence (the other pair being z34 and z35, which we discuss below). Both items had a similar setup, with one on the product rule (z18) and the other on the quotient rule (z19).

We also made changes to the ETH s21t that were not directly related to the IRT results. We substituted items z30 and z34 because, upon closer inspection, we thought we could improve on these items by rephrasing them to make it harder for students to eliminate the incorrect answer options; we return to this in the next section. Finally, we decided to remove items z35 and z36 because we had the general feeling that the test was perhaps too long and the low performance in the very last items could perhaps be explained by exhaustion instead of lack of knowledge in these areas (Figure 9).

Figure 9. Expected score for each item in the ETH s21t as a function of ability, based on the two-parameter IRT model. The highlighted items were identified for removal.

5.2. Creating replacement items

Perhaps the most challenging step is to devise new items, where the goal is for them to have desired IRT parameters (e.g. a particular difficulty level, or high discrimination). The challenge comes from the fact that there are no definitive rules about how features of an item will affect the IRT parameters. Nevertheless, the process can be guided by what has been learned from the previous IRT analysis (e.g. about what is easy/hard for this group of students). In addition, ideas from mathematics education literature (such as the MATH taxonomy) can be a useful guide.

For the Edinburgh MDT, we set out to create replacements for the three items that had been identified as providing low information, with a focus on their place in the MATH taxonomy. We noted that there were no Group C items on the test, so we decided to introduce one new item of this type (i.e. relating to the construction of mathematical arguments). And, since items from Group B of the MATH taxonomy were among the most informative on the test, we decided to add two new Group B questions. While the MATH taxonomy was our focus, we did also account for the topics covered by the questions. We did not set out to cover exactly the same topics, but in practice it was helpful to use those topics as a guide to stimulate ideas for new questions with a ‘twist’ to address different skills. A small group of lecturers contributed a total of 10 possible new items. The group independently reviewed all the items, then met to agree which three questions to include.

We created three new items, shown in Figure 10. The new Group C item (E11 in Figure 10) invites students to engage with (likely) new definitions and to construct a counterexample to a given statement. The two new Group B items were inspired by two of the items that were removed. E10 shows a pair of equations where some coefficients are variables rather than numbers, and students are asked whether solutions exist in various cases (rather than a routine calculation of the intersection of two lines, as in e2). E7 presents a problem in context, where one possible solution method is to compute the angle between two vectors in ${\mathbb{R}}^3$ (rather than simply asking directly for such a computation, as in e8).

Figure 10. New items added to the Edinburgh MDT.

For the ETH s21t, the replacement items were either close modifications of existing items, or new items created to address a particular topic. The items can be seen in Appendix 1. We modified three items, with aim of eliminating opportunities for students to answer using simpler techniques than intended. The first item we decided to change was z12, about identifying graphs of exponential functions with rational exponents. This turned out to be an easy item with low discrimination: essentially it can be solved by recognizing the effect of exponents being positive or negative and larger/smaller than 1. We replaced this with Z11, where students need to compare the growth of two given functions of this type.

The second item we modified was z30, on the graphical interpretation of the fundamental theorem of calculus. Our aim with this item was to check students' understanding of the effect of different graph behaviours on the resulting area function. However, since the given graph was a straight line through the origin, students were perhaps too easily led to recognize the parabola as the correct answer option. In the replacement item, Z26, the given graph is piecewise linear and has two options that would be plausible just from recognizing the first part should be a parabola.

The third item we modified was z34, on the equation of a plane. There were no distractors offered with the correct x, y, z coefficients, so students could perhaps too easily identify the correct option. In the replacement item, Z30, we added a distractor with the correct x, y, z coefficients so that students also had to check whether the given point lies on the plane to determine the correct option.

We also created two new items, about the vector and scalar products (Z31 and Z32). These replaced simpler vector geometry items that we had removed because they were too easy. We identified the vector and scalar products as topics for the replacement items since these play an important role in many engineering mathematics classes. Moreover, the experience of those teaching first-year students at ETH suggests that the students are mostly only able to carry out routine procedural computations with vectors (if they have been taught about them at all at school).

6. Re-analysing the test

Once the new version of the test has been completed by students, a variation of the analysis outlined in Section 4 can be used to evaluate the impact of the changes. In the following sections, we report on the key results of this analysis for each of the tests, to conclude our investigation of RQ2 (on whether the tests can be improved). Full details of the analysis can be seen for the Edinburgh MDT at https://osf.io/jqc3h/ and for the ETH s21t at https://osf.io/uybeh/.

The approach to the analysis is broadly similar, but there are key differences. First, the IRT model needs to account for having data from two versions of a test. Where the two versions of the test have many items in common, the data from both versions can be combined into one large dataset, where scores are missing for some items depending on which version of the test students completed. By fitting an IRT model with this single dataset, the item parameters are established on the same scale. This is known as concurrent parameter estimation (Jodoin et al., 2003). While other approaches are possible, we use this method because having the IRT parameters on the same scale makes it straightforward to compare them.

Another difference in the approach is that it is not possible to carry out factor analysis as a check of unidimensionality before fitting the IRT model. This is because the combined dataset has many missing values (e.g. students who took the new version of the test have no results for items that were removed), and R's factanal function does not accept missing data. Instead, we proceed directly to fitting the IRT model, then use Yen's $Q_3$ (DeMars, 2010, p. 48) to check for any dependence between items after controlling for θ. This gives a score for each pair of items, with scores above 0.2 regarded as problematic.

6.1. Edinburgh MDT

The new version of the Edinburgh MDT was first administered in September 2017. We gathered data from five cohorts of students, up to and including the 2021/22 academic year. The analysis is based on a total of 5433 students' attempts at the new version of the test (along with 3214 attempts at the original version³).

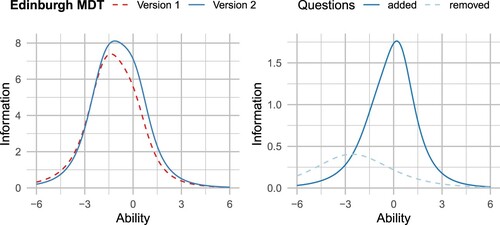
The goal of the refinement process was to increase the information in the test, by replacing three items that were among the least informative. As shown in Figure 11, this goal was achieved. The information curve for the new version of the test is attaining higher values, particularly around the mean ability level.

Figure 11. Comparison of the information curves for the two versions of the Edinburgh MDT. The left panel shows the test information function pre- and post-revisions. The right panel shows the sum of the item information curves for those items that were removed and those that were added.

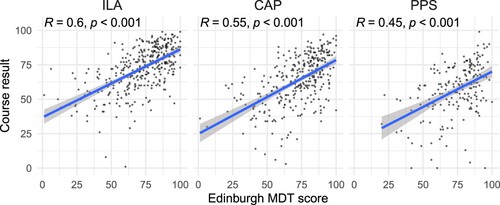
A second way of evaluating the changes is in terms of their effect on the predictive validity of the test. We previously observed that Edinburgh MDT scores were moderately correlated with results in first-year courses (see Figure 7). We repeated this analysis for the 2017–18 cohort and found that the correlation with first-year results had increased (see Figure 12). For instance, the correlation with the first-year linear algebra course has increased to R = 0.6 for the new version of the test (up from R = 0.49 for the original version).

Figure 12. Scatterplots of Edinburgh MDT scores against results in the three first-year mathematics courses: ILA (linear algebra), CAP (calculus) and PPS (proofs and problem solving), for the 2017–18 cohort. Regression lines are shown in each panel, and the text at the top of each panel shows the Pearson correlation coefficient.

While the overall picture is very positive, the analysis does still show some issues that could be addressed in a future round of refinement. For instance, the test still includes two items on the chain rule (now labelled E16 and E17). The $Q_3$ score for this pair of items was 0.27, suggesting that performance on these items is (perhaps unsurprisingly) not independent. Based on this observation, a future version of the test may only need to retain one of these items. Moreover, the test information function still has a slight skew toward the lower end of the ability scale. In light of this, a future version of the test could include a few more difficult items to provide more information at higher ability levels.

6.2. ETH s21t

The new version of the ETH s21t was administered in 2019, 2020 and 2021. From these three cohorts of students, we analysed a total of 6238 attempts (together with the 3433 attempts at the original version of the test, as in Section 4.2).

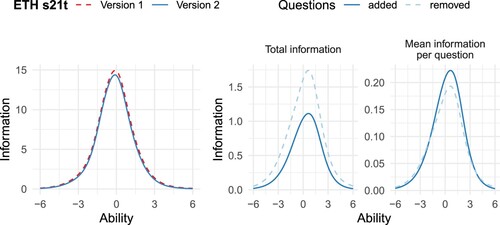
The goal was to slightly shorten the test, while retaining as much information as possible. The test information curves in Figure 13 show that, in fact, the new version of the test provides slightly lower overall information than the original version. However, since the test was shortened (9 items removed and only 5 added), this is not a like-for-like comparison. Focusing on the information provided by the items that were removed/added shows that the new items had lower total information than the ones that were removed (as shown in the central panel in Figure 13). However, after dividing this by the number of items in each group to consider the average information provided by the items, we see that the new items are in fact slightly more informative than the items they replaced (see the rightmost panel in Figure 13).

Figure 13. Comparison of the information curves for the two versions of the ETH s21t. The left panel shows the test information function pre- and post-revisions. The centre panel shows the sum of the item information curves for those items that were removed and those that were added. The panel on the right shows the mean information per item for the same two groups of items.

For the three items that we modified, aiming to increase their difficulty, there was partial success. For the exponentials item, changing from simply identifying one function's parameters (z12) to comparing the growth of two functions (Z11) saw the difficulty increase from $-1.11$ to $-0.48$. For the item on the graphical interpretation of the Fundamental Theorem of Calculus, where a linear function (z30) was replaced with a piecewise linear one (Z26), the difficulty increased from $-1.10$ to $-0.15$. However, for the item on the equation of a plane (z34 replaced by Z30), the difficulty remained very similar ($-0.52$ and $-0.59$ respectively). The change in this case was relatively minor, with only the distractors changing, so perhaps more substantial changes would be needed to make a more difficult item on this topic.

Two other new items were added, on the topic of vector and scalar products (Z31 and Z32 respectively). These both had positive difficulty parameters, placing them among the more difficult items on the test. Interestingly, their IRT parameters are quite close to those of the two items that were previously at the end of the test (z35 and z36 about planes, both of which were removed). For a future version of the test, it would be interesting to vary the order of the items, to check whether test fatigue is affecting students' performance toward the end of the test.

7. Discussion

We have described and applied a method for improving a mathematics diagnostic test that incorporates the use of item response theory. Our examples show how the approach can be used with multiple-choice tests (such as the ETH s21t) or with tests that award partial credit (such as the Edinburgh MDT). In each case, the IRT analysis enabled us to make improvements to the test by identifying the least effective items and replacing them.

Our first research question was, for each test, ‘how well does the test perform its function’. The results in Section 4 showed that both tests were already performing well. In particular, the IRT parameters were generally within acceptable ranges, and the overall test information functions (Figure 6) showed that both tests were giving a good level of information across a wide range of student abilities. Moreover, for the Edinburgh MDT, we were able to link test scores with performance in first-year courses, and we observed a moderate correlation (e.g. R = 0.49 with results in the semester 1 course in linear algebra). These results support the tests being used as intended purposes, such as advising students about their strengths and weaknesses (as discussed in Section 3).

Next, we sought to make improvements to both tests, addressing our second research question (can the test be improved based on insight gained from statistical analysis?). In Section 5, we described the process that we used to identify items that were relatively poorly-performing and to create replacements for them. Our analysis of the new versions of the tests (in Section 6) showed that in most cases the changes were successful in making the tests more informative about students' abilities.

For the Edinburgh MDT, we were able to measure the correlation with results in first-year mathematics courses. Correlation with important outcomes is a routine way of judging the effectiveness of tests (American Educational Research Association et al., 2014). The revised version of the test has substantially higher correlations than the previous version (e.g. from R = 0.49 to R = 0.6 for the linear algebra course). This result underlines the potential for our approach to improve not only the IRT measures, but other metrics for the reliability and validity of a diagnostic test.

A possible concern is that some of our data was gathered during the Covid-19 pandemic, which has caused widespread disruption to education. However, the refinement process took place well before the pandemic, so our analysis of the changes was not affected. For both tests, the pattern of results for the revised version is remarkably similar before and during the pandemic, particularly in light of concerns about the impact of the pandemic on learning in secondary schools. Of course, both institutions attract students who are among the most highly-performing in their cohort, so we do not wish to make any general claims – except to highlight that the pattern of diagnostic tests results provided useful information for both institutions at the start of the 2020–21 academic year, showing that incoming students were performing at a similar level to previous cohorts. Similarly, other institutions were able to use their diagnostic test results to obtain a clearer picture of the impact on incoming students' preparedness for their studies (see, e.g. Hodds, 2021).

A further concern is about the data cleaning process, for the Edinburgh MDT in particular (discussed in Section 4.2). Since students may abandon their online attempts, our data included several cases that could potentially paint a misleading picture about items' difficulty (particularly toward the end of the test). We set out to identify abandoned attempts based only on the scores that were available to us. Filtering our data in this way did have an effect on the results; repeating the analysis without removing these attempts produces a different factor structure and IRT parameters. We believe our filtering approach was appropriate, and the results presented here best reflect the properties of the items, because students who abandon their attempts will not be looking to make inferences about their preparedness based on the test score. Others looking to follow our approach will similarly need to consider which responses to include in their analysis.

More generally, the effort involved in understanding and implementing the IRT models may be offputting, particularly when simpler approaches based on classical test theory are available. While we have not carried out a full analysis based on classical test theory, we did compute facility values (i.e. mean scores) and these did not highlight the issues with items that we identified using the IRT analysis. We found the item information functions from IRT to be particularly helpful in identifying which items were providing the most/least information about students of a given ability level, and targeting our changes accordingly. We hope that the model we have provided, along with reusable R scripts at https://github.com/georgekinnear/diagnostic-test-irt, will help others to apply IRT more readily.

Acknowledgments

This project was supported with funding from the Principal's Teaching Award Scheme at the University of Edinburgh and from the Swiss-European Staff Mobility Programme at ETH Zurich. Thanks are due to the other project team members in Edinburgh: Tereza Burgetova, Joanne Ruth Imanuel and Chito Wong (who carried out the initial version of the statistical analysis); Chris Sangwin and Toby Bailey (who contributed to the analysis and design of replacement items). Mine Çetinkaya-Rundel provided valuable help with the R code. We also thank colleagues at ETH Zurich for their contributions: Heinz Rasched (who carried out initial statistical analysis of the s21t) and Alexander Caspar (who contributed to the analysis and design of replacement items).

Data availability statement

The supporting data and code is openly available at https://doi.org/10.17605/osf.io/bxwh9.

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes

1 The essential idea and interpretation of the item information curves is the same for the GPCM used to analyse the Edinburgh MDT. For details, see DeMars (2010, pp. 80–83) or De Ayala (2008, Chapter 8).

2 further details about the non-specialist stream can be found in section 4.2 at https://osf.io/pr3m7/

3 Note that this is 7 fewer than in the original analysis in Subsection 4.2, since a small number of students repeated a year of study and therefore completed both versions of the test; we retained their best result for the analysis.

Appendix 1.

ETH s21t: revised items