Toward a unified account of definitions in mathematics education research: a systematic literature review

Abstract

In this paper, we provide a conceptual framework of the central aspects of mathematical definitions discussed in the mathematics education literature. Based on a systematic literature review, we found that characterizations of definitions in the mathematics education literature can be classified into five main themes: requirements, preferred features, role and function, nature, and types of definition. Within each theme, a refined set of aspects was found by means of inductive coding. We discuss each aspect and point out areas where we believe further research is needed. The framework can be used both as a research tool and a didactical tool, as it highlights many aspects of mathematical definitions that call for attention by teachers and researchers.

KEYWORDS:

• Mathematical definition
• literature review
• mathematics education
• teacher education
• reasoning
• definition roles
• definition nature
• definition requirements
• definition features

1. Introduction

What is the definition of a mathematical definition? Philosophers of mathematics, such as Whitehead, Russell, Frege, and Wittgenstein, have contemplated this question without reaching clear answers (McGuinness, 1984; Weiner, 1990; Whitehead & Russell, 1912; Wittgenstein & Bosanquet, 1989). This is perhaps evidence for a view that there cannot be a definition of mathematical definition, or at least not a trivial one. Consequently, practitioners of mathematics must come to their own understanding of what mathematical definitions entail. Nonetheless, there are examples of agreed-upon rules by which mathematical definitions should abide (e.g. Edwards & Ward, 2008; Van Dormolen & Zaslavsky, 2003). Rather than being normative in nature, these rules may be better described as advice for best practices.

Students involved in mathematical activity are expected to prove mathematical statements. These can be algebraic proofs using only symbols but also representation-based proofs (Schifter, 2009) and generic examples (Balacheff, 1988; Stylianides, 2007; Stylianides & Stylianides, 2009). Definitions are essential ingredients in a mathematical proof, which means that students, just as mathematicians, need to consult and use definitions. For example, if one wishes to prove that the product of two even numbers is even, then it is necessary to use definitions of ‘even number’ and ‘product’.

While mathematicians seem to have a common understanding of the nature and use of mathematical definitions (Parameswaran, 2010), research shows that students do not necessarily share this understanding (Edwards & Ward, 2004). Mathematical definitions are stipulated (formal definitions that determine the one and only meaning of a term), but some students may see them as extracted (everyday definitions or dictionary definitions of words), that is to say, merely a description of something. In the language of Tall and Vinner (1981), their concept image may override the concept definition, which has been exemplified by Edwards and Ward (2004).

To support further investigation into students’ deductive reasoning and proving, it is important to know which aspects of mathematical definitions are relevant, discussed and highlighted in the mathematics education literature. Although this literature is rich in discussions about mathematical definitions, the many aspects of definitions that are addressed in the literature have not been collected in a coherent framework. In an effort to build such a coherent framework for mathematical definitions, we conducted a systematic literature review to answer the following research question:

How are mathematical definitions characterized in the mathematics education literature?

2. Methodology

To answer our research question, we conducted a literature review to examine the research on aspects of mathematical definitions in the field of mathematics education. We followed the guidelines by Arksey and O’Malley (2005): (1) identifying the research question, (2) identifying relevant studies, (3) study selection, (4) charting the data, and (5) collating, summarizing, and reporting the results.

Our main goal was to collect papers that addressed mathematical definitions as objects themselves (i.e. definitions being (one of) the object(s) of study) or that contained characterizations of mathematical definitions in general. A systematic literature search was therefore carried out to find academic publications that considered mathematical definitions in mathematics education. A coding process was then conducted on the raw material.

2.1. Sample

We employed a systematic, but not exhaustive, search following guidelines provided by Arksey and O’Malley (2005) and Lipsey and Wilson (2001). In the initial search, a publication was deemed relevant if it met the following inclusion criteria: the publication (1) was related to mathematical definitions, (2) had a didactical focus, and (3) was published in a peer-reviewed journal, peer-reviewed conference proceeding, or book.

The databases used to conduct the search were the Educational Resources Information Center (ERIC) and Scopus. Our search criteria within these databases were identical and as follows: both ‘mathematics’ and ‘definition’ in the title, abstract, or keywords/descriptor, and ‘education’ in any field. After this main search, we used the search engines’ exclusion functionalities. Details on this process are outlined in Appendix B.

This yielded a total of $n=1493$ publications (ERIC $n=619$, Scopus $n=874$). The search results were then exported to the ‘ris’ or ‘nbib’ file format. Scopus allows a search result to be exported with abstracts, while for the ERIC results, we retrieved the abstracts manually. To remove duplicates (both across the databases and within each) we used a Python script that programmatically determined the similarity of papers by comparing the ratio of similarity (as text strings) of the abstracts and title. After manually confirming and removing duplicates, we were left with $n=1253$ papers.

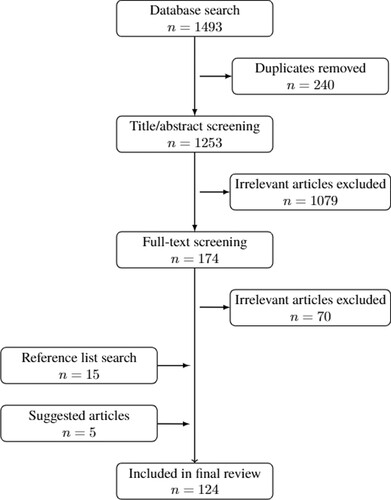
The sample was then further examined in a two-step process. First, papers were assessed by their titles and abstracts, and papers not fitting with the inclusion criteria were discarded ($n=1079$). Many of those papers were publications in fields other than mathematics education that still contained the inclusion search words.

The remaining 174 candidate articles were further scrutinized by reading the papers. Upon reading the papers, $n=70$ publications were deemed irrelevant and excluded. The inclusion criteria in this process were as follows: (1) mathematical definitions were (one of) the main object(s) of study, or (2) general characterizations of mathematical definitions were explicitly mentioned. In this process, we first conducted a digital search for the word definition in each of the papers to get an overview. Many of the excluded papers were publications in the field of mathematics education that contained the word definition in, for example, the data materials, as examples, or as part of tasks given to informants, but did not address them as objects or mention any general characterizations. In the cases where it was unclear if statements in a paper were general characterizations of mathematical definitions, the paper was either included, or great care was taken to ascertain that the points had appeared elsewhere in the reviewed literature.

To mitigate publication bias, we examined the bibliography of the refined sample to reveal potentially relevant publications not included in the database searches. This resulted in $n=15$ additional publications.

After conducting the analysis and writing down our results, additional publications were suggested as potential candidates by colleagues and peers who read the paper. The steps described above were carried out on those papers, which resulted in $n=5$ additional publications. The analysis procedure described in the next section was also applied to these additional papers.

This literature search strategy resulted in a final sample of $n=124$ publications (see Appendix B). A flow chart of the search strategy is outlined in Figure 1.

Figure 1. Systematic review search strategy.

2.2. Analysis

The data analysis was conducted in a multi-step process. As a first step, the first authors read the papers in the data set and highlighted quotes and paragraphs concerned with mathematical definitions. These paragraphs were then extracted from the selected papers and collected in a common list. Duplicate entries in this list were then removed.

Next, the quotes and paragraphs were coded openly in an inductive manner by the first authors individually. Paragraphs that addressed mathematical definitions as objects or described characterizations of definitions in general were extracted from the data and collected in a common list. Duplicates were then removed as in the first step described above. In this process, we looked for statements like ‘definitions must be’, ‘definitions should’, ‘definitions are’, ‘definitions are used’, and so on. Both steps had to be carried out qualitatively and manually, especially because not all statements contained the word ‘definition’, and because, in some cases, we had to interpret the statements to decide if they were general characterizations or not. This was first done individually, and then in a discussion group, to reach an agreement.

Subsequently, codes with common themes were merged individually by the first authors (Mayring, 2000). Obviously equivalent statements were merged first, i.e. statements that only differed in their phrasing. As a final step, a further refinement of the themes was reached by another pass of inductive coding within each theme in the previous step, both individually and in a discussion group. For example, ‘a definition should be minimal’ and ‘definitions should be economical’ were deemed to be sufficiently related to be merged into the theme Minimality, even though they do not necessarily mean exactly the same thing. Another example is the statement that a definition should ‘allow to discriminate between instances and non-instances’ and the criterion of ‘existence’ of at least one instance of the defined concept. The first statement says that it should be possible to decide if an example is an element of the example space defined, while the second states that the example space cannot be empty. Although they are not saying the same thing, they both deal with the example space of the defined concept and were placed under the theme Exemplification. The differences between such statements are explained in the results section.

For every coding pass, each first author conducted individual coding, after which a discussion of the proposed categorizations was carried out, and a final agreement on categorization was reached.

3. Descriptive overview

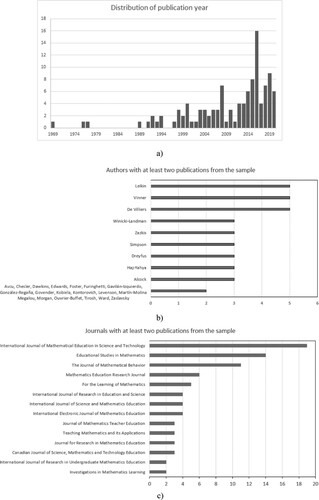
The systematic literature search yielded 124 publications from journal articles, conference papers, book chapters, and books. The years of publication of the sample range from 1969 to 2022; Figure 2(a) shows a bar chart of the distribution of publication years. A total of 202 different authors were present in the sample, and Figure 2(b) shows authors with multiple publications. The publications in the top five most frequent journals amounted to approximately 44% of the entire sample. Figure 2(c) shows a bar chart of the most frequent journals in the sample.

Figure 2. Graphical visualization of selected statistics about the sample.

4. Four main themes for characteristics of mathematical definitions

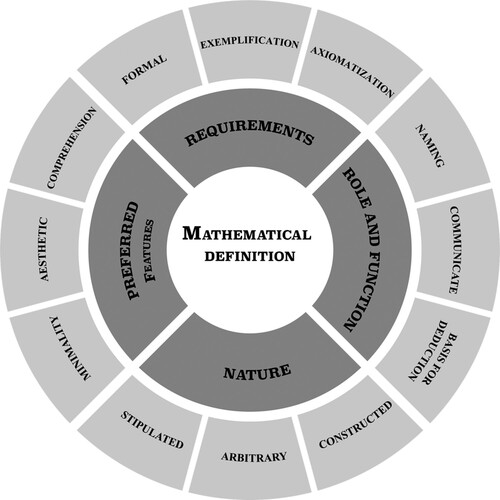
Our analysis revealed five emergent themes for how researchers in mathematics education characterize mathematical definitions. Four themes (Nature, Requirements, Preferred Features, and Role and Function) included characteristics of mathematical definitions, and are summarized in Figure 3. The fifth theme, Type, was qualitatively different from the other themes. Rather than a collection of characteristics, Type describes definitions as a two-dimensional construct. Therefore, it does not appear in Figure 3 but is described in Section 5. In the following sections, we present each theme with its corresponding categories, as well as statements and quotes from the source literature. Statements from the literature appear in italics.

Figure 3. The four main themes with corresponding categories.

4.1. Nature

We found an emerging theme that dealt with definitions on a meta-mathematical level, namely aspects relating to the intrinsic properties of mathematical definitions. This theme can be thought of as properties of mathematical definitions as meta-mathematical objects, that is to say global descriptors of mathematical definitions as constructs in mathematical science.

4.1.1. Stipulated

Mathematical definitions are stipulated (Vinner, 1991) as opposed to extracted (lexical). Extracted definitions explain how a word is used by people, often through examples. This can be thought of as an a posteriori or descriptive definition (e.g. Foster, 2014; Foster & de Villiers, 2015; Ouvrier-Buffet, 2010). Stipulated definitions are formal (e.g. Van Dormolen & Zaslavsky, 2003) and rigorous (e.g. Poincaré, 1969; Zazkis & Leikin, 2008) and determine the one and only meaning of a term. Terms used in a stipulated definition are placed in a new context and have only the meaning that is stated in the definition. All previous meanings of the term (if there are any) are irrelevant. The term obtains a new meaning, and previous associations of the term must be disregarded. Stipulated definitions have no truth value, as opposed to extracted definitions (Bayda & Sutliff, 2020). What this means is that extracted definitions are not always true, and they do not capture the essence of a concept completely. A chair can be defined in a dictionary as something you can sit on that usually has four legs and a rest for the back, but most people would accept a chair with three legs and no rest for the back. From the context, one would disallow the chair of a research committee. Stipulated definitions, on the other hand, are free from connotations, especially from everyday usage of the terms.

Foster (2014) used the term prescriptive to describe the stipulative property of mathematical definitions, that is, mathematical definitions prescribe the only correct meaning of a term. Others have dubbed this notion as a priori (De Villiers, 1994) or constructive (Foster & de Villiers, 2015).

An example of the relevance of this property to mathematics education is found in the work of Edwards and Ward (2004), who studied how students understand and use definitions. They found that some students, unlike mathematicians, view mathematical definitions as extracted rather than stipulated. This view profoundly impacted the students’ mathematical reasoning, and the researchers concluded that even if a student can recite a definition, it does not mean that the student understands the definition. They also found that, in some cases, these students were unable to appropriately use a definition that they seemingly understood and was available to them.

4.1.2. Arbitrary

There may be many equivalent definitions of a concept. The choice of statement to use as a definition for the concept is arbitrary, and the other equivalent definitions become theorems that give necessary and sufficient conditions for the concept (e.g. Leikin & Zazkis, 2010; Levenson, 2012; Üreyen, 2006; Vinner, 1991; Winicki-Landman & Leikin, 2000; Zaslavsky & Shir, 2005). Of course, this does not mean that the choice of definition among a set of equivalent definitions is random. Definitions are chosen for a purpose (Usiskin et al., 2008), and there can be both didactical and mathematical reasons for making this choice. For example, Harel et al. (2008) suggest in their research that if students are not aware that definitions are carefully chosen for a purpose, it is unlikely that they will go beyond just memorizing them.

Two equivalent definitions may highlight different aspects of a concept, and thus they may lead to different mathematical activities (Morgan, 2005). For example, consider the following two equivalent definitions of an even number: (1) An even number is a number that can be divided into two equal groups. (2) An even number is a number for which the last digit is 0, 2, 4, 6, or 8. The two definitions are equivalent, but they highlight different aspects of even numbers. The first definition highlights that an even number is divisible by two and that if we have an even number of marbles, we can share them fairly among two children. The second definition does not highlight these properties but provides a procedure to determine if a symbolic number is even. If a student is asked to prove that an even number multiplied by an even number is even, then the two definitions above would most likely produce different arguments (and mathematical activities).

4.1.3. Constructed

Whether a mathematical concept is discovered (i.e. naming pre-existing objects) or constructed is a matter of one’s philosophical persuasion. The main position of the reviewed papers, however, is that mathematical definitions are constructed. De Villiers (1998), for instance, maintained that the act of defining is a central mathematical activity, in which concepts are constructed or defined ‘into being’. Morgan (2005, p. 111) states that ‘[definitions] are the product of human activity’.

Likewise, Burn (as cited in Morgan, 2005) stated that.

The research mathematician may come to his results starting from special cases, which will appear as corollaries in the final version, from which he gets his ideas, which is worked with until he has a proof. Then the theorem is what has been proved. At this point he formulates his definitions so as to make the theorem and proof as neat as possible.

Others have made similar claims (e.g. Chesler, 2012; Viirman, 2013; Fisher, 2016, Kobiela et al., 2022). In sum, the reviewed papers portrayed an image of mathematicians who construct definitions (in a shared community), and that definitions are under constant development, driven by a need. Students are, as we have pointed out earlier, expected to be involved in the proving processes, but we observe the importance of students also being involved in the defining processes and constructing their own definitions (Borasi, 1992; De Villiers, 1998; Zandieh & Rasmussen, 2010).

4.2. Requirements

Several of the publications in the sample presented criteria for the definition formulation and imperative features of definitions (e.g. Van Dormolen & Zaslavsky, 2003; Zaslavsky & Shir, 2005). Naturally, this became an emerging theme. Statements were further refined into three categories, which we describe below.

4.2.1. Formal

This category encompasses the local criteria for a definition, namely, criteria to which a definition formulation must adhere.

According to Chesler (2012), Sánchez and García (2013), and Johnson et al. (2014), a definition must be consistent and non-contradicting. It must be consistent with the mathematical theory formed thus far. Furthermore, it must be well-defined (Tay & Leong, 2012); that is to say, the meaning is unambiguous (Burroughs & Burke, 2016; Foster & de Villiers, 2015; Morgan, 2005, 2006).

For example, if we view $\mathbb{Q}$ as $\left(\mathbb{Z}\times \mathbb{Z}\right)/\sim$, where $\left(a,b\right)\sim \left(c,d\right)$ if $ad=bc$, and (make an attempt to) define $f:\left(\mathbb{Z}\times \mathbb{Z}\right)/\sim \to \mathbb{Z}$, where $f\left(a,b\right)=a+b$, then $f$ is not well defined, since $f\left(1,2\right)\ne f\left(2,4\right)$. Of course, this is transferable to fraction notation. A mathematician must often prove that a definition is well defined, especially when dealing with equivalence classes. In general, a definition must be invariant under which representatives are chosen in the equivalence classes.

We have not found any examples of well-definedness suitable at the elementary school level in the literature. However, we can perhaps imagine a young student defining even numbers to be every other (whole) number on the number line. While the statement is true, it is not a well-defined definition, because it could describe either the odd or the even numbers depending on which number the number sequence starts from.

4.2.2. Exemplification

A multitude of sources contained statements pointing to the importance of the existence of an example/instance of a definition. That is, there must exist at least one example of the defined concept (e.g. Avcu, 2019; Edwards & Ward, 2008; Van Dormolen & Zaslavsky, 2003). Every definition must allow discrimination between instances and non-instances (e.g. Avcu, 2019; Edwards & Ward, 2004; Johnson et al., 2014; Morgan, 2005, 2006; Sánchez & García, 2013).

A definition is also given within a representation system and must be invariant under change of representation (see Sánchez & García, 2013; Zaslavsky & Shir, 2005). For example, consider the following definitions. (1) A number of unifix cubes is an even number if the unifix cubes can be divided into two equal groups. (2) An even number $a$ is a number that can be written as a sum of two equal natural numbers (i.e. can be written as $a=b+b$, where $b\in \mathbb{N}$). The two definitions are structurally the same; however, two different representation systems are being used.

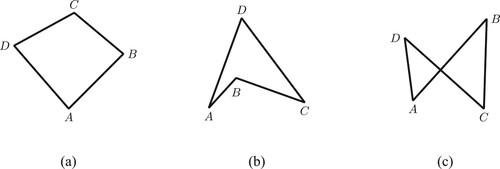
Moreover, the example space of a mathematical definition may yield degenerate instances (Van Dormolen & Zaslavsky, 2003), specifically, unwanted instances of the mathematical definition that are not in accordance with our intuition of the mathematical concept. For example, Van Dormolen and Zaslavsky (2003) give as an example the following definition of quadrilaterals:

Definition. A quadrilateral is a set of four points $A,B,C,D$ of which no three are collinear, and four segments $AB,BC,CD$ and $DA$.

This definition will result in a quadrilateral of one of three shapes (see Figure 4). Van Dormolen and Zaslavsky (2003) point out that although all of the shapes fit the definition, some would consider Figure 4(c) to be a degenerate quadrilateral. Furthermore, there are reasons to exclude Figure 4(c) as a valid quadrilateral. For example, the theorem of interior angle sum of a quadrilateral would no longer be valid (unless we consider the intersection of the two edges, but then we would have six interior angles). Even more so, the term interior angle would be difficult to interpret in a meaningful manner.

Figure 4. Three quadrilaterals that satisfy the definition.

4.2.3. Axiomatization

The global ecosystem in which the definition formulation lives was emphasized in several sources (see Miller, 2018; Van Dormolen & Zaslavsky, 2003; Winicki-Landman & Leikin, 2000). This category may be thought of as the global criterion for a definition formulation. A definition is part of a deductive system, in a hierarchical and noncircular manner within itself and across existing axioms, definitions, and theorems (e.g. Aktaş, 2015; Avcu, 2019; Morgan, 2005; Sánchez & García, 2013; Wong et al., 2014). Thus, the formulations must be consistent within this frame of reference. A definition of a concept may employ only previously defined concepts; that is, the concept at hand is a special case of a more general concept (Van Dormolen & Zaslavsky, 2003). For example, an even number is a special case of a number, continuous function is defined by the more general concept of a function, a rectangle is a particular quadrilateral, and so on. The criterion of axiomatization ensures that new concepts are defined by means of already defined concepts, and the graph of concepts (there is a directed edge between two concepts if one is a special case of the other) gives an acyclic directed graph. Didactically, this would mean that a definition should only contain concepts that are known in the given community (Winicki-Landman & Leikin, 2000). However, according to Morgan (2005) and Aktaş (2015), an exception should be made for the case of implicit definitions.

Moreover, equivalence frequently appears in the reviewed literature. If there are multiple formulations of a given concept, they have to be mathematically equivalent (e.g. Avcu, 2019; Megalou, 2018; Van Dormolen & Zaslavsky, 2003; Zazkis & Leikin, 2008). For example, a square may be defined as (1) a rhombus with right angles or (2) a quadrilateral with four mirror and four rotational symmetries. That these formulations yield the same mathematical object must be mathematically proven. Of course, this is closely related to the arbitrary nature of mathematical definitions.

4.3. Preferred features

Statements that were considered to be preferred features of mathematical definitions, but not absolute mathematical requirements, were collected under this theme. This involves both mathematical and didactical features. Three categories of preferred features were found: minimality, aesthetic, and comprehension.

4.3.1. Minimality

A definition should be economical and minimal (e.g. Vinner, 1991). Minimality means that no condition in a definition can be inferred from the other conditions; that is, there is no redundancy. If we remove one condition from a minimal definition, the example space becomes properly larger. Economical can, for example, be interpreted as a definition with as few words as possible.

In the literature we reviewed, the notion of minimality appears frequently, and there has been some discussion as to whether it should be a requirement or a preferred feature (see e.g. Zaslavsky & Shir, 2005). Leikin and Winicki-Landman (2000, p. 27), for example, claim that.

… [a] mathematical definition should be minimal, we accept this requirement as essential not only from an aesthetic point of view but also from a mathematical perspective.

On the other hand, Van Dormolen and Zaslavsky (2003, pp. 96–97), state that

[O]ften at the time when a concept is defined there may not be sufficient knowledge to determine whether it is minimal. […] In order to get a sound and rich mental image of the new concept, it can be advantageous to start with a description that does not satisfy the criterion of minimality.

Borasi (1992) used the term essentiality, which can be expressed as being a middle-ground approach to the notion of minimality. By that she means that we must only mention necessary terms and properties so that it is possible to distinguish an instance from a non-instance. The majority of the papers, however, either view minimality as a preferred feature (e.g. Leikin & Zazkis, 2010) or recognize that it is debatable whether it is required or not (Zazkis & Leikin, 2008; Ulusoy, 2021; Avcu, 2022). In doing so, they reason that, while a minimal definition is preferred, it may not be the most accessible from a didactical perspective (Avcu, 2022; Van Dormolen & Zaslavsky, 2003; Zaslavsky & Shir, 2005).

To mitigate the obstruction of learning due to minimal definitions, Zazkis and Leikin (2008) introduced the term barely-not-minimal, as definitions that use appropriate terminology and contain necessary and sufficient conditions without being minimal (Johnson et al., 2014, p. 288) (c.f. essentiality). For example, a rectangle can be defined as a parallelogram with four right angles. This definition is not minimal since it contains a theorem. It is sufficient to require a parallelogram to have a single right angle, from which it follows that all the angles are right angles. However, in certain circumstances, it is minimal enough.

4.3.2. Aesthetic

Arguably the most subjective of our categories, whether a definition is considered aesthetically pleasing is highly individual and context dependent. However, it is often mentioned in the literature that a definition should be elegant (e.g. Winicki-Landman & Leikin, 2000; Zandieh & Rasmussen, 2010; Zazkis & Leikin, 2008), precise (Levenson, 2012), or clear (Leikin & Winicki-Landman, 2000; Levenson, 2012; Miller, 2018). Minimal definitions are also considered to be more elegant.

One example, given by Vinner (1991), is the following two definitions of the absolute value of a real number $x$. (1) $\begin{array}{rl}|x|& =\{\begin{array}{ll}x& \text{if }x\ge 0\\ -x& \text{if }x<0\end{array}\end{array}$(1) (2) $\begin{array}{rl}|x|& =\sqrt{x^2}\end{array}$(2)

While both definitions are correct and equivalent (and even minimal), one can argue that (2) is a more elegant definition than (1) since (2) uses fewer words and symbols, and in some cases (2) might be a more convenient definition for proving certain results. However, it can also be argued that definition (1) in a better way illuminates the concept of the absolute value of a real number.

This shows that what is considered more elegant in a pure mathematical context is not necessarily more elegant, or even preferred, in a didactical context. Aesthetics are therefore highly dependent on the situation.

Clarity and precision are also considered to be aspects of comprehension, as discussed in the next section.

4.3.3. Comprehension

This category includes statements about features of definitions that facilitate teaching and learning. A definition used in schools should be didactically suitable (e.g. Poincaré, 1969; Winicki-Landman & Leikin, 2000; Zazkis & Leikin, 2008). The literature highlights intuitive (Ouvrier-Buffet, 2010; Zazkis & Leikin, 2008), understandable, precise, and clear definitions. According to Leikin and Winicki-Landman (2000), a definition must match students’ knowledge and needs. Definitions are also considered as starting points to understand the meaning of a concept (Ertekin et al., 2014; Yavuzsoy-Köse et al., 2019).

Furthermore, a definition is said to be formally operable for an individual, if that individual is able to use it in creating or (meaningfully) reproducing a formal argument (Bills & Tall, 1998). Burroughs and Burke (2016) use the term referential clarity when a definition has easily identifiable examples and is closely related to its natural language usage.

Comprehension is also tied to the arbitrary nature of mathematical definitions. As pointed out in Section 4.1.2, the choice of mathematical definitions might have some impact on mathematical activity (Morgan, 2005). Chesler (2021) showed that the choice of definition of a function had some influence on informants’ ability to use the definition.

4.4. Role and function

Another emerging theme in the literature was the role and function of mathematical definitions. Mathematical definitions play a significant role in the development and learning of mathematics. Definitions function as vessels of mathematical concepts in the mathematical discourse, and, alongside logic, they are the foundations of mathematical deductive proofs.

4.4.1. Naming

Mathematical definitions operate as necessary tools for naming a collection of objects or a phenomenon and introducing new notations (e.g. Leikin & Winicki-Landman, 2001; Miller, 2018; Winicki-Landman & Leikin, 2000). That is, they are used to ‘replace something with something else’. Zazkis and Leikin (2008, p. 133), for example, state that defining is giving a name. Although this is mentioned in the context of logical principles a mathematical definition must follow, we interpret this to be an important purpose rather than a requirement of a mathematical definition. Moreover, according to Robinson (as cited in Edwards & Ward, 2008), stipulated definitions are an explicit and self-conscious setting up of the meaning-relation between some word and some object, the act of assigning an object to a name (or a name to an object).

4.4.2. Communicate

A necessary role that mathematical definitions serve is to allow practitioners to communicate mathematical ideas efficiently (Gilboa et al., 2018, p. 440). Precise definitions are paramount for developing deductive arguments and conveying them to one’s peers (Alcock & Simpson, 2016, p. 5). Poincare (as cited in Johnson et al., 2014) highlights that mathematical definitions serve the role of vehicles for the communication of concepts. Mathematical definitions allow communication through creating uniformity in the meaning of concepts (Borasi, 1992). Students must use stipulated definitions to take part in a mathematical discourse, and these definitions allow students to communicate ideas, defend their reasoning, construct arguments, and draw logical conclusions. Furthermore, using stipulated definitions correctly is one way for students to demonstrate mathematical literacy (Bayda & Sutliff, 2020, p. 2).

4.4.3. Basis for deduction

Mathematical definitions are tools that mathematicians use to reach agreements about the nature and properties of mathematical objects (Tabach & Nachlieli, 2015). Moreover, mathematical definitions are the basis for logical derivation, used for deduction and structuring proofs, and they function as the foundation stone of mathematical thinking (Yavuzsoy-Köse et al., 2019) and lay the foundations of proving and problem-solving (Şen, & Güler, 2022). Definitions are constructs that extend our understanding of mathematical domains, and definitions that are fruitful in quickly enabling meaningful deductions in new domains are held in high regard (Burroughs & Burke, 2016).

Furthermore, mathematical definitions make it possible for mathematicians to classify mathematical objects (e.g. Zaslavsky & Shir, 2005; Alcock & Simpson, 2011), as well as to systematize existing knowledge and produce new knowledge (Yavuzsoy-Köse et al., 2019). To emphasize the importance of the use of mathematical definitions, Bills and Tall (1998) introduced the notion of formally operable definitions as a qualitative measure of whether an individual is able to employ the definition in a meaningful manner, that is to say, using it in creating or reproducing a formal argument. Among others (see e.g. Dawkins, 2014; Zaslavsky & Shir, 2005; Zazkis & Leikin, 2008), Morgan (2006) points to a definition’s usefulness and applicability as aspects to consider. A definition is stipulated with a purpose and chosen for a deliberate reason, for example to make theorems, to structure proofs, and to communicate. This also taps into the nature of definitions – they are constructs of human activity and driven by a (specific) need.

One example of the usefulness of a definition and its suitability for enabling meaningful deductions in new domains is the notion of generality or how generalizable a definition is (Burroughs & Burke, 2016). A definition is generalizable if it easily extends to other closely related domains, and Usiskin and Griffin (as cited in Burroughs & Burke, 2016) give an example of the definition of interior angle in Euclidean geometry; the definition based on the intersection of two half-planes easily extends to hyperbolic geometry. Martín-Molina et al. (2018) characterized how mathematicians construct new definitions by generalizing other existing definitions, and Kobiela et al. (2022), point out how definitions play an important role in constructing new definitions.

Definitions may therefore support the development of new definitions, both equivalent and non-equivalent. For example, the definition ‘a number of unifix cubes is an even number if we can pair two and two cubes such that no cube is left over’ does not extend to negative numbers, but the definition ‘an even number is a multiple of two’ easily does (the example space is extended). In abstract algebra a vector space is often defined with a (rather long) list of properties. However, we can define a vector space V to be an $R$-module, where $R$ is a ring, by simply requiring that $R$ is a field (the example space becomes properly smaller, i.e. all vector spaces are modules, but not all modules are vector spaces).

We note here that Leikin & Zaskis (2010) use generality somewhat differently; that is the ability to provide examples that are specific and precise rather than general descriptions.

5. Types of definitions as a fifth main theme

A multitude of types of definitions was described in the literature. This theme was not included in the above discussion and Figure 3 since we view this theme as independent of the other characteristics. We therefore describe this theme separately.

In some cases, there were several different names for the same type of definition. From the data analysis, we identified two independent categories (dimensions) of types of mathematical definitions. A priori, these categories are regarded as dichotomous categories. However, we do not rule out the possibility of mathematical definitions that do not exclusively belong to one category or the other.

Furthermore, it is possible to regard these dimensions as facets of the global and local aspect of mathematical definitions: procedural vs. structural (local) and inclusive vs. exclusive (global).

5.1. Inclusive vs. exclusive

A definition can be inclusive or exclusive (e.g. De Villiers, 1994; Usiskin et al., 2008; Winicki-Landman & Leikin, 2000, Butuner & Filiz, 2017). A definition is exclusive (partitional) when it describes only the concept at hand and excludes special cases as instances; that is, special cases, in the conventional hierarchical structure are regarded as unwanted degenerations. A definition is inclusive (hierarchical) when sets of more particular concepts are subsets of the more general concept. De Villiers (1994) gives as an example the classification of quadrilaterals: in the hierarchical classification, a square is a special case of a rectangle, while in the partitional classification the rectangle and square are considered as disjoint classes of quadrilaterals.

The term exclusive (partitional) is, to some degree, a result of a theme found in students’ perception and desire to specify concepts as narrowly as possible (e.g. De Villiers, 1994; Fujita, 2012; Leikin & Winicki-Landman, 2000). The research suggests that some students want, for example, the definition of a parallelogram to exclude the rhombus as a special type of parallelogram (De Villiers, 1994). There is also the particular case of the trapezoid, for which there are two schools of thought: one in which a rectangle is a special case of trapezoid (a trapezoid has at least one pair of parallel sides) and one where it is not (a trapezoid has exactly one pair of parallel sides).

This dimension can be thought of as a global aspect of mathematical definitions. That is to say, if one regards mathematics as a stratification of mathematical concepts, the conventional way to regard mathematics is as a highly connected hierarchical system of concepts, with chains of concepts where concepts are linked by level of generality (e.g. the hierarchical structure of quadrilaterals).

To clarify this, the convention in mathematics is to strive for hierarchical mathematical definitions. De Villiers (1994) argues that this perspective may yield a much more fruitful understanding of mathematics in general, and specifically of mathematical concepts.

5.2. Procedural vs. structural and static vs. dynamic

The literature under review described two forms of definition formulations. On the one hand, a mathematical concept can be given as the outcome of a prescribed process (procedural) (e.g. Borasi, 1992; Gilboa et al., 2018; Zaslavsky & Shir, 2005). Specifically, it describes a procedure in which the outcome will result in an instance of the mathematical concept. For instance, the algorithm for the construction of the perpendicular bisector is a procedural definition for the perpendicular bisector. On the other hand, it is possible to define the perpendicular bisector of a segment as a locus, that is the set of points that are equidistant from the endpoints of the segment. Thus, the concept is prescribed by defining the intrinsic structure (structural) of the concept (e.g. Borasi, 1992; Gilboa et al., 2018; Zaslavsky & Shir, 2005).

Raychaudhuri (2008) suggests two categories, namely static and dynamic definitions. A static definition is a definition in which the object being defined is generated by the property stated in the definition (Raychaudhuri, 2008, p. 163), Raychaudhuri gives the example of the definition of the additive inverse of a number $a$, where -$a$ is generated by a calculation given in the definition. A dynamic definition is a definition of an object that cannot be generated by the definition itself, that is, the process of generating the object is not explicitly stated in the definition.

6. Criteria for mathematical definitions

A question that inspired our investigation was what a definition of a mathematical definition could be. We do not aim to answer this question in its entirety. However, in the literature under review, we found a total of 12 different criteria or requirements for a mathematical definition. The term criterion was used by some of the authors of the sample, while others used phrasings such as ‘a definition must’ have an imperative feature or required property. Here, we use criterion as a collective term that encompasses all of the aforementioned terms and phrasing. The criteria are collected in Table 1, and an overview of which publications in the sample the criteria can be found is provided in Appendix A.

Table 1. A compiled list of criteria for a mathematical definition found in the sample.

Name of Criterion	Description
Hierarchy	A definition must describe any new concept as a special case of a general concept (Van Dormolen & Zaslavsky, 2003).
Equivalence	If more than one definition is given for the same concept, the equivalence of them must be proved (Van Dormolen & Zaslavsky, 2003).
Existence	It is necessary to prove that at least one instance of a newly defined concept exists (Van Dormolen & Zaslavsky, 2003).
Non-contradiction	All the properties stated in the definition should be able to coexist (Morgan, 2005).
Minimality	A definition should not contain properties that can be mathematically inferred from other parts of the definition (Vinner, 1991).
Elegance	When given a choice, definition that uses fewer words or symbols, or that looks “nicer,” should be chosen (Van Dormolen & Zaslavsky, 2003).
Axiomatization	A definition must fit into and be part of a deductive system (Van Dormolen & Zaslavsky, 2003).
Non-ambiguity	A definition must have a unique interpretation (Zaslavsky & Shir, 2005).
Degenerations	A definition may include degenerate (unexpected) instances that are non-intuitive (Van Dormolen & Zaslavsky, 2003).
Referential clarity	A definition must have easily identifiable examples, and the name of the concept must be closely related to its natural language usage (Burroughs & Burke, 2016).
Discrimination	A definition must allow instances and non-instances of the concept to be discriminated with certainty, consistency, and efficiency (Morgan, 2006).
Mathematical essence	A definition must capture and synthesize the mathematical essence of the concept (Morgan, 2006).

In this section, we have not made a distinction between which criteria were regarded as an imperative or as an optional criterion (this was done in Section 4). For instance, the criterion of minimality was in some publications considered as an imperative feature, whereas others regarded it as an optional or preferred feature (see Section 4.3.1). Appendix A, Table 2, shows that minimality was the most mentioned criterion.

The criteria in Table 1 are also included in our analysis of emerging themes (see Section 4); however, we must point out that in our analysis, not all of the criteria were regarded as strict mathematical requirements or rules. For instance, referential clarity is difficult to interpret as a strict criterion for a mathematical definition. In our analysis, we regard this criterion of didactical flavour as part of the function that a mathematical definition serves.

7. Discussion

The aim of this systematic literature review was to gather an overview of how researchers in mathematics education characterize mathematical definitions. The categorization is outlined in Figure 3, and it is presented in detail in Section 4. The framework offers a holistic view of mathematical definitions in the mathematics education literature and promotes a view of a mathematical definition as something more than a list of properties necessary and sufficient to characterize a mathematical concept. The framework has the potential to direct mathematics teachers, educators, and researchers’ attention to the wide range of aspects of mathematical definitions.

Our investigation revealed a list of 12 criteria for mathematical definitions described in the sample (see Table 1). However, the criteria were of varying degrees formal or logical, and one may thus ask whether all of them are necessary or if they are independent. Moreover, our analysis did not reveal any framework or paper that collects all aspects of mathematical definitions in the mathematics education literature. We see from the overview in Appendix A, Table 2, that no publication from the sample discusses all the aspects that we found. To the best of our knowledge, this paper provides the most comprehensive framework of mathematical definitions to date.

We observe that there is a high level of agreement on the different aspects of mathematical definitions that were discussed across the literature. The one point where there was slight controversy was whether minimality is a required property or a preferred feature of a mathematical definition (Zaslavsky & Shir, 2005). Interestingly, from Appendix A, Table 2, we see that the criterion of minimality was brought up the most in the reviewed literature. We decided to categorize minimality as a preferred feature primarily because it is not a requirement for the logical consistency of a definition – it only decreases the chance of an erroneous definition. Secondarily, there are strong didactical arguments for excluding minimality as a requirement in the context of teaching and learning (e.g. Johnson et al., 2014; Van Dormolen & Zaslavsky, 2003).

From our investigation, we detected a tension between purely mathematical aspects and didactical aspects of definitions. In some cases, the necessary and preferred criteria for mathematical definitions can even be obstacles for a learner. This tension is observable for several of the aspects that are discussed in the body of the literature we have reviewed. We will give a few examples.

First, regarding the nature of mathematical definitions, Edwards and Ward (2004) present empirical evidence that some students do not treat or understand mathematical definitions as mathematicians do. They show that some students do not regard mathematical definitions as stipulated, but rather as extracted. Another point to be made about the nature of definitions is about their arbitrary and constructed nature. Some teachers and students actually hold the position that there is only one correct definition for a concept. For example, Leikin and Winicki-Landman (2001, p. 72) state that ‘Our reflective discussions with the teachers showed that they were not always aware that there exists a possibility to define a concept in different ways’. Furthermore, even though mathematicians might prefer a minimal definition, this is not always preferred in a didactical context, as we previously mentioned. Another point is that of aesthetics and elegance. As we have pointed out, and in particular in the example of the absolute value of $x$ by Vinner (1991) in Section 4.3.2, what is considered elegant in one context might not be elegant in another. To underline the point even further, although Burroughs and Burke (2016) say that the name of the term in a definition should be closely related to its natural language usage, this is clearly not the case in mathematics research. We can argue that the mathematical terms natural, rational, complex, group, ring, field, function, factor, positive and negative, manifold, category, and even Fibonacci number, are not. They all have their own mathematical meanings, totally independent of any natural language usage. Furthermore, the term’s relation to natural language may change as the subject matter is developed. This is another example of a tension between the preferred features (and didactical aspects) of mathematical definitions and the nature of mathematical definitions in mathematical science.

It is clear that the most suitable definition at a certain level of education might not be the most preferred in a purely mathematical sense. Conversely, a mathematically sound and preferred definition, might not be the most suitable for students. These points might seem obvious, but consider the following example. It is sometimes suggested that multiplication can be introduced using an equal groups model or repeated addition (e.g. Van de Walle et al., 2019). Clearly, this restricted definition of multiplication breaks down when we want to extend the definition to rational or real numbers. We propose that it would be worthwhile to conduct more research into the observable tension among our categories of mathematical definitions.

We see mention in the body of literature under review of representation systems used in definitions. In particular, it is mentioned that a definition must be invariant under change of representation (see Sánchez & García, 2013; Zaslavsky & Shir, 2005). While definitions are arbitrary in nature, we note that the representation system used in a definition is of an arbitrary nature as well. Several representation systems can be used to define any given mathematical concept. Vice versa, a given representation system can be used to define different mathematical concepts. This arbitrariness raises some relevant questions. For example, how can we best make a choice between possible representation systems? Which representation system is didactically more suitable in a given situation? Which representation systems do teachers use and why? More research regarding the representations used in mathematical definitions seems warranted.

8. Concluding remarks

For students to be able to produce mathematical proofs, they have to know, at least to some degree, the nature and purpose of mathematical definitions. Dickerson and Pitman (2016) stress that students’ inability to produce proofs often has something do to with definitions. How students come to acquire the competencies necessary for producing deductive justification and how, and to what degree, these competencies can be taught are among the key open questions raised in Harel and Weber (2020)’s review of deductive reasoning. That students are not aware that definitions serve as the basis for deductive arguments may be one such missing competence, and this points toward the structure of deductive proof and the role of definitions in this structure as areas with particular potential for the design of new didactical interventions.

Several authors stress how important it is that teachers and educators have a robust understanding of mathematical definitions. For example, Avcu (2022) mentions the importance of knowledge about the process of defining, the nature, roles, and features of mathematical definitions, how definitions influence their pedagogical choices, and the various types of definitions.

It is interesting to note that some students who can recite definitions, and even seemingly understand and explain them, may still be unable to use them in a mathematically appropriate way in their reasoning and proving (Edwards & Ward, 2004). Based on this insight, Edwards and Ward (2004) recommend that.

The special nature of mathematical definitions should be treated as a concept in its own right, one that should be understood at some level by all college mathematics students.

and

[…] students also need to understand the specific role definitions play in mathematics. Thus in such courses the nature of mathematical definitions needs to be addressed more directly and more often. In particular, introduction to proof courses certainly should include a unit on the categorization and use of mathematical definitions.

We hope that our work, and the resulting framework, can help guide teachers, educators, and researchers to emphasize important aspects of mathematical definitions in both teaching and research in mathematics education.

Acknowledgements

This paper was referred to in Forbregd et al. (2022) before it was published in International Journal of Mathematical Education in Science and Technology.

Disclosure statement

No potential conflict of interest was reported by the authors.

Appendices

Appendix A. An overview of criteria in the sample.

Table 2. An overview of papers that consider different criteria for mathematical definitions.

Papers\Criterion	HI	EQ	EX	NC	MIN	ELG	AX	NAM	DEG	RCL	DC	ME
Aktaş (2015)	◊	◊		◊	◊	◊	◊		◊
Avcu (2019)				◊	◊			◊
Ayalon & Wilkie (2019)								◊
Bell & Woo (1998)								◊
Borasi (1992)											◊	◊
Burroughs & Burke (2016)	◊				◊			◊		◊
Chesler (2012)				◊				◊
Edwards & Ward (2008)	◊		◊			◊
Dawkins (2014)					◊
Foster (2014)								◊
Foster & de Villiers (2015)								◊
Gutiérrez & Jaime (1999)											◊
Johnson et. al. (2014)				◊	◊
Lavy & Mashiach-Eizenberg (2009)					◊	◊
Leikin & Winicki-Landman (2000)					◊
Leikin & Zazkis (2010)
Morgan (2005)				◊				◊			◊	◊
Morgan (2006)								◊			◊	◊
Sánchez & García (2013)	◊	◊	◊	◊	◊		◊				◊
Üreyen (2006)					◊
Van Dormolen & Zaslavsky (2003)	◊	◊	◊		◊	◊	◊		◊
Vinner (1991)					◊
Winicki-Landman & Leikin (2000)					◊
Zandieh & Rasmussen (2010)					◊	◊						◊
Zaslavsky & Shir (2005)		◊						◊
Zazkis & Leikin (2008)					◊	◊

Abbrevations: Hierarchy (HI), Equivalence (EQ), Existence (EX), Non-contradiction (NC), Minimality (MIN), Elegance (ELG), Axiomatization (AX), Non-ambiguity (NAM), Degenerations (DEG), Referential clarity (RCL), Discrimination (DC) and Mathematical essence (ME).

Appendix B. Search strategy details

The initial searches in Scopus and ERIC were as follows:

Table

Scopus:
(ABS(definition* AND mathematic*)
TITLE(definition* AND mathematic*) OR	N = 2215
KEY(definition* AND mathematic*))
AND ALL(education) AND
LIMIT-TO(LANGUAGE,English)
ERIC:
(abstract:(definition* AND mathematic*) OR
title:(definition* AND mathematic*) OR	N = 1361
descriptor:(definition* AND mathematic*))
AND education

The two search engines have very different inclusion/exclusion functionalities and levels of sophistication.

ERIC exclusion strategy:

We limited findings to peer-reviewed documents, resulting in $N=619$.

Scopus exclusion strategy:

Note that documents not written in English were excluded in the initial search. In subject area, we limited the search to social sciences, mathematics, and psychology. Further, we excluded the following, resulting in $N=874$, as shown in the screenshot:

The final and last search was conducted on 30 September 2022 on both engines.

Appendix C. Publications included in the review.

• Aktaş, M. C. (2015). Turkish high school students’ definitions for parallelograms: Appropriate or inappropriate? International Journal of Mathematical Education in Science and Technology, 47(4), 583–596. https://doi.org/10.1080/0020739x.2015.1124931
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2015.1124931 journal Turkish+high+school+students%E2%80%99+definitions+for+parallelograms%3A+Appropriate+or+inappropriate%3F author%3DM.+C.+Akta%C5%9F 2015 Akta%C5%9F%2C+M.+C.+%282015%29.+Turkish+high+school+students%E2%80%99+definitions+for+parallelograms%3A+Appropriate+or+inappropriate%3F+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+47%284%29%2C+583%E2%80%93596.+ 583-596 International+Journal+of+Mathematical+Education+in+Science+and+Technology 47 4 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2015.1124931 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_1_1 10.1080%252F0020739x.2015.1124931 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2015.1124931%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAkta%25C5%259F%26rft.aufirst%3DM.%2520C.%26rft.date%3D2015%26rft.atitle%3DTurkish%2520high%2520school%2520students%25E2%2580%2599%2520definitions%2520for%2520parallelograms%253A%2520Appropriate%2520or%2520inappropriate%253F%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D47%26rft.issue%3D4%26rft.spage%3D583%26rft.epage%3D596 %00empty%00}-->
• Alcock, L., & Simpson, A. (2002). Definitions: Dealing with categories mathematically. For the Learning of Mathematics, 22(2), 28–34.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Definitions%3A+Dealing+with+categories+mathematically author%3DL.+Alcock%26author%3DA.+Simpson 2002 Alcock%2C+L.%2C+%26+Simpson%2C+A.+%282002%29.+Definitions%3A+Dealing+with+categories+mathematically.+For+the+Learning+of+Mathematics%2C+22%282%29%2C+28%E2%80%9334. 28-34 For+the+Learning+of+Mathematics 22 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_2_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAlcock%26rft.aufirst%3DL.%26rft.date%3D2002%26rft.atitle%3DDefinitions%253A%2520Dealing%2520with%2520categories%2520mathematically%26rft.jtitle%3DFor%2520the%2520Learning%2520of%2520Mathematics%26rft.volume%3D22%26rft.issue%3D2%26rft.spage%3D28%26rft.epage%3D34 %00empty%00}-->
• Alcock, L., Simpson, A. (2011). Classification and concept consistency. Canadian Journal of Science, Mathematics and Technology Education, 11(2), 91–106.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F14926156.2011.570476 journal Classification+and+concept+consistency.+Canadian+Journal+of+Science author%3DL.+Alcock%26author%3DA.+Simpson 2011 Alcock%2C+L.%2C+Simpson%2C+A.+%282011%29.+Classification+and+concept+consistency.+Canadian+Journal+of+Science%2C+Mathematics+and+Technology+Education%2C+11%282%29%2C+91%E2%80%93106. 91-106 Mathematics+and+Technology+Education 11 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_3_1 10.1080%252F14926156.2011.570476 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F14926156.2011.570476%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAlcock%26rft.aufirst%3DL.%26rft.date%3D2011%26rft.atitle%3DClassification%2520and%2520concept%2520consistency.%2520Canadian%2520Journal%2520of%2520Science%26rft.jtitle%3DMathematics%2520and%2520Technology%2520Education%26rft.volume%3D11%26rft.issue%3D2%26rft.spage%3D91%26rft.epage%3D106 %00empty%00}-->
• Alcock, L., & Simpson, A. (2016). Interactions between defining, explaining and classifying: The case of increasing and decreasing sequences. Educational Studies in Mathematics, 94(1), 5–19. https://doi.org/10.1007/s10649-016-9709-4
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10649-016-9709-4 journal Interactions+between+defining%2C+explaining+and+classifying%3A+The+case+of+increasing+and+decreasing+sequences author%3DL.+Alcock%26author%3DA.+Simpson 2016 Alcock%2C+L.%2C+%26+Simpson%2C+A.+%282016%29.+Interactions+between+defining%2C+explaining+and+classifying%3A+The+case+of+increasing+and+decreasing+sequences.+Educational+Studies+in+Mathematics%2C+94%281%29%2C+5%E2%80%9319.+ 5-19 Educational+Studies+in+Mathematics 94 1 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10649-016-9709-4 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_4_1 10.1007%252Fs10649-016-9709-4 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10649-016-9709-4%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAlcock%26rft.aufirst%3DL.%26rft.date%3D2016%26rft.atitle%3DInteractions%2520between%2520defining%252C%2520explaining%2520and%2520classifying%253A%2520The%2520case%2520of%2520increasing%2520and%2520decreasing%2520sequences%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D94%26rft.issue%3D1%26rft.spage%3D5%26rft.epage%3D19 %00empty%00}-->
• Altiparmak, K., & Gürcan, G. (2021). Examination of 4th grade students’ definitions for square, rectangle and triangle geometric shapes. Education Quarterly Reviews, 4(3), 304–321.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.31014%2Faior.1993.04.03.340 journal Examination+of+4th+grade+students%E2%80%99+definitions+for+square%2C+rectangle+and+triangle+geometric+shapes author%3DK.+Altiparmak%26author%3DG.+G%C3%BCrcan 2021 Altiparmak%2C+K.%2C+%26+G%C3%BCrcan%2C+G.+%282021%29.+Examination+of+4th+grade+students%E2%80%99+definitions+for+square%2C+rectangle+and+triangle+geometric+shapes.+Education+Quarterly+Reviews%2C+4%283%29%2C+304%E2%80%93321. 304-321 Education+Quarterly+Reviews 4 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_5_1 10.31014%252Faior.1993.04.03.340 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.31014%252Faior.1993.04.03.340%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAltiparmak%26rft.aufirst%3DK.%26rft.date%3D2021%26rft.atitle%3DExamination%2520of%25204th%2520grade%2520students%25E2%2580%2599%2520definitions%2520for%2520square%252C%2520rectangle%2520and%2520triangle%2520geometric%2520shapes%26rft.jtitle%3DEducation%2520Quarterly%2520Reviews%26rft.volume%3D4%26rft.issue%3D3%26rft.spage%3D304%26rft.epage%3D321 %00empty%00}-->
• Altun, S. D. G., & Konyalioglu, A. C. (2019). The influence of mistake-handling activities on mathematics education: An example of definitions. European Journal of Educational Research, 8(2), 467–476.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.12973%2Feu-jer.8.2.467 journal The+influence+of+mistake-handling+activities+on+mathematics+education%3A+An+example+of+definitions author%3DS.+D.+G.+Altun%26author%3DA.+C.+Konyalioglu 2019 Altun%2C+S.+D.+G.%2C+%26+Konyalioglu%2C+A.+C.+%282019%29.+The+influence+of+mistake-handling+activities+on+mathematics+education%3A+An+example+of+definitions.+European+Journal+of+Educational+Research%2C+8%282%29%2C+467%E2%80%93476. 467-476 European+Journal+of+Educational+Research 8 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_6_1 10.12973%252Feu-jer.8.2.467 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.12973%252Feu-jer.8.2.467%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAltun%26rft.aufirst%3DS.%2520D.%2520G.%26rft.date%3D2019%26rft.atitle%3DThe%2520influence%2520of%2520mistake-handling%2520activities%2520on%2520mathematics%2520education%253A%2520An%2520example%2520of%2520definitions%26rft.jtitle%3DEuropean%2520Journal%2520of%2520Educational%2520Research%26rft.volume%3D8%26rft.issue%3D2%26rft.spage%3D467%26rft.epage%3D476 %00empty%00}-->
• Arnal-Palacián, M., Claros-Mellado, J., & Sánchez-Compaña, M. T. (2020). Infinite limit of sequences and its phenomenology. International Electronic Journal of Mathematics Education, 15(3), em0593. https://doi.org/10.29333/iejme/8279
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.29333%2Fiejme%2F8279 journal Infinite+limit+of+sequences+and+its+phenomenology author%3DM.+Arnal-Palaci%C3%A1n%26author%3DJ.+Claros-Mellado%26author%3DM.+T.+S%C3%A1nchez-Compa%C3%B1a 2020 Arnal-Palaci%C3%A1n%2C+M.%2C+Claros-Mellado%2C+J.%2C+%26+S%C3%A1nchez-Compa%C3%B1a%2C+M.+T.+%282020%29.+Infinite+limit+of+sequences+and+its+phenomenology.+International+Electronic+Journal+of+Mathematics+Education%2C+15%283%29%2C+em0593.+ em0593 International+Electronic+Journal+of+Mathematics+Education 15 3 https%3A%2F%2Fdoi.org%2F10.29333%2Fiejme%2F8279 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_7_1 10.29333%252Fiejme%252F8279 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.29333%252Fiejme%252F8279%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DArnal-Palaci%25C3%25A1n%26rft.aufirst%3DM.%26rft.date%3D2020%26rft.atitle%3DInfinite%2520limit%2520of%2520sequences%2520and%2520its%2520phenomenology%26rft.jtitle%3DInternational%2520Electronic%2520Journal%2520of%2520Mathematics%2520Education%26rft.volume%3D15%26rft.issue%3D3%26rft.spage%3Dem0593 %00empty%00}-->
• Asghari, A. H. (2008). Experiencing equivalence but organizing order. Educational Studies in Mathematics, 71(3), 219–234. https://doi.org/10.1007/s10649-008-9173-x
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10649-008-9173-x journal Experiencing+equivalence+but+organizing+order author%3DA.+H.+Asghari 2008 Asghari%2C+A.+H.+%282008%29.+Experiencing+equivalence+but+organizing+order.+Educational+Studies+in+Mathematics%2C+71%283%29%2C+219%E2%80%93234.+ 219-234 Educational+Studies+in+Mathematics 71 3 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10649-008-9173-x %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_8_1 10.1007%252Fs10649-008-9173-x url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10649-008-9173-x%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAsghari%26rft.aufirst%3DA.%2520H.%26rft.date%3D2008%26rft.atitle%3DExperiencing%2520equivalence%2520but%2520organizing%2520order%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D71%26rft.issue%3D3%26rft.spage%3D219%26rft.epage%3D234 %00empty%00}-->
• Avcu, R. (2019). A comparison of mathematical features of Turkish and American textbook definitions regarding special quadrilaterals. International Journal of Mathematical Education in Science and Technology, 50(4), 577–602. https://doi.org/10.1080/0020739x.2018.1529338
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2018.1529338 journal A+comparison+of+mathematical+features+of+Turkish+and+American+textbook+definitions+regarding+special+quadrilaterals author%3DR.+Avcu 2019 Avcu%2C+R.+%282019%29.+A+comparison+of+mathematical+features+of+Turkish+and+American+textbook+definitions+regarding+special+quadrilaterals.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+50%284%29%2C+577%E2%80%93602.+ 577-602 International+Journal+of+Mathematical+Education+in+Science+and+Technology 50 4 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2018.1529338 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_9_1 10.1080%252F0020739x.2018.1529338 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2018.1529338%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAvcu%26rft.aufirst%3DR.%26rft.date%3D2019%26rft.atitle%3DA%2520comparison%2520of%2520mathematical%2520features%2520of%2520Turkish%2520and%2520American%2520textbook%2520definitions%2520regarding%2520special%2520quadrilaterals%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D50%26rft.issue%3D4%26rft.spage%3D577%26rft.epage%3D602 %00empty%00}-->
• Avcu, R. (2022). Pre-service middle school mathematics teachers’ personal concept definitions of special quadrilaterals. Mathematics Education Research Journal (2022). https://doi.org/10.1007/s13394-022-00412-2
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs13394-022-00412-2 journal Pre-service+middle+school+mathematics+teachers%E2%80%99+personal+concept+definitions+of+special+quadrilaterals author%3DR.+Avcu 2022 Avcu%2C+R.+%282022%29.+Pre-service+middle+school+mathematics+teachers%E2%80%99+personal+concept+definitions+of+special+quadrilaterals.+Mathematics+Education+Research+Journal+%282022%29.+ %00empty%00 Mathematics+Education+Research+Journal 2022 %00null%00 https%3A%2F%2Fdoi.org%2F10.1007%2Fs13394-022-00412-2 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_10_1 10.1007%252Fs13394-022-00412-2 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs13394-022-00412-2%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAvcu%26rft.aufirst%3DR.%26rft.date%3D2022%26rft.atitle%3DPre-service%2520middle%2520school%2520mathematics%2520teachers%25E2%2580%2599%2520personal%2520concept%2520definitions%2520of%2520special%2520quadrilaterals%26rft.jtitle%3DMathematics%2520Education%2520Research%2520Journal%26rft.volume%3D2022 %00empty%00}-->
• Ayalon, M., & Wilkie, K. J. (2019). Exploring secondary students’ conceptualization of functions in three curriculum contexts. The Journal of Mathematical Behavior, 56, 100718. https://doi.org/10.1016/j.jmathb.2019.100718
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2019.100718 journal Exploring+secondary+students%E2%80%99+conceptualization+of+functions+in+three+curriculum+contexts author%3DM.+Ayalon%26author%3DK.+J.+Wilkie 2019 Ayalon%2C+M.%2C+%26+Wilkie%2C+K.+J.+%282019%29.+Exploring+secondary+students%E2%80%99+conceptualization+of+functions+in+three+curriculum+contexts.+The+Journal+of+Mathematical+Behavior%2C+56%2C+100718.+ 100718 The+Journal+of+Mathematical+Behavior 56 %00null%00 https%3A%2F%2Fdoi.org%2F10.1016%2Fj.jmathb.2019.100718 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_11_1 10.1016%252Fj.jmathb.2019.100718 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2019.100718%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DAyalon%26rft.aufirst%3DM.%26rft.date%3D2019%26rft.atitle%3DExploring%2520secondary%2520students%25E2%2580%2599%2520conceptualization%2520of%2520functions%2520in%2520three%2520curriculum%2520contexts%26rft.jtitle%3DThe%2520Journal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D56%26rft.spage%3D100718 %00empty%00}-->
• Bayda, N. I., & Sutliff, G. (2020). Comparing extracted and stipulated definitions in algebra 1 textbooks and Khan Academy. International Electronic Journal of Mathematics Education, 15(2), em0579. https://doi.org/10.29333/iejme/7601
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.29333%2Fiejme%2F7601 journal Comparing+extracted+and+stipulated+definitions+in+algebra+1+textbooks+and+Khan+Academy author%3DN.+I.+Bayda%26author%3DG.+Sutliff 2020 Bayda%2C+N.+I.%2C+%26+Sutliff%2C+G.+%282020%29.+Comparing+extracted+and+stipulated+definitions+in+algebra+1+textbooks+and+Khan+Academy.+International+Electronic+Journal+of+Mathematics+Education%2C+15%282%29%2C+em0579.+ em0579 International+Electronic+Journal+of+Mathematics+Education 15 2 https%3A%2F%2Fdoi.org%2F10.29333%2Fiejme%2F7601 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_12_1 10.29333%252Fiejme%252F7601 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.29333%252Fiejme%252F7601%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBayda%26rft.aufirst%3DN.%2520I.%26rft.date%3D2020%26rft.atitle%3DComparing%2520extracted%2520and%2520stipulated%2520definitions%2520in%2520algebra%25201%2520textbooks%2520and%2520Khan%2520Academy%26rft.jtitle%3DInternational%2520Electronic%2520Journal%2520of%2520Mathematics%2520Education%26rft.volume%3D15%26rft.issue%3D2%26rft.spage%3Dem0579 %00empty%00}-->
• Bell, G., & Woo, J. H. (1998). Probing the links between language and mathematical conceptualisation. Mathematics Education Research Journal, 10(1), 51–74. https://doi.org/10.1007/bf03217122
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2Fbf03217122 journal Probing+the+links+between+language+and+mathematical+conceptualisation author%3DG.+Bell%26author%3DJ.+H.+Woo 1998 Bell%2C+G.%2C+%26+Woo%2C+J.+H.+%281998%29.+Probing+the+links+between+language+and+mathematical+conceptualisation.+Mathematics+Education+Research+Journal%2C+10%281%29%2C+51%E2%80%9374.+ 51-74 Mathematics+Education+Research+Journal 10 1 https%3A%2F%2Fdoi.org%2F10.1007%2Fbf03217122 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_13_1 10.1007%252Fbf03217122 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fbf03217122%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBell%26rft.aufirst%3DG.%26rft.date%3D1998%26rft.atitle%3DProbing%2520the%2520links%2520between%2520language%2520and%2520mathematical%2520conceptualisation%26rft.jtitle%3DMathematics%2520Education%2520Research%2520Journal%26rft.volume%3D10%26rft.issue%3D1%26rft.spage%3D51%26rft.epage%3D74 %00empty%00}-->
• Berger, L. (2018). Attending to precision: Mathematical definitions in courses for pre-service and practicing teachers. PRIMUS, 28(8), 772–784.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F10511970.2018.1432732 journal Attending+to+precision%3A+Mathematical+definitions+in+courses+for+pre-service+and+practicing+teachers author%3DL.+Berger 2018 Berger%2C+L.+%282018%29.+Attending+to+precision%3A+Mathematical+definitions+in+courses+for+pre-service+and+practicing+teachers.+PRIMUS%2C+28%288%29%2C+772%E2%80%93784. 772-784 PRIMUS 28 8 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_14_1 10.1080%252F10511970.2018.1432732 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F10511970.2018.1432732%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBerger%26rft.aufirst%3DL.%26rft.date%3D2018%26rft.atitle%3DAttending%2520to%2520precision%253A%2520Mathematical%2520definitions%2520in%2520courses%2520for%2520pre-service%2520and%2520practicing%2520teachers%26rft.jtitle%3DPRIMUS%26rft.volume%3D28%26rft.issue%3D8%26rft.spage%3D772%26rft.epage%3D784 %00empty%00}-->
• Berman, A., & Shvartsman, L. (2016). Definitions are important: The case of linear algebra. European Journal of Science and Mathematics Education, 4(1), 26–32.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.30935%2Fscimath%2F9450 journal Definitions+are+important%3A+The+case+of+linear+algebra author%3DA.+Berman%26author%3DL.+Shvartsman 2016 Berman%2C+A.%2C+%26+Shvartsman%2C+L.+%282016%29.+Definitions+are+important%3A+The+case+of+linear+algebra.+European+Journal+of+Science+and+Mathematics+Education%2C+4%281%29%2C+26%E2%80%9332. 26-32 European+Journal+of+Science+and+Mathematics+Education 4 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_15_1 10.30935%252Fscimath%252F9450 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.30935%252Fscimath%252F9450%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBerman%26rft.aufirst%3DA.%26rft.date%3D2016%26rft.atitle%3DDefinitions%2520are%2520important%253A%2520The%2520case%2520of%2520linear%2520algebra%26rft.jtitle%3DEuropean%2520Journal%2520of%2520Science%2520and%2520Mathematics%2520Education%26rft.volume%3D4%26rft.issue%3D1%26rft.spage%3D26%26rft.epage%3D32 %00empty%00}-->
• Beynon, K. A., & Zollman, A. (2015). Lacking a formal concept of limit: Advanced non-mathematics students’ personal concept definitions. Investigations in Mathematics Learning, 8(1), 47–62. https://doi.org/10.1080/24727466.2015.11790347
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F24727466.2015.11790347 journal Lacking+a+formal+concept+of+limit%3A+Advanced+non-mathematics+students%E2%80%99+personal+concept+definitions author%3DK.+A.+Beynon%26author%3DA.+Zollman 2015 Beynon%2C+K.+A.%2C+%26+Zollman%2C+A.+%282015%29.+Lacking+a+formal+concept+of+limit%3A+Advanced+non-mathematics+students%E2%80%99+personal+concept+definitions.+Investigations+in+Mathematics+Learning%2C+8%281%29%2C+47%E2%80%9362.+ 47-62 Investigations+in+Mathematics+Learning 8 1 https%3A%2F%2Fdoi.org%2F10.1080%2F24727466.2015.11790347 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_16_1 10.1080%252F24727466.2015.11790347 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F24727466.2015.11790347%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBeynon%26rft.aufirst%3DK.%2520A.%26rft.date%3D2015%26rft.atitle%3DLacking%2520a%2520formal%2520concept%2520of%2520limit%253A%2520Advanced%2520non-mathematics%2520students%25E2%2580%2599%2520personal%2520concept%2520definitions%26rft.jtitle%3DInvestigations%2520in%2520Mathematics%2520Learning%26rft.volume%3D8%26rft.issue%3D1%26rft.spage%3D47%26rft.epage%3D62 %00empty%00}-->
• Bills, L., & Tall, D. (1998). Operable definitions in advanced mathematics: The case of the least upper bound. PME Conference, 2, 104–111.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Operable+definitions+in+advanced+mathematics%3A+The+case+of+the+least+upper+bound author%3DL.+Bills%26author%3DD.+Tall 1998 Bills%2C+L.%2C+%26+Tall%2C+D.+%281998%29.+Operable+definitions+in+advanced+mathematics%3A+The+case+of+the+least+upper+bound.+PME+Conference%2C+2%2C+104%E2%80%93111. 104-111 PME+Conference 2 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_17_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBills%26rft.aufirst%3DL.%26rft.date%3D1998%26rft.atitle%3DOperable%2520definitions%2520in%2520advanced%2520mathematics%253A%2520The%2520case%2520of%2520the%2520least%2520upper%2520bound%26rft.jtitle%3DPME%2520Conference%26rft.volume%3D2%26rft.spage%3D104%26rft.epage%3D111 %00empty%00}-->
• Bolondi, G., Ferretti, F., & Maffia, A. (2020). Monomials and polynomials: The long march towards a definition. Teaching Mathematics and its Applications, 39(1), 1–12.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}-->Web of Science ®<!--${googleScholarLinkReplacer: %00empty%00 journal Monomials+and+polynomials%3A+The+long+march+towards+a+definition author%3DG.+Bolondi%26author%3DF.+Ferretti%26author%3DA.+Maffia 2020 Bolondi%2C+G.%2C+Ferretti%2C+F.%2C+%26+Maffia%2C+A.+%282020%29.+Monomials+and+polynomials%3A+The+long+march+towards+a+definition.+Teaching+Mathematics+and+its+Applications%2C+39%281%29%2C+1%E2%80%9312. 1-12 Teaching+Mathematics+and+its+Applications 39 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_18_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBolondi%26rft.aufirst%3DG.%26rft.date%3D2020%26rft.atitle%3DMonomials%2520and%2520polynomials%253A%2520The%2520long%2520march%2520towards%2520a%2520definition%26rft.jtitle%3DTeaching%2520Mathematics%2520and%2520its%2520Applications%26rft.volume%3D39%26rft.issue%3D1%26rft.spage%3D1%26rft.epage%3D12 %00empty%00}-->
• Borasi, R. (1992). Learning mathematics through inquiry. Heinemann.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 book Learning+mathematics+through+inquiry author%3DR.+Borasi 1992 Borasi%2C+R.+%281992%29.+Learning+mathematics+through+inquiry.+Heinemann. %00empty%00 %00null%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_19_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Dbook%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBorasi%26rft.aufirst%3DR.%26rft.date%3D1992%26rft.btitle%3DLearning%2520mathematics%2520through%2520inquiry%26rft.pub%3DHeinemann %00empty%00}-->
• Breen, S., & O’Shea, A. (2019). Designing mathematical thinking tasks. PRIMUS, 29(1), 9–20.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F10511970.2017.1396567 journal Designing+mathematical+thinking+tasks author%3DS.+Breen%26author%3DA.+O%E2%80%99Shea 2019 Breen%2C+S.%2C+%26+O%E2%80%99Shea%2C+A.+%282019%29.+Designing+mathematical+thinking+tasks.+PRIMUS%2C+29%281%29%2C+9%E2%80%9320. 9-20 PRIMUS 29 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_20_1 10.1080%252F10511970.2017.1396567 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F10511970.2017.1396567%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBreen%26rft.aufirst%3DS.%26rft.date%3D2019%26rft.atitle%3DDesigning%2520mathematical%2520thinking%2520tasks%26rft.jtitle%3DPRIMUS%26rft.volume%3D29%26rft.issue%3D1%26rft.spage%3D9%26rft.epage%3D20 %00empty%00}-->
• Burroughs, E.A., Burke, M.J. (2016). By Definition: An Examination of the Process of Defining in Mathematics. In: Dewar, J., Hsu, Ps., Pollatsek, H. (eds) Mathematics Education. Association for Women in Mathematics Series, vol 7. Springer, Cham. https://doi.org/10.1007/978-3-319-44950-0_5
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2F978-3-319-44950-0_5 journal By+Definition%3A+An+Examination+of+the+Process+of+Defining+in+Mathematics author%3DE.A.+Burroughs%26author%3DM.J.+Burke%26 2016 Burroughs%2C+E.A.%2C+Burke%2C+M.J.+%282016%29.+By+Definition%3A+An+Examination+of+the+Process+of+Defining+in+Mathematics.+In%3A+Dewar%2C+J.%2C+Hsu%2C+Ps.%2C+Pollatsek%2C+H.+%28eds%29+Mathematics+Education.+Association+for+Women+in+Mathematics+Series%2C+vol+7.+Springer%2C+Cham.+ %00empty%00 Mathematics+Education.+Association+for+Women+in+Mathematics+Series 7 %00null%00 https%3A%2F%2Fdoi.org%2F10.1007%2F978-3-319-44950-0_5 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_21_1 10.1007%252F978-3-319-44950-0_5 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252F978-3-319-44950-0_5%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DBurroughs%26rft.aufirst%3DE.A.%26rft.date%3D2016%26rft.atitle%3DBy%2520Definition%253A%2520An%2520Examination%2520of%2520the%2520Process%2520of%2520Defining%2520in%2520Mathematics%26rft.aulast%3DDewar%26rft.aufirst%3DJ.%26rft.jtitle%3DMathematics%2520Education.%2520Association%2520for%2520Women%2520in%2520Mathematics%2520Series%26rft.volume%3D7%26rft.pub%3DSpringer%252C%2520Cham %00empty%00}-->
• Butuner, S.O., & Filiz, M. (2017). Exploring Turkish mathematics teachers’ content knowledge of quadrilaterals. International Journal of Research in Education and Science, 3(2), 395–408. DOI:10.21890/ijres.327898
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.21890%2Fijres.327898 journal Exploring+Turkish+mathematics+teachers%E2%80%99+content+knowledge+of+quadrilaterals author%3DS.O.+Butuner%26author%3DM.+Filiz 2017 Butuner%2C+S.O.%2C+%26+Filiz%2C+M.+%282017%29.+Exploring+Turkish+mathematics+teachers%E2%80%99+content+knowledge+of+quadrilaterals.+International+Journal+of+Research+in+Education+and+Science%2C+3%282%29%2C+395%E2%80%93408.+DOI%3A 395-408 International+Journal+of+Research+in+Education+and+Science 3 2 10.21890%2Fijres.327898 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_22_1 10.21890%252Fijres.327898 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.21890%252Fijres.327898%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DButuner%26rft.aufirst%3DS.O.%26rft.date%3D2017%26rft.atitle%3DExploring%2520Turkish%2520mathematics%2520teachers%25E2%2580%2599%2520content%2520knowledge%2520of%2520quadrilaterals%26rft.jtitle%3DInternational%2520Journal%2520of%2520Research%2520in%2520Education%2520and%2520Science%26rft.volume%3D3%26rft.issue%3D2%26rft.spage%3D395%26rft.epage%3D408 %00empty%00}-->
• Chesler, J. (2012). Pre-service secondary mathematics teachers making sense of definitions of functions. Mathematics Teacher Education and Development, 14(1), 27–40.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Pre-service+secondary+mathematics+teachers+making+sense+of+definitions+of+functions author%3DJ.+Chesler 2012 Chesler%2C+J.+%282012%29.+Pre-service+secondary+mathematics+teachers+making+sense+of+definitions+of+functions.+Mathematics+Teacher+Education+and+Development%2C+14%281%29%2C+27%E2%80%9340. 27-40 Mathematics+Teacher+Education+and+Development 14 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_23_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DChesler%26rft.aufirst%3DJ.%26rft.date%3D2012%26rft.atitle%3DPre-service%2520secondary%2520mathematics%2520teachers%2520making%2520sense%2520of%2520definitions%2520of%2520functions%26rft.jtitle%3DMathematics%2520Teacher%2520Education%2520and%2520Development%26rft.volume%3D14%26rft.issue%3D1%26rft.spage%3D27%26rft.epage%3D40 %00empty%00}-->
• Chesler, J. D. (2021). Minding the nouns and verbs: Definitions that respect knowledge development. Mathematics Education Research Journal, 33(1), 79–87.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs13394-019-00305-x journal Minding+the+nouns+and+verbs%3A+Definitions+that+respect+knowledge+development author%3DJ.+D.+Chesler 2021 Chesler%2C+J.+D.+%282021%29.+Minding+the+nouns+and+verbs%3A+Definitions+that+respect+knowledge+development.+Mathematics+Education+Research+Journal%2C+33%281%29%2C+79%E2%80%9387. 79-87 Mathematics+Education+Research+Journal 33 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_24_1 10.1007%252Fs13394-019-00305-x url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs13394-019-00305-x%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DChesler%26rft.aufirst%3DJ.%2520D.%26rft.date%3D2021%26rft.atitle%3DMinding%2520the%2520nouns%2520and%2520verbs%253A%2520Definitions%2520that%2520respect%2520knowledge%2520development%26rft.jtitle%3DMathematics%2520Education%2520Research%2520Journal%26rft.volume%3D33%26rft.issue%3D1%26rft.spage%3D79%26rft.epage%3D87 %00empty%00}-->
• Chorlay, R. (2019). A pathway to a student-worded definition of limits at the secondary-tertiary transition. International Journal of Research in Undergraduate Mathematics Education, 5(3), 267–314.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2Fs40753-019-00094-5 journal A+pathway+to+a+student-worded+definition+of+limits+at+the+secondary-tertiary+transition author%3DR.+Chorlay 2019 Chorlay%2C+R.+%282019%29.+A+pathway+to+a+student-worded+definition+of+limits+at+the+secondary-tertiary+transition.+International+Journal+of+Research+in+Undergraduate+Mathematics+Education%2C+5%283%29%2C+267%E2%80%93314. 267-314 International+Journal+of+Research+in+Undergraduate+Mathematics+Education 5 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_25_1 10.1007%252Fs40753-019-00094-5 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs40753-019-00094-5%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DChorlay%26rft.aufirst%3DR.%26rft.date%3D2019%26rft.atitle%3DA%2520pathway%2520to%2520a%2520student-worded%2520definition%2520of%2520limits%2520at%2520the%2520secondary-tertiary%2520transition%26rft.jtitle%3DInternational%2520Journal%2520of%2520Research%2520in%2520Undergraduate%2520Mathematics%2520Education%26rft.volume%3D5%26rft.issue%3D3%26rft.spage%3D267%26rft.epage%3D314 %00empty%00}-->
• Connor, J., Moss, L., & Grover, B. (2007). Student evaluation of mathematical statements using dynamic geometry software. International Journal of Mathematical Education in Science and Technology, 38(1), 55–63.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F00207390600967380 journal Student+evaluation+of+mathematical+statements+using+dynamic+geometry+software author%3DJ.+Connor%26author%3DL.+Moss%26author%3DB.+Grover 2007 Connor%2C+J.%2C+Moss%2C+L.%2C+%26+Grover%2C+B.+%282007%29.+Student+evaluation+of+mathematical+statements+using+dynamic+geometry+software.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+38%281%29%2C+55%E2%80%9363. 55-63 International+Journal+of+Mathematical+Education+in+Science+and+Technology 38 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_26_1 10.1080%252F00207390600967380 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F00207390600967380%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DConnor%26rft.aufirst%3DJ.%26rft.date%3D2007%26rft.atitle%3DStudent%2520evaluation%2520of%2520mathematical%2520statements%2520using%2520dynamic%2520geometry%2520software%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D38%26rft.issue%3D1%26rft.spage%3D55%26rft.epage%3D63 %00empty%00}-->
• Dahl, B. (2016). First-year non-STEM majors’ use of definitions to solve calculus tasks: Benefits of using concept image over concept definition? International Journal of Science and Mathematics Education, 15(7), 1303–1322. https://doi.org/10.1007/s10763-016-9751-9
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10763-016-9751-9 journal First-year+non-STEM+majors%E2%80%99+use+of+definitions+to+solve+calculus+tasks%3A+Benefits+of+using+concept+image+over+concept+definition%3F author%3DB.+Dahl 2016 Dahl%2C+B.+%282016%29.+First-year+non-STEM+majors%E2%80%99+use+of+definitions+to+solve+calculus+tasks%3A+Benefits+of+using+concept+image+over+concept+definition%3F+International+Journal+of+Science+and+Mathematics+Education%2C+15%287%29%2C+1303%E2%80%931322.+ 1303-1322 International+Journal+of+Science+and+Mathematics+Education 15 7 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10763-016-9751-9 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_27_1 10.1007%252Fs10763-016-9751-9 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10763-016-9751-9%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDahl%26rft.aufirst%3DB.%26rft.date%3D2016%26rft.atitle%3DFirst-year%2520non-STEM%2520majors%25E2%2580%2599%2520use%2520of%2520definitions%2520to%2520solve%2520calculus%2520tasks%253A%2520Benefits%2520of%2520using%2520concept%2520image%2520over%2520concept%2520definition%253F%26rft.jtitle%3DInternational%2520Journal%2520of%2520Science%2520and%2520Mathematics%2520Education%26rft.volume%3D15%26rft.issue%3D7%26rft.spage%3D1303%26rft.epage%3D1322 %00empty%00}-->
• Dawkins, P. C. (2014). How students interpret and enact inquiry-oriented defining practices in undergraduate real analysis. The Journal of Mathematical Behavior, 33, 88–105. https://doi.org/10.1016/j.jmathb.2013.10.002
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2013.10.002 journal How+students+interpret+and+enact+inquiry-oriented+defining+practices+in+undergraduate+real+analysis author%3DP.+C.+Dawkins 2014 Dawkins%2C+P.+C.+%282014%29.+How+students+interpret+and+enact+inquiry-oriented+defining+practices+in+undergraduate+real+analysis.+The+Journal+of+Mathematical+Behavior%2C+33%2C+88%E2%80%93105.+ 88-105 The+Journal+of+Mathematical+Behavior 33 %00null%00 https%3A%2F%2Fdoi.org%2F10.1016%2Fj.jmathb.2013.10.002 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_28_1 10.1016%252Fj.jmathb.2013.10.002 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2013.10.002%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDawkins%26rft.aufirst%3DP.%2520C.%26rft.date%3D2014%26rft.atitle%3DHow%2520students%2520interpret%2520and%2520enact%2520inquiry-oriented%2520defining%2520practices%2520in%2520undergraduate%2520real%2520analysis%26rft.jtitle%3DThe%2520Journal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D33%26rft.spage%3D88%26rft.epage%3D105 %00empty%00}-->
• Dawkins, P. C. (2018). Student interpretations of axioms in planar geometry. Investigations in Mathematics Learning, 10(4), 227–239.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F19477503.2017.1414981 journal Student+interpretations+of+axioms+in+planar+geometry author%3DP.+C.+Dawkins 2018 Dawkins%2C+P.+C.+%282018%29.+Student+interpretations+of+axioms+in+planar+geometry.+Investigations+in+Mathematics+Learning%2C+10%284%29%2C+227%E2%80%93239. 227-239 Investigations+in+Mathematics+Learning 10 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_29_1 10.1080%252F19477503.2017.1414981 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F19477503.2017.1414981%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDawkins%26rft.aufirst%3DP.%2520C.%26rft.date%3D2018%26rft.atitle%3DStudent%2520interpretations%2520of%2520axioms%2520in%2520planar%2520geometry%26rft.jtitle%3DInvestigations%2520in%2520Mathematics%2520Learning%26rft.volume%3D10%26rft.issue%3D4%26rft.spage%3D227%26rft.epage%3D239 %00empty%00}-->
• de Moura Fonseca, D. S. S., & de Oliveira Lino Franchi, R. H. (2016). Exploring the convergence of sequences in the embodied world using GeoGebra. Teaching Mathematics and Its Applications, 35(2), 88–101. https://doi.org/10.1093/teamat/hrw012
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1093%2Fteamat%2Fhrw012 journal Exploring+the+convergence+of+sequences+in+the+embodied+world+using+GeoGebra author%3DD.+S.+S.+de+Moura+Fonseca%26author%3DR.+H.+de+Oliveira+Lino+Franchi 2016 de+Moura+Fonseca%2C+D.+S.+S.%2C+%26+de+Oliveira+Lino+Franchi%2C+R.+H.+%282016%29.+Exploring+the+convergence+of+sequences+in+the+embodied+world+using+GeoGebra.+Teaching+Mathematics+and+Its+Applications%2C+35%282%29%2C+88%E2%80%93101.+ 88-101 Teaching+Mathematics+and+Its+Applications 35 2 https%3A%2F%2Fdoi.org%2F10.1093%2Fteamat%2Fhrw012 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_30_1 10.1093%252Fteamat%252Fhrw012 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1093%252Fteamat%252Fhrw012%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3Dde%2520Moura%2520Fonseca%26rft.aufirst%3DD.%2520S.%2520S.%26rft.date%3D2016%26rft.atitle%3DExploring%2520the%2520convergence%2520of%2520sequences%2520in%2520the%2520embodied%2520world%2520using%2520GeoGebra%26rft.jtitle%3DTeaching%2520Mathematics%2520and%2520Its%2520Applications%26rft.volume%3D35%26rft.issue%3D2%26rft.spage%3D88%26rft.epage%3D101 %00empty%00}-->
• De Villiers, M. (1994). The role and function of a hierarchical classification of quadrilaterals. For the Learning of Mathematics, 14(1), 11–18.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal The+role+and+function+of+a+hierarchical+classification+of+quadrilaterals author%3DM.+De+Villiers 1994 De+Villiers%2C+M.+%281994%29.+The+role+and+function+of+a+hierarchical+classification+of+quadrilaterals.+For+the+Learning+of+Mathematics%2C+14%281%29%2C+11%E2%80%9318. 11-18 For+the+Learning+of+Mathematics 14 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_31_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDe%2520Villiers%26rft.aufirst%3DM.%26rft.date%3D1994%26rft.atitle%3DThe%2520role%2520and%2520function%2520of%2520a%2520hierarchical%2520classification%2520of%2520quadrilaterals%26rft.jtitle%3DFor%2520the%2520Learning%2520of%2520Mathematics%26rft.volume%3D14%26rft.issue%3D1%26rft.spage%3D11%26rft.epage%3D18 %00empty%00}-->
• De Villiers, M. (1998). To teach definitions in geometry or teach to define? PME Conference, 2, 248–255.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal To+teach+definitions+in+geometry+or+teach+to+define%3F author%3DM.+De+Villiers 1998 De+Villiers%2C+M.+%281998%29.+To+teach+definitions+in+geometry+or+teach+to+define%3F+PME+Conference%2C+2%2C+248%E2%80%93255. 248-255 PME+Conference 2 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_32_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDe%2520Villiers%26rft.aufirst%3DM.%26rft.date%3D1998%26rft.atitle%3DTo%2520teach%2520definitions%2520in%2520geometry%2520or%2520teach%2520to%2520define%253F%26rft.jtitle%3DPME%2520Conference%26rft.volume%3D2%26rft.spage%3D248%26rft.epage%3D255 %00empty%00}-->
• Doruk, M., & Alper, Ç. (2020). Pre-service mathematics teachers’ concept definitions and examples regarding sets. International Journal of Psychology and Educational Studies 7(2), 21–36.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.17220%2Fijpes.2020.02.003 journal Pre-service+mathematics+teachers%E2%80%99+concept+definitions+and+examples+regarding+sets author%3DM.+Doruk%26author%3D%C3%87+Alper 2020 Doruk%2C+M.%2C+%26+Alper%2C+%C3%87.+%282020%29.+Pre-service+mathematics+teachers%E2%80%99+concept+definitions+and+examples+regarding+sets.+International+Journal+of+Psychology+and+Educational+Studies+7%282%29%2C+21%E2%80%9336. 21-36 International+Journal+of+Psychology+and+Educational+Studies 7 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_33_1 10.17220%252Fijpes.2020.02.003 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.17220%252Fijpes.2020.02.003%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDoruk%26rft.aufirst%3DM.%26rft.date%3D2020%26rft.atitle%3DPre-service%2520mathematics%2520teachers%25E2%2580%2599%2520concept%2520definitions%2520and%2520examples%2520regarding%2520sets%26rft.jtitle%3DInternational%2520Journal%2520of%2520Psychology%2520and%2520Educational%2520Studies%26rft.volume%3D7%26rft.issue%3D2%26rft.spage%3D21%26rft.epage%3D36 %00empty%00}-->
• Dickerson, D. S., & Pitman, D. J. (2016). An examination of college mathematics majors’ understandings of their own written definitions. Journal of Mathematical Behavior, 41, 1–9. https://doi.org/10.1016/j.jmathb.2015.11.001
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2015.11.001 journal An+examination+of+college+mathematics+majors%E2%80%99+understandings+of+their+own+written+definitions author%3DD.+S.+Dickerson%26author%3DD.+J.+Pitman 2016 Dickerson%2C+D.+S.%2C+%26+Pitman%2C+D.+J.+%282016%29.+An+examination+of+college+mathematics+majors%E2%80%99+understandings+of+their+own+written+definitions.+Journal+of+Mathematical+Behavior%2C+41%2C+1%E2%80%939.+ 1-9 Journal+of+Mathematical+Behavior 41 %00null%00 https%3A%2F%2Fdoi.org%2F10.1016%2Fj.jmathb.2015.11.001 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_34_1 10.1016%252Fj.jmathb.2015.11.001 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2015.11.001%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDickerson%26rft.aufirst%3DD.%2520S.%26rft.date%3D2016%26rft.atitle%3DAn%2520examination%2520of%2520college%2520mathematics%2520majors%25E2%2580%2599%2520understandings%2520of%2520their%2520own%2520written%2520definitions%26rft.jtitle%3DJournal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D41%26rft.spage%3D1%26rft.epage%3D9 %00empty%00}-->
• Durand-Guerrier, V. (2003). Which notion of implication is the right one? From logical considerations to a didactic perspective. Educational Studies in Mathematics, 53(1), 5–34. https://doi.org/10.1023/a:1024661004375
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1023%2Fa%3A1024661004375 journal Which+notion+of+implication+is+the+right+one%3F+From+logical+considerations+to+a+didactic+perspective author%3DV.+Durand-Guerrier 2003 Durand-Guerrier%2C+V.+%282003%29.+Which+notion+of+implication+is+the+right+one%3F+From+logical+considerations+to+a+didactic+perspective.+Educational+Studies+in+Mathematics%2C+53%281%29%2C+5%E2%80%9334.+ 5-34 Educational+Studies+in+Mathematics 53 1 https%3A%2F%2Fdoi.org%2F10.1023%2Fa%3A1024661004375 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_35_1 10.1023%252Fa%253A1024661004375 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1023%252Fa%253A1024661004375%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DDurand-Guerrier%26rft.aufirst%3DV.%26rft.date%3D2003%26rft.atitle%3DWhich%2520notion%2520of%2520implication%2520is%2520the%2520right%2520one%253F%2520From%2520logical%2520considerations%2520to%2520a%2520didactic%2520perspective%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D53%26rft.issue%3D1%26rft.spage%3D5%26rft.epage%3D34 %00empty%00}-->
• Edwards, B. S., & Ward, M. B. (2004). Surprises from mathematics education research: Student (mis)use of mathematical definitions. The American Mathematical Monthly, 111(5), 411–424. https://doi.org/10.1080/00029890.2004.11920092
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F00029890.2004.11920092 journal Surprises+from+mathematics+education+research%3A+Student+%28mis%29use+of+mathematical+definitions author%3DB.+S.+Edwards%26author%3DM.+B.+Ward 2004 Edwards%2C+B.+S.%2C+%26+Ward%2C+M.+B.+%282004%29.+Surprises+from+mathematics+education+research%3A+Student+%28mis%29use+of+mathematical+definitions.+The+American+Mathematical+Monthly%2C+111%285%29%2C+411%E2%80%93424.+ 411-424 The+American+Mathematical+Monthly 111 5 https%3A%2F%2Fdoi.org%2F10.1080%2F00029890.2004.11920092 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_36_1 10.1080%252F00029890.2004.11920092 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F00029890.2004.11920092%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DEdwards%26rft.aufirst%3DB.%2520S.%26rft.date%3D2004%26rft.atitle%3DSurprises%2520from%2520mathematics%2520education%2520research%253A%2520Student%2520%2528mis%2529use%2520of%2520mathematical%2520definitions%26rft.jtitle%3DThe%2520American%2520Mathematical%2520Monthly%26rft.volume%3D111%26rft.issue%3D5%26rft.spage%3D411%26rft.epage%3D424 %00empty%00}-->
• Edwards, B. S., & Ward, M. B. (2008). The role of mathematical definitions in mathematics and in undergraduate mathematics courses. In M. P. Carlson & C. Rasmussen (Eds.), Making the connection: research and teaching in undergraduate mathematics education (pp. 223–232). Mathematical Association of America. https://doi.org/10.5948/UPO9780883859759.018
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.5948%2FUPO9780883859759.018 book The+role+of+mathematical+definitions+in+mathematics+and+in+undergraduate+mathematics+courses author%3DB.+S.+Edwards%26author%3DM.+B.+Ward%26 2008 Edwards%2C+B.+S.%2C+%26+Ward%2C+M.+B.+%282008%29.+The+role+of+mathematical+definitions+in+mathematics+and+in+undergraduate+mathematics+courses.+In+M.+P.+Carlson+%26+C.+Rasmussen+%28Eds.%29%2C+Making+the+connection%3A+research+and+teaching+in+undergraduate+mathematics+education+%28pp.+223%E2%80%93232%29.+Mathematical+Association+of+America.+ 223-232 %00null%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_37_1 10.5948%252FUPO9780883859759.018 url_ver%3DZ39.88-2004%26rft.genre%3Dbook%26rft_id%3Dinfo%3Adoi%2F10.5948%252FUPO9780883859759.018%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DEdwards%26rft.aufirst%3DB.%2520S.%26rft.date%3D2008%26rft.atitle%3DThe%2520role%2520of%2520mathematical%2520definitions%2520in%2520mathematics%2520and%2520in%2520undergraduate%2520mathematics%2520courses%26rft.aulast%3DCarlson%26rft.aufirst%3DM.%2520P.%26rft.btitle%3DMaking%2520the%2520connection%253A%2520research%2520and%2520teaching%2520in%2520undergraduate%2520mathematics%2520education%26rft.spage%3D223%26rft.epage%3D232%26rft.pub%3DMathematical%2520Association%2520of%2520America %00empty%00}-->
• Ertekin, E., Yazici, E., & Delice, A. (2014). Investigation of primary mathematics student teachers’ concept images: Cylinder and cone. International Journal of Mathematical Education in Science and Technology, 45(4), 566–588.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F0020739X.2013.868537 journal Investigation+of+primary+mathematics+student+teachers%E2%80%99+concept+images%3A+Cylinder+and+cone author%3DE.+Ertekin%26author%3DE.+Yazici%26author%3DA.+Delice 2014 Ertekin%2C+E.%2C+Yazici%2C+E.%2C+%26+Delice%2C+A.+%282014%29.+Investigation+of+primary+mathematics+student+teachers%E2%80%99+concept+images%3A+Cylinder+and+cone.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+45%284%29%2C+566%E2%80%93588. 566-588 International+Journal+of+Mathematical+Education+in+Science+and+Technology 45 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_38_1 10.1080%252F0020739X.2013.868537 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739X.2013.868537%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DErtekin%26rft.aufirst%3DE.%26rft.date%3D2014%26rft.atitle%3DInvestigation%2520of%2520primary%2520mathematics%2520student%2520teachers%25E2%2580%2599%2520concept%2520images%253A%2520Cylinder%2520and%2520cone%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D45%26rft.issue%3D4%26rft.spage%3D566%26rft.epage%3D588 %00empty%00}-->
• Fernández-León, A., Gavilán-Izquierdo, J.M., González-Regaña, A.J., Martín-Molina, V., & Toscano, R. (2021). Identifying routines in the discourse of undergraduate students when defining. Mathematics Education Research Journal, 33(2), 301–319.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs13394-019-00301-1 journal Identifying+routines+in+the+discourse+of+undergraduate+students+when+defining author%3DA.+Fern%C3%A1ndez-Le%C3%B3n%26author%3DJ.M.+Gavil%C3%A1n-Izquierdo%26author%3DA.J.+Gonz%C3%A1lez-Rega%C3%B1a%26author%3DV.+Mart%C3%ADn-Molina%26author%3DR.+Toscano 2021 Fern%C3%A1ndez-Le%C3%B3n%2C+A.%2C+Gavil%C3%A1n-Izquierdo%2C+J.M.%2C+Gonz%C3%A1lez-Rega%C3%B1a%2C+A.J.%2C+Mart%C3%ADn-Molina%2C+V.%2C+%26+Toscano%2C+R.+%282021%29.+Identifying+routines+in+the+discourse+of+undergraduate+students+when+defining.+Mathematics+Education+Research+Journal%2C+33%282%29%2C+301%E2%80%93319. 301-319 Mathematics+Education+Research+Journal 33 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_39_1 10.1007%252Fs13394-019-00301-1 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs13394-019-00301-1%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DFern%25C3%25A1ndez-Le%25C3%25B3n%26rft.aufirst%3DA.%26rft.date%3D2021%26rft.atitle%3DIdentifying%2520routines%2520in%2520the%2520discourse%2520of%2520undergraduate%2520students%2520when%2520defining%26rft.jtitle%3DMathematics%2520Education%2520Research%2520Journal%26rft.volume%3D33%26rft.issue%3D2%26rft.spage%3D301%26rft.epage%3D319 %00empty%00}-->
• Fisher, B. (2016). Student-created definitions of sequence convergence: A case study. PRIMUS, 26(8), 770–787.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F10511970.2016.1172688 journal Student-created+definitions+of+sequence+convergence%3A+A+case+study author%3DB.+Fisher 2016 Fisher%2C+B.+%282016%29.+Student-created+definitions+of+sequence+convergence%3A+A+case+study.+PRIMUS%2C+26%288%29%2C+770%E2%80%93787. 770-787 PRIMUS 26 8 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_40_1 10.1080%252F10511970.2016.1172688 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F10511970.2016.1172688%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DFisher%26rft.aufirst%3DB.%26rft.date%3D2016%26rft.atitle%3DStudent-created%2520definitions%2520of%2520sequence%2520convergence%253A%2520A%2520case%2520study%26rft.jtitle%3DPRIMUS%26rft.volume%3D26%26rft.issue%3D8%26rft.spage%3D770%26rft.epage%3D787 %00empty%00}-->
• Flores, A., & Park, J. (2016). Students’ guided reinvention of definition of limit of a sequence with interactive technology. Contemporary Issues in Technology and Teacher Education, 16(2), 110–126.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Students%E2%80%99+guided+reinvention+of+definition+of+limit+of+a+sequence+with+interactive+technology author%3DA.+Flores%26author%3DJ.+Park 2016 Flores%2C+A.%2C+%26+Park%2C+J.+%282016%29.+Students%E2%80%99+guided+reinvention+of+definition+of+limit+of+a+sequence+with+interactive+technology.+Contemporary+Issues+in+Technology+and+Teacher+Education%2C+16%282%29%2C+110%E2%80%93126. 110-126 Contemporary+Issues+in+Technology+and+Teacher+Education 16 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_41_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DFlores%26rft.aufirst%3DA.%26rft.date%3D2016%26rft.atitle%3DStudents%25E2%2580%2599%2520guided%2520reinvention%2520of%2520definition%2520of%2520limit%2520of%2520a%2520sequence%2520with%2520interactive%2520technology%26rft.jtitle%3DContemporary%2520Issues%2520in%2520Technology%2520and%2520Teacher%2520Education%26rft.volume%3D16%26rft.issue%3D2%26rft.spage%3D110%26rft.epage%3D126 %00empty%00}-->
• Foster, C. (2014). Confidence trick: The interpretation of confidence intervals. Canadian Journal of Science, Mathematics and Technology Education, 14(1), 23–34. https://doi.org/10.1080/14926156.2014.874615
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F14926156.2014.874615 journal Confidence+trick%3A+The+interpretation+of+confidence+intervals.+Canadian+Journal+of+Science author%3DC.+Foster 2014 Foster%2C+C.+%282014%29.+Confidence+trick%3A+The+interpretation+of+confidence+intervals.+Canadian+Journal+of+Science%2C+Mathematics+and+Technology+Education%2C+14%281%29%2C+23%E2%80%9334.+ 23-34 Mathematics+and+Technology+Education 14 1 https%3A%2F%2Fdoi.org%2F10.1080%2F14926156.2014.874615 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_42_1 10.1080%252F14926156.2014.874615 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F14926156.2014.874615%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DFoster%26rft.aufirst%3DC.%26rft.date%3D2014%26rft.atitle%3DConfidence%2520trick%253A%2520The%2520interpretation%2520of%2520confidence%2520intervals.%2520Canadian%2520Journal%2520of%2520Science%26rft.jtitle%3DMathematics%2520and%2520Technology%2520Education%26rft.volume%3D14%26rft.issue%3D1%26rft.spage%3D23%26rft.epage%3D34 %00empty%00}-->
• Foster, C., & de Villiers, M. (2015). The definition of the scalar product: An analysis and critique of a classroom episode. International Journal of Mathematical Education in Science and Technology, 47(5), 750–761. https://doi.org/10.1080/0020739x.2015.1117148
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2015.1117148 journal The+definition+of+the+scalar+product%3A+An+analysis+and+critique+of+a+classroom+episode author%3DC.+Foster%26author%3DM.+de+Villiers 2015 Foster%2C+C.%2C+%26+de+Villiers%2C+M.+%282015%29.+The+definition+of+the+scalar+product%3A+An+analysis+and+critique+of+a+classroom+episode.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+47%285%29%2C+750%E2%80%93761.+ 750-761 International+Journal+of+Mathematical+Education+in+Science+and+Technology 47 5 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2015.1117148 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_43_1 10.1080%252F0020739x.2015.1117148 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2015.1117148%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DFoster%26rft.aufirst%3DC.%26rft.date%3D2015%26rft.atitle%3DThe%2520definition%2520of%2520the%2520scalar%2520product%253A%2520An%2520analysis%2520and%2520critique%2520of%2520a%2520classroom%2520episode%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D47%26rft.issue%3D5%26rft.spage%3D750%26rft.epage%3D761 %00empty%00}-->
• Fujita, T. (2012). Learners’ level of understanding of the inclusion relations of quadrilaterals and prototype phenomenon. The Journal of Mathematical Behavior, 31(1), 60–72. https://doi.org/10.1016/j.jmathb.2011.08.003
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2011.08.003 journal Learners%E2%80%99+level+of+understanding+of+the+inclusion+relations+of+quadrilaterals+and+prototype+phenomenon author%3DT.+Fujita 2012 Fujita%2C+T.+%282012%29.+Learners%E2%80%99+level+of+understanding+of+the+inclusion+relations+of+quadrilaterals+and+prototype+phenomenon.+The+Journal+of+Mathematical+Behavior%2C+31%281%29%2C+60%E2%80%9372.+ 60-72 The+Journal+of+Mathematical+Behavior 31 1 https%3A%2F%2Fdoi.org%2F10.1016%2Fj.jmathb.2011.08.003 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_44_1 10.1016%252Fj.jmathb.2011.08.003 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2011.08.003%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DFujita%26rft.aufirst%3DT.%26rft.date%3D2012%26rft.atitle%3DLearners%25E2%2580%2599%2520level%2520of%2520understanding%2520of%2520the%2520inclusion%2520relations%2520of%2520quadrilaterals%2520and%2520prototype%2520phenomenon%26rft.jtitle%3DThe%2520Journal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D31%26rft.issue%3D1%26rft.spage%3D60%26rft.epage%3D72 %00empty%00}-->
• Furinghetti, F. (2000). The history of mathematics as a coupling link between secondary and university teaching. International Journal of Mathematical Education in Science and Technology, 31(1), 43–51. https://doi.org/10.1080/002073900287372
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F002073900287372 journal The+history+of+mathematics+as+a+coupling+link+between+secondary+and+university+teaching author%3DF.+Furinghetti 2000 Furinghetti%2C+F.+%282000%29.+The+history+of+mathematics+as+a+coupling+link+between+secondary+and+university+teaching.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+31%281%29%2C+43%E2%80%9351.+ 43-51 International+Journal+of+Mathematical+Education+in+Science+and+Technology 31 1 https%3A%2F%2Fdoi.org%2F10.1080%2F002073900287372 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_45_1 10.1080%252F002073900287372 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F002073900287372%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DFuringhetti%26rft.aufirst%3DF.%26rft.date%3D2000%26rft.atitle%3DThe%2520history%2520of%2520mathematics%2520as%2520a%2520coupling%2520link%2520between%2520secondary%2520and%2520university%2520teaching%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D31%26rft.issue%3D1%26rft.spage%3D43%26rft.epage%3D51 %00empty%00}-->
• Furinghetti, F., & Paola, D. (2000). Definition as a teaching object: A preliminary study. PME Conference, 2, 289–296.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Definition+as+a+teaching+object%3A+A+preliminary+study author%3DF.+Furinghetti%26author%3DD.+Paola 2000 Furinghetti%2C+F.%2C+%26+Paola%2C+D.+%282000%29.+Definition+as+a+teaching+object%3A+A+preliminary+study.+PME+Conference%2C+2%2C+289%E2%80%93296. 289-296 PME+Conference 2 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_46_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DFuringhetti%26rft.aufirst%3DF.%26rft.date%3D2000%26rft.atitle%3DDefinition%2520as%2520a%2520teaching%2520object%253A%2520A%2520preliminary%2520study%26rft.jtitle%3DPME%2520Conference%26rft.volume%3D2%26rft.spage%3D289%26rft.epage%3D296 %00empty%00}-->
• Gilbertson, N. J., He, J., Satyam, V. R., Smith, J. P., & Stehr, E. M. (2016). The definitions of spatial quantities in elementary curriculum materials. Proceedings of 38th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (38th, Tucson, AZ, Nov 3-6, 2016).
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 other The+definitions+of+spatial+quantities+in+elementary+curriculum+materials author%3DN.+J.+Gilbertson%26author%3DJ.+He%26author%3DV.+R.+Satyam%26author%3DJ.+P.+Smith%26author%3DE.+M.+Stehr 2016 Gilbertson%2C+N.+J.%2C+He%2C+J.%2C+Satyam%2C+V.+R.%2C+Smith%2C+J.+P.%2C+%26+Stehr%2C+E.+M.+%282016%29.+The+definitions+of+spatial+quantities+in+elementary+curriculum+materials.+Proceedings+of+38th+annual+meeting+of+the+North+American+Chapter+of+the+International+Group+for+the+Psychology+of+Mathematics+Education+%2838th%2C+Tucson%2C+AZ%2C+Nov+3-6%2C+2016%29. %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_47_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Dother%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGilbertson%26rft.aufirst%3DN.%2520J.%26rft.date%3D2016%26rft.atitle%3DThe%2520definitions%2520of%2520spatial%2520quantities%2520in%2520elementary%2520curriculum%2520materials %00empty%00}-->
• Gilboa, N., Kidron, I., & Dreyfus, T. (2018). Constructing a mathematical definition: The case of the tangent. International Journal of Mathematical Education in Science and Technology, 50(3), 421–446. https://doi.org/10.1080/0020739x.2018.1516824
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2018.1516824 journal Constructing+a+mathematical+definition%3A+The+case+of+the+tangent author%3DN.+Gilboa%26author%3DI.+Kidron%26author%3DT.+Dreyfus 2018 Gilboa%2C+N.%2C+Kidron%2C+I.%2C+%26+Dreyfus%2C+T.+%282018%29.+Constructing+a+mathematical+definition%3A+The+case+of+the+tangent.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+50%283%29%2C+421%E2%80%93446.+ 421-446 International+Journal+of+Mathematical+Education+in+Science+and+Technology 50 3 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2018.1516824 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_48_1 10.1080%252F0020739x.2018.1516824 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2018.1516824%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGilboa%26rft.aufirst%3DN.%26rft.date%3D2018%26rft.atitle%3DConstructing%2520a%2520mathematical%2520definition%253A%2520The%2520case%2520of%2520the%2520tangent%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D50%26rft.issue%3D3%26rft.spage%3D421%26rft.epage%3D446 %00empty%00}-->
• Gokbulut, Y., & Sen, M. (2019). Primary teachers knowledge of quadrilaterals. Higher Education Studies, 9(2), 1–9.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.5539%2Fhes.v9n2p1 journal Primary+teachers+knowledge+of+quadrilaterals author%3DY.+Gokbulut%26author%3DM.+Sen 2019 Gokbulut%2C+Y.%2C+%26+Sen%2C+M.+%282019%29.+Primary+teachers+knowledge+of+quadrilaterals.+Higher+Education+Studies%2C+9%282%29%2C+1%E2%80%939. 1-9 Higher+Education+Studies 9 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_49_1 10.5539%252Fhes.v9n2p1 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.5539%252Fhes.v9n2p1%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGokbulut%26rft.aufirst%3DY.%26rft.date%3D2019%26rft.atitle%3DPrimary%2520teachers%2520knowledge%2520of%2520quadrilaterals%26rft.jtitle%3DHigher%2520Education%2520Studies%26rft.volume%3D9%26rft.issue%3D2%26rft.spage%3D1%26rft.epage%3D9 %00empty%00}-->
• Govender, R., & de Villiers, M. (2003). Constructive evaluation of definitions in a dynamic geometry context. Research in Mathematical Education, 7(1), 41–58.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Constructive+evaluation+of+definitions+in+a+dynamic+geometry+context author%3DR.+Govender%26author%3DM.+de+Villiers 2003 Govender%2C+R.%2C+%26+de+Villiers%2C+M.+%282003%29.+Constructive+evaluation+of+definitions+in+a+dynamic+geometry+context.+Research+in+Mathematical+Education%2C+7%281%29%2C+41%E2%80%9358. 41-58 Research+in+Mathematical+Education 7 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_50_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGovender%26rft.aufirst%3DR.%26rft.date%3D2003%26rft.atitle%3DConstructive%2520evaluation%2520of%2520definitions%2520in%2520a%2520dynamic%2520geometry%2520context%26rft.jtitle%3DResearch%2520in%2520Mathematical%2520Education%26rft.volume%3D7%26rft.issue%3D1%26rft.spage%3D41%26rft.epage%3D58 %00empty%00}-->
• Govender, R., & De Villiers, M. (2004). A dynamic approach to quadrilateral definitions. Pythagoras, 2004(59), 34–45.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal A+dynamic+approach+to+quadrilateral+definitions author%3DR.+Govender%26author%3DM.+De+Villiers 2004 Govender%2C+R.%2C+%26+De+Villiers%2C+M.+%282004%29.+A+dynamic+approach+to+quadrilateral+definitions.+Pythagoras%2C+2004%2859%29%2C+34%E2%80%9345. 34-45 Pythagoras 2004 59 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_51_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGovender%26rft.aufirst%3DR.%26rft.date%3D2004%26rft.atitle%3DA%2520dynamic%2520approach%2520to%2520quadrilateral%2520definitions%26rft.jtitle%3DPythagoras%26rft.volume%3D2004%26rft.issue%3D59%26rft.spage%3D34%26rft.epage%3D45 %00empty%00}-->
• Gutiérrez, A., & Jaime, A. (1999). Preservice primary teachers’ understanding of the concept of altitude of a triangle. Journal of Mathematics Teacher Education, 2(3), 253–275. https://doi.org/10.1023/a:1009900719800
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1023%2Fa%3A1009900719800 journal Preservice+primary+teachers%E2%80%99+understanding+of+the+concept+of+altitude+of+a+triangle author%3DA.+Guti%C3%A9rrez%26author%3DA.+Jaime 1999 Guti%C3%A9rrez%2C+A.%2C+%26+Jaime%2C+A.+%281999%29.+Preservice+primary+teachers%E2%80%99+understanding+of+the+concept+of+altitude+of+a+triangle.+Journal+of+Mathematics+Teacher+Education%2C+2%283%29%2C+253%E2%80%93275.+ 253-275 Journal+of+Mathematics+Teacher+Education 2 3 https%3A%2F%2Fdoi.org%2F10.1023%2Fa%3A1009900719800 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_52_1 10.1023%252Fa%253A1009900719800 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1023%252Fa%253A1009900719800%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DGuti%25C3%25A9rrez%26rft.aufirst%3DA.%26rft.date%3D1999%26rft.atitle%3DPreservice%2520primary%2520teachers%25E2%2580%2599%2520understanding%2520of%2520the%2520concept%2520of%2520altitude%2520of%2520a%2520triangle%26rft.jtitle%3DJournal%2520of%2520Mathematics%2520Teacher%2520Education%26rft.volume%3D2%26rft.issue%3D3%26rft.spage%3D253%26rft.epage%3D275 %00empty%00}-->
• Haj-Yahya, A. (2019). Can classification criteria constitute a correct mathematical definition? Pre-service and in-service teachers’ perspectives. International Journal of Research in Education and Science, 5(1), 88–101.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Can+classification+criteria+constitute+a+correct+mathematical+definition%3F+Pre-service+and+in-service+teachers%E2%80%99 author%3DA.+Haj-Yahya 2019 Haj-Yahya%2C+A.+%282019%29.+Can+classification+criteria+constitute+a+correct+mathematical+definition%3F+Pre-service+and+in-service+teachers%E2%80%99+perspectives.+International+Journal+of+Research+in+Education+and+Science%2C+5%281%29%2C+88%E2%80%93101. 88-101 perspectives.+International+Journal+of+Research+in+Education+and+Science 5 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_53_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHaj-Yahya%26rft.aufirst%3DA.%26rft.date%3D2019%26rft.atitle%3DCan%2520classification%2520criteria%2520constitute%2520a%2520correct%2520mathematical%2520definition%253F%2520Pre-service%2520and%2520in-service%2520teachers%25E2%2580%2599%26rft.jtitle%3Dperspectives.%2520International%2520Journal%2520of%2520Research%2520in%2520Education%2520and%2520Science%26rft.volume%3D5%26rft.issue%3D1%26rft.spage%3D88%26rft.epage%3D101 %00empty%00}-->
• Haj-Yahya, A. (2021). Students’ conceptions of the definitions of congruent and similar triangles International Journal of Mathematical Education in Science and Technology. https://doi.org/10.1080/0020739X.2021.1902008
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F0020739X.2021.1902008 journal Students%E2%80%99+conceptions+of+the+definitions+of+congruent+and+similar+triangles author%3DA.+Haj-Yahya 2021 Haj-Yahya%2C+A.+%282021%29.+Students%E2%80%99+conceptions+of+the+definitions+of+congruent+and+similar+triangles+International+Journal+of+Mathematical+Education+in+Science+and+Technology.+ %00empty%00 International+Journal+of+Mathematical+Education+in+Science+and+Technology %00empty%00 %00null%00 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739X.2021.1902008 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_54_1 10.1080%252F0020739X.2021.1902008 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739X.2021.1902008%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHaj-Yahya%26rft.aufirst%3DA.%26rft.date%3D2021%26rft.atitle%3DStudents%25E2%2580%2599%2520conceptions%2520of%2520the%2520definitions%2520of%2520congruent%2520and%2520similar%2520triangles%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology %00empty%00}-->
• Haj-Yahya, A., Hershkowitz, R., & Dreyfus, T. (2022). Investigating students’ geometrical proofs through the lens of students’ definitions. Mathematics Education Research Journal. https://doi.org/10.1007/s13394-021-00406-6
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs13394-021-00406-6 journal Investigating+students%E2%80%99+geometrical+proofs+through+the+lens+of+students%E2%80%99+definitions author%3DA.+Haj-Yahya%26author%3DR.+Hershkowitz%26author%3DT.+Dreyfus 2022 Haj-Yahya%2C+A.%2C+Hershkowitz%2C+R.%2C+%26+Dreyfus%2C+T.+%282022%29.+Investigating+students%E2%80%99+geometrical+proofs+through+the+lens+of+students%E2%80%99+definitions.+Mathematics+Education+Research+Journal.+ %00empty%00 Mathematics+Education+Research+Journal %00empty%00 %00null%00 https%3A%2F%2Fdoi.org%2F10.1007%2Fs13394-021-00406-6 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_55_1 10.1007%252Fs13394-021-00406-6 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs13394-021-00406-6%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHaj-Yahya%26rft.aufirst%3DA.%26rft.date%3D2022%26rft.atitle%3DInvestigating%2520students%25E2%2580%2599%2520geometrical%2520proofs%2520through%2520the%2520lens%2520of%2520students%25E2%2580%2599%2520definitions%26rft.jtitle%3DMathematics%2520Education%2520Research%2520Journal %00empty%00}-->
• Harel, G., Fuller, E., & Rabin, J. M. (2008). Attention to meaning by algebra teachers. Journal of Mathematical Behavior, 27(2), 116–127.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2008.08.002 journal Attention+to+meaning+by+algebra+teachers author%3DG.+Harel%26author%3DE.+Fuller%26author%3DJ.+M.+Rabin 2008 Harel%2C+G.%2C+Fuller%2C+E.%2C+%26+Rabin%2C+J.+M.+%282008%29.+Attention+to+meaning+by+algebra+teachers.+Journal+of+Mathematical+Behavior%2C+27%282%29%2C+116%E2%80%93127. 116-127 Journal+of+Mathematical+Behavior 27 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_56_1 10.1016%252Fj.jmathb.2008.08.002 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2008.08.002%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHarel%26rft.aufirst%3DG.%26rft.date%3D2008%26rft.atitle%3DAttention%2520to%2520meaning%2520by%2520algebra%2520teachers%26rft.jtitle%3DJournal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D27%26rft.issue%3D2%26rft.spage%3D116%26rft.epage%3D127 %00empty%00}-->
• Holguín, V. A. (2016). Stages identified in university students’ behavior using mathematical definitions. Proceedings of the 38th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. (38th, Tucson, AZ, Nov 3-6, 2016)
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 other Stages+identified+in+university+students%E2%80%99+behavior+using+mathematical+definitions author%3DV.+A.+Holgu%C3%ADn 2016 Holgu%C3%ADn%2C+V.+A.+%282016%29.+Stages+identified+in+university+students%E2%80%99+behavior+using+mathematical+definitions.+Proceedings+of+the+38th+Annual+Meeting+of+the+North+American+Chapter+of+the+International+Group+for+the+Psychology+of+Mathematics+Education.+%2838th%2C+Tucson%2C+AZ%2C+Nov+3-6%2C+2016%29 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_57_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Dother%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DHolgu%25C3%25ADn%26rft.aufirst%3DV.%2520A.%26rft.date%3D2016%26rft.atitle%3DStages%2520identified%2520in%2520university%2520students%25E2%2580%2599%2520behavior%2520using%2520mathematical%2520definitions %00empty%00}-->
• Johnson, H. L., Blume, G. W., Shimizu, J. K., Graysay, D., & Konnova, S. (2014). A teacher’s conception of definition and use of examples when doing and teaching mathematics. Mathematical Thinking and Learning, 16(4), 285–311. https://doi.org/10.1080/10986065.2014.953018
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F10986065.2014.953018 journal A+teacher%E2%80%99s+conception+of+definition+and+use+of+examples+when+doing+and+teaching+mathematics author%3DH.+L.+Johnson%26author%3DG.+W.+Blume%26author%3DJ.+K.+Shimizu%26author%3DD.+Graysay%26author%3DS.+Konnova 2014 Johnson%2C+H.+L.%2C+Blume%2C+G.+W.%2C+Shimizu%2C+J.+K.%2C+Graysay%2C+D.%2C+%26+Konnova%2C+S.+%282014%29.+A+teacher%E2%80%99s+conception+of+definition+and+use+of+examples+when+doing+and+teaching+mathematics.+Mathematical+Thinking+and+Learning%2C+16%284%29%2C+285%E2%80%93311.+ 285-311 Mathematical+Thinking+and+Learning 16 4 https%3A%2F%2Fdoi.org%2F10.1080%2F10986065.2014.953018 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_58_1 10.1080%252F10986065.2014.953018 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F10986065.2014.953018%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DJohnson%26rft.aufirst%3DH.%2520L.%26rft.date%3D2014%26rft.atitle%3DA%2520teacher%25E2%2580%2599s%2520conception%2520of%2520definition%2520and%2520use%2520of%2520examples%2520when%2520doing%2520and%2520teaching%2520mathematics%26rft.jtitle%3DMathematical%2520Thinking%2520and%2520Learning%26rft.volume%3D16%26rft.issue%3D4%26rft.spage%3D285%26rft.epage%3D311 %00empty%00}-->
• Kabaca, T. (2017). Understanding the hierarchical classification of quadrilaterals through the ordered relation according to diagonal properties. International Journal of Mathematical Education in Science and Technology, 48(8), 1240–1248. https://doi.org/10.1080/0020739x.2017.1334969
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2017.1334969 journal Understanding+the+hierarchical+classification+of+quadrilaterals+through+the+ordered+relation+according+to+diagonal+properties author%3DT.+Kabaca 2017 Kabaca%2C+T.+%282017%29.+Understanding+the+hierarchical+classification+of+quadrilaterals+through+the+ordered+relation+according+to+diagonal+properties.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+48%288%29%2C+1240%E2%80%931248.+ 1240-1248 International+Journal+of+Mathematical+Education+in+Science+and+Technology 48 8 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2017.1334969 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_59_1 10.1080%252F0020739x.2017.1334969 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2017.1334969%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DKabaca%26rft.aufirst%3DT.%26rft.date%3D2017%26rft.atitle%3DUnderstanding%2520the%2520hierarchical%2520classification%2520of%2520quadrilaterals%2520through%2520the%2520ordered%2520relation%2520according%2520to%2520diagonal%2520properties%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D48%26rft.issue%3D8%26rft.spage%3D1240%26rft.epage%3D1248 %00empty%00}-->
• Karakuş, F. (2015). Investigation into how 8th grade students define fractals. Kuram ve Uygulamada Egitim Bilimleri, 15, 825–836. https://doi.org/10.12738/estp.2015.3.2429
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.12738%2Festp.2015.3.2429 journal Investigation+into+how+8th+grade+students+define+fractals author%3DF.+Karaku%C5%9F 2015 Karaku%C5%9F%2C+F.+%282015%29.+Investigation+into+how+8th+grade+students+define+fractals.+Kuram+ve+Uygulamada+Egitim+Bilimleri%2C+15%2C+825%E2%80%93836.+ 825-836 Kuram+ve+Uygulamada+Egitim+Bilimleri 15 %00null%00 https%3A%2F%2Fdoi.org%2F10.12738%2Festp.2015.3.2429 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_60_1 10.12738%252Festp.2015.3.2429 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.12738%252Festp.2015.3.2429%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DKaraku%25C5%259F%26rft.aufirst%3DF.%26rft.date%3D2015%26rft.atitle%3DInvestigation%2520into%2520how%25208th%2520grade%2520students%2520define%2520fractals%26rft.jtitle%3DKuram%2520ve%2520Uygulamada%2520Egitim%2520Bilimleri%26rft.volume%3D15%26rft.spage%3D825%26rft.epage%3D836 %00empty%00}-->
• Kemp, A., & Vidakovic, D. (2021). Ways secondary mathematics teachers apply definitions in Taxicab geometry for a real-life situation: Midset. Journal of Mathematical Behavior, 62, 1–20.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2021.100848 journal Ways+secondary+mathematics+teachers+apply+definitions+in+Taxicab+geometry+for+a+real-life+situation%3A+Midset author%3DA.+Kemp%26author%3DD.+Vidakovic 2021 Kemp%2C+A.%2C+%26+Vidakovic%2C+D.+%282021%29.+Ways+secondary+mathematics+teachers+apply+definitions+in+Taxicab+geometry+for+a+real-life+situation%3A+Midset.+Journal+of+Mathematical+Behavior%2C+62%2C+1%E2%80%9320. 1-20 Journal+of+Mathematical+Behavior 62 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_61_1 10.1016%252Fj.jmathb.2021.100848 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2021.100848%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DKemp%26rft.aufirst%3DA.%26rft.date%3D2021%26rft.atitle%3DWays%2520secondary%2520mathematics%2520teachers%2520apply%2520definitions%2520in%2520Taxicab%2520geometry%2520for%2520a%2520real-life%2520situation%253A%2520Midset%26rft.jtitle%3DJournal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D62%26rft.spage%3D1%26rft.epage%3D20 %00empty%00}-->
• Kobiela, M., Iacono, H., Cho, S., & Chandrasekhar, V. (2022). Examining the potential of rehearsal interjections to support the teaching of mathematical practice: The case of mathematical defining. Journal of Mathematics Teacher Education. https://doi.org/10.1007/s10857-022-09545-4
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10857-022-09545-4 journal Examining+the+potential+of+rehearsal+interjections+to+support+the+teaching+of+mathematical+practice%3A+The+case+of+mathematical+defining author%3DM.+Kobiela%26author%3DH.+Iacono%26author%3DS.+Cho%26author%3DV.+Chandrasekhar 2022 Kobiela%2C+M.%2C+Iacono%2C+H.%2C+Cho%2C+S.%2C+%26+Chandrasekhar%2C+V.+%282022%29.+Examining+the+potential+of+rehearsal+interjections+to+support+the+teaching+of+mathematical+practice%3A+The+case+of+mathematical+defining.+Journal+of+Mathematics+Teacher+Education.+ %00empty%00 Journal+of+Mathematics+Teacher+Education %00empty%00 %00null%00 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10857-022-09545-4 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_62_1 10.1007%252Fs10857-022-09545-4 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10857-022-09545-4%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DKobiela%26rft.aufirst%3DM.%26rft.date%3D2022%26rft.atitle%3DExamining%2520the%2520potential%2520of%2520rehearsal%2520interjections%2520to%2520support%2520the%2520teaching%2520of%2520mathematical%2520practice%253A%2520The%2520case%2520of%2520mathematical%2520defining%26rft.jtitle%3DJournal%2520of%2520Mathematics%2520Teacher%2520Education %00empty%00}-->
• Kobiela, M., & Lehrer, R. (2015). The codevelopment of mathematical concepts and the practice of defining. Journal for Research in Mathematics Education, 46(4), 423–454.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.5951%2Fjresematheduc.46.4.0423 journal The+codevelopment+of+mathematical+concepts+and+the+practice+of+defining author%3DM.+Kobiela%26author%3DR.+Lehrer 2015 Kobiela%2C+M.%2C+%26+Lehrer%2C+R.+%282015%29.+The+codevelopment+of+mathematical+concepts+and+the+practice+of+defining.+Journal+for+Research+in+Mathematics+Education%2C+46%284%29%2C+423%E2%80%93454. 423-454 Journal+for+Research+in+Mathematics+Education 46 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_63_1 10.5951%252Fjresematheduc.46.4.0423 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.5951%252Fjresematheduc.46.4.0423%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DKobiela%26rft.aufirst%3DM.%26rft.date%3D2015%26rft.atitle%3DThe%2520codevelopment%2520of%2520mathematical%2520concepts%2520and%2520the%2520practice%2520of%2520defining%26rft.jtitle%3DJournal%2520for%2520Research%2520in%2520Mathematics%2520Education%26rft.volume%3D46%26rft.issue%3D4%26rft.spage%3D423%26rft.epage%3D454 %00empty%00}-->
• Kontorovich, I., & Zazkis, R. (2017). Mathematical conventions: Revisiting arbitrary and necessary. For the Learning of Mathematics, 37(1), 29–34.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Mathematical+conventions%3A+Revisiting+arbitrary+and+necessary author%3DI.+Kontorovich%26author%3DR.+Zazkis 2017 Kontorovich%2C+I.%2C+%26+Zazkis%2C+R.+%282017%29.+Mathematical+conventions%3A+Revisiting+arbitrary+and+necessary.+For+the+Learning+of+Mathematics%2C+37%281%29%2C+29%E2%80%9334. 29-34 For+the+Learning+of+Mathematics 37 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_64_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DKontorovich%26rft.aufirst%3DI.%26rft.date%3D2017%26rft.atitle%3DMathematical%2520conventions%253A%2520Revisiting%2520arbitrary%2520and%2520necessary%26rft.jtitle%3DFor%2520the%2520Learning%2520of%2520Mathematics%26rft.volume%3D37%26rft.issue%3D1%26rft.spage%3D29%26rft.epage%3D34 %00empty%00}-->
• Kontorovich, I. t. (2016). We all know that a0 = 1, but can you explain why? Canadian Journal of Science, Mathematics and Technology Education, 16(3), 237–246. https://doi.org/10.1080/14926156.2016.1189623
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F14926156.2016.1189623 journal We+all+know+that+a0+%3D+1%2C+but+can+you+explain+why%3F author%3DI.+t.+Kontorovich 2016 Kontorovich%2C+I.+t.+%282016%29.+We+all+know+that+a0+%3D+1%2C+but+can+you+explain+why%3F+Canadian+Journal+of+Science%2C+Mathematics+and+Technology+Education%2C+16%283%29%2C+237%E2%80%93246.+ 237-246 Canadian+Journal+of+Science%2C+Mathematics+and+Technology+Education 16 3 https%3A%2F%2Fdoi.org%2F10.1080%2F14926156.2016.1189623 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_65_1 10.1080%252F14926156.2016.1189623 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F14926156.2016.1189623%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DKontorovich%26rft.aufirst%3DI.%2520t.%26rft.date%3D2016%26rft.atitle%3DWe%2520all%2520know%2520that%2520a0%2520%253D%25201%252C%2520but%2520can%2520you%2520explain%2520why%253F%26rft.jtitle%3DCanadian%2520Journal%2520of%2520Science%252C%2520Mathematics%2520and%2520Technology%2520Education%26rft.volume%3D16%26rft.issue%3D3%26rft.spage%3D237%26rft.epage%3D246 %00empty%00}-->
• Lavy, I., & Mashiach-Eizenberg, M. (2009). The interplay between spoken language and informal definitions of statistical concepts. Journal of Statistics Education, 17(1). https://doi.org/10.1080/10691898.2009.11889502
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> PubMed<!--${googleScholarLinkReplacer: 10.1080%2F10691898.2009.11889502 journal The+interplay+between+spoken+language+and+informal+definitions+of+statistical+concepts author%3DI.+Lavy%26author%3DM.+Mashiach-Eizenberg 2009 Lavy%2C+I.%2C+%26+Mashiach-Eizenberg%2C+M.+%282009%29.+The+interplay+between+spoken+language+and+informal+definitions+of+statistical+concepts.+Journal+of+Statistics+Education%2C+17%281%29.+ 1 Journal+of+Statistics+Education 17 %00null%00 https%3A%2F%2Fdoi.org%2F10.1080%2F10691898.2009.11889502 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_66_1 10.1080%252F10691898.2009.11889502 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F10691898.2009.11889502%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLavy%26rft.aufirst%3DI.%26rft.date%3D2009%26rft.atitle%3DThe%2520interplay%2520between%2520spoken%2520language%2520and%2520informal%2520definitions%2520of%2520statistical%2520concepts%26rft.jtitle%3DJournal%2520of%2520Statistics%2520Education%26rft.volume%3D17%26rft.spage%3D1 %00empty%00}-->
• Leikin, R., & Winicki-Landman, G. (2000). On equivalent and non-equivalent definitions: Part 2. For the Learning of Mathematics, 20(2), 24–29.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal On+equivalent+and+non-equivalent+definitions%3A+Part+2 author%3DR.+Leikin%26author%3DG.+Winicki-Landman 2000 Leikin%2C+R.%2C+%26+Winicki-Landman%2C+G.+%282000%29.+On+equivalent+and+non-equivalent+definitions%3A+Part+2.+For+the+Learning+of+Mathematics%2C+20%282%29%2C+24%E2%80%9329. 24-29 For+the+Learning+of+Mathematics 20 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_67_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLeikin%26rft.aufirst%3DR.%26rft.date%3D2000%26rft.atitle%3DOn%2520equivalent%2520and%2520non-equivalent%2520definitions%253A%2520Part%25202%26rft.jtitle%3DFor%2520the%2520Learning%2520of%2520Mathematics%26rft.volume%3D20%26rft.issue%3D2%26rft.spage%3D24%26rft.epage%3D29 %00empty%00}-->
• Leikin, R., & Winicki-Landman, G. (2001). Defining as a vehicle for professional development of secondary school mathematics teachers. Mathematics Education Research Journal, 3, 62–73.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Defining+as+a+vehicle+for+professional+development+of+secondary+school+mathematics+teachers author%3DR.+Leikin%26author%3DG.+Winicki-Landman 2001 Leikin%2C+R.%2C+%26+Winicki-Landman%2C+G.+%282001%29.+Defining+as+a+vehicle+for+professional+development+of+secondary+school+mathematics+teachers.+Mathematics+Education+Research+Journal%2C+3%2C+62%E2%80%9373. 62-73 Mathematics+Education+Research+Journal 3 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_68_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLeikin%26rft.aufirst%3DR.%26rft.date%3D2001%26rft.atitle%3DDefining%2520as%2520a%2520vehicle%2520for%2520professional%2520development%2520of%2520secondary%2520school%2520mathematics%2520teachers%26rft.jtitle%3DMathematics%2520Education%2520Research%2520Journal%26rft.volume%3D3%26rft.spage%3D62%26rft.epage%3D73 %00empty%00}-->
• Leikin, R., & Zazkis, R. (2010). On the content-dependence of prospective teachers’ knowledge: A case of exemplifying definitions. International Journal of Mathematical Education in Science and Technology, 41(4), 451–466. https://doi.org/10.1080/00207391003605189
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F00207391003605189 journal On+the+content-dependence+of+prospective+teachers%E2%80%99+knowledge%3A+A+case+of+exemplifying+definitions author%3DR.+Leikin%26author%3DR.+Zazkis 2010 Leikin%2C+R.%2C+%26+Zazkis%2C+R.+%282010%29.+On+the+content-dependence+of+prospective+teachers%E2%80%99+knowledge%3A+A+case+of+exemplifying+definitions.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+41%284%29%2C+451%E2%80%93466.+ 451-466 International+Journal+of+Mathematical+Education+in+Science+and+Technology 41 4 https%3A%2F%2Fdoi.org%2F10.1080%2F00207391003605189 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_69_1 10.1080%252F00207391003605189 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F00207391003605189%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLeikin%26rft.aufirst%3DR.%26rft.date%3D2010%26rft.atitle%3DOn%2520the%2520content-dependence%2520of%2520prospective%2520teachers%25E2%2580%2599%2520knowledge%253A%2520A%2520case%2520of%2520exemplifying%2520definitions%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D41%26rft.issue%3D4%26rft.spage%3D451%26rft.epage%3D466 %00empty%00}-->
• Levenson, E. (2012). Teachers’ knowledge of the nature of definitions: The case of the zero exponent. The Journal of Mathematical Behavior, 31(2), 209–219. https://doi.org/10.1016/j.jmathb.2011.12.006
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2011.12.006 journal Teachers%E2%80%99+knowledge+of+the+nature+of+definitions%3A+The+case+of+the+zero+exponent author%3DE.+Levenson 2012 Levenson%2C+E.+%282012%29.+Teachers%E2%80%99+knowledge+of+the+nature+of+definitions%3A+The+case+of+the+zero+exponent.+The+Journal+of+Mathematical+Behavior%2C+31%282%29%2C+209%E2%80%93219.+ 209-219 The+Journal+of+Mathematical+Behavior 31 2 https%3A%2F%2Fdoi.org%2F10.1016%2Fj.jmathb.2011.12.006 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_70_1 10.1016%252Fj.jmathb.2011.12.006 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2011.12.006%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLevenson%26rft.aufirst%3DE.%26rft.date%3D2012%26rft.atitle%3DTeachers%25E2%2580%2599%2520knowledge%2520of%2520the%2520nature%2520of%2520definitions%253A%2520The%2520case%2520of%2520the%2520zero%2520exponent%26rft.jtitle%3DThe%2520Journal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D31%26rft.issue%3D2%26rft.spage%3D209%26rft.epage%3D219 %00empty%00}-->
• Linchesvky, L., Vinner, S., & Karsenty, R. (1992). To be or not to be minimal? Student teachers’ views about definitions in geometry. Proceedings of the Sixteenth International Conference for the Psychology of Mathematics Education, 2, 48–55.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal To+be+or+not+to+be+minimal%3F+Student+teachers%E2%80%99+views+about+definitions+in+geometry author%3DL.+Linchesvky%26author%3DS.+Vinner%26author%3DR.+Karsenty 1992 Linchesvky%2C+L.%2C+Vinner%2C+S.%2C+%26+Karsenty%2C+R.+%281992%29.+To+be+or+not+to+be+minimal%3F+Student+teachers%E2%80%99+views+about+definitions+in+geometry.+Proceedings+of+the+Sixteenth+International+Conference+for+the+Psychology+of+Mathematics+Education%2C+2%2C+48%E2%80%9355. 48-55 Proceedings+of+the+Sixteenth+International+Conference+for+the+Psychology+of+Mathematics+Education 2 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_71_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DLinchesvky%26rft.aufirst%3DL.%26rft.date%3D1992%26rft.atitle%3DTo%2520be%2520or%2520not%2520to%2520be%2520minimal%253F%2520Student%2520teachers%25E2%2580%2599%2520views%2520about%2520definitions%2520in%2520geometry%26rft.jtitle%3DProceedings%2520of%2520the%2520Sixteenth%2520International%2520Conference%2520for%2520the%2520Psychology%2520of%2520Mathematics%2520Education%26rft.volume%3D2%26rft.spage%3D48%26rft.epage%3D55 %00empty%00}-->
• Mamona-Downs, J.K., & Megalou, F.J. (2013). Students’ understanding of limiting behavior at a point for functions from R2 to R. Journal of Mathematical Behavior, 32(1), 53–68.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2012.09.004 journal Students%E2%80%99+understanding+of+limiting+behavior+at+a+point+for+functions+from+R2+to+R author%3DJ.K.+Mamona-Downs%26author%3DF.J.+Megalou 2013 Mamona-Downs%2C+J.K.%2C+%26+Megalou%2C+F.J.+%282013%29.+Students%E2%80%99+understanding+of+limiting+behavior+at+a+point+for+functions+from+R2+to+R.+Journal+of+Mathematical+Behavior%2C+32%281%29%2C+53%E2%80%9368. 53-68 Journal+of+Mathematical+Behavior 32 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_72_1 10.1016%252Fj.jmathb.2012.09.004 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2012.09.004%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMamona-Downs%26rft.aufirst%3DJ.K.%26rft.date%3D2013%26rft.atitle%3DStudents%25E2%2580%2599%2520understanding%2520of%2520limiting%2520behavior%2520at%2520a%2520point%2520for%2520functions%2520from%2520R2%2520to%2520R%26rft.jtitle%3DJournal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D32%26rft.issue%3D1%26rft.spage%3D53%26rft.epage%3D68 %00empty%00}-->
• Mariotti, M. A., & Fischbein, E. (1997). Defining in classroom activities. Educational Studies in Mathematics, 34, 219–248. https://doi.org/10.1023/A:1002985109323
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1023%2FA%3A1002985109323 journal Defining+in+classroom+activities author%3DM.+A.+Mariotti%26author%3DE.+Fischbein 1997 Mariotti%2C+M.+A.%2C+%26+Fischbein%2C+E.+%281997%29.+Defining+in+classroom+activities.+Educational+Studies+in+Mathematics%2C+34%2C+219%E2%80%93248.+ 219-248 Educational+Studies+in+Mathematics 34 %00null%00 https%3A%2F%2Fdoi.org%2F10.1023%2FA%3A1002985109323 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_73_1 10.1023%252FA%253A1002985109323 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1023%252FA%253A1002985109323%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMariotti%26rft.aufirst%3DM.%2520A.%26rft.date%3D1997%26rft.atitle%3DDefining%2520in%2520classroom%2520activities%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D34%26rft.spage%3D219%26rft.epage%3D248 %00empty%00}-->
• Martín-Molina, V., González-Regaña, A. J., & Gavilán-Izquierdo, J. M. (2018). Researching how professional mathematicians construct new mathematical definitions: A case study. International Journal of Mathematical Education in Science and Technology, 49(7), 1069–1082. https://doi.org/10.1080/0020739x.2018.1426795
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2018.1426795 journal Researching+how+professional+mathematicians+construct+new+mathematical+definitions%3A+A+case+study author%3DV.+Mart%C3%ADn-Molina%26author%3DA.+J.+Gonz%C3%A1lez-Rega%C3%B1a%26author%3DJ.+M.+Gavil%C3%A1n-Izquierdo 2018 Mart%C3%ADn-Molina%2C+V.%2C+Gonz%C3%A1lez-Rega%C3%B1a%2C+A.+J.%2C+%26+Gavil%C3%A1n-Izquierdo%2C+J.+M.+%282018%29.+Researching+how+professional+mathematicians+construct+new+mathematical+definitions%3A+A+case+study.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+49%287%29%2C+1069%E2%80%931082.+ 1069-1082 International+Journal+of+Mathematical+Education+in+Science+and+Technology 49 7 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2018.1426795 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_74_1 10.1080%252F0020739x.2018.1426795 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2018.1426795%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMart%25C3%25ADn-Molina%26rft.aufirst%3DV.%26rft.date%3D2018%26rft.atitle%3DResearching%2520how%2520professional%2520mathematicians%2520construct%2520new%2520mathematical%2520definitions%253A%2520A%2520case%2520study%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D49%26rft.issue%3D7%26rft.spage%3D1069%26rft.epage%3D1082 %00empty%00}-->
• Martín-Molina, V., González-Regaña, A. J., Toscano, R., & Gavilán-Izquierdo, J. M. (2020). Differences between how undergraduate students define geometric solids and what their lecturers expect from them through the lens of the theory of commognition. Eurasia Journal of Mathematics, Science and Technology Education, 16(12), em1917. https://doi.org/10.29333/ejmste/9159
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.29333%2Fejmste%2F9159 journal Differences+between+how+undergraduate+students+define+geometric+solids+and+what+their+lecturers+expect+from+them+through+the+lens+of+the+theory+of+commognition author%3DV.+Mart%C3%ADn-Molina%26author%3DA.+J.+Gonz%C3%A1lez-Rega%C3%B1a%26author%3DR.+Toscano%26author%3DJ.+M.+Gavil%C3%A1n-Izquierdo 2020 Mart%C3%ADn-Molina%2C+V.%2C+Gonz%C3%A1lez-Rega%C3%B1a%2C+A.+J.%2C+Toscano%2C+R.%2C+%26+Gavil%C3%A1n-Izquierdo%2C+J.+M.+%282020%29.+Differences+between+how+undergraduate+students+define+geometric+solids+and+what+their+lecturers+expect+from+them+through+the+lens+of+the+theory+of+commognition.+Eurasia+Journal+of+Mathematics%2C+Science+and+Technology+Education%2C+16%2812%29%2C+em1917.+ em1917 Eurasia+Journal+of+Mathematics%2C+Science+and+Technology+Education 16 12 https%3A%2F%2Fdoi.org%2F10.29333%2Fejmste%2F9159 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_75_1 10.29333%252Fejmste%252F9159 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.29333%252Fejmste%252F9159%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMart%25C3%25ADn-Molina%26rft.aufirst%3DV.%26rft.date%3D2020%26rft.atitle%3DDifferences%2520between%2520how%2520undergraduate%2520students%2520define%2520geometric%2520solids%2520and%2520what%2520their%2520lecturers%2520expect%2520from%2520them%2520through%2520the%2520lens%2520of%2520the%2520theory%2520of%2520commognition%26rft.jtitle%3DEurasia%2520Journal%2520of%2520Mathematics%252C%2520Science%2520and%2520Technology%2520Education%26rft.volume%3D16%26rft.issue%3D12%26rft.spage%3Dem1917 %00empty%00}-->
• Megalou, F. (2018). Students’ choices of definitions for the concept of limit of functions from R2 to R. International Journal of Mathematical Education in Science and Technology, 50(1), 141–156. https://doi.org/10.1080/0020739x.2018.1489073
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2018.1489073 journal Students%E2%80%99+choices+of+definitions+for+the+concept+of+limit+of+functions+from+R2+to+R author%3DF.+Megalou 2018 Megalou%2C+F.+%282018%29.+Students%E2%80%99+choices+of+definitions+for+the+concept+of+limit+of+functions+from+R2+to+R.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+50%281%29%2C+141%E2%80%93156.+ 141-156 International+Journal+of+Mathematical+Education+in+Science+and+Technology 50 1 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2018.1489073 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_76_1 10.1080%252F0020739x.2018.1489073 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2018.1489073%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMegalou%26rft.aufirst%3DF.%26rft.date%3D2018%26rft.atitle%3DStudents%25E2%2580%2599%2520choices%2520of%2520definitions%2520for%2520the%2520concept%2520of%2520limit%2520of%2520functions%2520from%2520R2%2520to%2520R%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D50%26rft.issue%3D1%26rft.spage%3D141%26rft.epage%3D156 %00empty%00}-->
• Miller, S. M. (2018). An analysis of the form and content of quadrilateral definitions composed by novice pre-service teachers. The Journal of Mathematical Behavior, 50, 142–154. https://doi.org/10.1016/j.jmathb.2018.02.006
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2018.02.006 journal An+analysis+of+the+form+and+content+of+quadrilateral+definitions+composed+by+novice+pre-service+teachers author%3DS.+M.+Miller 2018 Miller%2C+S.+M.+%282018%29.+An+analysis+of+the+form+and+content+of+quadrilateral+definitions+composed+by+novice+pre-service+teachers.+The+Journal+of+Mathematical+Behavior%2C+50%2C+142%E2%80%93154.+ 142-154 The+Journal+of+Mathematical+Behavior 50 %00null%00 https%3A%2F%2Fdoi.org%2F10.1016%2Fj.jmathb.2018.02.006 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_77_1 10.1016%252Fj.jmathb.2018.02.006 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2018.02.006%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMiller%26rft.aufirst%3DS.%2520M.%26rft.date%3D2018%26rft.atitle%3DAn%2520analysis%2520of%2520the%2520form%2520and%2520content%2520of%2520quadrilateral%2520definitions%2520composed%2520by%2520novice%2520pre-service%2520teachers%26rft.jtitle%3DThe%2520Journal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D50%26rft.spage%3D142%26rft.epage%3D154 %00empty%00}-->
• Moore, R. C. (1994). Making the transition to formal proof. Educational Studies in Mathematics, 27(3), 249–266.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2FBF01273731 journal Making+the+transition+to+formal+proof author%3DR.+C.+Moore 1994 Moore%2C+R.+C.+%281994%29.+Making+the+transition+to+formal+proof.+Educational+Studies+in+Mathematics%2C+27%283%29%2C+249%E2%80%93266. 249-266 Educational+Studies+in+Mathematics 27 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_78_1 10.1007%252FBF01273731 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252FBF01273731%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMoore%26rft.aufirst%3DR.%2520C.%26rft.date%3D1994%26rft.atitle%3DMaking%2520the%2520transition%2520to%2520formal%2520proof%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D27%26rft.issue%3D3%26rft.spage%3D249%26rft.epage%3D266 %00empty%00}-->
• Morgan, C. (2005). Word, definitions and concepts in discourses of mathematics, teaching and learning. Language and Education, 19(2), 102–116. https://doi.org/10.1080/09500780508668666
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F09500780508668666 journal Word%2C+definitions+and+concepts+in+discourses+of+mathematics%2C+teaching+and+learning author%3DC.+Morgan 2005 Morgan%2C+C.+%282005%29.+Word%2C+definitions+and+concepts+in+discourses+of+mathematics%2C+teaching+and+learning.+Language+and+Education%2C+19%282%29%2C+102%E2%80%93116.+ 102-116 Language+and+Education 19 2 https%3A%2F%2Fdoi.org%2F10.1080%2F09500780508668666 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_79_1 10.1080%252F09500780508668666 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F09500780508668666%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMorgan%26rft.aufirst%3DC.%26rft.date%3D2005%26rft.atitle%3DWord%252C%2520definitions%2520and%2520concepts%2520in%2520discourses%2520of%2520mathematics%252C%2520teaching%2520and%2520learning%26rft.jtitle%3DLanguage%2520and%2520Education%26rft.volume%3D19%26rft.issue%3D2%26rft.spage%3D102%26rft.epage%3D116 %00empty%00}-->
• Morgan, C. (2006). What is a definition for in school mathematics? In M. Bosch (Ed.), European Research in Mathematics Education IV: Proceedings of the Fourth Congress of the European Society for Research in Mathematics Education. Sant Feliu de Guíxols: FUNDEMI IQS - Universitat Ramon Llull.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 other What+is+a+definition+for+in+school+mathematics%3F author%3DC.+Morgan%26 2006 Morgan%2C+C.+%282006%29.+What+is+a+definition+for+in+school+mathematics%3F+In+M.+Bosch+%28Ed.%29%2C+European+Research+in+Mathematics+Education+IV%3A+Proceedings+of+the+Fourth+Congress+of+the+European+Society+for+Research+in+Mathematics+Education.+Sant+Feliu+de+Gu%C3%ADxols%3A+FUNDEMI+IQS+-+Universitat+Ramon+Llull. %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_80_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Dother%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMorgan%26rft.aufirst%3DC.%26rft.date%3D2006%26rft.atitle%3DWhat%2520is%2520a%2520definition%2520for%2520in%2520school%2520mathematics%253F%26rft.aulast%3DBosch%26rft.aufirst%3DM.%26rft.pub%3DFUNDEMI%2520IQS%2520-%2520Universitat%2520Ramon%2520Llull %00empty%00}-->
• Mosvold, R., & Fauskanger, J. (2013). Teachers’ beliefs about mathematical knowledge for teaching definitions. International Electronic Journal of Mathematics Education, 8(2-3), 43–61.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.29333%2Fiejme%2F273 journal Teachers%E2%80%99+beliefs+about+mathematical+knowledge+for+teaching+definitions author%3DR.+Mosvold%26author%3DJ.+Fauskanger 2013 Mosvold%2C+R.%2C+%26+Fauskanger%2C+J.+%282013%29.+Teachers%E2%80%99+beliefs+about+mathematical+knowledge+for+teaching+definitions.+International+Electronic+Journal+of+Mathematics+Education%2C+8%282-3%29%2C+43%E2%80%9361. 43-61 International+Electronic+Journal+of+Mathematics+Education 8 2-3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_81_1 10.29333%252Fiejme%252F273 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.29333%252Fiejme%252F273%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DMosvold%26rft.aufirst%3DR.%26rft.date%3D2013%26rft.atitle%3DTeachers%25E2%2580%2599%2520beliefs%2520about%2520mathematical%2520knowledge%2520for%2520teaching%2520definitions%26rft.jtitle%3DInternational%2520Electronic%2520Journal%2520of%2520Mathematics%2520Education%26rft.volume%3D8%26rft.issue%3D2-3%26rft.spage%3D43%26rft.epage%3D61 %00empty%00}-->
• Ndemo, Z., & Mtetwa, D. (2021). Mathematics education undergraduates’ personal definitions of the notion of angle of contiguity in kinematics. Journal of Research and Advances in Mathematics Education, 6(2), 111–127.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.23917%2Fjramathedu.v6i2.11130 journal Mathematics+education+undergraduates%E2%80%99+personal+definitions+of+the+notion+of+angle+of+contiguity+in+kinematics author%3DZ.+Ndemo%26author%3DD.+Mtetwa 2021 Ndemo%2C+Z.%2C+%26+Mtetwa%2C+D.+%282021%29.+Mathematics+education+undergraduates%E2%80%99+personal+definitions+of+the+notion+of+angle+of+contiguity+in+kinematics.+Journal+of+Research+and+Advances+in+Mathematics+Education%2C+6%282%29%2C+111%E2%80%93127. 111-127 Journal+of+Research+and+Advances+in+Mathematics+Education 6 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_82_1 10.23917%252Fjramathedu.v6i2.11130 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.23917%252Fjramathedu.v6i2.11130%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DNdemo%26rft.aufirst%3DZ.%26rft.date%3D2021%26rft.atitle%3DMathematics%2520education%2520undergraduates%25E2%2580%2599%2520personal%2520definitions%2520of%2520the%2520notion%2520of%2520angle%2520of%2520contiguity%2520in%2520kinematics%26rft.jtitle%3DJournal%2520of%2520Research%2520and%2520Advances%2520in%2520Mathematics%2520Education%26rft.volume%3D6%26rft.issue%3D2%26rft.spage%3D111%26rft.epage%3D127 %00empty%00}-->
• Ouvrier-Buffet, C. (2006). Exploring mathematical definition construction processes. Educational Studies in Mathematics, 63(3), 259–282.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2Fs10649-005-9011-3 journal Exploring+mathematical+definition+construction+processes author%3DC.+Ouvrier-Buffet 2006 Ouvrier-Buffet%2C+C.+%282006%29.+Exploring+mathematical+definition+construction+processes.+Educational+Studies+in+Mathematics%2C+63%283%29%2C+259%E2%80%93282. 259-282 Educational+Studies+in+Mathematics 63 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_83_1 10.1007%252Fs10649-005-9011-3 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10649-005-9011-3%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DOuvrier-Buffet%26rft.aufirst%3DC.%26rft.date%3D2006%26rft.atitle%3DExploring%2520mathematical%2520definition%2520construction%2520processes%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D63%26rft.issue%3D3%26rft.spage%3D259%26rft.epage%3D282 %00empty%00}-->
• Ouvrier-Buffet, C. (2010). A mathematical experience involving defining processes: In-action definitions and zero-definitions. Educational Studies in Mathematics, 76(2), 165–182. https://doi.org/10.1007/s10649-010-9272-3
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10649-010-9272-3 journal A+mathematical+experience+involving+defining+processes%3A+In-action+definitions+and+zero-definitions author%3DC.+Ouvrier-Buffet 2010 Ouvrier-Buffet%2C+C.+%282010%29.+A+mathematical+experience+involving+defining+processes%3A+In-action+definitions+and+zero-definitions.+Educational+Studies+in+Mathematics%2C+76%282%29%2C+165%E2%80%93182.+ 165-182 Educational+Studies+in+Mathematics 76 2 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10649-010-9272-3 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_84_1 10.1007%252Fs10649-010-9272-3 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10649-010-9272-3%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DOuvrier-Buffet%26rft.aufirst%3DC.%26rft.date%3D2010%26rft.atitle%3DA%2520mathematical%2520experience%2520involving%2520defining%2520processes%253A%2520In-action%2520definitions%2520and%2520zero-definitions%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D76%26rft.issue%3D2%26rft.spage%3D165%26rft.epage%3D182 %00empty%00}-->
• Öztürk, T., & Güven, B. (2022). A study on pre-service mathematics teachers’ criteria of proof evaluation. LUMAT: International Journal on Math, Science and Technology Education, 10(1), 210–241. https://doi.org/10.31129/LUMAT.10.1.1649
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.31129%2FLUMAT.10.1.1649 journal A+study+on+pre-service+mathematics+teachers%E2%80%99+criteria+of+proof+evaluation.+LUMAT%3A+International+Journal+on+Math author%3DT.+%C3%96zt%C3%BCrk%26author%3DB.+G%C3%BCven 2022 %C3%96zt%C3%BCrk%2C+T.%2C+%26+G%C3%BCven%2C+B.+%282022%29.+A+study+on+pre-service+mathematics+teachers%E2%80%99+criteria+of+proof+evaluation.+LUMAT%3A+International+Journal+on+Math%2C+Science+and+Technology+Education%2C+10%281%29%2C+210%E2%80%93241.+ 210-241 Science+and+Technology+Education 10 1 https%3A%2F%2Fdoi.org%2F10.31129%2FLUMAT.10.1.1649 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_85_1 10.31129%252FLUMAT.10.1.1649 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.31129%252FLUMAT.10.1.1649%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3D%25C3%2596zt%25C3%25BCrk%26rft.aufirst%3DT.%26rft.date%3D2022%26rft.atitle%3DA%2520study%2520on%2520pre-service%2520mathematics%2520teachers%25E2%2580%2599%2520criteria%2520of%2520proof%2520evaluation.%2520LUMAT%253A%2520International%2520Journal%2520on%2520Math%26rft.jtitle%3DScience%2520and%2520Technology%2520Education%26rft.volume%3D10%26rft.issue%3D1%26rft.spage%3D210%26rft.epage%3D241 %00empty%00}-->
• Özyildirim-Gümüş, F., & Şahiner, Y. (2017). Investigation on how pre-service elementary mathematics teachers write and use mathematical definitions. International Electronic Journal of Elementary Education, 9(3), 511–522.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Investigation+on+how+pre-service+elementary+mathematics+teachers+write+and+use+mathematical+definitions author%3DF.+%C3%96zyildirim-G%C3%BCm%C3%BC%C5%9F%26author%3DY.+%C5%9Eahiner 2017 %C3%96zyildirim-G%C3%BCm%C3%BC%C5%9F%2C+F.%2C+%26+%C5%9Eahiner%2C+Y.+%282017%29.+Investigation+on+how+pre-service+elementary+mathematics+teachers+write+and+use+mathematical+definitions.+International+Electronic+Journal+of+Elementary+Education%2C+9%283%29%2C+511%E2%80%93522. 511-522 International+Electronic+Journal+of+Elementary+Education 9 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_86_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3D%25C3%2596zyildirim-G%25C3%25BCm%25C3%25BC%25C5%259F%26rft.aufirst%3DF.%26rft.date%3D2017%26rft.atitle%3DInvestigation%2520on%2520how%2520pre-service%2520elementary%2520mathematics%2520teachers%2520write%2520and%2520use%2520mathematical%2520definitions%26rft.jtitle%3DInternational%2520Electronic%2520Journal%2520of%2520Elementary%2520Education%26rft.volume%3D9%26rft.issue%3D3%26rft.spage%3D511%26rft.epage%3D522 %00empty%00}-->
• Panaoura, A., Michael-Chrysanthou, P., Gagatsis, A., Elia, I., & Philippou, A. (2016). A structural model related to the understanding of the concept of function: Definition and problem solving. International Journal of Science and Mathematics Education, 15(4), 723–740. https://doi.org/10.1007/s10763-016-9714-1
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10763-016-9714-1 journal A+structural+model+related+to+the+understanding+of+the+concept+of+function%3A+Definition+and+problem+solving author%3DA.+Panaoura%26author%3DP.+Michael-Chrysanthou%26author%3DA.+Gagatsis%26author%3DI.+Elia%26author%3DA.+Philippou 2016 Panaoura%2C+A.%2C+Michael-Chrysanthou%2C+P.%2C+Gagatsis%2C+A.%2C+Elia%2C+I.%2C+%26+Philippou%2C+A.+%282016%29.+A+structural+model+related+to+the+understanding+of+the+concept+of+function%3A+Definition+and+problem+solving.+International+Journal+of+Science+and+Mathematics+Education%2C+15%284%29%2C+723%E2%80%93740.+ 723-740 International+Journal+of+Science+and+Mathematics+Education 15 4 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10763-016-9714-1 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_87_1 10.1007%252Fs10763-016-9714-1 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10763-016-9714-1%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DPanaoura%26rft.aufirst%3DA.%26rft.date%3D2016%26rft.atitle%3DA%2520structural%2520model%2520related%2520to%2520the%2520understanding%2520of%2520the%2520concept%2520of%2520function%253A%2520Definition%2520and%2520problem%2520solving%26rft.jtitle%3DInternational%2520Journal%2520of%2520Science%2520and%2520Mathematics%2520Education%26rft.volume%3D15%26rft.issue%3D4%26rft.spage%3D723%26rft.epage%3D740 %00empty%00}-->
• Pimm, D. (1993). Just a matter of definition. Educational Studies in Mathematics, 25(3), 261–277.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2FBF01273865 journal Just+a+matter+of+definition author%3DD.+Pimm 1993 Pimm%2C+D.+%281993%29.+Just+a+matter+of+definition.+Educational+Studies+in+Mathematics%2C+25%283%29%2C+261%E2%80%93277. 261-277 Educational+Studies+in+Mathematics 25 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_88_1 10.1007%252FBF01273865 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252FBF01273865%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DPimm%26rft.aufirst%3DD.%26rft.date%3D1993%26rft.atitle%3DJust%2520a%2520matter%2520of%2520definition%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D25%26rft.issue%3D3%26rft.spage%3D261%26rft.epage%3D277 %00empty%00}-->
• Poincaré, H. (1969). Mathematical definitions and teaching. The Mathematics Teacher, 62(4), 295–304.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.5951%2FMT.62.4.0295 journal Mathematical+definitions+and+teaching author%3DH.+Poincar%C3%A9 1969 Poincar%C3%A9%2C+H.+%281969%29.+Mathematical+definitions+and+teaching.+The+Mathematics+Teacher%2C+62%284%29%2C+295%E2%80%93304. 295-304 The+Mathematics+Teacher 62 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_89_1 10.5951%252FMT.62.4.0295 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.5951%252FMT.62.4.0295%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DPoincar%25C3%25A9%26rft.aufirst%3DH.%26rft.date%3D1969%26rft.atitle%3DMathematical%2520definitions%2520and%2520teaching%26rft.jtitle%3DThe%2520Mathematics%2520Teacher%26rft.volume%3D62%26rft.issue%3D4%26rft.spage%3D295%26rft.epage%3D304 %00empty%00}-->
• Randahl, M. (2016). The mathematics textbook at tertiary level as curriculum material—Exploring the teacher’s decision-making process. International Journal of Mathematical Education in Science and Technology, 47(6), 897–916. https://doi.org/10.1080/0020739x.2015.1133853
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2015.1133853 journal The+mathematics+textbook+at+tertiary+level+as+curriculum+material%E2%80%94Exploring+the+teacher%E2%80%99s+decision-making+process author%3DM.+Randahl 2016 Randahl%2C+M.+%282016%29.+The+mathematics+textbook+at+tertiary+level+as+curriculum+material%E2%80%94Exploring+the+teacher%E2%80%99s+decision-making+process.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+47%286%29%2C+897%E2%80%93916.+ 897-916 International+Journal+of+Mathematical+Education+in+Science+and+Technology 47 6 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2015.1133853 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_90_1 10.1080%252F0020739x.2015.1133853 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2015.1133853%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DRandahl%26rft.aufirst%3DM.%26rft.date%3D2016%26rft.atitle%3DThe%2520mathematics%2520textbook%2520at%2520tertiary%2520level%2520as%2520curriculum%2520material%25E2%2580%2594Exploring%2520the%2520teacher%25E2%2580%2599s%2520decision-making%2520process%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D47%26rft.issue%3D6%26rft.spage%3D897%26rft.epage%3D916 %00empty%00}-->
• Raychaudhuri, D. (2008). Dynamics of a definition: A framework to analyse student construction of the concept of solution to a differential equation. International Journal of Mathematical Education in Science and Technology, 39(2), 161–177.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F00207390701576874 journal Dynamics+of+a+definition%3A+A+framework+to+analyse+student+construction+of+the+concept+of+solution+to+a+differential+equation author%3DD.+Raychaudhuri 2008 Raychaudhuri%2C+D.+%282008%29.+Dynamics+of+a+definition%3A+A+framework+to+analyse+student+construction+of+the+concept+of+solution+to+a+differential+equation.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+39%282%29%2C+161%E2%80%93177. 161-177 International+Journal+of+Mathematical+Education+in+Science+and+Technology 39 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_91_1 10.1080%252F00207390701576874 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F00207390701576874%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DRaychaudhuri%26rft.aufirst%3DD.%26rft.date%3D2008%26rft.atitle%3DDynamics%2520of%2520a%2520definition%253A%2520A%2520framework%2520to%2520analyse%2520student%2520construction%2520of%2520the%2520concept%2520of%2520solution%2520to%2520a%2520differential%2520equation%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D39%26rft.issue%3D2%26rft.spage%3D161%26rft.epage%3D177 %00empty%00}-->
• Rowlett, P., Smith, E., Corner, A. S., O’Sullivan, D., & Waldock, J. (2019). The potential of recreational mathematics to support the development of mathematical learning. International Journal of Mathematical Education in Science and Technology, 50(7), 972–986. https://doi.org/10.1080/0020739x.2019.1657596
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2019.1657596 journal The+potential+of+recreational+mathematics+to+support+the+development+of+mathematical+learning author%3DP.+Rowlett%26author%3DE.+Smith%26author%3DA.+S.+Corner%26author%3DD.+O%E2%80%99Sullivan%26author%3DJ.+Waldock 2019 Rowlett%2C+P.%2C+Smith%2C+E.%2C+Corner%2C+A.+S.%2C+O%E2%80%99Sullivan%2C+D.%2C+%26+Waldock%2C+J.+%282019%29.+The+potential+of+recreational+mathematics+to+support+the+development+of+mathematical+learning.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+50%287%29%2C+972%E2%80%93986.+ 972-986 International+Journal+of+Mathematical+Education+in+Science+and+Technology 50 7 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2019.1657596 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_92_1 10.1080%252F0020739x.2019.1657596 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2019.1657596%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DRowlett%26rft.aufirst%3DP.%26rft.date%3D2019%26rft.atitle%3DThe%2520potential%2520of%2520recreational%2520mathematics%2520to%2520support%2520the%2520development%2520of%2520mathematical%2520learning%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D50%26rft.issue%3D7%26rft.spage%3D972%26rft.epage%3D986 %00empty%00}-->
• Sağlam, Y., & Dost, Ş. (2015). A qualitative research on example generation capabilities of university students. International Journal of Science and Mathematics Education, 14(5), 979–996. https://doi.org/10.1007/s10763-015-9624-7
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10763-015-9624-7 journal A+qualitative+research+on+example+generation+capabilities+of+university+students author%3DY.+Sa%C4%9Flam 2015 Sa%C4%9Flam%2C+Y.%2C+%26+Dost%2C+%C5%9E.+%282015%29.+A+qualitative+research+on+example+generation+capabilities+of+university+students.+International+Journal+of+Science+and+Mathematics+Education%2C+14%285%29%2C+979%E2%80%93996.+ 979-996 International+Journal+of+Science+and+Mathematics+Education 14 5 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10763-015-9624-7 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_93_1 10.1007%252Fs10763-015-9624-7 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10763-015-9624-7%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSa%25C4%259Flam%26rft.aufirst%3DY.%26rft.date%3D2015%26rft.atitle%3DA%2520qualitative%2520research%2520on%2520example%2520generation%2520capabilities%2520of%2520university%2520students%26rft.jtitle%3DInternational%2520Journal%2520of%2520Science%2520and%2520Mathematics%2520Education%26rft.volume%3D14%26rft.issue%3D5%26rft.spage%3D979%26rft.epage%3D996 %00empty%00}-->
• Sánchez, V., & García, M. (2013). Sociomathematical and mathematical norms related to definition in pre-service primary teachers’ discourse. Educational Studies in Mathematics, 85(2), 305–320. https://doi.org/10.1007/s10649-013-9516-0
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10649-013-9516-0 journal Sociomathematical+and+mathematical+norms+related+to+definition+in+pre-service+primary+teachers%E2%80%99+discourse author%3DV.+S%C3%A1nchez%26author%3DM.+Garc%C3%ADa 2013 S%C3%A1nchez%2C+V.%2C+%26+Garc%C3%ADa%2C+M.+%282013%29.+Sociomathematical+and+mathematical+norms+related+to+definition+in+pre-service+primary+teachers%E2%80%99+discourse.+Educational+Studies+in+Mathematics%2C+85%282%29%2C+305%E2%80%93320.+ 305-320 Educational+Studies+in+Mathematics 85 2 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10649-013-9516-0 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_94_1 10.1007%252Fs10649-013-9516-0 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10649-013-9516-0%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DS%25C3%25A1nchez%26rft.aufirst%3DV.%26rft.date%3D2013%26rft.atitle%3DSociomathematical%2520and%2520mathematical%2520norms%2520related%2520to%2520definition%2520in%2520pre-service%2520primary%2520teachers%25E2%2580%2599%2520discourse%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D85%26rft.issue%3D2%26rft.spage%3D305%26rft.epage%3D320 %00empty%00}-->
• Schüler-Meyer, A. (2020). Mathematical routines in transition: Facilitating students’ defining and proving of sequence convergence. Teaching Mathematics and its Applications, 39(4), 237–247.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1093%2Fteamat%2Fhrz019 journal Mathematical+routines+in+transition%3A+Facilitating+students%E2%80%99+defining+and+proving+of+sequence+convergence author%3DA.+Sch%C3%BCler-Meyer 2020 Sch%C3%BCler-Meyer%2C+A.+%282020%29.+Mathematical+routines+in+transition%3A+Facilitating+students%E2%80%99+defining+and+proving+of+sequence+convergence.+Teaching+Mathematics+and+its+Applications%2C+39%284%29%2C+237%E2%80%93247. 237-247 Teaching+Mathematics+and+its+Applications 39 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_95_1 10.1093%252Fteamat%252Fhrz019 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1093%252Fteamat%252Fhrz019%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSch%25C3%25BCler-Meyer%26rft.aufirst%3DA.%26rft.date%3D2020%26rft.atitle%3DMathematical%2520routines%2520in%2520transition%253A%2520Facilitating%2520students%25E2%2580%2599%2520defining%2520and%2520proving%2520of%2520sequence%2520convergence%26rft.jtitle%3DTeaching%2520Mathematics%2520and%2520its%2520Applications%26rft.volume%3D39%26rft.issue%3D4%26rft.spage%3D237%26rft.epage%3D247 %00empty%00}-->
• Seaman, C.E., Szydlik, J.E. (2007). Mathematical sophistication among preservice elementary teachers. Journal of Mathematics Teacher Education 10, 167–182. https://doi.org/10.1007/s10857-007-9033-0
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2Fs10857-007-9033-0 journal Mathematical+sophistication+among+preservice+elementary+teachers author%3DC.E.+Seaman%26author%3DJ.E.+Szydlik 2007 Seaman%2C+C.E.%2C+Szydlik%2C+J.E.+%282007%29.+Mathematical+sophistication+among+preservice+elementary+teachers.+Journal+of+Mathematics+Teacher+Education+10%2C+167%E2%80%93182.+ 167-182 Journal+of+Mathematics+Teacher+Education 10 %00null%00 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10857-007-9033-0 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_96_1 10.1007%252Fs10857-007-9033-0 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10857-007-9033-0%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSeaman%26rft.aufirst%3DC.E.%26rft.date%3D2007%26rft.atitle%3DMathematical%2520sophistication%2520among%2520preservice%2520elementary%2520teachers%26rft.jtitle%3DJournal%2520of%2520Mathematics%2520Teacher%2520Education%26rft.volume%3D10%26rft.spage%3D167%26rft.epage%3D182 %00empty%00}-->
• Şen, C., & Güler, G. (2022). Examining the effectiveness of teaching through definitions in the definition and conceptualization of number sets by pre-service mathematics teachers. Hacettepe Egitim Dergisi, 37(3), 969–993.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Examining+the+effectiveness+of+teaching+through+definitions+in+the+definition+and+conceptualization+of+number+sets+by+pre-service+mathematics+teachers author%3DC.+%C5%9Een%26author%3DG.+G%C3%BCler 2022 %C5%9Een%2C+C.%2C+%26+G%C3%BCler%2C+G.+%282022%29.+Examining+the+effectiveness+of+teaching+through+definitions+in+the+definition+and+conceptualization+of+number+sets+by+pre-service+mathematics+teachers.+Hacettepe+Egitim+Dergisi%2C+37%283%29%2C+969%E2%80%93993. 969-993 Hacettepe+Egitim+Dergisi 37 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_97_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3D%25C5%259Een%26rft.aufirst%3DC.%26rft.date%3D2022%26rft.atitle%3DExamining%2520the%2520effectiveness%2520of%2520teaching%2520through%2520definitions%2520in%2520the%2520definition%2520and%2520conceptualization%2520of%2520number%2520sets%2520by%2520pre-service%2520mathematics%2520teachers%26rft.jtitle%3DHacettepe%2520Egitim%2520Dergisi%26rft.volume%3D37%26rft.issue%3D3%26rft.spage%3D969%26rft.epage%3D993 %00empty%00}-->
• Shaker, H., & Berger, M. (2016). Students’ difficulties with definitions in the context of proofs in elementary set theory. African Journal of Research in Mathematics, Science and Technology Education, 20(1), 80–90.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F10288457.2016.1145449 journal Students%E2%80%99+difficulties+with+definitions+in+the+context+of+proofs+in+elementary+set+theory author%3DH.+Shaker%26author%3DM.+Berger 2016 Shaker%2C+H.%2C+%26+Berger%2C+M.+%282016%29.+Students%E2%80%99+difficulties+with+definitions+in+the+context+of+proofs+in+elementary+set+theory.+African+Journal+of+Research+in+Mathematics%2C+Science+and+Technology+Education%2C+20%281%29%2C+80%E2%80%9390. 80-90 African+Journal+of+Research+in+Mathematics%2C+Science+and+Technology+Education 20 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_98_1 10.1080%252F10288457.2016.1145449 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F10288457.2016.1145449%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DShaker%26rft.aufirst%3DH.%26rft.date%3D2016%26rft.atitle%3DStudents%25E2%2580%2599%2520difficulties%2520with%2520definitions%2520in%2520the%2520context%2520of%2520proofs%2520in%2520elementary%2520set%2520theory%26rft.jtitle%3DAfrican%2520Journal%2520of%2520Research%2520in%2520Mathematics%252C%2520Science%2520and%2520Technology%2520Education%26rft.volume%3D20%26rft.issue%3D1%26rft.spage%3D80%26rft.epage%3D90 %00empty%00}-->
• Shield, M. (2004). Formal definitions in mathematics. The Australian Mathematics Teacher, 60(4), 25–28.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Formal+definitions+in+mathematics author%3DM.+Shield 2004 Shield%2C+M.+%282004%29.+Formal+definitions+in+mathematics.+The+Australian+Mathematics+Teacher%2C+60%284%29%2C+25%E2%80%9328. 25-28 The+Australian+Mathematics+Teacher 60 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_99_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DShield%26rft.aufirst%3DM.%26rft.date%3D2004%26rft.atitle%3DFormal%2520definitions%2520in%2520mathematics%26rft.jtitle%3DThe%2520Australian%2520Mathematics%2520Teacher%26rft.volume%3D60%26rft.issue%3D4%26rft.spage%3D25%26rft.epage%3D28 %00empty%00}-->
• Soto-Johnson, H., Hancock, B., & Oehrtman, M. (2016). The interplay between mathematicians’ conceptual and ideational mathematics about continuity of complex-valued functions. International Journal of Research in Undergraduate Mathematics Education, 2(3), 362–389. https://doi.org/10.1007/s40753-016-0035-0
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2Fs40753-016-0035-0 journal The+interplay+between+mathematicians%E2%80%99+conceptual+and+ideational+mathematics+about+continuity+of+complex-valued+functions author%3DH.+Soto-Johnson%26author%3DB.+Hancock%26author%3DM.+Oehrtman 2016 Soto-Johnson%2C+H.%2C+Hancock%2C+B.%2C+%26+Oehrtman%2C+M.+%282016%29.+The+interplay+between+mathematicians%E2%80%99+conceptual+and+ideational+mathematics+about+continuity+of+complex-valued+functions.+International+Journal+of+Research+in+Undergraduate+Mathematics+Education%2C+2%283%29%2C+362%E2%80%93389.+ 362-389 International+Journal+of+Research+in+Undergraduate+Mathematics+Education 2 3 https%3A%2F%2Fdoi.org%2F10.1007%2Fs40753-016-0035-0 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_100_1 10.1007%252Fs40753-016-0035-0 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs40753-016-0035-0%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DSoto-Johnson%26rft.aufirst%3DH.%26rft.date%3D2016%26rft.atitle%3DThe%2520interplay%2520between%2520mathematicians%25E2%2580%2599%2520conceptual%2520and%2520ideational%2520mathematics%2520about%2520continuity%2520of%2520complex-valued%2520functions%26rft.jtitle%3DInternational%2520Journal%2520of%2520Research%2520in%2520Undergraduate%2520Mathematics%2520Education%26rft.volume%3D2%26rft.issue%3D3%26rft.spage%3D362%26rft.epage%3D389 %00empty%00}-->
• Stavrou, S. G. (2014). Common errors and misconceptions in mathematical proving by education undergraduates. Issues in the Undergraduate Mathematics Preparation of School Teachers, 1, 1–8.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Common+errors+and+misconceptions+in+mathematical+proving+by+education+undergraduates author%3DS.+G.+Stavrou 2014 Stavrou%2C+S.+G.+%282014%29.+Common+errors+and+misconceptions+in+mathematical+proving+by+education+undergraduates.+Issues+in+the+Undergraduate+Mathematics+Preparation+of+School+Teachers%2C+1%2C+1%E2%80%938. 1-8 Issues+in+the+Undergraduate+Mathematics+Preparation+of+School+Teachers 1 %00null%00 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_101_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DStavrou%26rft.aufirst%3DS.%2520G.%26rft.date%3D2014%26rft.atitle%3DCommon%2520errors%2520and%2520misconceptions%2520in%2520mathematical%2520proving%2520by%2520education%2520undergraduates%26rft.jtitle%3DIssues%2520in%2520the%2520Undergraduate%2520Mathematics%2520Preparation%2520of%2520School%2520Teachers%26rft.volume%3D1%26rft.spage%3D1%26rft.epage%3D8 %00empty%00}-->
• Tabach, M., & Nachlieli, T. (2015). Classroom engagement towards using definitions for developing mathematical objects: The case of function. Educational Studies in Mathematics, 90(2), 163–187. https://doi.org/10.1007/s10649-015-9624-0
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10649-015-9624-0 journal Classroom+engagement+towards+using+definitions+for+developing+mathematical+objects%3A+The+case+of+function author%3DM.+Tabach%26author%3DT.+Nachlieli 2015 Tabach%2C+M.%2C+%26+Nachlieli%2C+T.+%282015%29.+Classroom+engagement+towards+using+definitions+for+developing+mathematical+objects%3A+The+case+of+function.+Educational+Studies+in+Mathematics%2C+90%282%29%2C+163%E2%80%93187.+ 163-187 Educational+Studies+in+Mathematics 90 2 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10649-015-9624-0 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_102_1 10.1007%252Fs10649-015-9624-0 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10649-015-9624-0%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DTabach%26rft.aufirst%3DM.%26rft.date%3D2015%26rft.atitle%3DClassroom%2520engagement%2520towards%2520using%2520definitions%2520for%2520developing%2520mathematical%2520objects%253A%2520The%2520case%2520of%2520function%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D90%26rft.issue%3D2%26rft.spage%3D163%26rft.epage%3D187 %00empty%00}-->
• Tay, E. G., & Leong, Y. H. (2012). Explaining definitions in secondary school mathematics: a0. Australian Senior Mathematics Journal, 26(3), 28–37.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Explaining+definitions+in+secondary+school+mathematics%3A+a0 author%3DE.+G.+Tay%26author%3DY.+H.+Leong 2012 Tay%2C+E.+G.%2C+%26+Leong%2C+Y.+H.+%282012%29.+Explaining+definitions+in+secondary+school+mathematics%3A+a0.+Australian+Senior+Mathematics+Journal%2C+26%283%29%2C+28%E2%80%9337. 28-37 Australian+Senior+Mathematics+Journal 26 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_103_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DTay%26rft.aufirst%3DE.%2520G.%26rft.date%3D2012%26rft.atitle%3DExplaining%2520definitions%2520in%2520secondary%2520school%2520mathematics%253A%2520a0%26rft.jtitle%3DAustralian%2520Senior%2520Mathematics%2520Journal%26rft.volume%3D26%26rft.issue%3D3%26rft.spage%3D28%26rft.epage%3D37 %00empty%00}-->
• Tirosh, D. (1999). Finite and infinite sets: Definitions and intuitions. International Journal of Mathematical Education in Science and Technology, 30(3), 341–349. https://doi.org/10.1080/002073999287879
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F002073999287879 journal Finite+and+infinite+sets%3A+Definitions+and+intuitions author%3DD.+Tirosh 1999 Tirosh%2C+D.+%281999%29.+Finite+and+infinite+sets%3A+Definitions+and+intuitions.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+30%283%29%2C+341%E2%80%93349.+ 341-349 International+Journal+of+Mathematical+Education+in+Science+and+Technology 30 3 https%3A%2F%2Fdoi.org%2F10.1080%2F002073999287879 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_104_1 10.1080%252F002073999287879 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F002073999287879%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DTirosh%26rft.aufirst%3DD.%26rft.date%3D1999%26rft.atitle%3DFinite%2520and%2520infinite%2520sets%253A%2520Definitions%2520and%2520intuitions%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D30%26rft.issue%3D3%26rft.spage%3D341%26rft.epage%3D349 %00empty%00}-->
• Tossavainen, T., Suomalainen, H., & Mäkäläinen, T. (2016). Student teachers’ concept definitions of area and their understanding about two-dimensionality of area. International Journal of Mathematical Education in Science and Technology, 48(4), 520–532. https://doi.org/10.1080/0020739x.2016.1254298
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2016.1254298 journal Student+teachers%E2%80%99+concept+definitions+of+area+and+their+understanding+about+two-dimensionality+of+area author%3DT.+Tossavainen%26author%3DH.+Suomalainen%26author%3DT.+M%C3%A4k%C3%A4l%C3%A4inen 2016 Tossavainen%2C+T.%2C+Suomalainen%2C+H.%2C+%26+M%C3%A4k%C3%A4l%C3%A4inen%2C+T.+%282016%29.+Student+teachers%E2%80%99+concept+definitions+of+area+and+their+understanding+about+two-dimensionality+of+area.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+48%284%29%2C+520%E2%80%93532.+ 520-532 International+Journal+of+Mathematical+Education+in+Science+and+Technology 48 4 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2016.1254298 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_105_1 10.1080%252F0020739x.2016.1254298 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2016.1254298%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DTossavainen%26rft.aufirst%3DT.%26rft.date%3D2016%26rft.atitle%3DStudent%2520teachers%25E2%2580%2599%2520concept%2520definitions%2520of%2520area%2520and%2520their%2520understanding%2520about%2520two-dimensionality%2520of%2520area%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D48%26rft.issue%3D4%26rft.spage%3D520%26rft.epage%3D532 %00empty%00}-->
• Tsamir, P., Tirosh, D., Levenson, E., Barkai, R., & Tabach, M. (2015). Early-years teachers’ concept images and concept definitions: Triangles, circles, and cylinders. ZDM Mathematics Education, 47(3), 497–509.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs11858-014-0641-8 journal Early-years+teachers%E2%80%99+concept+images+and+concept+definitions%3A+Triangles%2C+circles%2C+and+cylinders author%3DP.+Tsamir%26author%3DD.+Tirosh%26author%3DE.+Levenson%26author%3DR.+Barkai%26author%3DM.+Tabach 2015 Tsamir%2C+P.%2C+Tirosh%2C+D.%2C+Levenson%2C+E.%2C+Barkai%2C+R.%2C+%26+Tabach%2C+M.+%282015%29.+Early-years+teachers%E2%80%99+concept+images+and+concept+definitions%3A+Triangles%2C+circles%2C+and+cylinders.+ZDM+Mathematics+Education%2C+47%283%29%2C+497%E2%80%93509. 497-509 ZDM+Mathematics+Education 47 3 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_106_1 10.1007%252Fs11858-014-0641-8 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs11858-014-0641-8%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DTsamir%26rft.aufirst%3DP.%26rft.date%3D2015%26rft.atitle%3DEarly-years%2520teachers%25E2%2580%2599%2520concept%2520images%2520and%2520concept%2520definitions%253A%2520Triangles%252C%2520circles%252C%2520and%2520cylinders%26rft.jtitle%3DZDM%2520Mathematics%2520Education%26rft.volume%3D47%26rft.issue%3D3%26rft.spage%3D497%26rft.epage%3D509 %00empty%00}-->
• Ulusoy, F. (2021). Prospective early childhood and elementary school mathematics teachers’ concept images and concept definitions of triangles. International Journal of Science and Mathematics Education, 19(5), 1057–1078.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1007%2Fs10763-020-10105-6 journal Prospective+early+childhood+and+elementary+school+mathematics+teachers%E2%80%99+concept+images+and+concept+definitions+of+triangles author%3DF.+Ulusoy 2021 Ulusoy%2C+F.+%282021%29.+Prospective+early+childhood+and+elementary+school+mathematics+teachers%E2%80%99+concept+images+and+concept+definitions+of+triangles.+International+Journal+of+Science+and+Mathematics+Education%2C+19%285%29%2C+1057%E2%80%931078. 1057-1078 International+Journal+of+Science+and+Mathematics+Education 19 5 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_107_1 10.1007%252Fs10763-020-10105-6 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10763-020-10105-6%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DUlusoy%26rft.aufirst%3DF.%26rft.date%3D2021%26rft.atitle%3DProspective%2520early%2520childhood%2520and%2520elementary%2520school%2520mathematics%2520teachers%25E2%2580%2599%2520concept%2520images%2520and%2520concept%2520definitions%2520of%2520triangles%26rft.jtitle%3DInternational%2520Journal%2520of%2520Science%2520and%2520Mathematics%2520Education%26rft.volume%3D19%26rft.issue%3D5%26rft.spage%3D1057%26rft.epage%3D1078 %00empty%00}-->
• Unlu, M., & Horzum, T. (2018). Mathematics teacher candidates’ definitions of prism and pyramid. International Journal of Research in Education and Science, 4(2), 670–685.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.21890%2Fijres.438373 journal Mathematics+teacher+candidates%E2%80%99+definitions+of+prism+and+pyramid author%3DM.+Unlu%26author%3DT.+Horzum 2018 Unlu%2C+M.%2C+%26+Horzum%2C+T.+%282018%29.+Mathematics+teacher+candidates%E2%80%99+definitions+of+prism+and+pyramid.+International+Journal+of+Research+in+Education+and+Science%2C+4%282%29%2C+670%E2%80%93685. 670-685 International+Journal+of+Research+in+Education+and+Science 4 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_108_1 10.21890%252Fijres.438373 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.21890%252Fijres.438373%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DUnlu%26rft.aufirst%3DM.%26rft.date%3D2018%26rft.atitle%3DMathematics%2520teacher%2520candidates%25E2%2580%2599%2520definitions%2520of%2520prism%2520and%2520pyramid%26rft.jtitle%3DInternational%2520Journal%2520of%2520Research%2520in%2520Education%2520and%2520Science%26rft.volume%3D4%26rft.issue%3D2%26rft.spage%3D670%26rft.epage%3D685 %00empty%00}-->
• Üreyen, M. (2006). The role of definition in students’ understanding with particular reference to the concavity of a function. International Journal of Mathematical Education in Science and Technology, 37(5), 600–604. https://doi.org/10.1080/00207390600595090
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F00207390600595090 journal The+role+of+definition+in+students%E2%80%99+understanding+with+particular+reference+to+the+concavity+of+a+function author%3DM.+%C3%9Creyen 2006 %C3%9Creyen%2C+M.+%282006%29.+The+role+of+definition+in+students%E2%80%99+understanding+with+particular+reference+to+the+concavity+of+a+function.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+37%285%29%2C+600%E2%80%93604.+ 600-604 International+Journal+of+Mathematical+Education+in+Science+and+Technology 37 5 https%3A%2F%2Fdoi.org%2F10.1080%2F00207390600595090 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_109_1 10.1080%252F00207390600595090 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F00207390600595090%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3D%25C3%259Creyen%26rft.aufirst%3DM.%26rft.date%3D2006%26rft.atitle%3DThe%2520role%2520of%2520definition%2520in%2520students%25E2%2580%2599%2520understanding%2520with%2520particular%2520reference%2520to%2520the%2520concavity%2520of%2520a%2520function%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D37%26rft.issue%3D5%26rft.spage%3D600%26rft.epage%3D604 %00empty%00}-->
• Usiskin, Z., Willmore, E., Witonsky, D., & Griffin, J. (2008). The classification of quadrilaterals: A study of definition. Information Age Publishing.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 book The+classification+of+quadrilaterals%3A+A+study+of+definition author%3DZ.+Usiskin%26author%3DE.+Willmore%26author%3DD.+Witonsky%26author%3DJ.+Griffin 2008 Usiskin%2C+Z.%2C+Willmore%2C+E.%2C+Witonsky%2C+D.%2C+%26+Griffin%2C+J.+%282008%29.+The+classification+of+quadrilaterals%3A+A+study+of+definition.+Information+Age+Publishing. %00empty%00 %00null%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_110_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Dbook%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DUsiskin%26rft.aufirst%3DZ.%26rft.date%3D2008%26rft.btitle%3DThe%2520classification%2520of%2520quadrilaterals%253A%2520A%2520study%2520of%2520definition%26rft.pub%3DInformation%2520Age%2520Publishing %00empty%00}-->
• Van Dormolen, J., & Zaslavsky, O. (2003). The many facets of a definition: The case of periodicity. The Journal of Mathematical Behavior, 22(1), 91–106.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1016%2FS0732-3123%2803%2900006-3 journal The+many+facets+of+a+definition%3A+The+case+of+periodicity author%3DJ.+Van+Dormolen%26author%3DO.+Zaslavsky 2003 Van+Dormolen%2C+J.%2C+%26+Zaslavsky%2C+O.+%282003%29.+The+many+facets+of+a+definition%3A+The+case+of+periodicity.+The+Journal+of+Mathematical+Behavior%2C+22%281%29%2C+91%E2%80%93106. 91-106 The+Journal+of+Mathematical+Behavior 22 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_111_1 10.1016%252FS0732-3123%252803%252900006-3 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252FS0732-3123%252803%252900006-3%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DVan%2520Dormolen%26rft.aufirst%3DJ.%26rft.date%3D2003%26rft.atitle%3DThe%2520many%2520facets%2520of%2520a%2520definition%253A%2520The%2520case%2520of%2520periodicity%26rft.jtitle%3DThe%2520Journal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D22%26rft.issue%3D1%26rft.spage%3D91%26rft.epage%3D106 %00empty%00}-->
• Viirman, O. (2013). The functions of function discourse—University mathematics teaching from a commognitive standpoint. International Journal of Mathematical Education in Science and Technology, 45(4), 512–527. https://doi.org/10.1080/0020739x.2013.855328
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1080%2F0020739x.2013.855328 journal The+functions+of+function+discourse%E2%80%94University+mathematics+teaching+from+a+commognitive+standpoint author%3DO.+Viirman 2013 Viirman%2C+O.+%282013%29.+The+functions+of+function+discourse%E2%80%94University+mathematics+teaching+from+a+commognitive+standpoint.+International+Journal+of+Mathematical+Education+in+Science+and+Technology%2C+45%284%29%2C+512%E2%80%93527.+ 512-527 International+Journal+of+Mathematical+Education+in+Science+and+Technology 45 4 https%3A%2F%2Fdoi.org%2F10.1080%2F0020739x.2013.855328 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_112_1 10.1080%252F0020739x.2013.855328 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F0020739x.2013.855328%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DViirman%26rft.aufirst%3DO.%26rft.date%3D2013%26rft.atitle%3DThe%2520functions%2520of%2520function%2520discourse%25E2%2580%2594University%2520mathematics%2520teaching%2520from%2520a%2520commognitive%2520standpoint%26rft.jtitle%3DInternational%2520Journal%2520of%2520Mathematical%2520Education%2520in%2520Science%2520and%2520Technology%26rft.volume%3D45%26rft.issue%3D4%26rft.spage%3D512%26rft.epage%3D527 %00empty%00}-->
• Vinner, S. (1976). The naive concept of definition in mathematics. Educational Studies in Mathematics, 7(4), 413–429.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2FBF00452223 journal The+naive+concept+of+definition+in+mathematics author%3DS.+Vinner 1976 Vinner%2C+S.+%281976%29.+The+naive+concept+of+definition+in+mathematics.+Educational+Studies+in+Mathematics%2C+7%284%29%2C+413%E2%80%93429. 413-429 Educational+Studies+in+Mathematics 7 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_113_1 10.1007%252FBF00452223 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252FBF00452223%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DVinner%26rft.aufirst%3DS.%26rft.date%3D1976%26rft.atitle%3DThe%2520naive%2520concept%2520of%2520definition%2520in%2520mathematics%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D7%26rft.issue%3D4%26rft.spage%3D413%26rft.epage%3D429 %00empty%00}-->
• Vinner, S. (1977). The concept of exponentiation at the undergraduate level and the definitional approach. Educational Studies in Mathematics, 8(1), 17–26.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2FBF00302501 journal The+concept+of+exponentiation+at+the+undergraduate+level+and+the+definitional+approach author%3DS.+Vinner 1977 Vinner%2C+S.+%281977%29.+The+concept+of+exponentiation+at+the+undergraduate+level+and+the+definitional+approach.+Educational+Studies+in+Mathematics%2C+8%281%29%2C+17%E2%80%9326. 17-26 Educational+Studies+in+Mathematics 8 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_114_1 10.1007%252FBF00302501 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252FBF00302501%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DVinner%26rft.aufirst%3DS.%26rft.date%3D1977%26rft.atitle%3DThe%2520concept%2520of%2520exponentiation%2520at%2520the%2520undergraduate%2520level%2520and%2520the%2520definitional%2520approach%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D8%26rft.issue%3D1%26rft.spage%3D17%26rft.epage%3D26 %00empty%00}-->
• Vinner, S. (1991). The role of definitions in the teaching and learning of mathematics. In D. Tall (Ed.), Advanced mathematical thinking (pp. 65–81). Springer Netherlands. https://doi.org/10.1007/0-306-47203-1_5
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2F0-306-47203-1_5 book The+role+of+definitions+in+the+teaching+and+learning+of+mathematics author%3DS.+Vinner%26 1991 Vinner%2C+S.+%281991%29.+The+role+of+definitions+in+the+teaching+and+learning+of+mathematics.+In+D.+Tall+%28Ed.%29%2C+Advanced+mathematical+thinking+%28pp.+65%E2%80%9381%29.+Springer+Netherlands.+ 65-81 %00null%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 %00empty%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_115_1 10.1007%252F0-306-47203-1_5 url_ver%3DZ39.88-2004%26rft.genre%3Dbook%26rft_id%3Dinfo%3Adoi%2F10.1007%252F0-306-47203-1_5%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DVinner%26rft.aufirst%3DS.%26rft.date%3D1991%26rft.atitle%3DThe%2520role%2520of%2520definitions%2520in%2520the%2520teaching%2520and%2520learning%2520of%2520mathematics%26rft.aulast%3DTall%26rft.aufirst%3DD.%26rft.btitle%3DAdvanced%2520mathematical%2520thinking%26rft.spage%3D65%26rft.epage%3D81%26rft.pub%3DSpringer%2520Netherlands %00empty%00}-->
• Vinner, S., & Dreyfus, T. (1989). Images and definitions for the concept of function. Journal for Research in Mathematics Education, 20(4), 356–366.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.2307%2F749441 journal Images+and+definitions+for+the+concept+of+function author%3DS.+Vinner%26author%3DT.+Dreyfus 1989 Vinner%2C+S.%2C+%26+Dreyfus%2C+T.+%281989%29.+Images+and+definitions+for+the+concept+of+function.+Journal+for+Research+in+Mathematics+Education%2C+20%284%29%2C+356%E2%80%93366. 356-366 Journal+for+Research+in+Mathematics+Education 20 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_116_1 10.2307%252F749441 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.2307%252F749441%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DVinner%26rft.aufirst%3DS.%26rft.date%3D1989%26rft.atitle%3DImages%2520and%2520definitions%2520for%2520the%2520concept%2520of%2520function%26rft.jtitle%3DJournal%2520for%2520Research%2520in%2520Mathematics%2520Education%26rft.volume%3D20%26rft.issue%3D4%26rft.spage%3D356%26rft.epage%3D366 %00empty%00}-->
• Wilhelmi, M. R., Godino, J. D., & Lacasta, E. (2007). Didactic effectiveness of mathematical definitions: The case of the absolute value. International Electronic Journal of Mathematics Education, 2(2), 72–90.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.29333%2Fiejme%2F176 journal Didactic+effectiveness+of+mathematical+definitions%3A+The+case+of+the+absolute+value author%3DM.+R.+Wilhelmi%26author%3DJ.+D.+Godino%26author%3DE.+Lacasta 2007 Wilhelmi%2C+M.+R.%2C+Godino%2C+J.+D.%2C+%26+Lacasta%2C+E.+%282007%29.+Didactic+effectiveness+of+mathematical+definitions%3A+The+case+of+the+absolute+value.+International+Electronic+Journal+of+Mathematics+Education%2C+2%282%29%2C+72%E2%80%9390. 72-90 International+Electronic+Journal+of+Mathematics+Education 2 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_117_1 10.29333%252Fiejme%252F176 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.29333%252Fiejme%252F176%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DWilhelmi%26rft.aufirst%3DM.%2520R.%26rft.date%3D2007%26rft.atitle%3DDidactic%2520effectiveness%2520of%2520mathematical%2520definitions%253A%2520The%2520case%2520of%2520the%2520absolute%2520value%26rft.jtitle%3DInternational%2520Electronic%2520Journal%2520of%2520Mathematics%2520Education%26rft.volume%3D2%26rft.issue%3D2%26rft.spage%3D72%26rft.epage%3D90 %00empty%00}-->
• Winicki-Landman, G., & Leikin, R. (2000). On equivalent and non-equivalent definitions: Part 1. For the Learning of Mathematics, 20(1), 17–21.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal On+equivalent+and+non-equivalent+definitions%3A+Part+1 author%3DG.+Winicki-Landman%26author%3DR.+Leikin 2000 Winicki-Landman%2C+G.%2C+%26+Leikin%2C+R.+%282000%29.+On+equivalent+and+non-equivalent+definitions%3A+Part+1.+For+the+Learning+of+Mathematics%2C+20%281%29%2C+17%E2%80%9321. 17-21 For+the+Learning+of+Mathematics 20 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_118_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DWinicki-Landman%26rft.aufirst%3DG.%26rft.date%3D2000%26rft.atitle%3DOn%2520equivalent%2520and%2520non-equivalent%2520definitions%253A%2520Part%25201%26rft.jtitle%3DFor%2520the%2520Learning%2520of%2520Mathematics%26rft.volume%3D20%26rft.issue%3D1%26rft.spage%3D17%26rft.epage%3D21 %00empty%00}-->
• Wong, C. L., Chu, H., & Yap, K. C. (2014). Developing a framework for analyzing definitions: A study of “The Feynman Lectures.” International Journal of Science Education, 36(15), 2481–2513.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Taylor & Francis Online<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--> Web of Science ®<!--${googleScholarLinkReplacer: 10.1080%2F09500693.2014.893594 journal Developing+a+framework+for+analyzing+definitions%3A+A+study+of+%E2%80%9CThe+Feynman+Lectures.%E2%80%9D author%3DC.+L.+Wong%26author%3DH.+Chu%26author%3DK.+C.+Yap 2014 Wong%2C+C.+L.%2C+Chu%2C+H.%2C+%26+Yap%2C+K.+C.+%282014%29.+Developing+a+framework+for+analyzing+definitions%3A+A+study+of+%E2%80%9CThe+Feynman+Lectures.%E2%80%9D+International+Journal+of+Science+Education%2C+36%2815%29%2C+2481%E2%80%932513. 2481-2513 International+Journal+of+Science+Education 36 15 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_119_1 10.1080%252F09500693.2014.893594 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1080%252F09500693.2014.893594%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DWong%26rft.aufirst%3DC.%2520L.%26rft.date%3D2014%26rft.atitle%3DDeveloping%2520a%2520framework%2520for%2520analyzing%2520definitions%253A%2520A%2520study%2520of%2520%25E2%2580%259CThe%2520Feynman%2520Lectures.%25E2%2580%259D%26rft.jtitle%3DInternational%2520Journal%2520of%2520Science%2520Education%26rft.volume%3D36%26rft.issue%3D15%26rft.spage%3D2481%26rft.epage%3D2513 %00empty%00}-->
• Yavuzsoy-Köse, N., Y. Yilmaz, T., Yeşil, D., & Yildirim, D. (2019). Middle school students’ interpretation of definitions of the parallelogram family: Which definition for which parallelogram? International Journal of Research in Education and Science, 5(1), 157–175.
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: %00empty%00 journal Middle+school+students%E2%80%99+interpretation+of+definitions+of+the+parallelogram+family%3A+Which+definition+for+which+parallelogram%3F author%3DN.+Yavuzsoy-K%C3%B6se%26author%3DT.+Yilmaz%26author%3DD.+Ye%C5%9Fil%26author%3DD.+Yildirim 2019 Yavuzsoy-K%C3%B6se%2C+N.%2C+Y.+Yilmaz%2C+T.%2C+Ye%C5%9Fil%2C+D.%2C+%26+Yildirim%2C+D.+%282019%29.+Middle+school+students%E2%80%99+interpretation+of+definitions+of+the+parallelogram+family%3A+Which+definition+for+which+parallelogram%3F+International+Journal+of+Research+in+Education+and+Science%2C+5%281%29%2C+157%E2%80%93175. 157-175 International+Journal+of+Research+in+Education+and+Science 5 1 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_120_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DYavuzsoy-K%25C3%25B6se%26rft.aufirst%3DN.%26rft.date%3D2019%26rft.atitle%3DMiddle%2520school%2520students%25E2%2580%2599%2520interpretation%2520of%2520definitions%2520of%2520the%2520parallelogram%2520family%253A%2520Which%2520definition%2520for%2520which%2520parallelogram%253F%26rft.jtitle%3DInternational%2520Journal%2520of%2520Research%2520in%2520Education%2520and%2520Science%26rft.volume%3D5%26rft.issue%3D1%26rft.spage%3D157%26rft.epage%3D175 %00empty%00}-->
• Yim, J., Chong, Y. O., Song, S. H., & Kwon, S. (2008). A case study on the local organization of two mathematically gifted seventh-grade students. Journal for the Education of the Gifted, 32(2), 211–229.
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.4219%2Fjeg-2008-851 journal A+case+study+on+the+local+organization+of+two+mathematically+gifted+seventh-grade+students author%3DJ.+Yim%26author%3DY.+O.+Chong%26author%3DS.+H.+Song%26author%3DS.+Kwon 2008 Yim%2C+J.%2C+Chong%2C+Y.+O.%2C+Song%2C+S.+H.%2C+%26+Kwon%2C+S.+%282008%29.+A+case+study+on+the+local+organization+of+two+mathematically+gifted+seventh-grade+students.+Journal+for+the+Education+of+the+Gifted%2C+32%282%29%2C+211%E2%80%93229. 211-229 Journal+for+the+Education+of+the+Gifted 32 2 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_121_1 10.4219%252Fjeg-2008-851 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.4219%252Fjeg-2008-851%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DYim%26rft.aufirst%3DJ.%26rft.date%3D2008%26rft.atitle%3DA%2520case%2520study%2520on%2520the%2520local%2520organization%2520of%2520two%2520mathematically%2520gifted%2520seventh-grade%2520students%26rft.jtitle%3DJournal%2520for%2520the%2520Education%2520of%2520the%2520Gifted%26rft.volume%3D32%26rft.issue%3D2%26rft.spage%3D211%26rft.epage%3D229 %00empty%00}-->
• Zandieh, M., & Rasmussen, C. (2010). Defining as a mathematical activity: A framework for characterizing progress from informal to more formal ways of reasoning. The Journal of Mathematical Behavior, 29(2), 57–75. https://doi.org/10.1016/j.jmathb.2010.01.001
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1016%2Fj.jmathb.2010.01.001 journal Defining+as+a+mathematical+activity%3A+A+framework+for+characterizing+progress+from+informal+to+more+formal+ways+of+reasoning author%3DM.+Zandieh%26author%3DC.+Rasmussen 2010 Zandieh%2C+M.%2C+%26+Rasmussen%2C+C.+%282010%29.+Defining+as+a+mathematical+activity%3A+A+framework+for+characterizing+progress+from+informal+to+more+formal+ways+of+reasoning.+The+Journal+of+Mathematical+Behavior%2C+29%282%29%2C+57%E2%80%9375.+ 57-75 The+Journal+of+Mathematical+Behavior 29 2 https%3A%2F%2Fdoi.org%2F10.1016%2Fj.jmathb.2010.01.001 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_122_1 10.1016%252Fj.jmathb.2010.01.001 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1016%252Fj.jmathb.2010.01.001%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DZandieh%26rft.aufirst%3DM.%26rft.date%3D2010%26rft.atitle%3DDefining%2520as%2520a%2520mathematical%2520activity%253A%2520A%2520framework%2520for%2520characterizing%2520progress%2520from%2520informal%2520to%2520more%2520formal%2520ways%2520of%2520reasoning%26rft.jtitle%3DThe%2520Journal%2520of%2520Mathematical%2520Behavior%26rft.volume%3D29%26rft.issue%3D2%26rft.spage%3D57%26rft.epage%3D75 %00empty%00}-->
• Zaslavsky, O., & Shir, K. (2005). Students’ conceptions of a mathematical definition. Journal for Research in Mathematics Education, 36(4), 317–346. http://www.jstor.org/stable/30035043
  <!--${if: isGetFTREnabled}--><!--${/if:}--> <!--${ifNot: isGetFTREnabled}--><!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}-->Web of Science ®<!--${googleScholarLinkReplacer: %00empty%00 journal Students%E2%80%99+conceptions+of+a+mathematical+definition author%3DO.+Zaslavsky%26author%3DK.+Shir 2005 Zaslavsky%2C+O.%2C+%26+Shir%2C+K.+%282005%29.+Students%E2%80%99+conceptions+of+a+mathematical+definition.+Journal+for+Research+in+Mathematics+Education%2C+36%284%29%2C+317%E2%80%93346.+ 317-346 Journal+for+Research+in+Mathematics+Education 36 4 %00empty%00 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_123_1 %00empty%00 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DZaslavsky%26rft.aufirst%3DO.%26rft.date%3D2005%26rft.atitle%3DStudents%25E2%2580%2599%2520conceptions%2520of%2520a%2520mathematical%2520definition%26rft.jtitle%3DJournal%2520for%2520Research%2520in%2520Mathematics%2520Education%26rft.volume%3D36%26rft.issue%3D4%26rft.spage%3D317%26rft.epage%3D346 %00empty%00}-->
• Zazkis, R., & Leikin, R. (2008). Exemplifying definitions: A case of a square. Educational Studies in Mathematics, 69(2), 131–148. https://doi.org/10.1007/s10649-008-9131-7
  <!--${if: isGetFTREnabled}-->

  <!--${/if:}--> <!--${ifNot: isGetFTREnabled}-->Crossref<!--${/ifNot:}--><!--${if: isGetFTREnabled}--><!--${/if:}--><!--${googleScholarLinkReplacer: 10.1007%2Fs10649-008-9131-7 journal Exemplifying+definitions%3A+A+case+of+a+square author%3DR.+Zazkis%26author%3DR.+Leikin 2008 Zazkis%2C+R.%2C+%26+Leikin%2C+R.+%282008%29.+Exemplifying+definitions%3A+A+case+of+a+square.+Educational+Studies+in+Mathematics%2C+69%282%29%2C+131%E2%80%93148.+ 131-148 Educational+Studies+in+Mathematics 69 2 https%3A%2F%2Fdoi.org%2F10.1007%2Fs10649-008-9131-7 %00empty%00 %00null%00 getFTREnabled FULL_TEXT %00empty%00}--><!--${sfxLinkReplacer: e_1_3_4_1_5_124_1 10.1007%252Fs10649-008-9131-7 url_ver%3DZ39.88-2004%26rft.genre%3Darticle%26rft_id%3Dinfo%3Adoi%2F10.1007%252Fs10649-008-9131-7%26rfr_id%3Dinfo%3Asid%2Fliteratum%253Atandf%26rft.aulast%3DZazkis%26rft.aufirst%3DR.%26rft.date%3D2008%26rft.atitle%3DExemplifying%2520definitions%253A%2520A%2520case%2520of%2520a%2520square%26rft.jtitle%3DEducational%2520Studies%2520in%2520Mathematics%26rft.volume%3D69%26rft.issue%3D2%26rft.spage%3D131%26rft.epage%3D148 %00empty%00}-->