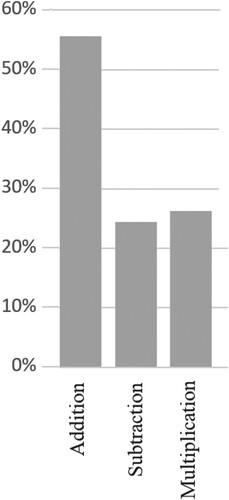Grade six students’ multidigit arithmetic strategy adaptivity and flexibility: evaluating a novel tri-phase assessment tool

Abstract

In this paper we present a novel adaptation of a tri-phase assessment tool, originally devised to investigate students’ linear equations-related strategy flexibility, to evaluate Danish grade-six students’ multidigit arithmetic-related strategy adaptivity and flexibility. Participants, 731 students, median age 12 years and drawn from 20 demographically different schools, completed a series of positive integer addition, subtraction and multiplication tasks designed to elicit shortcut strategies. First, students solved each task by means of their preferred strategy, with those using a shortcut strategy being defined as showing adaptivity for that task. Second, students solved the same tasks by means of whatever alternative strategies they could devise; those that offered at least two strategies were defined as showing flexibility for that task. Third, for each task, students were asked to indicate which of their strategies they believed was optimal. Statistical analyses, based on the total number of tasks on which students demonstrated adaptivity or flexibility, found students to be more flexible than adaptive, with 55% of students showing moderate or high levels of flexibility but only 21% for adaptivity. Both strategy adaptivity and flexibility, which differed according to operation, were implicated in students’ solution accuracy, with adaptivity being a stronger predictor than flexibility.

KEYWORDS:

• Adaptivity
• flexibility
• strategy use
• shortcut strategies
• multidigit arithmetic
• elementary school

1. Introduction

Researchers have increasingly come to view the solving of mathematics tasks efficiently, creatively, flexibly and adaptively as a core goal of mathematics education (Verschaffel et al., 2009). Indeed, since the mathematics reforms of the 1990s, flexibility and adaptivity in strategy choice have become accepted elements of mathematical proficiency (Baroody, 2003; Hickendorff, 2018; Xu et al., 2017) and, despite a lack of evidence supporting the feasibility of such goals for all students (Torbeyns et al., 2009a), an important developmental goal for mathematics learning (Baroody & Dowker, 2003; Hatano & Oura, 2003; McMullen et al., 2016; Torbeyns & Verschaffel, 2016). Moreover, evidence is increasingly showing that arithmetic-related strategy adaptivity has long-term developmental implications for many aspects of children’s learning of mathematics (Sunde et al., 2023).

1.1. Defining adaptivity and flexibility

A precursor to such work can be found in early research on the development and manifestation of adaptive expertise in the context of mathematics learning, both generally (De Corte, 2007; Hatano, 1988; Verschaffel et al., 2009) and in respect of arithmetic (Hickendorff, 2018; McMullen et al., 2016, 2020, 2022; Nemeth et al., 2019; Torbeyns et al., 2009a). However, over the last few years, research into the development of students’ adaptive expertise (McMullen et al., 2016) has been complemented by an emphasis on flexibility. Indeed, (Nemeth et al., 2019) write of a ‘consensus among mathematics researchers and educators that the abilities to use various strategies for solving a problem (flexibility) as well as to use efficient strategies (adaptivity) are important mathematical competencies students should gain’.

However, the distinction between the two constructs has not always been transparent (Heinze et al., 2009), for example, some scholars seem to construe adaptivity as subsuming flexibility. For example, McMullen and his colleagues have suggested that the flexible application of number-related knowledge is an important component of arithmetical adaptivity (McMullen et al., 2016, 2020). Others, see also Baroody (2003) see them as synonyms, as with Hickendorff’s (2018, p. 578) somewhat expedient position that in her ‘paper, flexibility and adaptivity are used interchangeably as selecting the optimal strategy for a given problem in a given setting for a given person’. The more widely accepted view, as argued by Blöte et al. (2000) and Star and Rittle-Johnson (2008), sees adaptivity as subsumed by flexibility, as with Schneider et al.’s (2011, p. 1527) argument that one ‘source of competence is procedural flexibility, where learners know multiple procedures and apply them adaptively to a range of situations’ and Rathgeb-Schnierer and Green’s (2017, p. 3) position that ‘flexibility in mental calculation includes two central features: the knowledge of different solution methods and the ability to adapt them appropriately’.

Clarification of this latter view can be found in Verschaffel et al.’s (2009) well-known review paper. After initially treating flexibility and adaptivity as synonymous, they concluded that 'the term “flexibility” is primarily used to refer to switching (smoothly) between different strategies, whereas the term “adaptivity” puts more emphasis on selecting the most appropriate strategy' (Verschaffel et al., 2009, p. 337, original emphasis). Others, as do we in this paper, have accepted this distinction (Heinze et al., 2009), although, as evidenced in Xu et al. (2017), the vocabulary may change. The latter refer to potential flexibility and practical flexibility in ways that indicate a strong resonance with flexibility and adaptivity respectively. Importantly, further clarifying Verschaffel et al.’s (2009) conclusions, although possessing a variety of strategies and being able to switch smoothly between these strategies can be considered an essential stepping-stone towards adaptivity, merely applying different solution strategies on a series of similar mathematical items or problems can hardly be considered as evidence of adaptivity (Verschaffel et al., 2009, p. 339).

Importantly, two key inferences can be drawn from Verschaffel et al.’s (2009) distinction. First, flexibility can be seen as a precondition for adaptivity (Verschaffel et al., 2007) and, second, ‘whether a strategy is adaptive or not, does not depend on speed and accuracy’ (Nemeth et al., 2019, p. 2). Finally, to illustrate our construal of the distinction between flexible and adaptive strategy use, we draw on an example from Threlfall (2002, p. 31), who writes that the adding of one number to another first by adding the tens and then the ones separately is more suited to 55 + 24 than to 33 + 29, whereas rounding a number before adding, and then compensating, is more suited to 33 + 29 than to 55 + 24.

Thus, a student who knows Threlfall’s two strategies can be construed as flexible. A student who chooses the more appropriate of the two strategies can be construed as adaptive. Importantly, there is some consensus with respect to the necessary precursors of strategy flexibility and adaptivity; a synthesis of the work of Hatano and Inagaki (1986), Hickendorff (2018), Hickendorff et al. (2019), Threlfall (2002) and Verschaffel et al. (2009) indicates that evaluating strategy appropriateness requires students to

• attend to the differing task characteristics, the implicated operations and the extent to which the numbers involved point the solver towards appropriate and efficient strategies;

• draw on an appropriately developed conceptual knowledge, not least because the identification of appropriate strategies or the invention of new ones, say, is dependent on a depth understanding of the numbers involved and their relations to each other;

• draw on an appropriate procedural knowledge;

• be conscious of contextual matters such as whether speed is privileged over accuracy.

In this paper, we focus on the strategy selection and use of Danish grade six students with respect to multidigit addition, subtraction and multiplication. Our reasons for so doing are several, and some of these are discussed later, but here we offer four. First, Danish grade six students’ strategy selection and use have not yet been researched. Therefore, this study should not only address a significant gap but contribute to the international literature on the topic. Second, national assessments of Danish students’ mathematics-related competence have shown low levels of division-related competence. Therefore, a study of division-related strategy selection is unlikely to prove productive. Third, as Sunde et al. (2020) observe, the Danish curriculum and assessment model forms the basis of PISA’s assessment framework. Therefore, investigating Danish students’ strategy use is important in relation to understanding Danish students’ PISA-related achievement. Fourth, as we outline below, much strategy-related research has exploited a choice/no choice research design, which, even in the choice condition, typically restrict the choices available. Therefore, this study draws on an approach to data collection that is not only novel in the context of multidigit arithmetic but also allows students, unconstrained by researcher-imposed strategies, to exploit their preferred strategies.

1.2. Strategy choice in the context of arithmetic

Our reading of the literature on children’s strategy selection and use in the context of arithmetic is that more attention has been paid to children in the first four years of elementary education than the latter. Frequently motivated by an interest in understanding the extent to which the curricular introduction of standard algorithms influences children’s strategy choice, much work has been undertaken in the European context, including Flemish studies of students in grades two, three and four (Torbeyns et al., 2009a), grade three (De Smedt et al., 2010; Torbeynset al., 2009b) and grade four (Torbeyns & Verschaffel, 2016). Elsewhere can be found French studies of students in grades three and five (Lemaire & Brun, 2017), German studies of students in grade two (Blöte et al., 2001), grade three (Heinze et al., 2018, 2009; Nemeth et al., 2019; Sievert et al., 2019) and grades three and four (Selter, 2001), Hungarian studies of students in grade four (Csíkos, 2016), Italian studies of students in grades three and five (Lucangeli et al., 2003) and Dutch studies of students in grade four (Hickendorff, 2020). Overall, these studies have indicated that cultural norms, including when and how standard algorithms are introduced, may influence greatly the strategies children later elect to use.

In similar vein, the limited number of studies involving older students, have found, for example, that Flemish grade six students flexibly apply indirect addition strategies to small difference subtraction tasks, even when the instructional setting emphasises direct subtraction (Peters et al., 2013; Torbeyns et al., 2018; Van Der Auwera et al., 2022). Elsewhere, when allowed to choose, Dutch grade six students privilege standard algorithms across all operations (Hickendorff, 2018), while French students in grades five and seven exploit various strategies dependent on the context of the problem and, in particular, whether the subtractions under scrutiny are presented vertically or horizontally (Lemaire & Callies, 2009). Other studies, of limited interest to this paper, have focused on the division strategies of Dutch grade six students (Fagginger Auer et al., 2016) or those of both Dutch and Flemish students in grades five and six (Hickendorff et al., 2018). Such studies have not only shown the influence on students’ strategy choices of standard algorithms but, importantly, highlighted how researcher decisions with respect to which strategies and task types are under scrutiny inevitably influence any conclusions. Importantly, by way of understanding more fully the relationship between adaptivity, flexibility and accuracy, McMullen et al. (2016) found the adaptive number knowledge of grade six Finnish students to be strongly related to both their conceptual knowledge of arithmetic and their arithmetic fluency. They conclude that ‘being able to produce a large number of arithmetic sentences on these tasks is not merely about being able to quickly calculate simple arithmetic problems, but requires a better understanding of the relationship between numbers and arithmetic operations’ (p. 179).

1.3. Approaches to the measurement of strategy flexibility and adaptivity

Previous studies have used a variety of tools to measure students’ adaptivity and flexibility. From the perspective of adaptivity, this entails evaluating when a strategy is appropriate or efficient for the item being solved (Luwel et al., 2009; Nemeth et al., 2019). Many studies, as indicated above, have adopted a choice/no choice approach, which typically entails students being tested under two differing conditions. For each task in the choice condition, children are typically invited to choose between a range of strategies offered to them. In the no choice condition, they are instructed to use one or other of the same strategies (Torbeyns et al., 2004). The researcher-selected strategies are dependent on the nature of the study being undertaken and, importantly, the operations under scrutiny. Various studies (see Hickendorff, 2020; Lemaire & Callies, 2009; Si et al., 2016; Torbeyns et al., 2006; Torbeyns et al., 2009b; Torbeyns et al., 2018; Torbeyns & Verschaffel, 2013, 2016) have exploited this approach, arguing that by comparing students’ responses in the two conditions, typically involving evaluations of speed and accuracy, researchers are able to determine an individual’s adaptivity. However, despite the undoubted success of the choice/no choice approach, the very tight restrictions on choice imposed in both conditions necessarily mask novel approaches students may otherwise bring to the task. By way of contrast, a number of studies have attempted to elicit students’ preferred strategies, albeit in different ways and contexts. For example, Blöte et al. (2001) invited German grade two students to solve two-digit addition and subtraction tasks in two different ways and record all the steps of each method, with flexible students being defined by their ability to provide two such methods. In the Finnish context, McMullen et al. (2016) ‘asked students to come up with as many arithmetic calculation sentences as they could which used a set of numbers to equal a target number’ (p. 175). For example, the first of the four tasks had a target of 16, and the integers 2, 4, 8, 12 and 32 as potential operands. The advantage of such an approach, which can also be construed as a disadvantage, is that no particular operation is privileged. In similar vein, Torbeyns et al. (2009a) examined second, third and fourth grade students’ two-digit addition and subtraction strategies by first inviting them to solve all given items as accurately and as quickly as possible by means of a preferred strategy, and then by inviting them to generate at least two different strategies for each item.

From the perspective of flexibility, studies with a clear focus on evaluating students’ preferred strategies rather than those imposed by researchers include the work of Rittle-Johnson and Star (2007). Here, focused on students’ flexibility in the solving of linear equations, they adopt a three-part assessment, ‘designed to tap three components of flexibility—the abilities to generate, recognize, and evaluate multiple solution methods for the same problem’ (p. 564). The ‘generate’ element invited students to solve each of two given equations in two different ways. In the ‘recognise’ element, students were shown two equations and, in each case, invited to write down ‘all possible steps that could be done next’ (p. 565). The ‘evaluate’ element, also involving two equations, presented the first line of an unconventional or novel solution and invited students to comment on the strategy’s efficiency. This three-pronged approach leads us to the work of Xu et al. (2017), which, as is explained below, will form the methodological underpinning of the study presented here. As with Rittle-Johnson and Star’s work, Xu et al. (2017) have three foci: the strategies students choose to use when solving linear equations, whether students have access to strategies additional to their preferred, and importantly, how they interpret the efficacy of these different strategies. Their three-phase assessment, which they label a Tri-phase Flexibility Assessment model (hereafter TriFA), draws on elements of the studies discussed above, and incorporates the processes of generation, recognition and evaluation found in Rittle-Johnson and Star (2007). During the first phase, students are invited to solve each assessment item with a strategy of their choice. In the second phase, students are invited to solve the same tasks but with as many different strategies as they can. Finally, during phase three, students are invited to identify the most efficacious of all the strategies they have offered. Overall, the total of number of strategies yielded by phases one and two offer an indication of student flexibility, while their responses to phases one and three offer an indication of student adaptivity.

2. The current study

In addition to those discussed above, the current study is motivated by at several additional factors. First, much of the research undertaken over the last 25 years has focused on both single and multidigit of addition and subtraction, with few studies examining strategy choice in relation to multiplication (Hickendorff et al., 2019). Second, most arithmetic-related studies have focused on younger students, with few considering the strategies students use at different ages. Third, and we reiterate this due to its methodological importance, one consequence of the choice/no choice research design is that studies rarely offer authentic opportunities for children to show their preferred strategies. Fourth, the sample sizes of most of the choice-no choice studies discussed above were relatively small and involved time-intensive procedures. For example, Van Der Auwera et al.’s (2022) recent study involved only 50 students at each grade level and a data collection procedure that involved each student solving tasks in each of three conditions on three days separated by at least one day and never more than one week. Our goal, therefore, was to identify an approach that would facilitate the collection of, essentially, cohort-level data in time-efficient ways that would allow older students authentic opportunities to demonstrate their preferred arithmetic strategies in secure contexts. In light of these matters, the research presented in this paper, focused on Danish grade six students, is framed by the questions:

• How is strategy adaptivity manifested in students’ approaches to multidigit arithmetic?

• How is strategy flexibility manifested in students’ approaches to multidigit arithmetic?

• How is student arithmetical accuracy associated with adaptivity and flexibility?

• How appropriate is the TriFA model for addressing such questions?

2.1. Methods

As indicated above, many of the tools used in previous research on students’ arithmetic-related strategies, while appropriate for the contexts in which they were used, do not allow for the uncovering of students ‘first choice’ or ‘go to’ strategies. Consequently, partly in response to Xu et al.’s (2017) invitation to adapt it for topic areas other than the linear equations for which it was developed, the TriFA approach was adopted. In addition to eliciting students’ preferred strategies, the TriFA is appropriate for whole-class settings, which means that large numbers of students from representative samples of schools can be assessed. Moreover, students will meet the test in familiar, comfortable and unthreatening contexts and, greatly simplifying procedural matters, all three phases can be completed within a single lesson.

In using a TriFA, we are conscious of earlier criticism of free-choice methods, which argue that such approaches are prone to bias, due to the nature of the tasks themselves and those who solve them. For example, Siegler and Lemaire (1997, pp. 71–72) write that.

if a less accurate strategy is used mainly on easy problems and a more accurate strategy is used primarily on difficult ones, the more accurate strategy may produce lower percentages of correct answers (due to its being used on harder problems) and thus appear to be less accurate. Similarly, if good students tend to rely on Strategy A and less good students tend to rely on Strategy B, Strategy A may appear to yield superior performance even if it is no better than the alternative (for example, because the good students are more careful in executing it).

While we concede the general arguments against free-choice approaches, their validity tends to diminish if the criterion for speed is removed. That is, if one’s goals are focused solely on whether students have a range of strategies available to them, and can identify which of those strategies is the more effective then speed is of little relevance. Moreover, in this study our interest in accuracy is concerned less with particular strategies than its relationship to both adaptivity and flexibility in general.

2.2. Adapting the TriFA for arithmetic

Xu et al.’s (2017) study draws on the notion of an innovative strategy, which they define as ‘the strategy for that problem that had the fewest steps and with the most simplified computations’ (p. 3). In our view, the adjective innovative implies that students’ strategies are novel, yet one cannot infer from students’ solutions whether such strategies are newly-invented or pre-existing. Consequently, drawing on Torbeyns et al. (2009a) and Hickendorff (2018), we refer to shortcut strategies, whereby the solution process is facilitated by appropriate modifications to a task’s numbers and/or operations in ways that both simplify the arithmetic and reduce the number of steps from those of the standard algorithm. In other words, this study is characterised by an emphasis on students attending to task features in order to make decisions about what strategies they employ.

Importantly, two equivalent tests of naked arithmetic tasks (Fuchs et al., 2010) were developed to ensure that any outcomes would not be the consequence of idiosyncratic responses to a particular item and that students sitting in adjacent seats would solve different tasks. Table 1 shows the tasks used to elicit students’ strategies for multidigit addition, subtraction and multiplication. Each task was designed to elicit the various strategies highlighted in the literature (Hickendorff, 2020; Sievert et al., 2019; Torbeyns et al., 2009a). With respect to addition, both sets included an item that could directly be solved by recognising a sum to one hundred (482 + 218 = 400 + 200 + (82 + 18) = 700). Both sets included a three-digit item to prompt the use of compensation as a shortcut strategy (199 + 323 = 200 + 323 − 1 = 522). Both sets included an item that can be addressed by a combination of compensation and a sum to one hundred (349 + 154 = 300 + 100 + 50 + 50 + 3 = 503). Finally, the hundreds digit for each three-digit addition item were chosen to ensure a three-digit sum.

Table 1. Multidigit items used across the different operations.

Addition		Subtraction		Multiplication
Set 1	Set 2	Set 1	Set 2	Set 1	Set 2
482 + 218	384 + 216	502−18	504−476	5 · 26	5 · 24
153 + 249	349 + 154	963−499	704−17	15 · 18	12 · 15
298 + 483	199 + 323	514−486	673−199	19 · 21	29 · 31

Both sets of subtraction tasks, adapted from (Hickendorff, 2020), included a task with 99 as a subtrahend to elicit compensation as a strategy for large difference numbers (963 − 499 = 964 − 500). Both sets, to prompt the use of indirect addition, included small difference tasks (504 − 476). Both sets included a large difference task to elicit a shortcut sequential strategy (704 − 17 = 704 − 10 − 7 = 687).

Finally, the three multiplication items shown in Table 1 were also designed to elicit different types of shortcut strategies. Each set included one item designed to elicit either compensation or partitioning as shortcut strategies (5 × 26 = 5 × 25 + 5 × 1 or 5 × 26 = 5 × 20 + 5 × 6). Each set included an item with 15 as either multiplicator or multiplicand with various opportunities for the use of different shortcut strategies (15 × 18 can be addressed by partitions like 10 × 18 + 5 × 18 or 10 × 15 + 8 × 15 or simplifications like 5 × 54 = 5 × 50 + 5 × 4). Each set included an item whose numbers fitted the model (a-b)², designed to elicit compensation strategies (29 × 31 = 29 × 30 + 29 or 29 × 31 = 30 × 31 − 31).

2.3. Participants

Schools in five demographically different municipalities in Jutland, the central region of Denmark, were contacted to elicit their participation. This yielded 20 schools, both large and small, urban and rural, and 731 grade-six pupils, with a median age of 12 years. Prior to the granting of permission for their children’s participation, all parents received information two letters. The first was through their child’s schools’ communication platform and, the second was by means of an email that included legal information about GDPR. Of all families contacted, only one requested that their child not be included.

2.4. Implementing TriFA

Over a period of four weeks, members of the project team undertook the TriFA with each participating class. In each case, the complete assessment was completed in under an hour according to the timeline shown in Table 2, which was intended to act as a guide, although actual times varied slightly according to differences in class size and questions posed by students about the assessment and its implementation. Each phase was preceded by an oral introduction and instructions for its completion, including alerting students to the research focus of the assessment and, importantly, promising that it would have no impact on their grades.

Table 2. Recommended timeline for the TriFA implementation.

Time in minutes	Activity
0–4	Introduction and instructions for phase 1
5–25	Phase 1 implementation
26–29	Instructions for phase 2
30–50	Phase 2 implementation
51–52	Instructions for phase 3
53–56	Phase 3 implementation

During the first phase, as indicators of their preferred strategies and adaptivity, students solved each task once, by whatever means they thought was appropriate. Students offering shortcut strategies rather than standard algorithms were construed as adaptive. During the second phase, as an indicator of strategy flexibility, students solved the same tasks again by whatever alternative strategies they were able to generate. In the third phase, as a further indication of strategy adaptivity, students evaluated the strategies generated in the first two phases to identify which they believed was optimal (Xu et al., 2017).

Procedurally, each student received a booklet comprising one page for each test item; Figure 1 shows the page for 482 + 218. Acknowledging that the instructions were written in Danish, it is probably important for the reader to know that in Scandinavian languages (Danish, Norwegian and Swedish) the verbs to count and to calculate are the same; in Danish, as shown in Figure 1, it is regne. Children typically learn from the context what the verb is inviting them to do and acquire at a young age an understanding that the verb represents a general invitation to find a solution. This is the case here and the manner of the tasks’ presentation would not rule out the possibility of a student actually counting on.

Figure 1. Exemplar solution sheet for phases 1, 2 and 3.

During phase 1, students wrote their solution strategy in the large box at the top of the page. Acknowledging each task’s design characteristics, and drawing on Hickendorff (2018), students were asked to examine the numbers involved before deciding how to solve it. Where they used a mental strategy, they were asked to write as best they could the various stages of their mental reasoning. In addition, students received a second sheet, see Figure 2, on which they were asked to write the answer, but no working, to each task of phase 1. These answer sheets, which would be used later to evaluate students’ accuracy, were collected before phase 2 was introduced. During phase 2, students were invited to return to each of the tasks of phase 1 and, in the smaller boxes on each page, write any additional solutions they could. Finally, in phase 3, students were asked to tick, in the small circle, which of their solutions they believed was the best.

Figure 2. Exemplar answer sheet for phase 1.

2.5. Coding

As indicated above, a shortcut strategy is construed as involving an appropriate modification of a task’s numbers and/or operations in ways that both simplify the arithmetic and reduce the number of steps from those of the standard algorithm. With respect to adaptivity, any phase one task solved by means of a shortcut strategy was recorded as having been solved adaptively. The rationale for this decision was based on two key characteristics of the project’s design. First, every task was designed to elicit shortcut strategies. Second, students were instructed at the start of phase one to pay attention to task characteristics before attempting their solution. Taken together, students who chose to use a standard algorithm for a particular task during phase one were deemed not to have demonstrated adaptivity on that task. With respect to flexibility, any task solved, over phases one and two, by two or more solutions was recorded as having been solved flexibly.

Two experts in the field independently undertook the development of a coding schedule for the various strategies used with the different items. These were then compared and contrasted to produce an agreed set of shortcut strategies for each item. In the case of uncertainty or disagreement, the opinion of a third expert was sought and a resolution achieved. Table 3, by way of exemplar, shows the set of agreed shortcut strategies for the item 482 + 218.

Table 3. Examples of shortcut strategies for 482 + 218, inspired by Sievert et al. (2019).

Split	Simplifying	Compensation	Jumping /Adding on
82 + 18 = 100 400 + 200 = 600 600 + 100 = 700	500 + 200 = 700 or 480 + 220 = 700	480 + 218 = 698 698 + 2 = 700	482 + 210 = 692 692 + 8 = 700

Each student’s solutions were coded by the first author and at least one of several research assistants trained to code the TriFA. Students’ answers, as recorded on the answer sheet of Figure 2, were coded as correct, incorrect or incomplete. In addition, drawing on the solutions presented in their solution booklets, the total number of strategies and whether or not those strategies were shortcut were recorded. Inter-rater reliability, based on comparisons of 60 sets of grade 6 codes from each research assistant and the first author, yielded the following. First, with respect to the accuracy of students’ answers, the average Cohen Kappa for accuracy between the first author and the research assistants was 0.93, which is indicative of exceptionally high inter-rater reliability (Landis & Koch, 1977; McHugh, 2012). Any differences were typically unrelated to the correctness of a student’s answer but whether it was incorrect or incomplete. The Cohen Kappa for the number of strategies was, at 0.73, substantial, while that for determining whether students’ strategies were shortcut was, while moderate at 0.54, a little disappointing. Our view is that the differing levels of inter-coder reliability reflect the differing complexities of the three forms of coding. That being said, every disagreement, irrespective of its source, was checked by the first author for explanations attributable to misinterpretations of the definitions found in the coding guide. In the event of any uncertainty, the opinion of a third expert was sought and the disagreement resolved.

2.6. Analytical procedures

To facilitate analyses and following the approaches of Hästö et al. (2019), where a version of the TriFA was used to measure students’ flexibility with linear equations, students were grouped according to pre-specified levels of adaptivity and flexibility. With respect to adaptivity, and in accordance with the project’s emphasis on task characteristics (Hickendorff, 2018, 2019; Threlfall, 2002; Verschaffel et al., 2009) students were grouped, as shown in Table 5, according to the number of phase-one tasks they solved by means of shortcut strategies. With respect to flexibility, and drawing on the results of phases one and two, similar groupings are shown in Table 9, based on the number of tasks solved by the individual student in two or more ways. For both groupings, accuracy, according to the number of items solved correctly, was calculated separately for each level of adaptivity and level of flexibility, separately. In other words, students were not grouped by their level of accuracy.

Finally, in this section, t-tests were conducted to determine the comparability of the different sets of items. The figures of Table 4 show, with respect to adaptivity, flexibility and accuracy, no statistically significant differences between the outcomes of the two sets, thus warranting our combining the data into a single set.

Table 4. Two-sample t tests conducted to ensure compatibility of the different item sets.

	Level of adaptivity		Level of flexibility		Total Accuracy
	t	p	t	p	t	p
Set 1 (n = 365) & set 2 (n = 366)	−1.567	0.118	−0.687	0.493	−0.718	0.473

Table 5. Levels of adaptivity and corresponding accuracy.

		731 students and 9 test items
		Items solved adaptively (By means of shortcut strategies)	Number of students (Percentage)	Mean accuracy as a percentage of correctly solved items
Adaptivity	None	0	331 (45)	65
	Low	1–2	242 (33)	72
	Medium	3–6	133 (18)	77
	High	7–9	25 (3)	92

3. Results

The results are presented in four parts. First, drawing on the results of phase 1, we examine students’ strategy adaptivity and the relationship between adaptivity and accuracy. Second, drawing on the data from phases 1 and 2, we examine students’ strategy flexibility and the relationship between flexibility and accuracy. Third we examine the relationship between adaptivity and flexibility. Fourth, we examine differences in students’ adaptivity and flexibility, across the three operations and phases of assessment. Throughout, we have worked to a statistical threshold of p < .001 for determining the significance of any results.

3.1. Adaptivity and accuracy

The figures of Table 5 show, with respect to phase one, the distribution of students’ adaptivity levels. As can be seen, very high numbers of students showed little or no adaptivity, while very few students demonstrated high levels of adaptivity. The figures also indicate generally high levels of accuracy and, unsurprisingly, a strong tendency for accuracy to increase with adaptivity.

To investigate more fully the connections between adaptivity and accuracy, students’ levels of accuracy were determined according to the protocol shown in Table 6. Following this, the figures of Table 7 show the distribution of students’ accuracy across the different adaptivity levels, with a chi square test (LR χ² = 53.75, p < .0001) confirming that high levels of adaptivity resonate with high levels of accuracy.

Table 6. Protocol for grouping students by the number of correctly solved items.

Accuracy level	9 items
Low	0–2
Medium low	3–4
Medium high	5–6
High	7–9

Table 7. Accuracy levels as a proportion of all students at each level of adaptivity.

		Accuracy
		Low	Medium low	Medium high	High
Adaptivity	None (n = 331)	9	24	22	45
	Low (n = 242)	4	14	26	57
	Medium (n = 133)	1	5	33	62
	High (n = 25)	0	0	4	96

A one-way ANOVA $(F(3,727)=17.89,p<.0001)$, warranted by evidence that with large samples parametric procedures are preferable to non-parametric even when data are skewed (Blanca et al., 2017; Fagerland, 2012; Vickers, 2005), confirmed a strong positive relationship between adaptivity and accuracy. That is, students with higher levels of adaptivity are significantly more accurate than students with low or no adaptivity. Moreover, the results of a Tukey’s HSD Post hoc test for multiple comparisons (Table 8) show that students’ mean accuracy increased from all lower to higher performing adaptivity group, and that these increases were significant between None and all higher levels of adaptivity and for low and high levels of adaptivity. In this respect, it can be seen, for example, that students with high levels of adaptivity score, on average, 2.45 points more in accuracy (max score = 9).

Table 8. Tukey Post hoc tests showing differences in mean accuracy score of the different adaptivity levels alongside tests of significance.

Levels of adaptivity	Difference in accuracy	t	p
None – Low	0.63 (0.18)	3.61	.002
None – Medium	1.10 (0.21)	5.18	<.0001
None – High	2.45 (0.43)	5.71	<.0001
Low – Medium	0.47 (0.22)	2.10	.154
Low – High	1.82 (0.44)	4.18	<.0001
Medium – High	1.35 (0.45)	2.99	.015

Table 9. Frequency (percentage) of students in each level of flexibility.

		731 students and 9 test items
		Items solved flexibly	Number of students (Percentage)	Mean accuracy as a percentage correctly solved items
Flexibility	None	0	173 (24)	59
	Low	1–2	150 (21)	67
	Medium	3–6	308 (42)	75
	High	7–9	100 (14)	83

3.2. Flexibility and accuracy

With respect to flexibility, as shown in Table 9, students were grouped according to the number of items they solved by means of more than one strategy, whether shortcut or standard algorithms. The figures indicate not only that more than half of all students (56%) demonstrate moderate or high levels of flexibility but that these figures are considerably higher than the corresponding figures for adaptivity shown in Table 5. That said, as with adaptivity, the general tendency is for accuracy to increase with flexibility. The figures of Table 10 show, confirmed by a one-way ANOVA (F(3,727) = 32.49, p < .0001), that increases in flexibility typically correspond to increases in accuracy. The exception lies with those students with no flexibility, whose accuracy is broadly equally distributed across the three higher levels of accuracy. In addition, the results of a Tukey’s HSD Post hoc test for multiple comparisons (Table 11) show that students’ mean accuracy increased across all possible pairings, from a lower to a higher-performing flexibility group, and that these increases were significant across all dyads with the exception of that between medium and high levels of flexibility, which marginally failed to register as significant. Indeed, the figures show that high flexibility student scored, on average, 2.19 points (on a 0–9 scale) higher in accuracy than the no flexibility students.

Table 10. Accuracy levels as a proportion of all students at each level of flexibility.

		ACCURACY
		LOW	MEDIUM LOW	MEDIUM HIGH	HIGH
FLEXIBILITY	None (n = 173)	12	28	27	33
	Low (n = 150)	9	16	27	48
	Medium (n = 308)	2	12	26	60
	High (n = 100)	1	7	16	76

Table 11. Tukey Post hoc tests showing differences in mean accuracy score of the different flexibility levels alongside tests of significance.

Levels of flexibility	Difference in accuracy	t	p
None – Low	0.72 (0.23)	3.21	.007
None – Medium	1.49 (0.19)	7.81	<.0001
None – High	2.19 (0.25)	8.63	<.0001
Low – Medium	0.77 (0.20)	3.85	.001
Low – High	1.46 (0.26)	5.62	<.0001
Medium – High	0.69 (0.23)	2.98	.016

3.3. The relationship between adaptivity and flexibility

While the data presented thus far show that both strategy adaptivity and strategy flexibility are implicated in student accuracy, it is important to consider which, if any, is the more influential. The figures of Table 12 show, for each adaptivity level, the percentage of students at each flexibility level. A chi square test (χ² = 64.57, p < .0001) confirms that such a distribution is unlikely to be due to chance. While there are some indications that high/low levels of adaptivity may equate to high/low levels of flexibility respectively, the overall picture is more complex. Across the two rows corresponding to low and medium adaptivity, the flexibility distributions are, to all practical purposes, identical. Also, regardless of their adaptivity levels, the proportion of students evaluated as having medium flexibility is higher than chance would have indicated. However, a one-way ANOVA indicates statistically significant different levels of flexibility across the adaptivity levels $F=(3,727)=17.30,p<.0001$. Indeed, the figures of Table 13 show, for each level of adaptivity, positive increases in flexibility (score 0–9). With one exception, the difference in flexibility from low to medium adaptivity, this positive difference was statistically significant. Overall, the mean flexibility score across all levels of adaptivity was 3.19 (SD = 2.79), highlighting the significance of the 3.39 flexibility difference between no adaptivity and high adaptivity students. In sum, confirming flexibility as a precursor to adaptivity, the figures indicate that higher levels of adaptivity appear related to higher levels of flexibility.

Table 12. Flexibility as a percentage of the students at each adaptivity level.

		FLEXIBILITY
		NONE	LOW	MEDIUM	HIGH
ADAPTIVITY	None (n = 331)	32	23	34	11
	Low (n = 242)	19	19	49	12
	Medium (n = 133)	15	19	49	17
	High (n = 25)	4	12	40	44

Table 13. Tukey Post hoc test showing differences in Flexibility (score 0–9) for different levels of adaptivity.

Levels of adaptivity	Difference in flexibility	t	p
None – Low	0.88 (0.23)	3.83	.001
None – Medium	1.20 (0.28)	4.32	<.0001
None – High	3.39 (0.56)	6.01	<.0001
Low – Medium	0.32 (0.29)	1.11	.683
Low – High	2.51 (0.57)	4.42	<.0001
Medium – High	2.19 (0.59)	3.71	.001

By way of contrast, the figures of Table 14 show, for each flexibility level, the percentage of students at each level of adaptivity. A chi square test (χ² = 30.26, p = .0004) confirms that the distribution is unlikely to be due to chance. For each level of flexibility, high proportions of students demonstrate low or no adaptivity. Indeed, two-thirds of high flexibility students were shown to have no or low adaptivity. Moreover, the proportions of students showing high levels of adaptivity, irrespective of their flexibility level, seem remarkably low. In other words, the figures of Table 14 suggest that flexibility has a limited predictive power with respect to adaptivity. That being said, a one-way ANOVA shows significant differences for adaptivity (0–9) across the different levels of flexibility$(F(3,727)=14.21,p<.0001)$. Indeed, the figures of Table 15 show, for each flexibility dyad a positive increase in adaptivity, which, in four cases was statistically significant. Overall, the mean adaptivity score across all levels of flexibility was just 1.39 (on a 0–9 scale), highlighting the significance of the 1.48 adaptivity difference between no flexibility and high flexibility students. In sum, the data suggest that access to multiple strategies is no guarantee that grade six students will either use shortcut strategies as a first choice or recognise them as optimal.

Table 14. Adaptivity as a percentage of the students at each level of flexibility.

		Adaptivity
		None	Low	Medium	High
Flexibility	None (n = 173)	61	27	12	1
	Low (n = 150)	50	31	17	2
	Medium (n = 308)	37	39	21	3
	High (n = 100)	36	30	23	11

Table 15. Post hoc Tukey test showing differences in adaptivity (score 0–9) for different levels of flexibility.

Levels of flexibility	Difference in adaptivity	t	p
None – Low	0.32 (0.21)	1.50	.441
None – Medium	0.67 (0.18)	3.76	.001
None – High	1.48 (0.24)	6.24	<.0001
Low – Medium	0.36 (0.19)	1.91	.224
Low – High	1.17 (0.24)	4.78	<.0001
Medium – High	0.80 (0.21)	3.71	.001

To investigate further the relationship between students’ flexibility and adaptivity, we examined those items that students identified as being solved optimally against when students first used a shortcut strategy. The figures of Table 16 show that when students’ first use of shortcut strategies was during phase 1, then 76% of optimal solutions identified in phase 3 were shortcut. By way of contrast, when students’ first use of shortcut strategies was during phase 2, then only 25% of optimal solutions identified in phase 3 were shortcut. Put another way, adaptive students, defined as those who introduce shortcut strategies in phase 1, are three times more likely to identify shortcut strategies as optimal than students who introduce shortcut strategies in phase 2.

Table 16. Percentage of students who, during phase 3, identified a shortcut strategy as the optimum in relation to when they first introduced a shortcut strategy.

When shortcut strategy first used	Percentage of shortcut solutions identified as optimum
Phase 1	76
Phase 2	25

3.4. Adaptivity, flexibility and the different operations

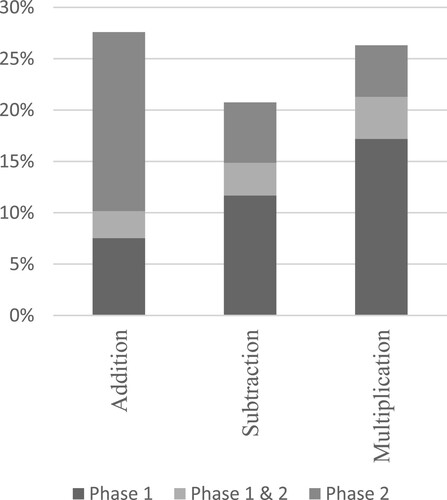
Figure 3 shows, for each operation, the percentage of phase 1 items solved by shortcut strategies (light grey), the percentage of phase 2 items solved only with shortcut strategies (dark grey) and the percentage of items solved with shortcut strategies in both phases 1 & 2 (mid-grey). It can be seen that while the use of solely shortcut strategies in both phases 1 and 2 is, in relative terms, rare, the proportion of phase-one items solved by shortcut strategies increases across the operations. Overall, confirming the generally low levels of adaptivity, the figures indicate a tendency for most students to invoke standard algorithms at some point.

Figure 3. Percentage of tasks solved uniquely by shortcut strategies at each phase of the study

Finally, Figure 4 shows the percentage of all items solved by more than one strategy, whether shortcut or not. It can be clearly seen that students demonstrate most flexibility when engaged in additive tasks, while their flexibility with respect to both subtraction and multiplication is, typically, around half that of addition. One interpretation, confirming the above, is that once standard algorithms become established, particularly with respect to subtraction and multiplication, students do not expect to engage with shortcut strategies, with the consequence that even when prompted, they may be unable to offer alternatives to the standard algorithms.

Figure 4. Flexibility by operation.

4. Discussion

In this paper, through an analysis of their use of shortcut strategies (Hickendorff, 2018; Torbeyns et al., 2009a, 2009b) and a novel application of a Tri-phase Flexibility Assessment (TriFA) (Xu et al., 2017), we have evaluated the strategy adaptivity and strategy flexibility of Danish grade six students with respect to multidigit arithmetic. Flexibility was defined as the ability to solve the same task by means of more than one strategy, while adaptivity depended on whether students’ first choice strategy or perception of which of their proposed strategies was optimal was shortcut. The multidigit arithmetic tasks used in the assessment were designed to elicit various forms of shortcut strategies based on particular task and operation characteristics. In the following, we discuss the outcomes of this study.

From the perspective of adaptivity, as measured by the number of items solved by means of shortcut strategies, the majority of students appeared limited. Indeed, more than three-quarters of the 731 participating students were assessed as possessing either low or no adaptivity. When set against a reform-oriented Danish curriculum that encourages the development of number-based strategies rather than standard algorithms (Ministry of Children and Education, 2019) these seem disappointingly problematic. The reasons for this apparent failure of Danish students to acquire the expected competences are not clear, although, acknowledging research internationally, it would not be surprising to find it due to instructional practices and parental interventions that privilege standard algorithms, as found in Flanders (Torbeyns & Verschaffel, 2013, 2016), France (Lemaire & Brun, 2017), Germany (Selter, 2001), Hungary (Csíkos 2016) and Italy (Lucangeli et al., 2003). However, such low proportions may not be as disappointing as the figures indicate. A similar free choice study of Dutch sixth grade students, who typically experience a European curriculum with an emphasis on number-based strategies, found students disinclined to use shortcut strategies, even when, as in the study reported here, tasks were chosen to elicit them (Hickendorff, 2018). In particular, she found, with respect to addition, subtraction and multiplication, an average of 12% of tasks solved by means of shortcut strategies, figures substantially less than the 22% represented above in Figure 3. That being said, highlighting the problematic nature of comparing the outcomes of different but conceptually similar studies, the lower figure found by Hickendorff may have been a consequence of the fact that only one-third of the addition, subtraction and multiplication tasks of her study were prefaced by an instruction to take a close look at the numbers and try to solve the task as cleverly as possible (Hickendorff, 2018, p. 583). Indeed, she found that such an instruction, which all students in our study received for all tasks, led to a significantly higher use of shortcut strategies on addition and multiplication but not subtraction. This subtraction-related lack of shortcut strategies, even when prompted, resonates well with the results of Figure 3, and may be a consequence of students’ familiarity and confidence with positive integer addition (and possibly multiplication) as a process of growth, where adding is joining, as opposed to subtraction construed as a process of separation or taking away (Bruno & Martinón, 1999).

That being said, perhaps the most important result concerning students’ adaptivity is its relationship to accuracy. The figures of Tables 5 and 7 show relatively high levels of accuracy across the different levels of adaptivity, although it is equally clear that accuracy increases with increasing adaptivity. Such findings seem to conflict with those of a Flemish study, albeit one focused solely on subtraction, that found no variation in strategy use across different attainment groups (Torbeyns et al., 2018). Importantly, the figures of Table 8 show quite clearly that adaptive students are significantly more likely to be accurate than non-adaptive students. Interestingly, while these findings resonate closely with a Finnish study that found adaptivity to be closely related to grade six students’ arithmetic fluency and knowledge of arithmetic concepts (McMullen et al., 2016), they conflict with those of Hickendorff (2018), who found no significant impact of shortcut strategy use on students’ multidigit arithmetic accuracy. Also, Hickendorff (2018) found consistently high levels of achievement.

Moreover, with potentially important developmental implications for Danish students, McMullen et al. (2017) found that that Finnish students’ adaptive number knowledge, even after taking into account arithmetic conceptual knowledge and arithmetic fluency, is a strong predictor of later pre-algebra skills.

From the perspective of flexibility, as measured by the number of items solved by means of two or more strategies, almost half of all students were assessed as having little or no flexibility. Such results are not dissimilar to studies conducted in Flanders, where grade-three students, even after exposure to teaching focused on informal strategies, rarely show flexibility in their solutions to multidigit subtraction problems (De Smedt et al., 2010). However, a German study found that grade-two students taught in ways that emphasise conceptual understanding alongside procedural skills become more flexible than students taught in ways the emphasis only procedural skills. Indeed, in accordance with our definition of flexibility, conceptually-based instruction enabled most students (84% with respect to addition and 62% with respect to subtraction) to offer two solutions to each task (Blöte et al., 2001). Unfortunately, many studies nominally addressing strategy flexibility conflate flexibility and adaptivity, making comparisons problematic (see, for example, Nunes et al., 2020). That being said, the relatively low levels of strategy flexibility identified above resonate with studies of students’ equation-solving flexibility, whether at grade eight (Schneider et al., 2011), grade nine (Newton et al., 2010) or grade eleven (Hästö et al., 2019). In other words, strategy flexibility is poorly manifested both internationally and across topics, further confirming the tendency for students, having learnt standard algorithms, to reject or ignore alternatives (Csíkos, 2016; Hickendorff, 2020; Lemaire & Brun, 2017; Lucangeli et al., 2003; Selter, 2001; Torbeyns & Verschaffel, 2013, 2016).

Furthermore, although the data indicate that flexibility is implicated in accuracy, the relationship is less robust than that between adaptivity and accuracy. Indeed, the results accord well with those of a TriFA-related study of Finnish grade eleven students’ strategy flexibility with respect to linear equations, whereby a ‘“triangle” type relation between accuracy and flexibility’ was found with, essentially, ‘no students with high flexibility and low accuracy’ but some ‘with low flexibility but high accuracy’ (Hästö et al., 2019, p. 5).

Overall, the results indicate that the relationship between flexibility and adaptivity is complex. Indeed, while it seems clear that adaptive students are typically flexible, the reverse cannot be said with the same degree of confidence; flexible students are not typically adaptive. Such findings, which resonate with an earlier study, whereby equation-solving experts were consistently able to exhibit strategy flexibility but were inconsistent in their selection of the most efficient strategy (Star & Newton, 2009), challenge earlier assertions that flexibility can be seen as a precondition for adaptivity (Verschaffel et al., 2007). The findings also confirm earlier research that exposure to standard algorithms tends to limit students’ ability to trust alternative, number-based, shortcut strategies. Indeed, students whose preferred strategy is shortcut are more able to make judgements about strategy appropriateness than students whose first strategy is not shortcut. Further, the evidence indicates that adaptivity is a stronger predictor of accuracy than flexibility, highlighting the importance of adaptivity as an educational objective (Baroody, 2003; Hickendorff, 2018; Xu et al., 2017).

Finally, as found in earlier studies, strategy choice is strongly dependent on the operation (Torbeyns et al., 2009b). For example, irrespective of whether their preferred strategy was shortcut, when considering alternative approaches, students were not only more able to offer shortcut strategies for additive than either subtractive or multiplicative tasks but that additive tasks prompted the greatest flexibility. Interestingly, while multiplicative tasks yielded the highest proportion of preferred shortcut strategies, relatively few students were able to offer a second shortcut strategy. Finally, subtraction seemed to limit students’ use of shortcut strategies more than either addition or multiplication. As above, such findings confirm that once standard algorithms become established, particularly with respect to subtraction, students do not expect to engage with shortcut strategies, with the consequence that even when prompted, they may be unable to offer alternatives to the standard algorithms. In sum, we hypothesis that students’ decisions with respect to their preferred strategies are influenced not only by what they have been taught (Csíkos, 2016; Hickendorff, 2020; Lemaire & Brun, 2017; Lucangeli et al., 2003; Selter, 2001; Torbeyns & Verschaffel, 2013, 2016) but, importantly, by what they have been led to trust and internalise as desirable.

5. Reflections on method

In this paper, with respect to multidigit arithmetic, we have investigated the relationship between the strategy adaptivity, strategy flexibility and solution accuracy of Danish grade six students. In so doing, we have successfully exploited a novel adaptation of a Tri-phase Flexibility Assessment model (TriFA) previously used to uncover students’ strategy use when solving linear equations (Xu et al., 2017), and for the reasons outlined below, would recommend similar adaptations to colleagues working in different content domains.

We have shown the adapted TriFa to be a simple and quick to implement diagnostic tool suitable for assessing large numbers of students in an unthreatening and familiar environment. Each phase of the assessment offers unique insights into students’ strategy choices that can be examined and reported at both individual and class levels, as well as facilitating the planning of didactical activities. Phase one offers insights into what strategies students choose to use, with those turning to shortcut strategies being defined as adaptive. Phase two offers insights into students’ strategy repertoires and whether they can be defined as flexible. Finally, phase three offers insights into when, if ever, students identify shortcut strategies as optimal.

We have shown that by not restricting students’ strategy choice or privileging speed has facilitated our identifying an important distinction between adaptivity and flexibility (Rathgeb-Schnierer & Green, 2017). Indeed, moving beyond studies that construe flexibility and adaptivity as synonyms (Baroody, 2003; Hickendorff, 2018) or those that see adaptivity as a component of flexibility (Blöte et al., 2000; Rathgeb-Schnierer & Green, 2017; Schneider et al., 2011; Star & Rittle-Johnson, 2008), we have shown that the TriFA has facilitated a nuanced understanding not only of the interrelationship of flexibility and adaptivity but also their differential impact on accuracy. We have shown how the TriFa has yielded results that both resonate and contrast with studies undertaken elsewhere, particularly in culturally comparable European contexts, confirming that students’ strategy choices are influenced by cultural norms and expectations (Hatano & Inagaki, 1986; Lin et al., 2007), particularly systemic decisions concerning the introduction of standard algorithms (Csíkos, 2016; De Smedt et al., 2010; Hickendorff, 2020; Lemaire & Brun, 2017; Lucangeli et al., 2003; Nemeth et al., 2019; Torbeyns & Verschaffel, 2016), and importantly, researchers’ methodologies; choice/no choice studies typically yield different results from free-choice and confirm the significance of our novel methodology.

Overall, the TriFA has proved a powerful tool in support of our quest to understand students’ arithmetic task-related strategy choices, albeit at just one grade level, and the relationship of those choices to accuracy. Also, by way of a pointer towards future research, there remains a question that has yet to be addressed adequately; why, even in contexts like Denmark and the Netherlands, where national curricula privilege informal strategies above standard algorithms, do students reject efficient number-based shortcut strategies? Is the teaching of shortcut strategies, as implied by Torbeyns et al. (2009a), simply not feasible? Is it a consequence, as implied by Skott (2004), of loosely-framed curricula leading to a plethora of didactical approaches, each unique to the individual teacher? Elsewhere in Scandinavia, researchers have identified commonly articulated but differently enacted strategies (Andrews & Larson, 2017; Andrews & Nosrati, 2018), but in the context of Denmark, little is known about how teachers present mathematics to their students, a problem in need of resolution.

Finally, we close by inviting teachers to reflect on how they choose the tasks they present their students. Do the textbooks they use encourage the learning of shortcut strategies or subordinate them to standard algorithms? If the latter, what alternative resources do teachers have available to them? Have their teacher education programmes provided them with the skills to adapt tasks, like those used in this study, in ways that will facilitate students recognising the number relationships that simplify what they choose to do?

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by Danmarks Frie Forskningsfond [grant number #9038-00045B.].