Examining primary school educators' preferences for using digital versus non-digital games to support mathematics instruction

Abstract

Both digital and non-digital games have been shown to be effective for supporting student engagement in mathematics. However, little is known about educator preferences for a particular game mode (i.e. digital versus non-digital), and what factors influence these preferences. To address this gap, 111 Australian primary school educators completed a questionnaire reporting on their usage of, and preferences for using, digital compared with non-digital games to support mathematics instruction. Participants were considerably more likely to use non-digital games than digital games in their classrooms, and the majority indicated a clear preference for using non-digital games. Thematic analysis revealed several themes that explained why many participants preferred non-digital games, with the most frequently coded theme being for pedagogical reasons such as: that they were better for promoting collaboration and communication; that they afforded opportunities for students to use manipulatives; and that they were easily adapted and differentiated for specific groups of students. Other notable themes included: assessment, in particular, the perception that when students played non-digital games it was easier to observe their understanding; access to, and limited awareness of, suitable digital resources; and managing the setup and delivery of the game. Implications of the findings are discussed.

KEYWORDS:

• Primary education
• mathematics education
• game-based learning
• digital games
• non-digital games
• teacher perspectives

1. Introduction

Game-based learning (GBL) has received substantial interest from education researchers and practitioners (Ariffin et al., 2014). In mathematics education, this interest has at least partially stemmed from a desire to make mathematics education more engaging for students. Previous research has shown that students become less interested in learning mathematics and more likely to dislike mathematics as they progress through schooling (Thomson et al., 2017). However, learning mathematics through game play has been identified as engaging and motivational for learning (Bragg, 2003, 2006b; Bright et al., 1985; White & McCoy, 2019).

Studies focused on the efficacy of educational games in mathematics generally focus on one mode of game, either digital or non-digital, and have compared games in this particular mode with non-game activities or traditional instruction (e.g. Abdullah et al., 2012; Bragg, 2012; Kamii et al., 2005; Miller & Robertson, 2011). Moreover, whereas much of the research into mathematical games has focused on the impact of games on student academic outcomes and affect, far fewer studies are concerned with how teachers choose to use games to support mathematics instruction (Russo et al., 2021). Consequently, there are gaps in the research literature, both in terms of studies that directly compare digital and non-digital games in mathematics education, as well as those that consider specifically how and why teachers choose to use games. The current study endeavours to address these gaps by examining primary school educators’ preferences for using digital compared to non-digital games to support mathematics instruction, and their reasons for holding these preferences.

1.1. Defining games

A game can be defined as

an activity often classified as fun, governed by precise rules that involve varying degrees of strategy or chance, and one or more players who cooperate or compete (with self, the game, one another, or a computer) through the use of knowledge or skill in an attempt to reach a specified goal. (Jaffe, 2019, p. 300)

Jaffe (2019) categorised games into three genres: Games, Simulations and Simulation Games. Games included both non-digital (e.g. board and card games), and digital games. Furthermore, educational games ‘are believed to provide learning benefits that last beyond the game for all participants’ (p. 300). Similarly, Talan et al.’s (2020) definition takes a broad view of GBL that includes any instructional activity specific to teaching mathematics based on the use of games, whether they are conducted traditionally (non-digital classroom games) or via digital technology (computers, consoles, tablets, etc.). In contrast, Gough’s (1999) definition of games does not include students playing a game on their own. He suggests, ‘a game needs to have two or more players, who take turns, each competing to achieve a “winning” situation of some kind, each able to exercise some choice about how to move at any time through the playing’ (p. 12). The view of games adopted in the current study aligns with these definitions, and includes both digital and non-digital games, played in pairs, small groups or teams, or as a large group. Moreover, our study focused on educational games; specifically, games that might be used by teachers to support mathematics learning and instruction in the primary mathematics classroom.

1.2. Affordances of non-digital games

As noted earlier, much of the literature involving the use of games in the primary mathematics classroom has investigated student outcomes related to playing non-digital games, with fewer studies focused on how and why teachers use such games. In particular, studies have shown that non-digital GBL in mathematics education improves achievement in mathematics knowledge and skills (Asplin et al., 2006; Bragg, 2006a: Bright et al., 1983; Ramani & Siegler, 2008; White & McCoy, 2019); including for low-performing students (Kamii et al., 2005; Karnes et al., 2021). For example, Bragg (2006a) reported that 9–12-year-old students started to question their own misconceptions in relation to multiplication and division of decimals through playing Guestimate (Swan, 1996). Students were required to estimate the result of multiplying some ‘messy’ number that usually included a decimal portion with another number (often less than one). The game playing helped students to wrestle with a common misconception that multiplication always makes the number bigger (McIntosh et al., 1997). In another example, the findings of Asplin et al. (2006) showed that the mental computation knowledge and skills of Grade 6 students could be improved by playing a commercial card game (Numero) four times a week for ten weeks.

Furthermore, playing mathematical card games beyond the classroom in the home environment has been shown to improve students’ achievement. For example, Casey et al. (2020) revealed that the addition accuracy of 6–7-year-old students in the United States improved after playing informal card games at home with their mother. Indeed, the results from the Trends in International Mathematics and Science Study, involving over 60 countries, reported that children who frequently played card or number games at home had higher than average mathematics achievement (Mullis et al., 2012).

Beyond improved mathematics understanding and achievement, playing non-digital games has been associated with a number of other benefits. Specifically, it has been shown that playing non-digital mathematical games can: reduce anxiety in learning mathematics (Alanazi, 2020); increase students’ growth mindset (White & McCoy, 2019); and encourage active learning, cooperation, and interactivity (Ernest, 1986). Game play has also been shown to improve students’ use of mathematical vocabulary (Andayani et al., 2022) and increase students’ proficiency with mathematical reasoning (McFeetors & Palfy, 2018). Moreover, Bragg (2012) found that playing mathematical games was associated with an increase in the time students spent discussing mathematics whilst engaging with a task, which is of particular significance given the importance of discourse for supporting mathematics learning (Hiebert & Wearne, 1993; Seegar, 2001; Sfard, 2001). Moreover, in the same study, Bragg (2012) also found that playing games helped to maximise students’ time-on-task. Specifically, it was reported that students spent 93% of class-time exhibiting on-task behaviours when playing games, compared with 72% of the time when participating in other mathematically rich, non-game activities. Given that student engagement is a multifaceted construct with behavioural, cognitive, and affective components (Skinner, 2016), Bragg’s findings in relation to mathematical discourse (representing cognitive engagement) and time-on-task (representing behavioural engagement) are particularly notable. They suggest that the capacity of games to engage students goes beyond the well-established notion that games promote affective engagement through being perceived as fun and enjoyable to play (Russo et al., 2023).

1.3. Affordances of digital games

Studies into the use of digital games in mathematics instruction in the primary grades have found that many of the cognitive and affective outcomes for students are similar to those for non-digital games. For example, Abdullah et al. (2012) reported that the use of computer-based video games that supplement conventional teaching had a significant effect on retention and mastery of multiplication tables of Year 3 students, compared with those who only received the conventional instruction. Similarly, Miller and Robertson (2011), utilising a randomised control trial design, showed that primary students (aged 10–11-year-old) in the experimental group had 50% greater gains in accuracy, and twice the gain in speed of mental calculation skills, compared with students in the control group. The students in the experimental group used a commercial off-the-shelf computer game, whilst the control group continued their normal classroom routines. Additionally, Miller and Robertson found that students in the digital games group reported a small but significant improvement in attitude towards school compared with the control group. Employing a quasi-experimental approach, Hung et al. (2014) reported that digital GBL improved fifth grade students learning about symmetry, promoted their self-efficacy, and enhanced their motivation to engage with mathematics, compared with students in the control group who received teacher-directed instruction. They also reported a decrease in mathematics anxiety between the pre- and post-questionnaires for both the digital GBL group and the e-learning group, which was not apparent in the control group.

Focussing on studies published between 2015 and 2020, Barz et al. (2023) conducted a meta-analysis on the effect of digital GBL on cognitive, metacognitive, and affective-motivational learning outcomes, compared with traditional teaching methods. While the meta-analysis did not solely focus on mathematics content, and included both primary and secondary school students, the findings indicated that there was a medium effect for both overall learning and cognitive learning and a small effect for affective-motivational learning outcomes. However, there was no significant effect of digital GBL on metacognitive learning outcomes.

1.4. Comparing the affordances of digital and non-digital games

The studies discussed thus far have generally focused on either digital or non-digital games, while some have compared the impact of one or the other against traditional teaching or non-GBL approaches. We have identified no studies that directly compared the effectiveness of using digital and non-digital games for teaching mathematics in the primary years. The closest we could find to illuminating this issue was conducted by Talan et al. (2020).

Talan et al.’s (2020) meta-analysis incorporated 154 empirical studies undertaken between 2004 and 2019, and was focused on evaluating the effects of playing digital and non-digital educational games on student achievement. The studies included students of all ages (preschool through to university) and a range of school subjects (e.g. science, mathematics, foreign languages). Overall, the findings indicated that educational games, when considered collectively, had a medium positive effect on academic achievement. However, Talan et al. reported that when measuring academic achievement the effect size was higher for interventions employing non-digital games compared with digital games. The authors cautioned that this does not negate the many studies that show the merit of digital games and noted the dramatic improvement in gaming technology in recent decades.

As a further commentary on the implications of Talan et al.’s (2020) findings for our current study, it is noteworthy that the seven studies included in the meta-analysis that focused on the impact of non-digital games on mathematics achievement in a primary education context were all unpublished Masters or Doctoral theses; whereas seven out of the twelve studies focused on digital games in the equivalent context were published in peer-reviewed journals. To the extent that these different sources can serve as a proxy for study quality and methodological rigour, it makes comparison between the impact of different game modes problematic. Indeed, the tendency for many of the intervention-type studies in primary mathematics education that incorporate non-digital games to remain as unpublished theses also explains the relative absence of such studies from similar systematic reviews and meta-analyses that have used stricter inclusion criteria (e.g. Abdul Jabbar & Felicia, 2015).

When comparing digital and non-digital games more generally, we note that, despite the many similarities in outcomes, there are at least two discrete differences worth considering. Non-digital games can incorporate physical activity, sometimes outside the classroom (Bahrami et al., 2012; Cichy et al., 2020), which is generally not the case when technology is involved. By contrast, digital games differ from non-digital games in that they unfold in an interface principally ‘regarded as an entertainment medium’ (Cojocariu & Boghian, 2014, p. 641), whereas non-digital games often repurpose resources and representations designed for educational ends as game objects (e.g. calculators, Bragg, 2006a; fraction walls, Clarke & Roche, 2010; number charts, Russo, 2018; number lines, Bofferding, 2014). Framed in this manner, designing and implementing digital games for the purpose of teaching mathematics might be captured by the phrase making entertainment educational, whereas for non-digital games, it is perhaps making education entertaining. This of course does not negate the notion that both digital and non-digital games can be enjoyable and promote positive emotions.

Beyond primary mathematics education in particular, a small number of studies have directly compared the student experience when engaging with digital and non-digital versions of a particular game. For example, Fang et al. (2016) investigated students’ preference for a board game (Monopoly) and Jenga when each is played in its physical table format compared with two digital formats (on a desktop computer and on a tablet). Students reported greater satisfaction with, and a visceral preference for (attraction to form, texture and colour), games when played in their physical table format over either of the technological interfaces. The physical table format was also more conducive to social interaction. Collectively these findings led Fang et al. to conclude that students valued the more ‘tangible’ experiences offered through a physical table game.

These preferences for more tangible, physical experiences revealed in the Fang et al. (2016) study may overlap with the benefits of using tactile materials or manipulatives in primary school classrooms. For example, researchers and educators have reported that incorporating concrete manipulatives improves student knowledge, engagement, and enjoyment in learning mathematics (Roche et al., 2023; Swan & Marshall, 2010; Vessonen et al., 2021). Indeed, a survey conducted by Swan and Marshall (2010) confirmed that teachers strongly supported the use of manipulatives, especially in the early primary grades. For example, 83% and 48% of teachers indicated they used manipulatives daily in Foundation and Year 1, respectively. However, this dropped to 9% in Year 6.

1.5. Virtual and physical manipulatives

Moyer (2001) noted that physical manipulatives have become popular in the mathematics classroom, in part because it has been argued, by both researchers and theorists (e.g. Piaget, 1952), that multiple representations or ‘embodiments’ of a concept support students’ understanding. Moreover, manipulatives in particular are valued by mathematics educators because they have both visual and tactile appeal for students, can make learning more enjoyable for both teachers and learners, and serve to promote image making that can be used when mentally manipulating abstract ideas (Moyer, 2001). Skemp (1987) theorised that students’ experiences with physical objects form the basis of later abstract thinking, whilst Stein and Bovalino (2001) argued that manipulatives such as pattern blocks, tiles, and cubes ‘contribute to the development of well-rounded, interconnected understandings of mathematical ideas’ (p. 1). Physical manipulatives may also enhance mathematical communication opportunities. For instance, Kosko and Wilkins (2010) have shown there is a positive correlation between how often a child is observed discussing mathematics problems with other children, and how often they are observed working with manipulatives. This seems an important finding, given what is known about the importance of student mathematical discourse to support mathematical learning (Stein et al., 2008).

However, Moyer (2001) also reported that the teachers in their study viewed manipulatives as ‘fun’ but not necessarily useful for teaching and learning mathematics. Furthermore, Stein and Bovalino (2001) also cautioned that, rather than allowing students to construct mathematical meaning through the manipulative, that manipulatives can instead be used in a mechanical or teacher directed way, thereby supporting procedural learning without the associated conceptual understanding. The key implication that can be drawn from the literature is that manipulatives have the potential to support students’ learning and development in mathematics, provided they are used appropriately.

Interestingly, Larkin (2016) suggested that ‘when concrete materials become digitised, their usefulness may diminish as they become distanced from the concrete nature of the resource; thus limiting their ability to be enacted by students’ (p. 15). Additionally, Swan and Marshall (2010) advocated for the delay in the introduction of virtual manipulatives until students have had experience with the ‘real thing’ (p. 14). The authors noted from their classroom observations that younger children had difficulty understanding a two-dimensional representation of a three-dimensional object, and that when objects are displayed on an interactive whiteboard the students do not have access to the objects.

In contrast to these views, some researchers and educators have reported that the introduction of virtual manipulatives into primary schools led to gains in mathematics achievement, time-on-task, motivation, and/ or enjoyment of mathematics learning (Baturo et al., 2003; Steen, 2006). Indeed, Moyer-Packenham and Westenskow (2013) conducted a meta-analysis synthesising the findings of 66 research articles and concluded that virtual manipulatives used in the teaching of mathematics have the potential to promote learning and engagement. The effect size varied across grade levels, with virtual manipulatives being associated with large effects in Grades 9–12 and at University-level, a moderate effect at Preschool to Grade 4, a small effect in Grades 5–6, and no effect in Grades 7–8.

To conclude this section, it is worth noting that any framing of virtual and physical manipulatives as being an either/ or choice is of course overly simplistic. For example, a study by Doias (2013) indicated that combining the use of concrete and virtual manipulatives showed measurable improvements in mathematics that surpassed that of using concrete manipulatives alone.

1.6. Teacher preferences for game use and barriers inhibiting their use

Mathematical games are commonly used in Australian primary schools to support mathematics teaching and learning (Russo et al., 2021; Russo & Russo, 2020). Russo et al. (2021) surveyed 248 primary teachers across all the primary years (Foundation to Year 6) and found that 79% of teachers reported playing mathematics games more than once a week. Moreover, recent research by the same authors has shed light on the characteristics of games that primary teachers and other mathematics leaders and educators consider educationally valuable. Specifically, they value games that are ‘suitably challenging, engaging, enjoyable, modifiable to support different learners, and transformable into an investigation or broader mathematical inquiry’ (Russo et al., 2023, p. 1). Importantly from the perspective of the current study, Russo et al. (2021) also revealed that, when asked to describe their favourite mathematical game, teachers preferred games that required minimal or no materials (e.g. cards, dice games, pen and paper), with only 4% of teachers mentioning a game involving any form of interaction with digital technology (e.g. calculators, interactive number charts), and only 1% specifically choosing a digital game.

Teachers’ motivation to incorporate digital games and the associated technologies may be influenced by their beliefs about the potential effectiveness of using technology for learning more generally (Ertmer et al., 2012). Stieler-Hunt and Jones (2015) investigated the reasons why some primary and secondary teachers in Australia embraced the use of digital GBL. The results indicated that the positive beliefs that teachers held regarding the use of digital GBL stemmed from experiencing success with their use in the classroom, personal experiences with digital GBL, and exposure to information that promoted the use of digital GBL. Furthermore, these teachers tended to hold positive attitudes towards information and communication technologies (ICT) more generally and had been invited to use ICT by someone in authority. They also felt that using digital GBL set them apart from other teachers. However, Stieler-Hunt and Jones (2017) also reported that teachers who are advocates for digital GBL sometimes felt resentment from colleagues, curriculum concerns, and that there was insufficient advocacy or acceptance of digital GBL at the school level. Classroom concerns included: the difficulty in finding links between curriculum and digital games; the fear of ‘losing control’ of the class; as well as the logistics of managing game use.

However, not all teachers are positive about the use of technology and its benefits for learning. Ertmer (1999) identified two types of barriers that impact on whether teachers’ use technology in the classroom. These were described as external barriers and internal barriers. External barriers included resources (hardware and software), training, and support. Internal barriers were defined as teachers’ confidence, beliefs about how students learned, and the value of technology for teaching and learning. In relation to the value of technology, Cabellos et al. (2023) reported that primary preservice teachers perceived that the use of video games in education (though not specifically mathematics) was less likely to promote learning than secondary teachers. Furthermore, Kaimara et al. (2021) reported that a major obstacle to pre-service teachers adopting digital GBL was the lack of availability of resources such as devices and software, and the lack of relevant training for teachers, school administrators, and policy makers.

Given the reluctance of some teachers to embrace digital game-play to support learning, some researchers have advocated for professional learning in this area (Chee et al., 2015; Cojocariu & Boghian, 2014; Meletiou-Mavrotheris & Prodromou, 2016). Chee et al. (2015) argued for professional support to maximise potential learning from digital games, while Cojocariu and Boghian (2014) proposed that primary teachers should be taught the relevance of GBL and appropriate methods and techniques to include them during instruction. In support of these ideas, Meletiou-Mavrotheris and Prodromou (2016) found that pre-service teachers had more positive perceptions of digital GBL and felt more competent to select, evaluate, and utilise digital games as an instructional tool, after participating in an instructional intervention focused on the knowledge, skills, and experience needed to integrate educational games into the mathematics curriculum.

Given the prevalence in which Australian primary teachers use mathematical games, and despite the evidence being ambiguous about the relative merits of digital versus non-digital games, the current study sought to investigate primary school educators’ preferences for utilising each particular game mode (digital vs non-digital) to support mathematics instruction. In addition, we also considered if educators’ preferences are moderated by the size of the group that they intend to use a game with (whole-class vs small-group), and their beliefs about the relative affordances of each game mode.

The research questions guiding this study included:

• To what extent do primary school educators have game mode preferences (digital vs non-digital) when using games to support mathematics learning?

• To what extent does game structure (whole-class vs small-group) moderate primary school educators’ game mode preferences (digital vs non-digital) when using games to support mathematics learning?

• What are the relative affordances of digital games compared with non-digital games for supporting mathematics learning according to primary school educators?

2. Methodology

2.1. Data collection

An anonymous online questionnaire was used to collect insights about educators’ preferences for the use of digital and non-digital games using Qualtrics.¹ Snowball sampling was employed to ensure the questionnaire’s widespread distribution. Specifically, the first author dispatched the questionnaire link via email to 15 contacts situated across the three largest Australian states (Victoria, New South Wales and Queensland). Additionally, social media platforms were harnessed to engage participants directly. The questionnaire was in the field for three months (1st June 2023 – 31st August 2023). The sole requisite for inclusion in the resultant analysis was that the respondent was a classroom teacher, specialist teacher, or instructional leader currently working in an Australian primary school, and that they had completed all relevant quantitative items from the questionnaire (see below). One-hundred and twenty respondents completed all relevant parts of the questionnaire, with nine of these individuals being subsequently excluded because they resided outside of Australia, were not currently teachers, or taught at a secondary or tertiary level only. This resulted in 111 study participants.

The questionnaire included demographic information (current role and years of teaching experience), quantitative items (Likert scale items and items requiring a quantitative response), and qualitative items (open response items). The quantitative and qualitative items reported on in the current paper were divided into two sections, those items covering whole-class mathematical games and small-group mathematical games. These items are described below.

2.1.1. Whole-class mathematical games²

1a) Out of every 100 mathematics lessons you teach, about how frequently do you play a whole-class mathematical game? (Quant; Accepted response range 0 to 100)

1b) What is your favourite whole-class mathematical game to use in the classroom? (Qual)

2a) Out of every 100 mathematics lessons you teach, about how frequently do you play a whole-class digital mathematical game? (e.g. a game from a website or app projected onto an electronic whiteboard) (Quant; Accepted response range 0 to 100)

2b) Out of every 100 mathematics lessons you teach, about how frequently do you play a whole-class non-digital mathematical game? (e.g. a game using only whiteboards, pen/ paper, oral language) (Quant; Accepted response range 0 to 100)

3a) Overall, do you prefer to use digital or non-digital whole-class mathematical games? (Quant) (Strongly prefer digital games – 1; Somewhat prefer digital games – 2; Neutral – 3; Somewhat prefer non-digital games – 4; Strongly prefer non-digital games – 5).

3b) Please explain your preference (Qual)

2.1.2. Small-group mathematical games³

4a) Out of every 100 mathematics lessons you teach, about how frequently do you play small-group mathematical games? (Quant; Accepted response range 0 to 100)

4b) What is your favourite small-group mathematical game to use in the classroom? (Qual)

5a) Out of every 100 mathematics lessons you teach, about how frequently do your students play small-group digital mathematical games? (e.g. a game from a website or app that students play on a device) (Quant; Accepted response range 0 to 100)

5b) Out of every 100 mathematics lessons you teach, about how frequently do your students play small-group non-digital mathematical games? (e.g. a game using only whiteboards, pen/ paper, oral language) (Quant; Accepted response range 0 to 100)

6a) Overall, do you prefer to use digital or non-digital small-group mathematical games? (Quant)

6b) Please explain your preference (Qual)

All participants were working in primary schools in Australia. Participants were comparatively experienced teachers on average, with a mean of 14.1 years teaching experience (SD = 8.0 years; Median = 12 years) in a school setting. Most participants were current classroom teachers (n = 81; 73%), with many teaching multiple year levels and some with an additional leadership or specialist role.

2.2. Data analysis

2.2.1. Quantitative items

Quantitative analysis was undertaken with the support of SPSS Statistics, v. 26. Descriptive statistics are presented and differences between participant preferences and usage of digital and non-digital games are explored. In terms of our inferential analysis, when comparing participant preferences for non-digital versus digital games across settings (whole-class versus small-group), paired-samples t-tests and independent-samples t-tests were used, as all relevant statistical assumptions were met. By contrast, as participant reported usage of digital games was strongly positively skewed, and therefore a normal distribution could not be assumed, Wilcoxon signed-rank tests and spearman rank-order correlations were instead employed for this analysis.

2.2.2. Qualitative items

Initially, educators’ open responses that explained their preference of mode for small-group games or whole-class games were sorted between those that indicated they preferred digital games, non-digital games, or were neutral. The written explanations for their choice of game mode were then analysed using qualitative line-by-line coding as outlined by Braun and Clarke (2006). The following stages were conducted: (1) familiarisation with the data, (2) generating initial codes, (3) searching for themes, (4) reviewing themes, (5) defining and naming themes, and (6) producing a report and coding framework. Initially, sub-themes were identified that sought to explain the reasons for educators’ preferences for mode of game (digital and non-digital) for each of the two group settings when playing games (small-groups and whole-class). In most cases, the responses were coded holistically to a specific sub-theme to maintain context (Bazeley, 2007), and most responses were assigned to one sub-theme (63% and 61%, for questions 3b and 6b, respectively). However, some responses were coded to more than one sub-theme as appropriate. For example, the response for Participant #84 was assigned two sub-themes. The participant wrote: ‘I value student talk, collaboration and seeing their thinking’, and this was assigned to Better for promoting collaboration, interactions, and communication, as well as Easier to observe students’ understanding. The mean number of sub-themes to which educators’ responses were coded was 1.3 and 1.2 for questions 3b and 6b, respectively. The final stage in the analytical process involved grouping the emergent sub-themes into seven main themes. The coding framework and percentages of educators coded to each theme and sub-theme are presented in Tables 6 and 7 in the Results section.

3. Results: quantitative analysis

3.1. Comparing frequency of game use across game mode

Primary school educators typically used both whole-class games and small-group games during the majority of their mathematics lessons, with the median participant reporting that they used games in each of these settings in three out of every five lessons (see Table 1). Importantly from our perspective in the current study, participants were far more likely to report using non-digital games than digital games. Specifically, comparing the median responses using a series of Wilcoxon signed-rank tests, participants reported using non-digital games approximately three times as frequently in a whole-class setting (Z = 6.463, p < .001, r = .61). and five times as frequently in a small-group setting (Z = 7.555, p < .001, r = .72). Moreover, whilst there was no statistically significant difference in how frequently participants used non-digital games across settings (Z = 1.498, p = .134), again comparing the median responses revealed that participants were approximately twice as likely to report using digital games with the whole-class than in small-groups (Z = 4.274, p < .001, r = .41).

Table 1. Percentage of lessons in which participants reported playing games by setting by game mode.

	Median	Q1	Q3	Min	Max
Whole-Class Games: Overall	63%	31%	80%	9%	100%
Whole-Class Games: Digital	20%	10%	40%	0%	95%
Whole-Class Games: Non-Digital	51%	22%	79%	6%	100%
Small-Group Games: Overall	60%	30%	78%	0%	100%
Small-Group Games: Digital	11%	3%	25%	0%	100%
Small-Group Games: Non-Digital	60%	30%	80%	0%	100%

Finally, Table 2 reveals that whilst there were no significant correlations between participants’ level of teaching experience and their tendency to use games, upper primary school teachers were somewhat more likely to use digital games in a small-group setting than their lower primary school counterparts.

Table 2. Spearman correlation coefficients by setting by game mode: teaching experience and year level taught.

	Teaching experience (years)	Year level taught
Whole-Class Games: Overall	.14	.03
Whole-Class Games: Digital	–.02	.11
Whole-Class Games: Non-Digital	.08	.01
Small-Group Games: Overall	.03	–.10
Small-Group Games: Digital	–.01	.27*
Small-Group Games: Non-Digital	.04	–.10

*p = .017.

3.2. Examining participant preferences for non-digital games

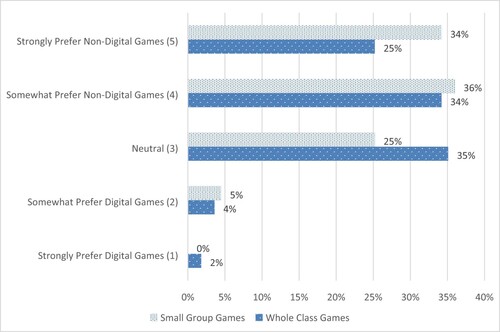
Consistent with our finding that primary school educators used non-digital games more frequently than digital games, participants had, on average, a clear preference for using non-digital games over digital games in both whole-class (M = 3.77, SD = 0.93) and small-group settings (M = 4.00, SD = 0.88), with the median response for both settings being ‘somewhat prefer non-digital games (4)’. Figure 1 indicates that approximately 60% to 70% of participants preferred using non-digital games, whereas only around 5% of participants preferred digital games. However, closer analysis does reveal a notable difference in preferences across setting. Specifically, comparison of mean game mode preference scores using a paired samples t-test indicates that educators were somewhat more likely to prefer non-digital games for use in small-group settings relative to whole-class settings, t(110) = 3.23, p = .002, d = 0.31; although perhaps unsurprisingly participant preferences across settings were also strongly correlated (r = .67, p < .001).

Figure 1. Participant preferences for non-digital versus digital games by setting.

Table 3 compares mean game mode preference scores for those participants with more than 10 years teaching experience with those who have 10 or less years teaching experience. Results of an independent-samples t-test reveal that more experienced educators had stronger preferences for using non-digital games compared with their less experienced counterparts, and this was the case for using games in both whole-class settings (t(109) = 2.23, p = .023, d = 0.44) and small-group settings (t(109) = 3.19, p = .002, d = 0.60). More generally, teaching experience was weakly-to-moderately correlated with a preference for non-digital games (whole-class, r = 0.27, p = .005; small-group, r = 0.30, p = .001).

Table 3. Mean game mode preference scores by setting by experience level.

	Mean	SD	N
Whole-Class Games: Overall	3.77	0.93	111
More than 10 years experience	3.94	0.82	66
10 or less years experience	3.53	1.04	45
Small-Group Games: Overall	4.00	0.88	111
More than 10 years experience	4.21	0.76	66
10 or less years experience	3.69	0.97	45

Note: A mean score above 3 indicates an average preference for non-digital games over digital games, with a higher score indicating a stronger preference.

Table 4 displays mean game mode preference scores for the subset of participants (n = 78) who were current classroom teachers and exclusively taught in either lower primary (Foundation to Year 2) or upper primary (Year 3 to Year 6) to establish whether year level taught impacted on teachers’ relative preference for non-digital games. Independent-sample t-tests indicate that participants who currently taught in the lower primary year levels were more likely to prefer using non-digital games in small-group settings (t(76) = 2.21, p = .030, d = 0.53), although there were no statistically significant differences in whole-class settings (t(76) = 0.97, p = .333).

Table 4. Mean game mode preference scores by setting by year level taught.

	Mean	SD	N
Whole-Class Games: Lower Primary	3.79	0.88	28
Whole-Class Games: Upper Primary	3.58	0.91	50
Small-Group Games: Lower Primary	4.18	0.82	28
Small-Group Games: Upper Primary	3.74	0.85	50

Notes: A mean score above 3 indicates an average preference for non-digital games over digital games, with a higher score indicating a stronger preference. Also note that this table only includes those participants who taught exclusively in lower primary (F-2) or upper primary (3–6) year levels.

To summarise the results of our quantitative analysis, Australian primary school educators typically reported using mathematical games in the majority of their mathematics lessons, however, were far more inclined (three to five times more likely) to use non-digital games than digital games, particularly in small-group settings. Consistent with this reported differential usage, around two-thirds of participants indicated that they preferred non-digital games over digital games, with most of the remaining participants responding neutrally regarding their preference for a given game mode. Moreover, there was some evidence that more experienced educators, and lower primary teachers, had relatively stronger preferences for non-digital games. The focus of our analysis now shifts to the qualitative data generated from the open-ended items, in order to shed light on the reasons that Australian primary school educators generally preferred non-digital over digital games.

4. Results: qualitative analysis

Table 5 provides the number of participants who indicated a preference for digital games, non-digital games, or did not have a game mode preference (i.e. were neutral) for each group setting (small-groups or whole-class), as well as the number of participants who explained their preference. These explanations provided the qualitative data for the current study. As noted in the method section, these data were analysed thematically, and first grouped into sub-themes before being distilled into main themes that explained participants’ preferences for a particular game mode. These main themes included: pedagogical reasons; assessment; access to, or awareness of, suitable digital resources; managing the setup and delivery; student affect and behaviours; technology; and beliefs about digital games.

Table 5. Participant preferences for each game mode by setting and the number of participants who provided an explanation for their preferences.

	Whole-class: Preference	Whole-class: Reason	Small-group: Preference	Small-group: Reason
Prefer digital	n = 6	n = 5	n = 5	n = 4
Prefer non-digital	n = 66	n = 63	n = 78	n = 66
Neutral	n = 39	n = 34	n = 28	n = 19
Total	111	102	111	89

We will now consider in turn the results of our analysis explaining participant preferences for either non-digital games, or digital games, as well as those who indicated that they did not have a particular preference. Illustrative quotations from participants will be presented to help elaborate the analysis.

4.1. Reasons for preferring non-digital games

Table 6 presents the seven main themes that emerged from our qualitative analysis that captured why most participants preferred non-digital games. The first point to note is that generally the explanations provided for preferring non-digital games were not contingent on setting, with similar reasons emerging for both small-group games and whole-class games. Consequently, the remainder of our description of the qualitative analysis will consider the two settings together.

Table 6. Reasons for preferring non-digital games by game setting.

Main theme	Small Group Setting N = 66 (%)	Whole class setting N = 63 (%)	Sub-theme	Small Group Setting N = 66 (%)	Whole class setting N = 63 (%)
Pedagogical reasons	32 (48%)	37 (59%)	Better for promoting collaboration interactions, and communication	18 (27%)	13 (21%)
			More ‘hands on’ or use of manipulatives	8 (12%)	17 (27%)
			Easily adapted/differentiated	7 (11%)	9 (14%)
			Prefer less screen time and technology use	6 (9%)	3 (5%)
Assessment	14 (21%)	12 (19%)	Easier to observe student understanding	11 (17%)	10 (16%)
			Easier to monitor time on task (engagement)	4 (6%)	2 (3%)
Access to, or awareness of suitable ‘digital’ resources	11 (17%)	11 (17%)	Lack of awareness of (hard to find) quality or suitable ‘digital’ games	9 (14%)	8 (13%)
			Easier access to suitable non-digital resources	2 (3%)	3 (5%)
Managing the set up and delivery	10 (15%)	7 (11%)	Managing the set up and delivery	10 (15%)	7 (11%)
Student affect and behaviours	17 (26%)	14 (22%)	Students more engaged/Games more engaging	8 (12%)	7 (11%)
			Promotes cooperation/turn taking	4 (6%)	2 (3%)
			Less distracted	4 (6%)	4 (6%)
			Less arguments	2 (3%)
			Digital games can be over-stimulating		1 (2%)
Difficulties with technology	9 (14%)	13 (21%)	Limited access to technology for digital games	6 (9%)	7 (11%)
			Technical issues with digital games	3 (5%)	5 (8%)
			Lack of expertise with technology		1 (2%)
Beliefs about the limited nature of digital games	5 (8%)	6 (9%)	Digital games only promote basic recall of number facts	5 (8%)	6 (10%)

Around half of participants who indicated that they preferred non-digital games had their explanation for this preference coded to the theme pedagogical reasons. In particular, participants valued the opportunities for collaboration and communication that playing a non-digital game facilitated, as well as the tactile nature of the learning experience as students engaged with hands-on manipulatives. Illustrative quotations include:

I value student talk, collaboration. Encourage students to communicate with their peers, share their methods and allow greater interactions. (Participant #85)

The non-digital games promote dialogue and there is more interaction between students. (Participant #170)

The opportunity to use hands-on materials is a big reason why I prefer non-digital games. (Participant #20)

I like the physical nature of materials. Blocks, counters, dice etc. I find they work well for hands on kids. (Participant #149)

The prevalence of the two aforementioned pedagogical sub-themes seems to imply that educators viewed non-digital games as more consistent with constructivist learning principles (Cooperstein & Kocevar-Weidinger, 2004), as students are afforded opportunities to interact meaningfully with their learning environment to develop their understanding of mathematical ideas. However, there is also perhaps a more tacit implication that non-digital games offer a ‘healthier’ learning experience than digital games. Indeed, the sub-theme ‘prefer less screen time and technology use’ implies that some educators believed there was particular value in pursuing activities that did not involve devices, given the ubiquity of technology across so much of education and recreation. For example:

(There is) enough technology at home. (Participant #82)

It's good for them to not be on their devices, as we have a one to one iPad program at the school. (Participant #139)

The final pedagogical sub-theme related to the fact that participants appreciated the level of control they had in being able to adapt a non-digital game for a particular content focus and to differentiate learning opportunities to meet their students’ learning needs:

(With) a non-digital game I can adapt on the fly to match the content I’m covering. (Participant #75)

I find non-digital games give more scope to extend or scaffold students. (Participant #138)

In small groups I can influence the members in the group and have some children that can support or extend others. (Participant #162)

Beyond pedagogy, another notable theme to emerge that explained preferences for non-digital games was that of assessment. In particular, some participants noted that it was easier to observe a student’s level of understanding of a mathematical concept when they were playing a non-digital game compared with a digital game. For example:

I feel like I can assess the game easier when it’s not digital. I can see what they are doing and see their recording clearly when it is not digital. (Participant #13)

I can see if they are counting or confidently outlining a region; physically manipulating sticks in the Place Value game – it is easy to see how they are moving them (e.g. by ones, by bundles etc.). (Participant #168)

The enhanced visibility of student mathematical behaviour when playing a non-digital game (relative to a digital game) is consistent with the previously noted idea that this game mode is more conducive to generating mathematical communication and interactions; all of which serves to make mathematical thinking more visible. However, this assessment theme also encompassed the notion that it is easier to monitor student time on task when they were playing a non-digital game, implying that participants again also preferred this game mode because it enhanced their sense of control:

(It’s) easier to check students are on task. (Participant #3)

(It’s) much easier to ensure students are on task with no screens. (Participant #175)

Non-digital shows me who is not just mimicking or pretending to participate. (Participant #84)

A further theme which helped to explain participant preferences for non-digital games was their lack of awareness of suitable digital resources:

A digital game I have to pre-search, play/check etc and even then, it isn’t usually what I’m looking for exactly. (Participant #75)

I have no knowledge of great digital games that can be played whole class or in groups. (Participant #58)

I found it is hard to find games online which match what you are trying to teach the kids. (Participant #120)

This can be contrasted with the resources required to facilitate non-digital games, which tended to be readily available and well known to participants:

Dice or deck of cards are readily available. (Participant #141)

My own knowledge of good mathematical games tends towards non-digital. (Participant #190)

Even when participants were aware of digital games, they tended to perceive them as pedagogically limited. This indeed was another theme to emerge, that of educators’ beliefs about the limited nature of digital games. Several participants viewed digital games as having limited utility because they did not provide students with opportunities to solve problems in multiple ways and to develop computational flexibility, but rather were narrowly focused on accurate and rapid recall of number facts. For instance:

I find that most digital games focus on fluency rather than understanding. (Participant #168)

I'm not really aware of many small group maths games that aren't fluency related. (Participant #22)

Often the answer is required with little knowledge of strategy or understanding in online games. (Participant #12)

Often digital platforms are only one player, are grounded more in fast recall of facts. (Participant #58)

Given that teachers are generally time poor (Ainley & Carstens, 2018), it seems reasonable that if relevant and pedagogically rich digital games are not known to them already, they will tend to incorporate non-digital games that they are both more familiar with, and for which the relevant resources are already present in the classroom environment. Indeed, difficulties with technology more generally, including a lack of access, expertise, as well as its reported unreliability, was another theme describing educators’ relative preference for non-digital games over digital games:

Limited access to technology can make digital games more challenging to use. (Participant #4)

We don't have an interactive whiteboard which I feel restricts the use of digital games … We don't have the resources for most students to access a digital device. (Participant #55)

A related concern is the issue of classroom management, which manifested in our study through the theme managing the setup and delivery of a game. Evidently many participants found using a non-digital game easier to navigate with their students, particularly in the early years of primary school:

(Non-digital games are) easier to manage and navigate for students in younger years. (Participant #64)

Digital anything with P-1s (Foundation, Year 1) can be a logistical and supervision nightmare. (Participant #153).

Transition into the learning experience is easier for my students when they DON'T have access to iPads. (Participant #160).

The last theme that helped partially to explain why some educators preferred non-digital games related to student affect and behaviours, which was in fact the second most frequently coded theme after pedagogical reasons. In particular, a subset of participants noted that non-digital games appeared to be more engaging for students, due to the opportunities to manipulate physical objects and interact directly with peers:

Kids seem more engaged with manipulatives and partners. (Participant #79)

More engaging to play a game against another student when they have eye contact. (Participant #136)

Students seem more animated and therefore more engaged playing non-digital games. (Participant #142)

Other participants indicated that non-digital games were more engaging because digital devices could be distracting or over-stimulating:

Students gets distracted on computers. (Participant #150)

The class gets distracted by the technology and game play elements and don't fully utilize their math skills and number knowledge. (Participant #24)

I’m also concerned about their cognitive load and extra stimulation from technology. (Participant #76)

In addition, this theme also encompassed the idea that some participants believed engaging with non-digital games was an opportunity to develop students’ social and emotional skills, such as cooperating with others and turn-taking, particularly when working with younger students:

With Prep students, I feel that non-digital games are best in a small group because of their need to learn to work together and take turns. (Participant #152)

Teaching the Foundation students to play a non-digital game is teaching them the skills of turn taking and sharing. (Participant #55)

This can be contrasted with digital games, which were sometimes viewed as undermining of students’ capacity to work together, leading to arguments:

When using digital games, they argue over whose turn it is to operate the game, whereas non-digital games seem more efficient and cause less confrontation. (Participant #24)

The kids often end up arguing in small groups when using digital games. (Participant #59)

4.2. Reasons for preferring digital games

As noted in Table 7, only a small number of participants indicated that they preferred digital games over non-digital games. This preference could be attributed to one of two explanations: student affect and behaviours, and managing the setup and delivery. In almost every instance in which an educator offered an explanation for preferring a digital game in either a whole-class or small-group setting, it related to the idea that students were more engaged playing digital games compared with non-digital games:

I find student engagement is higher with digital games. (Participant #157)

Kids find it more engaging to use their devices or screens. (Participant #19)

One particular participant connected the idea of higher levels of student engagement with the relative ease of managing the setup and delivery of a digital game:

Table 7. Reasons for preferring digital games by game setting.

Main theme	Small Group Setting N = 4 (%)	Whole class setting N = 5 (%)	Sub-theme	Small Group Setting N = 4 (%)	Whole class setting N = 5 (%)
Managing the set up and delivery	1 (25%)	2 (40%)	Managing the set up and delivery	1 (25%)	2 (40%)
Student affect and behaviours	4 (100%)	4 (80%)	Students more engaged/Games more engaging	4 (100%)	4 (80%)

If I did not intend to work with the students I would slightly prefer a digital game as it often helps them stay on task and can avoid misinterpretation of the rules/mechanics. (Participant #2)

Other participants highlighted the ease of setting up a digital game as a reason in its own right for preferring games of this mode:

Easy to set up, easy for all students to see. (Participant #136)

Easier set up. (Participant #83)

It is noteworthy that none of the 111 participants put forward a pedagogical explanation for preferring digital games, in contrast to the frequency with which this theme emerged when coding explanations for preferring non-digital games.

Finally, participants who indicated that they did not have a definite preference for non-digital or digital games tended to explain this position by indicating that they had no preference as long as the game was appropriate for the content focus, or that their preference depended on one of several factors including:

• Access to technology

• Access to suitable materials (for non-digital games)

• Suitability of the games available for a given content focus or learning purpose

• The interests/ age level of the particular group of students

5. Discussion

The current study set out to investigate Australian primary school educators’ preferences for using non-digital as opposed to digital mathematical games, whether these preferences varied across game setting (whole-class versus small-group), and the reasons for these preferences. This was in response to an identified gap in the literature in terms of studies that have investigated how teachers use mathematical games, as opposed to their impact on student engagement and performance, as well as the paucity of studies that have directly compared non-digital and digital games. There are several notable findings worth considering that contribute to the literature about what we know about how teachers use mathematical games.

First, our overall findings are consistent with previous pre-pandemic research that indicates that game usage is prevalent within Australian primary schools, with the median teacher using mathematical games in the majority of their mathematics lessons (Russo et al., 2021; Russo & Russo, 2020). This suggests that games remain a central part of Australian primary school teachers’ instructional repertoire post-pandemic, and that further research focused on better understanding both how and why teachers use games is a worthwhile endeavour.

Secondly, although prior research has implied that teachers prefer non-digital games to digital games (e.g. Russo et al., 2021), the current study is the first that we are aware of that reveals directly that primary school educators have a strong preference for using non-digital games over digital games, and are far more inclined to report incorporating such games into their mathematics teaching practice. Perhaps unsurprisingly given evidence that older teachers are less inclined to utilise digital technologies or resources to support their mathematics instruction compared with younger teachers (Yao & Zhao, 2022), this tendency to prefer non-digital games was amplified for participants with more teaching experience (who were also presumably on average older); although notably this did not translate into any direct correlation between the reported use of games of a particular mode and levels of teaching experience.

Thirdly, although there was no difference in the overall frequency of game use by setting, participants were more inclined to prefer, and twice as likely to report using, digital games in whole-class settings compared with small-group settings. This preference was amplified for participants who taught students in the early years of primary school. These quantitative findings were indirectly supported by our qualitative analysis, which implied that participants were concerned about digital games from a social and emotional developmental perspective (e.g. too much screen time, too many arguments), as well as the notion that facilitating access to technology and managing the setup and delivery of a digital game were particularly problematic when working with younger students. It may be that participants believed that these issues could be at least partially mitigated against by the teacher facilitating access to a digital game with the whole-class, rather than letting students play digital games independently in small groups. However, the more immediate, pragmatic constraint on using digital games in small groups could of course be a lack of access to appropriate digital technology resources, which was indeed an issue identified by a number of participants; and one that may be amplified in the early primary years, given that many Australian schools adopt a ‘one-to-one’ device program in the upper primary years (Pope et al., 2015).

Collectively, these findings are consistent with previous research suggesting that access to technology and supportive resources is a substantial barrier to teachers adopting digital GBL (Ertmer, 1999; Kaimara et al., 2021), and that teachers of older students are more inclined to believe that digital games are effective for supporting learning than teachers of younger students (Cabellos et al., 2023). Moreover, it confirms that some teachers perceive there to be unique classroom management challenges faced when attempting to incorporate digital games into mathematics lessons, particularly involving younger students (Stieler-Hunt & Jones, 2017).

By contrast, some of the other reasons for preferring non-digital games to digital games resonated with the literature espousing the benefits of non-digital games more generally when compared to other activities or traditional instruction. For example, Ernest (1986) concluded that games can foster cooperation and interactivity, while one of the more frequent explanations provided by our study participants for preferring non-digital games to digital games was because they better fostered interaction, collaboration, and communication. However, in juxtaposition to the mathematical games’ literature overall, educators in our study placed less emphasis on benefits pertaining directly to mathematical thinking, learning, and performance, and more emphasis on the enhanced capacity to meet students’ social and learning needs through non-digital games. In particular, participants emphasised that they could adapt and differentiate a non-digital game for specific groups of students, whilst this mode of game was also more conducive to effective assessment and observation of student understanding; both actions which are consistent with a teacher enacting principles of student-centred mathematics learning (Bingolbali & Bingolbali, 2015; Black, 2007). An additional relative benefit highlighted by participants, and one also consistent with student-centred teaching approaches, is that non-digital games provide students with access to hands-on manipulatives, potentially enabling them to visualise and connect mathematical ideas (Moyer, 2001), and facilitating more mathematical talk (Kosko & Wilkins, 2010). By contrast, participants did not describe the benefits of digital games in terms of providing students with access to virtual manipulatives, perhaps reflecting the belief that digitised concrete materials are less useful because their two-dimensionality limits students’ ability to interact with them as mathematical objects (Larkin, 2016; Swan & Marshall, 2010), or simply reflecting participants limited knowledge of digital games that purposefully connect various mathematical representations and incorporate virtual manipulatives.

It is noteworthy that the idea that students experience a particular game mode as distinctively engaging was a theme that emerged explaining participants preferences for both digital games and non-digital games, albeit in different ways. This apparent paradox can be partially reconciled if one considers that student engagement is a multifaceted construct, with behavioural, cognitive and affective components (Skinner, 2016). For instance, whilst some students might prefer digital games because they find them particularly stimulating and enjoyable to play (affective engagement), it is possible that they are simultaneously less cognitively engaged, as they, in the words of one study participant, ‘get distracted by the technology and game play elements, and don’t fully utilise their math skills and number knowledge’. By contrast, other students who find enhanced opportunities for social interaction and hands-on experiences particularly affectively engaging may well prefer non-digital games, given that it may be that such students are, in the words of another participant, ‘more engaged with manipulatives and partners’. Future research could seek to explicitly establish how each game mode impacts each of the three components of student engagement, and attempt to build a profile of the types of students who might experience digital or non-digital games as particularly engaging.

6. Conclusions and implications

Our study had at least three limitations that need to be acknowledged, and which might be addressed through future research. First, participants were limited to Australian primary school educators, implying that future research could explore whether the strong preference for non-digital games revealed through the current study held up in other contexts (e.g. Australian secondary schools; other countries). Secondly, we relied exclusively on retrospective, self-report, questionnaire data to answer our research questions. Consequently, our findings would be complemented by future research that adopted different methodologies (e.g. classroom observations; lesson diaries). Finally, our questionnaire was disseminated through a snowball sampling approach using a number of key informants, as well as through social media. This of course means that participants in this study cannot be assumed to be representative of Australian primary educators overall. Having said this, we remain confident in the overall trends reported in the current study for at least two reasons. First, other studies have revealed similar rates of high game usage amongst Australian primary school teachers irrespective of whether they have used a snowball sampling/ social media dissemination strategy (Russo et al., 2021), or a convenience sample attending a system-level professional learning initiative unrelated to mathematical games (Russo & Russo, 2020). Second, to the extent that using an online questionnaire and online distribution channel generated some form of self-selection bias (Thompson et al., 2003), we might expect this to result in a higher proportion of participants preferring digital games relative to non-digital games than would otherwise be the case if we sampled the overall population of primary school educators. Consequently, we would contend that the strong preference for non-digital games revealed in the current study is likely to be a robust finding. However, clearly there would be benefit in replicating the current research with a larger, random sample of educators.

There are further implications for future research and practice implied by our study. In particular, our findings showed that educators lack awareness of high-quality digital resources and games that go beyond supporting students to develop accuracy and speed with arithmetic. We note that this was one of the more notable reasons why participants indicated a preference for non-digital games, beyond pedagogical reasons and classroom management concerns. However, given we did not attempt to measure participant’s knowledge of digital games, it is not possible to establish whether these views reflect an informed perspective, or are a result of limited exposure to digital games and resources. Consequently, given that a lack of awareness of how to identify and access high quality digital resources was viewed as an impediment to incorporating digital games (and a reason for preferencing non-digital games), it would be interesting if future research endeavoured to control for this factor through presenting educators with high quality digital games that could be directly compared with high quality non-digital games. It also suggests that there is value in providing professional learning that raises educator awareness of where such high-quality digital games and activities can be sourced.

To conclude, despite the ubiquitousness of technology across almost all facets of Australian society, and the proliferation of digital games to support young children’s mathematical learning, primary school educators remain comparatively disinclined to incorporate digital games into their mathematics instruction. This is despite primary mathematics education being at least somewhat reimagined through an extended period of remote learning brought about by the pandemic, a period through which playing non-digital games was more difficult to facilitate than digital games. It seems that primary school educators perceive there to be unique value in students’ experiencing non-digital games, due to the fact that they are socially mediated, embedded in the physical world, and co-constructed through the actions of teachers themselves. However, our results simultaneously imply that Australian primary mathematics educators need opportunities to broaden their awareness of how to access high-quality digital games, and to deepen their knowledge of how to effectively integrate digital resources into their classroom practice.

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes

1 Note that participation in the questionnaire was interpreted as implied consent to participate in the research. The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Ethics Committee of Monash University (Project 21806).

2 Prior to completing the relevant questions, participants were provided with the following explanation: A whole-class teacher facilitated learning experience involves the collective participation of all students in structured, collaborative activities under the guidance of the teacher. Examples might include a number talk, a teacher-led ‘mini-lesson’ to unpack a mathematical idea, or a whole-class mathematical game.

3 Prior to completing the relevant questions, participants were provided with the following explanation: A small-group learning experience involves two, three, or four students working together independently of the teacher. Examples might include students engaged in a collaborative problem-solving task, students completing a worksheet together, or students playing a small-group mathematical game.