?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.
?Mathematical formulae have been encoded as MathML and are displayed in this HTML version using MathJax in order to improve their display. Uncheck the box to turn MathJax off. This feature requires Javascript. Click on a formula to zoom.Abstract
This paper explores the position of the vertex centroid for a generalisation of Van Aubel’s theorem: specifically we look at what happens to the vertex centroid when directly similar quadrilaterals are placed on the sides of an arbitrary quadrilateral. After giving a simple proof that the position of the vertex centroid remains unchanged, the result is further generalised to directly similar triangles (or other directly similar shapes) on the sides of polygons using vectors. Not only are the results mathematically interesting, but can also provide an appropriate classroom opportunity for dynamic geometry exploration, and to build 2D models with clay and drinking straws (or thin wire) to illustrate and check the theoretical solutions.
1. Introduction
Archimedes (c.287–c.212 BC) of Syracuse extensively used the centroids (centres of gravity) of figures, and the law of the lever, to deduce the volumes of spheres, cones and pyramids (Hawking, Citation2006; Heath, Citation1897; Polya, Citation1954). By considering different weights at the vertices of a triangle, just like Giovanni Ceva (1648–1734) did, we can also deduce from the principles of mechanics, the celebrated concurrency theorem of Ceva (Hanna & Jahnke, Citation2002). Other obvious applications of centroids and ideas from mechanics are the theorems of Varignon, the Fermat-Torricelli point, Steiner networks, etc. (De Villiers & Jahnke, Citation2023).
Flores (Citation2002) has also shown how one can use the so-called ‘kinematic method’, involving the velocity of endpoints and vectors, to effectively derive and explain (prove) a range of different results within geometry. While historically, vectors were largely motivated, developed and described within physical science, it’s also a very useful technique to utilise in proofs in geometry as it immediately accounts for all cases.
In the following example, we will give another illustration of the value of applying centroids, similarity, as well as vectors in geometry, to not only easily derive and prove a vertex centroid result in plane geometry, but also to generalise it further to other plane figures.
2. The vertex centroid of a quadrilateral
With the centroid of a quadrilateral, we will consistently in this paper mean its ‘centre of mass/gravity’, determined by the placement of equal point masses at the four vertices of the quadrilateral. Geometrically, this ‘vertex’ centroid is located at the centre of the Varignon parallelogram formed by the midpoints of the sides of the quadrilateral. Equivalently, it is easy to prove geometrically that the ‘vertex’ centroid of a quadrilateral can also be located at the midpoint of the segment connecting the midpoints of the diagonals of the quadrilateral (Coxeter & Greitzer, Citation1967, p. 54). This can also easily be deduced using arguments about centroids. Suppose equal point masses are located at the vertices of a quadrilateral ABCD. Then clearly the two masses at A and C would balance at the midpoint of the diagonal AC, and similarly the two masses at B and D would balance at the midpoint of diagonal BD. Hence, if two masses from each pair of opposite vertices are placed at the respective midpoint of the diagonal connecting them, these two pairs would balance at the midpoint of the segment between the two midpoints of the diagonals.
Also note that the vertex centroid of a polygon does not necessarily coincide with the lamina centroid of the polygon area (this would be the balance point of a homogeneous plate of the polygon shape). For triangles the vertex centroid coincides with the lamina centroid. In the world of quadrilaterals this holds if and only if the quadrilateral is a parallelogram (Humenberger, Citation2023).
3. A generalisation of Van Aubel’s quadrilateral theorem
Van Aubel’s celebrated quadrilateral theorem states that if squares are constructed on the sides of any quadrilateral, then the segments connecting the centres of the squares on opposite sides are equal and perpendicular (Van Aubel, Citation1878). The theorem has been generalised to similar rectangles, similar rhombi and similar parallelograms on the sides of a quadrilateral (De Villiers, Citation1998; Silvester, Citation2006). In De Villiers (Citation2007/Citation2008), some properties of the centroids of similar quadrilaterals placed alternately, inwardly & outwardly, on the sides of a quadrilateral were explored.
Let’s now consider Van Aubel’s theorem generalised to similar quadrilaterals all placed outwardly or inwardly on the sides of a quadrilateral as follows:
Theorem 1:
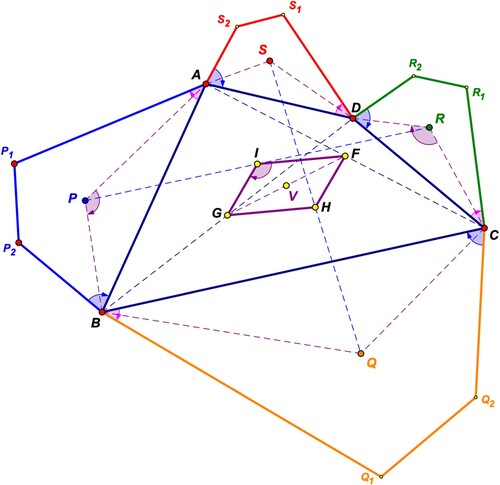
Given four points A, B, C, D, and four directly similar quadrilaterals AP1P2B, BQ1Q2C, CR1R2D, DS1S2A with respective vertex centroids P, Q, R, S. Further let F, G, H, I and V be the midpoints of the segments AC, BD, QS, PR and GF respectively (see Figure ). Then
IGHF is a parallelogram.
the vertex centroid of the whole configuration coincides with V, the original vertex centroid of the quadrilateral ABCD.
A dynamic geometry sketch illustrating the theorem is available online for the reader to explore at: http://dynamicmathematicslearning.com/van-aubel-centroid-generalization.html
Proof: As shown in De Villiers (Citation2023), result (i) easily follows from the so-called fundamental theorem of similarity given in DeTemple and Harold (Citation1996) that IGHF is a parallelogram, but for completeness, we repeat the proof here.
A useful special case of the fundamental theorem of similarity states that the midpoints of the segments connecting corresponding vertices of two directly similar figures form a figure similar to the other two. With regard to Figure , this means that GIF is similar to the two directly similar
’s BPA and DRC. In the same way,
FHG is similar to the directly similar
’s ASD and CQB. But since all the outwardly erected triangles are directly similar to each other, it follows that
GIF is similar to
FHG, and since they share the same side GF, they are congruent, which implies that IGHF is a parallelogram.
Note that as mentioned earlier, the vertex centroid of quadrilateral ABCD is located at V, the midpoint of GF. Now consider the quadrilateral formed by the vertex centroids P, Q, R and S of the respective quadrilaterals constructed on the sides. Clearly, the vertex centroid of PQRS would be located at the midpoint of IH. But since IGHF is a parallelogram as proved above, its diagonals bisect each other, and therefore the midpoint of IH (the vertex centroid of PQRS) must coincide with the vertex centroid, V, of ABCD. Since the vertex centroid of the four similar quadrilaterals on the sides coincides with that of the original quadrilateral ABCD, it follows that the vertex centroid of all the point masses put together from both PQRSFootnote1 and ABCD will also balance at V. This then completes the proof of Theorem 1.
The centroid generalisation of Van Aubel’s theorem as expressed in Theorem 1 is not new and appears in (Fritsch & Pickert, Citation2013). However, unlike here, it is proved there by means of complex numbers and algebra. More importantly, as pointed out in both Fritsch and Pickert (Citation2013) and De Villiers (Citation2023), note that the result is actually about directly similar triangles (with point masses placed at their respective apex vertices) on the sides of a quadrilateral, and not necessarily about similar quadrilaterals (and their corresponding vertex centroids) on the sides.
In the same vein as Theorem 1, and also using complex algebra, Ayoub (Citation1998) has shown that if three similar ’s AKB, BLC and CNA are constructed outwardly or inwardly on the sides of a
ABC, then the
’s KLN and ABC have the same centroid. However, the converse of this result is not true. As shown by Ayoub (Citation1998), a counter-example with three
’s AKB, BLC, and CNA on the sides of a
ABC can be constructed so that the
’s KLN and ABC have the same centroid, but the three triangles are not similar.
4. Further generalisation
Looking back at Theorem 1 and the given proof above, we wondered if it was possible to construct a straight forward proof (without using complex numbers and algebra) that would show either (1) the coincidence of the vertex centroids directly or (2) that IGHF is a parallelogram without having to use the fundamental theorem of similarity. At first we thought either of these two cases might be possible by just using centroids and simple applications of the lever principle of Archimedes, but were unable to find a way to do this. Finally we were forced to rely on vectors, but in the process of proving Theorem 1 in this way, we discovered the following interesting vertex centroid generalisation to plane polygons.
Theorem 2:
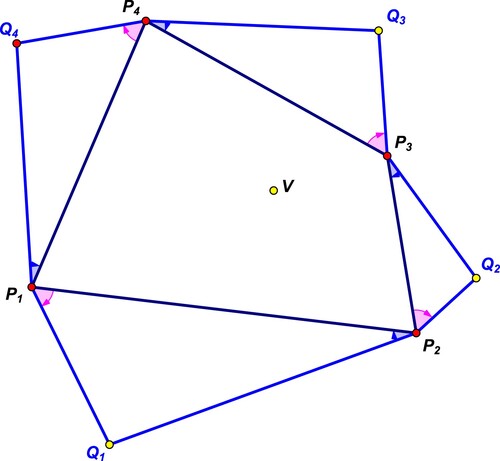
Let be an arbitrary polygon with vertex centroid
We erect directly similar triangles on the sides of the polygon:
,
, … ,
(in Figure , we have as an example
, and all triangles outwardly erected). Then the vertex centroid of the polygon coincides with
the vertex centroid of the initial polygon
.
Here one can experience once more that the ‘real home’ of centroids are coordinates and vectors, and the proof will be short and elucidating. In a way, this can already be seen in the well-known formula for the vertex centroid
(1)
(1)
Proof: First, we have a look at the four line segments . Since the erected triangles are all (directly) similar their lengths are the lengths of the polygon’s sides multiplied by a constant
:
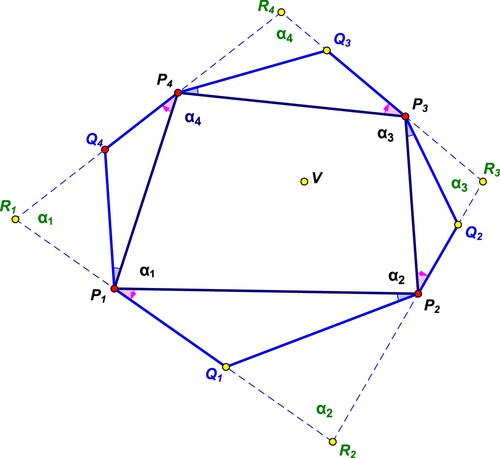
Let the interior angles of the initial polygon be . We can easily determine the angles between corresponding sides (rather their extensions) of the directly similar erected triangles, and we start with the angle between the straight lines
and
. Due to the similarity
and because the angle between the corresponding triangle sides
and
is
also the angle between the (extended) corresponding triangle sides
and
must be
(at
; this could be seen also via simple angle chasing; one could also involve the concept of spiral similarity; see Figure ).
Analogously, we can determine the other angles at
.
Now we turn to vectors. An immediate and important consequence of the considerations above is that the quadrilateral built up by the vectors (the endpoint of each vector should be considered as the initial point of the following oneFootnote2) is similar to the initial polygon
: its side lengths are the ones of the initial polygon multiplied by the constant
(see above), and both quadrilaterals have corresponding angles equal. This similarity is a neat additional result of our considerations, but more important for our purpose is that we finally have
(2)
(2)
WithFootnote3 this information, we can now easily calculate the vertex centroid of
(note
, analogous with the others):
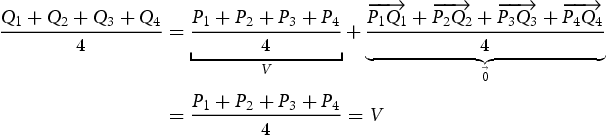
Another way of using Equation (2) without the formula Equation (1) would be the following: Equation (2) essentially tells us that if one moves the equal point masses at to
, respectively, there is no ‘overall change’, thus the vertex centroid does not change!
It is obvious that the whole argumentation holds true for initial polygons with arbitrary
.
Theorem 3a:
Let be an arbitrary polygon (not necessarily convex) with vertex centroid
We erect directly similar triangles on the sides of the polygon:
(in Figure , we have as an example
, and all triangles outwardly erected). Then the vertex centroid of the whole new configuration
coincides with
, the vertex centroid of the initial polygon.
Proof: This follows immediately from Theorem 2 since both ‘partial centroids’ (the one of and the one of
) coincide and the ‘overall centroid’ of the new configuration must lie somewhere on the line segment joining the two partial centroids.
Theorem 3b:
Now consider another way of building up a ‘new configuration’. Not only the points are added to the points
but we think of the union of the triangles
, (more precisely: the equal point masses at their vertices). Thus, at the points
we have a mass of 2 units each, at the points
we have a mass of 1 unit each. Then the vertex centroid of this kind of ‘new configuration’ is again
Theorem 3c:
There is still another way of building up a ‘new configuration’: Like in Theorem 3b, but now additionally the initial polygon is considered with its point masses 1 at its vertices. Thus, this kind of ‘new configuration’ has at the points
a mass of 3 units each and at the points
a mass of 1 unit each, again yielding
as its centroid.
The above theorems can be generalised immediately. Instead of the directly similar triangles (erected on the sides of the initial polygon ) one can take arbitrary directly similar polygons with
vertices, see Theorem 4.
Theorem 4:
Let be an arbitrary polygon (not necessarily convex) with vertex centroid
We erect directly similar
-gons on the sides of the polygon
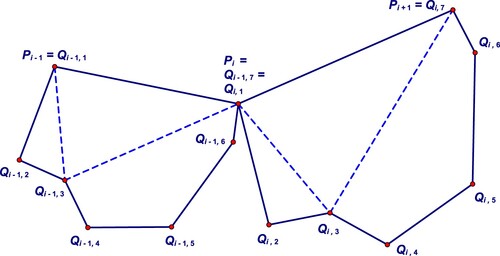
![]() (in Figure , we show only two consecutive such erected directly similar polygons with
(in Figure , we show only two consecutive such erected directly similar polygons with as an example). Then the vertex centroid of the whole ‘new configuration’ (in the sense of all three versions of Theorem 3a–3c) coincides with
.
Proof: The proof is given immediately by Theorem 4 itself. Note that for every fixed the triangles
,
, … ,
are all directly similar due to the similarity of the
-gons (in Figure indicated for
with dashed lines). Thus, by Theorem 1 the vertex centroid of the polygon
is
Since this holds for every
the vertex centroid of the whole ‘new configuration’ (in the sense of all three versions of Theorem 3) coincides with
.
5. Concluding remark
On a practical real world level, determining the centroids (centres of mass) of 2D and 3D objects is of paramount importance in civil, mechanical, shipping and aviation engineering. If engineers are not able to accurately determine centroids, rigid structures like walls, bridges, skyscrapers, etc. may easily fall over, boats may capsize in heavy seas, and cars may roll when going around a bend, or airplanes may not get the necessary lift to take off, or if in the air, may nosedive into the ground if they become unbalanced.
The vertex centroid results in this paper can also provide opportunity for including some real-world experimentation in the classroom as well. By using balls of clay (of equal mass) and some light connecting material like straws, students can build two-dimensional models of the theorems discussed here, and experimentally confirm the theoretical position of the vertex centroid by balancing the structure at that point with a sharp object like a pencil or knitting needle. (To make such a 2D structure stable and rigid, more straws will obviously need to be added to ‘triangulate’ it, and also to the vertex centroid to create a supportive ‘balancing point’ there). To engage students at high school or university in the mathematical exploration of some centroid properties such as these can therefore have considerable educational value.
Lastly, in the process of looking for a different alternative proof for Theorem 3.1, the decision to make use of vectors enabled us to discover an interesting further generalisation to polygons. Therefore, if the approach here is roughly replicated in an instructional context, it may be effectively used to illustrate to students the usefulness of proof, not only in explaining and understanding a result better, but in doing so, enabling further generalisation (compare De Villiers, Citation2012).
So far we have been unable to find mention of this centroid generalisation to polygons, but it might be mentioned in some engineering or physics textbook or appears in published papers on statics. Nonetheless, the original result that started this investigation, as well as its generalisation to polygons as expressed in the above theorems, deserve to be known better.
Disclosure statement
No potential conflict of interest was reported by the authors.
Notes
1 This corresponds to all the point masses placed at the vertices of the similar quadrilaterals.
2 This quadrilateral is not displayed in the figures.
3 Likewise, we have and the analogous relations would hold true for arbitrary
.
References
- Ayoub, A. B. (1998, June). Triangles with the same centroid. Mathematics Magazine, 71(3), 221–224. https://doi.org/10.1080/0025570X.1998.11996639
- Coxeter, H. S. M., & Greitzer, S. L. (1967). Geometry revisited. Mathematical Association of America.
- De Villiers, M. (1998). Dual generalizations of Van Aubel’s theorem. The Mathematical Gazette, 82(495), 405–412. https://doi.org/10.2307/3619886
- De Villiers, M. (2007/2008). A question of balance: An application of centroids. The Mathematical Gazette, 91(522), 525–528. & 92(523), 167-169. https://doi.org/10.1017/S0025557200182221
- De Villiers, M. (2012). An example of the explanatory and discovery function of proof. Pythagoras, 33(3), 1–8. https://doi.org/10.4102/pythagoras.v33i3.193
- De Villiers, M. (2023). An associated result of the Van Aubel configuration and its generalization. International Journal of Mathematical Education in Science and Technology, 54(3), 462–472. https://doi.org/10.1080/0020739X.2022.2034064
- De Villiers, M. D., & Jahnke, H.-N. (2023). How experimentation in mathematics can contribute to the learning of mathematics. In B. Sriraman (Ed.), Experimentation in mathematics education (pp. 2551–2586). Springer.
- DeTemple, D., & Harold, S. (1996). A round-up of square problems. Mathematics Magazine, 69(1), 15–27. https://doi.org/10.1080/0025570X.1996.11996375
- Flores, A. (2002). The kinematics method in geometry. PRIMUS, 12(4), 321–333. https://doi.org/10.1080/10511970208984038
- Fritsch, R., & Pickert, G. (2013, October). A quadrangle’s centroid of vertices and Van Aubel’s Square Theorem. Crux Mathematicorum, 39(8), 362–367.
- Hanna, G., & Jahnke, H. N. (2002, November). Arguments from Physics in mathematical proofs: An educational perspective. For the Learning of Mathematics, 22(No. 3), 38–45.
- Hawking, S. (2006). The method of Archimedes treating of mechanical problems – to Eratosthenes. In S. Hawking (Ed.), God created the integers (pp. 209–239). Penguin Books.
- Heath, T. L. (1897). The Works of Archimedes. Cambridge University Press.
- Humenberger, H. (2023). Centroids of quadrilaterals and a peculiarity of parallelograms. At Right Angles, November 2023.
- Polya, G. (1954). Mathematics and Plausible Reasoning: Induction and Analogy in Mathematics. (Vol. 1. pp. 155–158). Princeton.
- Silvester, J. (2006). Extensions of a theorem of Van Aubel. The Mathematical Gazette, 90(517), 2–12. https://doi.org/10.1017/S0025557200178969
- Van Aubel, H. (1878). Note concernant les centres des carr 'es construits sur les cot 'es dun polygon quelconque (French). Nouv Corresp Math, 4(4), 40–44.