A two-stage robust hub location problem with accelerated Benders decomposition algorithm

ABSTRACT

In this paper, a two-stage robust optimisation is presented for an uncapacitated hub location problem in which demand is uncertain and the level of conservatism is controlled by an uncertainty budget. In the first stage, locations for establishing hub facilities were determined, and allocation decisions were made in the second stage. An accelerated Benders decomposition algorithm was used to solve the problem. Computational experiments showed better results in terms of number of iterations and computation time for Benders decomposition with Pareto-optimal cuts in comparison with the classical Benders decomposition algorithm. According to numerical analysis, it was concluded that increasing the uncertainty budget also increased total costs for more established hubs. To determine the uncertainty budget in an appropriate manner, a new expected aggregate function was introduced. The numerical studies demonstrated the usefulness of the proposed method in defining the appropriate uncertainty budget in the presence of uncertainty.

KEYWORDS:

• Two-stage robust
• hub location problem
• demand uncertainty
• Benders decomposition algorithm
• Pareto-optimal cut

1. Introduction

Carrying out hub location consists of finding the best locations for establishing hubs and determining flow pathways. Network transportation costs are decreased by using hub facilities instead of direct connections, because that allows the utilisation of economies of scale. Transportation and telecommunication are important applications for hub location problems such as public and air transportation and delivery cargo systems. Since the work of O'Kelly (1986), hub location problems have become a popular area of research, and have gotten a lot of attention in recent decades. The first studies focused on basic hub locations, which are a type of discrete facility location problem. The set of assumptions that are considered for simplification in network design decisions are fully interconnected hub facilities, no direct connections, full transmitted flows, etc (Campbell and O'Kelly 2012; Contreras 2015).

Flow transportation via direct paths between origin-destination nodes raises costs, because vehicles that carry flows between origin-destination nodes may be empty on the return path, and this entails extra costs for the network. A hub as a connection point makes it possible to collect scattered flows and send them together, or vice versa. Determining the optimal locations of hubs in the network is a strategic decision and helps managers to reduce the costs of distribution networks. Therefore, this decision significantly affects the performance of the system. In addition, many companies and retailers locate their warehouses near hub facilities to improve flow transportation time and reduce transportation costs (for example, the Laura Ashley textile design company located their warehouses near FedEx hubs to improve responsiveness to customers). Hub facilities can also operate as assembly or production centres that can produce different types of commodities. In other words, different parts of commodities are sent to hub facilities, and then these parts are assembled and transshipped to their destinations. Therefore, proper selection of hub facilities and production planning can reduce transportation and production costs. The locations of hub facilities and warehouses are strategic decisions and affect production planning (Ghodratnama, Arbabi, and Azaron 2019). Therefore, hub location problems can be used in a wide range of real applications and studies, such as production research. The model presented in this paper can be used for sending commodities that are in hub facilities. In other words, commodities are produced in factories and sent to hubs for transshipment.

Optimisation of hub location problems, considering parameters such as demand, hub establishment costs, transportation costs, discount factors, and so on, using deterministic values that may in fact be uncertain in nature, may impose extra costs in the future. This is due to incorrect decisions made when considering deterministic values of parameters, which may affect establishment of hub facilities. There are some approaches to dealing with uncertainty, such as stochastic programming and robust optimisation. In stochastic programming, unlike robust optimisation, the probability distribution of uncertain parameters is known and an optimal solution is obtained by considering probability distribution or multiple scenarios. Stochastic programming is applied in different ways, such as two-stage, multi-stage and chance constrained approaches. In two-stage stochastic programming models, two types of decision variables, including the first and second stage decision variables, are considered. Robust optimisation is another way to deal with uncertainty, in which uncertain parameters are defined by interval uncertainty or discrete scenarios. Two-stage robust optimisation is a combination of stochastic programming and robust optimisation approaches, in that first-stage decision variables are determined by focusing on worst-case second-stage scenarios (Ben-Tal et al. 2004). Static robust optimisation ($R_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}}$) and adjustable robust optimisation ($R_{\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}}$) are two types of robust discrete optimisation (see : Bertsimas, Brown, and Caramanis (2011)). In $R_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}}$, all decisions are made before revealing uncertainty, while in the $R_{\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}}$ proposed by Ben-Tal et al. (2004), some decisions are made after revealing uncertainty. So the solution obtained by $R_{\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}}$ may be less conservative in comparison with $R_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}}$ ($R_{\mathrm{a}\mathrm{d}\mathrm{j}\mathrm{u}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}}\le R_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{c}}$).

The main contributions of this paper are as follows:

(1) Using two-stage robust optimisation for an uncapacitated multiple allocation hub location problem with uncertain demand. While recent work (on the robust optimisation approach and hub location problems) has focused on robust optimisation in which all decisions are made in one stage, in this study, decisions are made in two stages. Locations of hub facilities are decided in the first-stage without revealing uncertain demand, and flow pathway decisions are made in the second stage in the presence of uncertainty (wait-and-see decisions). (2) An accelerated Benders decomposition algorithm (Pareto-optimal cut) is used to solve the mathematical model more efficiently in comparison with the classical Benders decomposition algorithm. (3) A size reduction scheme is used to solve large-scale instances. This method finds near-optimal solutions in a very short time and with higher quality. (4) Also, a new expected aggregate function was introduced to determine appropriate uncertainty budgets for decision-makers.

The remainder of the paper is organised as follows: Section 2 pays attention to the literature review of the hub location problems and robust optimisation, Section 3 introduces the mathematical model of deterministic uncapacitated multiple allocation hub location problem and the proposed two-stage robust model with uncertain demand, Section 4 introduces classical and accelerated Benders decomposition algorithm. In Section 5 computational experiments are done for analysing the performance of Benders decomposition algorithm for the two-stage robust model, Section 6 pays attention to the managerial implications and finally Section 7 concludes the paper and suggests future studies.

2. Literature review

This section provides a comprehensive review covering the following three classes of studies for hub location problems: hub location research; production planning research on the concept of hub location problems; and robust optimisation approaches.

2.1. Hub location research works

The idea of hub location problems was initially introduced by Goldman (1969). O'Kelly (1986) later introduced a hub location problem for an air transportation network. O'Kelly (1987) proposed a mathematical model for a one-stop hub location problem. Then Campbell (1994) proposed a model in which the number of hubs is determined based on hub establishment and transportation costs. Farahani et al. (2013) studied solution methods and applications of hub location problems.

Ghaffarinasab and Kara (2019) proposed two models for hub location problems, uncapacitated single allocation hub location problems and uncapacitated single allocation p-hub median problems. They used the Benders decomposition algorithm to solve large-scale instances of these problems. Özgün Kibiroğlu, Serarslan, and Topcu (2019) presented hub location problems with the penalty cost in the objective function for hub facility congestion. Particle swarm optimisation (PSO) was used to solve the model in a shorter computation time. They showed that the proposed algorithm could find a good solution in less computation time in comparison with commercial solvers. Ghaffarinasab (2020) proposed a multiple allocation p-hub centre problem with unlimited capacity for hub facilities. Also, this author used the Benders decomposition algorithm for solving the proposed model in large-scale instances in an appropriate computation time. Shen, Liang, and Max Shen (2020) considered a backup path for avoidance of risk of random disruptions in addition to a primary path in a reliable hub location problem. The objective function of their model is designed to minimise the associated costs and penalty costs for unserved demand. da Costa Fontes and Goncalves (2019) proposed a new hub and spoke network considering the sub-hub structure. Transshipment of flows between origin-destination nodes for certain types of demand are allowed in their model, considering a sub-hub concept. They also used a variable neighbourhood decomposition search algorithm to solve large-size instances. Wandelt et al. (2020) proposed a contraction technique in six different hub location problems to reduce the complexity of the models and speed up the genetic, variable neighbourhood search and Benders decomposition algorithms. In contraction technique, the origin-destination flows of some nodes are merged into one existing node, the model is optimised, and the locations of hub facilities are determined. Then, the complete hub location model without contraction is solved, in which the hubs obtained in the previous step are fixed in a complete model. They solved the proposed model in instances with up to 5000 nodes using the contraction technique. Alumur et al. (2020) provided some new perspectives for hub location problems that can be considered for future work. They highlighted key gaps in the hub location problem literature and suggested opportunities for better models.

2.2. Production planning in hub location problem

Ghodratnama, Tavakkoli-Moghaddam, and Azaron (2012) proposed a hub covering problem with two objective functions. They also used a fuzzy approach to deal with uncertainty and solved their proposed bi-objective models using the Torabi and Hasini (TH) and Selim and Ozkarahan (SO) methods. They located hub facilities as factories and warehouses in a hub network. Ghodratnama, Tavakkoli-Moghaddam, and Azaron (2015) presented a fuzzy-robust multi-objective p-hub covering problem with scenario-based uncertainty. They also considered production facilities in their proposed mathematical model. They used the TH method to solve their multi-objective model. Ghodratnama, Arbabi, and Azaron (2018) proposed hub network design with production planning and congestion investigation. They located a central warehouse in hub facilities, and factories could be located near warehouses. Also, an Lp-metric method was used to solve their multi-objective model. Ghodratnama, Arbabi, and Azaron (2019) introduced a hub location–allocation problem considering a model that included production planning, supply chains, and queuing theory. They considered hub facilities as industrial townships. Also, manufacturing plants and warehouse congestion were considered in their proposed model.

2.3. Robust optimisation research works

Contreras, Cordeau, and Laporte (2011) presented a hub location problem with unlimited capacity for hubs and used two-stage stochastic programming to deal with uncertain demand and transportation costs. They used the Benders decomposition algorithm augmented with a sample average approximation method to obtain an optimal solution considering the appropriate number of scenarios. They showed that by considering uncertain demand and dependent transportation costs, a two-stage model is equivalent to a single-stage stochastic model or its associated deterministic expected value problem (EVP). In other words, neither uncertain demand nor dependent transportation costs affected the second-stage decision variables (allocation decisions). But they showed that when considering independent transportation costs, the corresponding stochastic problem is not equivalent to its EVP. However, in classical hub location problems considering capacity constraints on hub facilities or other assumptions, different scenarios of demand can affect location and allocation decisions, so the model can be considered as a two-stage stochastic model and is not equivalent to the EVP.

Alumur, Nickel, and Saldanha da Gama (2012) proposed single allocation and multiple allocation hub location problems with uncertain demand and hub establishment costs. They presented three formulations to deal with uncertainty. In the first model, hub establishment costs were uncertain, and the objective was minimising worst-case regret for all scenarios. The second model was formulated as two-stage stochastic programming with uncertain demand, but Contreras, Cordeau, and Laporte (2011) showed that the problem was equivalent to a model with expected values for demand. The third problem was modeled as robust-stochastic with uncertainty in both demand and hub establishment costs. Shahabi and Unnikrishnan (2014) presented robust optimisation for single and multiple allocation hub location problems with uncertain demand. The values for uncertain parameters belong to ellipsoidal interval uncertainty. They proposed a mixed integer nonlinear model and transformed it into a conic quadratic problem with a relaxation strategy. They showed that more hubs are established by the robust model compared with the deterministic model. According to the complexity of the model, their proposed robust model was solved in instances with up to a maximum of 25 nodes using a general commercial solver. Ghaffari-Nasab, Ghazanfari, and Teimoury (2015) presented a robust optimisation model for capacitated single and multiple allocation hub location problems with uncertain demand. Uncertain demand was considered in the capacity constraints, and they used an uncertainty budget to control conservatism. However, they used nominal values for demand in the objective function without considering uncertainty. In other words, demand parameters appeared in the objective function and hub capacity constraints, but they just considered uncertainty in the capacity constraints.

Habibzadeh Boukani, Farhang Moghaddam, and Pishvaee (2016) presented the same single and multiple allocation hub location problems, but the authors considered hub establishment costs and capacity as two sources of uncertainty. They used robust optimisation to deal with uncertainty, and defined several discrete scenarios and obtained the objective value for each scenario to minimise worst-case value. Merakli and Yaman (2016) proposed a robust model for an uncapacitated p-hub median problem with uncertain demand. Uncertain demand was modeled in two different ways: the hose and hybrid models. In the hose model, the only information about demand was the upper limit on the total flow adjacent to each origin-destination node, while the hybrid model included both lower and upper limits on each node. They used the Benders decomposition algorithm for large-scale instances and analysed the effect of uncertainty on the model. Previously mentioned papers used robust optimisation to deal with uncertainty, but these authors considered each uncertain parameter separately in their proposed models. Therefore, Zetina et al. (2017) proposed a model for an uncapacitated hub location problem and used robust optimisation to deal with uncertain demand and transportation costs. In this case, they proposed three models: a hub location problem with uncertain demand, a problem with uncertain transportation costs; and a problem with a combination of the two. The authors used the branch and cut algorithm for a case of uncertain demand and transportation costs. They analysed and examined the effect of uncertainty budgets on objective values and hub configurations, and also compared a robust solution with a deterministic solution. However, in comparison with our analyses, they did not analyse and suggest proper values for uncertainty budget.

Merakli and Yaman (2017) presented a multiple allocation hub location problem with capacity constraints and hose demand uncertainty. The authors used two kinds of Benders decomposition algorithms. For the Benders 2 algorithm, the sub-problem was decomposed into separate problems for each commodity. In each iteration, the optimality cuts for each commodity were added to the master problem. They showed that the Benders 2 decomposition algorithm with a multi-cut approach outperformed the other approaches and can solve Australian Post (AP) instances with up to 50 nodes. Talbi and Todosijević (2017) proposed a robust optimisation model for an uncapacitated multiple allocation hub location problem. They presented a new way to analyse robustness of solutions in the presence of uncertainty and used a variable neighbourhood search algorithm. However, a new robustness measure proposed in our paper, expected aggregate function, allowed for consideration of decision-makers' needs. de Sá, Morabito, and de Camargo (2018) proposed a model for a robust multiple allocation incomplete hub location problem with uncertain demand and hub establishment costs. Furthermore, the Benders decomposition algorithm and hybrid heuristic approaches were used to solve large-scale instances.

Due to the complexity of robust hub location problems, solving large-scale instances is challenging. To address this, Ghaffarinasab (2018) used an efficient tabu search algorithm-based matheuristic algorithm to solve large-scale instances up to 200 nodes. This author proposed a p-hub median problem and used robust optimisation to deal with uncertain demand. Three different models were proposed: hose, hybrid, and budget of uncertainty. The validity of the proposed matheuristic algorithm was evaluated for existing studies that used the Benders decomposition algorithm (Merakli and Yaman 2016). de Sá, Morabito, and de Camargo (2018) applied a Benders decomposition algorithm for an incomplete hub location problem with a service time requirement. They used a robust optimisation approach to deal with uncertain travel times and assumed that travel times belonged to a polyhedral uncertainty set. Up to 2018, robust hub location problem studies did not consider inter-hub flow discount factors as a source of uncertainty. Therefore, Rahmati and Bashiri (2018) proposed robust optimisation for a hub location problem with uncertain demand, hub establishment costs, and inter-hub flow discount factor. However, these uncertain parameters were considered separately in the model, and they could be considered simultaneously. Lozkins, Krasilnikov, and Bure (2019) presented robust optimisation for an uncapacitated multiple allocation hub location problem with a set of demand scenarios. Because of the complexity of the model (an increase in the number of scenarios), the authors used classical and improved Benders decomposition algorithms to solve the proposed model more efficiently. Ghaffarinasab, Zare Andaryan, and Ebadi Torkayesh (2020) proposed robust optimisation for single allocation p-hub median problem. They used two polyhedral uncertainty sets, a hose set and a hybrid set, and used a matheuristic algorithm to solve the problem. A tabu search algorithm and a mathematical model were used in their matheuristic algorithm. Li, Fang, and Wu (2020) used robust optimisation for a hub location problem and considered flows and fixed establishment costs as uncertain parameters in their proposed model. In their paper, in contrast to Shahabi and Unnikrishnan (2014), fixed hub establishment costs were considered to be uncertain and could be affected by total flows. It should be noted that various parameters, such as demand, transportation costs, and so on, are considered in these papers as sources of uncertainty. Compared to our proposed model, none of these papers analysed the conservatism of obtaining appropriate values for budget of uncertainty, and they also did not consider dealing with two-stage robust optimisation with uncertain demand in hub location problems.

In addition to hub location problems, robust optimisation is also used in other problems such as problems dealing with facility locations, supply chains, location transportation, and so on. Basciftci, Ahmed, and Shen (2020) presented a two-stage decision-dependent distributionally robust facility location problem in which moments of stochastic demand were interpreted as functions of facility-location decisions. These authors compared their model with a decision-dependent deterministic model, as well as stochastic programming and distributionally robust models without the decision-dependent assumption. Saif and Delage (2020) studied a capacitated facility location problem with distributionally robust optimisation. They used two algorithms based on column generation to solve a two-stage model. Ivanov et al. (2016) proposed a new method for robustness analysis of schedules that are formulated in continuous time in the state-space domain. Ivanov, Dolgui, and Sokolov (2016) presented robust analysis of schedule coordination in the presence of disruptions in capacities and supply with the help of attainable sets. Zeng and Zhao (2013) used adjustable robust optimisation to deal with uncertainty in a location transportation problem. They developed a decomposition algorithm to generate new columns and rows in each iteration and decrease the number of iterations and computational time. Bertsimas et al. (2013) and Lorca et al. (2016) proposed a two-stage model and a multi-stage robust model for a unit commitment problem. Bruni et al. (2017) presented an adjustable robust optimisation model for a resource-constrained project scheduling problem with uncertain activity duration, and used the Benders decomposition algorithm to solve the problem.

Table 1 provides a review of studies related to the robust hub location problem. The information in Table 1 is as follows: Column 1, author names; Columns 2 (static) and 3 (adjustable), the robust optimisation approach used in the study; Columns 4–9, the uncertain parameters that were considered in the model. Finally, Column 10 shows the solution approach used for solving the problems. The information in Table 1 allows the conclusion that adjustable robust optimisation was not used in hub location problems. In other words, most papers used robust optimisation with one-stage decisions. So in this paper, a two-stage robust optimisation approach was used for dealing with uncertain demand for uncapacitated hub location problems in which decisions were divided into two stages. In the first stage, decision variables were established without revealing uncertain parameters, while in the second stage, decision variables were set in the presence of uncertainty. Furthermore, an accelerated Benders decomposition algorithm with stronger cuts (Pareto-optimal cuts) and a size reduction scheme were used for solving the proposed problem in large-size instances. Also, to obtain appropriate uncertainty budget, a new expected aggregate function wasintroduced.

Table 1. Review of hub location problems based on robust optimisation.

	Uncertain approach		Uncertain parameter
Author(s)	SR	AR	w	c	f	α	cap	t	Solution approach
Alumur, Nickel, and Saldanha da Gama (2012)	✓		✓		✓				Commercial solver
Shahabi and Unnikrishnan (2014)	✓		✓						Commercial solver
Ghaffari-Nasab, Ghazanfari, and Teimoury (2015)	✓		✓						Commercial solver
Habibzadeh Boukani, Farhang Moghaddam, and Pishvaee (2016)	✓				✓		✓		Commercial solver
Merakli and Yaman (2016)	✓		✓						Commercial solver
Zetina et al. (2017)	✓		✓	✓					Branch and cut
Merakli and Yaman (2017)	✓		✓						Benders decomposition
Talbi and Todosijević (2017)	✓		✓						VNS
de Sá, Morabito, and de Camargo (2018)	✓		✓		✓				Benders decomposition
de Sá, Morabito, and de Camargo (2018)	✓							✓	Benders decomposition
Ghaffarinasab (2018)	✓		✓						Tabu search
Rahmati and Bashiri (2018)	✓		✓		✓	✓			Commercial solver
Lozkins, Krasilnikov, and Bure (2019)	✓		✓						Benders decomposition
Li, Fang, and Wu (2020)	✓		✓	✓					Commercial solver
Ghaffarinasab, Zare Andaryan, and Ebadi Torkayesh (2020)	✓		✓						Tabu search
This research		✓	✓						Benders decomposition

Notes: w = Demand, c = Transportation cost, f = Hub establishment cost, α = Discount factor, cap = Capacity of hubs, t = Time, SR = Static Robust, AR = Adjustable Robust.

3. Mathematical model

In this section, a deterministic model of uncapacitated multiple allocation hub location problem proposed by Hamacher et al. (2004) and a two-stage robust hub location problem with uncertain demand are introduced. In this problem, multiple allocation is allowed for commodities flow. According to the transportation cost, several different routes can be selected from each origin-destination nodes for sending commodities. In other words, flows from origin to destination nodes can be routed through different hub facilities. It is assumed that all nodes are hub candidates and the number of hub facilities that will be established is unknown. Hence, the set of hub facilities are determined according to the transportation and hub establishment costs. However in size reduction scheme, presented in this study, the number of hub candidates are decreased. Also, it is assumed that hub facilities have an unlimited capacity for incoming and outgoing flows.

3.1. Deterministic model of hub location problem

In this model, demand and transportation costs between each origin-destination nodes are known and deterministic. N and H are the sets of nodes and hubs ($H\subset N$), $w_{ij}$ is the demand originated at node $i\in N$ and destined to node $j\in N$, $f_k$ is the hub establishment cost, $d_{ij}$ is distances between node $i\in N$ and node $j\in N$, χ is the collection cost per unit, α is the inter hub flow discount factor and δ is the transfer cost. $c_{ijkl}$ determines the transportation cost from origin node ($i\in N$) to destination node ($j\in N$) through the hubs $k\in H$ and $l\in H$, respectively and is calculated by $c_{ijkl}=\chi d_{ik}+\alpha d_{kl}+\delta d_{lj}$. Two decision variables are used in this model, $z_k$ is a binary variable and is equal to 1 when a hub is established in node $k\in H$, otherwise gets zero value. $x_{ijkl}$ is the fraction of flows originated at node $i\in N$ and destined to node $j\in N$ by using hubs $k\in H$ and $l\in H$. The mathematical model of deterministic uncapacitated multiple allocation hub location problem is as follows: (1) $\begin{array}{rl}min& \sum _{k\in H}{f}_k{z}_k+\sum _{i\in N}^{}\sum _{k\in H}^{}\sum _{l\in H}^{}\sum _{j\in N}^{}{w}_{ij}{c}_{ijkl}{x}_{ijkl}\end{array}$(1) (2) $\begin{array}{r}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}:\\ & \sum _{k\in H}^{}\sum _{l\in H}^{}{x}_{ijkl}=1\mathrm{\forall }i\in N,j\in N\end{array}$(2) (3) $\begin{array}{rl}& \sum _{l\in H}^{}{x}_{ijkl}+\sum _{l\in H,l\ne k}^{}{x}_{ijlk}\le z_k\mathrm{\forall }i\in N,\\ & j\in N,k\in H\end{array}$(3) (4) $\begin{array}{rl}& z_k\in \left\{0,1\right\}\mathrm{\forall }k\in H\end{array}$(4) (5) $\begin{array}{rl}& x_{ijkl}\ge 0\mathrm{\forall }i\in N,j\in N,k\in H,\\ & l\in H\end{array}$(5) Expression (1(1) $\begin{array}{rl}min& \sum _{k\in H}{f}_k{z}_k+\sum _{i\in N}^{}\sum _{k\in H}^{}\sum _{l\in H}^{}\sum _{j\in N}^{}{w}_{ij}{c}_{ijkl}{x}_{ijkl}\end{array}$(1) ) is the objective function and minimises both hub establishment and transportation costs. Constraints (2(2) $\begin{array}{r}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}:\\ & \sum _{k\in H}^{}\sum _{l\in H}^{}{x}_{ijkl}=1\mathrm{\forall }i\in N,j\in N\end{array}$(2) ) guarantee that all demand from origin $i\in N$ to destination $j\in N$ must be served. Constraints (3(3) $\begin{array}{rl}& \sum _{l\in H}^{}{x}_{ijkl}+\sum _{l\in H,l\ne k}^{}{x}_{ijlk}\le z_k\mathrm{\forall }i\in N,\\ & j\in N,k\in H\end{array}$(3) ) ensure that there is no direct link between non hub nodes. On the other hand, demand have to be transported from one or two hubs. Constraints (4(4) $\begin{array}{rl}& z_k\in \left\{0,1\right\}\mathrm{\forall }k\in H\end{array}$(4) ) and (5(5) $\begin{array}{rl}& x_{ijkl}\ge 0\mathrm{\forall }i\in N,j\in N,k\in H,\\ & l\in H\end{array}$(5) ) determine the domains of decision variables.

3.2. The proposed two-stage robust hub location problem (TRHLP)

Adjustable robust or two-stage robust optimisation was introduced by Ben-Tal et al. (2004). In mentioned optimisation approach, decision variables are divided into two groups. The decision variables in the first group known as the first stage decision variables are determined when uncertain parameters have not been realised yet. The second stage decision variables are determined after revealing the uncertainties. The objective function of the two-stage robust optimisation is minimising a function of the first stage decision variables and a function of second stage decision variables in worst-case. There are some kinds of uncertainty sets such as box, ellipsoidal, polyhedral and combinations of these three types. Box uncertainty set was proposed by Soyster (1973). In this type of uncertainty, all of the uncertain parameters are equal to the worst case scenario. Therefore, considering this type of uncertainty leads to an excessive conservatism. Ellipsoidal uncertainty set, proposed by Ben-Tal, El Ghaoui, and Nemirovski (2009), have less conservatism in comparison with the previous one. Because only some of the uncertain parameters are equal to their corresponding worst case scenario. Also, the model by considering this type of uncertainty is nonlinear, because of using 2-norm for defining the uncertainties. Bertsimas and Sim (2003) proposed a mathematical model in which level of conservatism is controlled with an uncertainty budget and the model remains linear. When uncertainty budget gets a high value, the level of conservative increases and when it is equal to zero, the proposed model is equivalent to a deterministic form. Therefore in this paper, the same parameter is used in the proposed model which gives the possibility of analysing the model performance with different level of conservatism. In fact decision makers in companies may have different behaviour and conservatism level, so the model can be used for various situations of real applications.

In this paper, it is assumed that demand ($w_{ij}$) is uncertain and the deterministic value of demand is unknown in the planning time. So an interval value is considered to determine the value of demand parameter. The uncertainty set W associated with the demand for each origin-destination nodes is considered to be a polyhedral set and the uncertain parameter $w_{ij}$, is built around a nominal value ${\overline{w}}_{ij}$ and belongs to the interval $[{\overline{w}}_{ij}-{\hat{w}}_{ij},{\overline{w}}_{ij}+{\hat{w}}_{ij}]$, ${\hat{w}}_{ij}$ is deviation value of demand. ${\overline{w}}_{ij}+{\mu }_{ij}{\hat{w}}_{ij},|{\mu }_{ij}|\le 1,\mathrm{\forall }i,j\in N$ is an equivalent formulation for each demand with uncertainty. It is assumed that Γ is an uncertainty budget that controls the level of conservatism with $\sum _{i\in N}^{}\sum _{j\in N}^{}{\mu }_{ij}\le \mathrm{\Gamma }$ constraint. The deviation value for demand is ${\hat{w}}_{ij}\sim U[0,\mathrm{\Omega }\times {\overline{w}}_{ij}]$. Ω is a parameter that determines the maximum amount of deviation of demand from a nominal value which can take a positive value. Two-stage robust formulation for the uncapacitated hub location problem with uncertain demand is presented as follows: (6) $\begin{array}{rl}\underset{z}{min}& \sum _{k\in H}{f}_k{z}_k+\underset{w\in W}{max}\underset{x\in \mathrm{{\rm Y}}(z,w)}{min}\sum _{i\in N}^{}\\ & \sum _{k\in H}^{}\sum _{l\in H}^{}\sum _{j\in N}^{}{w}_{ij}{c}_{ijkl}{x}_{ijkl}\end{array}$(6) (7) $\begin{array}{rl}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}:& \\ & z_k\in \left\{0,1\right\}\mathrm{\forall }k\in H\end{array}$(7) where $\mathrm{{\rm Y}}(z,w)=\left\{x:\left(2\right),\left(3\right),\left(5\right)\right\}$. In Equation (6(6) $\begin{array}{rl}\underset{z}{min}& \sum _{k\in H}{f}_k{z}_k+\underset{w\in W}{max}\underset{x\in \mathrm{{\rm Y}}(z,w)}{min}\sum _{i\in N}^{}\\ & \sum _{k\in H}^{}\sum _{l\in H}^{}\sum _{j\in N}^{}{w}_{ij}{c}_{ijkl}{x}_{ijkl}\end{array}$(6) ), $z_k$ is the first stage decision variable and $x_{ijkl}$ is the second stage decision variable. The objective function in (6(6) $\begin{array}{rl}\underset{z}{min}& \sum _{k\in H}{f}_k{z}_k+\underset{w\in W}{max}\underset{x\in \mathrm{{\rm Y}}(z,w)}{min}\sum _{i\in N}^{}\\ & \sum _{k\in H}^{}\sum _{l\in H}^{}\sum _{j\in N}^{}{w}_{ij}{c}_{ijkl}{x}_{ijkl}\end{array}$(6) ) minimises the cost of the worst-case scenario. The max operator represents the demand scenario in W that generates the largest recourse cost, given the hub locations z. The min operator identifies the least costly solution, and the set $\mathrm{{\rm Y}}(z,w)$ represents possible recourse operations. This problem is NP-hard and the objective function have a max-min term and the model is non-linear, therefore there is a challenge and solving this model iscomplex.

Because of the objective function structure with a min (max–min) term, the proposed model can be solved only by using a decomposition approach like a Benders decomposition algorithm. In another word, this problem can not be solved by a commercial solver without any pre-processing. Hence, the proposed model can not be solved directly without implementing such algorithms. A decomposition approach is needed to ensure the possibility of solving the problem by a commercial solver. Therefore, Benders decomposition algorithm might be useful to solve the proposed model. In the next section, the Benders decomposition algorithm is describedmore.

4. Benders decomposition algorithm

Benders decomposition algorithm was proposed by Benders (1962). In Benders decomposition algorithm, model is divided in two separate problems including master and sub problems. Master problem is an MIP or IP model and binary or integer decision variables exist in the master problem. Sub problem is an LP model and consists of continuous decision variables. The sub problem of two-stage robust hub location problem is presented here: (8) $\begin{array}{rl}\underset{w\in W}{max}\underset{x\in \mathrm{{\rm Y}}(z,w)}{min}& \sum _{i\in N}^{}\sum _{k\in H}^{}\sum _{l\in H}^{}\sum _{j\in N}^{}{w}_{ij}{c}_{ijkl}{x}_{ijkl}\end{array}$(8) (9) $\begin{array}{r}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}:\\ & \sum _{k\in H}^{}\sum _{l\in H}^{}{x}_{ijkl}=1\mathrm{\forall }i\in N,j\in N\end{array}$(9) (10) $\begin{array}{rl}& \sum _{l\in H}^{}{x}_{ijkl}+\sum _{l\in H,l\ne k}^{}{x}_{ijlk}\le {\overline{z}}_k\mathrm{\forall }i\in N,\\ & j\in N,k\in H\end{array}$(10) (11) $\begin{array}{rl}& x_{ijkl}\ge 0\mathrm{\forall }i\in N,j\in N,\\ & k\in H,l\in H\end{array}$(11) Equation (8(8) $\begin{array}{rl}\underset{w\in W}{max}\underset{x\in \mathrm{{\rm Y}}(z,w)}{min}& \sum _{i\in N}^{}\sum _{k\in H}^{}\sum _{l\in H}^{}\sum _{j\in N}^{}{w}_{ij}{c}_{ijkl}{x}_{ijkl}\end{array}$(8) ) is still hard to solve because of max min term. In constraints (10(10) $\begin{array}{rl}& \sum _{l\in H}^{}{x}_{ijkl}+\sum _{l\in H,l\ne k}^{}{x}_{ijlk}\le {\overline{z}}_k\mathrm{\forall }i\in N,\\ & j\in N,k\in H\end{array}$(10) ) ${\overline{z}}_k$ is the obtained value from the master problem that is fixed in the sub problem. To consider the max-min term in the model, a dual form of the sub problem is considered. ${\alpha }_{ij}$ is dual variable corresponding to constraints (9(9) $\begin{array}{r}\mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{o}:\\ & \sum _{k\in H}^{}\sum _{l\in H}^{}{x}_{ijkl}=1\mathrm{\forall }i\in N,j\in N\end{array}$(9) ). $u_{ijk}$ is dual variable corresponding to decomposed constraints (10(10) $\begin{array}{rl}& \sum _{l\in H}^{}{x}_{ijkl}+\sum _{l\in H,l\ne k}^{}{x}_{ijlk}\le {\overline{z}}_k\mathrm{\forall }i\in N,\\ & j\in N,k\in H\end{array}$(10) ). Dual form of this problem is presented as follows: (12) $\begin{array}{rl}\underset{w\in W}{max}:& \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{\overline{z}}_k{u}_{ijk}\end{array}$(12) (13) $\begin{array}{r}\text{Subject to:}\\ & {\alpha }_{ij}-u_{ijk}-u_{ijl}\le w_{ij}{c}_{ijkl}\mathrm{\forall }i\in N,j\in N,\\ & k\in H,l\in H,k\ne l\end{array}$(13) (14) $\begin{array}{rl}& {\alpha }_{ij}-u_{ijk}\le w_{ij}\times (\chi d_{ik}+\delta d_{kj})\mathrm{\forall }i\in N,\\ & j\in N,k\in H\end{array}$(14) (15) $\begin{array}{rl}& u_{ijk}\ge 0\mathrm{\forall }i\in N,j\in N,k\in H\end{array}$(15) In constraints (13(13) $\begin{array}{r}\text{Subject to:}\\ & {\alpha }_{ij}-u_{ijk}-u_{ijl}\le w_{ij}{c}_{ijkl}\mathrm{\forall }i\in N,j\in N,\\ & k\in H,l\in H,k\ne l\end{array}$(13) ) and (14(14) $\begin{array}{rl}& {\alpha }_{ij}-u_{ijk}\le w_{ij}\times (\chi d_{ik}+\delta d_{kj})\mathrm{\forall }i\in N,\\ & j\in N,k\in H\end{array}$(14) ), exactly two and one hubs are considered for transfer flows between origin-destination nodes, respectively. Uncertain parameter still don't considered at this model. So constraints (13(13) $\begin{array}{r}\text{Subject to:}\\ & {\alpha }_{ij}-u_{ijk}-u_{ijl}\le w_{ij}{c}_{ijkl}\mathrm{\forall }i\in N,j\in N,\\ & k\in H,l\in H,k\ne l\end{array}$(13) ) and (14(14) $\begin{array}{rl}& {\alpha }_{ij}-u_{ijk}\le w_{ij}\times (\chi d_{ik}+\delta d_{kj})\mathrm{\forall }i\in N,\\ & j\in N,k\in H\end{array}$(14) ) should be changed. It should be noted that the worst-case value of uncertain parameter in primal problem is equal to the best-case of uncertain parameter in dual of sub problem (Jeyakumar and Li 2010). Robust counterpart of this model with considering uncertain demand is as follows: (16) $\begin{array}{rl}\underset{}{max}:& \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{\overline{z}}_k{u}_{ijk}\end{array}$(16) (17) $\begin{array}{r}\text{Subject to:}\\ & {\alpha }_{ij}-u_{ijk}-u_{ijl}\le {\overline{w}}_{ij}{c}_{ijkl}+{\hat{w}}_{ij}{c}_{ijkl}{\mu }_{ij}\\ & \mathrm{\forall }i\in N,j\in N,(k\ne l)\in H\end{array}$(17) (18) $\begin{array}{rl}& {\alpha }_{ij}-u_{ijk}\le ({\overline{w}}_{ij}+{\hat{w}}_{ij}{\mu }_{ij})(\chi d_{ik}+\delta d_{kj})\\ & \mathrm{\forall }i\in N,j\in N,k\in H\end{array}$(18) (19) $\begin{array}{rl}& \sum _{i\in N}^{}\sum _{j\in N}^{}{\mu }_{ij}\le \mathrm{\Gamma }\end{array}$(19) (20) $\begin{array}{rl}& 0\le {\mu }_{ij}\le 1\mathrm{\forall }i\in N,j\in N\end{array}$(20) (21) $\begin{array}{rl}& u_{ijk}\ge 0\mathrm{\forall }i\in N,j\in N,k\in H\end{array}$(21) First decision variable ($z_k$) is appeared in the master problem. Master problem of two-stage robust uncapacitated hub location problem can be stated as follows: (22) $\begin{array}{rl}min:& \sum _{k\in H}{f}_k{z}_k+\eta \end{array}$(22) (23) $\begin{array}{r}\text{Subject to:}\\ & \eta \ge \sum _{i\in N}^{}\sum _{j\in N}^{}{\overline{\alpha }}_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k{\overline{u}}_{ijk}\end{array}$(23) (24) $\begin{array}{rl}& \sum _{k\in H}^{}{z}_k\ge 1\end{array}$(24) (25) $\begin{array}{rl}& z_k\in \left\{0,1\right\}\mathrm{\forall }k\in H\end{array}$(25) Constraint (23(23) $\begin{array}{r}\text{Subject to:}\\ & \eta \ge \sum _{i\in N}^{}\sum _{j\in N}^{}{\overline{\alpha }}_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k{\overline{u}}_{ijk}\end{array}$(23) ) is the optimality cut which is generated in each iteration. Constraint (24(24) $\begin{array}{rl}& \sum _{k\in H}^{}{z}_k\ge 1\end{array}$(24) ) guarantees that at least one hub should be established. A pseudo code of the Benders algorithm for the proposed model is illustrated in Algorithm 1. With an initial value of ${\overline{z}}_k$, the dual sub problem is solved and the value of dual coefficients are obtained, if dual sub problem have unbound value an unbound modified problem should be solved and a feasibility cut is added in the master problem, else an optimality cut is generated based on the obtained variables of the dual sub problem and added in the master problem. These steps are continued until the algorithm to be converged. (26) $\begin{array}{rl}\underset{}{max}:& \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{\overline{z}}_k{u}_{ijk}\end{array}$(26) (27) $\begin{array}{r}\text{Subject to:}\\ & \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{\overline{z}}_k{u}_{ijk}=1\end{array}$(27) (28) $\begin{array}{rl}& {\alpha }_{ij}-u_{ijk}-u_{ijl}\le 0\mathrm{\forall }i\in N,j\in N,\\ & (k\ne l)\in H\end{array}$(28) (29) $\begin{array}{rl}& {\alpha }_{ij}-u_{ijk}\le 0\mathrm{\forall }i\in N,j\in N,k\in H\end{array}$(29) (30) $\begin{array}{rl}& \sum _{i\in N}^{}\sum _{j\in N}^{}{\mu }_{ij}\le 0\end{array}$(30) (31) $\begin{array}{rl}& 0\le {\mu }_{ij}\le 1\mathrm{\forall }i\in N,j\in N\end{array}$(31) (32) $\begin{array}{rl}& u_{ijk}\ge 0\mathrm{\forall }i\in N,j\in N,k\in H\end{array}$(32) Expressions (26(26) $\begin{array}{rl}\underset{}{max}:& \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{\overline{z}}_k{u}_{ijk}\end{array}$(26) )–(32(32) $\begin{array}{rl}& u_{ijk}\ge 0\mathrm{\forall }i\in N,j\in N,k\in H\end{array}$(32) ) are unbound modified problem for obtain dual variables for generate feasibility cut. In unbound modified problem for generating feasibility cut for the master problem, all constraints are transferred to the origin of coordinates. Therefore, all parameters in which no variable is multiplied take zero value in the unbound modified model. It should be noted that, constraints (30(30) $\begin{array}{rl}& \sum _{i\in N}^{}\sum _{j\in N}^{}{\mu }_{ij}\le 0\end{array}$(30) ) and (31(31) $\begin{array}{rl}& 0\le {\mu }_{ij}\le 1\mathrm{\forall }i\in N,j\in N\end{array}$(31) ) are redundant in the unbound modified problem and can be ignored, because the ${\mu }_{ij}$ takes zero value. To speed up the algorithm, accelerated Benders decomposition algorithm is used to achieve optimal solution in less iterations comparing with the classical Benders decomposition algorithm.

4.1. Pareto-optimal cuts

Magnanti and Wong (1981) proposed a method for classical Benders decomposition algorithm with faster convergence rate. This procedure seeks to find stronger cuts from the dual sub problem when there are alternative solutions. In other words this method selects stronger cut among generated cuts based on achieved alternative solutions by using an auxiliary mathematical model. A cut is called a Pareto-optimal cut if it dominate other available cuts. A cut generated using a solution $({\alpha }^a,u^a)$ achieved from the dual sub problem is stronger than $({\alpha }^b,u^b)$ if and only if: $\begin{array}{rl}& \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}^a-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k{u}_{ijk}^a\\ & \ge \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}^b-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k{u}_{ijk}^b\end{array}$ In addition of dual sub problem, one more model should be solved in each iteration to obtain the best stronger cut from all multiple solutions. In other words in each iteration, two different sub problems are solved associated to the current solution (${\overline{z}}_k$) and the core point ($z_k^o$). To obtain a Pareto-optimal cut, following model should be solved: (33) $\begin{array}{rl}max:& \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k^o{u}_{ijk}\end{array}$(33) (34) $\begin{array}{r}\text{Subject to:}\\ & \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k^{iter}{u}_{ijk}={\overline{Z}}_{dsp}\\ & \text{(16)--(20)}\end{array}$(34) $z_k^o$ is a core point and have a value between $[0,1]$ for binary variables and should be tuned. Constraint (34(34) $\begin{array}{r}\text{Subject to:}\\ & \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k^{iter}{u}_{ijk}={\overline{Z}}_{dsp}\\ & \text{(16)--(20)}\end{array}$(34) ) guarantees that the value of the dual sub problem should not be changed. Due to the constraint (34(34) $\begin{array}{r}\text{Subject to:}\\ & \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k^{iter}{u}_{ijk}={\overline{Z}}_{dsp}\\ & \text{(16)--(20)}\end{array}$(34) ), this additional problem (Pareto model) is much harder problem to solve in comparison with the dual sub problem. Hence Papadakos (2008) showd that with using a method, it is not necessary to consider dual sub problem objective function in the Pareto-optimal cut model and constraint (34(34) $\begin{array}{r}\text{Subject to:}\\ & \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k^{iter}{u}_{ijk}={\overline{Z}}_{dsp}\\ & \text{(16)--(20)}\end{array}$(34) ) can be removed from the Pareto model. He proved that with considering different core points in each iteration, the constraint (34(34) $\begin{array}{r}\text{Subject to:}\\ & \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k^{iter}{u}_{ijk}={\overline{Z}}_{dsp}\\ & \text{(16)--(20)}\end{array}$(34) ) can be ignored from the model. It is assumed that $z_{kt}^o$ and ${\overline{z}}_{kt}$ are core point and the master problem optimal solution in iteration t, respectively. Also λ is a parameter which can take a value between zero and one. The value of λ, empirically is considering equal to 0.5 ($\lambda =0.5$). According to the $z_{kt+1}^o=(1-\lambda )z_{kt}^o+\lambda {\overline{z}}_{kt}$ relations (and any convex combination), the value of the core points can be updated in each iteration. In other words in each iteration, core point value is updated according to the previous core point value and master problem solution. This new core point value is considered for Pareto-optimal cut model in the current iteration. So, for accelerating Benders decomposition algorithm with a stronger cut in each iteration, the dual sub problem corresponding to the (33(33) $\begin{array}{rl}max:& \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k^o{u}_{ijk}\end{array}$(33) ), (16(16) $\begin{array}{rl}\underset{}{max}:& \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{\overline{z}}_k{u}_{ijk}\end{array}$(16) )–(20(20) $\begin{array}{rl}& 0\le {\mu }_{ij}\le 1\mathrm{\forall }i\in N,j\in N\end{array}$(20) ) constraints, without constraint (34(34) $\begin{array}{r}\text{Subject to:}\\ & \sum _{i\in N}^{}\sum _{j\in N}^{}{\alpha }_{ij}-\sum _{i\in N}^{}\sum _{j\in N}^{}\sum _{k\in H}^{}{z}_k^{iter}{u}_{ijk}={\overline{Z}}_{dsp}\\ & \text{(16)--(20)}\end{array}$(34) ) is solved. A pseudo-code of the Pareto-optimal cut Benders algorithm is presented inAlgorithm 2.

5. Computational experiment

In this section, several computational experiments are done in order to analyse the performance of two-stage robust model as well as applied Benders decomposition algorithm. The well known sets of instances such as Australian Post (AP), Civil Aviation Board (CAB) and Turkish Network (TR) datasets are used in this paper for analysis. It should be noted that, hub establishment fixed cost is calculated based on the equations proposed by Correia, Nickel, and Saldanha da Gama (2018). These equations are asfollows: (35) $\begin{array}{rl}{o}_k& =\sum _{j\in N}^{}{w}_{kj},\mathrm{\forall }\mathrm{k}\in \mathrm{H}\end{array}$(35) (36) $\begin{array}{rl}{f}_k& =c\times \log \left(o_k\right),\mathrm{\forall }k\in H\end{array}$(36) Equations (35(35) $\begin{array}{rl}{o}_k& =\sum _{j\in N}^{}{w}_{kj},\mathrm{\forall }\mathrm{k}\in \mathrm{H}\end{array}$(35) ) and (36(36) $\begin{array}{rl}{f}_k& =c\times \log \left(o_k\right),\mathrm{\forall }k\in H\end{array}$(36) ) are used for calculating each hub establishment cost according to the flows entered to each hub. c is a cost factor and is determined as an input parameter. Large value for parameter c leads to establishment of few hubs. The values of χ and δ are equal to 1 and it is assumed that $\alpha \in \{0.2,0.5,0.8\}$. Because of economy of scale and also for saving money, α has smaller value in comparison with other coefficients (χ, δ) using in transferring demand. Uncertainty budget (Γ), denotes the number of parameters that have a deviation from their nominal values. Without loss of generality, it is assumed that ${\mathrm{\Gamma }}_{\mathrm{\%}}$ represent the percent of uncertain parameters that have deviation and belongs to the ${\mathrm{\Gamma }}_{\mathrm{\%}}\in \{0.1,0.2,\dots ,1\}$ set and the total number of demand parameters are equal to $|N|\times (|N|-1)$. For example, for a 10-node instance with 90 parameters ($10\times 9$), ${\mathrm{\Gamma }}_{\mathrm{\%}}=0.1$ means that 10 percent of demand parameter (9 parameter) have deviation from their nominal values. In the rest of the paper and experiments, for simplicity, uncertainty budget represent as ${\mathrm{\Gamma }}_{\mathrm{\%}}$. Two-stage robust hub location problem was solved by GAMS software and run in an Intel Core i7 with 3.7 GHz CPU and 32 GB of RAM.

5.1. Analysis on the initial core point

An analysis was done to obtain the optimum initial core points value for different values of uncertainty budgets. To find a better value for the initial core point, an experiment was designed and the number of iterations and CPU time (seconds) of the Pareto-optimal cut Benders decomposition algorithm were obtained for each initial core point and uncertainty budgets (${\mathrm{\Gamma }}_{\mathrm{\%}}$). The results for the AP 20-node instance are shown in Table 2. The numbers placed outside and inside the parentheses show the number of iterations and CPU time, respectively. The best initial core point with the smallest number of iterations and lowest CPU time (seconds) was selected for each level of uncertainty budget to be used for further analyses. As an example, when the uncertainty budget was equal to 0.1, the value of 0.25 for the initial core point had the lowest number of iteration (16) and CPU time (74 seconds) in comparison with the other initial core point values. Also, the best initial core point value was 0.25 for uncertainty budgets of 0.2 and 0.9. This analysis is not rational for obtaining the best value for the initial core point for large-scale instances. Therefore, the values obtained from Table 2 were used for other large-scale instances (AP 50-node and TR 81-node instances). The value of the initial core point for the CAB 25-node instance was also chosen according to Table 2. In short, the AP dataset, TR dataset, and part of the CAB dataset (with 25 nodes) were investigated in this study.

Table 2. Number of iterations and CPU time with different initial core points and Γ for AP 20-node instance.

	Uncertainty budget (${\mathrm{\Gamma }}_{\mathrm{\%}}$)
Core point	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
0.05	34 (157)	39 (180)	60 (278)	71 (328)	73 (338)	74 (342)	70 (324)	68 (315)	60 (278)	50 (231)
0.1	29 (134)	34 (157)	59 (273)	68 (315)	74 (342)	69 (319)	65 (301)	62 (287)	57 (264)	51 (236)
0.15	23 (106)	20 (93)	33 (153)	48 (217)	55 (254)	52 (241)	44 (204)	43 (199)	38 (176)	35 (162)
0.2	18 (83)	15 (74)	22 (102)	37 (171)	41 (190)	28 (130)	25 (116)	24 (111)	18 (83)	17 (79)
0.25	16 (74)	17 (69)	16 (74)	33 (153)	34 (157)	30 (139)	23 (106)	21 (97)	15 (69)	11 (51)
0.3	17 (79)	17 (79)	19 (88)	27 (125)	31 (143)	29 (134)	23 (106)	18 (83)	13 (60)	9 (42)
0.35	22 (102)	17 (82)	20 (97)	22 (102)	26 (120)	23 (106)	21 (88)	15 (69)	10 (46)	8 (37)
0.4	22 (100)	18 (76)	20 (93)	22 (104)	27 (127)	22 (102)	19 (93)	15 (72)	10 (49)	8 (39)
0.45	22 (103)	25 (83)	21 (97)	22 (105)	27 (125)	23 (106)	20 (93)	15 (71)	24 (48)	8 (40)
0.5	31 (143)	21 (116)	24 (111)	33 (153)	45 (208)	40 (185)	20 (130)	23 (106)	24 (111)	14 (65)
0.55	32 (148)	27 (125)	32 (149)	42 (194)	46 (213)	35 (162)	28 (138)	25 (115)	24 (111)	18 (83)
0.6	32 (146)	27 (123)	32 (148)	41 (190)	46 (217)	35 (164)	30 (137)	25 (119)	23 (111)	18 (85)
0.65	32 (149)	27 (125)	33 (153)	41 (190)	46 (214)	34 (157)	30 (136)	25 (117)	23 (106)	18 (84)
0.7	32 (147)	27 (124)	32 (148)	41 (192)	46 (218)	35 (162)	30 (146)	25 (119)	23 (106)	18 (88)
0.75	32 (148)	27 (127)	34 (157)	42 (194)	46 (217)	34 (157)	30 (142)	25 (120)	24 (111)	18 (87)
0.8	32 (150)	27 (126)	33 (153)	42 (196)	46 (213)	35 (162)	30 (139)	25 (116)	24 (115)	18 (86)
0.85	32 (139)	27 (123)	33 (154)	42 (195)	46 (214)	34 (157)	30 (138)	25 (116)	24 (110)	18 (89)
0.9	32 (147)	27 (124)	32 (148)	42 (194)	46 (216)	35 (162)	30 (137)	25 (117)	24 (113)	18 (83)
0.95	32 (148)	27 (125)	32 (143)	42 (198)	46 (217)	35 (164)	30 (142)	25 (118)	24 (109)	18 (87)

Note: Numbers in and out of parentheses are number of iterations and CPU time.

5.2. Performance evaluation of the Pareto-optimal cut Benders decomposition to solve the TRHLP model

Performance of the Pareto-optimal cut Benders decomposition algorithm was compared with the classical Benders decomposition algorithm under different values of uncertainty budgets (${\mathrm{\Gamma }}_{\mathrm{\%}}\in \{0.1,0.2,\dots ,1\}$) and discount factors ($\alpha \in \{0.2,0.5,0.8\}$). A time limit of 5 hours (18,000 seconds) is considered for CPU time (computation time). Table 3 shows that it is possible to conclude that the Benders decomposition algorithm with Pareto-optimal cut performs better than the classical Benders algorithm, considering number of iterations and CPU time (seconds) to convergence. As an example, when α and ${\mathrm{\Gamma }}_{\mathrm{\%}}$ are equal to 0.5, the Benders decomposition algorithm with Pareto-optimal cut converges to an optimal solution in 142 iterations and 5,454.38 seconds, while the classical algorithm required 901 iterations and did not converge to the optimal value in a predefined computation time (5 hours) with an 8.57% gap. The CPU time (seconds) of Pareto-optimal cut algorithm in average is half of the classical Benders decomposition algorithm.

Table 3. Comparison of the Pareto-optimal cut Benders decomposition algorithm with classical one for AP 50-node instance.

		Classical					Pareto
α	${\mathrm{\Gamma }}_{\mathrm{\%}}$	LB	UB	$\mathrm{\%}$ Gap	$\mathrm{\#}$ Iteration	CPU time (s)	LB	UB	$\mathrm{\%}$ Gap	$\mathrm{\#}$ Iteration	CPU time (s)
0.2	0.1	77,939.01	81,548.64	4.43	1,154	18,000	78,386.10	78,386.10	0	140	9943.85
	0.2	82,871.20	88,534.01	6.40	902	18,000	84,325.87	84,325.87	0	210	10,842.81
	0.3	85,432.37	91,787.19	6.92	649	18,000	88,269.83	88,269.83	0	194	10,388.69
	0.4	88,292.94	94,801.17	6.87	646	18,000	91,354.89	91,354.89	0	297	16,635.38
	0.5	90,558.03	98,710.37	8.26	645	18,000	93,721.03	93,721.03	0	282	16,502.75
	0.6	92,513.77	99,432.40	6.96	666	18,000	95,615.17	95,615.17	0	217	13,592.20
	0.7	93,980.97	102,610.06	8.41	657	18,000	97,215.76	97,215.76	0	190	12,327.36
	0.8	95,357.20	102,587.52	7.05	644	18,000	98,491.07	98,491.07	0	138	9374.95
	0.9	96,451.06	105,143.93	8.27	650	18,000	99,442.71	99,442.71	0	94	6990.08
	1	97,207.02	104,008.15	6.54	672	18,000	100,011.91	100,011.91	0	66	2313.88
0.5	0.1	94,262.60	94,262.60	0	696	7,676.30	94,262.60	94,262.60	0	117	4907.80
	0.2	102,365.34	102,365.34	0	943	9,393.27	102,365.34	102,365.34	0	110	4537.91
	0.3	106,828.03	110,395.54	3.23	921	18,000	108,034.90	108,034.90	0	108	4356.97
	0.4	111,169.98	117,029.39	5.01	1,004	18,000	112,396.49	112,396.49	0	121	4830.53
	0.5	114,438.56	125,170.63	8.57	901	18,000	115,921.20	115,921.20	0	142	5454.38
	0.6	117,420.13	121,554.73	3.40	985	18,000	118,810.25	118,810.25	0	133	5051.10
	0.7	119,784.43	126,043.37	4.97	953	18,000	121,223.39	121,223.39	0	157	5862.68
	0.8	121,833.41	124,817.18	2.39	999	18,000	123,183.40	123,183.40	0	160	5722.88
	0.9	123,334.31	126,578.63	2.56	887	18,000	124,756.85	124,756.85	0	156	5470.46
	1	124,544.98	130,956.92	4.90	980	18,000	125,821.31	125,821.31	0	135	4415.37
0.8	0.1	104,524.39	104,524.39	0	723	8518.27	104,524.39	104,524.39	0	114	5650.67
	0.2	114,382.19	114,382.19	0	750	8738.94	114,382.19	114,382.19	0	146	6053.82
	0.3	121,008.00	121,008.00	0	800	9468.76	121,008.00	121,008.00	0	156	6073.68
	0.4	126,134.90	126,134.90	0	804	9971.89	126,134.90	126,134.90	0	166	6497.57
	0.5	130,294.10	130,294.10	0	756	8293.17	130,294.10	130,294.10	0	176	6962.41
	0.6	133,728.35	133,728.35	0	784	9293.17	133,728.35	133,728.35	0	176	7001.22
	0.7	136,633.57	136,633.57	0	811	9987.25	136,633.57	136,633.57	0	184	7774.22
	0.8	139,051.80	139,051.80	0	858	9545.49	139,051.80	139,051.80	0	186	7502.77
	0.9	140,976.72	140,976.72	0	956	12,162.18	140,976.72	140,976.72	0	180	7358.77
	1	142,279.06	142,279.06	0	897	9,930.68	142,279.06	142,279.06	0	190	5989.30
Average				3.5	823.1	14,565.98			0	161.37	7546.21

Note: LB = Lower bound, UB = Upper bound.

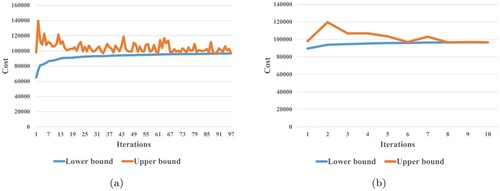
Figure 1(a) shows the convergence trend for the classical Benders decomposition algorithm in a case of an uncertainty budget of 0.9 for the AP 20-node instance. The value of the lower bound in each iteration must be greater than the value in the previous iterations. But this requirement does not apply to the upper bound. In other words, the upper bound can take a different value in each iteration that can be greater or smaller than the upper bounds in previous iterations. Figure 1(b) demonstrates the convergence trend for the Pareto-optimal cut Benders decomposition algorithm in a case of an uncertainty budget equal to 0.9 for the AP 20-node instance. Comparison of Figure 1(a-b) confirms the rapid convergence of the Pareto-optimal cut Benders decomposition to solve the proposed model, compared with the classical Benders decomposition model.

Figure 1. Convergence of (a) classical and (b) Pareto-optimal cut Benders decomposition algorithm for AP 20-node instance.

5.3. Sensitivity analysis on the model parameters

The impacts of model parameters such as uncertainty budget (${\mathrm{\Gamma }}_{\mathrm{\%}}$), maximum deviation value (Ω), and inter-hub flow discount factor (α) on the hub network configuration and its objective function (costs) were analysed.

Demand by customers can change during the year, with high or low fluctuations. For both high and low demand uncertainty during the year, the current locations of hub facilities are very important. Decisions about establishing hub facilities are strategic decisions, so the number and locations of hubs are very important for future incidents and can significantly affect transportation costs. Therefore, an analysis is needed to evaluate the effect of uncertainty on location and allocation decisions. Larger values of uncertainty budgets or maximum deviation value (Ω) may guarantee solution for high fluctuations in demand. Also, discount factor (α) tariff between hubs may change over time, and an analysis should be done for different values of discount factor. Moreover, parameters were investigated to establish which could illustrate the usefulness of the study's model, so that decision-makers for production hub facilities can use the proposed model for their decision-making according to the results of the sensitivity analysis carried out. The results for analysis of different values of uncertainty budgets and α with $\mathrm{\Omega }=1$ and $\mathrm{\Omega }=2$ for the AP 20-node instance, are reported in Tables 4 and 5, respectively. In the case of high values for uncertainty budget, the objective function (costs) will increase with more established hubs. In spite of uncertainty budget behaviour, fewer hubs will be established by increasing discount factor (α). Also, Ω has a direct effect on costs and the number of established hubs. In other words, increasing Ω, increases the number of established hub facilities and the objective function value. Also, Tables 6 and 7 show the results for the AP 50-node and CAB 25-node instances, respectively. The percent of the gap for these tables was reported as zero, because of the optimal values obtained within a predeterminedtime limit.

Table 4. Impact of uncertainty budget and α with $\mathrm{\Omega }=1$ for AP 20-node instance.

α	${\mathrm{\Gamma }}_{\mathrm{\%}}$	Cost	$\mathrm{\%}$ Gap	$\mathrm{\#}$ Iterations	CPU time (s)	Hub configuration
0.2	0.1	75,466.02	0	16	74.58	2,8,15,18
	0.2	81,367.25	0	15	67.53	2,8,15,18
	0.3	85,634.26	0	16	67.53	2,8,15,18
	0.4	88,936.20	0	22	91.58	2,8,15,18
	0.5	91,527.80	0	26	106.81	2,5,8,11,15,18
	0.6	93,162.38	0	22	97.92	2,5,8,11,15,18
	0.7	94,533.37	0	19	85.40	2,5,8,11,15,18
	0.8	95,659.90	0	15	71.53	2,5,8,11,15,18
	0.9	96,533.34	0	10	45.39	2,5,8,11,15,18
	1	97,035.53	0	8	16.90	2,5,8,11,15,18
0.5	0.1	82,672.30	0	11	47.24	2,9,18
	0.2	90,374.38	0	11	45.63	2,9,18
	0.3	95,715.18	0	12	49.95	2,9,18
	0.4	99,871.69	0	11	46.74	2,9,18
	0.5	103,338.82	0	19	74.64	2,9,18
	0.6	106,101.93	0	18	70.59	2,9,12,18
	0.7	108,179.99	0	17	76.74	2,9,12,18
	0.8	109,822.48	0	14	59.79	2,9,12,18
	0.9	111,140.80	0	17	72.96	2,9,12,18
	1	112,022.44	0	14	40.00	2,9,12,18
0.8	0.1	85,878.82	0	11	42.45	8,18
	0.2	94,994.82	0	12	22.95	8,18
	0.3	101,126.60	0	17	24.27	8,18
	0.4	105,643.30	0	18	24.59	2,9,18
	0.5	109,245.40	0	14	17.47	2,9,18
	0.6	112,326.39	0	17	24.55	2,9,18
	0.7	114,856.79	0	18	27.48	2,9,18
	0.8	116,918.78	0	18	26.30	2,9,18
	0.9	118,437.75	0	17	21.03	7,14,18
	1	119,379.74	0	16	17.00	7,14,18

Table 5. Impact of uncertainty budget and α with $\mathrm{\Omega }=2$ for AP 20-node instance.

α	${\mathrm{\Gamma }}_{\mathrm{\%}}$	Cost	$\mathrm{\%}$ Gap	$\mathrm{\#}$ Iterations	CPU time (s)	Hub configuration
0.2	0.1	86,124.31	0	20	37.24	2,8,15,18
	0.2	97,604.13	0	53	98.52	2,5,8,11,15,18
	0.3	104,029.84	0	43	79.39	2,5,8,11,18,20
	0.4	108,951.15	0	39	69.78	2,5,8,11,18,20
	0.5	112,971.81	0	36	63.41	2,5,8,11,18,20
	0.6	116,241.99	0	40	75.88	2,5,8,11,18,20
	0.7	119,019.42	0	38	70.18	2,5,8,11,18,20
	0.8	121,325.50	0	40	89.44	2,5,8,11,15,17,18
	0.9	122,985.86	0	31	67.67	2,5,8,11,15,17,18
	1	123,973.63	0	13	28.55	2,5,8,11,15,17,18
0.5	0.1	96,910.16	0	14	30.22	2,9,18
	0.2	112,314.31	0	24	49.07	2,9,18
	0.3	122,076.32	0	28	59.82	2,9,12,18
	0.4	129,551.00	0	39	88.80	2,9,12,18
	0.5	135,221.43	0	38	78.16	2,5,8,16,18,20
	0.6	139,532.19	0	29	58.08	2,5,8,16,18,20
	0.7	143,283.35	0	25	51.23	2,5,8,16,18,20
	0.8	146,431.61	0	31	65.39	2,5,8,16,18,20
	0.9	149,106.54	0	26	57.08	2,5,8,16,18,20
	1	150,833.50	0	22	38.00	2,5,8,12,14,18
0.8	0.1	102,630.64	0	14	23.35	7,18
	0.2	119,910.56	0	16	28.22	2,9,18
	0.3	131,086.39	0	17	29.42	2,9,18
	0.4	139,365.59	0	16	28.49	2,9,12,18
	0.5	146,100.41	0	16	26.65	2,9,12,18
	0.6	151,672.79	0	15	26.52	2,9,12,18
	0.7	156,152.37	0	17	28.31	2,9,12,18
	0.8	159,779.39	0	16	25.76	2,9,12,18
	0.9	162,654.51	0	15	24.32	2,9,12,18
	1	164,583.10	0	12	18.00	2,9,12,18

Table 6. Impact of uncertainty budget and α with $\mathrm{\Omega }=1$ for AP 50-node instance.

α	${\mathrm{\Gamma }}_{\mathrm{\%}}$	Cost	$\mathrm{\%}$ Gap	$\mathrm{\#}$ Iterations	CPU time (s)	Hub configuration
0.2	0.1	78,386.10	0	140	9,943.85	4,9,12,15,27,29,33,35,43
	0.2	84,325.87	0	210	10,842.81	4,7,9,12,15,27,29,33,35,43
	0.3	88,269.83	0	194	10,388.69	4,7,9,12,15,26,29,33,35,43
	0.4	91,354.89	0	297	16,635.38	4,7,9,12, 15,26,29,33,35,43
	0.5	93,721.03	0	282	16,502.75	3,5,7,9,12,15,26,29,33,35,38,43
	0.6	95,615.17	0	217	13,592.20	3,5,7,9,12,15,26,29,33,35,38,43
	0.7	97,215.76	0	190	12,327.36	3,5,7,9,12,15,26,29,33,35,38,43
	0.8	98,491.07	0	138	9,374.95	3,5,7,9,13,15,21,27,29,33,35,43,48
	0.9	99,442.71	0	94	6,990.07	3,5,7,9,13,15,21,27,29,33,35,43,48
	1	100,011.91	0	66	2,313.88	3,5,7,9,13,15,21,27,29,33,35,43,48
0.5	0.1	94,262.60	0	117	4,907.80	4,9,12,15,28,33,35
	0.2	102,365.34	0	110	4,537.91	4,9,12,15,28,33,35
	0.3	108,034.90	0	108	4,356.97	4,9,12,15,26,29,33,35
	0.4	112,396.49	0	121	4,830.53	4,9,12,15,26,29,33,35
	0.5	115,921.20	0	142	5,454.38	4,9,12,15,26,29,33,35
	0.6	118,810.25	0	133	5,051.10	4,9,12,15,26,29,33,35
	0.7	121,223.39	0	157	5,862.68	4,9,12,15,26,29,33,35
	0.8	123,183.40	0	160	5,722.88	4,9,12,15,18,29,33,35,37
	0.9	124,756.85	0	156	5,470.46	4,9,12,15,18,29,33,35,37,42
	1	125,821.31	0	135	4,415.37	4,9,12,15,27,29,33,35,37,42
0.8	0.1	104,524.39	0	114	5,650.67	3,15,28,32,35
	0.2	114,382.19	0	146	6,053.82	3,15,28,32,35
	0.3	121,008.00	0	156	6,073.68	3,9,15,32,35,39
	0.4	126,134.90	0	166	6,497.57	3,9,15,32, 35,39
	0.5	130,294.10	0	176	6,962.41	3,9,15,32,35,39
	0.6	133,728.35	0	176	7,001.22	3,9,15,32,35,39
	0.7	136,633.57	0	184	7,774.22	3,9,15,32,35,39
	0.8	139,051.80	0	186	7,502.77	3,9,15,32,35,39
	0.9	140,976.72	0	180	7,358.77	3,9,15,32,35,39
	1	142,279.06	0	190	5,989.30	3,9,15,32,35,39

Table 7. Impact of uncertainty budget and α with $\mathrm{\Omega }=1$ for CAB 25-node instance.

α	${\mathrm{\Gamma }}_{\mathrm{\%}}$	Cost	$\mathrm{\%}$ Gap	$\mathrm{\#}$ Iterations	CPU time (s)	Hub configuration
0.2	0.1	8,075,873,225	0	21	192.74	3,4,6,12,17
	0.2	8,684,194,322	0	19	172.49	4,6,12,17,20
	0.3	9,102,185,109	0	19	181.27	4,6,12,17,20
	0.4	9,430,098,195	0	17	175.16	4,6,12,17,20
	0.5	9,667,278,324	0	21	216.55	6,12,17,20,25
	0.6	9,838,958,249	0	17	193.51	6,12,17,20,25
	0.7	9,975,272,746	0	18	195.09	6,12,17,20,25
	0.8	10,087,132,408	0	19	203.82	6,12,17,20,25
	0.9	10,157,488,585	0	16	186.61	6,12,17,20,25
	1	10,273,704,079	0	11	46.00	6,12,17,20,25
0.5	0.1	10,926,837,994	0	7	62.47	3,4,17,25
	0.2	11,891,101,383	0	13	115.08	3,6,17,23,25
	0.3	12,461,833,181	0	11	101.06	3,6,17,23,25
	0.4	12,875,826,511	0	10	97.751	3,6,17,23,25
	0.5	13,178,648,180	0	11	111.31	3,6,17,23,25
	0.6	13,411,808,238	0	12	130.49	3,6,17,23,25
	0.7	13,585,689,892	0	10	110.986	3,6,17,23,25
	0.8	13,714,962,325	0	13	133.733	3,6,17,23,25
	0.9	13,831,526,420	0	8	78.79	3,6,17,23,25
	1	13,841,423,996	0	10	39.00	3,6,17,23,25
0.8	0.1	13,134,665,282	0	9	82.70	6,7,25
	0.2	14,333,311,160	0	11	106.00	6,17,25
	0.3	15,106,926,083	0	11	106.41	6,17,25
	0.4	15,657,195,449	0	13	123.72	6,17,25
	0.5	16,038,971,003	0	13	127.42	6,17,23,25
	0.6	17,051,701,929	0	8	82.11	6,17,23,25
	0.7	16,520,782,393	0	14	143.14	3,14,17,23,25
	0.8	16,668,894,357	0	13	136.38	3,14,17,23,25
	0.9	16,761,763,186	0	13	130.85	3,14,17,23,25
	1	16,809,385,472	0	11	42.00	3,14,17,23,25

5.4. Size reduction scheme

A method was proposed to solve an adjustable robust model in less computational time and with good solution quality. It is reasonable to say that, as usual, not all nodes were selected as hub facilities. Nodes with lower establishment costs and/or higher input and output flows can be selected as hub facilities. Computational time can be decreased by reducing the number of candidate points for establishing hubs.

The problem in large instances can be solved by some pre-processing. Some nodes that were selected as hub facilities in a deterministic model with worst-case values could also be selected as hubs for other uncertainty budgets. In other words, the hub facilities that were obtained from a deterministic model with worst-case values could generate a restricted set of candidate points for establishing hubs for other uncertainty budgets. To do so, the deterministic model was solved with worst-case values of uncertain parameters, and optimal locations of hubs were obtained. Then, the obtained nodes were considered as candidate hub nodes to solve the two-stage robust model. To ensure that all appropriate candidate hubs were considered, some other potential points were also added to the restricted list. Nodes were sorted from smallest to largest based on their establishment costs, and the top tier (10% of all nodes) was added to the restricted list. Moreover, nodes with larger total receiving and sending flow values (10% of all nodes) were added to the restricted list. Then the proposed model was solved by considering the restricted list only as candidate hubs. The results shown in Tables 8 and 9 confirm that, not only was the proposed approach to restricting candidate nodes for hub establishment efficient regarding computational time, but it also had acceptable quality. The average gap was 0.08%, which shows that good-quality solutions were obtained by using a preprocessing procedure.

Table 8. The impact of size reduction scheme for AP 50-node instances.

		Full size				Size reduction
α	${\mathrm{\Gamma }}_{\mathrm{\%}}$	$\mathrm{\#}$ Iterations	CPU time (s)	Cost	$\mathrm{\%}$ Gap	$\mathrm{\#}$ Iterations	CPU time (s)	Cost	$\mathrm{\%}$ Gap
0.2	0.1	140	9943.85	78,386.10	0	27	485.31	78,386.10	0
	0.2	210	10,842.81	84,325.87	0	27	584.66	84,325.87	0
	0.3	194	10,388.69	88,269.83	0	22	595.36	88,283.07	0.01
	0.4	297	16,635.38	91,354.89	0	35	1019.25	91,355.31	0.00
	0.5	282	16,502.75	93,721.03	0	34	985.47	93,739.03	0.01
	0.6	217	13,592.20	95,615.17	0	31	1141.51	95,654.82	0.04
	0.7	190	12,327.36	97,215.76	0	28	960.81	97,242.33	0.02
	0.8	138	9374.95	98,491.07	0	28	946.81	98,491.07	0
	0.9	94	6990.08	99,442.71	0	24	718.41	99,442.71	0
	1	66	2313.88	100,011.91	0	19	853.89	100,011.91	0
0.5	0.1	117	4907.80	94,262.60	0	20	327.95	94,614.11	0.37
	0.2	110	4537.91	102,365.34	0	17	267.83	102,519.70	0.15
	0.3	108	4356.97	108,034.90	0	18	769.46	108,116.98	0.07
	0.4	121	4830.53	112,396.49	0	20	781.46	112,486.71	0.08
	0.5	142	5454.38	115,921.20	0	22	408.86	116,033.79	0.09
	0.6	133	5051.10	118,810.25	0	20	522.60	118,895.21	0.07
	0.7	157	5862.68	121,223.39	0	24	641.45	121,243.33	0.01
	0.8	160	5722.88	123,183.40	0	26	429.24	123,183.40	0
	0.9	156	5470.46	124,756.85	0	21	474.46	124,756.85	0
	1	135	4415.37	125,821.31	0	18	535.25	125,821.31	0
0.8	0.1	114	5650.67	104,524.39	0	11	90.36	104,716.68	0.18
	0.2	146	6053.82	114,382.19	0	13	164.28	114,514.50	0.11
	0.3	156	6073.68	121,008.00	0	14	145.74	121,190.80	0.15
	0.4	166	6497.57	126,134.90	0	13	147.72	12,6357.91	0.17
	0.5	176	6962.41	130,294.10	0	11	173.43	130,553.98	0.19
	0.6	176	7001.22	133,728.35	0	14	131.22	133,929.96	0.15
	0.7	184	7774.22	136,633.57	0	12	137.58	136,775.04	0.10
	0.8	186	7502.77	139,051.80	0	12	148.80	139,221.21	0.12
	0.9	180	7358.77	140,976.72	0	12	166.54	141,164.20	0.13
	1	190	5989.30	142,279.06	0	9	101.61	142,477.33	0.13
Average		161.37	7546.21		0	20.07	495.24		0.08

Table 9. The impact of size reduction scheme for TR 81-node instance.

		Full size					Size reduction
α	${\mathrm{\Gamma }}_{\mathrm{\%}}$	$\mathrm{\#}$ Iterations	CPU time (s)	LB (M)	UB (M)	$\mathrm{\%}$ Gap	$\mathrm{\#}$ Iterations	CPU time (s)	Cost (M)	$\mathrm{\%}$ Imp	Hub configuration
0.2	0.1	15	18,000	48,977.31	51,531.57	4.96	22	5416.05	50,314.42	2.36	1,6,7,16,21,28,34,35,42
	0.2	13	18,000	53,784.11	56,612.59	5.00	38	10,478.99	54,255.64	4.16	6,7,16,21,25,27,33,34,35,38,42,55
	0.3	14	18,000	55,251.06	58,708.02	5.89	24	5036.96	56,684.24	3.45	6,7,16,21,25,27,33,34,35,38,42,55
	0.4	11	18,000	57,665.69	59,478.73	3.05	22	6656.31	58,464.60	1.71	6,7,16,21,25,27,33,34,35,38,42,55
	0.5	10	18,000	57,923.47	63,795.70	9.20	20	5554.28	59,790.98	6.28	6,7,16,21,25,27,33,34,35,38,42,55
	0.6	12	18,000	59,329.56	62,245.13	4.68	16	3553.15	60,805.56	2.31	6,7,16,21,25,27,33,34,35,38,42,55
	0.7	19	18,000	60,982.45	66,221.82	7.91	16	4741.45	61,568.93	7.03	6,7,16,21,25,27,33,34,35,38,42,55
	0.8	9	18,000	60,157.63	65,601.10	8.30	16	6432.83	62,131.81	5.29	6,7,16,21,25,27,33,34,35,38,42,55
	0.9	12	18,000	61,340.40	65,956.15	7.00	16	2598.36	62,503.68	5.23	6,7,16,21,25,27,33,34,35,38,42,55
	1	20	7907	62,686.98	62,686.98	0.00	15	2276.24	62,686.98	0.00	6,7,16,21,25,27,33,34,35,38,42,55
0.5	0.1	17	18,000	68,466.35	71,470.79	4.20	25	5956.75	69,120.69	3.29	1,6,7,16,21,34,35,42,60
	0.2	16	18,000	74,054.90	76,591.98	3.31	24	5944.08	74,941.79	2.15	1,6,7,16,21,34,35,42,60
	0.3	15	18,000	76,781.27	80,781.27	4.95	24	6754.38	78,675.41	2.61	1,6,7,16,21,34,35,42,60
	0.4	12	18,000	79,683.86	84,406.90	5.60	19	7330.83	81,202.88	3.80	1,6,7,16,21,25,34,35,42,60
	0.5	16	18,000	82,215.26	86,890.28	5.38	20	5836.47	83,080.64	4.38	1,6,7,16,21,25,34,35,42,60
	0.6	17	18,000	83,614.53	86,110.18	2.90	24	9636.38	84,504.11	1.87	1,6,7,16,21,25,34,35,42,60
	0.7	10	18,000	83,624.83	90,286.49	7.38	19	9095.08	85,561.12	5.23	1,6,7,16,21,25,34,35,42,60
	0.8	12	18,000	84,984.73	87,965.52	3.39	21	7625.76	86,310.53	1.88	1,6,7,16,21,25,34,35,42,60
	0.9	16	18,000	85,614.48	89,251.88	4.08	21	6167.41	86,810.46	2.74	1,6,7,16,21,25,34,35,42,60
	1	32	18,000	86,865.20	87,440.86	0.66	19	1434.58	87,059.02	0.44	1,6,7,16,21,25,34,35,42,60
0.8	0.1	11	18,000	82,995.06	86,065.19	3.57	40	11,213.44	84,641.80	1.65	1,6,16,21,34,35,60
	0.2	13	18,000	90,573.68	92,382.93	1.96	41	9986.36	91,961.40	0.46	1,6,7,16,21,34,35,60
	0.3	13	18,000	95,017.69	97,199.21	2.24	25	11,410.75	96,383.98	0.84	1,6,7,16,21,34,35,60
	0.4	9	18,000	98,299.22	101,447.36	3.10	27	8215.18	99,443.11	1.98	1,6,7,16,21,34,35,60
	0.5	17	18,000	100,854.67	105,603.29	4.50	25	12,162.45	101,707.67	3.69	1,6,7,16,21,34,35,60
	0.6	36	18,000	102,226.92	104,799.32	2.45	25	8531.20	103,401.66	1.33	1,6,7,16,21,34,35,60
	0.7	13	18,000	103,359.93	107,659.68	3.99	27	10,345.57	104,649.42	2.80	1,6,7,16,21,34,35,60
	0.8	15	18,000	104,476.74	107,110.01	2.46	23	9911.50	105,538.07	1.47	1,6,7,16,21,34,35,60
	0.9	6	18,000	101,238.04	112,051.86	9.65	22	8047.88	106,128.18	5.29	1,6,7,16,21,34,35,60
	1	48	17,129	106,422.94	106,422.94	0.00	23	1384.99	106,422.94	0.00	1,6,7,16,21,34,35,60
Average		15.97	17,651.98			4.39	23.3	6915.31		2.86

Table 9 shows the results for the TR 81-node instance in the full-size and size-reduction modes. CPU time of five hours (18,000 seconds) was considered in all cases. The results show the superiority of the size-reduction scheme to obtain a good solution in a shorter time, compared with the full-size mode. In other words, the size-reduction scheme improved the achieved solution by an average of 2.86% in comparison with the full-size mode in a shorter time (one-third the computational time).

5.5. Efficiency evaluation of the proposed model

The effect of incorrect decisions in terms of costs was analysed. Some organisations engage in risk-averse behaviour, so they make decisions considering worst-case scenario. However, this may lead to inefficient decisions. It is clear that considering uncertainty will impose costs on the organisation compared with the deterministic model, but it should be considered to achieve a reliable decision. So the trade-off between wrong decisions in both scenarios is analysed and interpreted.

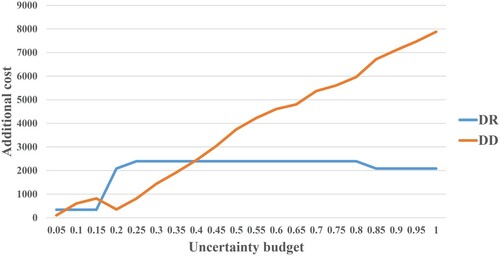
Figure 2 shows the additional costs imposed as a result of wrong decisions. These might be decisions based on deterministic values when uncertain parameters are involved, and vice versa. To calculate imposed costs, the model was solved with a specified uncertainty budget ${\mathrm{\Gamma }}_{\mathrm{\%}}\in \{0.05,0.1,\dots ,1\}$. Then the optimal solutions ($z_k$, $x_{ijkl}$) obtained were placed in a new robust model to be optimised. Robust deviation (RD) is a measure that calculates the cost difference between the new robust model (with wrong decisions) and the deterministic model. In the next stage, decision variables obtained by optimisation of the deterministic model ($z_k$, $x_{ijkl}$) were placed in the new deterministic model with a predefined ${\mu }_{ij}$ (obtained from optimisation of the robust model). Deterministic deviation (DD) calculates the cost difference between the new deterministic model (with wrong decisions) and the robust model. In cases with lower values for uncertainty budget, there were negligible financial losses. Based on results reported for selected datasets, it can be concluded that in much more uncertain environments, (${\mathrm{\Gamma }}_{\mathrm{\%}}>0.4$) making decisions using the robust model was more beneficial compared to the deterministic model. The objective function value is summarised as OFV for each model. For example, $OFV\left(HLP\right)$ denotes the objective function value of the HLP model. RD and DD is defined as follows: (37) $\begin{array}{rl}RD& =OFV\left(Robust\mathrm{d}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}|\mathrm{F}\mathrm{u}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{s}\mathrm{d}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\right)\\ & -\mathrm{O}\mathrm{F}\mathrm{V}\left(\mathrm{H}\mathrm{L}\mathrm{P}\right)\end{array}$(37) (38) $\begin{array}{rl}DD& =\mathrm{O}\mathrm{F}\mathrm{V}\left(\mathrm{D}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{d}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}|\mathrm{F}\mathrm{u}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{i}\mathrm{s}\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{i}\mathrm{n}\right)\\ & -\text{OFV(TRHLP)}\end{array}$(38)

Figure 2. Additional cost for wrong decisions, CAB 25-node instance.

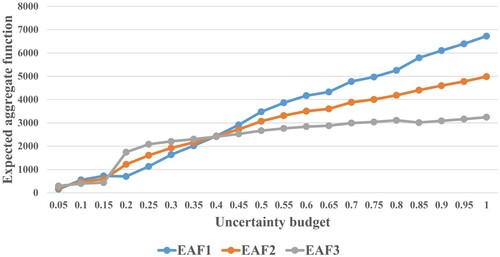
In both scenarios, it was observed that costs would be imposed on the network, so an aggregated expected imposed cost could be calculated using Equation (39(39) $EAF=RD\times (1-p)+DD\times \left(p\right)$(39) ). p was the probability of uncertainty occurrence. (39) $EAF=RD\times (1-p)+DD\times \left(p\right)$(39) Three different probabilities were considered for incorrect decisions. EAF1, EAF2 and EAF3 were expected aggregate functions with probabilities of 0.8, 0.5 and 0.2, respectively. Figure 3 shows that for ${\mathrm{\Gamma }}_{\mathrm{\%}}\ge 0.4$, it was more reasonable to decide using the uncertain model. The necessity of using the robust model increased as probability (p) increased. The opposite behaviour could be observed when the uncertainty budget were between 0.15 and 0.4.

Figure 3. Comparison between expected aggregate functions, CAB 25-node instance.

5.6. Comparison between static, adjustable robust and stochastic programming

Marandi and den Hertog (2018) showed that in a model with constraint-wise uncertainty, the objective function values of static robust and adjustable robust optimisation are the same. For constraint-wise uncertainty, two conditions should hold: (1) Any uncertain parameter should appear in only one constraint; and (2) the uncertainty set should be such that there is no correlation between the uncertain parameters of different constraints. Also, Bertsimas, Goyal, and Lu (2015) showed that for specific non-constraint-wise uncertainty, the same results held for static and adjustable robust optimisation. These authors examined different positions of uncertainty in the objective function and constraints, and showed that in these cases, static and adjustable robust optimisation had the same values. The uncertain parameter in our research was in the objective function, and could also be transferred into the constraint. Therefore, according to the constraint-wise uncertainty of the parameter, it was expected that the static and adjustable robust models would have the same objective values.

In the following, robust optimisation and stochastic programming are compared with each other. The probability distribution of the uncertain parameters was known in stochastic programming, and was considered in the model with several discrete scenarios ($S\in \{s_1,s_2,\dots ,s_n\}$) or chance constraints, while in classical robust optimisation, there is no information about the probability distribution of the parameters or uncertain parameters considered in the model with uncertainty sets.

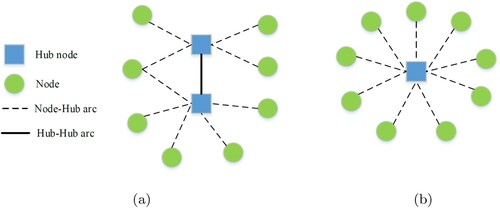
For this paper, it was assumed that the probability distribution of uncertain demand followed a uniform distribution, and scenarios were generated in which $w_{ij}^s\sim U[{\overline{w}}_{ij}-{\hat{w}}_{ij},{\overline{w}}_{ij}+{\hat{w}}_{ij}]$ represented demand parameters (origin-destination nodes) for each scenario s, and as before, ${\overline{w}}_{ij}$ and ${\hat{w}}_{ij}$ were average (deterministic) and deviation values of demand, respectively. Figure 4(a,b) show the network structure of the robust and stochastic models, respectively, for the AP 10-node instance. In these figures, the uncertainty budget value was considered to be equal to 1.0, and several scenarios were generated for the stochastic model. It should be noted that (Contreras, Cordeau, and Laporte 2011) showed that classical hub location problems with stochastic demand are equivalent to considering expected values of parameters in the deterministic model. In other words, different scenarios had no effect on second-stage (allocation) decisions. According to Figure 4, the number of established hubs is equal to 2 and 1 for the robust and stochastic models, respectively.

Figure 4. Network structure of (a) robust and (b) stochastic models, $\alpha =0.5$, AP 10-node instance.

Table 10 shows the optimal location of hubs in the stochastic and robust conditions with different values of Ω and discount factors (α). It is clear that the robust model was solved according to the worst-case values of uncertain demand (${\mathrm{\Gamma }}_{\mathrm{\%}}=1$), and that in the stochastic model, different scenarios were generated with a uniform distribution. As shown in Table 10, the optimal hubs in the stochastic and robust models were similar when $\mathrm{\Omega }=0.5$ and $\alpha =0.8$, while established hubs were different for other values of Ω and α. Furthermore, the results confirm that increasing discount factors leads to decreases in the number of established hubs, but Ω has a direct effect on the number of established hubs.

Table 10. Optimal hub configuration for CAB 25-node instance.

Ω	α	Stochastic	Robust
0.5	0.2	7, 14, 18	2, 8, 15, 16, 18
	0.5	8, 18	7, 14, 18
	0.8	8, 18	8, 18
1	0.2	7, 14, 18	2, 5, 8, 15, 16, 18
	0.5	8, 18	2, 8, 14, 16, 18
	0.8	8, 18	7, 14, 18

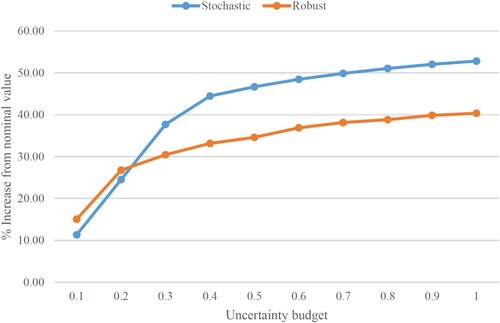
To evaluate the solutions of the robust and stochastic models, a simulation-based analysis was designed for different realisations of demand parameters using the AP 20-node instance. In this case, the robust and stochastic models were solved separately and their corresponding location decisions were extracted. Then the extracted location decisions of both models (robust and stochastic) are separately placed in the deterministic model. Then, according to each value for the uncertainty budget (${\mathrm{\Gamma }}_{\mathrm{\%}}\in \{0.1,0.2,\dots ,1\}$), different realisations of demand were considered. For example, when ${\mathrm{\Gamma }}_{\mathrm{\%}}$ was equal to 0.1, 10% of the demand parameters were randomly chosen, and their associated deviation values were added to their nominal values. It should be noted that this process was repeated several times, and every time, the objective function value of the deterministic model for each case (with the fixed location decisions extracted from the stochastic and robust models) was obtained. Finally, the average of all objective values in several experiments were compared. The solution performance of the robust and stochastic models for the AP 20-node instance, considering different values of uncertainty budgets, are analysed and illustrated in Figure 5. The results confirm better performance of the robust model solution in comparison with the stochastic model when the uncertainty budget is greater than 0.2.

Figure 5. Solution performance of robust and stochastic models, AP 20-node instance.

6. Managerial implications

Direct shipments of commodities that flow between origin-destination nodes increase total transportation costs. In other words, vehicles that transport commodities may not be completely full, or may be totally empty on the way back. Appropriate hub location can reduce transportation costs by using intermediate centres (hub facilities). In this case, flows are gathered in hub facilities and distributed to destinations, and economies of scale occur. It is obvious that hub location problems can be considered in a variety of applications, including airport and aviation industries (Karimi and Setak 2018; Masaeli, Alumur, and Bookbinder 2018; Madani, Shahandeh Nookabadi, and Hejazi 2018), supply chain management, and logistics (Wang and Cheng 2010; Ishfaq and Sox 2010) and transportation systems (Lin and Lee 2010; Gelareh and Pisinger 2011). Hub location problems have been used abundantly in the design of transportation and distribution systems, including postal delivery, air freight and passenger travel, trucking, express package delivery, and rapid transit systems. Uncertainty is part of reality in the real world, and exists in some parameters. For example, consumer behaviour affects the volume and supply of demand. While in some cases there is a lower degree of uncertainty (such as demand cancellation by customers), a higher degree of uncertainty may also occur. For example, the COVID-19 pandemic can be considered one of major sources of such uncertainty.

In air passenger travel, the COVID-19 pandemic led many countries to restrict and control the entry of passengers from other infected countries. For this reason, airline companies lost many passengers and their flights were cancelled or carried fewer passengers to their destinations through airport hubs. In this case, airline companies raised the price of their services to compensate for the costs that led to decreases in customer satisfaction. The Laura Ashley textile design company is an example of hub location in express package delivery. They located their warehouses near FedEx hubs to improve responsiveness to customers. During the COVID-19 pandemic, people have preferred to order their needs online instead of in face-to-face shopping, and the demand for such companies has greatly increased. It is clear that uncertainty has been imposed on these enterprises because of the pandemic. Therefore, it is necessary for decisions to be optimal for all scenarios in such cases. In other words, according to robust optimisation and decision-making based on the worst-case values of parameters guarantees the optimality and feasibility of all scenarios. Hence, decision-makers and managers need to make good decisions that take uncertainty into account. In hub location problems, decisions about locations of hub facilities are strategic decisions and have significant effects on total costs. Robust optimisation approach and it associated analyses, which were presented in this paper, are useful for helping decision-makers tackle uncertainty when choosing appropriate levels of conservatism. In robust optimisation with a polyhedral uncertainty set, decision-makers can control the level of conservatism or risks with an uncertainty budget. A higher value for an uncertainty budget raises costs and increases the level of conservatism in advance, but protects the system from future uncertainty. Some organisations display risk-averse behaviour, so make decisions considering worst case scenarios. However, this may lead to inefficient decisions. It is clear that considering uncertainty will impose costs on the organisation compared with the deterministic model, but it should be considered to achieve reliable decisions. In other words, deciding first with deterministic parameters may be very low-cost, but in the future, when uncertainty occurs, costs will rise sharply. In this case, companies may increase their product prices to compensate for transportation costs, which may lead to loss of customers, or at the very least, reductions in customer satisfaction. Therefore, managers should consider uncertainty in their decisions. Hence, this study carried out analyses of the trade-off between deterministic and uncertain conditions in obtaining appropriate values for uncertainty budgets for managerial decision-making. This approach can be used in different production and distribution companies when they deal withuncertainty.

7. Conclusion

In this paper, a two-stage robust optimisation approach was considered to deal with uncertain demand in an uncapacitated multiple allocation hub location problem. An accelerated Benders decomposition algorithm with stronger optimality cut (Pareto-optimal cut) was applied to solve the proposed model more efficiently. Also, a size-reduction scheme that reduced the number of candidate nodes for hub establishment was proposed to be used in the Benders decomposition algorithm. To determine the uncertainty budget in the right way, a new expected aggregate function was introduced. Computational experiments showed that the Benders decomposition algorithm with Pareto-optimal cuts required fewer iterations and less computation time compared with the classical Benders decomposition algorithm for all values of uncertainty budgets. The main findings of this research were as follows: (1) It was shown that using the proposed size-reduction scheme can speed up the algorithm. (2) It was concluded that, depending on the uncertainty budget, it might be more reasonable to use the deterministic or robust model. (3) The behaviour of imposed costs was evaluated using the proposed expected aggregate function. (4) The accelerated Benders decomposition algorithm with Pareto-optimal cut converged rapidly in comparison with the classical algorithm. (5) The values of uncertainty budget and deviation values have a direct effect on the objective function values (costs) and number of hub facilities. (6) The values of inter hub flow discount factors have a direct and opposite effect on the objective function values (costs) and number of hub facilities,respectively.

Future research could include modeling of the problem with the possibility of inclusion of more profitable demand in the hub location problems. Also, a multi-period model would allow transfer of flows between origin-destination nodes in any period. In this case, consistency of times or responsibility could be considered to benefit customers. For faster convergence in the Benders decomposition algorithm, a heuristic procedure could be applied to the algorithm.

Acknowledgments

The authors thank the anonymous reviewers for their useful comments and suggestions of revisions.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Notes on contributors

Reza Rahmati

Reza Rahmati is currently a Ph.D candidate in the Department of Industrial Engineering at Ferdowsi University of Mashhad, Iran. He received his M.Sc. degree in Industrial Engineering from Shahed University, Tehran, Iran in 2019. He is also received his B.Sc degree in Industrial Engineering from Torbat-e Heidarieh University, Iran in 2016. Reza's current research interests include the optimisation, operations research, uncertainty, sustainable hub location, robust optimisation, stochastic programming, fuzzy chance-constrained programming, location problems, exact and metaheuristic algorithms.

Mahdi Bashiri

Mahdi Bashiri has over 16 years of academic experience with a particular interest in operations and supply chain management, operations research, transportation planning, Heuristic and Matheuristic algorithms. Also he has participated in industrial and business projects in different levels. He has been involved in two UKRI funded projects. He has supervised more than 5 Ph.D. students and more than 60 M.Sc. students. He is an active reviewer for reputable academic journals. He is a recipient of the 2013 young national top scientist award from the Academy of Sciences of the Islamic Republic of Iran.

Erfaneh Nikzad

Erfaneh Nikzad received the B.Sc. Degree in industrial engineering from Alzahra University, in 2011, the M.Sc. degree in industrial engineering from Shahed University, Tehran, in 2014, and the Ph.D. Degree in industrial engineering from Shahed University, Tehran, Iran, in 2020. She currently works as a lecturer in West Tehran Branch, Islamic Azad University, Tehran, Iran. Her research interests include Vehicle Routing Problems, matheuristic algorithms, and stochastic programming.

Ali Siadat

Ali Siadat received his Ph.D. in robotics and digital signal processing from Institut National Polytechnique de Lorraine in France. He stated his carrier as associate professor in computer and industrial engineering at Arts et Metiers and became full professor in 2016 at the same engineering school. He was head of applied mathematics and computer Engineering department during 7 years and since 2019, he's Director of Design, Manufacturing and Control laboratory. He served also as Guest Professor in several universities in China, Iran, Morocco and Brazil. His research interests include artificial intelligence, information system, knowledge formalisation and operations research applied to production system fields. He has published over than 60 papers in distinguished scientific journals and more than 80 papers in international conferences and he supervised more than 25 Ph.D. theses. Ali Siadat is actively involved in Factories of the Future program in France and his research activities are drive usually with international collaborations and very closed to industries (STMicroelectronics, Siemens, PSA, Plastic Omnium …). His new research projects interest to integrated human factors to optimisation of production systems.