Inventory stacking with partial information

Abstract

An inventory stacking decision assigns positions to items which are stacked vertically, such as containers in container terminals and steel plates in steel plants. The performance of stacking decisions is greatly affected by the arrival and departure information on items. We study an inventory stacking problem with partial information based on industrial observation in a steel plant. On the inbound side, we investigate three levels of information on future arriving items and their effect on performance. On the outbound side, we study the impact of the retrieval sequence, which is often random. We develop models incorporating different availabilities of information and determine stacking strategies. The study shows that the stacking strategy and stacking performance depend highly on information quality and space utilisation. Especially, when the space utilisation is high, low-quality information deteriorates the performance and such information should be ignored. This contradicts the general belief that more information should bring better performance. The study further proposes a time window allocation approach to reduce the uncertainty in retrieval, and it is effective in improving stacking performance.

KEYWORDS:

• Stacking
• position assignment
• partial information
• reshuffles
• storage yard

1. Introduction

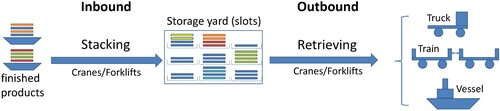
The storage of containers and steel plates often requires vertical stacking to conserve space, but such stacking often necessitates additional operations during the retrieval process. Retrieving an item located in a lower layer in a slot requires reshuffling all the items blocking it above, which can consume critical resources such as cranes and forklifts and add an extra workload. Thus, it is crucial to have a sound position assignment decision that defines the slot and position to allocate items and prepares for reshuffles in the vertical stacking system.

In this study, we explore a stacking problem that is inspired by a real case in a steel plant, in which the finished steel plates (items) are stacked vertically in a storage yard. Historically, the steel plant catered to a primary market with a limited customer base characterised by large order quantities. The employed stacking policy simply assigns several dedicated slots to a customer and groups items of the same retrieval week in the same slot. In recent years, however, competition has necessitated a shift towards the high-end niche market. As a result, the number of customers has substantially increased while each order has a small order quantity with customised specifications (size and thickness). Adherence to the previous stacking policy, which relies on the allocation of limited slots, is no longer feasible, prompting the need to stack items of different customers and retrieval times in the same slot to improve the usage of the storage yard.

Furthermore, there are some operational features of this stacking process. First, the inbound and outbound flows exhibit a high degree of asynchrony. Specifically, the inbound batches arrive consecutively, several batches during a day, from a production workshop, and each batch comprises items of different customers, each with distinct scheduled retrieval times. On the outbound side, items are retrieved by vehicles and the retrieval plan is on a longer time basis, often weekly.

Secondly, a stacking decision is needed when a batch arrives. We define target items as the items in the current arriving batch, and future items as the ones arriving in the future. The central problem is assigning positions (slot and layer) for all target items, and this decision is repeated in a rolling forward routine with a dynamic environment, i.e. the empty slots, available positions and other information keep changing.

Thirdly, the stacking decision needs to be made with partial information, which should have an important impact on the system performance. As the stacking decisions of each incoming batch directly affect the subsequent stacking decisions of future items, information on future items is essential from a long-term perspective. Concerning the information of future arriving items (inbound information), their quantity, arrival time and retrieval time are all crucial factors. However, collecting full information on future items seems impossible in practice. Concerning the future retrieval, the outbound information mainly pertains to the item retrieval time, which has a significant impact on their relative stacking sequence. Logistics planning, however, is often performed on a larger time interval (weekly), leading to vehicles arriving randomly within a designated time interval to retrieve items. Thus, the retrieval sequence of each item is unknown at the time of stacking, and this again results in partial information.

Fourthly, the storage yard still has relatively limited space in the steel plant. It can be viewed as a decoupling point, at which the steel production is converting from a continuous flow (production workshop) to a discrete flow (delivery). Its proper management should prevent the situation of blocking the continuous production flow, and in addition improve its operational performance, i.e. reduction of reshuffles. We present the aforementioned flow in Figure 1, in which different item colours indicate different retrieval times.

Figure 1. Logistics process of storage yard in the steel plant case.

However, even though there are studies investigating the stacking problems with partial information, the focus is often on either inbound or outbound side, for instance, container stacking problems (see Section 2). An investigation with the combination of partial information from both inbound and outbound perspectives is still missing in the literature for stacking problems. This paper therefore addresses the following research questions: (1) how to formulate and solve the stacking problem when both inbound and outbound have partial information, when decisions are made on a rolling forward basis? (2) how could different information settings (unknown, partial and full) affect decision-making and stacking performance? (3) what is the role of storage space in answering the above questions, and furthermore what is the possible managerial approach for improving the performance when the storage space is limited?

In this paper, we develop generalised stacking models that are applicable in various scenarios of information availability, especially different information settings on the inbound and outbound sides, and then we investigate the corresponding stacking performance and the value of information.

This study makes both theoretical contributions and practical contributions. On the one hand, the study contributes to the literature by examining the relationship between the information and stacking performance, which has not been explored thoroughly before. The study comprehends stacking position assignment models, taking into account full or partial retrieval information on future items, and highlights the crucial role of space utilisation in stacking performance. The proposed models can be applied and extended for stacking problems with other settings, including container terminals. In addition, to improve stacking performance, the study proposes a method for alleviating uncertainty, i.e. the time window method for reducing retrieval sequence uncertainty. On the other hand, the study results indicate that while decision-makers generally believe that additional information improves performance, this is not always the case. Rather, the information quality must be properly coped with the condition of resources to reap its benefits, when storage space is restricted. Further discussion of this phenomenon improves our understanding of the roots of reshuffles, the decision-making mechanism facing different resource conditions, as well as the trade-offs between information value and resource utilisation. The results therefore provide a good guideline for managers dealing with stacking problems.

2. Literature review

We review the literature on container stacking, which is most relevant to our stacking problems. Container stacking is a critical aspect in operating container terminals, and it has a significant impact on the overall terminal performance. Like the stacking problem of steel plates, container stacking involves the sequential arrival of containers at a yard and subsequently retrieval of the containers, making it a dynamic scheduling problem that requires real-time decision-making, as defined by Dolgui and Proth (2010). According to Steenken, Voß, and Stahlbock (2004), the stacking problem involves operational decision-making and is highly complex, necessitating advanced computational algorithms.

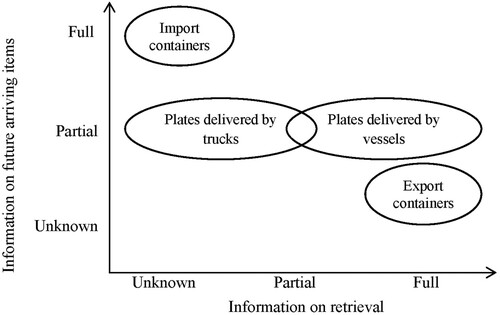
Gharehgozli et al. (2014) present a decision-tree heuristic to minimise container reshuffles at terminals, a time-consuming operation increasing ships’ berthing times. The heuristic employs a stochastic dynamic programming approach and generates generalised decision trees for large-scale problems. Numerical experiments reveal that shared-stacking outperforms dedicated-stacking policies. Zhang (2000) has developed distinct stacking models for import and export containers with different information availabilities. In the models of import containers, containers arrive in a (large) batch but the retrieval time of each container is uncertain as container vehicles arrive randomly in practice. The stacking positions are often assigned based on containers’ expected retrieval times. In the models of export containers, full information is sometimes assumed to be available, i.e. the arrival sequence of future containers is predefined and retrieval is in a large batch. However, according to Steenken, Voß, and Stahlbock (2004), lacking accurate information on the arrival time of containers is common in terminals. We argue that assuming partial information on arriving items in export containers, and respectively on retrieval times of import containers would generally be suitable for describing container stacking problems.

Kim, Park, and Ryu (2000) propose a method for stacking export containers with different weights. Heavy containers are assigned above light ones so that the heavy ones are first loaded on ships, thus container weights determine the retrieval sequence. In their model, the arrival time of each container is known in advance while its weight is uncertain until it arrives. With such information on future containers, a dynamic programming model is developed to minimise the reshuffles. Chen and Lu (2012) consider a similar problem for export containers with different levels of the weights and introduce a heuristic for stacking decisions. Park et al. (2023) design a dynamic stacking strategy for export containers with a data-driven principle, i.e. estimating container weights and correspondingly assigning positions. Cho et al. (2022) propose an online optimisation approach to overcome limitations of conventional container stacking models. The proposed approach updates data-driven information on weight classes, reducing the weight variance and facilitating flexible responses to uncertainties, leading to reduced container relocation times.

Azab and Morita (2022) propose a new optimisation problem, the Block Relocation Problem with Appointment Scheduling (BRPAS), to jointly address the appointment scheduling issues and minimising the number of relocations in container terminals. Two binary integer programming models are proposed and tested with examples from the literature, demonstrating improved coordination with appointment scheduling for container relocation operations. Kim and Hong (2006) and Wan, Liu, and Tsai (2009) focus on the position assignment for relocating blocking containers during the retrieving process, aiming at minimising future reshuffles. However, these models deal with decisions of retrieving containers rather than stacking.

Moreover, when dealing with partial information on future items, which will be the case in this study, the literature often assumes a scattered stacking strategy instead of a segregation strategy. The latter is commonly used in container terminals (Zhang et al. 2003). Since the container quantity of a vessel is often known in advance, the dedicated space and slots in a terminal can be readily defined. Thus, a segregation stacking strategy aims to minimise the reshuffles for a predefined number of containers in predefined slots. This stacking strategy can be seen as a ‘one-shot’ decision because the decision environment is static, and the decision is made only once. In practice in a container terminal, an area/space is often reserved for a dedicated vessel, to avoid dispersed allocation of containers and thereby travelling distance. To allocate spaces to vessels, Zhang et al. (2003) decompose the space allocation problem to balance the workload in sub-areas and minimise the retrieval travel distance.

When stacking decisions need to be made repeatedly for items in consecutively arriving batches, the information of arrival items is unknown or partially known, a scattered stacking strategy is often employed. In this case, the entire storage space is open for arriving items. However, the open space on the other hand stresses the importance of position assignment, to reserve sufficient empty slots for future items and thereby improve the long-run performance. Dekker, Voogd, and Asperen (2006) consider a category-stacking policy for containers under the scattered stacking strategy, in which containers have to be stacked on top of others within the same category. But this policy requires more storage space when the category number increases, which becomes an issue in our steel plant case. Zeng, Feng, and Yang (2019) propose a method to optimise the pickup sequence and improve container rehandling of import containers with partial retrieval information. A rehandling model is developed to minimise the reshuffles, and heuristic algorithms are proposed to solve the model. The experiments show that adjusting the pickup sequence within each group can greatly reduce the number of reshuffles, providing an efficient tool for improving operations based on truck group arrival information. This approach aims to reduce the uncertainty of item retrieval sequence; however, there are limited studies with similar concerns.

We also need to note that the scattered stacking strategy is less investigated in the literature, as this strategy faces the challenge of dynamically changing environment for decisions, in which case information and information updating become important. Chauhan, Gordon, and Proth (2007) stress the importance of information in scheduling, which will affect the resource efficiency and system performance. In addition, the scheduling problem in general is in particular interesting when outbound information (such as delivery date) can be part of negotiations with customers (Gordon, Proth, and Chu 2002). Furthermore, when performing operations during specified time windows, and assigning operations to specified resources, we can apply dispatching priority rules to simplify the algorithm complexity. In this case, the priority rules can be defined as integrating some future information, especially the near future information will present a good value, as discussed in Proth (2007).

In general, there is a limited number of studies investigating the stacking problem in an industry such as steel manufacturing, though many researchers mention its importance and similarity to the container stacking problem. Tang et al. (2002) and Tang and Ren (2010) both address the reshuffling problem for slabs, focusing on relocating blocking slabs in the retrieval process rather than position assignment in the stacking process. Kim, Koo, and Sambhajirao (2011) investigate a steel plate stacking problem, where plates arrive at a storage area with uncapacitated beds, with plate relocations (shifts) during the delivery stage. The problem’s complexity is demonstrated, and models are developed for small problems and lower bounds for larger ones. An iterative randomised approach is proposed and benchmarked with large problems. Ge et al. (2022) study a stacking problem for slabs and design an algorithm to pre-move slabs to minimise reshuffles in the retrieval process. The decisions on space size and space allocation have been investigated in several studies. Feng, Song, and Li (2022) show that space utilisation has a great impact on the performance of a storage yard in an import container scenario. Taleb-Ibrahimi, Castilho, and Daganzo (1993) and Kim and Kim (2002) focus on space allocation, with a similar conclusion.

In summary, there are two research gaps in the existing literature. Firstly, the conventional container stacking problem typically presents full information on either inbound or outbound side due to the associated vessel transportation (one large batch). The steel plate stacking problem involves uncertain information on both, with items inbounding randomly and outbounding with uncertain retrieval sequences. Our literature review reveals a research gap of the stacking problem with partial information on both inbound and outbound processes (see Figure 2), and therefore we fill this gap by addressing the complexity and challenges presented in such a problem. Secondly, the majority of stacking studies in the literature deal problems with static settings, whereas stacking problems with a dynamic environment and with a rolling-forward decision approach have been less investigated. With frequent item arrivals and retrievals in the steel plate stacking problem, a scattered stacking strategy should be applied to balance the reshuffles involving current items, and reserved space for less reshuffles involving future items. Furthermore, with partial information, should any managerial strategy be applied to reduce the information uncertainty and thereby improve the performance? This study tackles these issues and attempts to fill the research gap concerning stacking decisions in a dynamic environment.

Figure 2. The information structure of stacking problems.

3. A basic stacking model

This section develops a stacking model to assign items to minimise the retrieval reshuffles. The model is applied for each new arrival batch. Future items are excluded. In this section, we assume full information on retrieval time on the outbound side. Table 1 presents the notations.

Table 1. Notations.

Parameters	Explanation
Φ	Set of the target items, indexed by i, and |Φ| as the number of the set
Ωs	Set of the existing items in slot s, and |Ωs| as the number of the set
Ψ	Set of the future items, and |Ψ| as the number of the set
S	Number of slots, indexed by s
H	Maximal layer in one slot
K	The largest retrieval period
$k_i$	The retrieval period for item i, ranges in {1, 2, … , K}
Uk	Number of items to be retrieved in period k
$u_i^k$	The retrieval sequence for item i in period k ranges in {1, 2, … , Uk}
$l_i$	The arrival period for item i
$v_i^l$	The arrival sequence for item i in period l
E	Number of empty slots
Λ	Space utilisation
Decision variables	Explanation
$a_{is}$	A binary variable indicating whether item i is stacked in slot s
$b_{js}$	A binary variable indicating whether future item j is allocated to slot s
$d_{ijs}$	A binary variable showing whether item i and item j are stacked in slot s
$e_s$	A binary variable showing whether slot s is empty
CR	Number of cross-period reshuffles
IR	Number of within-period reshuffles
R	Number of total reshuffles, $R=CR+IR$

Table 2. The extensions of PA model with future item information.

	Information on future items
Models	Quantity	Retrieval time	Arrival time
PA
PA-Q	√
PA-QR	√	√
PA-QRA	√	√	√

Finally, we define $1|\{\cdot \}$ as a conditional function where the value equals to one under the condition $\{\cdot \}$.

3.1. Model formulation

Suppose we currently have a batch of target items denoted as Φ indexed by i, arriving simultaneously to be stacked with no sequence preference. Each item i has a retrieval time, defined by retrieval period $k_i$ and retrieval sequence $u_i^k$ in period k. A later retrieval is indicated by a larger $k_i$ and $u_i^k$. The space capacity is represented by S slots indexed by s, each of which has H vertical positions.

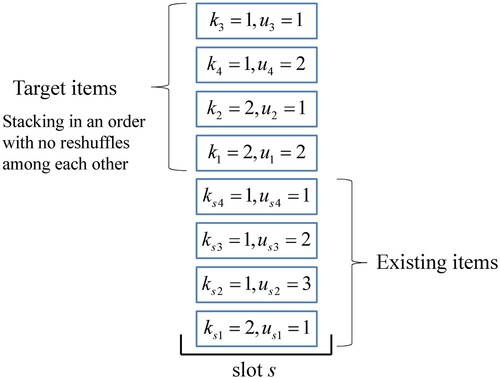
All items can be stacked on each other. When stacking a target item, reshuffles of existing items are not allowed. Hence, target items are always stacked above existing items. Since items are stacked vertically in slots, the decision assigns each target item a slot and specifies a position (which layer). This two-dimension allocation problem can be simplified as follows. To avoid unnecessary reshuffles, we should stack the target items from top to bottom in ascending order of retrieval times $k_i$ and sequence $u_i^k$ (see Figure 3). Hence for items in the same slot, the position assignment is determined directly. The remaining decision becomes slot assignment. A binary variable $a_{is}=1$ denotes i allocated to s. The solution space is reduced from ${\left({\sum }_{s=1}^S\left(H-|{\Omega }_s|\right)\right)}^{|\mathrm{\Phi }|}$ to $S^{|\mathrm{\Phi }|}$.

Figure 3. An example of position assignment.

An illustration example of position assignment with existing and target items.

The objective of the stacking problem is to minimise the reshuffles, which are defined as the additional movements of items due to the retrieval of items beneath. We distinguish cross-period reshuffles CR and within-period reshuffles IR. Consider two arbitrary items i and j. Let i stack above j, if j should be retrieved in an earlier period than i, i.e. $k_i>k_j$, retrieving j causes a cross-period reshuffle of i. If both items have the same retrieval period ($k_i=k_j=k$) but j has a smaller retrieval sequence index than i ($u_i^k>u_j^k$), retrieving j causes a within-period reshuffle of i.

An item may have several cross-period and within-period reshuffles. To determine the number of reshuffles of i, we compare the retrieval time and sequence of i with all beneath items. A comparison with other target items in the same slot is unnecessary, as these will be stacked in ascending order of retrieval (Figure 3). We now define $c{r}_i$ as the cross-period reshuffles of i and $i{r}_i$ as the within-period reshuffles. $\begin{array}{rl}c{r}_i& =\sum _{s=1}^S{a}_{is}\cdot \sum _{j\in {\Omega }_s}1|\left\{k_i>k_j\right\}\text{ ,}\mathrm{\forall }i\in \mathrm{\Phi }\\ i{r}_i& =\sum _{s=1}^S{a}_{is}\cdot \sum _{j\in {\Omega }_s}1|\left\{k_i=k_j\mathrm{\&}{u}_i^{k_i}=u_j^{k_j}\right\},\mathrm{\forall }i\in \mathrm{\Phi }\end{array}$Subsequently, we obtain the expressions of $CR={\sum }_{i\in \mathrm{\Phi }}c{r}_i$ and $IR={\sum }_{i\in \mathrm{\Phi }}i{r}_i$. We develop the basic position assignment model (PA model). (1) $\left(\text{PA Model}\right)minCR+IR-\alpha E$(1) s.t. (2) $\begin{array}{rl}& \sum _{s=1}^S{a}_{is}=1,i\in \mathrm{\Phi }\end{array}$(2) (3) $\begin{array}{rl}& \sum _{i\in \mathrm{\Phi }}{a}_{is}+|{\Omega }_s|\le H,s\in \left\{1,\dots ,S\right\}\end{array}$(3) (4) $\begin{array}{rl}& e_s\le 1-\left(\sum _{i\in \mathrm{\Phi }}{a}_{is}+|{\Omega }_s|\right)/\left(|\mathrm{\Phi }|+|{\Omega }_s|\right),s\in \left\{1,\dots ,S\right\}\end{array}$(4) (5) $\begin{array}{rl}& e_s\ge 1-\left(\sum _{i\in \mathrm{\Phi }}{a}_{is}+|{\Omega }_s|\right),s\in \left\{1,\dots ,S\right\}\end{array}$(5)

Equation (1) aims to minimise the reshuffles $CR+IR$ and maximise the number of empty slots E in a storage yard. Let $e_s$ be a binary variable, with $e_s=1$ indicating the slot being empty. Thus, we have $E={\sum }_{s=1}^S{e}_s$ as the number of empty slots. $\alpha$ is a weighting parameter to coordinate two objectives, i.e. reshuffles and empty slots. The empty slots are important for stacking future items, see details in Section 3.2.

Constraint (2) ensures each item only stacked in one slot. Constraint (3) illustrates the height limit. Constraints (4) and (5) ensure that $e_s$ is consistent with its definition. ${\sum }_{i\in \mathrm{\Phi }}{a}_{is}$ is the number of target items allocated to slot s. If slot s has no item, we have ${\sum }_{i\in \mathrm{\Phi }}{a}_{is}+|{\Omega }_s|=0$, which forces $e_s$ equal to one. If there is either an existing or a target item, we have $e_s<1$ in Constraint (4), which leads to $e_s=0$. Constraint (5) helps to reduce the computational time.

Further note that the number of reshuffles defined here is eventually an upper bound of actual reshuffles. According to our reshuffle definition, the reshuffled item will be put back to its original slot. In practice, it could be reshuffled to another slot without causing further reshuffles. However, such dynamic movements and reshuffles are rather difficult to formulate. It is similar to the container stack emptying problem (Wan, Liu, and Tsai 2009; Zhu et al. 2012). Furthermore, as several batches will arrive within one retrieval period, the slot configuration keeps changing. This makes the problem even more complicated. Therefore, an upper bound is a good estimation for the performance. In addition, in our industrial case, reshuffles are handled by forklifts and thus assigning an item back is practical.

3.2. Space criterion

In the objective function (1), the third term pertains to the effect of the scattered stacking strategy on future stacking decisions. The scattered stacking strategy allows items to be placed in any slot, including ones already containing items. The configuration resulting from the current stacking decision will affect future stacking decisions. When all slots are used, future items must be stacked on top of existing ones, thereby an increasing possibility of additional reshuffles. Given that the PA model considers only current target items, a scattered stacking strategy intends to distribute items over slots, thereby reducing the reshuffles involving existing items. However, this strategy is suboptimal when considering future items. In fact, a larger number of occupied slots indicates more possibilities of reshuffles due to future items, whereas a higher layer of occupied slots leads to more possibilities of reshuffling stacked items.

An alternative stacking strategy is reserving slots for future items, considering the number of empty slots (E). This approach balances the conflicting objectives of reducing reshuffles (current target items) and saving empty slots by assigning a weighting factor $\alpha$. When there is no empty slot, i.e. $E=0$, the weighting factor has no effect, and the objective is minimising the number of reshuffles. In other cases, $\alpha$ indicates the relative importance of empty slots. A larger value of $\alpha$ results in a greater emphasis on preserving empty slots, at the cost of increasing the number of reshuffles.

To further explore the relationship between reshuffles and space, let $R=CR+IR$, and $\mathit{A}$ the set of feasible solutions. Given a feasible solution $\chi$, $\chi \in \mathit{A}$, we calculate $R_{\chi }$ and $E_{\chi }$ in the objective function. With a given $\alpha$, Equation (1) can be written as $\vartheta \left(\alpha \right)=\underset{\chi \in A}{min}\left\{R_{\chi }-\alpha E_{\chi }\right\}$. Furthermore, with a given value R, the largest empty slot number is $E^{\ast }\left(R\right)=max\left\{E_{\chi }|R_{\chi }=R,\chi \in \mathit{A}\right\}$, and the solution $\left(R,E^{\ast }\left(R\right)\right)$ always dominates the others $\left\{\left(R_{\chi },E_{\chi }\right)|R_{\chi }=R,\chi \in \mathit{A}\right\}$ in terms of minimising the objective function (1). Define ${\mathrm{\Delta }}_R{E}^{\ast }\left(R\right)=E^{\ast }\left(R\right)-E^{\ast }\left(R-1\right)$, it is easy to have $0\le {\mathrm{\Delta }}_R{E}^{\ast }\left(R\right)\le 1$. When reducing a unit of reshuffles, it leads at most one extra empty slot or not. It implies that the change rate of empty slots is smaller than that of reshuffles. This principle helps to define the weight of two objectives: if reducing reshuffles is more important that saving space, we should let $0\le \alpha <1$; otherwise we have $\alpha >1$. The above analysis is based on the minimal reshuffle unit $\mathrm{\Delta }R=1$ in a deterministic model. However, in Sections 4 and 5 regarding partial information, we estimate the reshuffles based on distributions of stochastic variables, therefore the expected reshuffles could be less than one ($\mathrm{\Delta }R<1$). In this case to prioritise minimising reshuffles, we should set $0<\alpha <\mathrm{\Delta }R$. In our experiments, we consistently use an α value of 0.1.

3.3. Upper and lower bounds

The stacking decisions are made repeatedly with new arrivals. Each stacking decision generates a new slot configuration, which is the input for the next decision. It is important to evaluate the performance of a stacking model from a long-run perspective, but its analytical results are difficult to obtain, especially with partial information. Thus, we introduce bounds for the performance.

We first introduce two upper bounds. The first is a heuristic upper bound: target items are stacked one by one to a slot in descending order of their retrieval time and sequences. Thus, reshuffles among target items in the same batch will be eliminated (see Figure 3). The second is a random upper bound so that all items are stacked randomly in slots.

About the lower bound, one simple principle is to have information on future items to obtain global optimal decisions on both target and future items. We introduce a multiple-period stacking model (PA-MP model). Given that we have the full information of future items in the coming T periods, we make decisions to minimise the total reshuffles. (6) $\left(\text{PA}-\text{MP Model}\right)min\sum _i\sum _j\sum _s{\theta }_{ij}\cdot d_{ijs}$(6) s.t. (7) $\begin{array}{rl}& \sum _{s=1}^S{a}_{is}=1,i\in \mathrm{\Phi }\end{array}$(7) (8) $\begin{array}{rl}& a_{is}+a_{js}-1\le d_{ijs},\mathrm{\forall }i,j\in \mathrm{\Phi },i\ne j,s\in \left\{1,\dots ,S\right\}\end{array}$(8) (9) $\begin{array}{rl}& \sum _{i\in \mathrm{\Phi }}{\phi }_{it}{a}_{is}\le H,s\in \left\{1,\dots ,S\right\},t\in \left\{1,\dots ,T\right\}\end{array}$(9)

New notations include binary variable $d_{ijs}$, indicating whether i and j are both stacked in slot s, and binary parameter ${\phi }_{it}$, indicating that i is in the configuration in period t, i.e. i arrives earlier than period t and retrieves after period t, ${\phi }_{it}=1|\left\{k_i\ge t\mathrm{\&}{l}_i\le t\right\}$, and binary parameter ${\theta }_{ij}$, indicating that i arrives and retrieves earlier than j, and j arrives earlier than retrieval of i, i.e. i and j are both in a configuration for at least one period. ${\theta }_{ij}=1|\left\{l_j>l_{i}or\left\{l_j=l_i\mathrm{\&}{v}_j>v_i\right\}\right\}\mathrm{\&}\{k_j>k_{i}or\{k_j=k_i\mathrm{\&}{u}_j>u_i\left\}\right\}\mathrm{\&}\left\{k_i\ge l_j\right\}$.

Constraint (7) ensures one item is stacked in one slot. Constraint (8) ensures that $d_{ijs}$ equals to one only when both i and j are allocated in slot s. Otherwise minimising the objective will force $d_{ijs}=0$. Constraint (9) ensures the height limit. A reshuffle happens only when j arrives and leaves later than i, the term ${\theta }_{ij}\cdot d_{ijs}$ in the objective function (6) indicates one reshuffle only if i and j are both in one slot.

We then conduct a numerical experiment to compare all bounds, adopting the settings in Section 4.5. The performance is the expected reshuffles per item over 50 weeks. The result is shown in Figure 4. We also test the performance of having information on future items of different periods. The number after the ‘PA-MP’ notation indicates the number of periods T.

Figure 4. Comparison of PA model and upper and lower bounds.

The numerical results for the comparison of PA model and upper and lower bounds.

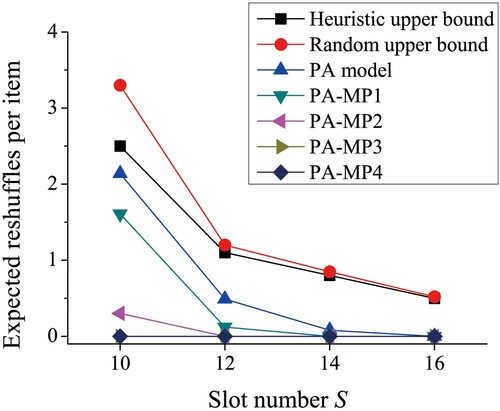
The experiment results highlight the importance of the number of slots in determining the performance of the models. As the number of slots increases, the performance of all models improves. In comparing the two upper bounds, the heuristic upper bound performs relatively better when the space is restricted. However, as the number of slots increases, the performance of both upper bounds becomes similar.

When the space is restricted, PA model is relatively close to the upper bound, indicating that optimisation without information about future items has limited advantages over simple heuristics. Furthermore, the large gap between PA model and PA-MP models demonstrates the value of incorporating information on future items. More specifically, information with more future periods in PA-MP models improves the performance, nevertheless, the marginal improvement from including more future periods declines. This suggests that information on items arriving soon is more valuable than items in the far future. In addition, as the number of slots increases, the information on future periods brings less benefits.

4. Partial information on the inbound side

In this section, we evaluate stacking performance by incorporating information on future items, including their quantity, arrival time and retrieval time. The retrieval time is described by the retrieval period and sequence within the period, while the arrival time is defined similarly.

Given the practical difficulties in collecting information about future items, we consider four scenarios, ranging from complete ignorance to full knowledge of future items. Specifically, we consider one scenario where all information is unknown, two scenarios with partial information and one scenario where all information is known, as shown in Table 2. The aim is to examine the extent to which partial information about future items affects stacking performance.

In this study, we focus on the arriving batches solely in the current period for three reasons. First, a retrieval operation can often result in a significant number of emptied slots, therefore a single-period model is already a good approximation. Secondly, including arriving batches in multiple periods would also pose significant challenges in terms of obtaining accurate information in practice. Thirdly, by limiting the consideration to the current period, we potentially have better insights in understanding the benefits and mechanism of incorporating partial information on future items.

4.1. Preliminary

In this paper, partial information refers to uncertain quantity, retrieval time and arrival time of future items. The deterministic variables k and v in Section 3 become stochastic here.

First, we present the stochastic retrieval time. Let k denote the stochastic integer variable of a retrieval time-period. An item can be retrieved in any period from the current period ($k=1$) to period K, i.e. $k\in \left\{1,\dots ,K\right\}$. Its probability mass function is $p_k(\cdot )$, the distribution function is $P_k(\cdot )$ and complementary distribution function is ${\overline{P}}_k(\cdot )$. With two items i and j, the probability of i being retrieved earlier than j is. (10) $Pr\left\{k_i<k_j\right\}=E_{k_i}\left[{\overline{P}}_K\left(k_i\right)\right]=\sum _{k_i=1}^K{p}_k\left(k_i\right)\cdot {\overline{P}}_k\left(k_i\right)={\eta }_k$(10) Further, let an integer variable u be the stochastic retrieval sequence with a known independent identical distribution (i.i.d.) for all items in the same retrieval period. The distribution depends on the number of items to be retrieved in period k which is denoted as $u^k$. Let $p_u(\cdot )$ and $P_u(\cdot )$ be its mass and distribution functions, respectively. If two items i and j are retrieved in the same period, the probability of i being retrieved earlier than j is (11) $Pr\left\{u_i<u_j\right\}=\sum _{u_i=1}^U{p}_u\left(u_i\right)P_u\left(u_i\right)={\eta }_u$(11) The stochastic arrival time is defined similarly. Since we only consider future items before the next retrieval in the decision models, all items belong to the same arrival time-period, but the arrival sequence differs. As items arrive in batches, the items in one batch have the same arrival sequence. Let an integer variable v be the stochastic arrival sequence and let V be the number of batches before the next retrieval, $v\in \left\{1,\dots ,V\right\}$. Suppose v is i.i.d. for all future items with probability mass function $p_v(\cdot )$, distribution function $P_v(\cdot )$ and complementary distribution function ${\overline{P}}_v(\cdot )$. With items i and j, the probability of i arriving in an earlier batch than j is (12) $Pr\left\{v_i<v_j\right\}=E_{v_i}\left[{\overline{P}}_v\left(v_i\right)\right]=\sum _{v_i=1}^V{p}_v\left(v_i\right)\cdot {\overline{P}}_v\left(v_i\right)={\eta }_v$(12) The probability of i arriving in the same batch as j is (13) $Pr\left\{v_i=v_j\right\}=E_{v_i}\left[p_v\left(v_i\right)\right]=\sum _{v_i=1}^V{p}_v{\left(v_i\right)}^2={\omega }_v$(13)

As $Pr\left\{v_i<v_j\right\}+Pr\left\{v_i=v_j\right\}+Pr\left\{v_i>v_j\right\}={\eta }_v+{\omega }_v+{\eta }_v=1$, we have ${\eta }_v+{\omega }_v/2=0.5$.

Also, note that the uncertain retrieval sequence influences the position of target items. If i and j are both target items, their relative positions are random due to their identical retrieval information. Thus, i could be stacked either above or below j, and $Pr\left\{\text{item }j\text{ above item }i\right\}\text{ = }0.5$.

4.2. Quantity information of future items

In this subsection, we investigate the impact of the information on the total quantity of future items in the current period. This is the most common case in reality (for instance our case company). We lack the exact information on the arrival and retrieval times of items but are aware of their distributions. We then extend PA model to PA-Q model with the knowledge of future item quantity denoted as $|\mathrm{\Psi }|$.

We first redefine the objective function and constraints. Since future items are always stacked above the existing and target items, retrieving future items causes no reshuffle of the existing and target ones. Hence, the reshuffles of target items are independent of future items so that CR and IR in PA model are still valid. On the other hand, the reshuffles of future items could be caused by retrieving the existing and target items. Suppose future items i and j are both allocated to the same slot, if the retrieval of i causes a reshuffle of j, j should be stacked above i, which indicates $v_i<v_j$ or $v_i=v_j$. Thus, the expected cross-period reshuffles of future item j caused by future item i in the same slot are. (14) $\begin{array}{rl}fc{r}_{i,j}& =1\cdot Pr\left\{v_i<v_j\mathrm{\&}{k}_i<k_j\right\}+1\\ & \cdot Pr\left\{v_i=v_j\mathrm{\&}\text{item }j\text{ above item }i\mathrm{\&}{k}_i<k_j\right\}\\ & ={\eta }_v\cdot {\eta }_k+{\omega }_v\cdot \delta \cdot {\eta }_k\\ & ={\eta }_k/2\end{array}$(14) Similarly, the expected within-period reshuffles of future item i caused by future item j are (15) $\begin{array}{rl}fi{r}_{i,j}& =1\cdot Pr\left\{v_i<v_j\mathrm{\&}{k}_i=k_j\mathrm{\&}{u}_i<u_j\right\}+1\\ & \cdot Pr\{v_i=v_j\mathrm{\&}\text{item }j\text{ above item }i\mathrm{\&}{k}_i\\ & =k_j\mathrm{\&}{u}_i<u_j\}\\ & ={\eta }_v\cdot {\omega }_k\cdot {\eta }_u+{\omega }_v\cdot \delta \cdot {\omega }_k\cdot {\eta }_u\\ & ={\omega }_k\cdot {\eta }_u/2\end{array}$(15) Let a binary variable $b_{js}=1$ indicate future item j allocated to slot s, then the cross-period reshuffle of future items is $FC{R}^Q$. (16) $\begin{array}{rl}FC{R}^Q& =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\phantom{\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}}\sum _{i\in {\mathrm{\Omega }}_s}Pr\left\{k_j>k_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot Pr\left\{k_j>k_i\right\}\right)+\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot fc{r}_{j,i}\right))\\ & =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\phantom{\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}}\sum _{i\in {\mathrm{\Omega }}_s}{\overline{P}}_k\left\{k_i\right\}+\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot {\overline{P}}_k\left(k_i\right)\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot {\eta }_k/2\right))\end{array}$(16) Similarly, the expected within-period reshuffles, including the within-period reshuffles among future items are (17) $\begin{array}{rl}FI{R}^Q& =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\phantom{\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}}\sum _{i\in {\mathrm{\Omega }}_s}Pr\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot Pr\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot fi{r}_{j,i}\right))\\ & =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\phantom{\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}}\sum _{i\in {\mathrm{\Omega }}_s}{p}_k\left\{k_i\right\}\cdot {\overline{P}}_u(u_i)\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot p_k\left(k_i\right)\cdot {\overline{P}}_u\left(u_i\right)\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot {\omega }_k\cdot {\eta }_k/2\right))\end{array}$(17) where ${\overline{P}}_u\left(u_i\right)=0.5$, i.e. the probabilities of retrieving a future item earlier or later than a target item of the same period k are the same.

We define the objective function as $minCR+IR+FC{R}^Q+FI{R}^Q-\alpha E$. Note that we still consider the space usage, with E defined the same as in PA model. We also consider future items in the restriction on the number of items in one slot. The corresponding constraint (3) is modified as (18) $\sum _{i\in \mathrm{\Phi }}{a}_{is}+|{\mathrm{\Omega }}_s|+\sum _{j\in \mathrm{\Psi }}{b}_{js}\le H,s\in \left\{1,\dots ,S\right\}$(18) An additional constraint is added as: (19) $\sum _{s=1}^S{b}_{js}=1,j\in \mathrm{\Psi }$(19)

4.3. Information with total quantity and retrieval time

We then examine another scenario. The exact retrieval time ($k$ and $u$) as well as the total quantity are known for future items. It usually occurs when customers appoint a specific delivery day, and this information is shared within the logistics system. However, due to the uncertain production process, the arrival time is still uncertain. This scenario becomes PA-QR model. Similarly, we redefine the reshuffle terms in the objective function. The expected cross-reshuffles and within-period reshuffles of future items are respectively (20) $\begin{array}{rl}FC{R}^{QR}& =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\phantom{\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}}\sum _{i\in {\mathrm{\Omega }}_s}1|\left\{k_j>k_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot 1|\left\{k_j>k_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot Pr\left\{v_i<v_j\right\}|\left\{k_i<k_j\right\}\right))\\ & =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\phantom{\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}}\sum _{i\in {\mathrm{\Omega }}_s}1|\left\{k_j>k_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot 1|\left\{k_j>k_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot {\eta }_v|\left\{k_i<k_j\right\}\right))\end{array}$(20) (21) $\begin{array}{rl}FI{R}^{QR}& =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}\\ & \times \left(\begin{array}{rl}& \sum _{i\in {\mathrm{\Omega }}_s}1|\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot 1|\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}(b_{is}\cdot Pr\{v_i<v_j\}\\ & |\left\{k_j=k_i\mathrm{\&}{u}_i<u_j\right\})\end{array}\right)\\ & =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}\\ & \times \left(\begin{array}{rl}& \sum _{i\in {\mathrm{\Omega }}_s}1|\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot 1|\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}(b_{is}\cdot {\eta }_v\\ & |\left\{k_j=k_i\mathrm{\&}{u}_i<u_j\right\})\end{array}\right)\end{array}$(21) Note that if the future item i and j arrive at the same batch ($v_i=v_j$) and are allocated into the same slot, they will be stacked according to an ascending order of k and u as in Section 3.1, hence no reshuffle occurs.

The objective function becomes $minCR+IR+FC{R}^{QR}+FI{R}^{QR}-\alpha E$. The constraints remain the same as in PA-Q model.

4.4. Full information on future arriving items

Finally, PA-QRA model includes full information on future items for the purpose of comparison. Besides the retrieval information, we also know the arrival sequence $v_i$ of future items. Thus, we can optimise the stacking decisions together with the target and future items.

In fact, the arrival sequence affects the reshuffles only involving future items. Hence, we simply modify the third term in the expressions of FCR and FIR of PA-QR model. (22) $\begin{array}{rl}FC{R}^{QRA}& =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\phantom{\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}}\sum _{i\in {\mathrm{\Omega }}_s}1|\left\{k_j>k_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot 1|\left\{k_j>k_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot 1|\left\{v_j>v_i\mathrm{\&}{k}_j>k_i\right\}\right))\end{array}$(22) (23) $\begin{array}{rl}FI{R}^{QRA}& =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}\\ & \times \left(\begin{array}{rl}& \sum _{i\in {\mathrm{\Omega }}_s}1|Pr\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot 1|\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}(b_{is}\cdot 1|\{v_j>v_i\mathrm{\&}{k}_j\\ & =k_i\mathrm{\&}{u}_j>u_i\left\}\right)\end{array}\right)\end{array}$(23)

The objective function becomes $minCR+IR+FC{R}^{QRA}+FI{R}^{QRA}-\alpha E$. The other constraints remain the same.

4.5. Values of future item information

This subsection investigates the benefits of incorporating various information in stacking decisions with as simulation study.

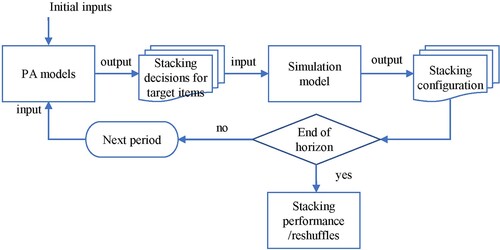
As items arrive and leave the storage yard consecutively, we have to measure the stacking performance in multiple periods. Thus, numerical experiments are employed. We develop a simulation for the operations in storage yards. The previously presented models are used to generate decisions in same simulation environment, and these optimisation models are solved using Cplex 12.6. The computational process is illustrated in a flow chart in Figure 5.

Figure 5. The flow chart of the computational process.

The computational process including PA models and simulation.

The parameters of the numerical experiments are as follows. We have a storage yard with slots, each has eight layers, $H=8$. We consider a stream of items in 50 weeks. Thirty-two items are retrieved at the end of each week. Half of these items arrive two weeks before the retrieval and the others arrive one week before. In total, 32 items arrive each week randomly allocated to 4 equal batches. At the end of each week, there are total 80 items, including 32, 32 and 16 items to be retrieved immediately, next week and in two weeks, respectively. We use discrete uniform distributions to generate retrieval period k, retrieval sequence u and arrival batch v. The retrieval sequence of items within the same retrieval period is random, and the probability of any sequence is the same. Similarly, the probability of retrieval time-period is similar as it depends largely on the number of customers. Hence, a uniform distribution is representative in these cases.

We vary the slot number as 10 to 16. Since the number of items is fixed, S also affects the expected space utilisation $\mathrm{\Lambda }$. When $S=10$, the space capacity $\mathrm{\Lambda }=100\mathrm{\%}$ right before the retrieval in each period. An increasing number of slots indicates decreasing in space utilisation. Let $\alpha =0.1$ to ensure the minimisation of reshuffles has a high priority as discussed previously. To evaluate the performance of the proposed models, we conducted the computational experiments for 30 different data streams, with a five-week warm-up period. The computational time of solving the optimisation model is around 1 s for the problem scale. It takes about 200 s to run a 50-week simulation with one data stream. We have also conducted calculations with data about 500 slots and 100 target items. The problem can be solved within approximately 5 s for each decision.

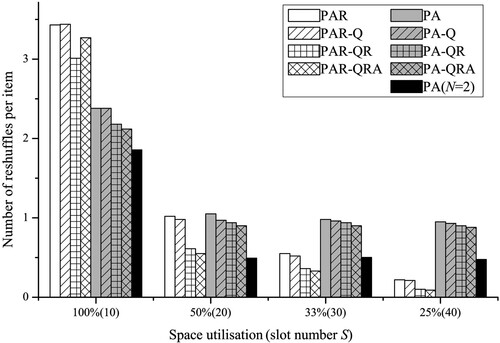
In Figure 6, as space utilisation is reduced and the average stacking height in slots is lowered, the reshuffles of all models are reduced greatly. However, the models with various future information perform differently regarding space utilisation. When the space utilisation is low, more future item information leads to better performance. But this is not true when space utilisation is very high.

Figure 6. Stacking performance with different future information.

A comparison of stacking performance with different future information.

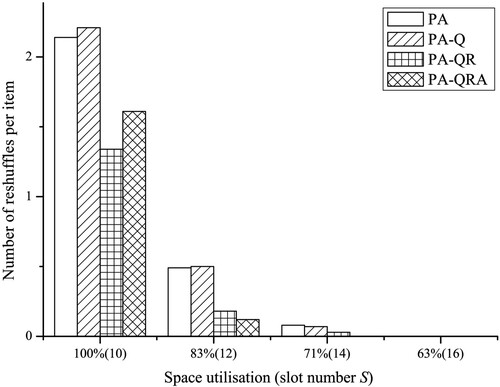
First, we find on average PA-Q model performs even worse than PA model with $\mathrm{\Lambda }=100\mathrm{\%}$. This is because PA-Q model contains much uncertain information about the arrival and retrieval times. In PA-Q objective function, major reshuffles occur with future items are estimated based on distributions of arrival and retrieval times. When the space utilisation is very high, there is little chance to reduce the expected reshuffles. The model will increase the reshuffles of target items in an attempt to reduce the expected reshuffles of future items, and this worsens the long-run performance. The phenomenon indicates that with high space utilisation, low-quality information on future items may not benefit decision-making compared with no information.

Second, when space is fully occupied, PA-QRA model averagely performs worse than PA-QR model. PA-QRA model can optimise the stacking decisions for arriving items within one week. However, the resulting configuration affects the performance of the successive weeks. Hence, a series of optimal decisions is probably not robust when space is limited, as the optimal decision is very sensitive with (slightly) changing settings in this case. The phenomenon indicates the unnecessity to collect full information on future items when space utilisation is very high, since the model with full information cannot guarantee better performance than partial information.

These results show difficulties to gain benefits by including information on future items when space utilisation is very high, whereas partial information with high quality can contribute positively. In practice, collecting information needs great effort. To improve stacking performance, managerial efforts should orientate on increasing space rather than collecting information on future items. As shown in Figure 6, lower space utilisation can reduce reshuffles substantially in all models.

5. Partial information on the outbound side

On the outbound side, the retrieval plan is made on a time-period basis. There is insufficient information on the retrieval sequence within one period (a week for instance) when a retrieval plan is made. Therefore, the retrieval information is partial, which means the retrieval period k is deterministic while the retrieval sequence u is unknown. It becomes difficult to assign the right positions to items to be retrieved in the same period. When the actual retrieval sequence deviates from the stacking sequence, additional reshuffles occur. One stacking policy is to ignore the uncertain retrieval sequence so that the decisions are based on the deterministic stacking models. In this case, we can employ PA models, implying $IR=0$ in the objective function (but positive in implementation). An alternative policy is including the uncertain information of retrieval sequence by using the distribution of retrieval sequence. This section is indicated for this purpose.

5.1. PA model with random retrieval sequence

We first develop PAR model based on PA model with the consideration of partial retrieval information. Future items are not considered in the decisions. Since the retrieval period k of items is known, the definition of CR remains the same whereas IR needs to be redefined due to the uncertain retrieval sequence u.

Suppose we have two items i and j to be retrieved in the same period, the probability of j being retrieved earlier than i is $Pr\left\{u_i>u_j\right\}={\eta }_u$ as discussed before. If i is stacked above j, the expected reshuffles that the retrieving j causes to i is $1\cdot {\eta }_u$. If both i and j are target items, their relative positions are random due to identical retrieval information, i.e. i can be either above or below j with $\delta =0.5$. We can estimate the within-period reshuffles as (24) $\begin{array}{rl}I{R}_{PR}& =\sum _{i\in \mathrm{\Phi }}\sum _{s=1}^S{a}_{is}\cdot (\phantom{\sum _{j\in \mathrm{\Phi }\mathrm{\setminus }i}}\sum _{j\in {\mathrm{\Omega }}_s}Pr\left\{u_i>u_j\right\}|\left\{k_i=k_j\right\}\\ & +\sum _{j\in \mathrm{\Phi }\mathrm{\setminus }i}{a}_{js}\cdot Pr\left\{\text{item }i\text{ above item }j\right\}\\ & \cdot Pr\left\{u_i>u_j\right\}|\left\{k_i=k_j\right\}\phantom{\sum _{j\in \mathrm{\Phi }\mathrm{\setminus }i}})\\ & =\sum _{i\in \mathrm{\Phi }}\sum _{s=1}^S{a}_{is}\cdot (\phantom{\sum _{j\in \mathrm{\Phi }\mathrm{\setminus }i}}\sum _{j\in {\mathrm{\Omega }}_s}{\eta }_u|\left\{k_i=k_j\right\}\\ & +\sum _{j\in \mathrm{\Phi }\mathrm{\setminus }i}{a}_{js}\cdot \delta \cdot {\eta }_u|\left\{k_i=k_j\right\})\end{array}$(24) The first term in the parentheses is the expected within-period reshuffles of target items caused by the retrieval of existing items. The second term is the expected reshuffles caused by the retrieval of other target items allocated in the same slots. Note that the second term exists due to the uncertain retrieval sequence, but not in PA model with full retrieval information. Even though, if several target items are allocated to the same slot, positions should be assigned accordingly, i.e. being stacked from top to bottom in ascending order of retrieval period $k_i$. Thus, there are only within-period reshuffles. We replace IR in PA model to define PAR model as $minCR+I{R}_{PR}-\alpha E$.

5.2. Future items with partial retrieval information

Moreover, the retrieval information of future items is also partial, i.e. deterministic $k$ and uncertain u. We extend PAR model to include various future information similar to Section 4.

The reshuffles are divided into four parts: CR and IR of the target items, and correspondingly FCR and FIR of the future items. Since the target items are always stacked beneath the future ones, retrieving future items does not cause reshuffles of the target ones. The expressions of CR and $I{R}_{PR}$ remain the same as in PAR model. Also, because k is known, FCR remains the same as in PA models with future information (PA-Q, PA-QR, PA-QRA). We then need to define the new expressions of FIR.

5.2.1. PAR-Q model

Similar to PA-Q model, PAR-Q model only includes the total quantity of future items before the next retrieval. It implies that we can only estimate the reshuffles based on the distribution of k and u. Redefine the expected number of within-period reshuffles as (25) $\begin{array}{rl}FI{R}_{PR}^Q& =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\sum _{i\in {\mathrm{\Omega }}_s}Pr\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot Pr\left\{k_j=k_i\mathrm{\&}{u}_j>u_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot fi{r}_{j,i}\right))\\ & =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\sum _{i\in {\mathrm{\Omega }}_s}{p}_k\left\{k_i\right\}\cdot {\eta }_u\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot p_k\left(k_i\right)\cdot {\eta }_u\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot {\omega }_k\cdot {\eta }_u/2\right))\end{array}$(25) The objective of PAR-Q model is defined as $minCR+I{R}_{PR}+FC{R}^Q+FI{R}_{PR}^Q-\alpha E$.

5.2.2. PAR-QR model

In PAR-QR model, we know additional partial retrieval information of future items, i.e. the retrieval period of a future item is known but the retrieval sequence is unknown. The new FIR is (26) $\begin{array}{rl}FI{R}^{QR}& =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}\\ & \times \left(\begin{array}{rl}& \sum _{i\in {\mathrm{\Omega }}_s}Pr\left\{u_j>u_i\right\}|\left\{k_j=k_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot Pr\left\{u_j>u_i\right\}|\left\{k_j=k_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}(b_{is}\cdot Pr\{v_i<v_j\mathrm{\&}{u}_j>u_i\}\\ & |\left\{k_j=k_i\right\})\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}(b_{is}\cdot Pr\{v_i=v_j\mathrm{\&}\text{item }j\\ & \text{above item }i\mathrm{\&}{u}_j>u_i\left\}|\right\{k_j=k_i\left\}\right)\end{array}\right)\\ & =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}(\phantom{\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}}\sum _{i\in {\mathrm{\Omega }}_s}{\eta }_u|\left\{k_j=k_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot {\eta }_u|\left\{k_j=k_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot 0.5\cdot {\eta }_u|\left\{k_j=k_i\right\}\right))\end{array}$(26) We define the objective of PAR-QR model as $minCR+I{R}_{PR}+FC{R}^{QR}+FI{R}_{PR}^{QR}-\alpha E$.

5.2.3. PAR-QRA model

In this model, we know partial retrieval information and the exact arrival sequence of the future items. Note that with partial retrieval information, we no longer have full information due to the lack of certain u. We redefine the within-period reshuffles as (27) $\begin{array}{rl}& FI{R}^{QRA}\\ & =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}\\ & \times \left(\begin{array}{rl}& \sum _{i\in {\mathrm{\Omega }}_s}Pr\left\{u_j>u_i\right\}|\left\{k_j=k_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot Pr\left\{u_j>u_i\right\}|\left\{k_j=k_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}(b_{is}\cdot Pr\{u_j>u_i\}\\ & |\left\{v_j>v_i\mathrm{\&}{k}_j=k_i\right\})\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}(b_{is}\cdot Pr\{\text{item }j\text{ above}\\ & \text{item }i\mathrm{\&}{u}_j>u_i\left\}|\right\{v_i=v_j\mathrm{\&}{k}_j=k_i\left\}\right)\end{array}\right)\\ & =\sum _{j\in \mathrm{\Psi }}\sum _{s=1}^S{b}_{js}\\ & \times \left(\begin{array}{rl}& \sum _{i\in {\mathrm{\Omega }}_s}{\eta }_u|\left\{k_j=k_i\right\}\\ & +\sum _{i\in \mathrm{\Phi }}\left(a_{is}\cdot {\eta }_u|\left\{k_j=k_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot {\eta }_u|\left\{v_j>v_i\mathrm{\&}{k}_j=k_i\right\}\right)\\ & +\sum _{i\in \mathrm{\Psi }\mathrm{\setminus }j}\left(b_{is}\cdot \delta \cdot {\eta }_u|\left\{v_j=v_i\mathrm{\&}{k}_j=k_i\right\}\right)\end{array}\right)\end{array}$(27) PAR-QR model is developed based on PAR and PA-QRA models with restrictions as $minCR+I{R}_{PR}+FC{R}^{QRA}+FI{R}_{PR}^{QRA}-\alpha E$.

5.3. Value of partial retrieval information

We then investigate how the partial retrieval information affects the stacking performance by employing a numerical experiment, with the same settings in Section 4.5. As retrieval sequence $u_i$ is random in Section 5, it is generated by a uniform distribution. As mentioned at the beginning of Section 5, we compare two policies. The first policy incorporates the uncertain retrieval sequence into decision models, which leads to a collection of PAR class models (PAR, PAR-Q, PAR-QR, PAR-QRA). The second one assumes the retrieval sequence to be the same for all items, indicating within-period reshuffles to be disregarded in stacking decisions ($IR=FIR=0$). It leads to a collection of PA class models (PA, PA-Q, PA-QR, PA-QRA). Both policies generate decisions in the same simulation environment.

5.3.1. Including vs. excluding uncertain retrieval sequence

Figure 7 reveals the performance of two model classes with different space utilisations. The light columns are the performance of PAR class whereas the dark ones are PA class.

Figure 7. Performance of stacking models with different information.

We observe that the two model classes perform differently with various space utilisations. As space increases (space utilisation is low), PAR models have decreasing reshuffles while the reshuffles of PA models decrease first and then become fairly constant. Comparing the performance, we see that PA models dominate PAR models when space utilisation is high. But as space increases, PAR models gradually outperform PA models. Thus, with an uncertain retrieval sequence, PAR models perform better only with sufficient empty spaces. Otherwise, they perform worse than models excluding the information on uncertain retrieval sequence. To explain the underlying principle, we present the reshuffle details in Table 3.

Table 3. Reshuffles per item in PA and PAR models.

	PAR models			PA models
$\mathrm{\Psi }\left(S\right)$	CR	IR	R	CR	IR	R
100% (10)	2.68	0.75	3.43	1.19	1.16	2.35
50% (20)	0.69	0.34	1.03	0.00	1.05	1.05
33% (30)	0.36	0.19	0.55	0.00	1.01	1.01
25% (40)	0.12	0.09	0.21	0.00	0.96	0.96

Including the stochastic sequence u, PAR model yields less IR but much more CR than PA model when the space is fully occupied ($S=10$, without any empty slot). The trade-off in the objective is between the confirmed CR determined by the deterministic retrieval period and the estimated IR based on the uncertain retrieval sequence. Since IR increases with the number of items in the same retrieval period allocated to one slot, PAR model reduces IR by spreading these items into more slots. As a result, the items arriving later are more likely to stack on existing ones which are likely retrieved earlier, therefore generating more cross-period reshuffles. When there is enough space, PAR model can reduce both CR and IR due to the relaxed space constraint.

Excluding the stochastic sequence u, PA model only minimises CR. It inclines to stacking together items of the same retrieval period to reduce CR. Meanwhile, it generates more IR. When the space utilisation is high, PA model dominates PAR model by generating fewer total reshuffles. However, since PA model excludes IR and space term $-\alpha E$ in the objective function, we see that with enough space its CR is minimised to zero whereas its IR has no improvement. The comparison result also applies to other models in PAR and PA classes.

The result implies that when the space utilisation is high, it is better to ignore the uncertain retrieval sequence and minimise the reshuffles only based on the deterministic retrieval period. Otherwise, the deterministic information will be diluted by uncertain information, and therefore the decision of critical resources refers to unreliable information and subsequently, the model generates an overall worse performance. When there is sufficient space, redundant resources can alleviate the negative consequence of uncertain information, thus we regain the benefits of including uncertain information.

5.3.2. Performance with future item information

Figure 7 displays the improvement of the models when considering partial information. The contribution of future item information reduces due to the partial retrieval information. In Section 4.5 we show that with full retrieval information, the models including information on future items can improve the performance significantly even if the space utilisation is high ($\mathrm{\Lambda }=83\mathrm{\%},71\mathrm{\%}$). However, with partial retrieval information, the models with high-quality information of future items present obvious improvement only when the space utilisation is medium and low ($\mathrm{\Lambda }\le 50\mathrm{\%}$). The potential for improvement is much smaller than the situation with full retrieval information.

5.4. Reducing uncertainty

The performance difference between PA and PAR models also varies with the level of uncertainty in the retrieval information. In our case, uncertainty refers to the unpredictability of the retrieval sequence of items belonging to the same retrieval period. Thus, a higher number of items to be retrieved during a period leads to a higher uncertainty.

One way to remove the retrieval sequence uncertainty of items within the same retrieval period is dividing a period into time windows and assign each item to a specific time window. Then retrieval vehicles arrive and retrieve items in the assigned time window. This results in a unique item retrieval sequence, which eliminates all within-period reshuffles. However, it is impractical to have such a short time window for vehicles, and it is unnecessary to assign a unique time window for each item. For example, if two items in the same time window are stacked in different slots, there is no reshuffle regardless of the retrieval sequence. To reduce reshuffles, we propose a time window assignment model that allocates items with the same retrieval period in the same slot into several time windows, while minimising within-period reshuffles. The method is presented as follows. We assume that the retrieval period is divided into N time windows, which are indexed by n. Within period k, there are $U_k$ items to be retrieved, which are indexed by i. The binary variable $x_{in}=1$ indicates whether item i is assigned to time window n. Additionally, an integer variable $N{P}_i$ represents the assigned window index of item i and $N{P}_i=\sum _{n=1}^{N}n\cdot x_{in}$. The binary variable $z_{ij}$ represents the comparison of the time window assignment between items i and j, with $z_{ij}=1$ indicating that i is assigned to an earlier time window than j.

Using the results of previous stacking models, we have the stacking sequence of items, depicted by a binary variable ${\upsilon }_{ij}$, with ${\upsilon }_{ij}=1$ indicating i stacking below j in the same slot. Thus, we formulate the 0–1 programming model as follows. (28) $\text{TWA model}:min\sum _{i=1}^{U_k}\sum _{j=1}^{U_k}{\upsilon }_{ij}\cdot z_{ij}\left(i\ne j\right)$(28) s.t. (29) $\begin{array}{rl}\sum _{n=1}^N{x}_{in}& =1\end{array}$(29) (30) $\begin{array}{rl}{z}_{ij}& \ge \frac{N{P}_j-N{P}_i}{N}+\frac{0.5}{N}\end{array}$(30) (31) $\begin{array}{rl}{z}_{ij}& \le \frac{N{P}_j-N{P}_i}{N}+1\end{array}$(31)

Constraint (29) indicates an item assigned to one time window. We do not restrict the number of items in one window. Constraints (30) and (31) ensure that $z_{ij}$ follows its definition. Note that the term $0.5/N$ in Constraint (31) forces $z_{ij}=1$ when i and j are in the same window. Subsequently, the model allocates items from the same slots into different windows to optimise the objective, minimising the within-period reshuffles in (28).

This model defines a partial sequence for retrieving items, therefore reducing the retrieval uncertainty. As the number of windows increases, reshuffles reduce. When $N=U_k$, each item has a dedicated time window, and the model determines the best retrieval sequence. However, a small N is realistic so that the time window is sufficiently large and retrieving trucks can follow the schedule in practice. We then investigate reshuffles in TWA model.

We use the same numerical experiments for stacking decisions following the position assignment models. TWA model is implemented at the beginning of each week so that all items retrieved in this week are allocated into two windows. Table 4 presents the results of implementing PA and PAR model with TWA strategy.

Table 4. Comparison between PA and PAR with TWA model ($N=2$).

	PAR models			PA models
$\mathrm{\Psi }\left(S\right)$	CR	IR	R	CR	IR	R
100% (10)	2.68	0.38	3.06	1.19	0.58	1.77
50% (20)	0.69	0.17	0.86	0.00	0.53	0.53
33% (30)	0.36	0.10	0.46	0.00	0.51	0.51
25% (40)	0.12	0.05	0.17	0.00	0.48	0.48

The result is encouraging because TWA model with two time windows already reduces about 50% IR for both models compared with Table 3. The total reshuffles in PA model are reduced significantly as it contains IR, whereas the improvement of PAR is smaller because its reshuffles are mainly CR on which TWA model has no impact. Despite the fact that PAR model outperforms PA model in situations where slot utilisation is very low or very high, the difference between the two models diminishes when using TWA policy. As N increases, PA model has $CR=0$ and will have less IR, while PAR always has CR as the lower bound of reshuffles.

Our study shows that allocating the retrieval items into different time windows brings significant benefits. It implies that reducing uncertainty after stacking decisions is very effective in dealing with partial information. It does not require additional space, which is often a valuable resource and sometimes a constraint. This insight is instructive to the storage management for both container terminals and steel plants. In container terminals, the space is usually hard to expand. In our case company, logistics manager can raise requirements for arriving times of retrieval vehicles, especially during the high demand season (high space utilisation).

In Figure 7, we add the result of PA ($N=2$) model as the combination of PA model and TWA model with $N=2$. It shows that PA ($N=2$) model always performs better than other PA class models which exclude uncertain retrieval sequences. It also performs no worse than PAR class models with consideration of partial retrieval information on target and future items, even when space utilisation is not high ($\mathrm{\Lambda }\ge 50\mathrm{\%}$). It implies that better retrieval information on target items is more valuable than future items. Priority should be given to reducing the corresponding retrieval uncertainty.

6. Conclusion

The current study addresses the impacts of different types of inbound and outbound information on stacking performance in the context of a vertical stacking problem with dynamic item inflows. The study focus is to examine the relationship between information availability and stacking performance, which has not been explored in depth in the previous literature. To fill this research gap, several position assignment models are developed and evaluated, taking into account full and partial information on retrieval times, and respectively information on quantity, arrival time and retrieval time of future items. This study thus comprehends the modelling literature of stacking problems. Corresponding to the problem structure in Figure 2, we position the models of this paper in Figure 8.

Figure 8. Stacking models for various information structures.

A framework for applying the stacking models for various information structures.

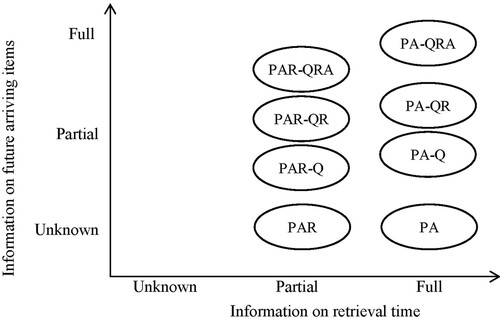
The study results confirm that different information settings (unknown, partial and full) do affect decision-making and stacking performance. Nevertheless, the outcome is not always intuitive, since it could be largely affected by other factors. Some interesting findings are highlighted below.

Firstly, the performance of stacking models depends not only on the quality of available information but also on the level of space utilisation. When space utilisation is high, the models that use low-quality partial information on future items perform worse than those excluding the information. In addition, models considering uncertain retrieval sequences result in a lower performance than those excluding these sequences. The observations suggest that the utilisation of partial information not necessarily improves stacking performance, but sufficient space is a foremost condition to ensure the added value of partial information.

Secondly, the study illustrates the effectiveness of reducing retrieval uncertainty in reducing reshuffles. To address this issue, a method is proposed for allocating the retrieval items into several time windows, which can be applied after stacking decisions. An implementation example is: previously retrieval vehicles are assigned to a specific week, but now these vehicles are further required to arrive and retrieve items either in the first half or the second half of that week, and thus items are assigned into two time windows. This method partially determines the retrieval sequence and reduces uncertainty, leading to improved stacking performance, as evidenced by the study results.

In conclusion, the study challenges the conventional belief that incorporating more information always leads to improved performance. Instead, the results suggest that the quality of information and space capacity should be considered jointly in decision-making. The study also highlights the importance of proactive approaches, such as increasing space and reducing retrieval uncertainty, as more effective methods for improving stacking efficiency. Thus, it is recommended to prioritise such proactive approaches instead of developing sophisticated models to utilise partial information.

There are several limitations of this study. One is the assumption that reshuffled items will be placed back to their original positions. Further research could explore strategies that relax this assumption, aiming at a better reduction in reshuffling. Furthermore, another assumption indicates that the decision models are mainly focusing on arriving batches in the current period, and the decision process is rolling forward. One alternative is considering multiple periods and investigating decision models in a defined planning horizon. This may need industrial cases to support such a stacking planning principle. Another focus of future research could be alternative strategies to reduce uncertainty. Developing propositions for the proposed staking models in this study should also be of great interest. Nevertheless, all suggested directions for future research would be very challenging from a modelling perspective, if not impossible.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The data that support the findings of this study are openly available at https://doi.org/10.57760/sciencedb.06774.

Additional information

Funding

This work was supported by National Natural Science Foundation of China [grant number 71873096].

Notes on contributors

Daqin Wang

Daqin Wang is an associate professor of Management Science and Engineering at Donghua University, China. His research includes production scheduling, supply chain and inventory optimisation. He has published research articles in international journals including International Journal of Production Economics, Computers and Operations Research, and others.

Ou Tang

Ou Tang is Professor of Production Economics at Linköping University, Sweden. His research includes production and inventory modelling, closed loop supply chains, supply chain risk management, sustainable supply chains, China-related operations management issues and energy policies. He has published more than 100 scientific articles in international journals including European Journal of Operational Research, International Journal of Production Economics, International Journal of Production Research, Production and Operations Management, and others. He serves as editor for the International Journal of Production Economics and is the past president of International Society of Inventory Research.

Lihua Zhang

Lihua Zhang is an associate professor of Industrial and Regional Economics at Tongji University, China. Her research mainly uses micro econometrics to study topics in the area of industrial structural change and technological innovation. She has published research articles in international journals including International Journal of Production Economics, Industrial and Corporate Change, Applied Economics Letters. Her research articles have also been published in a list of Chinese academic journals. She has been undertaking two research projects of China National Natural Science Foundation.