Decentralised fully probabilistic design for stochastic networks with multiplicative noise

ABSTRACT

In this paper, we present an innovative decentralised control framework, designed to address stochastic dynamic complex systems that are influenced by multiple multiplicative noise factors. Our advanced approach builds upon the foundation of conventional Decentralised Fully Probabilistic Design (DFPD) by refining the Riccati equation to accommodate multiple noise sources effectively. By embracing the inherent stochastic nature of complex systems, our methodology fully characterises their dynamic behaviours using probabilistic state–space models, delivering a comprehensive representation of subsystem components. Importantly, the DFPD approach also incorporates system and input constraints by characterising their corresponding ideal distributions, ensuring optimal functionality and performance while adhering to permissible boundaries. To further enhance system performance, we introduce a probabilistic message passing architecture that enables seamless communication between neighbouring subsystems and promotes harmonised decision-making among local nodes. To demonstrate the efficacy of our proposed framework, we employ a three-inverted pendulum system as a numerical example and compare its performance to that of the conventional DFPD. Through this comparison, we showcase the advantages of our novel decentralised control approach in handling complex systems with multiple noise factors.

KEYWORDS:

• Stochastic control
• fully probabilistic design
• multiplicative noise
• stochastic systems

1. INTRODUCTION

Complex systems are a major research focus due to their widespread presence in real life (Chen et al., 2021; Zhang & Zhou, 2022), spanning various domains such as electrical power grids (Herzallah & Zhou, 2021), cryogenic propellant loading systems (Ren et al., 2018) and social, biological and economic systems (Bunde & Bogachev, 2010; Mokshin et al., 2019). A key characteristic of these systems is their susceptibility to high levels of uncertainty, which has led to extensive literature on stochastic control for complex systems (Herzallah & Lowe, 2003; Li et al., 2017; Liu et al., 2022; Zhang & Zhou, 2022). However, most existing studies primarily focus on additive noise, which is insufficient for modelling complex industrial and mechanical processes, especially in networked systems with noisy communication channels (Antsaklis & Baillieul, 2007) and modern power networks with a high penetration of intermittent renewables (Y. Guo & Summers, 2019). In such systems, multiplicative noises (or state-dependent noises) are often employed to characterise the stochastic dynamics, as they can capture the dependence of noise on state and/or control input (Xing et al., 2020).

Moreover, multiple multiplicative noises are prevalent in a wide range of complex systems, and in many practical scenarios, systems may contain more than one multiplicative noise. For example, communication systems may experience fading channels, resulting in multiple multiplicative noises. Power systems, such as Phasor Measurement Units (PMUs) (Yang et al., 2014), employed in power quality monitoring, can also be affected by multiple multiplicative noises due to phase mismatches. Sensor networks (Ma et al., 2017) and image processing systems (X. Hu & Hu, 2015) are additional examples where multiple multiplicative noises play a significant role. To better describe various sources and channels of uncertainties, it is crucial to consider multiple multiplicative noises in stochastic system dynamics (J. Hu et al., 2013; Sotiropoulos & Kaznessis, 2008). This approach allows for the explicit incorporation of model uncertainty and inherent stochasticity, thereby improving the robustness properties of the controller (Gravell et al., 2020; L. Guo et al., 2021).

Despite the prevalence of multiple multiplicative noises, most existing stochastic control algorithms either focus on additive noises or assume single multiplicative noises within the system. Addressing multiple multiplicative noises can provide a more accurate representation of various sources and channels of uncertainty present in complex systems, warranting further research and attention. Some studies have begun to tackle multiple multiplicative noises both theoretically and practically. For instance, X. Hu and Hu (2015) proposed a variational method for removing multiple multiplicative noises in image processing systems, while Sotiropoulos Kaznessis (2008) investigated the recursive finite-horizon filtering problem for a class of nonlinear time-varying systems subject to multiple multiplicative noises, missing measurements and quantisation effects. Building on these foundations, Dong et al. (2015) addressed the event-based filtering problem for time-varying systems with fading channels and multiple multiplicative noises.

Extending the existing research that addresses multiple multiplicative noises in various contexts, this paper proposes a novel decentralised control framework for a class of complex networks subject to multiple multiplicative noises. Recognising that complex systems typically comprise large numbers of interacting nodes, the proposed control framework is designed in a decentralised manner. To enhance the system's performance, we employ a computational and communication approach called message passing, enabling individual subsystems to harmonise their actions by sharing information. This distinguishes our approach from traditional decentralised control methods, as stochastic message passing is not constrained by the homogeneity or conformability of the subsystem components. Furthermore, all system dynamics are characterised by probabilistic state–space models, providing a comprehensive description of the stochastic complex system components. Capitalising on the strengths of stochastic control methods, such as the Decentralised Fully Probabilistic Design (DFPD) (Herzallah & Kárn$\stackrel{`}{\mathrm{y}}$, 2017; Herzallah & Zhou, 2021; Zhou & Herzallah, 2020, 2021), our proposed framework demonstrates superiority over conventional deterministic control methods in addressing the inherent randomness of complex systems influenced by multiple multiplicative noises.

While most published papers on conventional FPD have primarily focused on additive noises, some research has expanded the method by taking multiplicative noise into account (Zhou et al., 2019). However, this approach is limited to centralised systems and does not effectively represent the various disturbances that agents encounter from multiple sources (L. Guo et al., 2021; J. Hu et al., 2013; Sotiropoulos & Kaznessis, 2008). To address these limitations, this paper extends the conventional DFPD by considering multiple multiplicative noises, making it more suitable for complex systems. In contrast to the extended FPD method presented in Zhou et al. (2019), the novel control method proposed in this paper employs a decentralised approach. Furthermore, our method surpasses existing DFPD methods in Zhou and Herzallah (2020, 2021) and Herzallah and Zhou (2021) by addressing not only additive noises but also multiple multiplicative noises. We go beyond the consideration of a single multiplicative noise, as in Zhou et al. (2019), by incorporating a series of multiplicative noises to accurately represent the various sources of disturbances affecting complex systems. This comprehensive approach enhances the applicability of the control method for real-world scenarios, making it a more effective solution for managing complex systems with multiple noise sources.

The contributions of this paper can be summarised as follows:

1. All system dynamics are described by probabilistic models, resulting in a comprehensive description of the stochastic complex system components.

2. Stochastic message passing is implemented to harmonise subsystems' actions under disturbances, without being limited by the homogeneity or conformability of the subsystem components.

3. Both multiplicative and additive noises are considered. The conventional DFPD is improved by evaluating the effect of multiple multiplicative noises, filling a gap in current DFPD research.

4. The novel DFPD is further enhanced to handle multiple multiplicative noises, representing various sources of disturbances.

The remainder of this paper is organised as follows: Section 2 presents the control problem statement. Section 3 introduces the probabilistic message passing framework, while Section 4 details the randomised optimal controller design for decentralised randomised complex systems with multiplicative noises. Section 5 demonstrates the effectiveness of the proposed framework through a three-inverted-pendulums example. Finally, the conclusion and future work are discussed in Section 6.

2. Problem statement

As we specified in the introduction part and model from J. Hu et al. (2013), consider each subsystem $i,i\in N$ with the following expressions: (1) $\begin{array}{rl}{x}_{i,k}& =(A_{i,1}+\sum _{l=1}^{P_i}{\rho }_{i,l}{\overline{A}}_{i,l})x_{i,k-1}+\sum _j^{N_i}{A}_{i,j,2}{x}_{j,k-1}\\ & +B_i{u}_{i,k-1}+w_{i,k,}\end{array}$(1) where $x_{i,k}\in {\mathrm{\Re }}^{n_i}$ is the state of subsystem i, $x_{j,k}\in {\mathrm{\Re }}^{n_j}$, $j\in N_i$ is the neighbouring subsystem which connects with subsystem i and $N_i$ is the total number of subsystems that subsystem i has connection with, $u_{i,k}\in {\mathrm{\Re }}^{m_i}$ represents the controlled input of local subsystem i. ${\rho }_{i,l}\in \mathrm{\Re }$, $l=1,2,\dots ,P_i$ are the multiplicative noises with the following distributions (2(2) $\begin{array}{rl}{\rho }_{i,l}& \sim N(0,{\overline{Q}}_{i,l}),l=1,\dots ,P_i,\end{array}$(2) ) while $w_{i,k}\in {\mathrm{\Re }}^{n_i}$ stands for the process noise with Gaussian distribution (3(3) $\begin{array}{rl}{w}_{i,k}& \sim N(0,M_i).\end{array}$(3) ). Note that $w_{i,k}$ and ${\rho }_{i,l}$ are mutually uncorrelated in k, l and i. Furthermore, matrices $A_{i,1}$, $A_{i,j,2}$, $B_i$, ${\overline{A}}_{i,l}$, $l=1,2,\dots ,P_i$ are the system parameters with appropriate dimensions. (2) $\begin{array}{rl}{\rho }_{i,l}& \sim N(0,{\overline{Q}}_{i,l}),l=1,\dots ,P_i,\end{array}$(2) (3) $\begin{array}{rl}{w}_{i,k}& \sim N(0,M_i).\end{array}$(3) We can see that the formulation expressed as Equation (1(1) $\begin{array}{rl}{x}_{i,k}& =(A_{i,1}+\sum _{l=1}^{P_i}{\rho }_{i,l}{\overline{A}}_{i,l})x_{i,k-1}+\sum _j^{N_i}{A}_{i,j,2}{x}_{j,k-1}\\ & +B_i{u}_{i,k-1}+w_{i,k,}\end{array}$(1) ) is complicated and hard to read. Therefore, to express the system in a clearer and more convenient manner, we extend the subsystem state by including the states from neighbouring nodes. As such, the extended state of subsystem i is donated as $z_{i,k}=[x_{i,k}^T,{\tilde{x}}_{i,k}^T]$, where $x_{i,k}$ is the refereed as to the internal state while ${\tilde{x}}_{i,k}=[\cdots ,x_{j,k}^T,\dots {]}_{j\in N_i}^T$, the states from neighbouring nodes is donated as subsystem i's external state. Using these new notations, Equation (1(1) $\begin{array}{rl}{x}_{i,k}& =(A_{i,1}+\sum _{l=1}^{P_i}{\rho }_{i,l}{\overline{A}}_{i,l})x_{i,k-1}+\sum _j^{N_i}{A}_{i,j,2}{x}_{j,k-1}\\ & +B_i{u}_{i,k-1}+w_{i,k,}\end{array}$(1) ) can be rewritten as follows: (4) $\begin{array}{rl}{x}_{i,k}& =(A_{i,1}+\sum _{l=1}^{P_i}{\rho }_{i,l}{\overline{A}}_{i,l})x_{i,k-1}+A_{i,2}{\tilde{x}}_{i,k-1}\\ & +B_i{u}_{i,k-1}+w_{i,k},\end{array}$(4) where $A_{i,2}=\left[\cdots A_{i,j,2}\cdots \right]$, $j\in N_i$. As introduced earlier, the external state ${\tilde{x}}_{i,k}$ represents the states from the neighbouring subsystems who have connections with subsystem i. In this framework, we offer an prior linear estimation of external state ${\tilde{x}}_{i,k-1}$ inside of subsystem i which is given as the following form: (5) ${\tilde{x}}_{i,k}=A_{i,3}{\tilde{x}}_{i,k-1}+{\tilde{w}}_{i,k},$(5) where $A_{i,3}=diag\left[A_{i,j,3}\right]$ is the estimated parameter which will be updated every step and $A_{i,j,3},j\in N_i$ are related to each external state ${\tilde{x}}_{i,j,k}$ corresponding to neighbouring nodes j, ${\tilde{w}}_{i,k}$ the estimated error that is assumed as Gaussian noise with zero mean and variance $Q_{i,2}$. Later on, the external state will be updated using the information passed from the neighbouring subsystems which will be explained in detail in Section 3.

To better characterise the stochastic nature of the considered system, in this paper, we describe the system dynamics using probabilistic models. Thus the system dynamics of internal state equation (4(4) $\begin{array}{rl}{x}_{i,k}& =(A_{i,1}+\sum _{l=1}^{P_i}{\rho }_{i,l}{\overline{A}}_{i,l})x_{i,k-1}+A_{i,2}{\tilde{x}}_{i,k-1}\\ & +B_i{u}_{i,k-1}+w_{i,k},\end{array}$(4) ) and external state equation (5(5) ${\tilde{x}}_{i,k}=A_{i,3}{\tilde{x}}_{i,k-1}+{\tilde{w}}_{i,k},$(5) ) can be represented as the following conditional distributions: (6) $\begin{array}{rl}& s\left(x_{i,k}|z_{i,k-1},u_{i,k-1}\right)\sim N({\mu }_{i,k},Q_{i,k,1})\end{array}$(6) (7) $\begin{array}{rl}& s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\sim N({\tilde{\mu }}_{i,k},Q_{i,2})\end{array}$(7) where (8) $\begin{array}{rl}{\mu }_{i,k}& =A_{i,1}{x}_{i,k-1}+A_{i,2}{\tilde{x}}_{i,k-1}+B_i{u}_{i,k-1}\\ Q_{i,k,1}& =\sum _{l=1}^{P_i}{\overline{A}}_{i,l}{x}_{i,k-1}{\overline{Q}}_{i,l}{x}_{i,k-1}^T{\overline{A}}_{i,l}^T+M_i\\ {\tilde{\mu }}_{i,k}& =A_{i,3}{\tilde{x}}_{i,k-1}\end{array}$(8) where ${\mu }_{i,k}$ and ${\tilde{\mu }}_{i,k}$ are the mean values and $Q_{i,k,1}$ and $Q_{i,k,2}$ are covariances.

Remark 2.1

Based on Equation (1(1) $\begin{array}{rl}{x}_{i,k}& =(A_{i,1}+\sum _{l=1}^{P_i}{\rho }_{i,l}{\overline{A}}_{i,l})x_{i,k-1}+\sum _j^{N_i}{A}_{i,j,2}{x}_{j,k-1}\\ & +B_i{u}_{i,k-1}+w_{i,k,}\end{array}$(1) ), we can see that $n_i$ represents state dimension of subsystem i, which is verified with $i,i=1,\dots ,N$. This is because of that the above formulation is not restricted by the homogeneity assumption of the components of the subsystems. Individual subsystems can be heterogeneous and can have different lengths.

Remark 2.2

From Equation (5(5) ${\tilde{x}}_{i,k}=A_{i,3}{\tilde{x}}_{i,k-1}+{\tilde{w}}_{i,k},$(5) ), we can see that the prior estimation of external state is only related to the former value of itself, where the controller of subsystem i has no control power over the external state. This is an realistic assumption since the external state represents the state from the neighbouring subsystems, thus shouldn't be affected by any variables from subsystem i.

From the system dynamic probabilistic model (6(6) $\begin{array}{rl}& s\left(x_{i,k}|z_{i,k-1},u_{i,k-1}\right)\sim N({\mu }_{i,k},Q_{i,k,1})\end{array}$(6) ), we can see that the internal state of subsystem i is decided by both internal and external states and controlled by the controller of subsystem i. In addition, the external state participates the controller design as well, in which way the control decision is made based on not only their own state information but also the state information from neighbouring nodes, thus making sure the global control objective can be achieved. Therefore, the external state is significant for subsystems and has major influence on both system internal state dynamics and control inputs. Note that the external state probabilistic model (7(7) $\begin{array}{rl}& s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\sim N({\tilde{\mu }}_{i,k},Q_{i,2})\end{array}$(7) ) only offers an prior estimation of external state, which will be updated to posterior external state using the obtained information passed from the neighbouring subsystems. The whole communication process is regarded as message passing framework and will be introduced in the next section.

3. Message passing framework

In this section, the probabilistic message passing methodology, which indicates how subsystems communicate with each other and keep each other informed about their newest state will be briefly introduced. As discussed in the previous section, we offered a brief prior external state estimation inside if subsystem i using the external state's previous values. After that, the prior estimation will be updated using external signals received as messages from neighbouring subsystems. In the meantime, the subsystem i will pass their new updated internal state to the neighbouring subsystems as well, thus providing coordination between the subsystems. To better understand this process, we divided this into two steps. The first step is regarded as Passing, which indicates how the information been passed to their neighbouring subsystems. For instance, for subsystem i's neighbouring nodes $j,j\in N_i$, after the latest probabilistic distribution of the interacting variables of subsystem j, $L_j(x_{j,k},{\tilde{x}}_{j,k},u_{j,k-1}\mid z_{j,k-1})=s(x_{j,k}\mid z_{j,k-1},u_{j,k-1})s({\tilde{x}}_{j,k}\mid {\tilde{x}}_{j,k-1})c(u_{j,k-1}\mid z_{j,k-1})$ obtained, subsystem j will then pass this information to its neighbouring subsystem i specifying the probabilistic description of its own internal state, $x_{j,k}$, which is given by, (9) $\begin{array}{rl}{\mathcal{M}}_{i\leftarrow j,k}& =\int s(x_{j,k},{\tilde{x}}_{j,k},u_{j,k-1}|z_{j,k-1})\mathrm{d}{\tilde{x}}_{j,k}\mathrm{d}{u}_{j,k-1}\\ & =\int s\left(x_{j,k}|z_{j,k-1},u_{j,k-1}\right)s\left({\tilde{x}}_{j,k}|{\tilde{x}}_{j,k-1}\right)\\ & \times c\left(u_{j,k-1}|z_{j,k-1}\right)\mathrm{d}{\tilde{x}}_{j,k}\mathrm{d}{u}_{j,k-1}\\ & =N({\mu }_{i\leftarrow j,k},{\mathrm{\Sigma }}_{i\leftarrow j,k}),\end{array}$(9) where (10) $\begin{array}{rl}{\mu }_{i\leftarrow j,k}& =A_{j,1}{x}_{j,k-1}+A_{j,2}{\tilde{x}}_{j,k-1}+B_j{\overline{u}}_{j,k-1},\\ {\mathrm{\Sigma }}_{i\leftarrow j,k}& =Q_{j,k,1}+B_j{\overline{\mathrm{\Gamma }}}_j{B}_j^T,\end{array}$(10) where $c(u_{j,k-1}\mid z_{j,k-1})$ is the randomised controller which will be designed in the following section, ${\overline{u}}_{j,k-1}$ and ${\overline{\mathrm{\Gamma }}}_j$ are the mean and covariance of randomised input $u_{j,k-1}$, respectively.

From Equation (9(9) $\begin{array}{rl}{\mathcal{M}}_{i\leftarrow j,k}& =\int s(x_{j,k},{\tilde{x}}_{j,k},u_{j,k-1}|z_{j,k-1})\mathrm{d}{\tilde{x}}_{j,k}\mathrm{d}{u}_{j,k-1}\\ & =\int s\left(x_{j,k}|z_{j,k-1},u_{j,k-1}\right)s\left({\tilde{x}}_{j,k}|{\tilde{x}}_{j,k-1}\right)\\ & \times c\left(u_{j,k-1}|z_{j,k-1}\right)\mathrm{d}{\tilde{x}}_{j,k}\mathrm{d}{u}_{j,k-1}\\ & =N({\mu }_{i\leftarrow j,k},{\mathrm{\Sigma }}_{i\leftarrow j,k}),\end{array}$(9) ), we can see that except the internal state, all the other variables have been integrated over. This is because that the subsystems only need to send information about their own state, thus the marginal distributions of the internal states need to be evaluated and packed to be passed to neighbouring subsystems.

After this information about the internal state of subsystem j is received by subsystem i, it will be used to update the prior external estimation of subsystem i, which will lead to the next step: Updating. To be more specific, the prior estimation (7(7) $\begin{array}{rl}& s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\sim N({\tilde{\mu }}_{i,k},Q_{i,2})\end{array}$(7) ) and new received message (9(9) $\begin{array}{rl}{\mathcal{M}}_{i\leftarrow j,k}& =\int s(x_{j,k},{\tilde{x}}_{j,k},u_{j,k-1}|z_{j,k-1})\mathrm{d}{\tilde{x}}_{j,k}\mathrm{d}{u}_{j,k-1}\\ & =\int s\left(x_{j,k}|z_{j,k-1},u_{j,k-1}\right)s\left({\tilde{x}}_{j,k}|{\tilde{x}}_{j,k-1}\right)\\ & \times c\left(u_{j,k-1}|z_{j,k-1}\right)\mathrm{d}{\tilde{x}}_{j,k}\mathrm{d}{u}_{j,k-1}\\ & =N({\mu }_{i\leftarrow j,k},{\mathrm{\Sigma }}_{i\leftarrow j,k}),\end{array}$(9) ) are fused using Bayesian rule by multiplying the two together, yielding (11) $\begin{array}{rl}s\left({\tilde{x}}_{i\leftarrow j;f_k}\right)& =N({\tilde{\mu }}_{i,j,k},Q_{i,2})N({\mu }_{i\leftarrow j,k},{\mathrm{\Sigma }}_{i\leftarrow j,k})\\ & =N({\mu }_{i\leftarrow j;f_k},{\mathrm{\Sigma }}_{i\leftarrow j;f_k}),\\ {\mu }_{i\leftarrow j;f_k}& ={\tilde{\mu }}_{i,j,k}+L_{i\leftarrow j,k}({\mu }_{i\leftarrow j,k}-{\tilde{\mu }}_{i,j,k}),\\ {\mathrm{\Sigma }}_{i\leftarrow j;f_k}& =Q_{i,2}-L_{i\leftarrow j,k}{Q}_{i,2}.\end{array}$(11) where (12) $L_{i\leftarrow j,k}=Q_{i,2}({\mathrm{\Sigma }}_{i\leftarrow j,k}+Q_{i,2}{)}^{-1}.$(12) These equations can then be used to update the parameter $A_{i,3}$ in Equation (5(5) ${\tilde{x}}_{i,k}=A_{i,3}{\tilde{x}}_{i,k-1}+{\tilde{w}}_{i,k},$(5) ) using linear optimisation methods. Note that we only offer a brief introduction and discussion of message passing methodology in this paper. For more details and the general results of the probabilistic message passing methodology, the readers are referred to Zhou and Herzallah (2020).

4. Randomised controller design

As discussed previously, the control decision is made based on both internal and external states, thus guaranteeing not only the local but also the global control goal can be achieved. After the posterior distribution of the external state obtained in the last section, we will then design the decentralised optimal randomised controller for individual subsystems. In this paper, the tracking problem is considered, which means that the control objective is for the internal state to follow a predefined reference state. Moreover, the fully probabilistic design (FPD) control method will be applied in this paper given the stochastic nature of systems.

4.1. General decentralised FPD control solution to the probabilistic state–space representation

As a randomised controller, FPD is designed to minimise the Kullback–Leibler divergence (KLD) between the probabilistic model of dynamics of the closed loop system and its desired joint distribution. With $\mathbf{H}$ being the control horizon, the KLD between the actual joint PDF $f\left(\mathbf{F}\right)$ of the observed data $\mathbf{F}=\left(x\right(\mathbf{H}),u(\mathbf{H}\left)\right)$ and the ideal joint PDF $f^I\left(F\right)$ is given by (13) $\mathcal{D}\left(f\Vert f^I\right)=\int f\left(\mathbf{F}\right)\ln \left(\frac{f\left(\mathbf{F}\right)}{f^I\left(\mathbf{F}\right)}\right)\mathrm{d}\mathbf{F}.$(13) Based on the chain rules (Zhou et al., 2019), the joint distribution of the probabilistic closed-loop of the system dynamics is evaluated as follows: (14) $f\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}s\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right),$(14) with (15) $\begin{array}{rl}& s\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & =s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right).\end{array}$(15) The ideal closed-loop distribution that determines the steady-state behaviour of the joint distribution can be factorised in the same form as Equation (14(14) $f\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}s\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right),$(14) ) with ideal system dynamic PDF $s^I(z_{i,k}|u_{i,k-1},z_{i,k-1})$ and ideal control input PDF $c^I\left(u_{i,k-1}|z_{i,k-1}\right)$, (16) $f^I\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}{s}^I\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c^I\left(u_{i,k-1}|z_{i,k-1}\right),$(16) where (17) $\begin{array}{rl}& s^I\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & =s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right).\end{array}$(17) Since the ${\tilde{x}}_{i,k-1}$ enters subsystem i as external signal whose behaviour cannot be changed by subsystem i, its corresponding ideal PDF is taken to be equal to its actual PDF.

The randomised controller can then be developed to minimise the KLD (13(13) $\mathcal{D}\left(f\Vert f^I\right)=\int f\left(\mathbf{F}\right)\ln \left(\frac{f\left(\mathbf{F}\right)}{f^I\left(\mathbf{F}\right)}\right)\mathrm{d}\mathbf{F}.$(13) ) between the actual joint PDF (14(14) $f\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}s\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right),$(14) ) and ideal joint PDF (16(16) $f^I\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}{s}^I\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c^I\left(u_{i,k-1}|z_{i,k-1}\right),$(16) ), which yields the performance index given as the following form: (18) $\begin{array}{rl}& -\ln \left(\gamma \right(z_{i,k-1}\left)\right)\\ & =\underset{c\left(u_{i,k-1}|z_{i,k-1}\right)}{min}\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times [\ln \left(\frac{\begin{array}{c}s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}{\begin{array}{c}{s}^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c^I\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}\right)-\ln (\gamma \left(z_{i,k}\right)\left)\right]\\ & \times \mathrm{d}(x_{i,k},{\tilde{x}}_{i,k},u_{i,k-1}),\end{array}$(18) where the first term in parenthesis in (18(18) $\begin{array}{rl}& -\ln \left(\gamma \right(z_{i,k-1}\left)\right)\\ & =\underset{c\left(u_{i,k-1}|z_{i,k-1}\right)}{min}\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times [\ln \left(\frac{\begin{array}{c}s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}{\begin{array}{c}{s}^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c^I\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}\right)-\ln (\gamma \left(z_{i,k}\right)\left)\right]\\ & \times \mathrm{d}(x_{i,k},{\tilde{x}}_{i,k},u_{i,k-1}),\end{array}$(18) ) represents the partial cost while the second term $-\ln \left(\gamma \right(z_{i,k}\left)\right)$ stands for the expected minimum cost-to-go function. Full derivation of (18(18) $\begin{array}{rl}& -\ln \left(\gamma \right(z_{i,k-1}\left)\right)\\ & =\underset{c\left(u_{i,k-1}|z_{i,k-1}\right)}{min}\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times [\ln \left(\frac{\begin{array}{c}s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}{\begin{array}{c}{s}^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c^I\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}\right)-\ln (\gamma \left(z_{i,k}\right)\left)\right]\\ & \times \mathrm{d}(x_{i,k},{\tilde{x}}_{i,k},u_{i,k-1}),\end{array}$(18) ) is provided in our previous publication (Zhou & Herzallah, 2020).

Therefore, the general decentralised optimal control law $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)$ for the subsystem i which minimises the KLD between the joint PDF (14(14) $f\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}s\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right),$(14) ) and ideal distribution (16(16) $f^I\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}{s}^I\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c^I\left(u_{i,k-1}|z_{i,k-1}\right),$(16) ) is given in following theorem based on the Fully Probabilistic Design (FPD) (Herzallah & Kárn$\stackrel{`}{\mathrm{y}}$, 2017; Kárn$\stackrel{`}{\mathrm{y}}$, 1996; Zhou & Herzallah, 2020),

Theorem 4.1

The optimal randomised control law which minimises the performance index (18(18) $\begin{array}{rl}& -\ln \left(\gamma \right(z_{i,k-1}\left)\right)\\ & =\underset{c\left(u_{i,k-1}|z_{i,k-1}\right)}{min}\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times [\ln \left(\frac{\begin{array}{c}s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}{\begin{array}{c}{s}^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c^I\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}\right)-\ln (\gamma \left(z_{i,k}\right)\left)\right]\\ & \times \mathrm{d}(x_{i,k},{\tilde{x}}_{i,k},u_{i,k-1}),\end{array}$(18) ) given the ith subsystem closed loop dynamic joint PDF (14(14) $f\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}s\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right),$(14) ) and the ideal PDF of the ith subsystem (16(16) $f^I\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}{s}^I\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c^I\left(u_{i,k-1}|z_{i,k-1}\right),$(16) ) is given by (19) $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)=\frac{\begin{array}{c}{c}^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\end{array}}{\gamma \left(z_{i,k-1}\right)},$(19) where (20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20)

for full derivation of Equations (19(19) $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)=\frac{\begin{array}{c}{c}^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\end{array}}{\gamma \left(z_{i,k-1}\right)},$(19) )–(20(20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20) ), please refer to Herzallah and Kárn$\stackrel{`}{\mathrm{y}}$ (2017) and Kárn$\stackrel{`}{\mathrm{y}}$ (1996).

Remark 4.1

Equations (19(19) $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)=\frac{\begin{array}{c}{c}^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\end{array}}{\gamma \left(z_{i,k-1}\right)},$(19) )–(20(20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20) ) offer the general solution of the decentralised fully probability design methodology, which are not restricted by the distributions of the subsystem dynamics or its ideal distribution. They could theoretically follow any arbitrary distribution. Moreover, note that the optimal controller $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)$ stands for the optimal solution for the current instant k to reach the control goal (18(18) $\begin{array}{rl}& -\ln \left(\gamma \right(z_{i,k-1}\left)\right)\\ & =\underset{c\left(u_{i,k-1}|z_{i,k-1}\right)}{min}\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times [\ln \left(\frac{\begin{array}{c}s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}{\begin{array}{c}{s}^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c^I\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}\right)-\ln (\gamma \left(z_{i,k}\right)\left)\right]\\ & \times \mathrm{d}(x_{i,k},{\tilde{x}}_{i,k},u_{i,k-1}),\end{array}$(18) ) while $c^I\left(u_{i,k-1}|z_{i,k-1}\right)$ represents the ideal controller for the instant k. With $k\to \mathrm{\infty }$, $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)$ should be gradually approach $c^I\left(u_{i,k-1}|z_{i,k-1}\right)$.

4.2. Optimal controller design for local subsystems

In this section, the decentralised FPD control law (19(19) $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)=\frac{\begin{array}{c}{c}^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\end{array}}{\gamma \left(z_{i,k-1}\right)},$(19) )–(20(20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20) ) will be implemented to each subsystem (4(4) $\begin{array}{rl}{x}_{i,k}& =(A_{i,1}+\sum _{l=1}^{P_i}{\rho }_{i,l}{\overline{A}}_{i,l})x_{i,k-1}+A_{i,2}{\tilde{x}}_{i,k-1}\\ & +B_i{u}_{i,k-1}+w_{i,k},\end{array}$(4) ) which is affected by multiple multiplicative noises and the analytical control solution will be presented. In this paper, the tracking problem is considered, meaning that the controller will be designed so that the internal state can follow a predefined desired trajectory. Therefore, the ideal distribution of the internal state can be represented as follows: (21) $s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\sim N(r_i,R_i),$(21) where $r_i$ is the mean of the distribution and $R_i$ is the covariance, which indicate the tracking error allowance.

The ideal distribution of the controller can also be defined as follows: (22) $c^I\left(u_{i,k-1}|z_{i,k-1}\right)\sim N(u_{r,i,k-1},{\mathrm{\Gamma }}_i),$(22) where ${\mathrm{\Gamma }}_i$ represents the desired covariance which indicates the admissible range of the optimal control input, and $u_{r,i,k-1}$ in (22(22) $c^I\left(u_{i,k-1}|z_{i,k-1}\right)\sim N(u_{r,i,k-1},{\mathrm{\Gamma }}_i),$(22) ) is the ideal mean of the optimal control signal which can be calculated as follows: (23) $\begin{array}{rl}\underset{k\to \mathrm{\infty }}{lim}E\left(x_{i,k}\right)& =r_i\\ & =\underset{k\to \mathrm{\infty }}{lim}E(A_{i,1}{x}_{i,k-1}+A_{i,2}{\tilde{x}}_{i,k-1}\\ & +B_i{u}_{i,k-1})\\ u_{r,i,k-1}& =(B_i^T{B}_i{)}^{-1}{B}_i^T\left\{\right(I-A_{i,1})r_i-A_{i,2}{\tilde{x}}_{i,k-1}\}.\end{array}$(23) As we specified earlier, the ideal distribution of the external state remains itself since the external state should not be controlled by the local controller.

With the ideal distributions (21(21) $s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\sim N(r_i,R_i),$(21) ) and (22(22) $c^I\left(u_{i,k-1}|z_{i,k-1}\right)\sim N(u_{r,i,k-1},{\mathrm{\Gamma }}_i),$(22) ) and the distributions of the subsystem dynamics (6(6) $\begin{array}{rl}& s\left(x_{i,k}|z_{i,k-1},u_{i,k-1}\right)\sim N({\mu }_{i,k},Q_{i,k,1})\end{array}$(6) ) and (7(7) $\begin{array}{rl}& s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\sim N({\tilde{\mu }}_{i,k},Q_{i,2})\end{array}$(7) ), the performance index (18(18) $\begin{array}{rl}& -\ln \left(\gamma \right(z_{i,k-1}\left)\right)\\ & =\underset{c\left(u_{i,k-1}|z_{i,k-1}\right)}{min}\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times [\ln \left(\frac{\begin{array}{c}s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}{\begin{array}{c}{s}^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c^I\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}\right)-\ln (\gamma \left(z_{i,k}\right)\left)\right]\\ & \times \mathrm{d}(x_{i,k},{\tilde{x}}_{i,k},u_{i,k-1}),\end{array}$(18) ) can be specified by the following theorem.

Theorem 4.2

Substituting the PDF of the system dynamics specified by Equations (6(6) $\begin{array}{rl}& s\left(x_{i,k}|z_{i,k-1},u_{i,k-1}\right)\sim N({\mu }_{i,k},Q_{i,k,1})\end{array}$(6) ) and (7(7) $\begin{array}{rl}& s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\sim N({\tilde{\mu }}_{i,k},Q_{i,2})\end{array}$(7) ), the ideal distribution of the system dynamics equation (21(21) $s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\sim N(r_i,R_i),$(21) ) and the ideal distribution of the controller equations (22(22) $c^I\left(u_{i,k-1}|z_{i,k-1}\right)\sim N(u_{r,i,k-1},{\mathrm{\Gamma }}_i),$(22) ) into (20(20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20) ) yield the following performance index: (24) $\begin{array}{rl}-\ln \left(\gamma \left(z_{i,k-1}\right)\right)& =0.5x_{i,k-1}^T{M}_{1k-1;i}{x}_{i,k-1}\\ & +x_{i,k-1}^T{M}_{2k-1;i}{\tilde{x}}_{i,k-1}\\ & +0.5{\tilde{x}}_{i,k-1}^T{M}_{3k-1;i}{\tilde{x}}_{i,k-1}\\ & +0.5S_{1,k-1;i}{x}_{i,k-1}\\ & +0.5S_{2,k-1;i}{\tilde{x}}_{i,k-1}+0.5{\omega }_{i,k-1},\end{array}$(24) where $\begin{array}{rl}{M}_{1k-1;i}& =A_{i,1}^T(M_{1k;i}+R_i^{-1})A_{i,1}\\ & -A_{i,1}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T(M_{1k;i}+R_i^{-1})A_{i,1}+\sum _{l=1}^{P_i}{\overline{\mathrm{\Phi }}}_{i,l}\\ M_{2k-1;i}& =A_{i,1}^T(M_{1k;i}+R_i^{-1})A_{i,2}+A_{i,1}^T{M}_{2k;i}{A}_{i,3}\\ & -A_{i,1}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i[B_i^T(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & -A_{i,1}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}\\ M_{3k-1;i}& =A_{i,3}^T{M}_{3k;i}{A}_{i,3}+A_{i,2}^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & -A_{i,2}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T\\ & \times (M_{1k;i}+R_i^{-1})A_{i,2}-A_{i,3}^T{M^T}_{2k;i}\\ & \times B_i\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}+2A_{i,2}^T{M}_{2k;i}{A}_{i,3}\\ & -2A_{i,2}^T(M_{1k;i}+R_i^{-1}{)}^T\\ & \times B_i\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}\end{array}$ (25) $\begin{array}{r}\\ S_{1,k-1;i}& =2\{(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,1}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T\times (M_{1k;i}+R_i^{-1})A_{i,1}\}\\ S_{2,k-1;i}& =2\{(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,2}\\ & +0.5S_{2,k;i}{A}_{i,3}+\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]+{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}\}\end{array}$(25) and where (26) ${\overline{\mathrm{\Phi }}}_{i,l}=tr\left({\overline{A}}_{i,l}^T{\overline{Q}}_{i,l}{M}_{1k;i}{\overline{A}}_{i,l}\right),l=1,2,\dots ,P_i$(26)

Proof.

To evaluate Equation (38(38) $\begin{array}{rl}{\dot{x}}_i& =\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{g}{l}-\frac{a_{i}k}{m{l}^2}}& 0\end{array}\right]x_i+\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{m{l}^2}}\end{array}\right]u_i\\ & +\sum _{j\ne i}^3\left[\begin{array}{cc}0& 0\\ {\displaystyle \frac{1}{m{l}^2}}& 0\end{array}\right]x_j,\end{array}$(38) ), we need to substitute the distributions of system dynamics (6(6) $\begin{array}{rl}& s\left(x_{i,k}|z_{i,k-1},u_{i,k-1}\right)\sim N({\mu }_{i,k},Q_{i,k,1})\end{array}$(6) ) and Equation (7(7) $\begin{array}{rl}& s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\sim N({\tilde{\mu }}_{i,k},Q_{i,2})\end{array}$(7) ) and the ideal distributions (21(21) $s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\sim N(r_i,R_i),$(21) ) and (22(22) $c^I\left(u_{i,k-1}|z_{i,k-1}\right)\sim N(u_{r,i,k-1},{\mathrm{\Gamma }}_i),$(22) ) into Equation (20(20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20) ).

Following the steps in Equation (20(20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20) ), first, we should calculate $\ln \left(\tilde{\gamma }\right(x_{i_k},{\tilde{x}}_{i_k}\left)\right)$ by substituting $s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)$ and $\ln \gamma \left(z_{i,k}\right)$ into the third equation in Equation (20(20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20) ), (27) $\begin{array}{rl}\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}\\ & =-0.5x_{i,k}^T{M}_{1k;i}{x}_{i,k}-x_{i,k}^T{M}_{2k;i}{\tilde{\mu }}_{i,k}\\ & -0.5{\tilde{\mu }}_{i,k}^T{M}_{3k;i}{\tilde{\mu }}_{i,k}\\ & -0.5S_{1,k;i}{x}_{i,k}-0.5S_{2,k;i}{\tilde{\mu }}_{i,k}\\ & -0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\end{array}$(27) And the next step is to evaluate $\text{β}(u_{i,k-1},z_{i,k-1})$ by completing the integration over $x_{i,k}$, (28) $\begin{array}{rl}\text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k}\\ & =-0.5{\mu }_{i,k}^T(-M_{1k;i}-R_i^{-1}){\mu }_{i,k}\\ & +{\mu }_{i,k}^T(M_{2k;i}{\tilde{\mu }}_{i,k}\\ & +0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i})\\ & +0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}+0.5{\tilde{\mu }}_{i,k}^T{M}_{3k;i}{\tilde{\mu }}_{i,k}\\ & +0.5S_{2,k;i}{\tilde{\mu }}_{i,k}+0.5{\omega }_{i,k}\\ & +0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & -0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(Q_{i,k,1}^{-1}-M_{1k;i}-R_i^{-1})\\ & \times Q_{i,k,1}),\end{array}$(28) then substituting $\text{β}(u_{i,k-1},z_{i,k-1})$ (28(28) $\begin{array}{rl}\text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k}\\ & =-0.5{\mu }_{i,k}^T(-M_{1k;i}-R_i^{-1}){\mu }_{i,k}\\ & +{\mu }_{i,k}^T(M_{2k;i}{\tilde{\mu }}_{i,k}\\ & +0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i})\\ & +0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}+0.5{\tilde{\mu }}_{i,k}^T{M}_{3k;i}{\tilde{\mu }}_{i,k}\\ & +0.5S_{2,k;i}{\tilde{\mu }}_{i,k}+0.5{\omega }_{i,k}\\ & +0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & -0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(Q_{i,k,1}^{-1}-M_{1k;i}-R_i^{-1})\\ & \times Q_{i,k,1}),\end{array}$(28) ) into $\gamma \left(z_{i,k-1}\right)$ in Equation (20(20) $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1},\\ \text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k},\\ -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)& =\int s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)\ln \gamma \left(z_{i,k}\right)\mathrm{d}{\tilde{x}}_{i,k}.\end{array}$(20) ), we have (29) $\begin{array}{rl}& \gamma \left(z_{i,k-1}\right)=\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1}\\ & =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\exp \left[0.5{\mu }_{i,k}^T\right(-M_{1k;i}-R_i^{-1})\\ & +{\mu }_{i,k}-{\mu }_{i,k}^T(M_{2k;i}{\tilde{\mu }}_{i,k}+0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i})\\ & -0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}-0.5{\tilde{\mu }}_{i,k}^T{M}_{3k;i}{\tilde{\mu }}_{i,k}\\ & -0.5S_{2,k;i}{\tilde{\mu }}_{i,k}-0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & +0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & +0.5tr\left(\right(Q_{i,k,1}^{-1}-M_{1k;i}-R_i^{-1}\left)Q_{i,k,1}\right)]\mathrm{d}{u}_{i,k-1}.\end{array}$(29) Substituting ${\mu }_{i,k}$ and ${\tilde{\mu }}_{i,k}$ Equations (8(8) $\begin{array}{rl}{\mu }_{i,k}& =A_{i,1}{x}_{i,k-1}+A_{i,2}{\tilde{x}}_{i,k-1}+B_i{u}_{i,k-1}\\ Q_{i,k,1}& =\sum _{l=1}^{P_i}{\overline{A}}_{i,l}{x}_{i,k-1}{\overline{Q}}_{i,l}{x}_{i,k-1}^T{\overline{A}}_{i,l}^T+M_i\\ {\tilde{\mu }}_{i,k}& =A_{i,3}{\tilde{x}}_{i,k-1}\end{array}$(8) ) into (29(29) $\begin{array}{rl}& \gamma \left(z_{i,k-1}\right)=\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\mathrm{d}{u}_{i,k-1}\\ & =\int c^I\left(u_{i,k-1}|z_{i,k-1}\right)\exp \left[0.5{\mu }_{i,k}^T\right(-M_{1k;i}-R_i^{-1})\\ & +{\mu }_{i,k}-{\mu }_{i,k}^T(M_{2k;i}{\tilde{\mu }}_{i,k}+0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i})\\ & -0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}-0.5{\tilde{\mu }}_{i,k}^T{M}_{3k;i}{\tilde{\mu }}_{i,k}\\ & -0.5S_{2,k;i}{\tilde{\mu }}_{i,k}-0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & +0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & +0.5tr\left(\right(Q_{i,k,1}^{-1}-M_{1k;i}-R_i^{-1}\left)Q_{i,k,1}\right)]\mathrm{d}{u}_{i,k-1}.\end{array}$(29) ), we can obtain the following form of $\gamma \left(z_{i,k-1}\right)$, $\begin{array}{rl}\gamma \left(z_{i,k-1}\right)& =\exp \{-0.5x_{i,k-1}^T\left[A_{i,1}^T\right(M_{1k;i}+R_i^{-1})A_{i,1}\\ & -A_{i,1}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i\left[B_i^T\right(M_{1k;i}+R_i^{-1})\\ & \times B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T\\ & \times (M_{1k;i}+R_i^{-1})A_{i,1}\phantom{A_{i,1}^T}]x_{i,k-1}\\ & -0.5{\tilde{x}}_{i,k-1}^T[A_{i,3}^T{M}_{3k;i}{A}_{i,3}\\ & +A_{i,2}^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & -A_{i,2}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & -A_{i,3}^T{M^T}_{2k;i}{B}_i\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T{M}_{2k;i}{A}_{i,3}+2A_{i,2}^T{M}_{2k;i}{A}_{i,3}\\ & -2A_{i,2}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i\end{array}$ $\begin{array}{r}\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}]{\tilde{x}}_{i,k-1}\\ & -x_{i,k-1}^T\left[\phantom{B_i^T}{A}_{i,1}^T\right(M_{1k;i}+R_i^{-1})A_{i,2}\\ & +A_{i,1}^T{M}_{2k;i}{A}_{i,3}-A_{i,1}^T(M_{1k;i}+R_i^{-1}{)}^T\\ & \times B_i\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & -A_{i,1}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i[B_i^T(M_{1k;i}+R_i^{-1})\\ & \times B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T{M}_{2k;i}{A}_{i,3}]{\tilde{x}}_{i,k-1}\\ & -[(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,1}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\end{array}$ (30) $\begin{array}{r}\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,1}\phantom{0.5S_{1,k;i}^T}]x_{i,k-1}\\ & -[(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,2}+0.5S_{2,k;i}{A}_{i,3}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}]{\tilde{x}}_{i,k-1}-0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}\\ & +0.5\left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times \left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]+{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1})\\ & -0.5u_{r,i,k-1}^T{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}\\ & -0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & +0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)\}\end{array}$(30) where (31) $\begin{array}{rl}& 0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)]\mathrm{d}{u}_{i,k-1}\\ & =-0.5n+0.5tr\left(M_{1k;i}{Q}_{i,k,1}\right)+0.5tr\left(R_i^{-1}{Q}_{i,k,1}\right),\end{array}$(31) and using the Lemma in Zhou et al. (2019), (32) $\begin{array}{rl}& 0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & =0.5tr\left(log\right(Q_{i,k,1}{R}_i^{-1}\left)\right)\\ & \times 0.5tr\left(Q_{i,k,1}{R}_i^{-1}\right)-0.5n\end{array}$(32) Thus, the last two items, $0.5\ln \left(|Q_{i,k,1}||R_i{|}^{-1}\right)-0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)$ in Equation (30(30) $\begin{array}{r}\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,1}\phantom{0.5S_{1,k;i}^T}]x_{i,k-1}\\ & -[(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,2}+0.5S_{2,k;i}{A}_{i,3}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}]{\tilde{x}}_{i,k-1}-0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}\\ & +0.5\left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times \left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]+{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1})\\ & -0.5u_{r,i,k-1}^T{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}\\ & -0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & +0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)\}\end{array}$(30) ) can be simplified as follows: (33) $\begin{array}{rl}& 0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)\\ & =0.5tr\left(Q_{i,k,1}{R}_i^{-1}\right)\\ & -0.5n+0.5n-0.5tr\left(M_{1k;i}{Q}_{i,k,1}\right)\\ & -0.5tr\left(R_i^{-1}{Q}_{i,k,1}\right)\\ & =-0.5tr\left(M_{1k;i}{Q}_{i,k,1}\right)),\end{array}$(33) where (34) $\begin{array}{rl}& tr\left(M_{1k;i}{Q}_{i,k,1}\right)\\ & =tr\left(M_{1k;i}(\sum _{l=1}^{P_i}{\overline{A}}_{i,l}{x}_{i,k-1}{\overline{Q}}_{i,l}{x}_{i,k-1}^T{\overline{A}}_{i,l}^T+M_i)\right)\\ & =\sum _{l=1}^{P_i}{x}_{i,k-1}^{T}tr\left({\overline{A}}_{i,l}^T{\overline{Q}}_{i,l}{M}_{1k;i}{\overline{A}}_{i,l}\right)x_{i,k-1}\\ & +tr\left(M_{1k;i}{M}_i\right)\\ & =\sum _{l=1}^{P_i}{x}_{i,k-1}^T{\overline{\mathrm{\Phi }}}_{i,l}{x}_{i,k-1}+tr\left(M_{1k;i}{M}_i\right).\end{array}$(34) Then we can obtain the result specified by Equations (24(24) $\begin{array}{rl}-\ln \left(\gamma \left(z_{i,k-1}\right)\right)& =0.5x_{i,k-1}^T{M}_{1k-1;i}{x}_{i,k-1}\\ & +x_{i,k-1}^T{M}_{2k-1;i}{\tilde{x}}_{i,k-1}\\ & +0.5{\tilde{x}}_{i,k-1}^T{M}_{3k-1;i}{\tilde{x}}_{i,k-1}\\ & +0.5S_{1,k-1;i}{x}_{i,k-1}\\ & +0.5S_{2,k-1;i}{\tilde{x}}_{i,k-1}+0.5{\omega }_{i,k-1},\end{array}$(24) ) and (38(38) $\begin{array}{rl}{\dot{x}}_i& =\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{g}{l}-\frac{a_{i}k}{m{l}^2}}& 0\end{array}\right]x_i+\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{m{l}^2}}\end{array}\right]u_i\\ & +\sum _{j\ne i}^3\left[\begin{array}{cc}0& 0\\ {\displaystyle \frac{1}{m{l}^2}}& 0\end{array}\right]x_j,\end{array}$(38) ) by substituting Equations (33(33) $\begin{array}{rl}& 0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)\\ & =0.5tr\left(Q_{i,k,1}{R}_i^{-1}\right)\\ & -0.5n+0.5n-0.5tr\left(M_{1k;i}{Q}_{i,k,1}\right)\\ & -0.5tr\left(R_i^{-1}{Q}_{i,k,1}\right)\\ & =-0.5tr\left(M_{1k;i}{Q}_{i,k,1}\right)),\end{array}$(33) ) and (34(34) $\begin{array}{rl}& tr\left(M_{1k;i}{Q}_{i,k,1}\right)\\ & =tr\left(M_{1k;i}(\sum _{l=1}^{P_i}{\overline{A}}_{i,l}{x}_{i,k-1}{\overline{Q}}_{i,l}{x}_{i,k-1}^T{\overline{A}}_{i,l}^T+M_i)\right)\\ & =\sum _{l=1}^{P_i}{x}_{i,k-1}^{T}tr\left({\overline{A}}_{i,l}^T{\overline{Q}}_{i,l}{M}_{1k;i}{\overline{A}}_{i,l}\right)x_{i,k-1}\\ & +tr\left(M_{1k;i}{M}_i\right)\\ & =\sum _{l=1}^{P_i}{x}_{i,k-1}^T{\overline{\mathrm{\Phi }}}_{i,l}{x}_{i,k-1}+tr\left(M_{1k;i}{M}_i\right).\end{array}$(34) ) back into Equation (30(30) $\begin{array}{r}\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,1}\phantom{0.5S_{1,k;i}^T}]x_{i,k-1}\\ & -[(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,2}+0.5S_{2,k;i}{A}_{i,3}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}]{\tilde{x}}_{i,k-1}-0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}\\ & +0.5\left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times \left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]+{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1})\\ & -0.5u_{r,i,k-1}^T{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}\\ & -0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & +0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)\}\end{array}$(30) ). The constant terms correspond to ${\omega }_{i,k}$ can be found in Equation (30(30) $\begin{array}{r}\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,1}\phantom{0.5S_{1,k;i}^T}]x_{i,k-1}\\ & -[(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,2}+0.5S_{2,k;i}{A}_{i,3}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}]{\tilde{x}}_{i,k-1}-0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}\\ & +0.5\left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times \left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]+{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1})\\ & -0.5u_{r,i,k-1}^T{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}\\ & -0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & +0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)\}\end{array}$(30) ) and is omitted here as it has no contribution to the controller evaluation. End of proof.

Following the above verification of the performance index, the next step is to evaluate the parameters of the optimal randomised controller distribution such that the KLD can be minimised. Based on Equation (19(19) $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)=\frac{\begin{array}{c}{c}^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\end{array}}{\gamma \left(z_{i,k-1}\right)},$(19) ), the optimal distribution of the local controller can be specified in the following theorem.

Theorem 4.3

The distribution of the optimal randomised controller minimising the cost-to-go function (18(18) $\begin{array}{rl}& -\ln \left(\gamma \right(z_{i,k-1}\left)\right)\\ & =\underset{c\left(u_{i,k-1}|z_{i,k-1}\right)}{min}\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times s\left({\tilde{x}}_{i,k}|{\tilde{x}}_{i,k-1}\right)c\left(u_{i,k-1}|z_{i,k-1}\right)\\ & \times [\ln \left(\frac{\begin{array}{c}s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}{\begin{array}{c}{s}^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ c^I\left(u_{i,k-1}|z_{i,k-1}\right)\end{array}}\right)-\ln (\gamma \left(z_{i,k}\right)\left)\right]\\ & \times \mathrm{d}(x_{i,k},{\tilde{x}}_{i,k},u_{i,k-1}),\end{array}$(18) ) is formulated as follows given the ideal distribution of subsystem i dynamics (21(21) $s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\sim N(r_i,R_i),$(21) ) and the ideal distribution of control signal (22(22) $c^I\left(u_{i,k-1}|z_{i,k-1}\right)\sim N(u_{r,i,k-1},{\mathrm{\Gamma }}_i),$(22) ), (35) $c\left(u_{i,k-1}|z_{i,k-1}\right)\sim N({\overline{u}}_{i,k-1},{\mathrm{\Gamma }}_{i,k-1}),$(35) where (36) $\begin{array}{rl}{\overline{u}}_{i,k-1}& =-K_{i,k-1}{z}_{i,k-1}+d_{i,k-1}\\ K_{i,k-1}& ={\mathrm{\Gamma }}_{i_{k-1}}{B}_i^T\left[\right(M_{1k;i}+R_i^{-1})A_i\\ & \times (M_{1k;i}+R_i^{-1})A_{i,2}+M_{2k;i}{A}_{i,3}],\\ {\mathrm{\Gamma }}_{i,k-1}& =({\mathrm{\Gamma }}_i^{-1}+B_i^T(M_{1k;i}+R_i^{-1})B_i{)}^{-1},\\ d_{i,k-1}& ={\mathrm{\Gamma }}_{i,k-1}[-0.5B_i^T{S}_{1,k;i}^T+B_i^T{R}_i^{-1}{x}_{r,i}\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}],\end{array}$(36) where ${\overline{u}}_{i_{k-1}}$ and ${\mathrm{\Gamma }}_{i_{k-1}}$ are the mean and covariance of the optimal randomised controller of subsystem i, respectively. Moreover, $K_{i,k-1}$ stands for the controller feedback gain while $d_{i,k-1}$ is a linear shift which manifests from the considered tracking problem.

Proof.

The results given in Equations (35(35) $c\left(u_{i,k-1}|z_{i,k-1}\right)\sim N({\overline{u}}_{i,k-1},{\mathrm{\Gamma }}_{i,k-1}),$(35) ) and (36(36) $\begin{array}{rl}{\overline{u}}_{i,k-1}& =-K_{i,k-1}{z}_{i,k-1}+d_{i,k-1}\\ K_{i,k-1}& ={\mathrm{\Gamma }}_{i_{k-1}}{B}_i^T\left[\right(M_{1k;i}+R_i^{-1})A_i\\ & \times (M_{1k;i}+R_i^{-1})A_{i,2}+M_{2k;i}{A}_{i,3}],\\ {\mathrm{\Gamma }}_{i,k-1}& =({\mathrm{\Gamma }}_i^{-1}+B_i^T(M_{1k;i}+R_i^{-1})B_i{)}^{-1},\\ d_{i,k-1}& ={\mathrm{\Gamma }}_{i,k-1}[-0.5B_i^T{S}_{1,k;i}^T+B_i^T{R}_i^{-1}{x}_{r,i}\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}],\end{array}$(36) ) can be evaluated by substituting $c^I\left(u_{i,k-1}|z_{i,k-1}\right)$ (16(16) $f^I\left(\mathbf{F}\right)=\prod _{k=1}^{\mathbf{H}}{s}^I\left(z_{i,k}|u_{i,k-1},z_{i,k-1}\right)c^I\left(u_{i,k-1}|z_{i,k-1}\right),$(16) ), $\text{β}(u_{i,k-1},z_{i,k-1})$ (28(28) $\begin{array}{rl}\text{β}(u_{i,k-1},z_{i,k-1})& =\int s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)\\ & \times [\ln \frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}\\ & -\ln \left(\tilde{\gamma }\right(x_{i,k},{\tilde{x}}_{i,k}\left)\right)\phantom{\frac{s\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}{s^I\left(x_{i,k}|u_{i,k-1},z_{i,k-1}\right)}}]\mathrm{d}{x}_{i,k}\\ & =-0.5{\mu }_{i,k}^T(-M_{1k;i}-R_i^{-1}){\mu }_{i,k}\\ & +{\mu }_{i,k}^T(M_{2k;i}{\tilde{\mu }}_{i,k}\\ & +0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i})\\ & +0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}+0.5{\tilde{\mu }}_{i,k}^T{M}_{3k;i}{\tilde{\mu }}_{i,k}\\ & +0.5S_{2,k;i}{\tilde{\mu }}_{i,k}+0.5{\omega }_{i,k}\\ & +0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & -0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(Q_{i,k,1}^{-1}-M_{1k;i}-R_i^{-1})\\ & \times Q_{i,k,1}),\end{array}$(28) ), and $\gamma \left(z_{i,k-1}\right)$ (30(30) $\begin{array}{r}\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,1}\phantom{0.5S_{1,k;i}^T}]x_{i,k-1}\\ & -[(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,2}+0.5S_{2,k;i}{A}_{i,3}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}]{\tilde{x}}_{i,k-1}-0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}\\ & +0.5\left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times \left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]+{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1})\\ & -0.5u_{r,i,k-1}^T{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}\\ & -0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & +0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)\}\end{array}$(30) ) into Equation (19(19) $c^{\ast }\left(u_{i,k-1}|z_{i,k-1}\right)=\frac{\begin{array}{c}{c}^I\left(u_{i,k-1}|z_{i,k-1}\right)\\ \times \exp [-\text{β}(u_{i,k-1},z_{i,k-1}\left)\right]\end{array}}{\gamma \left(z_{i,k-1}\right)},$(19) ). The details of the evaluation are omitted here.

Remark 4.2

The quadratic term $M_{1k-1;i}$ in the Riccati equation of the conventional DFPD is given by (37) $\begin{array}{rl}{M}_{1k-1;i}& =A_{i,1}^T(M_{1k;i}+R_i^{-1})A_{i,1}\\ & -A_{i,1}^T(M_{1k;i}+R_i^{-1}{)}^T{B}_i\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T(M_{1k;i}+R_i^{-1})A_{i,1}.\end{array}$(37) Comparing this equation to the quadratic term $M_{1k-1;i}$ in the Riccati equation of the DFPD proposed in this paper (30(30) $\begin{array}{r}\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,1}\phantom{0.5S_{1,k;i}^T}]x_{i,k-1}\\ & -[(0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}{)}^T{A}_{i,2}+0.5S_{2,k;i}{A}_{i,3}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i\\ & +{\mathrm{\Gamma }}_i^{-1}{]}^{-1}{B}_i^T(M_{1k;i}+R_i^{-1})A_{i,2}\\ & +\left(B_i^T\right[-0.5S_{1,k;i}^T+R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times B_i^T{M}_{2k;i}{A}_{i,3}]{\tilde{x}}_{i,k-1}-0.5x_{r,i}^T{R}_i^{-1}{x}_{r,i}\\ & +0.5\left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]\\ & +{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}{)}^T\\ & \times \left[B_i^T\right(M_{1k;i}+R_i^{-1})B_i+{\mathrm{\Gamma }}_i^{-1}{]}^{-1}\\ & \times \left(B_i^T\right[0.5S_{1,k;i}^T-R_i^{-1}{x}_{r,i}]+{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1})\\ & -0.5u_{r,i,k-1}^T{\mathrm{\Gamma }}_i^{-1}{u}_{r,i,k-1}\\ & -0.5{\omega }_{i,k}-0.5tr\left(M_{3k;i}{Q}_{i,2}\right)\\ & +0.5\ln \left(\left|Q_{i,k,1}\right|{\left|R_i\right|}^{-1}\right)\\ & -0.5tr\left(\right(-Q_{i,k,1}^{-1}+M_{1k;i}+R_i^{-1}\left)Q_{i,k,1}\right)\}\end{array}$(30) ), it becomes evident that the proposed DFPD Riccati equation includes an additional term $\sum _{l=1}^{P_i}{\overline{\mathrm{\Phi }}}_{i,l}$. The incorporation of this additional term is due to the consideration of multiple multiplicative noises in the optimisation process of the randomised controller. Consequently, the derived control solution not only accounts for the covariances of the multiple multiplicative noises but also simultaneously attempts to minimise these covariances, as they are state dependent. It can be inferred that by modifying the Riccati equation, the DFPD proposed in this paper exhibits an enhanced capability to handle multiple multiplicative noises. Furthermore, our method outperforms the extended FPD method in Zhou et al. (2019), which only considered a single multiplicative noise in a centralised approach. This improvement represents the main contribution of this paper.

5. IMPLEMENTATION PROCEDURE OF THE PROPOSED FRAMEWORK

The step-by-step implementation pseudocode of the proposed probabilistic decentralised control and message passing framework to the considered stochastic complex system with multiplicative noise is summarised in Algorithm 1. This algorithm is provided to assist implementation without having to go through the mathematical details.

6. Simulation

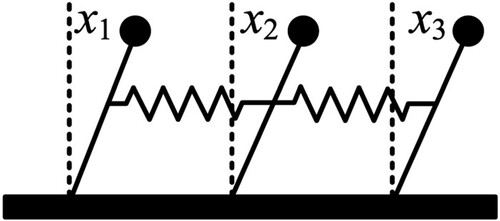
In this section, the proposed algorithm is tested on a three-inverted-pendulum system in Koo et al. (2015) to illuminate the effectiveness of the proposed control method. The structure of the system employed from Koo et al. (2015) is shown in Figure 1. From Figure 1, we can see that the system is consisting by three inverted pendulums whose arms are coupled with each other by springs. The state–space equation for each system is given by (38) $\begin{array}{rl}{\dot{x}}_i& =\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{g}{l}-\frac{a_{i}k}{m{l}^2}}& 0\end{array}\right]x_i+\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{m{l}^2}}\end{array}\right]u_i\\ & +\sum _{j\ne i}^3\left[\begin{array}{cc}0& 0\\ {\displaystyle \frac{1}{m{l}^2}}& 0\end{array}\right]x_j,\end{array}$(38) where g = 10 is the gravitational acceleration, l = 2 represents the length of the pendulum, $m=1$ is the mass of the pendulum and k = 5 stands for the spring constant. Besides, $a_i$ denotes the number of springs connected to the ith pendulum with $a_1=a_3=1$ and $a_2=2$ while $h_{ij}$ means the connection between ith pendulum and jth pendulum, which gives $h_{12}=h_{21}=h_{23}=h_{32}=1$ and $h_{ij}=0$ otherwise.

Figure 1. Three inverted pendulum system.

To apply our proposed method, the system is assumed of suffering from multiplicative noises and additive noises, which is very common in inverted pendulum system. The system (38(38) $\begin{array}{rl}{\dot{x}}_i& =\left[\begin{array}{cc}0& 1\\ {\displaystyle \frac{g}{l}-\frac{a_{i}k}{m{l}^2}}& 0\end{array}\right]x_i+\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{m{l}^2}}\end{array}\right]u_i\\ & +\sum _{j\ne i}^3\left[\begin{array}{cc}0& 0\\ {\displaystyle \frac{1}{m{l}^2}}& 0\end{array}\right]x_j,\end{array}$(38) ) can then be rewritten as following form after discretised, (39) $\begin{array}{rl}{x}_{i,t}& =(A_{i,1}+{\overline{A}}_{i,1}{\rho }_{i,1}+{\overline{A}}_{i,2}{\rho }_{i,2})x_{i,t-1}+A_{i,2}{\tilde{x}}_{i,t-1}\\ & +B_i{u}_{i,t-1}+w_{i,t}\\ {\tilde{x}}_{i,t}& =A_{i,3}{\tilde{x}}_{i,t-1}+{\tilde{w}}_{i,t}\end{array}$(39) where $A_{1,1}=A_{2,1}=A_{3,1}=I+h\left[\begin{array}{cc}0& 1\\ \frac{g}{l}-\frac{a_{i}k}{m{l}^2}& 0\end{array}\right]$, $B_1=B_2=B_3=h\left[\begin{array}{c}0\\ \frac{1}{m{l}^2}\end{array}\right]$, $A_{1,2}=A_{3,2}=h\left[\begin{array}{cc}0& 0\\ \frac{1}{m{l}^2}& 0\end{array}\right]$, $A_{2,2}=h\left[\begin{array}{cccc}0& 0& 0& 0\\ \frac{1}{m{l}^2}& 0& \frac{1}{m{l}^2}& 0\end{array}\right]$, $A_{i,3},i=1,2,3$ are initialised randomly. The distribution of noises are listed in Table 1. The noise parameters are listed in Table 2.

Table 1. Noise distribution.

Noise	Distribution	Noise	Distribution
${\rho }_{1,1}$	$N(0,0.0094)$	${\rho }_{1,2}$	$N(0,0.0098)$
${\rho }_{2,1}$	$N(0,0.009)$	${\rho }_{2,2}$	$N(0,0.0096)$
${\rho }_{3,1}$	$N(0,0.009)$	${\rho }_{3,2}$	$N(0,0.016)$
$w_1$	$N(0,0.001)$	${\tilde{w}}_1$	$N(0,0.001)$
$w_2$	$N(0,0.001)$	${\tilde{w}}_2$	$N(0,0.001)$
$w_3$	$N(0,0.0012)$	${\tilde{w}}_3$	$N(0,0.001)$

Table 2. Noise parameters.

Noise	Distribution	Noise	Distribution
${\overline{A}}_{1,1}$	$\left[\begin{array}{cc}-0.17& -0.54\\ -1.67& 1.58\end{array}\right]$	${\overline{A}}_{1,2}$	$\left[\begin{array}{cc}0.98& -0.01\\ 0.85& -0.89\end{array}\right]$
${\overline{A}}_{2,1}$	$\left[\begin{array}{cc}0.37& -2.10\\ 0.83& -0.39\end{array}\right]$	${\overline{A}}_{2,2}$	$\left[\begin{array}{cc}0.30& -0.74\\ -2.83& 1.34\end{array}\right]$
${\overline{A}}_{3,1}$	$\left[\begin{array}{cc}-0.40& 0.79\\ -2.09& 1.71\end{array}\right]$	${\overline{A}}_{3,2}$	$\left[\begin{array}{cc}-0.45& 0.36\\ 0.07& 1.63\end{array}\right]$

Figure 2. State $x_{1_1}$.

Figure 3. State $x_{1_2}$.

Figure 4. State $x_{2_1}$.

Figure 5. State $x_{2_2}$.

Figure 6. State $x_{3_1}$.

Figure 7. State $x_{3_2}$.

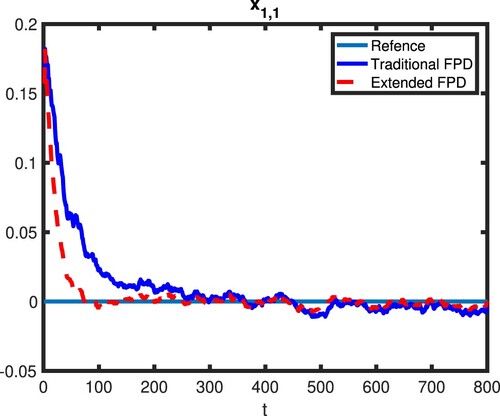
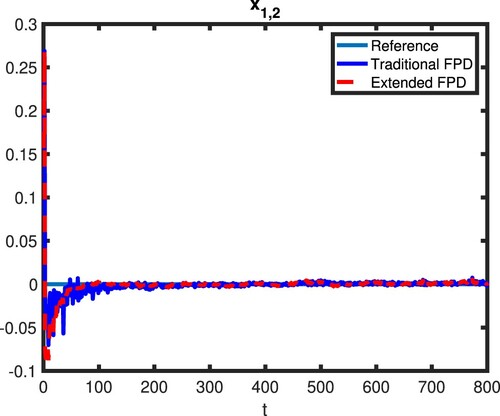
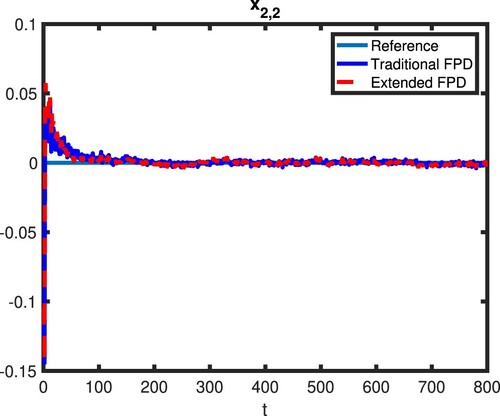
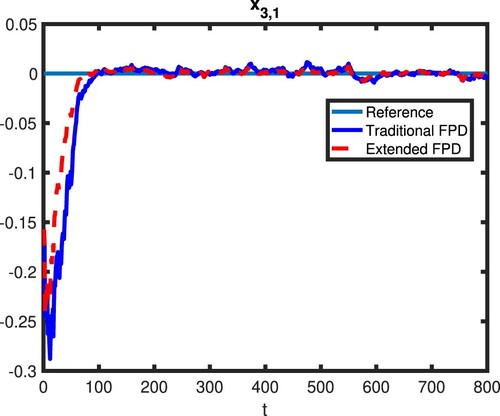
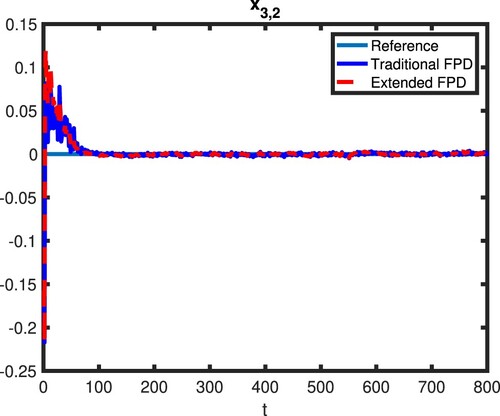
To validate the control performance of the decentralised randomised controller derived in this paper, the results are compared to the results obtained from the traditional DFPD. The state results of all three subsystems are shown in Figures 2–7. In these figures, the red dot lines represent the state's response controlled by the proposed extended DFPD while the blue solid lines are the state response controlled by the traditional DFPD. From these figures, we can see that both states controlled by extended DFPD and states controlled by traditional DFPD converge to zero in all three subsystems. Compared to the traditional DFPD, the converging speed of the proposed method is clearly faster with much fewer oscillations and smaller overshoots. This makes sense as the proposed method is designed to deal with multiple multiplicative noises. Therefore, the conclusion can be drawn that compared to the traditional DFPD, the extended DFPD can achieve a better performance in a decentralised manner for the subsystems that suffering from multiple multiplicative noises.

7. Conclusion

In this paper, a DFPD-based control framework for a class of stochastic dynamic complex systems with multiplicative noise has been proposed. The proposed control framework has improved the conventional DFPD by taking multiple multiplicative noises into consideration, rather than simply assuming the system noises are additional. To better cope with the stochastic nature of complex systems and to provide a more accurate description of the components of the subsystems, the systems' dynamical behaviours in this paper have been fully presented by probabilistic state–space models. Moreover, the probabilistic message passing method has been applied to provide communication between neighbouring subsystems. Numerical results also proved that the proposed control framework has better control performance than the original DFPD. Future research will take into account how the proposed framework might be applied to real-world systems. In addition, we will consider extending our framework to non-linear and non-Gaussian multi-agent systems.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Data availability statement

The authors confirm that the data supporting the findings of this study are available within the article [and/or] its supplementary materials.

Correction Statement

This article has been corrected with minor changes. These changes do not impact the academic content of the article.

Additional information

Notes on contributors

Yuyang Zhou

Yuyang Zhou received her B.Sc. in Electrical & Electricity Engineering School in The University of Manchester, United Kingdom, 2014 and Electrical & Engineering School in Beijing JiaoTong University, China, 2014, and later her Ph.D. in control theory from Electrical & Electricity Engineering School in The University of Manchester, United Kingdom, 2018. After that, she became a Research Associate for three years in the Faculty of Engineering and Applied Science at Aston University, Birmingham, United Kingdom. She currently is a lecturer in group of Engineering and Mathematics, School of Computing, Engineering and Built Environment, Edinburgh Napier University, United Kingdom. Her current research focuses on probabilistic and stochastic control, minimum entropy control, pdf control and decentralized control, time-delay systems, networked and complex systems control with applications to power grids and Kalman filtering.

Randa Herzallah

Randa Herzallah received her B.Sc. degree in Industrial Engineering, her M.Sc. degree in Industrial Engineering/Manufacturing and Design from Jordan University, Jordan, and her PhD degree in Control Theory from Aston University, Birmingham, UK. She is currently an Associate Professor at the Warwick Mathematics Institute at the University of Warwick. She previously held the positions of Reader in the College of Engineering and Physical Sciences at Aston University, UK, Associate Professor at Al-AHliyya Amman University, and Professor at Al-Balqa Applied University, Jordan. Her general research focus is on the general topic of systems modelling, optimization, design, and control. Her current research interests include nonlinear control theory, probabilistic, and stochastic control; intelligent control; pinning control; adaptive control; distributed and decentralized control; optimal control; signal processing; time-delay systems; networked and complex systems control with applications to power grids; and manufacturing systems and biomedical signals.

Qichun Zhang

Qichun Zhang received the B.Eng. degree in automation and the M.Sc. degree in control theory and control engineering from Northeastern University, China, in 2008 and 2010, respectively, and the Ph.D. degree in electrical and electronic engineering from The University of Manchester, U.K., in 2016. He is currently an Assistant Professor in Computer Science with the University of Bradford, U.K. Before joining the University of Bradford, he was a Senior Lecturer in Dynamics and Control with De Montfort University, a Senior Research Officer in Neural Engineering with the University of Essex, and an Academic Visitor with the Control Systems Centre, the University of Manchester. His research interests include stochastic systems optimisation, stochastic distribution control, non-Gaussian filtering, and biological computational modelling. He serves as an active reviewer and an Associate Editor of Journal of Intelligent Manufacturing.