Bedload transport: a walk between randomness and determinism. Part 2. Challenges and prospects

ABSTRACT

By the late nineteenth century, the scientific study of bedload transport had emerged as an offshoot of hydraulics and geomorphology. Since then, computing bedload transport rates has attracted considerable attention, but whereas other environmental sciences have seen their predictive capacities grow over time, particularly thanks to increased computing power, engineers and scientists are unable to predict bedload transport rates to within better than one order of magnitude. Why have we failed to improve our predictive capacity to any significant degree? A commonly shared view is that the study of bedload transport has more in common with the earth sciences than hydraulics: bedload transport rates depend on many processes that vary nonlinearly, involve various time and space scales, and are interrelated to each other. All this makes it difficult to view bedload as merely particle transport in a turbulent flow – something which can be studied in the laboratory in isolation from the natural environment. Over the last two decades, more emphasis has been put on the noisy dynamics characterizing bedload transport. This Vision Paper makes a strong case for recognizing noise (e.g. bedload transport rate fluctuations) as an intrinsic feature of bedload transport. Improving our predictive capacities requires a better understanding of the origins and nature of noise in bedload transport. This paper also reviews some of the challenges that need to be addressed in current research and teaching.

Keywords:

• Bedload transport
• bedload transport rate
• history of hydraulics
• morphodynamics
• random motion
• stochastic model

1. Introduction

The study of bedload transport is a lively, steadily developing field of science, but it faces one longstanding thorny issue: predicting bedload transport rates. After more than a century of research, it is still difficult to predict bedload transport rates more accurately than to within one order of magnitude (Recking, 2013a; Recking, Liébault, Peteuil, & Jolimet, 2012). A closely related problem is predicting the evolution of bed morphology. The twin problems of computing bedload transport rates and bed morphology are of paramount significance to a wide range of engineering and ecological issues (e.g. river and habitat restoration, flood protection, land use planning, risk analysis, water resources and biodiversity). The costs incurred in river management are huge. In Switzerland alone, floods involving bedload transport cause mean annual property damage of CHF 125 million (0.2% of the annual Swiss federal budget) (Badoux, Andres, & Turowski, 2014). The development of more accurate morphodynamic models could have a major societal impact, including the substantial financial savings and higher safety standards which more accurate predictions would engender.

In this article's companion paper (Ancey, 2020), I reviewed the various approaches to computing bedload transport and bed morphology. The present Vision Paper supplements this review, shifting the focus from the state of the art to the hot questions related to bedload transport theory. Among these questions are the scientific challenges yet to be addressed in our search for a better understanding of bedload transport and more accurate predictions. However, some of the questions as to why progress in our field is so slow are sensitive ones. In a previous Vision Paper devoted to bedload transport, Hager (2018) suggested that “research progress slowed down some 40 years ago as the advances were too small to generate adequate funding.” Not many readers will object to this observation. Hydraulics – and its offshoots such as the study of bedload transport – is regarded as an old-fashioned technical field by the “science managers” who rule academia today. I will not challenge Hager's view on the slowdown in the pace of discovery, but I will argue that we are on the verge of creating a new paradigm in bedload transport theory thanks to the latest technologies in instrumentation and innovative ideas. Further information is provided in the online supplementary material (see the public data repository https://doi.org/10.6084/m9.figshare.9892118).

2. Are there really noisy dynamics?

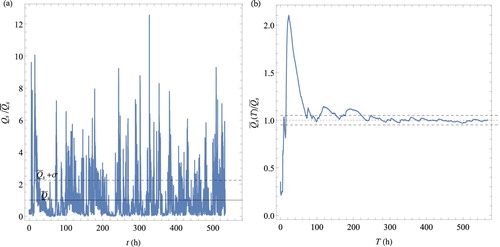
To substantiate this Vision Paper's content and to give it a personal touch, I start with laboratory and field data showing the significance of fluctuations in bedload transport rates. This will be the guiding theme throughout the paper. I will provide two examples. The first involves a typical laboratory experiment: an inclined flume is fed with sediment and water, and we wish to measure the bedload transport rate at the flume outlet. The key question is how long we will have to wait for an accurate estimate of the mean bedload transport rate ${\overline{Q}}_s$ when recording the instantaneous transport rate $Q_s$ at the flume outlet. Figure 1a shows how the bedload transport rate $Q_s$ varies with time t at the outlet of a 19-m-long flume under steady-state conditions (constant water discharge $Q_w$ and sediment feed rate $Q_{in}$). Fluctuations as large as $10Q_{in}$ occurred over the experiment duration (585 h). This fluctuating behaviour substantially affects the value of the mean transport rate. Figure 1b shows how the time-averaged transport rate ${\overline{Q}}_s\left(T\right)={\int }_0^T{Q}_s\left(t\right)\mathrm{d}t/T$ varies as a function of the sampling time T. Because of the huge fluctuations in $Q_s$, the time needed to obtain the mean sediment transport rate ${\overline{Q}}_s$ to within 5% is very long (about 210 h). Measuring ${\overline{Q}}_s$ over short lengths of time (e.g. a few minutes, as in many experimental protocols) could lead to errors of 100%.

Figure 1. (a) Time variation in the bedload transport rate $Q_s\left(t\right)$ measured in a 19-m-long flume with a 60-cm-wide outlet using accelerometers. Values are scaled with the feed rate $Q_{in}=5.0$ g s${}^{-1}$. The solid line shows the mean transport rate $\overline{Q}=4.82$ g s${}^{-1}$ scaled by $Q_{in}$, whereas the dashed line shows the fluctuation amplitude $\overline{Q}+\sigma$ (scaled by $Q_{in}$), where σ denotes the standard deviation ($\sigma =6.2$ g s${}^{-1}$). The sampling time for $Q_s\left(t\right)$ is 1 min. The bed was initially flat, with a mean slope of 1.6% and a final slope of 1.49% (its range of variation was 1.2–1.8%), and was composed of well-sorted natural gravel (diameter $5.5\pm 1.2$ mm). Water discharge at the inlet was $Q_w=15$ l s${}^{-1}$ (uncertainty 0.1%). The Shields number ranged from 0.05 to 0.1. (b) Variation in the time-averaged transport rate ${\overline{Q}}_s\left(T\right)={\int }_0^T{Q}_s\left(t\right)\mathrm{d}t/T$ with the sampling time T. The dashed lines show the 5% variation interval around the mean value (${\overline{Q}}_s\pm 5$%). Data from Dhont and Ancey (2018)

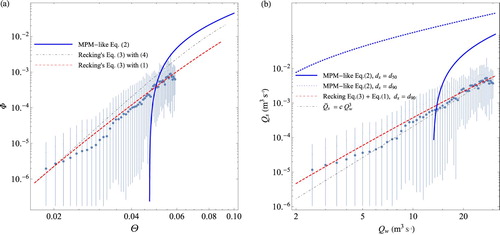
The second example shows field data collected on the Navisence, a mountain river in the Canton du Valais (Switzerland), which has been monitored since 2011 (Ancey, Bohorquez, & Bardou, 2014). Since monitoring began, the river has experienced a wide range of flow conditions, from low to intense sediment transport and two major floods, in 2013 and 2018. Transport rates were measured using geophones placed across a concrete sill of width W = 9 m (Wyss et al., 2016). The mean bed slope upstream of the sill is i = 3.2%. Like most mountain rivers, the Navisence flows over a bed of grains with a wide size distribution: $d_{30}=2$ cm, $d_{50}=8$ cm, and $d_{84}=30$ cm, where $d_x$ is a characteristic particle size such that x% of the sediment (in volume) is finer than $d_x$. See the electronic supplement for further information.

Figure 2a shows that the (dimensionless) transport rate varied over two orders of magnitude at low flow rates, and even during intense floods these rates exhibited large fluctuations covering one order of magnitude. It is tempting to compare these data with extant bedload transport equations. To that end, I have scaled the particle transport rate $Q_s$ and the bed shear stress: (1) $\begin{array}{r}\Phi =\frac{Q_s}{W\sqrt{g(s-1)d_x^5}}\mathrm{a}\mathrm{n}\mathrm{d}\Theta =\frac{\rho g{R}_{h}i}{g({\rho }_p-\rho )d_x}=\frac{R_{h}i}{(s-1)d_x}\end{array}$(1) where g is gravitational acceleration, $s={\rho }_p/\rho \sim 2.65$ is the particle-to-water density ratio (${\rho }_p$ is particle density, ρ is water density), and $R_h=Wh/(W+2h)$ is the hydraulic radius (h is water flow depth). The representative diameter $d_x$ is commonly assumed to be the median diameter $d_{50}$, but recent studies suggest that for mixtures made up of fine and coarse sediment, $d_{84}$ is a better choice (Recking, 2013a). I have plotted two empirical bedload transport equations. The first is a variant of the Meyer-Peter–Müller (MPM) Eq. (6(6) $\Phi =8{\left(\Theta -{\Theta }_c^{\ast }\right)}^{3/2}$(6) ) obtained by Wong and Parker (2006) after recompiling experimental data: (2) $\Phi =4.93(\Theta -{\Theta }_c{)}^{1.6}$(2) where ${\Theta }_c=0.047$ denotes the dimensionless critical Shields stress (related to incipient motion). This variant of the original MPM Eq. (6(6) $\Phi =8{\left(\Theta -{\Theta }_c^{\ast }\right)}^{3/2}$(6) ) is assumed to be better suited to gravel-bed rivers with a slope in excess of 2%. The second equation was derived by Recking (2013b): (3) $\Phi =\frac{14{\Theta }^{2.5}}{1+({\Theta }_c/\Theta {)}^4}$(3) with ${\Theta }_c=(5i+0.06)(d_{84}/d_{50}{)}^{4.4\sqrt{i}-1.5}$. Recking (2013b) suggested two ways of computing the Shields stress $\Theta$, either: (i) by using the definition Eq. (1(1) $\begin{array}{r}\Phi =\frac{Q_s}{W\sqrt{g(s-1)d_x^5}}\mathrm{a}\mathrm{n}\mathrm{d}\Theta =\frac{\rho g{R}_{h}i}{g({\rho }_p-\rho )d_x}=\frac{R_{h}i}{(s-1)d_x}\end{array}$(1) ) when information on h is available; or (ii) by taking this empirical equation reflecting flow resistance in coarse-bed rivers: (4) $\Theta =\frac{i}{(s-1)d_{90}\left(2/W+74p^{2.6}(gi{)}^p{q}^{-2p}{d}_{90}^{3p-1}\right)}$(4) with p = 0.23 and $q=Q_w/W$. Figure 2a shows that Recking's Eq. (3(3) $\Phi =\frac{14{\Theta }^{2.5}}{1+({\Theta }_c/\Theta {)}^4}$(3) ) closely matches the mean bedload transport rate curve, whereas Eq. (2(2) $\Phi =4.93(\Theta -{\Theta }_c{)}^{1.6}$(2) ) shows no agreement between the MPM's predictions and field data because of the value of ${\Theta }_c$. In the log–log representation of Fig. 2a, Recking's equation seems to do a good job of predicting the bedload transport rate, with relative errors mostly lower than 100%, but these errors are more significant at intermediate transport rates: a factor of three for $\Theta \sim 0.03$. How the Shields stress $\Theta$ is defined makes the difference at high transport rates: using the empirical flow resistance Eq. (4(4) $\Theta =\frac{i}{(s-1)d_{90}\left(2/W+74p^{2.6}(gi{)}^p{q}^{-2p}{d}_{90}^{3p-1}\right)}$(4) ) leads to errors up to a factor of three, whereas using the definition Eq. (1(1) $\begin{array}{r}\Phi =\frac{Q_s}{W\sqrt{g(s-1)d_x^5}}\mathrm{a}\mathrm{n}\mathrm{d}\Theta =\frac{\rho g{R}_{h}i}{g({\rho }_p-\rho )d_x}=\frac{R_{h}i}{(s-1)d_x}\end{array}$(1) ) leads to excellent agreement. When working with dimensional variables and comparing field data and empirical equations, the choice of the representative diameter is decisive. As shown by Fig. 2b, using the MPM-like Eq. (2(2) $\Phi =4.93(\Theta -{\Theta }_c{)}^{1.6}$(2) ) with $d_x=d_{90}$ in the definition of $\Theta$ in Eq. (1(1) $\begin{array}{r}\Phi =\frac{Q_s}{W\sqrt{g(s-1)d_x^5}}\mathrm{a}\mathrm{n}\mathrm{d}\Theta =\frac{\rho g{R}_{h}i}{g({\rho }_p-\rho )d_x}=\frac{R_{h}i}{(s-1)d_x}\end{array}$(1) ) leads to errors ranging from two to three orders of magnitude. A power-law function fitted to the data ${\overline{Q}}_s=c{Q}_w^3$ shows that despite large fluctuations, the mean transport rate is well correlated with water discharge $Q_w$. As found in a number of field investigations (Barry, Buffington, & King, 2004; Rickenmann, 2018), the dependence of $Q_s$ on $Q_w$ is more pronounced than that given by classic bedload equations, such as the MPM Eq. (6(6) $\Phi =8{\left(\Theta -{\Theta }_c^{\ast }\right)}^{3/2}$(6) ). Not only does this empirical equation fail to capture the right order of magnitude for ${\overline{Q}}_s$ but it also miscalculates terribly when computing the total amount of sediment transported by the river.

Figure 2. (a) The dimensionless bedload transport rate $\Phi$ as a function of the dimensionless bed shear stress (Shields number) Θ for the River Navisence (Zinal, Anniviers Valley, canton of Valais, Switzerland). The data were scaled using Eq. (1(1) $\begin{array}{r}\Phi =\frac{Q_s}{W\sqrt{g(s-1)d_x^5}}\mathrm{a}\mathrm{n}\mathrm{d}\Theta =\frac{\rho g{R}_{h}i}{g({\rho }_p-\rho )d_x}=\frac{R_{h}i}{(s-1)d_x}\end{array}$(1) ) with $d_x=d_{90}$. The error bars show the 95% confidence interval. We also show the empirical bedload transport equation proposed by Recking (2013b) and the MPM-like Eq. (2(2) $\Phi =4.93(\Theta -{\Theta }_c{)}^{1.6}$(2) ) proposed by Wong and Parker (2006). For Recking's equation, I considered two ways of computing the Shields stress Θ, either: (i) using the definition Eq. (1(1) $\begin{array}{r}\Phi =\frac{Q_s}{W\sqrt{g(s-1)d_x^5}}\mathrm{a}\mathrm{n}\mathrm{d}\Theta =\frac{\rho g{R}_{h}i}{g({\rho }_p-\rho )d_x}=\frac{R_{h}i}{(s-1)d_x}\end{array}$(1) ), where I used the recorded flow depth; or (ii) using Recking's flow resistance Eq. (4(4) $\Theta =\frac{i}{(s-1)d_{90}\left(2/W+74p^{2.6}(gi{)}^p{q}^{-2p}{d}_{90}^{3p-1}\right)}$(4) ). (b) The bedload transport rate $Q_s$ as a function of the water discharge $Q_w$. The same data are shown using dimensional variables instead. The dashed red line shows the scaling ${\overline{Q}}_s=c{Q}_w^3$ (with $c=2.1\times {10}^{-7}$ s${}^2$ m${}^{-2}$). I plotted Recking's equation (Recking, 2013b) (with $d_x=d_{90}$) and MPM-like Eq. (2(2) $\Phi =4.93(\Theta -{\Theta }_c{)}^{1.6}$(2) ), where Φ was transformed into $Q_s$ using Eq. (1(1) $\begin{array}{r}\Phi =\frac{Q_s}{W\sqrt{g(s-1)d_x^5}}\mathrm{a}\mathrm{n}\mathrm{d}\Theta =\frac{\rho g{R}_{h}i}{g({\rho }_p-\rho )d_x}=\frac{R_{h}i}{(s-1)d_x}\end{array}$(1) ) with $d_x=d_{90}$ (dashed line) or $d_x=d_{50}$ (solid line). See the online supplemental data for further information

These two examples show that bedload transport fluctuations are a ubiquitous feature of bedload transport rate records. The existence of wide fluctuations calls into question the very definition of the mean transport rate ${\overline{Q}}_s$ and suggests that timescales associated with $Q_s$ variations be more carefully considered. Questions around the definition of ${\overline{Q}}_s$ have as yet received no consensual answer. We are at a crossroads. We could continue to ignore the part played by fluctuations in bedload transport; after all, many physical systems (e.g. gases, turbulent flows) exhibit fluctuations at the microscopic scale, but their macroscopic behaviours can be described using deterministic principles alone. Conversely, we could consider that the dynamics of bedload transport cannot be modelled without a proper understanding of how fluctuations are created and how they affect bulk dynamics. Admittedly, turbulence can be described using empirical laws such as the Prandtl mixing layer concept, but all the modern theories of turbulence have aimed to provide a refined quantitative description and more accurate predictions of flows. The cornerstone of their modelling is the recognition that velocity fluctuation has a role in generating bulk stress.

3. A brief historical outlook

3.1. The hydraulic perspective

Paul du Boys is credited with the first (heuristic) attempt to predict bedload transport in gravel-bed rivers. By viewing bedload transport as sliding layers of grains, he developed an equation that provides the bedload transport rate $q_s$ per unit width as a function of the bottom shear stress ${\tau }_b$ (du Boys, 1879): (5) $q_s=\chi {\tau }_b({\tau }_b-{\tau }_c)$(5) where ${\tau }_c$ is the critical shear stress above which layers start sliding, and χ is a material coefficient. His work would probably have been forgotten had Grove Karl Gilbert not given him credit, a few decades later, for his ground-breaking concepts on moving particle layers and tractive force, in a seminal work on sediment transport (Gilbert & Murphy, 1914). Thus, Eq. (5(5) $q_s=\chi {\tau }_b({\tau }_b-{\tau }_c)$(5) ) contains two key elements that have commonly been used in bedload transport models since then: (i) bedload transport only occurs when bottom drag exceeds a critical value (an idea then formalized by Shields, 1936); and (ii) the bedload transport rate is a nonlinear function of the bottom shear stress. The latter element had long been debated. Scientists such as Schoklitsch (1934) and Bagnold (1980) argued that the key hydraulic variable should be the water discharge or stream power rather than the bottom shear stress. Laboratory experiments have confirmed that the bedload transport rate varies as a power-law function of the bottom shear stress, but not quadratically as in Eq. (5(5) $q_s=\chi {\tau }_b({\tau }_b-{\tau }_c)$(5) ). For instance, in the commonly used MPM equation, the bedload transport rate varies as ${\tau }_b^{3/2}$. In the absence of correction factors, the MPM equation can be written in a dimensionless form: (6) $\Phi =8{\left(\Theta -{\Theta }_c^{\ast }\right)}^{3/2}$(6) where ${\Theta }_c^{\ast }=0.047$ is the critical Shields stress and $d=d_{50}$ is the median particle diameter to be used in the definition of the Shields stress $\Theta$ in Eq. (1(1) $\begin{array}{r}\Phi =\frac{Q_s}{W\sqrt{g(s-1)d_x^5}}\mathrm{a}\mathrm{n}\mathrm{d}\Theta =\frac{\rho g{R}_{h}i}{g({\rho }_p-\rho )d_x}=\frac{R_{h}i}{(s-1)d_x}\end{array}$(1) ) (e.g. Wong & Parker, 2006).

Empirical approaches epitomized by the MPM Eq. (6(6) $\Phi =8{\left(\Theta -{\Theta }_c^{\ast }\right)}^{3/2}$(6) ) assume the bedload transport rate to be structurally dependent on hydraulic variables and then fit the resulting equation to laboratory data. Although the empirical equations were satisfactory when tested using laboratory data, it quickly appeared that they agreed poorly with field data (Gomez, 1991). This observation has led to two radically different strategies for improving the predictive capacity of bedload equations. For scientists such as Eugen Meyer-Peter, refining the bedload equation by involving more dependent variables (e.g. grain size) should lead to more accurate equations. For other scientists, better accuracy meant a better understanding of the physical mechanisms involved in bedload transport. New ideas about particle entrainment and transport emerged between the mid-1930s and the late 1940s. Among the various theoretical approaches to bedload transport, two ideas developed in the 1940s have attracted the most attention:

• For Hans Albert Einstein, bedload transport reflected the random nature of particle paths and exchanges between the bed and stream (Einstein, 1950). For steady, uniform flows, bedload transport rates could be calculated by matching the entrainment and deposition rates of particles. When the water discharge was increased, the bottom drag increased and fluctuated more widely, causing more particles to be entrained. It was Einstein's view that the main driver of bedload transport was the number of particles entrained. The mean bedload transport rate is defined as ${\overline{q}}_s=E\overline{l}$ where E denotes the particle entrainment rate, and $\overline{l}$ is the mean distance travelled by a particle between two resting phases.

• For his main theoretical challenger, Anton Kalinske, the main driver was particle velocity. Once entrained by the flow, particles moved at the velocity imposed by the fluid velocity distribution (Kalinske, 1947). As the number of moving particles was assumed to be constant, any variation in the bedload transport rate was related to changes in the particle velocity. Kalinske (1947) defined the mean bedload transport rate from the particle activity (that is, the volume of particles in motion per unit streambed area) γ and the mean particle velocity ${\overline{u}}_p$: ${\overline{q}}_s=\gamma {\overline{u}}_p$.

Einstein is often credited as the father of stochastic models of bedload transport. Although he used probabilistic concepts – as did Kalinske – his bedload equation is purely deterministic. The two viewpoints seem incompatible at first sight, but as shown by Furbish, Fathel, Schmeeckle, Jerolmack, and Schumer (2017), there are dual definitions of the bedload transport rate, which can be expressed as a function of particle activity γ or of the entrainment rate E (see also Section 4.4 in Ancey, 2020).

In the decades following Einstein's and Kalinske's contributions, various ideas were explored to infer the bedload transport rate $q_s$ from the mean behaviour of particles (Ali & Dey, 2019). For instance, Wiberg and Smith (1989) and Niño and García (1994) used Kalinske's definition $q_s=\gamma {\overline{u}}_p$, and calculated the particle velocity ${\overline{u}}_p$ from the mean force balance (including drag and gravitational forces, and bed friction). Particle activity was deduced from Bagnold's assumption, which states that the excess stress ${\tau }_b-{\tau }_c$ between the bottom shear stress and critical stress is associated with the energy $u_{\ast }({\tau }_b-{\tau }_c)$ that is available to dislodge and move particles ($u_{\ast }=\sqrt{{\tau }_b/\rho }$ is the friction velocity). This approach has gradually been abandoned. Seminara, Solari, and Parker (2002) showed that Bagnold's assumption was flawed. Furthermore, there is growing evidence that bedload transport rate fluctuations arise mainly from variations in particle activity rather than from mean particle velocity.

Was Einstein's intuition on the random nature of bedload transport just a flash in the pan? Although they were ignored for decades, the 2000s saw a revival of interest in the fluctuations of bedload transport and in bed morphology. As this article's companion paper reviewed the research done since the 2000s, I will simply outline the main directions of that research. Parker, Paola, and Leclair (2000) reformulated the Exner equation in probabilistic terms, opening the way for river morphodynamic models that are able to account for the effects of randomly distributed bed elevations on deposition and entrainment rates (Blom, 2008; Pelosi, Schumer, Parker, & Ferguson, 2016). David Furbish and his co-workers used statistical mechanics methods to show how particle entrainment, deposition and displacement are interrelated physically. Their work has shown that the random nature of particle displacements induces a Fick-like gradient in the particle flux. Consequently, the bedload transport rate is not only related to the particle flux $\gamma {\overline{u}}_p$ but also to its gradient (Furbish et al., 2017; Furbish, Haff, Roseberry, & Schmeeckle, 2012). My colleagues and I have made an analogy with population dynamics (deposition being similar to death, entrainment to birth and displacement to migration) and used the corresponding framework of jump Markov processes (Ancey, Bohorquez, & Heyman, 2015; Ancey & Heyman, 2014). Using this approach, the occurrence of large (non-Gaussian) $Q_s$ fluctuations resulted from a positive feedback mechanism in particle entrainment. As Furbish et al. (2012) showed in their statistical approach, we have found that defining the mean bedload transport rate ${\overline{Q}}_s$ over a control volume involves both the particle flux $\gamma {\overline{u}}_p$ (as Kaslinske defined it) and a fluctuating part that looks like particle diffusion (Ancey et al., 2015).

3.2. Views inspired from the literature on geomorphology

Within the hydraulics community, sediment transport has often been regarded as an isolated system whose variations are solely dictated by the water flow. As summarized by Church and Ferguson (2015), “the channel was regarded as a fixed container within which the flow set the conditions for transport”. The geomorphology community has considered the broader physical picture, looking at sediment transport over larger scales of space and time. Sediment transport is just one of the numerous processes involved in landscape dynamics. As we will see, efforts have been made to bridge the gap between the two perspectives.

The design of stable channels – that is, unlined earth channels “the banks and bed of which are not scoured objectionably by the moving water, and in which objectionable deposits of sediment do not occur” (Lane, 1955a, p. 1235) – gained considerable attention in the twentieth century because of increased settlement on floodplains. In the early part of the twentieth century, geomorphologists such as William Davis, Grove Karl Gilbert, Hoover Mackin and Leopold Lunn had started to think about river morphology. Sediment production (erosion), transport and deposition were addressed over larger scales of space and time. Special attention was paid to how the entire landscape was shaped by erosion and sediment transport, and how river morphology adapted to the constraints imposed by topography and sediment. Morphological processes were described and classified (Schumm, 2005). Geomorphologists also defined a number of important concepts such as capacity, competence, equilibrium and grade (Gilbert & Murphy, 1914; Mackin, 1948). Many of the concepts defined by geomorphologists are still avidly discussed due to the lack of a consensual quantitative framework (Phillips, 2011).

The concept of graded rivers is especially significant to hydraulic engineering because it is closely related to the design of stable channels. Mackin (1948, p. 464) defined a graded river as:

one in which, over a period of years, slope is delicately adjusted to provide, with available discharge and with prevailing channel characteristics, just the velocity required for the transportation of the load supplied from the drainage basin. The graded stream is a system in equilibrium; its diagnostic characteristic is that any change in any of the controlling factors will cause a displacement of the equilibrium in a direction that will tend to absorb the effect of the change.

Emory Lane gave a quantitative translation to this definition, today known as Lane's balance (Lane, 1955b): (7) $Q_{s}d\propto Q_{w}i$(7) that is, the channel adjusts to balance sediment load $Q_s$ and water discharge $Q_w$. In Lane's view, this equation was not a law that described bed equilibrium, but rather a mathematical expression that qualitatively indicated “the changes which will take place in a stream when a change of any one of the variables occurs” (Lane, 1955b). Although Lane's Eq. (7(7) $Q_{s}d\propto Q_{w}i$(7) ) supports the idea of an interplay between bed morphology, bedload and water discharge, in quantitative and sensitive terms, it remains rather vague about the underlying mechanisms. It is unclear over which temporal and spatial scales this condition of bed equilibrium holds true. Another criticism of the concept of bed equilibrium is the very existence of a goal function that would push the stream to reach equilibrium: admittedly, for humans, the river's role is to transport water and sediment, but there is no specific reason why a river would maximize its transport capacity and seek to maintain its bed at equilibrium (Phillips, 2010).

A key question is whether we can move one step further along the trail marked by Emory Lane. It was noted very early on in field investigations that both man-made and natural alluvial channel geometries showed a certain consistency when one tried to compare their channel width, depth and bed slope to bankfull discharge (e.g. Gleason, 2015; Julien & Wargadalam, 1995). This led to the formulation of the regime concept (closely related to the grade concept) (Graf, 1984). Although cross-sections may vary considerably from one river to another, the following scalings have been found for channel width W, flow depth h and velocity $\overline{u}$: (8) $W\propto Q^{{\alpha }_w},h\propto Q^{{\alpha }_h},\mathrm{a}\mathrm{n}\mathrm{d}\overline{u}\propto Q^{{\alpha }_u}$(8) where Q is the bankfull discharge (also called the channel-forming discharge), ${\alpha }_w\sim 1/2$, ${\alpha }_h\sim 1/3$ and ${\alpha }_u\sim 1/6$ (Gleas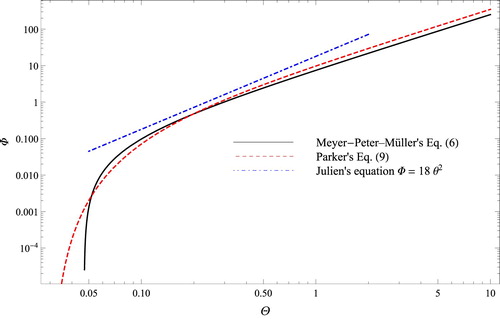on, 2015; Graf, 1984). The robustness and universality of these scalings have long intrigued scientists, who have tried to discover the channel self-adjustment mechanisms hidden behind them using rational arguments (e.g. shear stress redistribution, see Parker, 1978) or the principle of maximization/minimization of an ad hoc functional (Davies & Sutherland, 1983; Nanson & Huang, 2008), a principle often criticized for being unphysical (Gray, Ghidaoui, & Karney, 2018). Combining various scaling relationships, Parker (1979) proposed the following bedload transport equation for a straight gravel-bed river: (9) $\Phi =\frac{q_s}{\sqrt{(\mathrm{\Delta }\varrho -1)g{d}^3}}=11.2\frac{(\Theta -0.03{)}^{9/2}}{{\Theta }^3}$(9) which shows remarkable agreement with Einstein's bedload transport equation, as shown by Fig. 3 (see Eq. (11) in the companion paper for the definition of Einstein's equation). Refining the regime equations by taking sediment size into account, Julien (2002) revisited the Lane balance equation and obtained: (10) $Q_s{d}^{0.28}=9.1Q^{1.11}{i}^{1.44}$(10) for channels whose flow resistance can be described using the Manning–Strickler equation. The agreement between the dimensionless form of Eq. (10(10) $Q_s{d}^{0.28}=9.1Q^{1.11}{i}^{1.44}$(10) ), Parker's Eq. (9(9) $\Phi =\frac{q_s}{\sqrt{(\mathrm{\Delta }\varrho -1)g{d}^3}}=11.2\frac{(\Theta -0.03{)}^{9/2}}{{\Theta }^3}$(9) ) and the MPM Eq. (6(6) $\Phi =8{\left(\Theta -{\Theta }_c^{\ast }\right)}^{3/2}$(6) ) shown in Fig. 3 stems from the specific assumption used by Julien (2002) and Parker (1978).

Figure 3. Comparison between Parker's bedload transport Eq. (9(9) $\Phi =\frac{q_s}{\sqrt{(\mathrm{\Delta }\varrho -1)g{d}^3}}=11.2\frac{(\Theta -0.03{)}^{9/2}}{{\Theta }^3}$(9) ) (red dashed line) and the MPM Eq. (5) (black solid line), in which the flow intensity parameter Ψ has been substituted with the Shields number $\Theta =1/\mathrm{\Psi }$. Julien (2002) assumed the form $\Phi =18{\Theta }^2$ (dot-and-dashed blue curve) to adjust Lane's Eq. (10(10) $Q_s{d}^{0.28}=9.1Q^{1.11}{i}^{1.44}$(10) )

The apparent behaviour of the power-law Eqs (8(8) $W\propto Q^{{\alpha }_w},h\propto Q^{{\alpha }_h},\mathrm{a}\mathrm{n}\mathrm{d}\overline{u}\propto Q^{{\alpha }_u}$(8) ) of the flow variables has fascinated some scientists. However, it has been noted that the respective exponents in those power-law Eqs (8(8) $W\propto Q^{{\alpha }_w},h\propto Q^{{\alpha }_h},\mathrm{a}\mathrm{n}\mathrm{d}\overline{u}\propto Q^{{\alpha }_u}$(8) ) vary from one author to another, depending on the dataset, river features and the fitting protocol (particularly how bankfull discharge is defined) (Gleason, 2015). In the absence of an underlying theory explaining why the flow variables scale with some measure of water discharge, the trends displayed by Eqs (8(8) $W\propto Q^{{\alpha }_w},h\propto Q^{{\alpha }_h},\mathrm{a}\mathrm{n}\mathrm{d}\overline{u}\propto Q^{{\alpha }_u}$(8) ) may be more accidental than the tell-tale sign of a universal mechanism of channel formation. Many complex physical and biological systems exhibit power-law behaviours, but they often arise from unspecified reasons, for instance when the variable of interest is a by-product of mixing multiple heavy-tailed distributions (Stumpf & Porter, 2012). Various efforts have nevertheless aimed at developing this understanding without recourse to ad hoc assumptions. For instance, Parker, Wilcock, Paola, Dietrich, and Pitlick (2007) showed that for straight gravel-bed rivers, the power-law behaviours Eqs (8(8) $W\propto Q^{{\alpha }_w},h\propto Q^{{\alpha }_h},\mathrm{a}\mathrm{n}\mathrm{d}\overline{u}\propto Q^{{\alpha }_u}$(8) ) were the natural consequences of flow resistance, sediment transport and the threshold of incipient motion.

Although geomorphologists have mostly regarded bedload transport as a mechanism of bed equilibrium (Phillips, 2010), some have begun to consider rivers to be closer to punctuated equilibrium systems than to stable systems satisfying Lane's balance in Eqs (8(8) $W\propto Q^{{\alpha }_w},h\propto Q^{{\alpha }_h},\mathrm{a}\mathrm{n}\mathrm{d}\overline{u}\propto Q^{{\alpha }_u}$(8) ). Indeed, on sufficiently large spatial and temporal scales, rivers experience bursts of bedload transport with rapid changes in bed morphology over short time intervals interrupted by long periods of weak activity (stasis). Turbulence and self-organized critical systems have served as an analogue means of studying how a physical, noise-driven system adapts to external changes (Jerolmack & Paola, 2010). Similar views developed in hydraulics from the 1970s onward, when it was realized that a river bed's response to an external change was associated with a much longer timescale than the one characterizing water flow (Cunge & Perdreau, 1973). This led to morphodynamic models governed by the Exner equation, which describes how the bed evolves to balance the difference between the volumes of entrained and deposited sediment (Lanzoni & Seminara, 2002).

4. Open questions and prospects

4.1. Where are we today?

With advances in computational power and refined numerical models, sciences such as meteorology have steadily increased their predictive capabilities (Bauer, Thorpe, & Brunet, 2015). But what about hydraulics? Returning to the example in Fig. 2, one cannot but be amazed by the deviation between the trend shown by the field data $Q_s\propto Q_w^3$ and an MPM-like bedload transport equation $Q_s\propto Q_w$. Field surveys in other gravel-bed rivers have shown similar deviations between field data and empirical bedload equations (Barry et al., 2004; Recking, 2010; Recking et al., 2012; Rickenmann, 2018) of up to as large as one order of magnitude. Various explanations have been suggested, including the poor performance of empirical equations at capturing low sediment transport rates (near the threshold of incipient motion), the effect of grain sorting, surface processes such as bed armouring, the bedload transport rate's nonlinear dependence on flow rate and bed geometry, variations in sediment supply, and the effects of migrating bedforms (Recking, 2012; Yager, Venditti, Smith, & Schmeeckle, 2019). Yet, when recording high-resolution data over long periods, even simple flume experiments (without additional elements of complexity such as grain sorting) reveal the poor match between empirical bedload equations and the data. Figure 1a is a case in point: the fluctuations of $q_s$ are so wide that it is hard to be convinced that a simple relationship $q_s=q_s\left(q_w\right)$ can emerge from them. In a nutshell, on the one hand, the scaling of $q_s\propto q_w$ or $q_s\propto {\tau }_b^{3/2}$ have been consistently demonstrated by many laboratory experiments and numerical simulations since the 1930s. On the other hand, the coefficient of proportionality varies considerably from one laboratory experiment to another, and the exponent of the scaling can also vary significantly, especially when considering field data (Fig. 2).

One could legitimately wonder whether the present situation is much different from that of a nineteenth-century scientist, who, armed only with the Navier–Stokes equations and ignorant of what turbulence meant, might try to calculate the flow rate in a water stream. Naturally, the scientist's governing equations would have been correct, but velocity fluctuations make calculations extremely difficult. Approximations such as Prandtl's mixing length are a first step towards calculating the flow properties of turbulent flows. Returning to bedload transport, we are faced with three questions which have received few answers to date. First, is bedload transport driven by fluctuations? Second, if so, does this hold for all transport regimes? And third, as with closure equations for estimating turbulent viscosity, is it possible to relate the fluctuating components to the mean flow's properties? If we follow Furbish et al. (2017) and other authors, the tentative answers would be the following:

• First, bedload transport is essentially a noise-driven process at low transport rates. The mean bedload transport rate $⟨q_s⟩=⟨\gamma u_p⟩$ cannot be related solely to the mean flow properties (that is, the flow depth and mean velocity).

• Second, this has been shown for transport conditions referred by Furbish to as “rarefied”. The part played by fluctuations at high transport rates is less documented.

• Third, the transport rate's fluctuating part $⟨{\gamma }^{\prime }{u}_p^{\prime }⟩$ can be related to local flow properties through a Fick-like law: $⟨{\gamma }^{\prime }{u}_p^{\prime }⟩=-{\mathrm{\partial }}_x\left(D_r{\overline{u}}_p\right)$ (Section 4 in Ancey, 2019). Ancey and Heyman (2014) found the same result using a different approach. The existence of a particle flux gradient has important consequences in morphodynamic models, especially with regards to the development of bedforms arising from flow instabilities (Bohorquez & Ancey, 2015, 2016).

Although there is a growing number of papers dealing with bedload transport fluctuations, few scientists and engineers show awareness of the effects of fluctuations on bedload transport. Experimental protocols are a case in point: authors have often mentioned that they measured $q_s$ by taking the time average of the particle flux at the flume outlet, but Fig. 1b and field surveys (Bunte & Abt, 2005) have shown that their convergence to the mean value was usually slow. Other authors have mentioned that they waited until bed equilibrium had been reached, but in a context where everything fluctuates slowly, what does “bed equilibrium” mean? A look at recent guidelines and textbooks shows that the problem of fluctuations is almost never mentioned, although it may be the very essence of sediment transport, at least for some of its regimes.

4.2. Additional elements of complexity

The present paper provides a simplified physical picture of bedload transport. Numerous processes have been left aside despite their significance. The interplay between turbulence and sediment transport is certainly one of the most significant and the one that has attracted the most attention. I believe that disentangling how near-bed turbulence and bed structure affect bedload transport remains the single most significant challenge in the field. Interestingly, however, there is one issue which has received some partial answers and is connected with the above discussion on whether bedload transport is essentially a deterministic or stochastic process:

• On the one hand, several authors have developed analytical models for studying the conditions under which an individual particle exposed to a turbulent flow stays at equilibrium (Maurin, Chauchat, & Frey, 2018; Yager, Schmeeckle, & Badoux, 2018). This is a longstanding issue related to Shields' criterion of incipient motion. In these models, the authors ignored hydrodynamic fluctuations induced by turbulence and used mean values for the driving and resisting forces; they were able to provide realistic estimates of Shields' critical shear stress (Yager et al., 2018).

• On the other hand, there is accumulating evidence to show that particle entrainment is caused by drag and lift force fluctuations (not only their instantaneous values but also their durations) (Cameron, Nikora, & Marusic, 2019; Keylock, Lane, & Richards, 2014; Lamb, Brun, & Fuller, 2017b; Schmeeckle, Nelson, & Shreve, 2007; Valyrakis, Diplas, & Dancey, 2013).

Naturally, these two viewpoints are not incompatible. Because the force fluctuations are correlated with the friction velocity $u_{\ast }$ in many flow geometries, the effects of fluctuations can implicitly be incorporated into the drag and lift force coefficients. This link is not universal, however, as it depends crucially on bed roughness and bedforms. Stress-partitioning approaches have had some success in evaluating the relative parts played by particles and bedforms in near-bed turbulence (Scheingross, Winchell, Lamb, & Dietrich, 2013; Yager, Dietrich, Kirchner, & McArdell, 2012), but the physical picture is far from being comprehensive, notably for slopes exceeding 1%, for which flow shallowness and bed coarseness make turbulence more complex (Lamb, Brun, & Fuller, 2017a).

Several complexities are related to the effects of particle size variability. When the bed material is graded, finer particles are more easily entrained than coarser particles, and this has two major consequences: the development of armoured beds and the partial mobility of particles under low to moderate flow conditions (Parker & Toro-Escobar, 2002). Following on from Einstein's concept of hiding function and size-fraction calculation in bedload transport rates, a number of authors have tried to implement simple methods for taking size distribution into account. More recently, the growing perception that bedload transport is a granular flow has given a new impetus to research on grain sorting (Houssais & Jerolmack, 2016). In the field of granular flows, grain sorting is called particle segregation, and it plays a significant role in the dynamics of those flows, for example, by promoting levee formation, self-channelization, mobility feedback and accumulation of coarse particles at the front (Gray, 2018). A few mechanisms have been identified at the particle scale, such as kinetic sieving and squeeze expulsion (small particles fall into gaps that open up beneath them during shear whereas larger particles are squeezed upwards), but understanding of these mechanisms is still only partial. At the bulk scale, segregation can be described using nonlinear advection–diffusion equations (Gray, 2018). Extending segregation theory to bedload is attracting growing interest, but this is far from being a simple exercise. One major obstacle is the continuum assumption used in the segregation theory for granular flows: for bedload transport, particles move individually or in the form of thin flows (a few particle diameters in thickness), which makes the assumption of a continuum less realistic. Grain sorting is undoubtedly the great challenge of the years ahead.

Hydraulic engineers are prone to reducing rivers to surface flows, but they are more complex systems, interacting with the atmosphere, vegetation and groundwater (Brunner, Therrien, Renard, Simmons, & Hendricks Franssen, 2017; Gurnell, Bertoldi, Tockner, Wharton, & Zolezzi, 2016). Subsurface flow – primarily hyporheic flow – affects bedload transport by creating pressure fluctuations (Smart & Habersack, 2007; Tonina & Buffington, 2009), modifying near-bed turbulence (Lamb et al., 2017a; Sinha, Hardy, Blois, Best, & Sambrook Smith, 2017), interacting with bedforms (Bray & Dunne, 2017; Stonedahl, Harvey, & Packman, 2013) and causing water discharge to vary along the streambed. There is much work to be done on subsurface flows.

4.3. Links with morphodynamics

An examination of the technical literature on morphodynamics shows the predominance of theories based on stability analysis. In the companion paper (Section 3.2), we showed that stability analysis successfully predicts the development and migration of dunes and anti-dunes when bottom shear stress and depth-averaged velocity exhibit a phase lag. In Section 4 of the companion paper (Ancey, 2020), we saw that recent models based on mass balance considerations lead to the desired phase lag and provide consistent predictions. Stability analysis has also been applied to predict other bed morphologies (such as gravel bars, channel bifurcation and river meandering) with varying degrees of success depending on channel geometry and the timescales for water discharge and bank and bed evolution (e.g. Bolla Pittaluga, Coco, & Kleinhans, 2015; Redolfi, Zolezzi, & Tubino, 2016).

Not all bedforms arise from hydrodynamic instabilities, however. Many physical and biological systems have a fine-grained architecture (Cross & Greenside, 2009) made up of large numbers of simple elements that interact with each other through a limited number of rules. Physicists have imagined a simple representation of these systems in the form of cellular automata, that is, grids in which the cells evolve in response to the (discrete) states in their local neighbourhood. Cellular automata exhibit macroscopic patterns, which can persist for a long time or die out quickly and which can move around and interact with each other. In other words, cellular automata organize themselves, and macroscopic behaviour may emerge from a simple micro-behaviour follow with its own logic. Murray and Paola (1994) developed a cellular model to explain the development of braided rivers, and their work was followed up by several teams interested in modelling braided river or landscape dynamics (Coulthard & Van De Wiel, 2012). Although cellular automata successfully mimic landform morphologies, they perform poorly at predicting bedload transport rates and morphodynamics: cells redistribute masses of water and grains but not their momentum, and computations are sensitive to local bed slope (Williams, Brasington, & Hicks, 2016). One evolution of this approach has been to combine cellular automata with hydraulic models (Coulthard & Van De Wiel, 2012), and an interesting feature of these models is their deterministic chaos, a property well known by complex-system physicists – even governed by deterministic rules, cells quickly develop chaotic patterns. These morphological fluctuations are different from those studied in stochastic models (Section 4 in the companion paper), which reflect the random nature of particle motion. The question arises as to whether these different viewpoints are compatible and can be placed under a single umbrella theory.

More recently, authors such as Grégoire Mariéthoz and Philippe Renard have suggested that flow patterns such as meandering and braiding rivers can be generated using genetic algorithms that do not need prior knowledge of the rules of interaction between cells (Pirot, Straubhaar, & Renard, 2014). Using a method based on multiple-point statistics (extending kriging techniques based on two-point statistics) they were able to generate structured patterns that were statistically consistent with a “training image” of a river. This resembled the algorithm presented by Shannon (1948), whose introduction to information theory showed how to generate a text in English by combining words randomly selected from a book. After a few iterations, the text was grammatically correct even though the meaning was obscure. Shannon's algorithm (and subsequent methods based on random selection and recombination, such as the Metropolis–Hastings and genetic algorithms) raises fascinating questions when applied to natural processes. When looking at these processes at the bulk scale, where is the limit between random-looking and structured patterns? Do we need physics-based models to provide realistic predictions? What physical insights can be gained from the “random order” featured in bed geometries? Redolfi, Tubino, Bertoldi, and Brasington (2016) recently provided a tentative answer by showing that the irregular cross-sections in multiple-channel rivers were statistically equivalent to a single channel whose section satisfies the power-law function $b=k{d}^{\alpha }$, where b is the free-surface width (wetted width), h is the flow depth, and k and α are two parameters. They then calculated the bedload transport rate in this synthetic channel, and their experimental results agreed well with theory. Closely related methods are those based on maximum entropy (Furbish, Schmeeckle, Schumer, & Fathel, 2016) and Bayesian inference (Schmelter, Erwin, & Wilcock, 2012). One strength of entropy-based methods is their use of the physical information conveyed by data, thereby enforcing physical consistency. These studies have opened up new avenues of research combining statistical information and physics-based models. As high-resolution field survey data are increasingly available (LiDAR, structure from motion video, photogrammetry, laser scanning, etc.), data-driven approaches (e.g. machine-learning algorithms) are likely to be the next important stage in the development of bedload transport models. Not only do they offer the possibility of quantifying a model's uncertainties and calibrating its parameters, but they can also be used to reduce those uncertainties and, possibly, to reveal the missing elements in our physical understanding of bedload transport. Similar efforts are being made in other fields of physics, for instance in turbulence (Duraisamy, Iaccarino, & Xiao, 2019).

5. Further thoughts

5.1. Are we really lagging behind?

A look at recent forum papers and commentaries on hydraulics (and related fields) reveals the scientific community's growing concern about the slowdown in the pace of discoveries (Hager, 2018; Sivapalan & Blöschl, 2017). In the words of Sivapalan and Blöschl, we have entered an era of disenchantment. For those of us with academic responsibilities, required to seek financial support, take part in the recruitment of professors and sit on thesis juries, or in contact with university deans and the stakeholders in funding agencies, there has been a considerable change in how hydraulics is perceived by people outside the field, and it has not been a positive one. Hydraulics – and in turn its offshoots like bedload transport – has increasingly been considered an ageing field, one which can be relegated to colleges of higher education. In many universities, hydraulic facilities have been dismantled, retiring hydraulics professors have not been replaced, technical staff has been reduced, promotions delayed and budgets cut.

The history of science has shown that knowledge accumulates from small, incremental advances due to the work of multitudes of scientists and, exceptionally, from major ideas that revolutionize the field or create new fields from scratch (Mokyr, 1990). Phases of slow evolution and apparent stagnation alternate with phases of rapid evolution marked by major discoveries. The current slow evolution of our field is not exceptional. If we adopt a Schumpeterian view of creative destruction, neither is it a priori shocking to see some fields disappear as others emerge. Are we witnessing the gradual and natural disappearance of our field in part or in its entirety? Will there be new fields? Computational hydraulics has long had the wind in its sails, and some have even predicted the end of classic hydraulics. Although it holds promise, notably for studying bedload transport (Colombini, 2014), computational hydraulics cannot replace experimental and theoretical investigations (Hager & Boes, 2014). Will some new field of scientific endeavour sound the death knell of hydraulics?

According to American anthropologist David Graeber, the post-World War Two years saw the rise of what he called “bureaucratic capitalism”, which entirely reshaped the world since the USA had no competitor. The rising power of bureaucratic approaches to research has been well documented in America (Ginsberg, 2011; Stephan, 2012), and the trend is now worldwide. Graeber (2015) argued that “the increasing interpenetration of government, university, and private firms has led all parties to adopt language, sensibilities, and organizational forms that originated in the corporate world. While this might have helped somewhat in speeding up the creation of immediately marketable products – as this is what corporate bureaucracies are designed to do – in terms of fostering original research, the results have been catastrophic. (··· ) [Universities] have now become brands to be marketed to prospective students or contributors. Marketing and public relations thus come to engulf every aspect of university life.” In addition to the explosion of administrative staff and paperwork, Graeber explains that there has been a shift of emphasis from creativity to bureaucratic projects and, as a result, a decline in the number of major new ideas, inventions and discoveries. If academia was once a refuge for brilliant, quirky personalities, it has now become the realm of managers. Could Hans Albert Einstein (or his father, Albert) be tenured today?

As excessive as Graeber's view may seem at first glance, it is largely supported by evidence. If we focus on medical and pharmaceutical research, despite the massive investments which have taken place since the 1950s, research efficiency is now declining inexorably. Scannel, Blanckley, Boldon, and Warrington (2012) calculated that the cost of drug development doubled every nine years (a negative trend referred to as Eroom's law in a deliberate and sardonic backwards reference to Moore's law). Bowen and Casadevall (2015) confirmed the decline in efficiency in biomedical research since the 1960s, but they also reported that since the mid-2000s, the number of molecules approved annually by the US Food and Drug Administration has also decreased. This decline contrasts with the constant flux of press releases announcing breakthroughs in biomedical research, but it may also explain the explosion of cases of misconduct and the crisis of reproducibility in the medical sciences (Baker, 2016). Whereas in the 1980s, Peter and Olson (1983) were still wondering whether science was just marketing (and, indirectly, whether Kuhn's paradigm of scientific revolution still made sense), nobody even asks the question nowadays. Kuchner (2011) showed scientists how to sell their work more effectively, writing “scientists are always trying to be the first to do something. But of course, it doesn't always work out that way. (··· ) To remedy this problem you need to find or invent a new category you can be first in. For example, maybe your planet is the first planet discovered by the transit technique.” Lemaitre (2016) gave many specific examples of how prominent scientists had built their reputation like fashion designers. Another consequence of bureaucratic drift has been the implementation of metrics and evaluation (Muller, 2018). Stephan (2012) argued that “[the traditional] approach fails to meet the criterion of accountability. In recent years, this has proven to be the Achilles' heel of such a system, as the public, especially in Europe where the system had flourished, has demanded to know what they are getting for their investment in research – in terms of both the quality of the research and its contribution to economic development. Like it or not, a number of countries in Europe (··· ) have moved away from using unrestricted funds in supporting research to a system that allocates university resources on the basis of past performance or through peer review.”

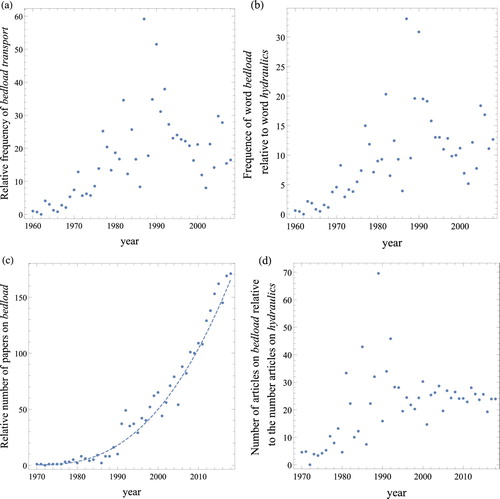
Is the study of bedload transport a field of research in decline? Let us examine a common, simple metric – the annual number of papers and books on bedload transport. Figure 4 shows some bibliometric data extracted from Web of Science and Google. The number of books and articles has steadily increased since the 1970s. The average annual growth rate in bedload transport articles over the last 50 years has been 11.3%, higher than the mean rate for all scientific papers, which ranges from 4% to 9% (Bornmann & Mutz, 2015; Pan, Petersen, Pammolli, & Fortunato, 2018). Because articles on hydraulics have followed a similar trend, the percentage of bedload transport articles within hydraulics has remained roughly constant (around 25% if we use the criteria of Fig. 4). From this quantitative perspective, scientific production is by no means waning. Quantity is admittedly not quality, but at least there is no evident sign of a decline in the former.

Figure 4. (a) Relative frequency of use of the terms “bedload transport” or “bed load transport” in written sources according to the Google Ngram script (Michel et al., 2011) from 1960 to 2008, scaled relative to the frequency of their use $f_0$ in 1960 ($f_0=2.13\times {10}^{-9}$). (b) Frequency of use of the terms “bedload transport” or “bed load transport” relative to the frequency of use of the word “hydraulics” according to Ngram. (c) Relative frequency of the annual number of articles R using the keywords “bedload transport” or “bed load transport” according to the Web of Science (WoS) Core Collection database from 1970–2018, scaled by the number of papers in 1970 (one paper). The dashed line shows the trend fitted to the data: $R=0.33+0.00801823t^{2.56}$ with t the time. (d) Variation in the number of papers on “bedload transport” or “bed load transport” relative to the number on “hydraulics” according to WoS

What of bedload transport's societal and scientific impact? If we consider the total costs incurred by national and local authorities in large river engineering and restoration projects (e.g. the third correction of the Rhone, in Switzerland, whose cost will exceed EUR 2 billion) or in risk analysis (e.g. whether the Vouglans reservoir would damage the Bugey nuclear plant in case of dam break), then it is essential to take bedload transport and its morphodynamic effects into account. Poor scientific analysis of the part played by bedload transport can have costly and enduring consequences. For instance, two additional correction campaigns have been necessary (1930–1960 and 2000–2020) to mitigate the effects of bed aggradation in the Rhone following the initial campaign from 1863–1894.

Thus, bedload transport remains something of a stubborn paradox of hydraulics. The above considerations on scientific output and real-world effects show that the study of bedload transport remains a living scientific field with the potential to influence a wide range of river engineering projects of huge economic importance. Despite this, it suffers from a poor image among university decision-makers, who perceive it to be an old-fashioned discipline. This image probably stems from the mode of funding: in the absence of private financial support, research is mainly funded by national science agencies. Furthermore, the economic added value of high-performance, innovative research is indirect: it takes years until the efficiency of sediment management can be evaluated.

5.2. Education

Many readers will certainly agree that “river engineering is an art as well as a science, and that modelling should therefore take into account two distinct elements: theoretical fluid mechanics and a multitude of practical issues”, as Knight (2013) claimed. By “art”, one usually emphasizes that hydraulics does not rely solely on explicit knowledge – that is, a collection of equations, rules and diagrams – but also on the implicit knowledge gained through personal experience and interaction with highly practised peers. The art of engineering is a delicate one, which involves “doing the best expert job possible in an uncertain world” (Collins & Pinch, 2002) by mixing various forms of knowledge. Because bedload transport lies at the border between geomorphology and hydraulics, the part played by empirical knowledge – gained by looking at how real-world rivers work – is essential to training engineers and scientists.

A few decades ago, students of bedload transport were faced with a complex scientific field mixing equations, rules of thumb, observations and empiricism. As summarized by Ramette (1979), “students will be left hungry, they will likely close the treatise, and conclude that this science has no connection with the essential notions of hydraulics that the school has taught them. This science is full of caveats on the validity domain of this or that correlation, and overall is an experimental field that even experienced professionals can only use cautiously.” And then these students will probably keep their distance from a field about which they have no understanding – a wise decision. In the digital age, experience and implicit knowledge are unable to compete with computers. Students and junior engineers take the predictions of numerical code at face value. Numerical codes are now standard tools in flood-hazard zoning and restoration projects, but few people seem aware that their results are fraught with inaccuracies (exceeding one order of magnitude, in many cases, with regards to bedload transport). Better communication about the limits of current models is thus paramount to avoid overconfidence in numerical models. Students need a better introduction to the strengths and weaknesses of computational thinking.

Over the last four decades, higher education has experienced major changes, including a substantial increase in the number of students (resulting in mass education) and the development of digital technologies and computational techniques (opening up new possibilities). This is not without its challenges and threats, such as the transformation of students into clients of academic services, rising doubts about students' levels of knowledge and the development of self-inflated egos (Nichols, 2017). For hydraulic engineers, there are two major concerns. The first is related to the misuse of computational tools, a point evoked above, discussed by Cunge (2014) and that I will not belabour: “the situation is catastrophic because apparently the students, as well as prospective employers, do not realize that essential is understanding of physics and of limitations of modelling software (Mouse, Mike, HEC, etc.) as well as facilitating software (ArcView, AutoCAD, etc.), not the skills of running these software packages.” The second is related to statistical innumeracy (the greatest irony for engineers) – a form of mathematical illiteracy in the handling of statistical concepts. Many engineering projects involve making decisions in an uncertain, risky world, and the optimal decision is the one that not only satisfies technical requirements but also draws inference from uncertain data and knowledge. The German psychologist, Gerd Gigerenzer, was alarmed by how physicians made erroneous diagnoses. He concluded that, “At present, high school education in some countries covers only little, if any, statistical thinking. Algebra, geometry, and calculus teach thinking in a world of certainty – not in the real world, which is uncertain. Medical schools routinely teach statistics but focus on methods such as significance tests rather than the kind of statistical thinking needed for sound diagnosis and risk assessment. As the widespread innumeracy in the medical profession reveals, data analysis is typically taught as a set of statistical rituals rather than a set of methods for statistical thinking” (Gigerenzer, 2003). Engineering schools are not immune to innumeracy either (and, in fact, this threat looms large over them). Reinforcing students' statistical thinking and teaching them how to reason on the basis of uncertain evidence (e.g. using Bayesian analysis) is of paramount importance.

6. Concluding remarks

This paper started with the observation that scientists and engineers are unable to predict bedload transport rates in rivers to better than one order of magnitude. This held true 70 years ago when Meyer-Peter and Müller published their bedload equation, and it has not changed to any significant degree since then. Existing methods fail to provide accurate estimates of bedload transport rates $Q_s$ because of their large temporal and spatial variability. The $Q_s$ fluctuations have long been regarded as “simple” noise created by the numerous processes involved in bedload transport (e.g. water turbulence, varying sediment supply and grain sorting) – noise that can be averaged out and thus left largely unaddressed. There is growing evidence, however, that $Q_s$ fluctuations do not flatten out when one removes the sources of that noise, and thus they appear to be intrinsic features of bedload transport. As with turbulence modelling, improving our predictive capacities for bedload transport will require a better understanding of how fluctuations are created and how they affect its bulk dynamics.

Notation

b	=	free-surface width (m)
d	=	mean particle diameter (m)
E	=	particle entrainment rate (kg s−1)
g	=	gravitational acceleration (m s${}^{-2}$)
h	=	water flow depth (m)
i	=	bed slope (%)
$\overline{l}$	=	leap length (m)
$q_s$	=	bedload transport rate per unit width (kg m−1 s−1)
Q	=	bankfull discharge (g s−1)
$Q_{in}$	=	sediment feed rate (g s−1)
$Q_s$	=	bedload transport rate (m3 s−1)
${\overline{Q}}_s$	=	mean transport rate (m4 s−1)
$Q_w$	=	constant water discharge (m3 s${}^{-1}$)
$R_h$	=	hydraulic radius (m)
s	=	particle-to-water density ratio (–)
t	=	time (s)
T	=	sampling time (s)
$u_{\ast }$	=	friction velocity (m s−1)
${\overline{u}}_p$	=	mean particle velocity (m s−1)
W	=	width (m)
γ	=	particle activity (m s−1)
$\Theta$	=	Shields stress (–)
${\Theta }_c^{\ast }$	=	dimensional critical shear stress (–)
$\rho$	=	water density (kg m−3)
${\rho }_p$	=	particle density (kg m−3)
${\tau }_b$	=	bottom shear stress (Pa)
${\tau }_c$	=	critical shear stress (Pa)
χ	=	material coefficient ((s2 m−1))
$\Phi$	=	dimensionless bedload transport rate (–)
Ψ	=	flow intensity (–)

Acknowledgments

The author thanks Vladimir Nikora, David Furbish, Philippe Frey, and Éric Bardou, who were generous with their time and critical advice.

Additional information

Funding

The author acknowledges the support of the Swiss National Science Foundation (Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung) (grant 200021_160083).