A Stochastic Model for Population and Well-Being Dynamics

Abstract

This article presents a stochastic dynamic model to study the demographic evolution per sexes and the corresponding well-being of a general human population. The main model variables are population per sexes and well-being. The considered well-being variable is the Gender-Related Development Index (GDI), a United Nations index. The model's objectives are to improve future well-being and to reach a stable population in a country. The application case consists of adapting, validating, and using the model for Spain in the 2000–2006 period. Some instance strategies have been tested in different scenarios for the 2006–2015 period to meet these objectives by calculating the reliability of the results. The optimal strategy is “government invests more in education and maintains the present health investment tendency.”

Keywords:

• Gender-Related Development Index (GDI)
• human population dynamics
• stochastic model
• United Nations' well-being

1. INTRODUCTION

According to the Human Development Reports (United Nations Development Program [UNDP], 1990–2008), human development goes far beyond when a country's income increases or decreases. This is mainly because it covers the creation of an environment where people can develop their maximum potential and continue with a productive and creative life according to their needs and interests. People are a country's real wealth; therefore, development involves extending opportunities.

In order to extend opportunities, development of human capabilities is essential in relation to the diversity of things that people can do during their lifetime. The most basic capabilities for human development are to be able to enjoy a long, healthy life (life expectancy at birth); to receive adequate education (adult literacy rate and combined primary, secondary and tertiary gross enrollment ratio); and to be able to access the resources needed to achieve a decent standard of living and participate in community life (gross domestic product); these are the well-being variables. Access to many other opportunities is considerably restricted or even impossible without these capabilities. Although this way of thinking about development is often forgotten when striving to accumulate wealth, philosophers, economists, and political leaders emphasize that the objective of development is the social well-being of the state.

The mathematical model presented herein has been constructed to contribute to this development. This model studies population dynamics in relation to one of the well-being variables measured by the indices of the United Nations (UN): the Gender-Related Development Index (GDI). A feature of this model is that it is abstract, that is, transferable to any country. This model intends to be a tool for the general study of the stability strategies of human populations and their well-being.

The application case consists in adapting, validating, and using the model for Spain in the 2000–2006 period. The model's objectives are to improve the future well-being and to reach a stable population in this country. Some strategies have been tested in different scenarios in the 2006–2015 period to meet these objectives. Thus, the searched model's solutions are those that increase the GDI and that minimize the difference between births and deaths to obtain a stable population. The optimal strategies indicate that meeting the model's objectives in Spain in the considered period is possible if its government invests more in education and maintains the present health investment tendency.

Another remarkable feature is that it is a stochastic model; that is, its estimates are obtained with its respective maximum and minimum values for a given confidence level. This manner of presenting the results provides a measure of their reliability, unlike deterministic models (Caselles, 1992a).

In order to contextualize the model, it is appropriate to compare it with other models that deal with population dynamics and that are used in different fields; for instance, the models of Kermack-McKendrick and Lotka-McKendrick, which are deterministic control models. The Kermack-McKendrick model permits the study of the evolution of infectious diseases (Inaba, 2001) and epidemics of plant diseases (Segarra, Jeger, & Vandenbosch, 2001). In sociology, it is applied to study the transmission and persistence of urban legends (Noymer, 2001) and to predict and control violent riots (Patten, 1999). Moreover, Bacaër, Abdurahman, and Ye (2006) used a Kermack-McKendrick model to study the AIDS epidemic. The Lotka-McKendrick model solves the crops optimizing control problem (Murphy & Smith, 1991; Anita, Iannelli, Kim, & Park, 1998; Barbu, Iannelli, & Martcheva, 2001). Another model given by the nonlinear system of equations of Gurtina-MacCam and McKendrick is provided by Feichtinger, Tragler, and Veliov (2003), who analyze an epidemic control model and a capital accumulation model. Similar approaches have been provided by Almeder (2004) and Kim (2006).

Takada and Caswell (1997) study the mature population in biology, while Chowdhury and Allen (2001) examine a stochastic approximation for the biological population given by a system of two differential equations taken from the model of von Foerster-McKendrick after considering age a discrete variable. Clemons, Hariharan, and Quinn (2001) present another article about biological population dynamics, which discusses the periodic solutions emerging from the Hopf bifurcation for the McKendrick models in which fertility and mortality rates depend explicitly on time.

Other works that study the stability of nonlinear models are also worth mentioning. The classic work by Webb (1985) is interesting because it addresses significant applications. Mischler, Perthame, and Ryzhik (2002) introduces the maturity variable into the study of solutions' stability, while Norhayati and Wake (2003), who follow the same objective, include a competition term for natural resources. Farkas (2004) focuses on the stability of nonlinear McKendrick equations with fertility and mortality rates. Finally, Guo and Sun (2005) study the optimization of birth with a structured McKendrick model by using a dynamic-programming–based method of approximation to study the case of population in China. In this model, the predictions for the 1989–2014 period are compared with an objective that they call “ideal population.”

There are other works that incorporate new variables into the aforementioned models. For example, Schoen (1988) incorporates two new variables—marriage between males and females and fertility rate—and carries out a demographic analysis. Alho and Spencer (2005) develop a theory and a notation for multistate life tables, that is, a stationary population model and its stability to consider marriages, divorces, and fertility rates in the general linear model of growth context based on the Leslie-Matrix's method, which they apply to different economic situations. Land, Yang, and Yi (2005) study the life table and control the interaction of both sexes for this very purpose. Finally, besides the continuous approximation given by McKendrick models, there are some relevant discrete methods that consider population dynamics structured by sexes. These models are a generalization of the classical stable population theory, which handles dynamic change through the Leslie matrix. The work by Caswell and Weeks (1986) examines the dynamic consequences of considering sexes in demographic patterns, as well as chaos and extinction. In addition, Pollak (1986, 1990) generalizes the classical stable population theory through births from the matching matrix model.

With regard to the direct precedents of this article, Micó and Caselles (1998) study space-time population dynamics. The work by Micó, Caselles, and Soler (2006) examines population dynamics as a function of age. More recently, Micó, Caselles, Soler, Sanz, and Martínez (2008) study its distribution per sexes as well as consider its age dependence. These models attempt to respond to a general demographic standpoint, they are applicable to both biological populations and human populations, and they focus on the existence of a stable population.

However, a literature review shows that there is a lack of studies about the dynamics of human populations which consider both sexes; cover demographic processes such as births, deaths and migration; and depend on well-being variables.

A recent work that considers well-being variables is that of Caselles, Micó, Soler, and Sanz (2008). It proposes a deterministic human population model by distinguishing neither sexes nor ages, where birth and death rates depend on the Human Development Index (HDI) variable, a basic variable that the UN considers to describe the well-being of countries. In addition, emigration and immigration rates are calculated as explicit functions of time. Other variables the UN considers (UNDP, 1990–2008) to describe the well-being of countries include the (Human Poverty Index for developing countries (HPI-1), Human Poverty Index for Organisation for Economic Co-operation and Development (OECD) countries (HPI-2), GDI, and Gender Empowerment Measure (GEM).

This article focuses on well-being using the GDI. The use of the GDI allows the study of the same characteristics as the HDI but by differentiating genders. Thus, differentiating genders introduces innovation in relation to the model presented by Caselles et al. (2008). The GDI fits men and women's average achievement in development of the following dimensions:

	a long, healthy life, given by life expectancy at birth;
	knowledge, given by the adults' literacy rate (with a two-thirds weight) and the combined primary, secondary, and tertiary gross enrolment ratio (with a one-third weight); and
	a decent standard of living, given by estimated earned income (purchasing power parity [PPP] in U.S. dollars).

The GDI assumes complete equality of achievement of life expectancy, literacy, and standards of living are realistic goals for a society.

Section 2 details the procedure to calculate the GDI (UNDP, 1990–2008) and includes three steps:

	In Step 1, an index for each dimension and each sex is calculated. Note that the GDI assumes an equal weight between the variables needed to calculate it.
	In Step 2, the two indices (for men and women) corresponding to each dimension are combined with a formula that includes the parameter ϵ, representing the aversion to inequality in each particular country or each particular case. Thus by considering ϵ = 0, no aversion to inequality (in this case, the GDI would equal the HDI) is introduced, while the indices corresponding to men and women are averaged weighted with the respective rates. The parameter value ϵ > 1 referring, for instance, to life expectancy signifies that a government could obtain better GDI results by concentrating its health efforts on improving the life expectancy of the lesser developed sex than on distributing the same effort equally between both sexes. The ϵ = 2 value has been chosen to calculate the GDI (Anand & Sen, 1994).
	In Step 3, the GDI is calculated as an equal-weighting average of the three indices corresponding to the three dimensions. The justification for the equal-weighting average was that it was simple and convenient, and there was no rationale for unequal weights. A statistical justification of this method can be found in the work by Hagerty and Land (2007), who demonstrated that the equal-weights method is a minimax estimator insofar as it minimizes extreme disagreements on weights.

Hence, the main article's contribution is to present a general dynamic demographic and stochastic model that involves well-being. To the best of our knowledge, the scientific literature does not include a dynamic demographic model that comprises well-being variables. The well-being index considered is the GDI. Because the GDI is a UN index, the model becomes general, that is, applicable to any country. Another of the article's contributions is the way to introduce randomness into stochastic demographic models: not only in input variables but also in certain functions (as Caselles, 1992a, suggests). Such a model can be used, for instance, to design adequate strategies to improve the well-being in a country or to make a certain population stable by calculating the reliability of the results in all cases.

The methodology used in the present study to build the model is the general modeling methodology (GMM) proposed by Caselles (1992a, 1992b, 1993, 1994, 2008), which can be implemented using the Intelligent System Models' Generator SIGEM. The model has been implemented in this environment, and both the validation and simulations in the application case have been developed with the support of this environment.

The remainder of this article is organized as follows: Section 2 presents and explains the model equations. Section 3 provides the application case corresponding to Spain, a country belonging to the OECD whose historical data are fitted to the functions obtained in Section 2; the model is validated, and some instance simulations are performed. Finally, Section 4 presents the conclusions drawn and suggests some future research into this subject.

2. DEMOGRAPHIC AND WELL-BEING MODEL

Due to the complexity of the model, this section provides only a scheme about what is programmed. For the purpose of being brief and practical, online Appendices D and E, respectively, list all the variables and equations involved in the model.

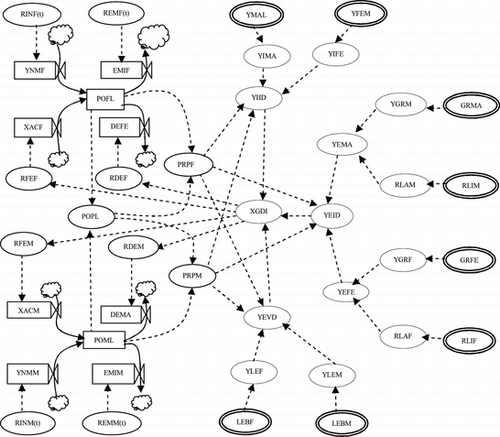
The relationships between the most relevant variables involved in the model can be seen in the Forrester's diagram presented in Figure 1. This is the characteristic diagram of system dynamics. It is a translation of the causal diagram terminology, which facilitates writing equations when they are computer-scheduled.

FIGURE 1 Forrester's diagram (simplified).

In order to interpret the Forrester's diagram, the variables are classified into different types:

	Level variables require an initial value (an input variable), and the following values are updated. They are represented by a square because they can be compared with tanks where a fluid is stored.
	Flow variables can be compared with the stopcocks that regulate the flow to or from a fluid tank. They are represented by a characteristic icon.
	Auxiliary variables are intermediate variables used to calculate flows or strict output variables (they are not used in other calculations and are usually variables employed to optimize). They are represented by a circle or an ellipse.
	Setting variables are not controlled input variables.
	Control variables are input variables whose value can be assigned by the decision maker or by the person who uses the model.
	Constants are system parameters with a known and fixed value.

All the input variables and constants are represented by a double-lined circle or an ellipse. Sources or sinks are represented by a cloud (they are the source of the inflows or the end of the outflows of tanks).

The summary structure of the model is as follows: male and female population dynamics are influenced by fertility, death, emigration, and immigration rates. All these rates depend on the GDI well-being variable. The search for these dependencies is the central goal in constructing the model. Besides, the GDI is calculated from population and input variables.

The starting point is the demographic model presented by Micó et al. (2006), which has no age structure:

where RFEF is the female fertility rate, RFEM is the male fertility rate, RDEF is the females death rate, RDEM is the males death rate, REMF is the female emigration rate, REMM is the male emigration rate, RINF is the female immigration rate, RINM is the male immigration rate, POFL is the female population at the end of the year, and POML is the male population at the end of the year. Moreover in (1) and (2), all the variables depend on time .

The dynamics of the emigration and immigration rates are obtained by explicit time-dependence. This hypothesis is also considered for all the rates in Marchetti, Meyer, and Ausubel (1996), Micó and Caselles (1998), and Chowdhury and Allen (2001). The work by Caselles et al. (2008) introduces a more detailed hypothesis: dependence on a well-being variable (specifically the HDI) of the birth and death rates. Based on the same idea, the present article considers that fertility and death rates are determined from the GDI (see Forrester's diagram, Figure 1), which introduces the innovation of gender distinction in relation to well-being into the model.

From this point onwards, subscript i represents sexes for all the variables: i = 1 for males and i = 2 for females. The dependences of the fertility rates (RFEM and RFEF, herein defined respectively as male and female births per woman) on the GDI are represented as:

In addition, if n _i (t) functions represent births, they can be written as:

Mathematical structures (3) and (4) considered for the fertility rates (that could be extrapolated to any country) are described as functions of the GDI variable as follows:

Mathematical structures (7) and (8), as well as that corresponding to death rates, have been found by a trial-and-error process and by the help of the functions finder and fitter tool Regint (Caselles, 1998, 2008). The work by Marchetti et al. (1996) demonstrates that fertility and death rates can be fitted by a sum of logistic functions. Our data show a joint tendency to complete cycles (see Figures A5 to A8 in online Appendix A). A cycle can be formulated as an increasing logistics, followed by a decreasing logistics. However, the available real data correspond to the short term, which prevents computing the rates as a sum of logistics. Mathematical structures (7) and (8) are the best option found to model the cycles for this short term.

Moreover, this cycle tendency of fertility rates in relation to well-being was also discovered by Canh (2003). In online Figures A5 and A6, the real data for the case of Spain show that when the GDI is greater than 0.94, fertility rates start to lower. The rational explanation provided by Canh is that when a country's well-being increases (due to social improvements, such as female incorporation into working life, and improved health, education and economy), then its fertility rates decline.

On the other hand, the male and female death rates (RDEM and RDEF, respectively) are represented as follows:

Death rates are defined as male deaths and female deaths, respectively, per unit of male or female population. They also depend on the GDI. The mathematical structures considered for these rates are:

Note that we obtain the same function for death rates as for fertility rates. This is due to the same reason: the need to represent cycles (see Figures A7 and A8 in online Appendix A). Note in these figures (in the case of Spain) that when the GDI is greater than 0.89, death rates start to drop.

The rational explanation of this change in tendency of death rates for high well-being values is provided by Dugarte (2000): for developed countries, high well-being produces an aged population, thus a drop in deaths. In order to also support this assertion, fertility rates show a positive linear correlation with life expectancy (see Figures F1 and F2 in online Appendix F). Furthermore, an aging population increases death rates but decreases birth rates for a given GDI value.

At the same time, the GDI is calculated as described in the UN's Human Development Reports (UNDP, 1990–2008). A summarized description of this index is presented below for an easier understanding of the whole model. Calculation of the GDI involves three steps:

	Step 1. The female and male indices in each dimension are calculated according to this general formula:
	Step 2. The female and male indices in each dimension are combined in such a way to penalize the differences in achievement between men and women. The resulting index is calculated according to this general formula: Parameter ϵ measures aversion to inequality. In the GDI, ϵ = 2.
	Step 3. The GDI is calculated by combining the three equally distributed indices in a non weighted average.

The entire process and corresponding equations are presented below (by taking Table 1 into account).

TABLE 1 Goalposts for Calculating the GDI

Indicator	Maximum value	Minimum value
Female life expectancy at birth (years)	87.5	27.5
Male life expectancy at birth (years)	82.5	22.5
Adult literacy rate (%)	100	0
Combined gross enrollment ratio (%)	100	0
Estimated earned income (PPP US$)	40000	100

2.1. Equally Distributed Life Expectancy Index

The first step to compute this index is to calculate the separate indices for female and male achievements in life expectancy using the general formula for the dimension indices:

where YLEF is the index of female life expectancy at birth, YLEM is the index of male life expectancy at birth, LEBM is male life expectancy at birth, and LEBF is female life expectancy at birth.

Next, the female and male indices are combined to create the equally distributed life expectancy index using the general formula for equally distributed indices.

where PRPF is females proportion, PRPM is males proportion, and YEVD is the index of equally distributed life expectancy at birth.

2.2. Equally Distributed Education Index

First, the indices for the adult literacy rate and the combined primary, secondary, and tertiary gross enrolment ratio are calculated separately for females and males. Calculating these indices is straightforward since the indicators used have already been normalized between 0 and 100.

Literacy rate for adults: where RLIF is the female literacy rate, RLIM is the male literacy rate, RLAF is the female literacy rate for adults, and RLAM is the male literacy rate for adults.

Gross rate registered for primary, secondary, and tertiary levels: where GRFE is the rate of female gross registered to primary, secondary, and tertiary levels; GRMA is the rate of male gross registered to primary, secondary, and tertiary levels; YGRF is female gross rate registered to primary, secondary, and tertiary levels; and YGRM is male gross rate registered to primary, secondary, and tertiary levels.

Second, the education index, which gives a two-thirds weight to the adult literacy index and a one-third weight to the gross enrollment index, is computed separately for females and males:

where YEFE is the female education index and YEMA is the male education index.

Finally, the female and male education indices are combined to create the equally distributed education index:

where YEID is the equally distributed education index.

2.3. Equally Distributed Interior Gross Product Index

First, female and male earned incomes (PPP, US$) are estimated. Then the income index is calculated for each gender.

where YFEM is female income, YMAL is male income, YIFE is the female income index, and YIMA is the male income index.

To calculate YFEM and YMAL, the input variables RLFM, RLFF, and GDPR, male and female labor force and gross interior product, respectively, are necessary (see the respective equations in online Appendix E).

Finally, the female and male income indices are combined to create the equally distributed income index:

where YIID is the equally distributed income index.

2.4. Gender-Related Development Index

The GDI is the nonweighted average of the three component indices: the equally distributed life expectancy index, the equally distributed education index, and the equally distributed income index.

LEBM, LEBF, RLIF, RLIM, GRFE, and GRMA are input variables influencing YEVD and YEID. Moreover, RLFM, RLFF, and GDPR are input variables influencing YIID (through YMAL and YFEM; see Figure 1 and online Appendix E for a better understanding).

Finally, the male and female migration balances m _i (t) are considered and defined as immigration minus emigration:

where RINM and RINF are the male and female immigration rates, respectively; REMM and REMF are the male and female emigration rates, respectively; and POML and POFL are the male and female populations, respectively.

The functions considered both for immigrations and emigrations derive from logistics with positive parameters, as in the work by Micó et al. (2006):

The mathematical structures of the fitted functions corresponding to the emigration rate and immigration rate are also those indicated by Marchetti et al. (1996) for time rates, that is, logistic functions (or sums of them).

The structure considered for the time-dependence of the input variables, mentioned when describing well-being indices, is the sum of the logistic functions. Logistic functions can be interpreted in a saturation of resources and their use in demography has proved most useful (Marchetti et al., 1996).

3. APPLICATION CASE

The historical population data used in this article to validate the model have been obtained from the Spanish National Institute of Statistics database (http://www.ine.es) for the 1998–2007 period.

This section is divided into three subsections: In Subsection 3.1 the functions defined in Section 2 (birth, death, emigration, and immigration rates) are fitted to the historical data; in Subsection 3.2 the model is validated; and in Subsection 3.3, the data are extrapolated, and some instance strategies and scenarios are simulated to meet some objectives.

3.1. Fitting Functions

Online Appendix E provides the complete set of equations corresponding to the application case. Most of the equations not mentioned in Section 2, which appear in online Appendix E, are straightforward.

The functions required for calculating the birth and death rates per sexes (RFEM, RFEF, RDEM, and RDEF) are fitted by using the Regint tool (Caselles, 1998, 2008) and are shown in Tables A5 to A8 in online Appendix A. Information about the independent variable of such functions (the GDI well-being index) is extracted from the UN Human Development Reports for the 1999–2008 period. To validate them, the residuals have been analyzed and parameter R ² has been calculated. Figures A5, A6, A7, and A8 in online Appendix A present the corresponding graphical and numerical representations.

The independent variable for the immigration and emigration rates per gender (REMM, REMF, RINM, and RINF) is time. Tables A1 to A4 in online Appendix A show the fitted functions. The historical data about immigration corresponding to the 1998–2007 period originate from the Spanish National Institute of Statistics (http://www.ine.es). The information corresponding to emigration was obtained differently because of complete information exists only from the year 2002. The information from 1998 to 2001 was estimated by multiplying the information corresponding to these years in the city of Valencia (which appears in its website, http://www.ayto-valencia.es) by the proportion between the number of inhabitants in the city of Valencia and the number of inhabitants in Spain. This estimation procedure is acceptable since the evolution of the emigration rates for Valencia and Spain are almost parallel in the 2002–2007 period. The best fitted functions were obtained with the Nonlinear Regression program of MATHEMATICA 7.0. Afterward, Regint was employed to obtain the information needed and not supplied by MATHEMATICA 7.0. All this information is contained in online Appendix A, where Figures A1–A4 show how the obtained functions are a good approximation to the historical data.

The stochastic form of the functions corresponding to the aforementioned rates is made up of two parts. The first part calculates the mean value (represented by h in online Appendix E) using the corresponding fitted function. The second part calculates the corresponding standard deviation (represented by s in online Appendix E). All this is in accordance with the method proposed by Caselles (1992a, 2008). Thus, a generic variable such as Y would be obtained as: Y = h + s · ϵ(t). Where ϵ(t) is a N(0, 1), and h takes the following structure: h = a + b ₁ T ₁ + b ₂ T ₂ + … + b _m T _m , where a, b ₁, …, b _m are parameters, T ₁, …, T _m are transformed functions of the independent variables, and s is calculated by the following formula:

where s _yx is the standard deviation of regression, n is the number of data points, the components of vector τ are the differences between the transformed functions T _i of the independent variables and its respective average, and C is the inverse matrix of the variance-covariance matrix corresponding to the transformed functions. For instance, the following equation appears in online Table A5:

In this case, the transformed functions considered are T ₁ = GDI and T ₂ = Cos(μ₆ · GDI).

3.2. Model Validation

The considered field of study is Spain from 1999 to 2006. Model validation has been performed for both the deterministic and the stochastic versions of the model.

When the model is considered to be deterministic, its validation has been done in the following way. The model has been written as a set of finite difference equations and the solutions have been calculated with Euler's approximation. This method has been chosen because some papers, like that by Djidjeli, Price, Temarel, and Twizell (1998), explain that Euler's method is the most appropriate to solve this kind of equations. In addition, Djidjeli et al. made a comparison with Runge-Kutta's model, stating that this model often leads to false results, and they present a numerical case. Letellier, Elaydi, Aguirre, and Alaoui (2004) indicate that Euler's method is often used with discrete models, but with only a short discretization time, these solutions are equivalent to the continuous model.

These equations have been programmed using the automatic programming tool SIGEM with the functions fitted in Subsection 3.1. The results have been obtained for the 2000–2006 period, and validation has been performed graphically by superposing the results obtained for each year and the historical data, and numerically by calculating the determination coefficients and by testing the randomness of the residues. The validation process has been considered successful for three reasons:

	The graphical superposition of the historical and calculated data in the first years is very good.
	The determination coefficients, R 2 , are very high. R 2 is a useful index for a global fitting between datasets: where (x i , y i ) are the data to be compared, and μ x and μ y are the respective average values.
	Randomness of the results has been verified by means of the maximum relative error.

To check this information, see Figures A9, A10 and A11 in online Appendix A. Deterministic validation may be considered successful because all the R ² are greater than 0.9 and the relative errors do not exceed 5%.

Nevertheless, the stochastic version of the model was that used for simulation because it helps determine the reliability of the results (each result is obtained with its respective confidence interval or with its respective average value and standard deviation). One way of determining whether the stochastic model is validated consists in:

	observing that all the results are normally distributed (to do this, a χ 2 test is done automatically in the program generated by SIGEM); and
	creating a 95% confidence interval, for instance, for each outcome and verifying that all the historical data are within this interval.

The results corresponding to this kind of validation are provided in online Appendix A, in Figures A12, A13, and A14 and in Tables A9, A10 and A11. They confirm that the model is validated for Spain for 2000 to 2006.

3.3. Forecasting

Before making predictions with the model, we extrapolated all the input variables to define (below) the relevant strategies and scenarios. To perform this extrapolation, the input variables are firstly fitted in relation to time (with Regint). All the fitting functions are logistic sums (as explained in Section 2). These functions are extrapolated with confidence intervals using the Extrapol program (available at http://www.uv.es/caselles). These extrapolations are graphically shown in online Appendix C. The Extrapol program calculates the mean values (tendency values) and the limits of a 95% confidence interval for each extrapolated year. Depending on each variable, an extrapolated value (maximum, minimum, or mean) is assigned to each future scenario each year.

Once everything has been sketched and built, the model can be used to simulate the behavior of the system. Two simulations are performed with the model corresponding to two goals: A and B.

A. To Determine How to Reach a Stable Population

The specific objective here is to reach a stable population in 2015. The corresponding objective-variable is named SOST _ij . This variable states the difference between births and deaths for each year of the 2006–2015 period, and I = 1, 2, 3 describe strategies, while j = 1, 2, 3 describe scenarios.

The considered strategies, scenarios, and objective-variables are named as in Table 2. The variable to optimize is

where p _j are the probabilities that experts assign to the three scenarios.

TABLE 2 Concrete SOST_ij when Combining Strategies and Scenarios

	Scenario 1	Scenario 2	Scenario 3
Strategy 1	SOST 11	SOST 12	SOST 13
Strategy 2	SOST 21	SOST 22	SOST 23
Strategy 3	SOST 31	SOST 32	SOST 33

B. To Determine How to Improve Well-Being (GDI)

The specific objective is to increase well-being (GDI) in 2015. The corresponding objective-variable is named XGDI _ij . This variable represents well-being (GDI) in each year in the 2006–2015 period, and I = 1, 2, 3 describe strategies, while j = 1, 2, 3 describe scenarios.

The considered strategies, scenarios and objective-variables are named as in Table 3. The variable to optimize is

where p _j are the probabilities that experts assign to the three scenarios.

TABLE 3 Concrete XGDI_ij when Combining Strategies and Scenarios

	Scenario 1	Scenario 2	Scenario 3
Strategy 1	XGDI 11	XGDI 12	XGDI 13
Strategy 2	XGDI 21	XGDI 22	XGDI 23
Strategy 3	XGDI 31	XGDI 32	XGDI 33

On the one hand, and in the model context, the economic variables (GDPR, RLFM, and RLFF) are assumed to be scenario variables given the difficulty to control them. On the other hand, those variables related to health (LEBF and LEBM) and education (RLIF, RLIM, GRFE, and GRMA) are assumed to be control variables because the relevant authorities may be able to carry out mechanisms that drive the system toward the specified objective. The instance strategies and scenarios considered are

	Strategy 1: Increasing investment in health and maintaining its tendency in education. For this purpose, the average-extrapolated-line values of LEBM (online Figure C3) increase by 2%, while those of LEBF (online Figure C9) increase by 4% (tentative values). Besides, RLIM, RLIF, GRMA, and GRFE maintain the average-extrapolated-line values (online Figures C2, C3, C7, and C8, respectively).
	Strategy 2: Increasing investment in education and maintaining its tendency in health. For this purpose, the average-extrapolated-line values of GRMA and GRFE increase by 10%, while variables RLIM and RLIF increase by 2.5% and 4%, respectively (tentative values). Besides, LEBM and LEBF maintain the values of the average-extrapolated-line (online Figures C3 and C9, respectively).
	Strategy 3: Increasing investment equally in education and health. For this case, the LEBM and LEBF values increase by half the percentage specified for Strategy 1 over its respective average-extrapolated-line, and the values for RLIM, RLIF, GRMA and GRFE increase by half the percentage specified in Strategy 2 over their respective average-extrapolated-line values.
	Scenario 1: Increasing economic variables RLFM, RLFF and GDPR. We chose the maximum values of the extrapolated confidence intervals (see online Figures C4, C5, and C6).
	Scenario 2: Decreasing economic variables RLFM, RLFF and GDPR. We chose the minimum values of the extrapolated confidence intervals (see online Figures C4, C5, and C6).
	Scenario 3: Maintaining the tendency of economic variables RLFM, RLFF and GDPR. We chose the mean values of the extrapolated confidence intervals (see online Figures C4, C5, and C6).

A hypothetical probability is assigned to each scenario:

	Scenario 1: p 1 = 0.4;
	Scenario 2: p 2 = 0.35; and
	Scenario 3: p 3 = 0.25.

The corresponding calculations were performed with the simulator generated by SIGEM and with MATHEMATICA 7.0. Online Appendix B presents the results and the corresponding data. Online Tables B1 to B9 show the SOST _ij and XGDI _ij values. The optimal strategies to reach goals A and B are chosen by observing the evolution of zopt1 and zopt2 (see online Figures B1 and B2, respectively). Thus online Figure B1 depicts that the best demographic stability in 2015 corresponds to Strategy 2 (the minimum value of zopt1). That is, Strategy 2 minimizes the difference between births and deaths in 2015. A similar conclusion is deduced by observing online Figure B2: the highest increase in well-being in 2015 corresponds to Strategy 2. These conclusions relate with the probabilities assigned to the three scenarios; see Eqs. (35) and (36). The major increases in stability and well-being correspond to Scenario 1 (economic increase) (see online Tables B1 to B9).

4. DISCUSSION

An abstract human population dynamics model, which is stochastic and distinguishes sexes, has been presented. It includes the main well-being variable defined by the UN when sexes are considered: the GDI. With simulations, it enables us to obtain the possible consequences of different strategies in different scenarios, and provides the results over time either with their respective confidence intervals or their respective mean and standard deviation.

Nevertheless, two types of models have been studied: deterministic and stochastic. The deterministic model uses new generalized functions for emigration, immigration, birth and death rates and demonstrates that they are valid for Spain (inside OECD) with the fitting coefficient R ² values greater than those obtained in previous studies (Sanz, Micó, Caselles, Soler, & Amigó, 2009). On the other hand, the stochastic model seems the more appropriate for the problem posed in this article because it takes into account the “noise” or uncertainty by calculating the reliability of the results. Both types of models have been validated for Spain in 2000–2006 with the criteria in place.

Two instance application cases referring to Spain are described. Two objectives have been considered: a stable population, that is, a minimum difference between deaths and births, (application case A) and a high well-being level (application case B) for 2015. Three scenarios and three strategies have been considered for them. The strategies are priority investment in health (Strategy 1), priority investment in education (Strategy 2), and investing in both fields in the same proportion (Strategy 3). The scenarios are increasing economy, decreasing economy, and maintaining the economy tendency.

The simulation of both cases in the nine strategy/scenario combinations has verified that the best strategy for our purposes is that which increases investment in education and maintains the current health investment tendency. For the case of Spain in this article, the instance percentages used are an increase of 2.5% and 4% in the literacy rates of men and women, respectively, and a 10% increase in the gross enrolment ratios of men and women. Meanwhile, life expectancy at birth maintains its tendency values. These percentages are tentative; a specialized agency would be responsible for estimating optimal ones.

As a future research line into this topic, the next step could be to validate this model for all the countries in the world where the necessary data are available. A first task could be to verify that the formulas obtained for migration, fertility, and death rates are actually generic because they are validated for all these countries. Another interesting future contribution could be the study of the relationship among fertility rates, death rates, and the remaining well-being variables defined by the UN: HDI, HPI-2 and GEM. On the other hand, the HPI-1 could also be considered in future works for the non OECD countries context. It would be interesting to test if this index could be interchanged with the HPI-2 in the corresponding formulas, or could be included in the other transformed functions added to such formulas. Finally, another possible ambitious work would be to attempt to find a model involving several countries or regions. Thus, migration rates could be fitted in accordance with the well-being variables. This kind of model might help to build a stable world society by minimizing generational relief-type problems.

SUPPLEMENTARY MATERIAL

Supplemental data for this article can be accessed on the publisher's website at http://dx.doi.org/10.1080/0022250X.2011.629064.

Notes

Note. GDI = Gender-Related Development Index; PPP = purchasing power parity.