Morphological Transition of Schooling in 19th-Century France

Abstract

The transformation over time of level sets—the sets of states for which a given function takes a given value—has no reason to be regular, especially in social science, where the structure of these level sets of a given variable may be altered by a fluctuating demography or disrupted by unexpected events, and where the actors contribute to shaping their space through investment policies. The pioneering construction of graphic derivatives of set-valued maps renews the understanding of dynamic level sets in social science. The exemplary case of schooling in 19th-century France shows the set derivatives of level sets and illustrates how the Franco-Prussian War of 1870–1871 disturbed the directions taken in 1867. A comparison of the observed changes of level sets with those observed under rational theoretical policies leads to the conclusion that the actors behaved with the ambition of optimizing the overall schooling incidence while reducing the gap between boys and girls.

Keywords:

• dynamical systems
• France
• mutational equations
• schooling

1. INTRODUCTION

In social science, diffusion has been used to describe the spread of a disease, acquisition of a skill, or the social changes that result when innovations in customs, beliefs, tools, and techniques are adopted by one group of people from another (review in Rogers, 1983). Modeling diffusion often relies on the chance of one member of the population being influenced by another (Bayley, 1976; Bartholomew, 1982). For example, in Medical Innovation (Coleman, Katz, & Menzel, 1966), doctors are assumed to respond to other doctors working in the same city but not to those in other cities. The assumption of homogeneity of time and space was relaxed by Hernes (1972) and Diekman (1989) on population marriage rates and by Strang and Tuma (1993) who developed a class of diffusion models incorporating spatial and temporal heterogeneity. Cartograms have been improved by techniques relating to diffusion from physics (Gastner & Newman, 2004). Aggregate models based on cointegration techniques or on short-term fluctuations can also test the presence of diffusion in their spatial and historical variations, as in the exemplary case of the fertility transition (Bonneuil, 1997; Bonneuil & Dassouki, 2006, 2007).

In natural and social sciences, processes may also draw shapes that are not necessarily regular sets. This holds true especially with historical spatial data (Flint, 2002; Gregory & Ell, 2005; St-Hilaire, Moldofsky, Richard, & Beaudry, 2007; DeBats, 2008). The application I shall develop is the variation over time of level sets of the schooling incidence over the French territory. A level set of a function f for a given value, say λ, is the set of all points x for which f(x) = λ (see a rigorous definition in Appendix A). All users of topographic maps have followed level lines to figure out hills or peaks or valleys. Schooling does not “spread” in the same way that a disease or a custom does by contact between individuals or among groups of individuals. The process requires investment in money, in organization, and in people; it is tuned by the demography of the pupil population and by the filling of classroom places that also depends on decision making and resource constraints.

The differentiation between schooling for boys and girls reflected political and societal regulation, and the rivalry between the confessional and secular systems also obeyed the law. The interesting case is a country where schooling is developing over time and heterogeneously in space, and for which sufficiently reliable data are available. Nineteenth-century France is such a well-documented case, and I shall develop on it.

Why not work with level sets of schooling incidences rather than with their contingent derivatives defined below and which capture the change of sets? Level sets of schooling incidences do not represent conditions of change; rather, they merely cumulate the past changes, as prevalence does in epidemiology. The set derivatives are specifically devoted to informing us about the change of the moment. The difference between level sets and their set derivatives is the same as between stocks and flows, or in demography, age pyramid and life expectancy.

The difference between set derivatives and linearly interpolated values between two dates is the same as between a tangent at a point of a circumference and a chord between two distant points. Set derivatives are specifically designed to know what the movement of the set is at a given date, no matter the nonlinearity of the variations.

After presenting the concept of set derivative, I shall introduce the concept of mutational maps and show its relevance for understanding the social history of schooling in 19th-century France. Mutational maps consist of sets of set derivatives, which represent the tendency for change at a given moment as a tangent gives the tendency to change in a simple curve. In history, as I pointed out above, processes are seldom regular, and this is the case for schooling. Then, the comparison of the value extrapolated from the mutation map with the actual successive value highlights the nonlinearity of the process and the importance of the accident brought by history. Thus, the 1870–1871 Prussian war abruptly modifies the extrapolation of the spatial expansion of schooling France. I shall compute and represent maps of derivatives of level sets for the distribution of schooling incidences over time. To inform on the structure of these observed set derivatives, I shall use the latter as an independent variable in simultaneous regressions involving four key policies and changes in the total number of schools, in the total number of pupils per school, in the total number of unschooled children, in schooling incidences, in the sex difference of schooling incidences, in the proportion of urban population, in life expectancy, and in fertility. These maps of set derivatives are as useful as transition probabilities in a process, while maps of schooling rates are as useful as the table of prevalence in an epidemiological study. Maps of set derivatives then complete the portrayal of a spatial phenomenon, in informing us about the directions the spatial process was taking at a given date. The comparison of the map of rates obtained from the set derivatives from time t and the map of what actually occurred at time t + 1 reveals the part taken by innovation in the historical process.

2. MORPHOLOGICAL TRANSITION

A correspondence is a map associating a set to a point (literary presentation in Bonneuil, 2010). Zolésio (1976) and Céa (1981) introduced a concept of the differential of a correspondence and of a set. The equation expressing the differential of a set is called a “mutational equation,” as it extends the usual concept of a differential equation, which usually applies to functions. Aubin (1999) suggested kinds of differential equations governing the variation of sets in the general framework of metric spaces, which are spaces where a distance can be defined. (We are no longer limited to standard linear calculus.)

The set derivative of a set K(t) at time t is identified to a correspondence F(t) defining a set-valued vector field changing the set K(t). When F(t) is a constant set B(t), candidates for set derivatives are the structuring sets of mathematical morphology. When F(t) is a point-to-point function, we find the ideas of shape optimization. When the shapes K(t) are level sets of a regular function, the set derivative of K(t) is the normal derivative of the shape, and we again find the shape evolution governed by partial differential equations. In the social sciences and especially in history, functions are unlikely to be regular. Mutational equations (Gorre, 1997), which require only a metric space, are useful to consider real phenomena. The set-valued feature of set derivatives allows us to study not only the alteration in the boundaries of sets but also the growth of these sets. During an infinitesimal duration dt, a state x(t) at time t moves to its multiple successors x(t + dt), which constitute the set . The alteration of the set K(t) is then directed toward a given goal (in the application below, improved schooling incidences) and can be “controlled” (in the application, by maintaining existing schools and opening new ones, and by provision of teachers and staff).

In Appendix A, I present the mathematics of transformation of sets, so-called mutational calculus. Here I suggest the usefulness of the concept for understanding the application. A set-valued dynamic F is a correspondence or a set-valued map, which associates a whole set of admissible velocities x′(t) to a given state x(t) indexed by time t:

Figure 1 shows an example of an attainable set under a dynamic F after a time h either from a given state x ₀ in (a) or from a given set K ₀ in (b). The set-valued map associating the set of attainable states after time h to the state x ₀ is denoted θ _F (h, x ₀). It also associates the union θ _F (h, K ₀) of the sets of attainable states stemming from all states of the set K ₀ to the set K ₀. Figure 2, a detail of Figure 3, shows the case of the level set 90%–100% of the schooling incidence for girls in eastern France. In 1837, this level set covers three départements (Haute-Marne, Meurthe, Meuse), and its set derivative is small; in 1850, it is reduced to the départements of Haute-Marne and Meuse but is nevertheless heading for expansion, which is realized in 1867, when it encompasses Ardennes, Aube, Côte d'Or, Doubs, Jura, Marne, Haute-Marne, Meuse, Haute-Saône, Vosges, and Territoire de Belfort. In 1876, the départementsof Ardennes, Marne, and Territoire de Belfort have fallen under 90%, while the more southern départements of Ain, Hautes-Alpes, and Savoie have reached this level. The situation in 1850 resembles the extrapolation which can be done from the situation in 1837 and from the set derivatives indicated by arrows, and similarly from 1850 to 1867. In contrast, the extension of the 90–100 level set in 1876 differs from the extrapolation from 1867, notably for the most northern départements of Ardennes, Marne, and Territoire de Belfort, which suffered the most from the Prussian invasion.

Figure 1 (a) Example of an attainable set made of successors of an initial point x ₀ and (b) example of a mutation of a set K ₀. Arrows represent normal set derivatives.

Figure 2 Example of the mutation of the level set 90%–100% in northeastern France (to be found again on Figure 3).

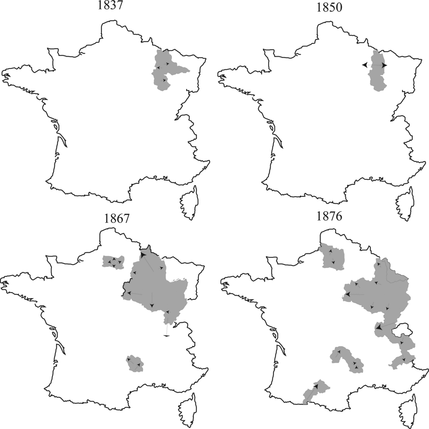
Figure 3 Girls schooling: Level sets in grey and their set derivatives as arrows with length representing |ϕ| and direction as . Deciles of level sets correspond, respectively, to schooling incidences of 21%, 31%, 42%, 51%, 60%, 67%, 72%, 78%, and 84%.

When K(t) is a level set of a function (t, x) → f(t,x), Aubin (1999) showed that one such morphological transition ϕ of K(t) is defined by (sketch of the proof in Appendix A):

where is the unit normal to K(t) at x, and and are the partial derivatives with respect to time t and space x. The transformation ϕ then combines changes in time , changes in space , with the unit normal, which is the most “natural” direction, in which the set is being transformed. We are accustomed to classical diffusion coming from physics, and may find mutational calculus “complicated.” First, escaping from the framework of classical diffusion implies different thinking, made necessary by the fact that social sciences have little reason to respond to processes like the diffusion of heat or epidemics. Second, the expression of Eq. (2) remains rather simple. The difficulty lies in the concept of derivative of sets. This is exactly my project to present it. Social sciences offer novel challenges compared to physics: Can we address them without concepts designed to deal with its specifics?

3. CONTROLLED DYNAMICS OF SCHOOLING AND DATA

The object is not to retrace the history of the statistics of schooling, work which Luc (1985, 1986) has performed at length, nor to give an econometric analysis of the convergence of schooling incidences, as Diebolt (1999) has done, nor to chart the growth of elementary schooling (Grew & Harrigan, 1991). But, rather, the object is to present schooling as an exemplary case of a controlled spatial process. The geographical division of France into a maximum (in 1867) of 89 départements, the key administrative territorial unit at that time, forms an approximately regular grid over the French territory and offers an exceptional opportunity to capture spatial processes at a fine level in the 19th century (Bonneuil, 1997; Bonneuil & Rosental, 1999; Bonneuil, Bringé, & Rosental, 2008).

In the case of 19th-century France, large amounts of human and material resources were made available for schooling starting in 1837. Against a background of modest population growth at an annual rate of 1.3% in 1836, 1850, and 1876 (Bonneuil, 1997)—with the annexing of Nice and Savoy in 1860 adding 669,000 inhabitants, and the loss of Alsace and Lorraine in 1871 subtracting one and a half million— the total number of state-run schools for girls increased from 4,178 in 1850 to 6,570 in 1867 and to 9,417 in 1876, an annual increase of 2.7% and 4%, respectively; the total number of boys schools increased from 33,201 in 1850 to 35,774 in 1867 to 36,399 in 1876, or 0.4% and 0.2% annual increases on average. The total number of private and clerical-run schools for girls increased from 17,011 in 1850 to 21,645 in 1867 and decreased to 19,709 in 1876; the figures for boys are 6,189 in 1850, 6,683 in 1867, and 6,022 in 1876. The average total number of girls per school remained at 78 in 1850, 1867, and 1876, while for boys it increased from 46 in 1850 to 56 in 1867 and 58 in 1876.

Retracing the history of statistics on schooling, Luc (1985, 1986) called for a critical approach when interpreting published figures, whose biases are multiple. The data I use here are those corrected by him and by Diebolt (1999). Statistics from the earliest surveys were ill-matched due to differences over school type (under clerical or secular control) and pupils (the proportion of girls varied between départements), though after 1829 considerable efforts were made to obtain correct information and homogeneous data sets and to adjust for successive reforms in the recording of pupils (Luc, 1985).

I am grateful to Claude Diebolt for allowing me access to his data, namely total population size of 5–15 year olds by département, the total number of schooled children in private or public schools under secular or clerical control available only for 1837, 1850, 1867, and 1876, which are the years of interest to capture the schooling transition. Though they must be treated with caution, these data are unique in showing a society where schooling was increasing, where political will was clearly at work to promote schooling across the national territory, and where schooling incidences were altered by a fluctuating demography. (The fertility decline, having begun as early as the mid-18th century in Normandy, Garonne Valley, and Champagne, was underway throughout France; the mortality decline temporarily disturbed by epidemics, such as the cholera in 1832 or the Franco-Prussian War of 1870–1871 [Bonneuil, 1997].) After correction along the lines indicated by Luc (1985, 1986) the data are adequate to portray the mutation of level sets of schooling incidence.

On March 15, 1876, a commission of statistics on primary schools was set up in the Ministry of Education with the purpose of publishing detailed statistics on a 5-year basis. Eight volumes were published prior to World War I. The second presents the comparative statistics on primary schools from 1829 to 1877. The other volumes deal with school years 1881–1882, 1886–1887, 1891–1892, 1896–1897, 1901–1902, and 1906–1907. The sixth volume (1896–1897) summarizes the improvement in primary schooling under the Third Republic. Most data, before correction, come from the report by Jules Ferry, Minister of Public Education and Arts (Éducation publique et des Beaux-Arts), to the President of the Republic on January 25, 1880. Ferry (as cited in Diebolt, 1999) noted the immense improvement in primary schooling: between 1837 and 1877 the total number of pupils had increased by 82%, the total number of schools by 36% (secular schools by 75%), and girls schools had multiplied four-fold; the total number of teachers increased by 85%, with a pupil–teacher ratio falling from 53 to 48. Diebolt (1999) shows that in a context of a general increase in operating costs, the disparities between départements declined rapidly: The discrepancy between the départements best and worst endowed with schools was 1 to 4 in 1856, 1 to 3 in 1867, and 1 to 2 in 1876. The total number of teachers increased from 63,409 in 1840 to 108,799 in 1863 (Diebolt, 1999). As Ferry, cited by Diebolt, claimed, one remarkable fact was the rapid increase in schooling by age class between 1850 and 1877.

Diebolt (1999) notes that the total number of teachers grew even faster than the total number of schools, from 63,409 in 1840 to 110,709 in 1876, responding to the dramatic increase in schooled children and thus limiting the increase in pupils per class. Operating expenditure rose from 25 million to 68 million francs as a result of a policy of allocating more resources to education, for building new schools, hiring teachers, and improving their pay.

The schooling incidence among children aged 5–15, for département i, sex s = 1 for boys and s = 2 for girls, and date t is

where is the population size of boys (s = 1) or girls (s = 2) aged 5–15 at date t and the total number of schooled boys (s = 1) or girls (s = 2). These numbers depend on the total number of schools and on the capacity filled in each school:

where is the average total number of pupils of sex s per school and is the total number of schools for pupils of sex s.

Differentiating the schooling incidence yields (omitting superscript s for sex and subscript i for département):

Underlying the variation in schooled children, the available controls are then the net growth of schools u ₁ : = e′(t) and the net growth of pupils per school u ₂ : = α′(t), under a budget constraint. The characteristics of the household that might affect schooling choices for their children is included in u ₂: my perspective is from the state measuring the attendance of children, not from the households. All schools—both public and private, secular and clerical—are included. The population growth rate is a given, not a control. Even if actors finance schools in number and capacities of value , these controls combine in the variation of schooled children (through the equation for sex s and department i omitted).

4. RESULTS

4.1. Mutational Maps in 19th-Century French Schooling

The mutation of the level sets in an empirical case requires treatment of the data. First, a bidimensional smoothing with scattered data ¹ of schooling incidences on the grid formed over France's territory by the chief cities of all the départements is made for each available date, yielding a space-time continuous manifold in four dimensions. The smoothing operator passes exactly by the observed points (coordinates of the chief city and schooling rate in the corresponding department). Second, the derivatives and are computed on this manifold ² to obtain ϕ. The whole operation certainly depends on the smoothing operator whose flexibility is fine tuned so as to both pass through the observed data and avoid spurious interpolations. The smoothing operator is built on successive certain polynomials, in number m for each dimension, which is then divided into m + 1 support intervals, delimited by m knots. The larger this number, the closer the smoothing operator passes to all empirical points, but with the danger of keeping or creating meaningless unevenness. The smaller this number, the smoother the manifold, but with the danger of ignoring meaningful variations. Practically, five knots in abscissa and five in ordinate yield a satisfactory adjustment on the grid of the map of France. The level sets of schooling incidence are represented together with the set derivatives ϕ on Figure 3 for girls and on Figure 4 for boys.

Figure 4 Boys schooling: Level sets in grey and their set derivatives as arrows with length representing |ϕ| and direction as . Deciles of level sets correspond, respectively, to schooling incidences of 35%, 46%, 52%, 61%, 68%, 73%, 78%, 85%, and 92%.

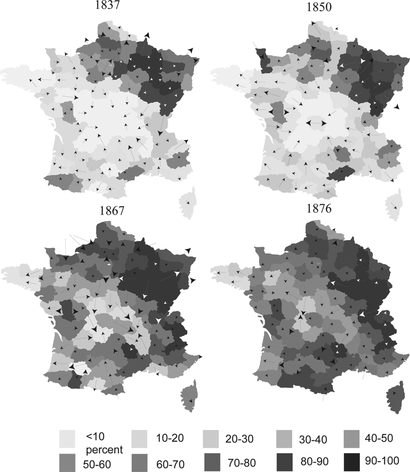
Schooling tended to spread over the French territory, and because it increased more or less everywhere level sets of low schooling incidence contracted at the expense of higher level sets. Figures 3 and 4 show that the most mobile level sets were those of intermediate low value (deciles 20–30, 30–40, and 50–60) in 1837, of intermediate high values (40–50, 70–80, and above all 50–60 deciles) in 1855, of high values (70–80 and 80–90) in 1867, and, with a lower magnitude, in 1876. The mean value of set derivatives is coherent with the maps of level sets because the process is close to linear in general. However, from 1867 to 1876, the discrepancy between the set derivatives in 1867 and the observed map of level sets in 1876 conveys the disruption caused by the Franco-Prussian War of 1870–1871. The effect is especially acute in the northeastern region which of course suffered most from the Prussian invasion. The level set of 90%–100% shrunk between 1867 and 1876, although set derivatives in 1867 allow us to forecast an extension. The extension was stopped by the war and the ensuing period of political indecision, under the political leadership of Adolphe Thiers, between 1871 and 1877. Taking a partition as thin as deciles runs the risk of the data being not detailed enough but also allows us to identify the abrupt growth of level sets 70–80 and 80–90, and the stagnation of the 90–100 level set from 1867 to 1876.

An aggregated index measuring the mean set derivative of a level set K(t) is

which, in the application of French schooling, is approximated by

Table 1 represents that observed mean absolute set derivative by decile and by date. This value gives the overall mobility of the level set, whatever the direction. It reveals two parallel waves, one for boys and one for girls, covering deciles 30–40 to 60–70 in 1837, deciles 40–50 to 70–80 in 1850, deciles 70–80 to 90–100 in 1867, and decile 80–90 in 1876. The possibility of revealing these waves retrospectively helps to vindicate the choice of deciles over larger quantiles. The waves not only move along the distribution of deciles but also swell gradually between 1837 and 1867, to die away in 1876. This phenomenon attests to the acceleration of schooling brought about by the resolute intervention of the state to complete and possibly supplant the education supply of private and church schools.

Table 1 Observed Mean Absolute Values × 100 of |ϕ|

	Boys				Girls
	1837	1850	1867	1876	1837	1850	1867	1876
0–10	10	5	—	—	4	5	30	—
10–20	15	5	13	—	5	8	9	—
20–30	8	8	9	2	3	3	16	1
30–40	255	6	9	8	244	5	7	6
40–50	15	197	10	4	15	248	9	3
50–60	326	500	41	3	382	524	9	1
60–70	296	38	12	8	199	47	23	9
70–80	31	183	1579	2	34	232	1701	10
80–90	9	2	1586	13	24	12	1268	5
90–100	12	28	208	5	17	14	105	5

4.2. Influence of Demography and of Investment on Mutations of Level Sets

The set derivatives of sets are likely to be determined by the demography and economy of investment in schools and in teachers. A simple regression of the set derivative on economic variables is unsatisfactory because the decision of investment is likely to respond to a conscious policy rather than to result directly from economic development. Schools in 19th-century France came from decisions centralized in the Ministry of Education rather than from local initiatives, as may be the case in other countries. Comparing set derivatives of sets with those that would result from plausible policies allows me to investigate the structure of investment decisions in the observed set derivatives, in addition to demography which modifies counts independently of schooling policy.

One policy could be to open new schools and to fill schools such as to increase the total number of schooled children as a constant fraction of the needs (Policy 1):

where w ₁(t) is constant for all départements. This solution, for a population growth rate equal to the mean population growth ρ over a given five-year period, allows an analytical solution to Eq. (2), giving, after derivation with respect to time and to space (superscript s for sex and subscript i for département omitted):

where ϕ₁(t, i) is the set derivative under policy 1 of the level set covering département i at time t, ∇ is the gradient operator, x ₁ is longitude, and x ₂ latitude.

Three other key policies come from optimizing an interesting criterion:

	either maximize the mean schooling incidence at time t (Policy 2 yielding set derivative ϕ2(t, i)):
	minimize the sum of variances of schooling incidences over the territory at time t (Policy 3 yielding set derivative ϕ3(t, i)): with the mean schooling incidence at date t for sex s—this corresponds to a policy of convergence, a pattern explored by Diebolt (1999); or
	minimize the gap between boys and girls on a local (départemental) basis (Policy 4 yielding set derivative ϕ4(t, i)):

This was the policy initiated by Ministers of Public Education Frédéric de Falloux, in the Falloux law of 1850, which required each township (commune) to open a school for girls, and Victor Duruy, who introduced the Duruy law of April 10, 1867, to develop girls' schools and offer free school access for boys and girls in townships that solicited it.

For estimating the outcomes of each of these four policies at date t ₂ = 1850, 1867, 1876, I started from the previous date t ₁ = 1837, 1850, 1867, respectively, with the actual data. The budget constraint at time t was taken as proportional to the total number of pupils actually observed at date t. In each case, I obtained the optimal solution by simulated annealing, a stochastic optimization method in large dimension. The dimension is here equal to the total number N of départements, which was 86 in 1850, 89 in 1867, and 87 in 1876. Kirkpatrick, Gelatt, and Vecchi (1983) showed that simulated annealing converges to the globally optimal solution, provided a proper schedule is used. Moreover, I implemented many restarts to reduce the possibility that numerical approximation did not yield a local minimum.

In the regression of ϕ on ϕ₁, ϕ₂, ϕ₃, and ϕ₄, the influences of the total number of pupils per school, of the boy-girl schooling gap, and of the difference to the national mean schooling incidence are not added as covariates because they are already contained in the set derivative modulus ϕ _j , j = 1, 2, 3, 4, which are more convenient for the regression of ϕ, being themselves set derivatives and not proxies. Introducing life expectancy and fertility—migration concerns mainly only the départment of Seine (with the city of Paris)—and schooling incidence directly into the regression leads to lack of identifiability of the system, but they intervene indirectly, through the regressions of ϕ _j , j = 1, 2, 3, 4, which are endogenous. The population growth rate is a consequence of mortality and fertility and for colinearity reasons does not appear among the covariates. The influence of epidemics and war then is conveyed not only through the variable “life expectancy” but also through the variable “fertility,” which was depressed during the Franco-Prussian War, especially in eastern France (Bonneuil, 1997). In the mostly rural economy of 19th-century France, the variation of life expectancy also captures the seasonal variation of agricultural productivity by type of prevailing local economy. Fertility also captures part of familial circumstances, which would interfere with the decision to send children to school.

The endogenous variables ϕ _j , j = 1, 2, 3, 4 are regressed on covariates which are rendered stationary to get rid of temporal autocorrelations. The usual procedure is to consider the first difference ΔX = X(t + h) − X(t) for the variable X(t) at two consecutive dates of observation t and t + h. Equation (5) indicates that it is better to work with growth rates, which has the same power of reducing temporal auto-correlation in monotone trends (in fact exponential trends, but there are few dates available, so it makes no difference from an econometric point of view). Consider the operator Δ as rather denoting an approximate growth rate: ΔX = (X(t + h) − X(t))/(hX(t)). Moreover, the ϕ and ϕ _j , j = 1, 2, 3, 4 are themselves differentials and are to be compared with first differences or with growth rates. As the statistics of number of schools exists only in 1850, 1867, and 1876, only three points in time are available. Differencing yields two points, 1850 to 1867 and 1867 to 1876.

The set derivative modulus ϕ₁ corresponding to the building of schools as a constant proportion of the needs is endogenous and regressed on schooling incidence and on the total number of unschooled children. The set derivative modulus ϕ₂ corresponding to the maximization of the mean schooling incidence is endogenous and regressed on the schooling incidence. There are no variables available really relevant to put in the regression of the set derivative modulus ϕ₃ corresponding to the minimization of the variance of schooling incidences. Then ϕ₃ can be considered as an exogenous variable. The modulus ϕ₄ corresponding to the reduction of the boy–girl difference of schooling incidences is regressed on this latter variable. The total number of unschooled children is endogenous and regressed on the total number of schools, the total number of pupils per school, life expectancy, and fertility, because mechanically, a high fertility and a low mortality are likely to increase this number. The total number of schools is endogenous and regressed on the proportion of urban population—does there exist a preference for cities?—on the boy–girl gap—do authorities build schools for girls rather than for boys?—and on the mean number of schools in the neighboring départements, to account for spatial autocorrelations. A spatial correlation would mean that the building of schools would respond to regional rather than local projects. It makes sense for this variable, because it stems from administrative decisions, but little sense for variables which did not respond to a policy of homogenization across the national territory, such as the total number of unschooled children or the total number of pupils per school. I considered this latter variable as covariate, meaning that schools would be built to reduce the population per existing school. However, this regression, for all periods and both sexes, always yields a negative coefficient, which is not meaningful and shows that the causal link is the other way round. (It is the task of the econometrician to impose the causal links to estimate.) I also considered the total number of unschooled children among the covariates on the assumption that new schools would be built where they were most needed. The coefficient is negative in the regression from 1867 to 1876, which makes no sense, and positive from 1850 to 1867, which is coherent with this policy in this period. The demographic variables influence the total number of children, not directly the total number of schools, and then must appear as such. I have no data on teachers' costs, but this variable is captured by the total number of schools because schools and teachers went together and teachers were paid on a national basis. The total number of pupils per school is endogenous and should depend on the total number of schools and on mortality and fertility; the schooling incidence, finally, is also endogenous and results from the identity of Eq. ( 5).

One possible variable is the availability of transport means to schools, but the 19th-century transportation revolution either concerned cities (first with horse-drawn tramcars, then electrical ones after 1870 in Paris), or consisted in steam trains which were of little use for children to go to school every day (Lepetit, 1986). Moreover, if people had benefited from more transport availability to schools, the increase in the total number of schools should have slowed down, and we observe the opposite. Thus, local transport means from home to schools is not likely to have varied in this period. Schooling was made compulsory only in March 1882 with Jules Ferry's law, and prior to this date parents could keep their children away from school. But this changes nothing to the question of the observed dynamics of level sets of schooling incidences, and does not change the policies of school supply which were decided at the national level. The attitude of parents toward school and the spatial dynamic of level sets are not the same question.

It is tempting to consider the process made of the eight mentioned endogenous variables as multispell, where the spells would be the two points in time 1850–1867 and 1867–1876. However, there is no reason why the process would be the same in the two periods. On the contrary, the period 1850–1867 corresponded to the advent of Second Empire with important reforms of public education (the laws of Falloux in 1850 and Duruy in 1867), and the period 1867–1876 to its fall, to the Franco-Prussian War, and to the reorganizing of the country under the Third Republic. I then estimate a system of 32 simultaneous equations, eight for 1850–1867 and eight for 1867–1876 for each sex:

where S is the system, for each sex and each period:

where , n is the total number of unschooled children, l ₀ is life expectancy at birth, I _f is a fertility index (the “Coale” index; Bonneuil, 1997), is the mean total number of schools in neighboring départements, and a _ij , i = 0, …, 7, j = 1, … are parameters to be estimated. Encompassing these equations in a single system allows the possibility to test equalities of coefficients applying in different periods, and compare the mutations of level sets between the two periods. The regression was done with the procedure SYSLIN of SAS.

The estimation of Eq. (14) is done jointly for 1850–1867 and for 1867–1876 and for both sexes. The estimates for boys in 1850–1867 is:

where the asterisk (*) denotes significance at the 5% level and where numbers in parentheses are standard deviations. This system (15) shows that the observed set derivatives of sets of schooling incidence are associated with the maximization of schooling incidence for boys, and that this variable is not significantly related to other available variables. For girls in 1850–1867, the estimates are:

These set derivatives in System (16) are significantly associated with the boy–girl gap, in coherence with the Falloux and the Duruy laws. In this period, then, the level sets of schooling incidence seemed to carry on a general policy of raising the education level at the national level for boys, which went through the reduction of the boy–girl discrepancy. In 1867–1876, the estimates of Eq. (14) for boys are:

The policy of reduction of the boy–girl gap affects (coefficient −1.14 of ϕ₄ in Eq. (17)) the opening of new schools for boys, resources being constrained, but the objective of improving schooling incidences remains (coefficient 1.15 of ϕ₂ in Eq. (17)). The modulus ϕ₂ is higher for départements with low schooling incidence and lower for those with a high incidence, reflecting the willingness of the Ministry of Education to invest in locations where schooling was most needed. The schooling rate results from the exact account of Eq. (5). Then ϕ₂ positively correlated with ϕ depends on the growth rate of the total number of schools, on the total number of pupils, and on demography. Through the first variable, the locations of investment into new schools form pockets of territory (for example Brittany or the Loire Valley, as shown in Figures 3 and 4) rather than archipelagos of départements. This spatial arrangement produces spatial autocorrelations, which are captured by the variable “mean number of schools in neighboring départements.” Demography intervenes mechanically through the second variable with a positive coefficient: the longer children lived, the more likely they were to be in fuller schools, and conversely, an epidemic was likely to deplete the school population. The adjustment consisting in opening new schools must catch up with the changing demographic landscape. In 1867–1876, the estimates of Eq. (14) for girls are:

The reduction of the boy–girl gap is no longer significantly associated with ϕ, which is negatively correlated with ϕ₂. This apparently strange result comes from the targeting of schools for girls in cities to the detriment of the territory as a whole. This fact is reflected by the positive coefficient of the proportion of people living in cities in the regression of the total number of girls' schools. The policy of reduction was still at work, but efforts were concentrated in cities. Consequently, rural areas were relatively deprived, which yields a negative coefficient for ϕ₂ on ϕ. We still have the mechanistic relationships of demography and of the total number of schools on the total number of pupils per school.

5. CONCLUSION

In social sciences, the changing spatial structure of a variable can respond to controlled policies rather than to diffusion models inherited from physics and in use to describe the spread of an epidemic or a cultural trait. To capture the changing conditions of a spatial structure such as level sets (and to go beyond the mere description of the schooling incidence itself, which gives the state of the system and not the spatial change) I suggested first to introduce derivatives of sets and mutational equations. The key concept is the set derivative, or morphological transition. It allowed me to associate a velocity to each point of the territory, and to infer the set of velocities of a level set; it allowed me to go beyond the usual linear interpolation on which the change is usually conjectured.

The case of schooling is a counterexample of classical diffusion because neighboring locations have no reason to behave similarly if no investment is made and is an example of a controlled transformation of a space. I wrote down the equations at work in the construction of the schooling incidence. I computed the set derivatives of level sets of schooling incidence from smoothing techniques and using a unique data set of a schooling revolution in progress. I drew maps of schooling incidence with their set derivatives at four dates and for both sexes. As soon as the change was no longer linear, as in the case of France before and after the Franco-Prussian War of 1870–1871, the linear interpolation is misleading for informing us on the conditions of change. The morphological transition in 1867 is captured by the modulus of set derivatives ϕ, which describe the course of schooling from the viewpoint of 1867 but which was interrupted by the war of 1870–1871.

I computed the set derivatives which would be obtained under four key policies. Notably, I could obtain analytical expression in the case of constant fraction of the needs. The search for determinants of the observed set derivatives was done through a multiprocess regression, which showed the role played by the ambition to allocate new schools so as to maximize the overall mean schooling incidence while reducing the gender gap on a local basis. Spatial convergence turned out to be a consequence of these policies rather than an objective. This result does not appear from the study of schooling incidences, because, once again, these are quantities cumulated over time, and this is one advantage of the study of set derivatives of level sets. The wave phenomenon revealed by the computation of mean absolute values of set derivative modulus, with its acceleration and its dying away in 1876, is another result hard to observe on the basis of schooling incidences alone.

Morphological transitions are then adequate to inform us on change, especially in historical time which does not conform to the regular processes of diffusion in physics or epidemiology. Morphological transitions are designed to capture the dynamics of sets in the social sciences or in biology, of which level sets are an exemplary case.

Notes

¹With imsl_f_scattered_2d_interp of imsl C.

²With routines bs3in and bs3dr of fortran imsl.

APPENDIX A: TRANSFORMATIONS OF SETS

Figure 1 shows an example of an attainable set under a dynamic F of Eq. (1) from a given state x ₀ or alternatively from a given set K ₀. The set of solutions stemming from x ₀ is denoted

where x(.) is a trajectory with t varying. The associated attainable set (represented on Figure 1, left-hand side) is obtained as

and the attainable set of a given set K ₀ is

For F a Lipschitz set-valued map from the metric space X to X with compact convex values, the map θ _F defined by

is a morphological transition of the space of nonempty compact subsets of the finite dimensional vector space X. If, in addition,

where “dist” is an appropriate distance (namely the Pompeiu-Hausdorff distance (Aubin, 1999, pp. xxv), then θ _F is the mutation in the forward direction 1.

Level sets are particular sets. For a given value λ ∈ R, the λ-level set is defined as

for f a smooth nondegenerate function.

Aubin (1999) showed that for a differentiable function f : R ⁺ × X → R such that:

1.	∀ t ≥ 0, and are Lipschitz on a neighborhood N(t) of K(t)
2.	∃ η > 0, M ≥ η such that ∀ (s, x) ∈ [t, t + 1] × N(t), and
3.	∀ t ≥ 0, K(t) is compact,

then if K(t) : = {x ∈ X such that f(t, x) = λ} is not empty, the Lipschitz map ϕ(t) defined as

belongs to the mutation of the tube K(.) at t in the forward direction.

The restriction of the mutation ϕ(t) to K(t) is:

where is the unit normal to K(t) at x. The proof is in Aubin (1999, pp. 145–146).

APPENDIX B: COMPUTER PROGRAMS USED AT EACH STAGE TO CONSTRUCT THE VECTORS

	Prepare a file with year, identification of spatial division, coordinate of the chief city, value of the variable (here the schooling rates for boys and for girls).
	Run a spline program which builds a rectangular grid surface f(t, x) in a 3D space at given time t: two spatial coordinates and the variable under study (the schooling rate for boys for example) from the map of the country and its scattered points (with imsl_f_scattered_2d_interp of imsl C).
	Gather the time series of surfaces f(t, x) and compute the differentials and at regular points f(t, x) of the boundary of each geographical subdivision, with the help of bs3in and bs3dr of Fortran imsl for example.
	Compute ϕ(t)(x), the modulus of the set derivative at this point of the boundary of the spatial subdivision (here the French départment). To get a readable map, take the mean value and the mean direction over the boundary of the départment.