Explaining cooperation in the finitely repeated simultaneous and sequential prisoner’s dilemma game under incomplete and complete information

ABSTRACT

Explaining cooperation in social dilemmas is a central issue in behavioral science, and the prisoner’s dilemma (PD) is the most frequently employed model. Theories assuming rationality and selfishness predict no cooperation in PDs of finite duration, but cooperation is frequently observed. We therefore build a model of how individuals in a finitely repeated PD with incomplete information about their partner’s preference for mutual cooperation decide about cooperation. We study cooperation in simultaneous and sequential PDs. Our model explains three behavioral regularities found in the literature: (i) the frequent cooperation in one-shot and finitely repeated N-shot games, (ii) cooperation rates declining over the course of the game, and (iii) cooperation being more frequent in the sequential PD than in the simultaneous PD.

KEYWORDS:

• Cooperation
• incomplete information
• prisoner’s dilemma
• repeated play
• sequential play

1. Introduction

Social dilemmas are situations in which individually rational and selfish behavior leads to undesirable outcomes for all involved. Such outcomes can only be averted if individuals cooperate, neglecting their immediate material interests. Explaining the (non)occurrence of such cooperation is a central issue in the behavioral sciences (e.g., Buchan, Croson, & Dawes, 2002; Dawes, 1980; Fehr & Gächter, 2002; Fehr & Gintis, 2007; Kollock, 1998; Willer, 2009), and the two-person prisoner’s dilemma (PD) game arguably is the model most used to examine it (e.g., Axelrod, 1984). The PD is a binary form of the more general public goods game (e.g., Dijkstra, 2013; Ledyard, 1995). Famous examples of social dilemmas are the tragedy of the commons (Hardin, 1968; Ostrom, 1990) and trench warfare in WWI as described and analyzed by Axelrod (1984). Everyday life is rife with social dilemmas, from efforts to reduce pollution or maintain a valuable community resource (Bouma, Bulte, & van Soest, 2008) to attempts at overthrowing oppressive political regimes (Opp, Voss, & Gern, 1995). In all these cases, all individuals would prosper if the collective goals were reached, but no individual has sufficiently strong incentives to contribute to their achievement.

The traditional theoretical approach based on the assumptions of rationality and selfishness (e.g., Olson, 1965) predicts no cooperation to occur in social dilemmas of finite duration. Whenever the individuals involved accurately foresee the end of their relations (“the end of the game”), the theory predicts that no one will ever cooperate (i.e., everyone will always “defect”). Moreover, the actual duration of the social relations is predicted not to matter for cooperation as long as the exact duration is common knowledge. However, in many observed social dilemma situations of finite duration, be it in the laboratory or in observational studies, cooperation is frequent or even very frequent (Sally, 1995).

Many explanations of this unexpected degree of cooperation modify the model of the individual agent such that (s)he prefers mutual cooperation over defecting on a cooperating partner. One prominent explanation is the social exchange heuristic (Dijkstra, 2012; Kiyonari, Tanida, & Yamagishi, 2000; Simpson, 2004; Yamagishi, Terai, Kiyonari, Mifune, & Kanazawa, 2007). Through the heuristic, individuals come to perceive mutual cooperation as a more desirable outcome than defecting on a cooperating partner. After having thus transformed the payoffs, individuals are assumed to choose their strategies rationally. There is experimental support for the claim that experimental subjects evaluate mutual cooperation as more desirable than successful cheating (Kiyonari et al., 2000; Rilling et al., 2002), and the model we present in this article is an elaboration of this notion (see also Dijkstra & van Assen, 2013).

Changing assumptions in the model of the agent to explain observed outcomes attracts the justified criticism of “assuming what needs to be explained.” In this critical view, micro-assumptions are too easily adapted to render macro-outcomes intelligible, thus evading the true intellectual challenge of explaining cooperation between selfish individuals. Although we generally subscribe to this tenet of scientific parsimony (cf. Occam’s razor), we also believe science should offer true explanations of observed phenomena (cf. Watts, 2014). In light of observational and experimental evidence on cooperation in (prisoner’s) dilemmas, we find it very hard to maintain that theoretical explanations modifying the micro-model of the agent are always ad hoc. Rather, such explanations accord with the criterion of conceptual integration advocated by Tooby, Cosmides, and Cosmides (1992), which states that no scientific explanation should be based on assumptions that are clearly falsified in other fields of inquiry. The universal selfishness assumption is such an assumption. Additionally, several authors offer explicit arguments as to why the assumption of selfishness should be modified. In particular, Yamagishi et al. (2007) justify the social exchange heuristic by arguing that in the human ancestral environment, mistakenly assuming that a social relationship was of indefinite length (when it was in fact one-shot) was likely a much less grave mistake than mistakenly assuming a one-shot relation (when it was in fact a long-lasting one). Since the very large majority of social relations in the human ancestral environment were of indefinite duration, a hard-wired heuristic over-valuing mutual cooperation was adaptive. In line with this, Clark and Sefton (2001, p. 62) propose that “subjects may misperceive themselves to be playing a repeated game,” when interpreting their experimental results. Indeed, classical anthropology provides evidence for the claim that anonymous, one-shot interactions and isolated exchanges are historically recent (Malinowski, 1922; Mauss, 1923–1924), and contemporary observational work by Diekmann and colleagues (Diekmann, Jann, Przepiorka, & Wehrli, 2014) suggests that strong reciprocity (Fehr & Gintis, 2007) and altruistic preferences are part and parcel of the human constitution.

In our model, we will assume agents to make their decisions as described by the social exchange heuristic, which involves a reevaluation of the mutually cooperative outcome. We do not change any other assumptions of the standard rational model. In particular, we will assume agents are fully rational expected utility maximizers who rationally update their beliefs. We readily concede that these, too, are empirically questionable assumptions. We retain these assumptions for reasons of analytical tractability, and because we want to examine if we can accurately model behavioral regularities in one-shot and repeated play of the PD by one minimal change to the standard model (i.e., incorporating the social exchange heuristic).

Even if a preference for mutual cooperation makes the occurrence of cooperation in finitely repeated interactions understandable, a new problem presents itself: how do people know whether or to what extent their interaction partners prefer mutual cooperation? We argue that they do not know. Given that people are heterogeneous in terms of their preferences and that preferences are not directly observable, all an individual knows for sure is her own preference for mutual cooperation. She is uncertain about the preferences of her interaction partner. This state of affairs gives rise to an assurance problem: individuals preferring mutual cooperation over defecting on a cooperating partner may not dare cooperate, feeling too uncertain about the preferences of their partners. We say that individuals preferring mutual cooperation over successful cheating have “assurance game preferences,” because for them the game is an assurance game if they play against each other. The assurance problem thus arises from the incompleteness of information on the other player’s preferences, i.e,. they do not know the other player has assurance game preferences as well. Famously, Kreps, Milgrom, Roberts, and Wilson (1982) show how cooperation between two rational and selfish individuals can be sustained up to the last few stages of a finitely repeated PD game if there is incomplete information concerning the rationality of one or both of the partners. Based on experiments on finitely repeated PDs, Andreoni and Miller (1993) conclude that observed behavior is largely consistent with the incomplete information account.

A crucial feature of incomplete information is that individuals can update their information based on observations. Thus, uncertainty about the preferences of one’s partner can be reduced by drawing inferences from the partner’s behavior. This suggests that the assurance problem can be mitigated or perhaps solved by repeated interaction between the same two partners, or by the fact that one partner can observe the other’s behavior before choosing herself. In this article we, therefore, build a theoretical model of how individuals in a finitely repeated PD with incomplete information about their partner’s preference for mutual cooperation decide about cooperation. This model allows us to study the assurance problem in repeated and sequential PDs.

Apart from showing how repetition and sequential choices may solve the assurance problem, our model accounts for three behavioral regularities found in the literature, as follows: (i) the frequent occurrence of cooperation in one-shot and finitely repeated N-shot games (e.g., Sally, 1995), (ii) cooperation rates declining over the course of the game (Cooper, DeJong, Forsythe, & Ross, 1996; Dawes & Thaler, 1988; Fehr & Gächter, 2002), and (iii) cooperation being more frequent in the sequentially played PD (where one player’s decision is revealed before the other chooses) than in the simultaneously played PD (Hayashi, Ostrom, Walker, & Yamagishi, 1999; Yamagishi et al., 2007; Kiyonari et al., 2000, but not found by Bolle & Ockenfels, 1990).

Our model has three distinctive features. First of all, it makes empirically grounded assumptions about players’ preferences for mutual cooperation and recognizes that individuals are heterogeneous in this respect. Second, preferences for mutual cooperation are continuous, allowing the modeling of a diverse and continuous set of “player types.” Third, players know their own preferences but are uncertain about the preferences of their partner. Our model explains many observed aspects of cooperation in finite PDs with what we believe is a minimal and justifiable change in assumptions compared to the standard rational selfishness approach.

With our model, we explore the possibilities for cooperation and the solution of the assurance problem in one-shot PDs (players making a single decision), two-shot PDs, and (finite) N-shot PDs, in which players play with the same partner throughout. Our model allows us to distinguish the problems of assurance (due to uncertainty about one’s partner’s preferences) and efficiency (concerning the expected material payoffs). In addition, we address the issue of the move structure in a PD: what changes if one individual gets to decide about cooperation after she has observed the decision of the other? Repetition and move structure affect cooperation, i.e., solving the assurance problem, since both affect learning; repeated interactions and observations of what one’s partner did in the current interaction allow individuals to draw inferences about the preferences of the partner.

In the next section, we explicate our model formally, but here we give a verbal description. Individuals (henceforth called players) playing a PD game put a “premium” on the mutual cooperation outcome. This premium is a psychological payoff they get in addition to the material payoffs of the game. Players know their own premium but are uncertain about the premium of their partner. Thus, the premium is private information. Moreover, the premium can have any real value and can thus also be negative. This allows the modeling of various types of players, ranging from spiteful ones (players disliking mutual cooperation to the extent of preferring mutual defection over it) to altruistic ones (players who have a strong taste for mutual cooperation, who cooperate even though the probability that the other player cooperates is very small), passing through players with standard PD preferences (with defection as their dominant strategy) and players with assurance game preferences (who prefer mutual cooperation over successful cheating). Given their preferences, we assume players choose their strategies rationally. Learning about the premium of the partner based on the partner’s behavior is also done rationally.

2. The relation between our model and previous models

Many models explain cooperation in the PD by changing the preferences of the agents. In this section, we briefly discuss the most important contributions and relate them to our model.

Consequentialist (aspects of) models assume agents’ utilities solely depend on the final payoff vector, whereas what we dub procedural (aspects of) models assume agents value other aspects of the outcome, such as the behaviors leading to the outcome, the (imputed) intentions of players, etc. For instance, Andreoni (1990) assumes people may positively value others’ payoffs as well as their own (pure altruism; consequentialist) or positively value the act of cooperating itself (warm-glow giving; procedural) (see also Dawes & Thaler, 1988). Andreoni’s (1990) model assumes complete information model and is applied to one-shot public goods game, calibrating it on data of charitable giving.

An important class of consequentialist models assume players have an aversion to inequality; For instance, Fehr and Schmidt (1999) build a model in which players’ utilities depend negatively on self-centered payoff inequality. They analyze a set of one-shot games, and compare the simultaneous and sequential PD in a complete information context. Bolton and Ockenfels (2000) build a similarly consequentialist model of inequality aversion, fitting it to a list of stylized facts from many experimental games. Their analysis is also confined to one-shot games. Tutic and Liebe (2009) build a consequentialist model, assuming that a player’s degree of inequality aversion depends on pre-existing status differences between players. These authors analyze one-shot games with complete information.

An important class of procedural models assume players’ utilities depend on (beliefs about) other players’ preferences or intentions. Rabin (1993) builds a model of intention-based utilities for two-player normal form games, in which a player’s utilities depend on her beliefs about the intentions of the other player. The intentions ego attributes to alter are dependent on the beliefs ego has about (i) the behavior of alter, and (ii) the beliefs of alter concerning ego’s behavior (second order beliefs). Rabin (1993) implicitly assumes complete information regarding the degree to which players value others’ intentions (at any rate, he does not explicitly model incomplete information), and he does not analyze repeated play. Dufwenberg and Kirchsteiger (2004) build a similar intention-based model applicable to general extensive form games. They analyze a number of games, explaining a set of stylized facts. As in the Rabin (1993) model, the uncertainty (asymmetric information) concerning the “kindness parameters” of other players is not explicitly modeled.

Levine’s (1998) model has both consequentialist and procedural features. In it, players are assumed to positively (altruism) or negatively (spite) value payoffs for others. In addition, players’ utilities depend on (beliefs about) the altruism of others. The altruism (spite) parameter is explicitly modeled as being private information, but the parameter that weights the degree of others’ altruism (spite) is not. The model is fitted to a set of experimental datasets, culminating in an estimated distribution of the altruism (spite) parameter. Only one-shot games are analyzed. Falk and Fischbacher (2006) also propose a model with both consequentialist and procedural (intention-based) utility components. They assume complete information regarding the social preference parameters, and base their model on questionnaire evidence of ‘kindness evaluations’ in bilateral distribution decisions. These authors discuss a set of games, including the sequential PD, but do not compare the latter to the simultaneous PD. In the spirit of Rabin (1993) and Levine (1998), Nax, Murphy, and Ackermann (2015) also build a model of interactive preferences, in which the utility of ego depends on the preferences of alter. They analyze their model in the context of a repeatedly played public goods game, calibrating it on their experimental data. The repeated nature of the game is not analyzed strategically, but is handled by assuming a fixed updating (“learning”) rule. Players are assumed to best respond in each round given their beliefs, as if each round were a separate one-shot game.

Finally, we mention a number of important articles offering experimental evidence (sometimes combined with theoretical modeling) on the operation of social preferences in social dilemmas. Clark and Sefton (2001) report an experimental study of one-shot sequential PDs. They reject explanations of their data in terms of altruism or warm-glow giving, favoring a reciprocity explanation instead. Moreover, reciprocation becomes less likely in their data, as it becomes more expensive. Analyzing experimental behavior in a finitely repeated public goods experiment using a random utility model, Palfrey and Prisbrey (1997) also reject altruism explanations of the data, but do find (limited) evidence of warm-glow giving, in addition to a fairly large impact of sheer decision errors. The analysis these authors report does not account for the strategic aspects of repetition. Aksoy and Weesie (2013) study one-shot asymmetric, simultaneous PDs. These authors consider theoretical models in which utilities depend on the outcome for the other player (consequentialist preferences, such as inequality aversion) and on the behavior of ego (procedural). Based on their experimental data, they reject the inequality aversion model and find support for their social orientation (“altruism”) and normative model (on norms in this context see also Bichierri, 2006).

The article closest to ours is no doubt Bolle and Ockenfels (1990). One of their micro-level models (indeed, the one best fitting their experimental data) is identical to ours. These authors theoretically and empirically compare one-shot sequential and simultaneous PDs, predicting (but not finding) higher cooperation rates in the former than in the latter, as we do. However, contrary to our approach, they do not allow for the existence of spiteful players, do not identify the assurance problem; nor do they separate it from the efficiency problem or analyze repeated play.

We present a model specifically for the two-person PD. Contrary to the other models presented in this section, ours partly follows a heuristics approach. The heuristics approach to decision making assumes that players have modular brains (Barkow, Cosmides, & Tooby, 1992; Gigerenzer & Selten, 2001; Gigerenzer & Todd, 1999) containing “scripts” for important, recurrent decision situations. In particular, the argument of the social exchange heuristic is that situations of repeated social exchange constituted an important class of adaptive problems in the human ancestral environment, to such an extent that the development of a special cognitive module has been adaptive. These social exchange situations are PD structured (e.g., Barkow et al., 1992, Chapter 3), and especially the fact that the vast majority of ancestral human social exchange interactions were of indefinite duration has made a (positive) re-evaluation of the cooperative outcome adaptive. Note that such a model is not consequentialist, since utilities depend on the chosen “strategy profile” (i.e., combination of actions, or outcome) rather than on (properties of) the resulting payoff vector.

Overall, we give a fuller treatment of the PD along the dimensions of “move structure” (sequential vs. simultaneous) and repetition (one-shot, two-shot, N-shot) using an incomplete information model, than any of the other “alternative preference” models. Ours is the only model we know of separating the assurance problem and the efficiency problem, leading to the proposition of a new experimental test (see the Conclusions section). Finally, the fact that multiple models can explain (different aspects of) cooperation in the PD is in itself a good thing. We concur with Ullmann-Margalit (1977, p. 17), when she writes that “[a]ny reduction of one theory (or type of theory) to another carries the prospect of being a clarificatory achievement …”

3. Game, preferences, and equilibrium concept

Table 1 presents the basic PD we investigate. Each of two players (1 and 2) decides to either cooperate (C) or defect (D). By cooperating, player j incurs a cost of 1, and this cooperative act yields a benefit of a to both players i and j. This yields the payoffs denoted by Arabic numerals and Latin letters in Table 1. In each cell, the expression before the comma denotes the payoffs of player 1, and the expression after the comma denotes the payoffs of player 2, with denoting the premium for mutual cooperation for players . We impose , which for yields the classic PD structure where choosing D dominates choosing C.

Table 1. The payoff matrix of the stage game prisoner’s dilemma with premium for mutual cooperation ().

		Player 2
		C	D
Player 1	C	,	a, a + 1
	D	a + 1, a	1, 1

The premium’s interpretation is that upon mutual cooperation {C, C} each player j receives a “psychological payoff” of in addition to the material payoff of . This allows us to model players with standard PD preferences (), assurance game preferences (), and spiteful players who dislike mutual cooperation (). Players with assurance game preferences prefer mutual cooperation over defecting on a cooperating partner, and have PD preferences otherwise. Spiteful players prefer mutual defection over mutual cooperation and have PD preferences otherwise. Note that “almost pure altruism” is captured by our model through high values of theta (). Such high values render cooperation the most attractive strategy under even the slightest probability that the partner will cooperate.

Throughout the article, we assume that players have complete information on the material payoffs of the game and that the premium for mutual cooperation is private information. Thus, player j knows with certainty the value of but is uncertain (i.e., has incomplete information) about the value of player i. We model this uncertainty by introducing a common knowledge cumulative distribution function on the thetas in the population, where is the probability that the theta of player i does not exceed some real number. We assume that is continuous and that the density is strictly positive for any . The fact that is continuous implies that in our analysis we do not have to reckon with mixed strategy equilibria, since any type that is indifferent between cooperating and defecting has probability 0 of occurring. Pairs of players are randomly drawn from the population, and each player knows her own theta and . In our theoretical propositions below, we will assume can be any real number. However, in the two running examples, we limit the range of possible values of for computational convenience. In these examples, we highlight the consequences this has for the existence of player types.

In the simultaneous move game players 1 and 2 decide on what to play (C or D) without knowledge of the choice made by the other player. In the sequential move game player 1 (the “first mover”) chooses without knowing player 2’s move, but player 2 (the “second mover”) learns player 1’s choice before making her own. We study both move structures under different temporal regimes: the one-shot game (where the game is played only once), the two-shot game, and the finitely repeated N-shot game. The payoffs in the two-shot and N-shot game are the undiscounted sums of the payoffs earned in each repetition (displayed in Table 1).

For each possible value of , a strategy of player j specifies what player j should do (C, D, or a probability mixture of C and D) in each repetition of the game, for each possible history of the game until that point. A Nash equilibrium in this game is a pair of strategies such that neither player can earn a strictly higher expected payoff by unilaterally changing her strategy. In this article, we employ a refinement of Nash equilibrium called Bayes-Nash equilibrium (BNE). A BNE is a Nash equilibrium with the additional requirement that players update their beliefs about the premium of the other player rationally using Bayes’ rule, whenever possible. Mutual defection in each round of the game (whether played simultaneously or sequentially) is an equilibrium for any P(). With our model, we investigate conditions under which equilibria exist such that cooperation occurs in at least one round. In the next section, we present our analysis and its results. Formal derivations and proofs are relegated to the Appendix as much as possible, and the main text gives the intuitions.

4. One-shot game

4.1. Simultaneous play and the assurance problem

Suppose there is a BNE and let denote the equilibrium probability that player i cooperates. Player j will cooperate if and only if given the expected payoffs of cooperation are at least as large as the expected payoffs of defecting. Dijkstra and Van Assen (2013) prove that this condition gives the result that under each BNE and for each player there is a threshold such that players j with defect and others cooperate with , and

(1)

(see Appendix for derivation).

Dijkstra and Van Assen (2013) show that implies , which in turn implies . In other words, provided the population contains players with PD preferences (i.e., ), there exists an assurance problem in the simultaneous one-shot game under incomplete information; some players j who prefer mutual cooperation over successful cheating (those with assurance game preferences, i.e., with ) choose D nonetheless.¹ Consequently, some pairs of players who both prefer mutual cooperation over successful cheating, fail to cooperate. Note that under complete information (when players’ thetas are common knowledge) all pairs of assurance game players would cooperate. However, as we will see below, this does not imply that efficiency under complete information is always higher than under incomplete information.

We define efficiency as or the surplus of the players’ expected material payoffs in the game (E(X)) over the minimum average material payoff (1, corresponding to mutual defection), over the total range of game’s average material payoffs (where the maximum payoff, 2a, corresponds to mutual cooperation). Note that we do not include the psychological payoffs in the definition of efficiency. The reason is that we want to express the costs and benefits of the incompleteness of information in terms of the standard (material) PD payoffs. Let and , with and being the proportions of players cooperating in the game under incomplete and complete information, respectively. In the Appendix we show that efficiency is higher under incomplete information than under complete information if P₁ > 0 and P₂ approaches 0. In other words, the efficiency of the game under incomplete information exceeds that of the game under complete information if there is a substantial proportion of players with spiteful or PD preferences (P₁), and simultaneously the proportion of players with assurance preference that do not cooperate in the equilibrium under incomplete information (P₂) is small. The intuition is that if the proportions of cooperating players under both information conditions are sufficiently similar (P₂ is small), a weighted sum (weights sum to 1) of all four cells of Table 1 (under incomplete information) yields a higher average expected material payoff than a weighted sum of the diagonal cells only (under complete information).

To illustrate the nature of the assurance problem and efficiency of the game with and without complete information, consider Example 1 from Dijkstra and van Assen (2013). Whereas efficiency in Example 1 is still higher under complete than incomplete information, later on we will slightly modify it to Example 2 where efficiency is highest under incomplete information.

Example 1. Suppose , and let be uniform on the unit interval. Suppose the one-shot game is played simultaneously. Then there is a pure strategy equilibrium in which both players defect.

In addition, there is a single symmetric, pure strategy BNE with positive cooperation probability of ½, i.e., .²

The parameters in Example 1 mean that there are no spiteful players in the population, but only players with standard PD preferences (having ) and assurance game preferences (having ). The assurance problem in Example 1 is illustrated by the fact that under complete information all players from the latter category cooperate if they encounter another player with assurance preferences (the probability of this encounter equals , whereas only 2/3 of these same players (namely, those with ) achieve mutually beneficial cooperation under incomplete information. Efficiency under complete information equals (which equals the probability that both players’ premiums exceed 0.25). Efficiency under incomplete information equals (both actors independently cooperating with probability 0.5 results in an expected payoff equal to the average of all four payoffs, which equals 1.25, exactly halfway the mutual defection and mutual cooperation payoffs), meaning that for Example 1 efficiency is higher in the game with complete information. Thus, there are costs associated with incomplete information in the simultaneous game. Both the cooperation rates and efficiencies of the simultaneous one-shot game of Example1 can be found in the upper left cell of Table 2.

Table 2. Proportion of player’s cooperation (first pair of numbers in cell, first number in each pair referring to player 1), proportion of mutual cooperation (second number), and efficiency (third number) in the simultaneous and sequential one-shot game of Example 1 and Example 2.

	Example 1		Example 2
	Complete info	Incomplete info	Complete info	Incomplete info
Simultaneous	(0.75, 0.75)^§	(0.5, 0.5)	(0.375, 0.375)^§	(0, 0)
	0.5625	0.25	0.1406	0
	0.5625	0.5	0.1406	0
Sequential	(0.75, 0.75)	(1,0.75)	(0.2813, 0.375)	(0.2917, 0.375)
	0.75	0.75	0.2813	0.1094
	0.75	0.875	0.2813	0.2005

Note. ^§Under complete information these numbers represent the proportion of players preferring mutual cooperation over unilateral defection.

4.2. Sequential play

Suppose the game of Table 1 is played sequentially, player 1 being the first mover and player 2 the second mover. In any BNE, player 2 responds with D after player 1 played D. Thus, player 1’s expected payoffs in any BNE of playing D equal 1. Let denote player 2’s BNE probability of playing C after player 1 played C. The threshold premium for player 1 is then given by Eq. (2a) (see Appendix for derivation):

(2a)

In a BNE all players 1 with defect and all others cooperate. After observing cooperation of player 1, player 2 compares his payoffs for mutual cooperation and unilateral defection and his BNE threshold is simply,

(2b)

Since by the assurance problem in the simultaneous one-shot game we had , the equilibrium thresholds for both players in the sequential game are strictly below the equilibrium threshold in the one-shot simultaneous game, under the same, . Thus, in our model sequential play in the one-shot game implies an increase in cooperation compared to simultaneous play and alleviates the assurance problem. This increasing cooperation (reduced assurance problem) arises through a two-step learning process. First, player 2 observes player 1’s behavior, rendering uncertainty about player 1’s theta irrelevant for his (player 2’s) decision: Any player 2 with (i.e., with assurance game preferences) dares to cooperate and players 2 do not experience the assurance problem. Second, player 1 foresees this when making her decision and upwardly adjusts the probability that player 2 will answer cooperation with cooperation.

An assurance problem in the sequential game arises if players 1 exist with . In other words, an assurance problem for players 1 occurs whenever some nonspiteful players 1 dare not cooperate due to uncertainty about the type of player 2. Note that the assurance problem is different from the one we employed in the simultaneous game. This is caused by the fact that cheating on a cooperating partner is out of reach for player 1 in the sequential game. Therefore, the correct comparison is between the outcomes of mutual defection and mutual cooperation, and the assurance problem is said to be manifest whenever not all players 1 who prefer mutual cooperation over mutual defection (i.e., nonspiteful players) dare cooperate. Equation (2a) immediately shows that whenever the assurance problem is manifest. We reconsider Example 1, but now played sequentially.

Example 1 continued. Recall that and is uniform on [0, 1]. From (2b), it follows that 75% of players 2 cooperate. Substituting 0.75 in (2a) yields Since no spiteful players exist in this example, all players’ premiums exceed . Hence, no assurance problem exists and all players 1 cooperate. Efficiency equals 0.875. Note that both the cooperation rates and efficiency are larger than in the simultaneous game.

Under complete information, the proportions of players’ cooperation and mutual cooperation both equal 0.75, resulting in an efficiency of 0.75 as well, which is lower than the efficiency of 0.875 under incomplete information. Thus, counterintuitively, incomplete information increases efficiency in this sequential game: incomplete information yields a benefit. Note that only player 2 profits from the incomplete information; the players’ expected payoffs are 1.3125 (player 1) and 1.5625 (player 2), whereas they are 1.375 in the complete information game for both players (see lower-left cell of Table 2). The assurance problem in the sequential game is illustrated in Example 2, which is similar to Example 1 but for a including spiteful players.

Example 2. Suppose , and let be uniform on the [−1, 1] interval. Assuming sequential play, players 2 cooperate with probability . Hence, , with a proportion of of players 1 cooperating. The assurance problem occurs because (nonspiteful) players 1 exist with . The proportion of mutual cooperation equals 0.1094, and efficiency equals 0.2005. Cooperation and efficiency are higher under complete information, again signifying the cost of incomplete information. Under complete information, again 37.5% of players 2 cooperate; 75% of players 1 (those with ) prefer mutual cooperation over mutual defection; hence, the proportions of players 1 cooperating, mutual cooperation, and efficiency, all equal 0.2813. The characteristics of the corresponding simultaneous game are again summarized in Table 2.³

To summarize, the assurance problem may arise in both the simultaneous and sequential game under incomplete information. Counterintuitively, efficiency can be higher under incomplete information than under complete information in both the sequential and simultaneous games. Finally, the assurance problem is less severe (i.e., cooperation is more frequent) and efficiency is higher in the sequential game than in the corresponding simultaneous game, both under incomplete and complete information.

5. Two-shot game

5.1. Simultaneous play

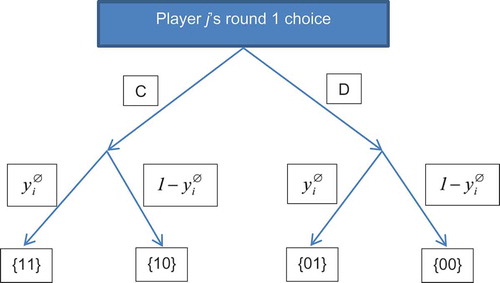
In the two-shot simultaneously played game there are four possible histories at the start of round two. Letting “0” denote a player’s defection and “1” his cooperation, we denote these 4 histories as {00}, {10}, {01}, and {11}, where the first and second elements indicate the actions of players j and i respectively. Contingent on these histories players form their round 2 beliefs, yielding 4 different round 2 beliefs for player j concerning . Denote player j’s round 2 beliefs conditional on history h by . Substantively, the round 2 beliefs are the updated beliefs a player holds about the likely values of the theta of the other player after observing that player’s round 1 behavior.

Let denote the BNE probability that player i cooperates in round 2, conditional on some history h that has a strictly positive probability of occurring under the BNE. Then we obtain round 2 BNE threshold

(3)

such that players j with defect and others cooperate, with . Note how Eq. (3) amount to nothing more than the one-shot game threshold applied to each possible round 2 history in the two-shot game.

Let denote player i’s BNE probability of cooperation in round 1 (after the “empty history”). We can then depict player j’s round 1 decision in the following decision tree (see Figure 1). In the histories shown at the bottom of Figure 1 player j’s round 1 behavior is the first element in each pair.

Figure 1. Player j’s decision tree of round 1 in the simultaneous two-shot game.

Based on Figure 1, we present player j’s expected payoffs of first round cooperation and defection in the Appendix. In order to investigate the assurance problem in the two-shot and N-shot games, we call a BNE round k unassured if any player j with (i.e., with assurance game preferences) should defect in round k under this equilibrium. All other BNE are round k assured. Then the following proposition can be proved.

5.1.1. Proposition 1 (Two-shot simultaneous game trigger strategies)

In any round 1 assured BNE of the simultaneously played two-shot game, any round 1 defection leads to mutual defection in round 2.

Using Proposition 1, we find the expression for the round 1 equilibrium threshold for round 1 assured BNE to be (see Appendix for derivation)

(4)

With and , Eqs. (3) and (4) characterize round 1 assured BNE in the simultaneously played two-shot game. In the Appendix we also show that round 1 assurance implies , i.e., under round 1 assured BNE fewer players cooperate in round 2 (after mutual cooperation in round 1) than in round 1, corresponding to an end game effect. Note that the contra-positive of Proposition 1 is that, if in any BNE it is not true that , this BNE cannot be round 1 assured. Hence, (or “trigger strategies”) is a necessary condition for BNE to be round 1 assured.

It is instructive to analyze some examples, especially observing that “trigger strategies” are necessary but not sufficient for reaching round 1 assurance. In addition, the examples will show once more that the incomplete information does not imply inefficiency (see Table 3).

Table 3. Proportion of player’s cooperation (first pair of numbers in cell, first number in each pair referring to player 1), proportion of mutual cooperation (second number), and efficiency (third number) in both rounds of the simultaneous and sequential two-shot game of Example 1 and Example 2; round 2 calculations based on entire population.

		Example 1		Example 2
	Round	Complete info	Incomplete info	Complete info	Incomplete info
Simultaneous	1	(0.75, 0.75)^§	(0.2675,	(0.375,	(0.4768,
		0.5625	0.2675)	0.375)^§	0.4768)
		0.5625	0.0716	0.1406	0.2273
			0.2675	0.1406	0.4768
	2	(0.75, 0.75)^§	(0.0721,	(0.375,	(0.3039,
		0.5625	0.0721)	0.375)^§	0.3039)
		0.5625	0.0052^§§	0.1406	0.0923
			0.0193^§§§	0.1406	0.1448
Sequential	1	(0.75, 0.75)	(1, 1)	(0.281,	(0.715,
		0.75	1	0.281)	0.702)
		0.75	1	0.281	0.5019
				0.281	0.6085
	2	(0.75, 0.75)	(1, 0.75)	(0.281,	(0.641,
		0.75	0.75	0.281)	0.375)
		0.75	0.875	0.281	0.2404
				0.281	0.3452

Note. ^§Under complete information, these numbers represent the proportion of players preferring mutual cooperation over unilateral defection.

^§§ Only a proportion of 0.0716 of all players mutually cooperate in round 1. Since , only a proportion of of all players mutually cooperate in round 2.

^§§§ A proportion of 0.0052 of all players get the 1.5 payoff for mutual cooperation in round 2. A proportion of is involved in unilateral defection, whereas the remaining proportion of 0.9666 is involved in mutual defection.

Example 1 continued. Suppose , let be uniform on the unit interval, and consider the simultaneously played two-shot game. Since in a round 1 assured BNE we must have , the conditional cumulative probability of given mutual cooperation in round 1 is and . Substituting in Eqs. (3) and (4) yields and . The only feasible solution to these equations is and , yielding and . Because , the equilibrium is not round 1 assured, illustrating that the “trigger strategies” of Proposition 1 are not sufficient. Note that because the premium threshold was smaller in the one-shot game (0.5), the assurance problem is not attenuated by repetition, but worsened considerably. The upper-left cell of Table 3 shows the proportions of cooperation and mutual cooperation and the efficiency for the incomplete and complete information versions of the two-shot game of this example. Comparison shows that efficiency under incomplete information is lower than under complete information in both rounds of the simultaneous game, indicating the costs of incomplete information in the two-shot game of Example 1. For a case where repetition both dissipates the assurance problem and improves efficiency in both round 1 and 2, reconsider example 2.

Example 2 continued. Suppose , let be uniform on , and consider the simultaneously played two-shot game. From and , we obtain , and . Substituting in (3) and (4) yields and . A solution to this set of equations is and , yielding and . Comparison of the complete and incomplete information versions of this game in the upper-right cell of Table 3 shows that the round 1 assurance problem is solved under incomplete information. What is more, the incomplete information game is more efficient than the complete information game in both rounds 1 and 2, again showing that incomplete information can increase efficiency and yield a benefit.

Comparing the equilibria of Example 1 and Example 2 under incomplete information yields a counterintuitive result or paradox: In the two-shot game, the probability of cooperation is higher in Example 2 than in Example 1, while the only difference between the two examples is that in Example 2 individuals are included who like mutual cooperation less than the individuals in Example 1 (i.e., individuals with in [−1,0) are added to the population of players in Example 1 to obtain the game of Example 2). The explanation of the paradox is that even though these added players dislike mutual cooperation (their thetas being negative), those in the range [−0.5,0) do prefer mutual cooperation over mutual defection. The game being two-shot, some of these players have an interest in cooperating in round 1. This decreases the first round threshold in Example 2 compared to the first round threshold in Example 1. To conclude, adding players who do not prefer mutual cooperation above successful cheating may still increase (mutual) cooperation in finitely repeated games.

In the solution found in Example 2 above, there is no assurance problem in round 1, but there is in round 2. This raises the question of whether we can find equilibria that have both round 1 and round 2 assurance, and particularly, BNE that separate players with assurance game preferences from the rest in terms of behavior. In such a separating BNE players with assurance game preferences would never have to worry about being cheated after mutual cooperation in round 1. Proposition 2 addresses this question.

5.1.2. Proposition 2 (Two-shot simultaneous game constancy of thresholds)

In the simultaneously played two-shot game, a round 1 assured BNE that meets Eqs. (3) and (4) with exists if and only if (i) and (ii) for .

Proposition 2 implies that for any given family of probability distributions, the condition for assurance throughout the game is very restrictive, since the distribution must be characterized by exactly . The distribution of example 2, for instance, has . For this distribution, a separating BNE does not exist: round 1 assurance entails having some players with PD preferences cooperate in round 1, which implies an assurance problem in round 2. For a beta probability distribution with and a separating BNE does exist.

In addition, Proposition 2 shows that under Eqs. (3) and (4) the round 1 and round 2 threshold can be equal only whenever . This explains the counterintuitive feature of the equilibrium found in example 1, where the round 2 threshold was strictly above the round 1 threshold even though the latter was already well above . Thus, under the BNE in example 1, players who mutually cooperated in round 1 would know with certainty that both of them had assurance game preferences (this would in fact be common knowledge), but still some of them (those with thetas below the round 2 threshold) would have to defect in round 2 under equilibrium play. Thus, Proposition 2 shows that we will observe end game effects in BNEs under Eqs. (3) and (4) whenever .

5.2. Sequential play

In the sequential game, call a BNE round k unassured if any player 1 with (i.e., nonspiteful players) or any player 2 with (i.e., with assurance game preferences) should defect in round k under this equilibrium. All other BNE are round k assured. Moreover, since spiteful players 1 (i.e., with ) always play D, round k assurance in the sequentially played game requires that the round k threshold for player 1 exactly equals .

5.2.1. Proposition 3 (Two-shot sequential game trigger strategies)

In any round 1 assured BNE in the sequentially played two-shot game, any defection by players 1 or 2 leads to mutual defection in round 2.

Proposition 3 implies that in our search for round 1 assured BNE in the sequentially played two-shot game we again need to consider only “trigger strategy profiles.” Thus, Proposition 3 is the sequential game version of Proposition 1. Letting and denote player i’s round k equilibrium threshold and cooperation probability, respectively, and using Proposition 3, we can derive the round 1 and round 2 thresholds for players 1 and 2, under round 1 assured BNE (see Appendix for derivation):

(5a)

(5b, equation (2b) repeated), and

(6a)

Note that Eqs. (5) imply that : Under round 1 assured BNE fewer players 2 cooperate in round 2 after mutual cooperation in round 1, than in round 1. Proposition 4 tells us that in the presence of spiteful players there is no round 1 assured equilibrium in the two-shot sequential game. Note how this implies a decrease in severity of the assurance problem compared to the one-shot case in which the mere presence of players with PD preferences rendered player 1 assurance infeasible.

5.2.2. Proposition 4 (Two-shot sequential game assurance problem)

If , there exists no round 1 assured player 1 threshold in the two-shot sequential game.

Finally, the round 2 threshold for player 1 in round 1 assured BNE is simply

(6b)

In the Appendix we also show that round 1 assurance implies . By Eqs. (6a) and (6b), this in turn implies : in round 1 assured BNE in the sequential game player 2’s cooperation probabilities (weakly) decrease over the two rounds. Even if the equilibrium is not round 1 assured, Eqs. (5) and (6) define an equilibrium under the trigger strategy profile.⁴ The continued example 2 below illustrates Proposition 4. Both continued examples 1 and 2 again illustrate how incomplete information can increase efficiency.

Example 2 continued. Suppose , let be uniform on the [−1, 1] interval, and suppose the sequential game is played twice. Round 1 assurance would require that all nonspiteful players 1 (with ) cooperate. However, since we know by Proposition 4 that there is no round 1 assured BNE. Nevertheless, repeating the game twice strongly decreases the severity of the assurance problem and increases efficiency compared to the one-shot game; using (5) and (6) we find , , , and , which are lower than in the one-shot game, although the BNE in this two-shot sequential game is strictly speaking round 1 unassured (since ). Finally, comparing the lower-right cells of Tables 2 and 3 reveals that both rounds of the incomplete information two-shot game are more efficient than both complete and incomplete information versions of the 1-shot game.

Example 1 continued. Suppose , let be uniform on the unit interval, and suppose the sequential game is played twice. Using (5) and (6) yields negative values for , , and , and gives . Setting , , implies and . Using Eqs. (A.6)--(A.9) in the Appendix shows that under this equilibrium all players 1 cooperate in both rounds, and all players 2 cooperate in round 1. There is no assurance problem, and efficiency in both rounds is higher under incomplete information than under complete information (lower-left cell of Table 3): Incomplete information entails a net benefit.

Concerning the issue of whether a BNE can be assured in both rounds of the two-shot sequentially played game, we have seen that this can indeed be the case for the player 2 thresholds (e.g., Example 1). Proposition 5, however, shows that for the player 1 thresholds, this is only feasible if there are no players with spiteful or PD preferences in the population (i.e., ).

5.2.3. Proposition 5 (Two-shot sequential game constancy of thresholds)

In the two-shot sequential game, a BNE meeting Eqs. (5) and (6), (i) with exists if and only if , (ii) with exists only if , and (iii) with exists only if .

Proposition 5 means that separating the players 1 with assurance game preferences from the spiteful and PD players from the outset is impossible. Proposition 5 also shows that if we want an assured equilibrium for player 1 in both rounds, we are back at the assurance problem of the one-shot game. In addition, Proposition 5 shows that constant thresholds for player 1 are only possible if the player 2 thresholds strictly increase. In other words, we must have player 2 end game effects. Finally, the proposition shows that constant thresholds for player 2 can only exist if player 1 does not cooperate in round 2. Summarizing, a mutually cooperative relationship without end game effects (i.e., with constant thresholds for both players) is impossible under Eqs. (5) and (6) in the two-shot sequential game.

To summarize the results of the two-shot game, in the simultaneous two-shot game the round 1 assurance problem can be solved, contrary to what was the case in the one-shot game. In the sequentially played two-shot game, the round 1 assurance problem (with respect to player 1’s threshold) can also be solved, but only if there are no spiteful players in the population. In both the simultaneously and the sequentially played game round 1 assured BNE necessitate the play of trigger strategies and imply the occurrence of end game effects (except under very restrictive conditions). For both the simultaneous and sequential games, the existence of round 1 assured BNE generally depends on players’ (updated) beliefs (i.e., on the (conditional) distributions of premiums), implying that one-shot game and two-shot game thresholds cannot be directly compared. The exception is player 2’s thresholds in the sequentially played games, which are never higher in the two-shot game than in the one-shot game. A similar point arises when comparing the sequential and simultaneous two-shot games: existence of round 1 assured BNE depends on players’ (updated) beliefs, rendering general conclusions about the thresholds infeasible. Finally, the examples demonstrate that incomplete information two-shot games (both sequential and simultaneous) can be more efficient than their complete information counterparts, and that adding players who prefer successful cheating may still improve cooperation in repeated games under incomplete information.

5.3. N-shot game

We now briefly show that our two-shot game results concerning trigger strategies (propositions 1 N and 3 N) and end game effects (propositions 2 N and 5) generalize to the finitely repeated N-shot game. The conclusions related to the assurance problem, the comparisons between sequential and simultaneous play, and between complete and incomplete information are similar to those formulated for the two-shot game. For illustration, we also provide equilibria of the five-shot games of Example 1 and Example 2.

5.4. Simultaneous play

When finding BNE in the simultaneously played N-shot game, beliefs are uniquely defined by Bayes’ rule along the equilibrium path, i.e., along histories that have a nonzero probability of occurring. If in addition we explicitly assume that players’ beliefs are well-defined at any history h, including those with zero probability (see Fudenberg & Tirole, 1991), Proposition 1 can be generalized to simultaneously played N-shot games.

5.4.1. Proposition 1 N (N-shot simultaneous game trigger strategies in Round K assured BNE)

In any BNE of the simultaneously played N-shot game that is round k assured after history h_k, any round k defection after history h_k leads to mutual defection until the end of the game.

Proposition 1 N implies that players play trigger strategies under round 1 assured BNE: Defection in round 1 leads to mutual defection until the end of the game. The Appendix provides the players’ expected payoffs under round 1 assured BNE.

Proposition 1 N shows that mutual defection until the end of the game ensues after defection in a round in which the equilibrium threshold is not above . The set of trigger strategies in which any defection is followed by mutual defection in the next round is a subset of these strategy profiles, and we concentrate on these general trigger strategies in the remainder. Since, under general trigger strategies, players only (possibly) cooperate after a history of uninterrupted mutual cooperation, we can simplify our notation. Similar to what we did in the two-shot sequentially played game, we let be the equilibrium probability of cooperation by player i in round k, after a history of uninterrupted mutual cooperation. Proposition 6 states that under general trigger strategies all BNE consist of a sequence of thresholds, one for each round.

5.4.2. Proposition 6 (N-shot simultaneous game sequence of equilibrium thresholds)

Under general trigger strategies, all BNE in the simultaneously played N-shot game have thresholds at each round k history of uninterrupted mutual cooperation with , such that all players j with defect in round k and all others cooperate.

Propositions 1 N and 6 together imply that . We can now characterize BNE under general trigger strategies for the simultaneously played N-shot game. For any round k and we get (see Appendix for derivation)

(7)

with by convention. Equation (7) is a direct generalization of (3) for two-shot games. Proposition 2 N shows that having a BNE that separates the players with assurance game preferences from all players throughout the game is impossible when N > 2, and that having constant thresholds in at least three consecutive rounds is possible only under very restrictive conditions. Hence, Proposition 2 N implies that end game effects exist in the N-shot simultaneously played game.

5.4.3. Proposition 2 N (N-shot simultaneous game constancy of thresholds)

In the simultaneously played N-shot game with N > 2, (i) there is no BNE satisfying equations (7) with for and all rounds k, and (ii) BNE satisfying equations (7) with can only exist if and .

For completeness, we now present equilibria for Examples 1 and 2, played simultaneously for five rounds. The five-shot games illustrate that the threshold of cooperation is increasing over rounds in the equilibria, in accordance with propositions 1 N and 6. In particular, in both examples, we find no equilibrium thresholds that are equal in three consecutive rounds, as the requirements of Proposition 2 N (ii) are not met.

Example 1 continued. Suppose , and let be uniform on the unit interval. Suppose the game is played simultaneously for 5 rounds. Then a symmetric BNE is , leading to .

Example 2 continued. Suppose , let be uniform on , and consider the simultaneously played game repeated five times. Then a symmetric BNE is , leading to .

5.5. Sequential play

In the sequentially played game round 1 assurance requires that all players 1 with and all players 2 with cooperate in round 1. Thus, assuming a round 1 assured BNE, any defection by any player in round 1 reveals that the defecting player is spiteful and is followed by mutual defection in round 2. Proposition 3 N concerning trigger strategies is a straightforward generalization of Proposition 3 to the N-shot game.

5.5.1. Proposition 3 N (N-shot sequential game trigger strategies in Round K assured BNE)

In any round k assured BNE in the sequentially played N-shot game, any defection by players 1 and 2 in round k leads to mutual defection in all subsequent rounds.

We again concentrate on the set of general trigger strategies in which any defection is followed by mutual defection in the next round, which is a subset of the strategy profiles from Proposition 3 N. Proposition 7 establishes that under general trigger strategies BNE consist of sequences of thresholds, one threshold for each player in each round.

5.5.2. Proposition 7 (N-shot sequential game sequence of equilibrium thresholds)

Under general trigger strategies, all BNE in the sequentially played N-shot game have thresholds at each round k history of uninterrupted mutual cooperation with , such that all players j with defect in round k and all others cooperate, with .

By Proposition 7, we have for any round k, and (see Appendix for derivation)

(8)

(9a)

and

(9b)

Equation (8) is a direct generalization of Eqs. (6a) and (6b), and Eq. (9b) is the direct generalization of (5a). Equation (9a) reflects the fixed nature of the final threshold for player 2.

It is immediate from Eq. (8) that a BNE under general trigger strategies having for every round k is possible if and only if for every round k. Since , Eq. (9a) implies that this is possible if and only if . Thus, Proposition 5 that was proved for the two-shot case also holds for the N-shot case: under Eqs. (8) and (9), (i) BNE that separate nonspiteful players 1 from all other players throughout the game exist if and only if there are only players with assurance game preferences in the population; (ii) player 1 thresholds that are equal in rounds k and k + 1 exist only if player 2 thresholds strictly increase in these rounds; and (iii) player 2 thresholds that are equal in rounds k and k + 1 exist only if player 1 cooperates with probability zero in round k + 1. This establishes that end game effects for at least one player occur in sequentially played N-shot games.

Finally, we present equilibria for Examples 1 and 2, played sequentially for 5 rounds. The equilibria of the five-shot games illustrate that thresholds weakly increase, as implied by Proposition 7. Example 1 illustrates that equilibrium thresholds can be equal for both players in consecutive rounds if the support of P() is restricted to a finite range (contrary to what we assume in the derivations of our propositions). Example 2 illustrates the fact that existence of equilibria depends on P() and that repeating the game is not guaranteed to lead to more cooperation.

Example 1 continued. Suppose , and let be uniform on the unit interval and suppose the sequential game is played for 5 rounds. Then and is a BNE with cooperation probability equal to 1 for both players in all five rounds, except for player 2 in round 5, for whom we have .

Example 2 continued. Suppose , let be uniform on the [−1, 1] interval, and suppose the sequential game is played for five rounds. Through numerical search (Generalized Reduced Gradient method in Excel), we were not able to find any equilibrium with positive cooperation probabilities, other than the one identified in the two-shot case, followed by three rounds of mutual defection. In any case, no round 1 assured BNE exists.

6. Conclusions

The model we developed in this article is based on the empirically supported notion that people value mutual cooperation in a PD game over and above its material payoff consequences. We theorized that the degree to which this is true differs from individual to individual and that this degree is private information: People are assumed to have an accurate assessment of their own preferences for mutual cooperation, and know the distribution of others’ preferences. Our model accommodates a variety of player types, ranging from spiteful players who prefer mutual defection over mutual cooperation to players with assurance game preferences who prefer mutual cooperation over successful cheating, passing through players with true PD preferences. With this model we showed that an assurance problem may occur: Pairs of players with assurance game preferences (who would have preferred to cooperate under complete information) dare not do so due to incomplete information caused by the invisibility of preferences. Subsequently, we showed how this problem might be alleviated through sequential and repeated play, which facilitate learning. Additionally, we derived the following results, all in accordance with observed behavioral regularities, in both simultaneously and sequentially played one-shot and repeated PD games.

First of all, cooperation is possible in one-shot and finitely repeated PD games. Moreover, cooperation is easier to attain in the sequentially played one-shot PD than in the simultaneously played one-shot PD; both players in the sequential one-shot game have lower cooperation thresholds than players in the one-shot simultaneously played game (the assurance problem is less severe in the former game). However, in both games there may be an assurance problem in the sense that not all players who would have preferred to cooperate if the game were one of complete information dare to cooperate under incomplete information. Second, we derive the counterintuitive result that incomplete information games can be more efficient than the corresponding complete information games. Hence, solving the assurance problem by revealing all information might harm efficiency, and the two are separate problems. Third, repeating the game improves the chances of cooperation (i.e., reduces or obliterates the round 1 assurance problem) but end game effects are endemic. Thus, in both the simultaneously played and sequentially played PDs, there will generally be relationships that start off with mutual cooperation but turn sour before the end of the game. Moreover, we derived the counterintuitive result that in repeated games adding players who prefer successful cheating above mutual cooperation may increase cooperation. Fourth, separating BNE that solve the assurance problem once and for all, in the sense that all players with assurance game preferences cooperate and all others defect, are generally not feasible, except under very restrictive conditions. The assurance problem can thus generally be suppressed only in the first rounds of the game, only to surface in later rounds.

In future research we aim to extend our analyses and experimentally test our model. First, our result that conditions for cooperation are better in the one-shot sequentially played game than in the one-shot simultaneously played game has consequences for the mechanism design of social dilemmas. Interesting here is whether players, who are free to design the move structure of the PD, will prefer the sequential over the simultaneous game. What will impede selecting the sequential game is that the expected payoffs of players with PD preferences are lower as first mover in the sequential than in the simultaneous game. Moreover, players with assurance game preferences as first mover are worse off than all other player types in the sequential game. So these players may prefer the simultaneously played game over the sequentially played game. The question of mechanism design of the social dilemma is therefore also an interesting question to be investigated experimentally. In such an experiment, we would endeavor to independently measure participants’ theta parameter and then predict that their choices in the mechanism design problem depend on its value.

Second, a different experimental test of our model is suggested by the fact that efficiency can be higher under incomplete information than under complete information. In this experiment, we would screen participants for low values of theta (selfishness, say). We would then use a standard PD game, with an added random material payoff for mutual cooperation that is either public or private information. Choosing the right payoffs and distribution of the random payoff component would enable us to create treatments in which the average expected payoff net of the random payoff (i.e., efficiency) is higher under incomplete information than under complete information. We could then test this prediction.

Third, we consider extending our theoretical analyses to more players, including N-person games and network games. For instance, Dijkstra and van Assen (2013), using the same model of players’ preferences, show that cooperation is more frequent in dense groups or networks satisfying a condition called degree independence. We aim to analyze repeated N-person and network games, to examine how cooperation may evolve in these repeated games under our model assumptions, depending on network structure, number of repetitions, and the structure of the game (simultaneous or sequential).

Notes

¹ Dijkstra and Van Assen (2013) call this an efficiency problem, but see below for why we avoid this term.

² Finally, there is an infinite set of mixed strategy equilibria in which one or both of the players randomize when their theta is ½. Note how these mixed equilibria do not affect the threshold value, due to our assumptions on P().

³ Under incomplete information, (1) has no solution, and hence all players defect. Under complete information, 37.5% of players with assurance preferences encounter each other with probability , which results in the same efficiency.

⁴ The probabilities are defined by , , and .

Appendix: Proofs and derivations

Derivation of Eq. (1)

Player j will cooperate if and only if . This yields threshold such that players j with defect and others cooperate, with .

Conditions for higher efficiency under incomplete information than under complete information

Let and , with and being the proportions of players cooperating in the game under incomplete and complete information, respectively. Then the efficiency of the game under incomplete information equals

,

and the efficiency under complete information equals

.

Subtracting the numerators yields , with , , and . It follows that dif < 0, if P₁ > 0 and P₂ approaches 0, because then both A and B approach zero, with dif approaching.

Derivation of Eq. (2a)

Player 1’s expected payoffs in any BNE of playing D equal . Since player 2 will respond to C with C only if we have , and player 1’s expected payoffs of playing C equal . Setting yields Eq. (2a).

Derivation of player j’s expected payoffs in the simultaneous two-shot game

Player j’s expected payoffs from cooperation in round 1 are as follows:

(A.1)

Player j’s expected payoffs from defection in round 1 are as follows:

(A.2)

The elements and in (A.1) and (A.2) capture the expected round 1 behavior of player i (see Figure 1). The first elements within any pair of square brackets denote the round 1 payoffs earned by player j contingent on the round 1 behavior of player i. The expected round 2 payoffs earned by player j depend on her own round 2 behavior and the expected behavior of player i in round 2. Since players are assumed to maximize their expected payoffs, we capture this with the elements.

Proposition 1 (Two-shot simultaneous game trigger strategies)

Proof. Consider a round 1 assured BNE, and suppose player i defects in round 1. Since no player i with defects in round 1, player j infers that and i will defect (i’s dominant strategy) in round 2 as well; hence, j’s single best response is to defect in round 2. Q.E.D.

Derivation of Eq. (4)

Proposition 1 means that . This implies that (A.1) and (A.2) can be rewritten as

(A.3)

and

(A.4)

respectively.

Because (A.3) is increasing in whereas (A.4) is constant in , round 1 assured BNE are strictly monotonous in theta, implying there exists a unique round 1 threshold such that all players j with cooperate in round 1 and all others defect for . Round 1 assurance also implies that players with weakly prefer round 2 defection over round 2 cooperation, after mutual cooperation in round 1, and hence . To prove this, suppose it is not true. Then for these players j it would hold that . Solving for the round 1 threshold, this implies that , which means the proposed equilibrium is unassured. Hence, in any round 1 assured equilibrium , or equivalently for all players j with . Thus, for players j with , we can rewrite (A.3) as

(A.5)

Equation (4) is found by equating (A.4) and (A.5) and solving for .

Proposition 2 (Two-shot simultaneous game constancy of thresholds)

Proof. The equality implies. By Eq. (3), this implies for. The fact that implies by Eq. (4) that . Hence, we have, implying and finally by substitution of. To prove sufficiency, substitute in (3), yielding. Substituting and in Eq. (4) yields the requirement . Since by condition (ii) , this requirement is met and a BNE with the desired characteristics exists. Q.E.D.

Proposition 3 (Two-shot sequential game trigger strategies)

Proof. The proof rests on a standard backward induction argument.

First, consider a round 2 defection by player 1 (first mover). Player 2’s unique best reply in round 2 is then to defect, too. Second, consider a round 1 defection by player 2 (second mover). Cooperating in round 2 can only be part of a best reply for player 1, if player 1 believes there is a nonzero probability that player 2 has . But any BNE for which this is true, and in which player 2 defected in round 1, would be round 1 unassured. Thus, in a round 1 assured BNE player 1 defects in round 2 after a round 1 defection by player 2. Finally, consider a round 1 defection by player 1 (first mover). Player 2 knows that (i) in round 2 only players 1 with will possibly cooperate, and (ii) if he (player 2) defects in round 1, mutual defection will follow in round 2. Thus, after player 1 defected in round 1, player 2 will only cooperate in round 1 if player 2 believes there is a non-zero probability that . But given that player 1 defected in round 1, this can only be true in an unassured BNE. Hence, in a round 1 assured BNE, player 2 defects in round 1, after player 1 defected in round 1. Q.E.D.

Derivation of Eqs. (5) and (6)

Under the trigger strategy profiles, we can specify the expected payoffs of playing C and D in round 1. Denote these expected payoffs by and , with indexing the players. Since player 2 plays only after learning player 1’s round 1 move, and since by Proposition 3 we already know player 2’s (round 1 assured) BNE behavior after a round 1 defection by player 1, we specify player 2’s expected payoffs contingent on player 1 having cooperated in round 1. Letting denote the cooperation probability of player i in round k contingent on a history of perfect cooperation, we get that in round 1 certain BNE,

(A.6)

(A.7)

(A.8)

(A.9)

In any round 1 assured BNE in the sequentially played two-shot game there is a pair of thresholds and such that all players 1 with defect in round 1 and all others cooperate, and all players 2 with defect in round 1 after player 1 cooperated in round 1 and all others cooperate. To see this, note that for both players i the relevant expected payoff of round 1 cooperation ((A.7) and (A.9)) are strictly increasing in , whereas the expected payoffs of round 1 defection ((A.6) and (A.8)) are constant in . Thus, for both players i there exists a unique such that for all and otherwise. Now we can derive Eqs. (5) and (6).

Round 1 assurance means , which implies that for players 2 with , allowing us to rewrite (A.9) as for players 2 with . Setting to find the expression for yields Eq. (5a). The round 2 threshold for player 2 (Eq. (5b)) is straightforward. The maximization problem in Eq. (A.7) can be solved by noting that under round 1 assured equilibria, after mutual cooperation in round 1, players 1 with (weakly) prefer round 2 defection over round 2 cooperation. To prove this, suppose it is not true. We would then have . This inequality implies , which means the proposed equilibrium would be round 1 unassured. Hence, for any round 1 assured BNE , or equivalently , allowing us to rewrite (A.7) as for players 1 with . Setting this equation equal to (A.6) to find the expression for yields Eq. (6a).

Note that since all players 1 with (weakly) prefer defection in round 2 and all others prefer cooperation, this implies .

Proposition 4 (Two-shot sequential game assurance problem)

Proof. We already know that round 1 assurance requires . Equation (6a) therefore proves that in any round 1 assured BNE . Since , and since by Eq. (5a) , we have that whenever there is no round 1 assured equilibrium. Q.E.D.

Proposition 5 (Two-shot sequential game constancy of thresholds)

Proof. (i) It immediately follows from Eqs. (6a) and (6b) that can only occur if , which can only be the case if . Having requires . Sufficiency follows straightforwardly from noting that if all players 2’s best reply is to cooperate after player 1’s cooperation in any round, yielding , after which substitution in (6a) and (6b) gives the required result.

(ii) By Eqs. (6), implies , which implies .

(iii) By Eqs. (5) implies .

Q.E.D.

Proposition 1 N (N-shot simultaneous game trigger strategies, in round k assured BNE)

Proof. Suppose the players have reached round k after history h_k, and suppose player i defects. Since the BNE is assured given this round and history, no player i with defects under the BNE. Thus, player j infers that . Since all players i with defect in any equilibrium in round N no matter the round N history, player j´s single best response is to defect in round N, regardless of the history and his premium. Now the standard backward induction argument leads to the conclusion that the unique best response for both players is to defect from round k + 1 onwards. Q.E.D.

Derivation of expected payoffs in the N-shot game

Let denote player j’s expected payoff from round 2 onwards, after mutual cooperation in round 1. Since in every round player j’s expected payoffs are increasing in after mutual cooperation in the previous round, and is a weighted sum of these per round payoffs, is increasing in . We can now write the expected payoff of player j under any round 1 assured BNE contingent on her cooperation and defection as, respectively,

(A.10)

and

(A.11)

It is immediate from Eqs. (A.10) and (A.11) that there exists a unique such that all players j with defect in round 1 and all others cooperate. Thus, round 1 assured BNE have a round 1 equilibrium threshold.

Proposition 6 (N-shot simultaneous game sequence of equilibrium thresholds)

Proof. The proof follows immediately from the fact that the payoff of defection in any round k is constant in , whereas the payoff of cooperation is increasing in , there exists a such that all players j with defect and all others cooperate. Q.E.D.

Derivation of Eq. (7)

Consider the round k continuation game after k-1 rounds of mutual cooperation. Defection in round k gives an expected payoff for player j of . By Proposition 6, we know that . Thus, players j with (weakly) prefer defection over cooperation in round k + 1, and their expected payoff of cooperation in round k is . Requiring that cooperation and defection be equally attractive for players with yields Eq. (7).

Proposition 2 N (N-shot simultaneous game constancy of thresholds)

Proof. (i) Suppose , . By Eq. (7), this can only be the case whenever , which implies . By Eq. (7), , which implies . Since , and together imply . (ii) Suppose , for some round k. This implies . By Eq. (7), this implies , from which it is immediate that . Q.E.D.

Proposition 7 (N-shot sequential game sequence of equilibrium thresholds). Under trigger strategy profiles, all BNE in the sequentially played N-shot game have thresholds at each round k history of uninterrupted mutual cooperation with, such that all players j with defect in round k, and all others cooperate.

Proof. Consider the round k continuation game after a history of mutual cooperation, and suppose . Under trigger strategy profiles, player 1’s expected payoff of defection in round k in this continuation game is , which is constant in . Let denote player 1’s expected equilibrium continuation payoff in the round k + 1 continuation game after cooperation in round k. Then is nondecreasing in . Player 1’s expected continuation payoff of cooperation in round k, , is then strictly increasing in , and there exists a such that all players 1 with defect and all others cooperate. Now consider player 2. Playing D in round k yields player 2 a continuation payoff of , which is constant in . Let denote player 2’s expected equilibrium continuation payoff in the round k + 1 continuation game after cooperation in round k. Then is nondecreasing in . Player 2’s expected continuation payoff of cooperation in round k, , is then strictly increasing in , and there exists a such that all players 2 with defect, and all others cooperate. Q.E.D.

Derivation of Eqs. (8) and (9)

Note that players 1 who defect from round k onward get a continuation payoff of . Since , players 1 with (weakly) prefer cooperation over defection in round k + 1. Cooperation in round k followed by defection from round k + 1 onwards yields them a round k continuation payoff of . Requiring that in round k these players be indifferent between cooperation and defection yields , which is easily rewritten into Eq. (8). Next, we find expressions for under trigger strategy profiles. When , we have Eq. (9a). Now suppose , and assume a history of uninterrupted cooperation up to and including player 1’s move in round k. Defection in round k yields a continuation payoff of for player 2. Players 2 with (weakly) prefer to defect in round k + 1. Cooperation in round k followed by defection from round k + 1 onwards yields these players a continuation payoff of . Requiring that these players 2 be indifferent between defection and cooperation in round k yields Eq. (9b).