A note on application of superhomogénéisation factors to integro-differential neutron transport equations

Abstract

The present article focuses on the application of the SPH factor method to the integro-differential neutron transport equation. While leakage-related parameters are arbitrarily corrected by the SPH factors, the correction procedure for these parameters affects the calculation accuracy. We treat two correction procedures named the simultaneous correction and the direct correction, and compare them with each other in one-dimensional colorset assembly problems. Through numerical testing, we find that the simultaneous SPH correction gives better accuracy than the direct SPH correction, and the higher-order SPH-corrected calculations show better accuracy than the low-order ones. Furthermore, to consider the flux discontinuity between different types of assemblies, the improved SPH method proposed by Yamamoto and the SPH method with the Selengut normalization condition are also tested. Numerical results reveal that the both methods significantly improve the calculation accuracy and that the latter method is more robust than the former method.

Keywords :

• homogenization
• SPH factor
• discontinuity factor

1. Introduction

Reactor core calculations are vital for operations of fission reactors, and high accuracy is required in order to effectively utilize nuclear energy from fissile nuclides such as uranium and plutonium. Numerical methods for reactor core calculations have been evolved so far by efforts of many researchers and engineers working on the fields of the reactor physics and the numerical method. Significant advance in the computer technology also contributes to this evolution.

The ultimate goal of the development of reactor core calculation method is to realize a numerical procedure to solve the governed neutron transport equation as is within a practical computing time. Even with the current high-performance computers, however, this goal cannot be attained. Hence it is inevitable to use some approximations and numerical techniques in the reactor core calculations.

The homogenization is one of the important techniques in the reactor core calculations. Due to the geometrical complexity of fuel assemblies in fission reactors, the direct modeling of the fuel assemblies in a whole core calculation requires quite a heavy computational burden. Thus, in the usual reactor core calculations, fuel assemblies are homogenized in a simple calculation model such as a single fuel assembly with the reflective boundary conditions, and the homogenized fuel assemblies are treated in a subsequent whole core calculation. In the recent development, the homogenization in a smaller scale, not a fuel assembly but a unit pincell in an assembly, has been done and a more accurate whole core calculation, so called a pin-by-pin calculation, within a practical computation time has been realized. Since there are a large number of papers related to the homogenization technique, we refer to a good review paper written by Sanchez here [1].

In the homogenization, it is expected to preserve the reaction rate and the leakage rate between a heterogeneous system and a homogenized system. Koebke has pointed out that the homogenization with simple flux-volume weighting cannot preserve both of them and that an additional factor is required [2]. While several techniques have been proposed to address this issue, these are settled down to two different theories; the superhomogénéisation (SPH) factor method [3,4] and the generalized equivalence theory [5]. In the SPH factor method, homogenized cross-sections are corrected by the SPH factors. On the other hand, in the generalized equivalence theory, the flux discontinuity factors are assigned to the surface neutron flux of the system and homogenized cross-sections are not corrected. Both theories have been successfully utilized so far.

In the current reactor core calculation procedure, the diffusion equation or the simplified P₃ (SP₃) equation is employed for a whole core problem. Recently, further improvement has been attempted by Yamamoto [6] and Yamamoto et al. [7]. They intend to use the high-order equation, that is the integro-differential transport equation, for a whole core calculation instead of the diffusion equation or the SP₃ equation. Since the generalized equivalence theory has been originally developed for the diffusion-theory calculations, Yamamoto et al. have been extending this theory to be applicable to the integro-differential transport equation.

On the other hand, the SPH factor method provides a homogenized system equivalent to a heterogeneous system with a help of the SPH factors. The interesting property of this method is that a degree of approximation introduced to the homogenized system calculation can be different from that to the heterogeneous system calculation. That is, the SPH factor method can consider differences in a degree of approximation in operators, and the fineness of energy groups and spatial meshes between heterogeneous and homogenized systems in the “equivalence”. For example, the SPH factor method can provide an equivalence between a high-order heterogeneous solution with the large number of energy groups and a low-order homogenized solution with the smaller number of energy groups.

Yamamoto has interestingly pointed out in his paper [6] that the cross-section correction procedure with the SPH factors is different between for the diffusion equation and for the integro-differential transport equation. In the latter case, the SPH factors are multiplied to all the types of cross-sections such as total, partial, scattering, etc. On the other hand, in the former case, the SPH factors are multiplied to diffusion coefficients which are proportional to an inverse of total (or transport) cross-sections. Yamamoto has derived the SPH factor correction procedure for the integro-differential equation which is consistent with that for the diffusion equation [6].

It is guaranteed that the SPH factor method preserves the reaction rate and the leakage rate through the homogenization if the reflective boundary conditions are assigned in both heterogeneous and homogenized systems. Thus, choice of the cross-section correction procedure with the SPH factors does not matter in this case. In usual reactor core calculations, however, homogenization is done with a single-assembly calculation with the reflective boundary conditions, and the homogenized assemblies are located on the reactor with boundary conditions depending on the position in a reactor core. Thus the reaction rate and the leakage rate of the homogenized assembly in a whole-core calculation cannot be rigorous even if the SPH factor method is applied. In this case, the cross-section correction procedure may affect the accuracy of the homogenized calculation.

In the present article, we will test several cross-section correction procedures with the SPH factors for one-dimensional colorset assembly problems and quantify the errors of each correction procedure. Calculations with different-order operators will be also carried out for the homogenized systems, and a merit of introducing the high-order operators will be quantified. Furthermore, a problem of the usual SPH method, that it cannot consider the flux discontinuity between different types of assemblies, will be addressed.

2. The SPH factor method

2.1. Definition of the SPH factor

Let us consider a heterogeneous system. A macro region C_m is defined as a collection of regions i. Cross-section in the heterogeneous system Σ _i is homogenized over a macro region C_m . The homogenization is usually done with flux-volume weighting and homogenized cross-section Σ _m is obtained as

where and V_i are a neutron flux calculated in the heterogeneous system and a volume of region i, respectively.

In order to ensure a preservation of a reaction rate through the homogenization, the SPH factor α is introduced to correct Σ _m as

and the SPH factor is defined as

where is a neutron flux calculated in the homogenized system and V_m is a volume of a macro region C_m .

As pointed out by Hébert [4], there are an infinite number of SPH factor sets that preserve the reaction rate. This brings an extra degree of freedom and the additional normalization condition should be considered to determine the unique set of the SPH factors. Usually the following neutron flux normalization is posed [4]:

The above mentioned procedure is refereed to as the second generation SPH factor method in Hébert's paper [4].

Since the neutron flux in the homogenized system depends on the SPH-corrected homogenized cross-sections , the SPH factor set is obtained through iterative calculations.

2.2. SPH correction procedures for homogenized cross-sections

In this subsection, explicit expressions are provided for the transport and diffusion equations with the SPH-corrected homogenized cross-sections. We will refer to these equations as SPH-corrected equations. For simplicity, we consider a one-dimensional one-group problem with isotropic scattering and an external source.

A SPH-corrected integro-differential transport equation is written as

where ψ(x,μ) is angular neutron flux at position x directed with angular cosine μ, Σ _t and Σ _s are total and scattering cross-sections, and s is an external isotropic source. The SPH factor is multiplied to Σ _t and Σ _s . On the other hand, a SPH-corrected diffusion equation is written as

where the diffusion coefficient D is defined as D = 1/(3Σ _t ) and Σ _α  = Σ _t  − Σ _s . In the SPH-corrected diffusion equation, not the SPH factor but its inverse is multiplied to the total cross-section as pointed out by Yamamoto [6]. Since the leakage rate is proportional to D, both the reaction rate and the leakage rate are simultaneously corrected by the SPH factors in the SPH-corrected diffusion equation. In the present article, we will call this SPH correction procedure simultaneous correction. On the other hand, in the SPH-corrected integro-differential transport equation the SPH factor is multiplied to Σ _t which affects both the neutron absorption and the neutron leakage. When Σ _t is increased, the neutron absorption is increased and the neutron leakage is decreased. Thus, the SPH factor in the integro-differential transport equation gives different effects on the reaction rate and the leakage rate from that in the diffusion equation. We will call this SPH correction procedure direct correction.

If the boundary conditions in the homogenized system is same as those in the heterogeneous system in which homogenization is done, the SPH-corrected equation yields the equivalent reaction rates and leakage rates. Thus there is no difference among these correction procedures with the SPH factors. In a usual procedure for reactor core calculations, however, the boundary condition of each fuel assembly is different between a whole-core system and a single-assembly model. Thus these two correction procedures may give different results. This is the main interest in the present study.

Yamamoto has derived the SPH-corrected integro-differential transport equation with the simultaneous correction, which is consistent with the SPH-corrected diffusion equation [6]. This procedure is briefly described in the following.

The SPH-corrected P₁ equation which is equivalent to the SPH-corrected diffusion equation can be written as

where

Yamamoto has extended this concept to the higher order P _N equation as

In order to obtain the consistent integro-differential transport equation, these equations are rewritten as

Thus the simultaneously SPH-corrected integro-differential transport equation can be obtained as

where

Numerical calculations based on this expression seem cumbersome since the high-order Legendre components in the scattering source should be considered even in an isotropic scattering case.

In Yamamoto's formula, the SPH factor is multiplied to the total cross-sections for the even moments of neutron flux, and its inverse is multiplied to those for the odd moments. From a view point of preserving the reaction rate and the leakage rate related to φ₀, correction procedure to the total cross-sections for high moments of neutron flux can be arbitrarily chosen. If we intend to obtain the “rigorously” equivalent homogenized system, however, we have to introduce the SPH factors which are dependent on the total cross-sections for the angular flux moments. Let us show a simple example here. One-dimensional P₃ equations can be expressed in a set of diffusion-like equations composed of only the even-order moments of angular neutron flux as

In order to obtain homogenized equations rigorously equivalent to these equations, we have to preserve the reaction rates related to both the P₀ and P₂ components of angular neutron flux. Thus we have to introduce different SPH factors to the total cross-sections multiplied by φ₀ and φ₂. This discussion is consistent with the concept of the discontinuity factor for the SP₃ equation derived by Kozlowski et al. [8]. In this “rigorous” procedure, the total cross-sections multiplied by the even-moments should be homogenized with the corresponding moment-volume weighting to preserve the reaction rate of these moments. This homogenization procedure is problematic since these moments can take both positive and negative values and the homogenized cross-sections can take unphysical values. Thus this theoretically rigorous treatment is considered impractical.

Here, in order to obtain the simple expression of the simultaneously SPH-corrected integro-differential transport equation, we change the set of equations derived by Yamamoto slightly as follows.

With this procedure, the SPH-corrected integro-differential transport equation can be written as

In a comparison with Equation (19), this equation can be much more easily handled with the numerical calculations. In the following, we will use a set of Equations (25)–(28) or Equation (29) as the SPH-corrected transport equation with the simultaneous correction procedure.

3. Calculation

3.1. Calculation configurations and conditions

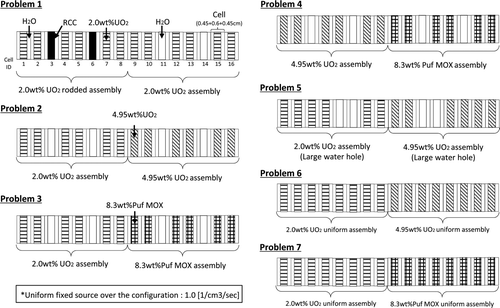
Numerical calculations are done for a set of one-dimensional colorset assembly problems constructed by Yamamoto et al. [9].

Calculation configurations are shown in Figure 1 . These calculation configurations simulate colorset assembly geometry that two different types of assemblies are adjacent. Thickness of fuel and moderator are 0.6 cm and 0.9 cm, respectively, thus the cell-pitch is 1.5 cm. Number of energy group is one and uniform fixed source over the configuration, whose intensity is 1.0 (1/cm³/s), is assumed. This assumption captures the situation in thermal energy groups of light water reactor assembly calculation [9]. Cross-sections used in these calculations are shown in Table 1 .

Figure 1. Calculation configurations.

Table 1. List of cross-sections.

Material	Cross-section (1/cm)
	Absorption	Total
4.95 wt.% UO2	0.38	0.75
2.00 wt.% UO2	0.18	0.55
RCC	7.6	7.6
MOX (8.3 wt.% Puf)	2.0	2.3
H2O	0.019	1.3

In this test, we focus on a cell-averaged absorption reaction rate. Reference values are obtained for the colorset assembly by diamond-differencing discrete-ordinates transport calculations with 16-point double Gaussian angular quadrature set. In order to obtain cell-homogenized cross-sections for each assembly, single assembly calculations are also carried out by the same discrete-ordinates transport method. Cell-homogenized cross-sections are calculated by the flux-volume weighting and the cell-homogenized diffusion coefficients are defined from the homogenized total cross-sections. Then, the cell-homogenized colorset assembly calculations are carried out by two neutron transport computer programs. One is the same as the one used for the reference calculations and the other one is based on the finite-difference P _N method. Since 35 spatial meshes are assigned for each unit cell in all the calculations, truncation errors on the spatial valuable are negligible.

The SPH factors are also obtained in single-assembly calculations. Calculations for a cell-homogenized assembly are carried out with the above mentioned neutron transport methods, and SPH factors for each numerical method are determined to reproduce the reference cell-wise reaction rates.

In order to ease a comparison in accuracy among various calculation cases, maximum and mean values of relative errors in cell-wise absorption reaction rates ε _m are focused on. The maximum error ε_max is obtained as

and the mean value of error ε_mean is calculated as

where m denotes the macro region: a unit cell, and M denotes the number of unit cells (16 in the present problems).

3.2. Results and discussions

Improvement in calculation accuracy attained by the application of the SPH factors is quantified first. Tables 2 and 3 show the results obtained without and with using the SPH factor corrections, respectively. In this case, the direct SPH correction is applied. The SPH correction significantly reduces homogenization errors except for problems 6 and 7. Since each assembly in the problems 6 and 7 is composed of the same unit cell, the SPH factors are 1.0. Thus the SPH correction does not change the results of these problems. It is also found in the SPH-corrected results that the high-order P _N method gives smaller errors than the low-order methods and the P₅ results are almost consistent with the S₁₆ results.

Table 2. Maximum and mean values of errors in cell-wise absorption reaction rate (without SPH factors, unit:%).

Problem	P1		P3		P5		S16
	Maximum	Mean	Maximum	Mean	Maximum	Mean	Maximum	Mean
1	12.5	4.8	6.4	2.7	5.9	2.5	5.6	2.4
2	8.5	2.2	5.2	1.4	4.8	1.3	4.7	1.3
3	20.5	4.6	13.7	3.2	12.8	3.0	12.4	3.0
4	20.5	4.7	13.7	3.2	12.8	3.1	12.4	3.0
5	6.8	1.9	3.9	1.1	3.8	1.1	3.7	1.0
6	2.5	0.4	1.8	0.3	1.7	0.3	1.7	0.3
7	9.8	1.3	7.5	1.0	7.2	1.0	7.0	1.0

Table 3. Maximum and mean values of errors in cell-wise absorption reaction rate (with SPH factors, direct correction, unit:%).

Problem	P1		P3		P5		S16
	Maximum	Mean	Maximum	Mean	Maximum	Mean	Maximum	Mean
1	1.9	0.32	1.0	0.22	1.1	0.22	1.0	0.22
2	2.1	0.37	1.5	0.23	1.4	0.22	1.4	0.22
3	7.8	1.10	5.6	0.80	5.3	0.78	5.2	0.76
4	4.7	0.62	3.1	0.42	2.9	0.40	2.8	0.39
5	2.0	0.34	1.4	0.21	1.3	0.21	1.3	0.20
6	2.5	0.42	1.8	0.28	1.7	0.27	1.7	0.26
7	9.8	1.33	7.5	1.03	7.2	1.00	7.0	0.98

Secondly, the simultaneous correction is adopted to the SPH-corrected calculations. The result is shown in Table 4 . In comparison with the result shown in Table 3, the simultaneous correction clearly results in smaller errors than the direct correction in the same-order calculations. As in the results of the direct correction, the P₅ results are consistent with the S₁₆ results.

Table 4. Maximum and mean values of errors in cell-wise absorption reaction rate (with SPH factors, simultaneous correction, unit:%).

Problem	P1		P3		P5		S16
	Maximum	Mean	Maximum	Mean	Maximum	Mean	Maximum	Mean
1	1.6	0.30	1.1	0.24	1.1	0.25	1.1	0.25
2	2.0	0.33	1.4	0.21	1.4	0.20	1.3	0.20
3	4.7	0.56	3.0	0.37	3.1	0.36	2.8	0.35
4	2.8	0.32	1.5	0.19	1.6	0.18	1.4	0.17
5	1.8	0.29	1.3	0.19	1.3	0.18	1.2	0.18

As shown in the previous section, there is another procedure to apply the SPH factors to the high-order P _N equation, that is Yamamoto's method shown in Equations (11)–(14). So the comparison is done between the different SPH correction procedures for the high-order P _N equation. Furthermore, in order to see the effect of the SPH correction to the total cross-sections multiplied by the high-order neutron flux moments, we also carry out another calculation in which the total cross-sections multiplied by the high-order neutron flux moment (larger than the first moment) are not corrected by the SPH factor. Table 5 shows result of the P₅ calculations. While Yamamoto's procedure gives the smallest errors, no significant differences are observed among three methods. The SPH correction for high-order total cross-sections does not affect calculation accuracy in the present benchmark problems.

Table 5. Maximum and mean values of errors in cell-wise absorption reaction rate (with SPH factors, simultaneous correction, P₅, unit:%).

Problem	Present		Yamamoto		No correction
	Maximum	Mean	Maximum	Mean	Maximum	Mean
1	1.1	0.25	1.1	0.23	1.1	0.24
2	1.4	0.20	1.3	0.20	1.3	0.20
3	2.9	0.36	2.5	0.33	2.8	0.33
4	1.5	0.18	1.2	0.19	1.4	0.18
5	1.2	0.18	1.2	0.18	1.2	0.18

From above numerical calculations, we have found that the SPH method with the simultaneous correction provides more accurate results than that with the direct correction. Also we have found that the accuracy improvement can be achieved by introducing the higher-order calculations such as P₅ and S₁₆ calculations since the neutron transport effect between different adjacent assemblies can be better captured by the higher-order calculations. Errors in the cell-wise absorption rates of the simultaneously SPH-corrected P₅ calculations are listed in Table 6 .

Table 6. Errors in cell-wise absorption reaction rate (with SPH factors, simultaneous correction, P₅, unit:%).

Cell ID	Problem
	1	2	3	4	5	6	7
1	−0.00	0.01	0.03	0.01	0.01	0.01	−0.00
2	−0.00	0.01	0.02	0.01	0.01	0.00	−0.01
3	0.05	0.02	0.06	0.03	−0.00	0.00	−0.04
4	0.15	−0.01	0.02	0.04	−0.02	−0.01	−0.12
5	0.33	−0.05	−0.03	0.05	0.01	−0.06	−0.30
6	0.05	−0.00	0.15	0.21	0.01	−0.17	−0.77
7	0.53	−0.35	−0.48	0.03	−0.30	−0.50	−2.05
8	1.13	−1.35	−2.94	−1.50	−1.24	−1.70	−7.15
9	−1.12	1.18	0.40	0.11	1.07	1.48	3.30
10	−0.40	0.14	1.08	0.56	0.10	0.29	1.73
11	−0.08	−0.10	0.34	0.18	−0.10	0.04	0.37
12	−0.08	−0.01	0.12	0.06	−0.06	−0.01	0.06
13	−0.03	−0.02	0.02	0.01	−0.01	−0.01	0.01
14	0.00	−0.02	0.00	−0.00	−0.01	−0.01	0.00
15	−0.00	−0.01	0.00	0.00	−0.01	−0.01	0.00
16	0.00	−0.01	0.01	0.01	−0.00	−0.00	0.00

Even using the above SPH-correction techniques, however, non-negligible errors are observed in the cells around the boundary between different types of assemblies. These errors come from the following facts; the conventional SPH factor method cannot consider the flux discontinuity between different assemblies and the cell-homogenized cross-sections are obtained with a single assembly model. The problem due to the former can be partly overcome by introducing the improved SPH method proposed by Yamamoto et al. [10]. In the improved SPH method, the flux discontinuity between assemblies is calculated from the following equation:

where DF_SPH is a flux discontinuity factor for the improved SPH method, φ^het,sur is the surface flux of assembly obtained by a cell-heterogeneous calculation, and φ^hom,SPH,sur is the surface flux of assembly obtained by a cell-homogenized calculation using the SPH factors. Since DF_SPH is dependent on the cell surfaces, the direct use of DF_SPH reduces the merit of the SPH factor method. To overcome this problem, an assumption that DF_SPH is constant throughout the assembly surface is introduced in the improved SPH method. Then the discontinuity factor is defined for each cell and can be incorporated by dividing all (SPH-corrected) cross-sections in the assembly [9]. Thus the inverse of DF_SPH can be regarded as an additional SPH factor in the simultaneously SPH-corrected P _N equation.

Under the diffusion approximation, surface partial current J _± can be expressed by the surface flux φ^sur and the surface net current J as

Since the surface net current is zero in the reflective boundary conditions, the partial current can be simply written as

As pointed out by Sanchez [1], the introduction of discontinuity factor is equivalent to the preservation of partial surface current under the diffusion approximation since Equation (32) can be transformed as

Thus, the improved SPH method can be regarded as a family of the SPH factor method with the Selengut normalization condition [11], and is related to the third generation SPH factor method developed by Hébert and Mathonniére [12].

Calculations with the improved SPH method are carried out with the simultaneously SPH-corrected S₁₆ method. For a comparison, the SPH-corrected calculations with the Selengut normalization condition are also conducted. Results are summarized in Table 7 . By introducing these improved methods, homogenization errors are significantly reduced especially for the problems 6 and 7. It is noteworthy to indicate that the improvement achieved by introducing the Selengut normalization condition is larger than that of the improved SPH method. This is because the simultaneously SPH-corrected integro-differential equation presently used is an approximated form as shown in Equations (25)–(28) and the flux discontinuity factor cannot be regarded as the inverse of the SPH factors in a rigorous sense. Thus, the improved SPH method in the present calculations does not preserve the surface neutron flux. This result suggests that the SPH method with the Selengut normalization condition is more robust since it directly preserves the surface neutron flux between heterogeneous and homogenized systems.

Table 7. Maximum and mean values of errors in cell-wise absorption reaction rate (with SPH factors, improved methods, simultaneous correction, P₅, unit:%).

Problem	Improved SPH		Selengut normalization		Flux-volume normalization
	Maximum	Mean	Maximum	Mean	Maximum	Mean
1	0.6	0.18	0.5	0.13	1.1	0.25
2	0.7	0.15	0.3	0.11	1.3	0.20
3	1.7	0.49	1.5	0.27	2.8	0.35
4	1.7	0.42	1.1	0.18	1.4	0.17
5	0.6	0.14	0.2	0.11	1.2	0.18
6	0.3	0.09	0.3	0.09	1.7	0.26
7	1.4	0.24	1.4	0.24	7.0	0.98

Table 8 shows the cell-wise errors in absorption reaction rates of the S₁₆ calculations with the Selengut-normalization SPH method. Significant accuracy improvement around the boundary can be observed in comparison with the results shown in Table 6.

Table 8. Errors in cell-wise absorption reaction rate (with SPH factors, Selengut normalization, S₁₆, unit:%).

Cell ID	Problem
	1	2	3	4	5	6	7
1	−0.00	0.02	0.05	0.01	0.02	0.02	0.04
2	0.00	0.03	0.06	0.02	0.03	0.02	0.06
3	0.04	0.06	0.14	0.05	0.04	0.03	0.09
4	0.13	0.06	0.15	0.07	0.05	0.05	0.15
5	0.30	0.07	0.22	0.13	0.14	0.08	0.25
6	−0.11	0.24	0.66	0.39	0.24	0.11	0.40
7	0.17	0.13	0.58	0.46	0.16	0.09	0.58
8	0.52	−0.21	0.05	0.07	−0.15	−0.28	0.14
9	−0.53	0.24	−1.49	−1.11	0.19	0.39	−1.39
10	−0.13	−0.21	0.66	0.33	−0.23	−0.17	0.54
11	0.06	−0.27	0.23	0.12	−0.25	−0.15	0.12
12	−0.00	−0.09	0.08	0.04	−0.14	−0.09	0.02
13	0.01	−0.05	0.01	0.01	−0.06	−0.05	0.00
14	0.02	−0.04	0.00	0.00	−0.04	−0.02	−0.00
15	0.01	−0.02	0.00	0.00	−0.02	−0.01	0.00
16	0.01	−0.01	0.00	0.00	−0.02	−0.01	0.00

4. Conclusion

The present article focuses on the application of the SPH factor method to the integro-differential neutron transport equation. The SPH factor method is to obtain equivalent homogenized cross-sections which reproduce the reaction rate and the leakage rate of a heterogeneous system. That is achieved by searching the proper set of SPH-corrected cross-sections so as to preserve the reaction rate. Since the reflective boundary conditions are usually posed and there is no net leakage in the boundary surface, preservation of the leakage rate is attained implicitly. Thus leakage-related parameters such as diffusion coefficients or total cross-sections are arbitrarily adjusted by the SPH factors. In the present article, we have treated two correction procedures; the simultaneous correction and the direct correction.

The SPH-corrected cross-sections are guaranteed to reproduce the reaction rate and the leakage rate of the reference heterogeneous system if the same reflective boundary conditions are assigned in a homogenized system. In usual reactor core calculations, however, this situation is not true, hence the different SPH-correction procedure shows different accuracy. We have tested these different procedures to one-dimensional colorset assembly problems and quantified the errors of each procedure. Furthermore, reference calculations have been done with the S _N transport method and several low-order methods have been also tested.

Through numerical testing, the following observations have been obtained:

•	The simultaneous SPH correction gives better accuracy than the direct SPH correction.
•	The higher-order SPH-corrected calculations show better accuracy than the low-order SPH-corrected calculations.
•	The SPH correction for total cross-sections multiplied by the high-order neutron flux moments does not significantly affect the accuracy.

The second point motivates to improve the existing reactor core calculation method by replacing the diffusion or SP₃ method by the high-order method such as the S _N method as a whole-core calculation engine.

Furthermore, to consider the flux discontinuity between different adjacent assemblies, the improved SPH method proposed by Yamamoto has been tested, and significant accuracy improvement has been observed. It has also been shown that the improved SPH method is similar to the SPH method with the Selengut normalization condition, and that the former method is more robust since it directly preserves the surface neutron flux.

The present numerical study has compared several procedures of the SPH method for the integro-differential neutron transport equation, and has proposed the procedure expected to show the best performance among them. To give theoretical foundation to the present conclusion and to confirm it by testing for more realistic problems are necessary for future works.