Development of numerical analysis method of flow-acoustic resonance in stub pipes of safety relief valves

Abstract

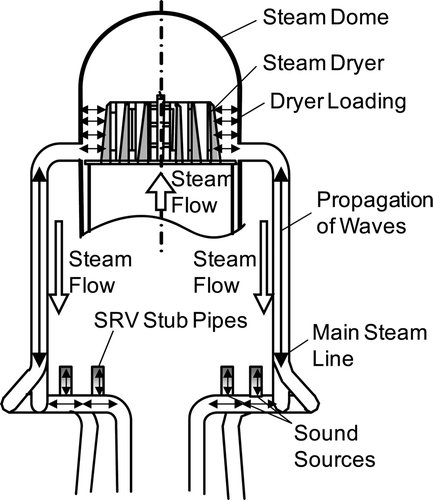
The boiling water reactors (BWRs) have steam dryer in the upper part of the pressure vessel to remove moisture from the steam. The steam dryer in the Quad Cities Unit 2 nuclear power plant was damaged by high-cycle fatigue due to acoustic-induced vibration during extended power uprate operation. The principal source of the acoustic-induced vibration was flow-acoustic resonance at the stub pipes of the safety relief valves (SRVs) in the main steam lines (MSLs). The acoustic wave generated at the SRV stub pipes propagates throughout the MSLs and eventually reaches and damages the steam dryer. Therefore, for power uprate operation of the BWRs, it has been required to predict the flow-acoustic resonance at the SRV stub pipes. The purpose of this article was to propose a numerical analysis method for evaluating the flow-acoustic resonance in the SRV stub pipes. The proposed method is based on the finite difference lattice Boltzmann method (FDLBM). So far, the FDLBM has been applied to flow-acoustic simulations of laminar flows around simple geometries at low Reynolds number. In order to apply the FDLBM to the flow-acoustic resonance simulations of turbulent flows around complicated geometries at the high Reynolds number, we developed computationally efficient model by introducing new function into the governing equation. The proposed method was compared with the conventional FDLBM in the cavity-driven flow simulation. The proposed method was validated by comparisons with the experimental data in the 1/10-scale test of BWR-5 under atmosphere condition. The following three results were obtained; the first is that the proposed method can reduce the computing time by 30% compared with the conventional FDLBM; the second is that the proposed method successfully simulated the flow-acoustic resonance in the SRV stub pipes of the BWR-5, and the pressure fluctuations of the simulation results agreed well with those of the experimental data; and the third is the mechanism of the flow-acoustic resonance in the SRV stub pipes. Acoustic waves causing the flow-acoustic resonance in the SRV stub pipes are generated by the unsteady vortices in the SRV stub pipes.

Keywords:

• boiling water reactor
• power uprate operation
• steam dryer
• safety relief valve
• flow-acoustic resonance
• numerical analysis
• computational fluid dynamics
• finite difference lattice Boltzmann method

1. Introduction

In recent years, extended power uprate (EPU) operation has been implemented in many boiling water reactors (BWRs) in the United States. The BWR in the Quad Cities Unit 2 (QC-2) experienced a significant increase in steam moisture in the main steam lines (MSLs) at EPU operation [1]. Inspection showed that the steam dryer which is installed in the upper part of the pressure vessel had been damaged by high-cycle fatigue due to acoustic-induced vibration. DeBoo et al. [2] investigated sound sources of the acoustic-induced vibration using actual plant data. Their results showed that the principal source was flow-acoustic resonance at the stub pipes of the safety relief valves (SRVs) in the MSLs. It was likely that the acoustic wave generated in the SRV stub pipes propagated from the SRV stub pipes to the steam dryer throughout the MSLs and eventually reached and damaged the steam dryer (Figure 1). Therefore, for power uprate operation of the BWRs, the flow-acoustic resonance at the SRV stub pipes needs to be predicted. We have started a research program to develop evaluation methods for the steam dryer vibration [3]. The purpose of this article is to propose a numerical analysis method for evaluating the flow-acoustic resonance in the SRV stub pipes.

Figure 1. Propagation of acoustic-induced vibration from SRV to the steam dryer.

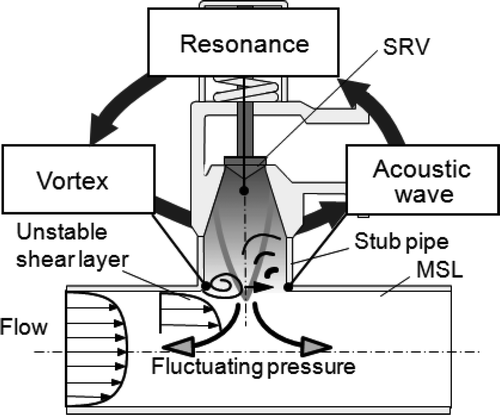
The flow-acoustic resonance may occur in a piping system with closed side branches, such as the SRV stub pipe. The flow-acoustic resonance is produced by interaction between acoustic wave and an unstable shear layer across the SRV stub pipe (Figure 2). The unstable shear layer promotes and enhances the formation of vortices in the SRV stub pipe. These vortices trigger the formation of the acoustic wave. If the vortex shedding frequency is close to the acoustic resonance frequency of the SRV stub pipe, the vortex shedding frequency is locked in the acoustic resonance frequency and then the flow-acoustic resonance occurs. When the resonance occurs, the amplitude of the acoustic wave can be several times higher than the dynamic pressure in the MSLs. Many experimental studies [4–10] related to flow-acoustic resonance of closed side branches have been reported. Jungowski et al. [4] investigated the effect of the diameter ratio on the Strouhal number and the amplitude of the acoustic wave. Bruggeman et al. [5] proposed a theoretical model for the acoustic sources responsible for the flow-acoustic resonance in a piping system with closed side branches. Ziada and Buhlmann [6] demonstrated that side branches in close proximity are particularly liable to resonance. Kriesels et al. [7] studied the detailed behavior of the flow in a piping system with two opposite closed side branches of equal length in a cross configuration. Visualization of the flow-acoustic resonance was also studied by Ziada [8], Dequand et al. [9], and Li et al. [10].

Figure 2. Mechanism of flow-acoustic resonance at the SRV stub pipe.

On the other hand, a numerical analysis is helpful for the prediction of occurrence of the flow-acoustic resonance and the easy understanding of phenomena of the flow-acoustic resonance in the stub pipes of the SRVs. However, a numerical analysis of the flow-acoustic resonance is difficult due to the need to capture interaction between the vortex and the acoustic wave in the SRV stub pipe. In particular, pressure fluctuations of the acoustic wave are very small compared with those of the vortex when the flow-acoustic resonance begins to occur. Therefore, the numerical analysis method which can accurately capture the acoustic wave is required for the flow-acoustic simulations. The compact finite difference scheme [11–16] is often applied to the computational aero-acoustics (CAA) simulations. However, the compact finite difference scheme is liable to become unstable and requires large computational effort compared with the traditional finite difference schemes due to its implicit algorithms [17]. Recently, the finite difference lattice Boltzmann method (FDLBM) [18–26] has been verified as an alternative method which can accurately capture the acoustic wave. The FDLBM is the numerical analysis method which is developed from the lattice Boltzmann method (LBM) [27–38]. Unlike conventional computational fluid dynamics (CFD) methods based on discretizations of the fluid dynamics equations, the LBM is based on the kinetic equation of the molecular gas dynamics. Chen and Doolen [38] presented the view that the LBM is not only computationally comparable with traditional numerical analysis methods, but it is also easy to program and to include new physics because of the simple form of the equation of this method. The FDLBM in which the kinetic equation is discretized by the finite difference scheme has been developed for improvements of numerical stability of the LBM. Tsutahara et al. [23] has reported that interaction between the vortex and the acoustic wave can be well captured by the FDLBM in the simulation of the flow around the two-dimensional circular cylinder.

The FDLBM is considered to be appropriate to the numerical analysis method for the flow-acoustic resonance simulations at the SRV stub pipes. However, so far, the FDLBM has been applied to flow-acoustic simulations of laminar flows around simple geometries such as two-dimensional circular cylinder at low Reynolds number because of its computational cost [23]. In this article, we developed computationally efficient model in order to apply the FDLBM to the flow-acoustic resonance simulations of turbulent flows around complicated geometries such as the SRV stub pipes. The developed method was compared with the conventional FDLBM in the cavity-driven flow simulation. The developed method was validated by comparisons with the experimental data in the 1/10-scale test of BWR-5 under atmosphere condition. The mechanism of the flow-acoustic resonance at the SRV stub pipes was also discussed by the simulation results.

2. Numerical method

2.1. Finite difference Lattice Boltzmann method

In this section, we introduce the FDLBM developed by Tsutahara et al. [23] The FDLBM is different from traditional CFD methods and is based on the molecular gas dynamics. The FDLBM can be derived from the Boltzmann equation which is a basic equation of the molecular gas dynamics. In the FDLBM, the density ρ and the flow velocity u _α  are given from the velocity distribution function f_i taking the moments of the molecular velocities c_{i α}  as

where the respective subscripts i and α indicate the molecular velocity direction and the spatial direction in the Cartesian coordinates. I is the number of directions of the molecular velocities.

The equation to be solved in the FDLBM is the following kinetic equation (discrete-velocity Bhatnagar-Gross-Krook (BGK) equation):

where t and x _β are the time and the Cartesian coordinates, respectively. The first term of the right-hand side shows the lattice BGK collision operator. is the local equilibrium distribution function which is calculated by the macroscopic variables. The relaxation time τ which represents the rate of approach to equilibrium state is proportional to the coefficient of molecular viscosity μ. The last term of the right-hand side operates for maintaining numerical stability of the FDLBM when the molecular viscosity is set to small value. As the molecular velocity model, which defines the number of the molecular velocities and the form of the local equilibrium distribution function, a three-dimensional 15-velocity model (D3Q15) [33] or a three-dimensional 39-velocity model (D3Q39) [23] is used. The spatial derivatives of the Equation (3) are discretized by the third-order upwind scheme. The two-stage second-order Runge-Kutta method is used for the time integration of Equation (3). The calculation procedure of the FDLBM is shown in Figure 3.

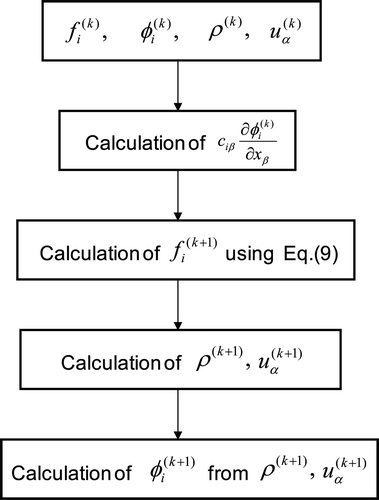
Figure 3. Calculation procedure of the conventional FDLBM [23].

2.2. Computational acceleration

In order to apply the FDLBM to the numerical analysis of the flow-acoustic resonance at the SRV stub pipes, there is the need for improvements of its computational efficiency. In this section, we develop improvements for computational acceleration of the FDLBM. Most of the computations of the FDLBM are occupied by the calculation of the spatial-derivative terms and the calculation of the equilibrium distribution function. Equation (3) includes three spatial-derivative terms. Uniting these derivative terms leads to computational acceleration of the FDLBM. To do this, we proposed a new function φ _i instead of the equilibrium distribution function . The new function consists of the distribution function and the equilibrium distribution function.

where the new function satisfies the following equations:

A, which was proposed by Tsutahara et al. [23], is a constant corresponding to the molecular (laminar) viscosity μ. B, which we introduce, is the variable related to the turbulent viscosity μ _T . A and B are defined by the following equations:

where c represents the speed of sound. We proposed a new governing equation of the FDLBM using the new function φ _i :

Calculation procedure of the developed method is shown in Figure 4. Computational efficiency of the FDLBM can be increased by using Equation (9) instead of Equation (3) because the number of the spatial-derivative terms is reduced. By the Chapman-Enskog analysis, it is shown that Equation (9) is equal to Equation (3). In this analysis, the distribution function f_i and the function φ _i are expanded about the equilibrium distribution function :

where ε is small parameter. Substituting Equations (10) and (11) in Equation (9), the following equation is obtained.

With some algebraic calculations, the Navier-Stokes equations are derived from Equation (12). As the molecular velocity model, a three-dimensional 13-velocity model (D3Q13) [26] whose computational efficiency is superior to that of D3Q15 is employed. The molecular velocities c of D3Q13 are shown in Figure 5 and Table 1. The speed of sound c and the pressure p are obtained by and p = pc ², respectively. Isothermal compressible fluid in which the speed of sound is constant is derived from D3Q13. In the low Mach number flows, error of isothermal assumption becomes O(Ma²) [39]. The error is negligible in our simulations since the Mach number is less than 0.2. In this model, the function φ _i is shown as

Figure 4. Calculation procedure of the developed method.

Figure 5. Distribution of the molecule velocities c_{i α}  [26].

Table 1. Cartesian components of the molecule velocities [26], where and .

i	cix	ciy	ciz
1	0	0	0
2	0	c 1	c 2
3	0	−c 1	c 2
4	0	c 1	−c 2
5	0	−c 1	−c 2
6	c 2	0	c 1
7	−c 2	0	c 1
8	c 2	0	−c 1
9	−c 2	0	−c 1
10	c 1	c 2	0
11	−c 1	c 2	0
12	c 1	−c 2	0
13	−c 1	−c 2	0

The four-stage second-order Runge-Kutta method is used for the time integration of Equation (9) because we can use a large Courant-Friedricks-Lewey (CFL) number cΔt/Δx in three-dimensional simulations compared with the two-stage second-order Runge-Kuuta method. The four-stage second-order Runge-Kutta method is as follows.

In order to increase simulation accuracy, the spatial derivative of Equation (9) is discretized by the sixth-order central-difference scheme as follows.

The turbulent viscosity is calculated by the lattice Boltzmann subgrid model [38]. As the lattice Boltzmann subgrid model, we employ the Smagorinsky eddy viscosity model, which computes the turbulent viscosity μ _T from the local shear rate and the filter size:

where S _αβ  is the resolved strain rate tensor and is the local intensity of the strain tensor. The velocity distribution function is filtered by the Favre averaging. The filter size Δ is computed as the cubic root of the grid volume. The Smagorinsky coefficient C is computed by the dynamic Smagorinsky model [40].

2.3. Validation of the developed method

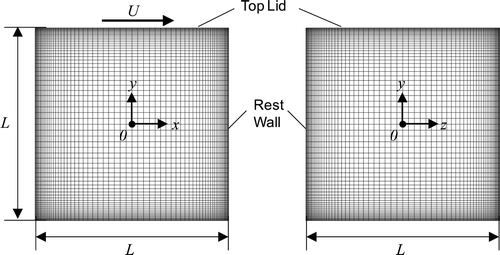
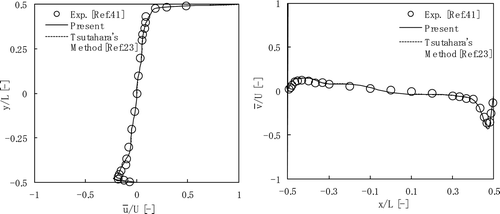
In this section, the proposed method is compared with the FDLBM developed by Tsutahara et al. [23] with respect to computational efficiency. Both methods are discretized by the same numerical schemes. Comparison between the developed method and Tsutahara's method is shown in Table 2. The analysis object is the cavity-driven flow at the Reynolds number of 12,000 [41]. The flow is induced by the top lid that moves in the x-direction. The non-uniform grid for the computation is shown in Figure 6. The grid number is 71×71×71, and the minimum grid width is 0.002L. The CFL number is 1.0. On the rest wall, the non-slip boundary condition is applied. On the top lid, the Neumann type boundary condition is applied for the density and the velocity is constant. The flow velocity of the simulation results are shown in Figure 7. Both simulation results agree well with the experimental result. The developed method can reduce the computing time by 30% compared with the conventional FDLBM.

Figure 6. Computational grid for simulation of the cavity driven flow.

Figure 7. Time-averaged flow in the cavity driven flow simulation.

Table 2. Comparison between the developed method and the conventional FDLBM [23].

Item	Developed method	Tsutahara's model [23]
Governing equation	Equation (9)	Equation (3)
Molecular velocity model	D3Q13	D3Q13
Spatial discretization	Sixth-order central difference	Sixth-order central difference
Time integration	Four-step second-order Runge-Kutta	Four-step second-order Runge-Kutta
Turbulence model	Dynamic Smagorinsky	Dynamic Smagorisnsky

3. Acoustic resonance simulations

3.1. Analysis conditions

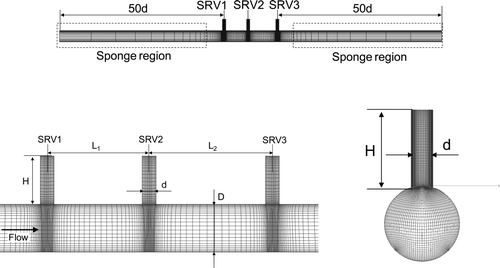
We applied the developed method to simulations of the flow-acoustic resonance in the SRV stub pipes. Our analysis object is the SRV stub pipes of the 1/10-scale test apparatus [3] illustrated in Figure 8. The 1/10-scale test apparatus was made with reference to a BWR-5. In these simulations, we focused on the SRV stub pipes which consist of three side branches. The configuration of the SRV stub pipes is shown in Figure 8(b). Fluctuating pressures induced by the flow-acoustic resonance are measured on the top of the three stub pipes. Air at ordinary temperature is used as fluid instead of steam flow. Physical properties of the fluid are shown in Table 3.

Figure 8. Schematic presentation of the test facility [3].

Table 3. Physical properties of the fluid.

Item	Value
Temperature	20 [deg C]
Density	1.204 [kg/m^3]
Pressure	101.3 [kPa]
Speed of sound	343.7 [m/s]
Molecular viscosity	1.808 × 10^−5 [Pa s]

The multi-block structure grid which is shown in Figure 9 is used for three-dimensional simulations of the flow-acoustic resonance in the SRV stub pipes. The total number of grid points is about 1,500,000. The non-dimensional minimum grid width Δx/d is 0.01. The CFL number is 1.0. On the wall boundary, the flow velocity is given by the wall function defined by the Spaulding law and the density is given by the Neumann type boundary condition. On the inlet boundary, the velocity is constant and the Neumann type boundary condition is applied for the density. On the outlet boundary, the density is constant and the Neumann type boundary condition is applied for the velocity. In order to prevent acoustic waves generated in the SRV stub pipes from reflecting at inlet or outlet boundaries, sponge regions which attenuate the acoustic waves by numerical viscosity are placed as shown in Figure 9(a).

Figure 9. Computational grid for simulations of the flow-acoustic resonance.

The non-dimensional parameters of this problem are the Reynolds number Re and the Strouhal number St. The Strouhal number St is defined by the following equation:

where f_r is the resonant frequency of the SRV stub pipe:

U is the mean flow velocity in the main pipe. The Strouhal number St is changed from 0.30 to 0.71. The Reynolds number Re is also changed from 120,000 to 350,000.

3.2. Results and discussion

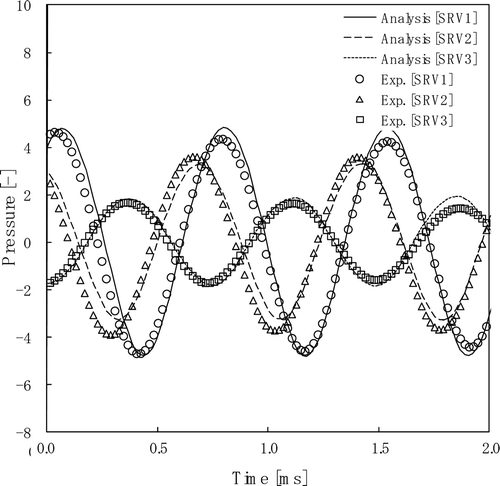
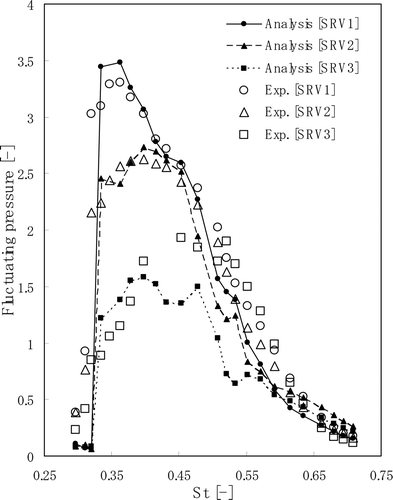
We note that the large fluctuating pressure induced by the flow-acoustic resonance occurs at the flow condition under which the flow velocity is excessively increased compared with the velocity at normal operation. Time variation of pressure fluctuations on the top of the SRV stub pipes at the Strouhal number of 0.36 is shown in Figure 10. The pressure is normalized by the dynamic pressure in the main pipe. The results show a substantial sinusoidal waveform. Large pressure fluctuations occur due to the flow-acoustic resonance in the SRV stub pipes. The numerical results show good agreement with the experimental data. The amplitudes of the pressure fluctuations defined as effective value of time variation of pressure fluctuations are plotted against the Strouhal number in Figure 11. The stub pipe of SRV1 placed upstream induces the largest pressure fluctuation. The amplitude of the pressure fluctuation becomes 3.5. The Strouhal number corresponding to the largest fluctuating pressure is approximately 0.36. The numerical results of SRV1 and SRV2 show good agreement with the experimental data. The numerical results of SRV3 are slightly different from the experimental data. The reason is likely that SRV3 is affected by vortices which come from SRV1 and SRV2.

Figure 10. Pressure fluctuations on the top of the SRV stub pipes at St = 0.36.

Figure 11. Amplitudes of the pressure fluctuations as functions of the Strouhal number.

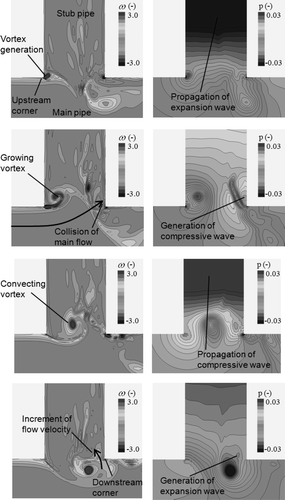
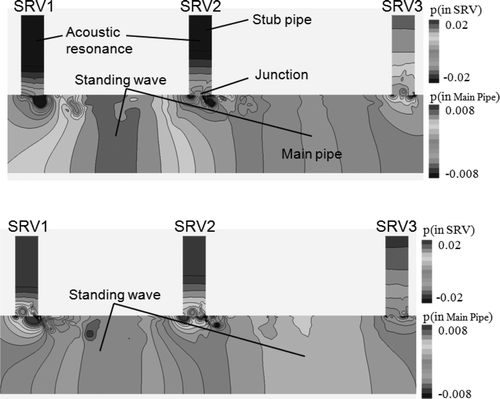
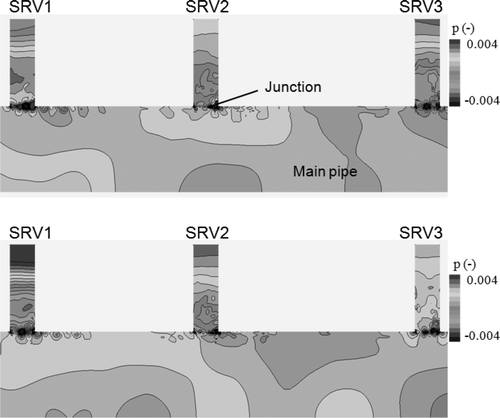
In order to investigate the mechanism of the flow-acoustic resonance, we show vorticity field and pressure field of the SRV1 of the simulation results in Figure 12, where T represents the cycle of the unsteady vortex motion. The vorticity ω is non-dimensionalized by the diameter of the stub pipe d and the speed of sound c. The pressure p is non-dimensionalized by c ² and the density ρ. Anti-clockwise vorticity is defined as positive. The Strouhal number is 0.36 which corresponds to the flow condition where the largest fluctuating pressure occurs in these simulations and experiments. The vortex is periodically generated at the upstream corner (Figure 12(a)). The vortex grows and is convected downward (Figure 12(b) and (c)). Finally, the vortex moves into the main pipe, passing through the neighborhood of the downstream corner (Figure 12(d)). When the vortex is located at the upstream corner, a compressive wave is generated around the downstream corner due to collision of the main flow with the downstream corner (Figure 12(b)). When the vortex is located at the downstream corner, the flow velocity around the downstream corner is increased by the vortex-induced velocity. As a result, an expansion wave is generated around the downstream corner. Acoustic resonance in the SRV stub pipes is shown in Figure 13. The first quarter-wave resonance occurs in all stub pipes. The standing wave is observed between SRV1 and SRV2 because their phases are almost the same. Pressure distribution in the SRV stub pipes at the Strouhal number of 0.29 which corresponds to the flow condition of the small pressure fluctuations is shown in Figure 14. The first quarter-wave resonance does not occur in all stub pipes. The standing wave in the main pipe is not observed in this case.

Figure 12. Unsteady motion of the vortex at the stub pipe of SRV1 (left, vorticity; right, pressure).

Figure 13. Pressure distribution in the SRV stub pipes at St = 0.36.

Figure 14. Pressure distribution in the SRV stub pipes at St = 0.29.

4. Conclusions

In this article, we proposed a numerical analysis method based on the FDLBM for evaluating the flow-acoustic resonance in the SRV stub pipes. In order to apply the FDLBM to the flow-acoustic resonance simulations, we developed computationally efficient model by introducing new function into the governing equation. The developed method was compared with the conventional FDLBM in the cavity-driven flow. The developed method was validated by comparisons with the experimental data in the 1/10-scale test of BWR-5. The mechanism of the flow-acoustic resonance was also discussed by the simulation results. The following results were obtained.

1.	In order to increase computational efficiency of the FDLBM, we developed a new function which consists of the distribution function and the equilibrium distribution function. The simplified governing equation of the FDLBM was proposed by introducing the new function. It was found that the developed method can reduce the computing time by 30% compared with the conventional FDLBM.
2.	The developed method was applied to the numerical analyses of the flow-acoustic resonance in the SRV stub pipes of the 1/10-scale test of BWR-5. The developed method successfully simulated the flow-acoustic resonance at the SRV stub pipes of the BWR-5. Time variation of the pressure fluctuations becomes substantially sinusoidal waveform. The pressure fluctuations of the simulation results agreed well with those of the experimental data.
3.	Acoustic waves causing the flow-acoustic resonance in the SRV stub pipes were generated by the unsteady vortices in the SRV stub pipes. When the vortex was located at the upstream corner, a compressive wave was generated around the downstream corner due to a collision of the main flow with the downstream corner. When the vortex was located at the downstream corner, the flow velocity around the downstream corner was increased by the vortex-induced velocity. As a result, an expansion wave was generated around the downstream corner.

Acknowledgements

We would like to thank Prof. Fujii and Dr. Nonomura of ISAS-JAXA for many enlightening discussions about the compact finite difference scheme and insightful comments.