Abstract
The count-loss effect in determination of neutron decay constant by pulsed neutron source method was investigated. It was found that overestimation of neutron decay constant due to count-loss effect is seen while underestimation appears superiorly as the intensity of pulsed neutron source is getting higher. It was further demonstrated that the well-known count-loss correction procedures are not effective for overestimation although they suppress underestimation. Therefore, the pulsed neutron source method should be modified so as to have robustness against the count-loss effect.
1. Introduction
Measurement of subcriticality (i.e., negative reactivity) is one of the most important subjects in the field of reactor physics since it is closely related to the nuclear criticality safety. The pulsed neutron source method that can measure the subcriticality through determination of neutron decay constant is the most popular one [Citation1], and has been applied to many subcritical reactor systems [Citation2–6]. Experimental investigations based on pulsed neutron source method are still being pursued to meet a renewed necessity of subcriticality measurement (or monitoring) for accelerator-driven systems [Citation7–11]. In future researches on criticality management of fuel debris generated in the severe accident of light water reactors [Citation12], it is expected that the pulsed neutron source method will play important roles.
Owing to a great amount of efforts devoted by many researchers [Citation13–19], the pulsed neutron source method is now regarded to be the most reliable and established one for measuring the subcriticality. Nevertheless, a further discussion on pulsed neutron source method is provided in the present paper since it is needed to investigate an unresolved issue, i.e., the count-loss effect in determination of neutron decay constant.
It is well known that the radiation counting system (that consists of a radiation detector and instrumentation circuits) inevitably involves the count-loss process owing to the dead time, i.e., the minimum duration of time for separating a couple of detection events in radiation detector into two output pulse signals [Citation20]. Therefore, one is not always able to extract accurate information on radiation filed of interest from the radiation counting system owing to the count-loss effect.
It is naturally expected that the count-loss effect also appears in the pulsed neutron source method that employs the neutron counting system (i.e., a neutron detector and instrumentation circuits). One, hence, often intends to eliminate the count-loss effect by introducing the well-known count-loss correction procedures [Citation20] in determining the neutron decay constant. However, elimination of count-loss effect that is brought by these count-loss correction procedures has not been verified yet. Furthermore, the characteristics of count-loss effect in determination of neutron decay constant themselves have not been well understood yet. The goal of present paper is to investigate these two subjects on the basis of the neutron observation probability that is derived by explicitly considering the count-loss process in neutron counting system and the periodic burst of pulsed neutrons.
In the following section, derivation of neutron observation probability is provided. The count-loss effect in determination of neutron decay constant by pulsed neutron source method is then discussed in Section 3. Verification of count-loss correction procedures for eliminating the count-loss effect is described in the same section. Finally, the conclusion is summarized in Section 4.
2. Theory of pulsed neutron source method with count-loss process
2.1. Degweker’s formulation
It is well known that there are two different models for count-loss process that correspond to the idealized responses of radiation counting system, i.e., the paralyzable and non-paralyzable ones [Citation20]. In the present paper, the paralyzable count-loss process is assumed for simple discussion. We would like to note here that the real counting system involves a count-loss process that is not one of either of these two models but an intermediate one between them. However, the difference between these two models is small when the frequency of neutron capture events in neutron detector is low, so that this assumption brings few problems for this region.
In 1989, Degweker paid attention to the fact that the neutron counting system that involves the paralyzable count-loss process with dead time τ can generate an output pulse signal at time t when the neutron detector captures no neutrons within the preceding time interval (t − τ, t) as shown in and developed a rigorous formulation approach for treating the count-loss process [Citation21] on the basis of the backward master equation formalism [Citation22–25]. According to Degweker, one derives the neutron observation probability within infinitesimal time interval dt around t (or the expectation value of number of neutrons observed within dt around t) that explicitly considers the paralyzable count-loss process in neutron counting system, i.e., p(τ, t)dt, as follows:
(1)
Here,
(2)
is the source-induced probability that Z1 and Z2 neutrons are captured by the neutron detector within the respective time intervals (t − T1 − T2, t − T2) and (t − T2, t) that are mutually adjacent and non-overlapping under the condition that an extraneous neutron source is introduced at time 0. The timing diagram of is illustrated in .
Figure 1. Illustration of paralyzable count-loss process.
Figure 2. Timing diagram of source-induced probability .
One understands from Equation (Equation1(1) ) that p(τ, t)dt is derived when the analytical expression of
is obtained. In the Degweker’s formulation, however, one does not obtain
but the following probability generating function (PGF) for simple mathematical manipulation, i.e.,
(3)
Using this PGF, Equation (Equation1(1) ) is re-written as follows:
(4)
In the following subsections, to derive the neutron observation probability that explicitly considers the count-loss process in neutron counting system and the periodic burst of pulsed neutrons, the analytical expression of is obtained within the one-point reactor approximation model with one group of neutron energy and no delayed neutrons.
2.2. Source-induced probability generating function
Let us suppose a zero-power subcritical reactor system that is coupled with a pulsed neutron source and introduce the following probability:
(5) This is the source-induced probability that Z1 and Z2 neutrons are captured by the neutron detector within the respective time intervals (t − T1 − T2, t − T2) and (t − T2, t) under the condition that the pulsed neutron source is introduced into the subcritical reactor system at time t0 (≤t). The terminal condition of
is read as
(6) The corresponding PGF and its terminal condition are as follows:
(7)
(8)
The time dependence of pulsed neutron source intensity S(t) is illustrated in and is expressed as
(9)
(10) where H(t) is the Heaviside’s step function, Sc and S0 the respective intensity factors of constant and pulsed components, W the pulse width, and T0 the pulse period (0 ≤ W < T0). In the present paper, to avoid complicated mathematical manipulation due to discontinuity of S(t), the Fourier series expansion is alternatively utilized, i.e.,
(11) with the following notations,
(12)
(13)
(14)
(15)
(16)
(17)
Figure 3. Time dependence of pulsed neutron source intensity S(t).
Let us consider where introduction of pulsed neutron source is delayed by Δt0. Assuming that the time interval (t0, t0 + Δt0) is small enough to neglect any twofold source events, one can establish the following probability balance equation [Citation24]:
(18)
where
(19)
is the single-particle-induced probability that Z1 and Z2 neutrons are captured by the neutron detector within the respective time intervals (t − T1 − T2, t − T2) and (t − T2, t) under the condition that an initial neutron is injected into the subcritical reactor system at time 0. The terminal condition of P(Z1, T1, Z2, T2, t) is read as
(20)
Multiplying xZ11xZ22, then performing summation from zero to infinity with respect to Z1 and Z2, one obtains the following equation from Equation (Equation18(18) ):
(21) where
(22)
(23) By letting Δt0 → 0 after some rearrangement, the following differential equation is obtained:
(24) This equation can be solved with the terminal condition given in Equation (Equation8
(8) ), i.e.,
(25) When setting t0 = 0, the following equations,
(26)
(27)
(28)
(29) are obtained. Here, g(x1, T1, x2, T2, t) is defined as
(30)
(31)
In the following subsection, the analytical expression of g(x1, T1, x2, T2, t) is obtained by considering the elementary processes of neutron interactions in subcritical reactor system.
2.3. Single-particle-induced probability generating function
The neutron interactions in subcritical reactor system are described by
(32) where λc is the probability that one neutron is captured per unit time by materials excluding neutron detector in subcritical reactor system, λf the probability that one neutron undergoes a fission reaction per unit time, λd the probability that one neutron is captured per unit time by the neutron detector, v the velocity of neutrons, and Σx the macroscopic cross sections of corresponding interaction types x = c, f, d.
The probability that n neutrons are generated per fission reaction is denoted by
(33) and the rth order factorial moment of number of neutrons generated per fission reaction is defined as follows:
(34)
Here, let us consider P(Z1, T1, Z2, T2, t − Δt) where injection of initial neutron is delayed by Δt. Neglecting any twofold neutron interactions within infinitesimal time interval (0, Δt), the following probability balance equation can be established [Citation25]:
(35) The respective terms in right-hand side correspond to mutually exclusive neutron interactions within (0, Δt). Here, Rn(Z1, T1, Z2, T2, t) is the multi-particle-induced probability that Z1 and Z2 neutrons are captured by the neutron detector within the respective time intervals (t − T1 − T2, t − T2) and (t − T2, t) under the condition that n neutrons are simultaneously injected at time 0. This probability can be easily constructed with P(Z1, T1, Z2, T2, t). For example, Rn(Z1, T1, Z2, T2, t) with respect to n = 0, 1, 2, 3 are written as follows:
(36)
(37)
(38)
(39) On the other hand, by using the Heaviside’s step function H(t), Δ1(t) and Δ2(t) are defined as
(40)
(41) These functions are introduced to describe the status of counting gates by taking zero when closed or unity when opened. Furthermore, Δ0(t) is defined as follows:
(42)
Multiplying xZ11xZ22, then performing summation from zero to infinity with respect to Z1 and Z2, one obtains the following equation from Equation (Equation35(35) ):
(43) Hence, the following backward master equation is obtained by making some rearrangement, then letting Δt → 0:
(44) Rewriting Equation (Equation44
(44) ) by using g(x1, T1, x2, T2, t), the Pál–Bell equation [Citation22,Citation23] of two-interval version is obtained as
(45) where α is the neutron decay constant that is defined as
(46)
To solve the Pál–Bell equation of two-interval version, the two-forked approximation that neglects the higher order components than third of the second term in the right-hand side of Equation (Equation45(45) ) is introduced, i.e.,
(47) Regarding the two-forked approximation, Furuhashi and Izumi pointed out that the contributions from higher order components than the third are negligible except in reactor systems with far large subcriticalities [Citation26,Citation27].
To solve Equation (Equation47(47) ) efficiently, let us divide g(x1, T1, x2, T2, t) into three regions as
(48)
(49)
(50) with the following boundary conditions:
(51)
(52)
(53) Although Equation (Equation49
(49) ) is non-linear, it is of the Ricatti type that can be solved analytically. One, hence, obtains the solution as follows:
(54)
(55)
(56)
(57)
(58)
(59)
2.4. Neutron observation probability
When T1 + T2 < t, Equations (Equation28(28) ) and (Equation29
(29) ) are calculated as
(60)
(61) Hence, by using a function θk(u, t) that is defined as
(62)
the concrete expressions of ΓDC(x1, T1, x2, T2, t) and ΓMOD(x1, T1, x2, T2, t) for T1 + T2 < t are obtained as follows:
(63)
(64)
Therefore, by substituting Equations (Equation63(63) ) and (Equation64
(64) ) into Equations (Equation26
(26) ) and (Equation27
(27) ), one obtains the analytical expression of
for T1 + T2 < t.
Here, some arrangement with respect to is made to take actual experimental conditions of pulsed neutron source method into account. First, in actual experiments, the neutron counting rate is measured as a function of time after periodic burst of pulsed neutrons. Let us hence introduce a new parameter Δ that is the time after jth burst of pulsed neutrons and set t − T2 = jT0 + Δ as shown in . Second, in actual experiments, measurement is started when the steady state is realized by the pulsed neutron source after a long waiting time. Therefore, let us take limitation j → ∞ as follows:
(65) where
(66)
(67)
Figure 4. Timing diagram of neutron observation probability p(τ, Δ).
As seen in Equation (Equation4(4) ), the neutron observation probability that explicitly considers the count-loss process in neutron counting system and the periodic burst of pulsed neutrons, i.e., p(τ, Δ)dΔ, is derived by using
as
(68) Let us hence calculate the T2 → dΔ limitation of
as the Maclaurin expansion with the elimination of higher order terms of dΔ as
(69) where
(70)
(71)
Their concrete expressions are written as follows:
(72)
(73)
(74)
(75) The analytical expression of p(τ, Δ)dΔ can now be derived from Equation (Equation68
(68) ) as
(76) where
(77)
(78)
(79)
(80) Using the following notation,
(81) their concrete expressions are obtained as follows:
(82)
(83)
(84)
(85)
(86)
(87)
(88)
(89) Therefore, the analytical expression of p(τ, Δ)dΔ is derived as follows:
(90)
(91)
(92)
(93)
(94)
Here, let us substitute τ = 0 into Equation (Equation90(90) ). As a result, one obtains the following expression:
(95) On the other hand, the conventional analytical expression of pulsed neutron source method that does not include the count-loss process is written as follows:
(96) One confirms that Equation (Equation95
(95) ) is the Fourier series expansion of Equation (Equation96
(96) ).
3. Discussions
3.1. Determination of neutron decay constant
Let us suppose that there exists no constant component of pulsed neutron source (i.e., Sc = 0) for simple discussion. Under such a condition, p(τ, Δ) given in Equation (Equation90(90) ) is re-written as follows:
(97)
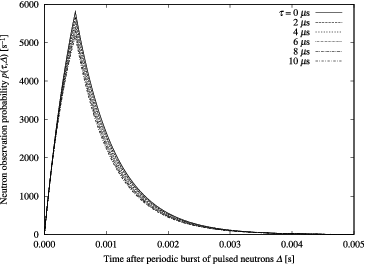
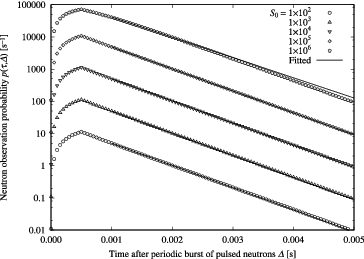
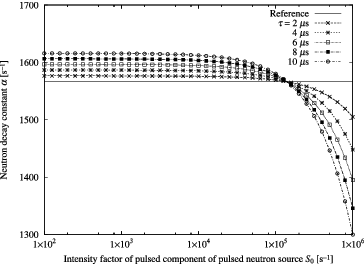
In order to grasp the count-loss effect in determination of neutron decay constant α by conventional formula of pulsed neutron source method Ωe−αΔ, different p(τ, Δ) curves were plotted by substituting the parameters listed in , where a typical thermal subcritical reactor system for pulsed neutron source method with subcriticality of 3 %Δk/k and neutron decay constant of 1566.3 s−1 is supposed, into Equation (Equation97(97) ) (see ), then α was determined by the least square fitting technique using conventional formula for 2W ≤ Δ < T0 (see ). Thus obtained α was plotted in . Here, we note that the fitting range 2W ≤ Δ < T0 is a typical one in actual experiments of pulsed neutron source method. One finds that the conventional formula overestimates α when the intensity factor of pulsed component S0 is not high and underestimates α when S0 is high.
Figure 5. Examples of neutron observation probability p(τ, Δ) (for Sc = 0 and S0 = 5 × 104).
Figure 6. Examples of fitted curve (for Sc = 0 and τ = 4 μs).
Figure 7. Neutron decay constant α determined by conventional formula.
Table 1. Parameters for plotting neutron observation probability p(τ, Δ).
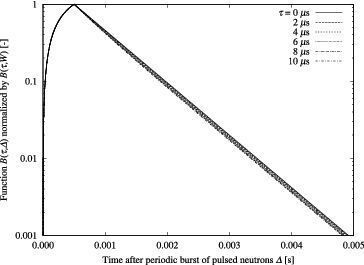
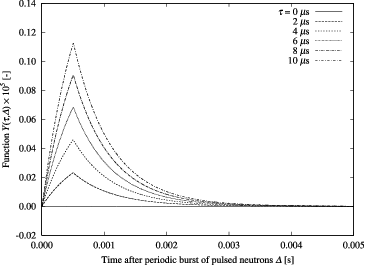
To acquire further understanding on count-loss effect in determination of α, B(τ, Δ) normalized by B(τ, W), Y(τ, Δ), and exp [−S0Y(τ, Δ)] for τ = 4 μs were plotted in –, respectively. In , one observes faster decaying behaviors of B(τ, Δ) for W ≤ Δ as τ is getting larger. On the other hand, although Y(τ, Δ) itself has an obvious dependency on Δ (see ), it is found in that exp [−S0Y(τ, Δ)] is almostunity when S0 is not high. Therefore, with regard to not high S0, the faster decaying behavior of B(τ, Δ) is responsible for overestimation of α, since the decaying behavior of p(τ, Δ) is almost identical to that of B(τ, Δ).
Figure 8. Examples of function B(τ, Δ) (normalized by B(τ, W)).
Figure 9. Examples of function Y(τ, Δ).
Figure 10. Examples of function exp [−S0Y(τ, Δ)] (for τ = 4 μs).
![Figure 10. Examples of function exp [−S0Y(τ, Δ)] (for τ = 4 μs).](/cms/asset/0af07508-79d5-4ed8-8023-26cbba8bd3e4/tnst_a_900459_f0010_b.gif)
On the other hand, one finds in that exp [− S0Y(τ, Δ)] has a clearer dependency on Δ as S0 is getting higher. Hence, with regard to high S0, p(τ, Δ) shows slower decaying behaviors that result in underestimation of α since it is proportional to the product of B(τ, Δ) and exp [−S0Y(τ, Δ)]. Furthermore, underestimation of α appears superiorly as S0 is getting higher.
3.2. Verification of count-loss correction procedures
It is well known that the relations between true counting rate n and observed counting rate m for paralyzable and non-paralyzable count-loss processes are expressed as follows [Citation20]:
(98)
(99)
By solving them with respect to n, one gets
(100)
(101)
In the pulsed neutron source method, the correction procedures based on Equations (Equation100(100) ) and (Equation101
(101) ) are often introduced to eliminate the count-loss effect. To verify these count-loss correction procedures, the following corrected p(τ, Δ) curves, i.e., pcorr, p(τ, Δ) and pcorr, np(τ, Δ), were plotted by using the parameters listed in :
(102)
(103) Regarding the pcorr, p(τ, Δ) and pcorr, np(τ, Δ) curves thus obtained, α was determined by the least square fitting technique using conventional formula Ωe−αΔ for 2W ≤ Δ < T0 as plotted in and . It is clearly seen in these figures that the both count-loss correction procedures suppress underestimation of α. However, it is confirmed that these correction procedures are not effective for overestimation.
Figure 11. Neutron decay constant α determined by conventional formula with paralyzable count-loss correction.
Figure 12. Neutron decay constant α determined by conventional formula with non-paralyzable count-loss correction.
4. Conclusion
The count-loss effect in determination of neutron decay constant by pulsed neutron source method was investigated on the basis of the neutron observation probability that was derived by explicitly considering the count-loss process in neutron counting system and the periodic burst of pulsed neutrons. It was found that overestimation of neutron decay constant due to count-loss effect is seen while underestimation appears superiorly as the intensity of pulsed neutron source is getting higher. It was further demonstrated that the well-known count-loss correction procedures that are often introduced to eliminate the count-loss effect are not effective for overestimation although they successfully suppress underestimation. Therefore, the pulsed neutron source method should be modified so as to have robustness against the count-loss effect.
On the basis of the conclusion provided in the present paper, a modification of pulsed neutron source method will be proposed and discussed in a forthcoming paper.
Acknowledgements
The authors would like to express their thanks to Dr Teruhiko Kugo for his valuable comments.
Related Research Data
References
- Simmons BE, King JS. A pulsed neutron technique for reactivity determination. Nucl Sci Eng. 1958;3:595–608.
- Kaneko Y, Sumita K. Determination of neutron multiplication, (I) Concept. J Nucl Sci Technol. 1967;4:400–407.
- Sumita K, Kaneko Y. Determination of neutron multiplication, (II) Experiments and analysis. J Nucl Sci Technol. 1967;4:491–502.
- Akino F, Yasuda H, Kaneko Y. Determination of large negative reactivity by integral versions of various experimental methods. J Nucl Sci Technol. 1980;17:593–615.
- Kitamura Y, Yamauchi H, Yamane Y, Misawa T, Ichihara C, Nakamura H. Experimental investigation of variance-to-mean formula for periodic and pulsed neutron source. Ann Nucl Energy. 2004;31:163–172.
- Pázsit I, Kitamura Y, Wright J, Misawa T. Calculation of the pulsed Feynman-alpha formulae and their experimental verification. Ann Nucl Energy. 2005;32:986–1007.
- Soule R, Assal W, Chaussonnet P, Destouches C, Domergue C, Jammes C, Laurens J-M, Lebrat J-F, Mellier F, Perret G, Rimpault G, Servière H, Imel G, Thomas GM, Villamarin D, Gonzalez-Romero E, Plaschy M, Chawla R, Kloosterman JL, Rugama Y, Billebaud A, Brissot R, Heuer D, Kerveno M, Le Brun C, Liatard E, Loiseaux J-M, Méplan O, Merle E, Perdu F, Vollaire J, Baeten P. Neutronic studies in support of accelerator-driven systems: the MUSE experiments in the MASURCA facility. Nucl Sci Eng. 2004;148:124–152.
- Jammes C, Geslot B, Rosa R, Imel G, Fougeras P. Comparison of reactivity estimations obtained from rod-drop and pulsed neutron source experiments. Ann Nucl Energy. 2005;32:1131–1145.
- Persson C-M, Fokau A, Serafimovich I, Bournos V, Fokov Y, Routkovskaia C, Kiyavitskaya H, Gudowski W. Pulsed neutron source measurements in the subcritical ADS experiment YALINA-Booster. Ann Nucl Energy. 2008;35:2357–2364.
- Pyeon CH, Hervault M, Misawa T, Unesaki H, Iwasaki T, Shiroya S. Static and kinetic experiments on accelerator-driven system with 14 MeV neutrons in Kyoto University Critical Assembly. J Nucl Sci Technol. 2008;45:1171–1182.
- Pyeon CH, Lim J-Y, Takemoto Y, Yagi T, Azuma T, Kim H, Takahashi Y, Misawa T, Shiroya S. Preliminary study on the thorium-loaded accelerator-driven system with 100 MeV protons at the Kyoto University Critical Assembly. Ann Nucl Energy. 2011;38:2298–2302.
- Izawa K, Uchida Y, Ohkubo K, Totsuka M, Sono H, Tonoike K. Infinite multiplication factor of low-enriched UO2-concrete system. J Nucl Sci Technol. 2012;49:1043–1047.
- Gozani T. A modified procedure for the evaluation of pulsed source experiments in subcritical reactors. Nukleonik. 1962;4:348–349.
- Garelis E, Russell JL. Theory of pulsed neutron source measurements. Nucl Sci Eng. 1963;16:263–270.
- Aizawa O, Yamamuro N. Spectral correction to the Garelis–Russell formula. J Nucl Sci Technol. 1967;4:623–625.
- Aizawa O. Reactivity analysis by spectral corrected Garelis–Russell method. J Nucl Sci Technol. 1969;6:498–507.
- Kosály G, Valkó J. Investigation of the area-ratio method of pulsed reactivity determination. J Nucl Energy. 1971;25:297–315.
- Kosály G, Fischer A. On integral-versions of the area-ratio method of pulsed neutron reactivity measurements. J Nucl Energy. 1972;26:17–26.
- Kosály G, Valkó J, Fischer A. Theory of the area-ratio method of subcriticality determination. Atomkernenergie. 1974;23:251–259.
- Knoll GF. Radiation detection and measurement. 2nd ed. New York (NY): Wiley; 1979; p. 95–99.
- Degweker SB. Effect of deadtime on the statistics of time correlated pulses – application to the passive neutron assay problem. Ann Nucl Energy. 1989;16:409–416.
- Pál L. On the theory of stochastic processes in nuclear reactors. Nuovo Cimento. 1958;7 (Suppl.):25–42.
- Bell GI. On the stochastic theory of neutron transport. Nucl Sci Eng. 1965;21:390–401.
- Pázsit I. The backward theory of stochastic particle transport with multiple emission sources. Phys Scr. 1999;59:344–351.
- Pázsit I, Yamane Y. The backward theory of Feynman- and Rossi-alpha methods with multiple emission sources. Nucl Sci Eng. 1999;133:269–281.
- Furuhashi A, Izumi A. Third moment of the number of neutrons detected in short time intervals. J Nucl Sci Technol. 1968;5:48–59.
- Furuhashi A. Analyzing neutron count trios into two- and three-forked components. J Nucl Sci Technol. 1969;6:156–158.