Application of correction technique using leakage index combined with SPH or discontinuity factors for energy collapsing on pin-by-pin BWR core analysis

Abstract

A correction technique to capture the spectral interference effect on collapsed cross sections is combined with the superhomogenization (SPH) factor or the discontinuity factor (DF) and is applied to the pin-by-pin core analysis for boiling water reactors (BWRs). The spectral interference effect has relationship with variations of neutron leakage in each pin-cell from the viewpoint of neutron balance. In order to correct collapsed cross sections, a new correction technique, in which the neutron leakage in each pin-cell is used as a correction index, was proposed in the previous study. By this correction technique, the reference coarse group cross sections are well reproduced and the calculation accuracies are improved. However, the reference fine group calculation results could not be reproduced since the correction technique cannot reduce energy collapsing errors. Thus, we combine the correction technique with the SPH factor or the DF to reduce energy collapsing errors. In order to verify and discuss the applicability of the correction technique with the SPH factor or the DF, two-dimensional benchmark calculations considering typical characteristics of BWR cores are carried out. The correction technique with the DF more accurately reproduces the reference fine group calculation results than that with the SPH factor.

Keywords:

• pin-by-pin
• BWR core analysis
• spectral interference effect
• energy collapsing
• leakage index
• SPH factor
• discontinuity factor

1. Introduction

In the conventional boiling water reactor (BWR) core analysis, which consists of lattice physics and core calculations, first, lattice physics calculations are performed in single-assembly geometries with the reflective boundary condition and heterogeneous fine group (dozens to a few hundred groups) cross sections and neutron fluxes are obtained. By these calculation results, spatial homogenization and energy collapsing are carried out, then finally assembly-homogenized coarse group (1–3 group(s)) cross sections for core calculations are calculated [1,2]. Core calculations are performed with these assembly-homogenized coarse group cross sections and crucial core parameters (e.g., power peaking factor) are estimated. However, neutron fluxes in single-assembly geometries, which are used for the spatial homogenization and the energy collapsing, are generally different from those in core geometries. The spatial and the energetic distribution of neutron fluxes become different in core geometries by the spectral interference effect due to the adjacent loadings of different types of fuel assemblies. Namely, appropriate cross sections for core calculations (i.e., cross sections directly homogenized and collapsed in core geometries) are different from those calculated in lattice physics calculations. Therefore, corrections of cross sections considering the spectral interference effect are necessary.

Recently, as a next generation core analysis method, the pin-by-pin fine mesh core calculation method for BWR core analysis has been studied [3,4]. In recent studies, in order to evaluate important parameters for highly heterogeneous cores (e.g., mixed-oxide (MOX) or high-burnup fuel loaded cores), finer energy group structures are used. For example, 8- or 9-group structure is used in the recent studies of the pin-by-pin approach for light water reactor core analysis [3–5]. However, the spectral interference effect on the energy collapsing should be still taken into account even if we utilize such finer energy group structure.

In our previous study, we propose a new correction technique in order to capture the spectral interference effect and to correct coarse group cross sections [6]. In this correction technique, we assume that the spectral interference effect has relationship with variations of neutron leakage from the viewpoint of neutron balance. Moreover, a leakage index (LI), which is similar to a macroscopic cross section related to the neutron leakage, is newly used as a correction index. Through the mathematical derivations using the generalized perturbation theory based on the diffusion theory, the variations of coarse group cross sections due to the spectral interference effect are approximately represented by the linear combination of variations of coarse group LIs. From the verification calculation results in the previous study, it is confirmed that the correction technique using LI (i.e., the LI correction technique) can well reproduce the reference coarse group cross sections (i.e., cross sections directly collapsed with consideration of the spectral interference effect) [6]. It should be remembered that even if the reference coarse group cross sections, which are collapsed with actual neutron spectrum in core geometries, are used, the coarse group calculations do not reproduce the reference fine group calculation results. The root cause of this inconsistency is the energy collapsing error, which should be considered in addition to the spectral interference effect. Namely, though the LI correction technique can well reproduce the reference coarse group calculation results, this cannot reduce the errors between the fine and the coarse group calculation results. Therefore, in order to reproduce the reference fine group calculation results, combinations of the LI correction technique with other correction techniques, which reduce the energy collapsing errors, are necessary.

In the present paper, we focus on the superhomogenization (SPH) factor and the discontinuity factor (DF), which can reduce the energy collapsing errors [7,8]. Then, we try to combine the LI correction technique with either the SPH factor or the DF in the present paper (i.e., the LI correction technique with the SPH factor and that with the DF are investigated). Since the LI correction technique is proposed in our latest study, the performance of such combination has not been investigated and confirmed so far. Only the spectral interference effect on energy collapsing of cross sections is investigated in the present paper, but the spectral interference effect on spatial homogenization of cross sections is not investigated. The similar investigation for the spectral interference effect on spatial homogenization will be necessary in order to fully verify the applicability of the LI correction technique with the SPH factor or the DF in the practical use. However, it is not discussed in the present paper since we focus on the energy collapsing error.

Concepts of combination of the correction techniques are described in Section 2. The verification results

of the LI correction technique with the SPH factor or the DF are shown in Section 3 through numerical benchmark calculations. Finally, the concluding remarks are given in Section 4.

2. Methodology

In this section, first, the overview of the LI correction technique is described in order to make the present paper self-explanatory. Then, the concepts of combinations of the LI correction technique with the SPH factor or the DF are shown.

2.1. Overview of LI correction technique

The conventional core analysis consists of lattice physics and core calculations. Coarse group cross sections for core calculations are obtained by collapsing fine-group cross sections with fine-group neutron fluxes through lattice physics calculations in single-assembly geometries: (1) $${\Sigma }_{x,G}=\frac{{\sum }_{g\in G}{\Sigma }_{x,g}{\phi }_g}{{\sum }_{g\in G}{\phi }_g},$$(1) where Σ and φ are the macroscopic cross section and the neutron flux, respectively. The subscripts x, g, and G represent the reaction type (e.g., fission and absorption), the fine group index, and the coarse group index, respectively. However, the neutron fluxes used in Equation (1) (i.e., calculated in single-assembly geometries) are different from those obtained in core geometries, since the spatial and the energetic distributions of neutron fluxes in core geometries become different by the spectral interference effect. Thus, coarse group cross sections, which are calculated through lattice physics analyses in single-assembly geometries, become different from the appropriate coarse group cross sections for core calculations.

In order to correct coarse group cross sections considering the spectral interference effect, we focus on neutron leakages in each pin-cell and consider the relationship between the variations of coarse group cross sections and neutron leakage. In order to express the neutron leakage, we newly introduce the LI defined by (2) $${\mathrm{LI}}_g\left(\overrightarrow{r}\right)\equiv \frac{{\int }_S\overrightarrow{J_g}\left(\overrightarrow{r}\right)·\overrightarrow{n}\left(\overrightarrow{r}\right)dS/\phantom{{\int }_S\overrightarrow{J_g}\left(\overrightarrow{r}\right)·\overrightarrow{n}\left(\overrightarrow{r}\right)dS{\int }_{V}dV}{\int }_{V}dV}{{\phi }_g\left(\overrightarrow{r}\right)},$$(2) which is an index parameter related to neutron leakage and is defined as a volume-averaged neutron leakage. From the viewpoint of neutron balance in the k-effective eigenvalue calculation, the LI is calculated by (3) $$\begin{array}{c}\hfill {\mathrm{LI}}_g\left(\overrightarrow{r}\right)=\frac{\frac{{\chi }_g\left(\overrightarrow{r}\right)}{k_{\mathrm{eff}}}{\sum }_{g^{\text{'}}}\nu {\Sigma }_{f,g^{\text{'}}}\left(\overrightarrow{r}\right){\phi }_{g^{\text{'}}}\left(\overrightarrow{r}\right)+{\sum }_{g^{\text{'}}\ne g}{\Sigma }_{s,g^{\text{'}}\to g}\left(\overrightarrow{r}\right){\phi }_{g^{\text{'}}}\left(\overrightarrow{r}\right)-{\Sigma }_{r,g}\left(\overrightarrow{r}\right){\phi }_g\left(\overrightarrow{r}\right)}{{\phi }_g\left(\overrightarrow{r}\right)}.\end{array}$$(3)

From Equation (3), the dimension of LI is the same as macroscopic cross sections. Namely, the LI is considered as a macroscopic cross section related to the neutron leakage. By using the LI in Equation (2) and by considering the perturbations of LI, we approximately represent the variations of coarse-group cross sections as the linear combination of variations of coarse group LIs: (4) $$\begin{array}{ccc}\hfill d{\Sigma }_{x,m,G}& \approx & {\sum }_{G^{\text{'}}}{a}_{x,m,G,G^{\text{'}}}dL{I}_{m,G^{\text{'}}}\hfill \\ & =& {\sum }_{G^{\text{'}}}{a}_{x,m,G,G^{\text{'}}}\left(L{I}_{m,G^{\text{'}}}-L{I}_{m,G^{\text{'}}}^{\mathrm{single}}\right),\hfill \end{array}$$(4) where a is the coupling coefficients of LIs. The superscript single represents single-assembly calculations. In order to calculate the coupling coefficients of LIs in Equation (4), we perform various simplified colorset assembly calculations, which consist of the target and the simplified fuel assemblies described in Section 3.1, and simulate actual impacts of spectral interference effect in core geometries. In the present study, Equation (4) is used for all reaction types of cross sections (i.e., absorption, fission, and production cross sections, scattering matrices, and diffusion coefficients) since they are collapsed with neutron fluxes as Equation (1).

Note that the detailed mathematical descriptions of derivations of Equation (4) can be found in [6].

2.2. Combination of LI correction technique with SPH factor or DF

In the previous subsection, the overview of the LI correction technique is described. The LI correction technique based on Equation (4) can reduce errors due to the spectral interference effect and well reproduces the reference coarse group cross sections. However, even if the reference coarse group calculation results are well reproduced, errors due to the energy collapsing of cross sections still exist (i.e., the reference fine group calculation results are not reproduced). Thus, it is necessary to combine the LI correction technique and other correction methods, which reduce the energy collapsing errors.

It is possible to reduce the energy collapsing errors by the SPH factor or the DF. For the energy collapsing of cross sections, these are calculated as (5) $$\begin{array}{c}\hfill {\mu }_G=\frac{{\sum }_{g\in G}{\phi }_g}{{\phi }_G},\end{array}$$(5) (6) $$\begin{array}{c}\hfill f_G=\frac{{\sum }_{g\in G}{\phi }_{s,g}}{{\phi }_{s,G}},\end{array}$$(6) where φ, φ_s, μ, and f are the region-averaged neutron flux, the region-surface neutron flux, the SPH factor, and the DF, respectively. The subscript g and G represent the fine energy group and the coarse energy group indices, respectively. In the present study, the SPH factor and the DF are calculated in each pin-cell mesh and in every surfaces of pin-cell mesh, respectively.

Similar to coarse group cross sections, the SPH factor and the DF in core geometries are also different from those in single-assembly geometries by the spectral interference effect. Thus, the variations of the SPH factor and the DF would be taken into account. In our preliminary investigations, we tried to simultaneously correct the coarse group cross sections and the SPH factor by the LI correction technique. However, this approach encountered the following difficulty.

In order to estimate the variations of SPH factor due to the spectral interference effect, calculations of the SPH factor in every simplified colorset assembly geometry are necessary in order to simulate actual impacts of spectral interference effect in core geometries. Thus, the calculation procedure of LI correction technique becomes very complicated. Moreover, in the LI correction technique based on the diffusion theory, the LI defined in Equation (3) is used to correct the coarse group cross sections and the neuron fluxes are necessary to estimate the LI. If the SPH factor simultaneously changes with the coarse group cross sections, the corrections of coarse group cross sections and SPH factor would conflict each other over the variations of neutron fluxes. As the results of such conflict, the calculation procedure of LI correction technique becomes unstable from the viewpoint of numerical calculation. When the equivalence between the SPH factor and the DF (i.e., the SPH factor corresponds to the inverse of region-averaged DF) is considered, the simultaneous correction of coarse group cross sections and DF would present the same problems as the SPH factor.

Therefore, in the present study, we assume that dependences of SPH factor and DF on the spectral interference effect are not significant. Namely, the SPH factor and the DF, which are calculated in single-assembly geometries, are used during the calculation procedure of LI correction technique. With this approximation, we can avoid the instabilities of numerical calculations of LI correction technique.

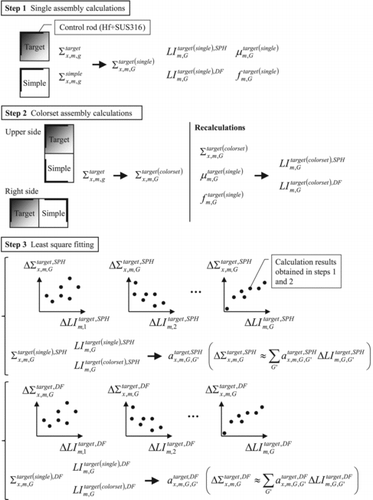
The overview of calculation procedure of LI correction technique with the SPH factor or the DF is shown in Figure 1.

Figure 1. Overview of the calculation procedure of LI correction technique with SPH factor and DF.

As shown in Figure 1, first, single-assembly calculations are carried out for target and simplified fuel assemblies. Coarse group cross sections (Σ^{target(single)}_{x, m, G}) are collapsed in single-assembly geometries and the SPH factor and the DF (μ^{target(single)}_{m, G} and f^{target(single)}_{m, G}) are calculated. By utilizing the calculation results (i.e., the neutron fluxes and the k-effective) and the SPH factor, coarse group LIs (LI^{target(single), SPH}_{m, G}) are estimated. Similarly, by utilizing the calculation results and the DF, coarse group LIs (LI^{target(single), DF}_{m, G}) are also estimated. Note that the coarse group LIs, which are obtained with the SPH factor or the DF, are calculated as (7) $$\begin{array}{c}\hfill {\mathrm{LI}}_{m,G}^{\mathrm{SPH}}=\frac{\frac{{\chi }_{m,G}}{k_{\mathrm{eff}}^{\mathrm{SPH}}}{\sum }_{G^{\text{'}}}{\mu }_{m,G^{\text{'}}}\nu {\Sigma }_{f,m,G^{\text{'}}}{\phi }_{m,G^{\text{'}}}^{\mathrm{SPH}}+{\sum }_{G^{\text{'}}\ne G}{\mu }_{m,G^{\text{'}}}{\Sigma }_{s,m,G^{\text{'}}\to G}{\phi }_{m,G^{\text{'}}}^{\mathrm{SPH}}-{\mu }_{m,G}{\Sigma }_{r,m,G}{\phi }_{m,G}^{\mathrm{SPH}}}{{\mu }_{m,G}{\phi }_{m,G}^{\mathrm{SPH}}},\end{array}$$(7) (8) $$\begin{array}{c}\hfill {\mathrm{LI}}_{m,G}^{\mathrm{DF}}=\frac{\frac{{\chi }_{m,G}}{k_{\mathrm{eff}}^{\mathrm{DF}}}{\sum }_{G^{\text{'}}}\nu {\Sigma }_{f,m,G^{\text{'}}}{\phi }_{m,G^{\text{'}}}^{\mathrm{DF}}+{\sum }_{G^{\text{'}}\ne G}{\Sigma }_{s,m,G^{\text{'}}\to G}{\phi }_{m,G^{\text{'}}}^{\mathrm{DF}}-{\Sigma }_{r,m,G}{\phi }_{m,G^{\text{'}}}^{\mathrm{DF}}}{{\phi }_{m,G}^{\mathrm{DF}}}.\end{array}$$(8)

Note that μ_{m, G}φ^SPH_{m, G} in the coarse group calculation is equivalent to the summation of fine group neutron fluxes. Furthermore, in the coarse group calculations with the DF, φ^DF_{m, G} is equivalent to the summation of fine group neutron fluxes. Thus, the coarse group LIs obtained by Equation (7) or (8) is consistent with those obtained by the fine group calculation results.

Second, fine group calculations are carried out in colorset assembly geometries, which consist of the target and the simplified fuel assemblies. Coarse group cross sections (Σ^{target(colorset)}_{x, m, G}), which are directly collapsed in colorset assembly geometries, are estimated. By the coarse group cross sections (Σ^{target(colorset)}_{x, m, G}), the SPH factor, or the DF (μ^{target(single)}_{m, G} or f^{target(single)}_{m, G}), and the neutron fluxes in the target and the simplified fuel assemblies, the LIs (LI^{target(colorset), SPH}_{m, G} and LI^{target(colorset), DF}_{m, G}) in the target fuel assembly are calculated by Equations (7) and (8), respectively.

The colorset assembly geometries should be chosen to cover actual impacts of spectral interference effect. Thus, similar to our previous study, we assume that actual impacts of spectral interference effect can be simulated by two assembly geometries with reflective boundary condition, in which the target and the simplified fuel assemblies are adjacently loaded [6]. As shown in [6], utilizations of such two assembly geometries and the simplified fuel assemblies are justified due to the following viewpoints.

1. The spectral interference effect is mainly observed in the assembly peripheral meshes. Thus, the actual impacts of spectral interference effect can be decomposed into the impact from each assembly surface.

2. BWR fuel assemblies have geometric symmetries. Thus, two types of two assembly geometries shown in Figure 1 can cover the impacts of spectral interference effect on each assembly surface.

3. In order to consider the control rod insertion on actual operating core, larger colorset assembly geometries (e.g., 4×4 colorset assembly geometries) should be used and larger computational load is necessary. Thus, the treatment of control rod insertion is approximated.

4. The enrichment distribution of adjacent fuel assemblies is unknown in prior to core calculations. Moreover, the spectral interference effect is mainly observed in the assembly peripheral meshes. We consider that the averageenrichment of fuel assembly has larger impact on the spectral interference effect than the enrichment distribution in a fuel assembly. Therefore, the uniform enrichment distribution is used for simplified fuel assemblies in order to simplify colorset assembly geometries and to reduce computational load.

Finally, the coupling coefficients of LIs (a^{target, SPH}_{x, m, G, G′} and $a_{x,m,G,G^{\text{'}}}^{\mathrm{target},\mathrm{DF}}$) are calculated for each pin-cell. The least squares approximation for the relationship between the variations of coarse group cross sections (ΔΣ^{target, SPH}_{x, m, G} or ΔΣ^{target, DF}_{x, m, G}) and those of coarse group LIs (ΔLI^{target, SPH}_{m, G} or ΔLI^{target, DF}_{m, G}) obtained in steps (1) and (2) is used to estimate the coupling coefficients.

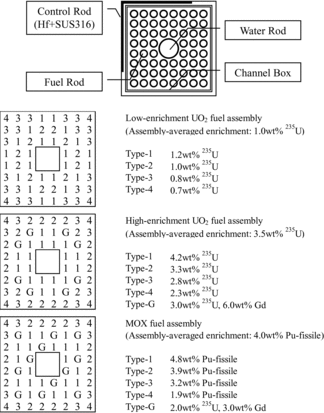
In the present study, three types of 8×8 BWR fuel assemblies shown in Figure 2 are used for the target fuel assemblies [9].

Figure 2. 8×8 BWR fuel assemblies used in present study.

In the conventional and the next-generation BWR core designs, 9×9 and 10×10 BWR fuel assemblies are also used in addition to the 8×8 BWR fuel assembly shown in Figure 2 [9,10]. We think that the average enrichment or Pu content of a fuel assembly has larger impact on the spectral interference effect than the assembly geometries (e.g., the number and the radius of fuel rods). Thus, we use the 8×8 BWR fuel assembly as a typical one and consider several fuel rod enrichments of ²³⁵U or Pu-fissile.

As shown in Figure 2, the low-enrichment UO₂ (assembly-averaged enrichment: 1.0 wt% ²³⁵U), the high-enrichment UO₂ (assembly-averaged enrichment: 3.5 wt% ²³⁵U), and the MOX (assembly-averaged enrichment: 4.0 wt% Pu-fissile) fuel assemblies are used. The geometry of these 8×8 fuel assembly are taken by [9]. The fuel rod enrichment distributions are manually decided with the considerations for the positions of Gd-bearing fuel rods and the fuel rod enrichment distributions in [9,10].

Six types of fuel assemblies with the uniform enrichment distribution are used for simplified fuel assemblies. The fuel rod enrichments are 1.0 wt% ²³⁵U, 3.0 wt% ²³⁵U, 5.0 wt% ²³⁵U, 3.0 wt% Pu-fissile, 4.0 wt% Pu-fissile, and 5.0 wt% Pu-fissile. Enrichments of ²³⁵U and Pu-fissile are chosen to cover the values used in typical BWR fuel assemblies. The geometry of simplified fuel assemblies is the same with that of target fuel assemblies (i.e., the simplified fuel assemblies are also 8×8 BWR fuel assemblies).

Note that the above design conditions of target and simplified fuel assemblies (i.e., the geometry and the enrichment distribution of target and simplified fuel assemblies) are the same with those described in [6].

3. Numerical calculations

3.1. Calculation conditions and preparations for correction

3.1.1. Preparation of pin-cell averaged cross sections

The pin-cell averaged cross sections used in the present study are calculated by the HELIOS code in 47 energy groups [11]. In the HELIOS code, the depletion calculation is performed in single-assembly geometry with the reflective boundary condition. The void fraction, the control rod position, and the power density are fixed during the depletion calculation. Through the depletion calculations, we obtain the pin-cell averaged fine group cross sections at 0, 15, 30, 45, and 60 GWd/t (assembly-averaged exposure). The fine group cross sections at 0, 15, 30, 45, and 60 GWd/t are used to construct the two assembly geometries shown in Section 2.2 and the 4×4 colorset assembly geometries as described later. The heterogeneous 47-group cross sections are homogenized in each pin-cell and the SPH method is applied for 47-group pin-cell averaged cross sections in single-assembly geometries in order to reduce the spatial homogenization errors [7].

3.1.2. Estimations of coupling coefficients of leakage index

As shown in Section 2.2, the two assembly calculations, which consist of the target and the simplified fuel assemblies, are carried out and the perturbations of boundary conditions due to the spectral interference effect are simulated. Then, the coupling coefficients of LIs are calculated with this condition. In the present paper, we carry out 36 patterns of two assembly calculations for one target fuel assemblies. These 36 patterns of two assembly geometries are determined by the combinations of calculation conditions for simplified fuel assemblies as follows:

1. Fuel rod enrichment of simplified fuel assembly (six patterns): 1.0 wt% ²³⁵U, 3.0 wt% ²³⁵U, 5.0 wt% ²³⁵U, 3.0 wt% Pu-fissile, 4.0 wt% Pu-fissile, and 5.0 wt% Pu-fissile.

2. Assembly-averaged exposure (three patterns): 0, 30, and 60 GWd/t.

3. Loading position of simplified fuel assemblies (two patterns): upper and right sides for the target fuel assembly.

Note that the assembly-averaged void fraction is 40% and the void fraction distribution is assumed as uniform. From [12], an in-channel void distribution has a considerable impact on the calculation results (e.g., the k-infinity and the pin-by-pin fission rate distribution). However, consideration of an in-channel void distribution is beyond the scope of the present paper, which aims verifications of simultaneous utilization of the LI corrections and the SPH or the DF correction. Treatment of in-channel void distribution is an important issue to be addressed in future work.

The above calculation conditions to estimate the coupling coefficients of coarse group LIs are the same with those described in [6]. Moreover, the relationships between the variations of coarse group cross sections and LIs, which are obtained through 36 patterns of two assembly calculations, sufficiently cover those obtained through 4×4 colorset assembly calculations as described in later.

3.1.3. Calculation geometry and number of energy groups

In order to verify the present LI correction technique with the SPH factor or the DF, two-dimensional (2D) benchmark problems considering typical characteristics of BWR cores are carried out. In the benchmark problems, we consider the energy collapsing of cross sections from 47 to 4 and 8 energy groups, whose structures are shown in Table 1 [11,13].

Table 1. Energy group structure.

4-group structure	8-group structure	Lower energy boundary (eV)
First group	First group	2.2313E+06
	Second group	8.2085E+05
	Third group	9.1188E+03
Second group	Fourth group	1.3007E+02
	Fifth group	3.9279E+00
Third group	Sixth group	6.2506E−01
Fourth group	Seventh group	1.4572E−01
	Eighth group	1.0000E−04

Through the numerical verifications with 4 and 8 energy group structures, we confirm that present LI correction technique with the SPH factor or the DF can be used for several energy group structures.

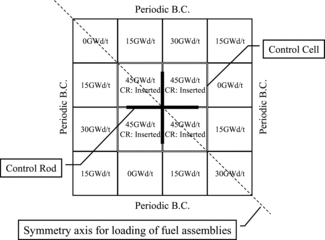
In the present paper, we use 4×4 colorset assembly geometry with the periodic boundary condition shown in Figure 3, which consists of three different types of 8×8 BWR fuel assemblies shown in Figure 2.

Figure 3. Geometry of 4×4 colorset assemblies.

In Figure 3, the 2×2 fuel assemblies, which are located in the center of 4×4 colorset assembly geometry, simulate a control cell and have the same specifications (i.e., the assembly-averaged exposure and the type of fuel assembly are the same). For other fuel assemblies loaded around the control cell, the assembly-averaged exposures are fixed as shown in Figure 3 and the types of fuel assemblies are randomly determined considering the diagonal symmetry of 4×4 colorset assembly geometry. Through these procedures, we determine approximately 6500 patterns of 4×4 colorset assembly geometries, which are combinations of three types of fuel assemblies for the control cell and surrounding seven assemblies (i.e., 3⁸ patterns). The assembly-averaged void fraction is 40%, which is an average value of void fraction in actual BWR cores. It should be remembered that consideration of an in-channel void distribution is beyond the scope of the present paper as described previously. Since we assume that the cycle length is 15 GWd/t and consider the loading pattern of fuel assemblies in the beginning of cycle, the assembly-averaged exposure is chosen from 0, 15, 30, or 45 GWd/t.

Note that the above calculation conditions are the same with those described in [6].

3.2. Verification procedure to correct coarse group cross sections

In the present LI correction technique with the SPH factor or the DF, the coarse group cross sections are corrected by the following procedures. Note that the SPH factor and the DF are not corrected (i.e., those calculated in single assembly geometries are used).

1. Single assembly calculations in coarse group are carried out for all types of fuel assemblies. Through such single assembly calculations, the LI^single_{m, G} in Equation (4) is calculated.

2. Target 4×4 colorset assembly calculation in coarse group is carried out with the uncorrected coarse group cross sections and the SPH factor or the DF, which are obtained in single assembly geometries. The LIs in the target 4×4 colorset assembly geometries are calculated using the neutron fluxes and the k-effective obtained in this step.

3. Based on Equation (4), the corrections of coarse group cross sections are estimated using the LIs obtained in steps (1) and (2) and the coupling coefficients of LIs pre-calculated in Section 2.2.

4. Target 4×4 colorset assembly calculation in coarse group is carried out with the corrected coarse group cross sections obtained in step (3) and the SPH factor or the DF. The LIs are updated using the neutron fluxes and the k-effective of target 4×4 colorset assembly calculation.

5. Steps (3) and (4) are repeated until the k-infinity and the pin-by-pin fission rate distribution of the target 4×4 colorset assembly calculation are converged.

As shown above, the iteration of core calculations is necessary in order to correct the coarse group cross sections by the present LI correction technique. In actual core analysis, cross sections are also corrected by the thermal-hydraulic feedback effect. The coarse group cross sections can be simultaneously corrected by the present LI correction technique and the thermal-hydraulic feedback effect and thus, the computational time would not be significantly increased even if present LI correction technique is applied. Also, note that the number of iterations required for the present LI correction technique with the SPH factor and that with the DF are comparable, which is confirmed through the verification calculations described in the next subsection.

3.3. Verification results and remarks

3.3.1. Impact of LI correction technique, SPH factor, and DF

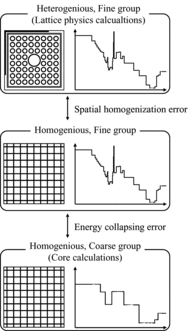
In general, in order to reproduce heterogeneous fine group calculations by homogeneous coarse group calculations, the spatial homogenization and the energy collapsing errors should be taken into account as shown in Figure 4.

Figure 4. Treatments of spatial and energy dependences in lattice physics and core calculations.

However, in the present paper, we only focus on the reduction of energy collapsing error. Reduction of the spatial homogenization error is out of the scope of the present paper. Therefore, in the present verifications, the pin-averaged 47-group cross sections obtained by the HELIOS code in single-assembly geometries are used as the reference cross sections, which corresponds to the middle part in Figure 4. Moreover, the core calculations are performed with the pin-averaged 4- or 8-group cross sections, which correspond to the lower part in Figure 4. In this context, the direct comparison with the HELIOS calculations (i.e., the upper part in Figure 4) would be an open issue to be addressed in future work. For the fine group (47-group) and the coarse group (4- or 8-group) calculations, the diffusion method is used.

In order to discuss the impacts of the LI correction technique, the SPH factor, and the DF, we compare the k-infinities and the pin-by-pin fission rate distributions on several 4×4 colorset assembly geometries. The pin-by-pin (cell-homogenized) calculations in the single and the colorset assembly geometries are performed by the diffusion method, in which the finite difference method is used for the spatial discretization. The present spatial discretization method would be different from typical pin-by-pin calculation method. However, in general, spatial discretization error is not very large in a pin-by-pin calculation since spatial mesh size is small. Therefore, the difference of spatial discretization method would not have significant impact on the calculation results. However, confirmation on this issue will be desirable as a future study.

The absolute value of relative difference of k-infinity and the root-mean-square (RMS) difference of pin-by-pin fission rate distribution are calculated as (9) $$\begin{array}{c}\hfill \Delta k_{inf}=\left|\frac{k_{inf}^{\mathrm{calculated}}-k_{inf}^{\mathrm{reference}}}{k_{inf}^{\mathrm{reference}}}\right|,\end{array}$$(9) (10) $$\begin{array}{c}\hfill \Delta R_{f,\mathrm{RMS}}=\sqrt{\frac{{\sum }_{m\in \mathrm{fuel}\mathrm{mesh}}{\left(R_{f,m}^{\mathrm{calculated}}-R_{f,m}^{\mathrm{reference}}\right)}^2}{N_{\mathrm{fuel}\mathrm{mesh}}},}\end{array}$$(10) where Δk_inf, ΔR_f,RMS, R_f,m, and N_{fuel mesh} are the absolute value of relative difference of k-infinity, the RMS difference of pin-by-pin fission rate distribution, the pin-by-pin fission rate on fuel mesh m, and the total number of fuel meshes, respectively. The superscript calculated represents the calculations with the coarse group cross sections corrected (or not corrected) by the present LI correction technique with the SPH factor or the DF. The superscript reference represents those with the reference cross sections. Note that the reference cross sections have been corrected by the SPH method in order to reduce the spatial homogenization errors in single assembly geometries.

In the present verifications, the six types of calculation results in Table 2 are compared with the reference calculation results (i.e., the 47-group calculation results).

Table 2. Types of calculation results used in the present verifications.

	LI correction	SPH
	technique	factor	DF
None	–	–	–
LI	○	–	–
SPH	–	○	–
DF	–	–	○
LI + SPH	○	○	–
LI + DF	○	–	○

Note: –: not applied, ○: applied.

The absolute value of relative difference of k-infinities and the RMS difference of pin-by-pin fission rate distributions are summarized in Tables 3 and 4. These are calculated in approximately 6500 patterns of 4×4 colorset assembly geometries with 4- and 8-group cross sections.

Table 3. Summary of 4-group calculation results considering errors due to spectral interference effect and energy collapsing.

		None	LI	SPH	DF	LI + SPH	LI + DF
Control rod: withdrawn
$\Delta k_{inf}$ (pcm)	Average	106	87	57	44	37	20
	Maximum	403	310	172	142	81	45
ΔRf, RMS (%)	Average	1.19	1.01	0.77	0.59	0.49	0.26
	Maximum	1.51	1.16	1.28	1.01	0.82	0.47
Control rod: inserted
$\Delta k_{inf}$ (pcm)	Average	137	95	100	89	46	31
	Maximum	465	328	221	196	90	63
ΔRf, RMS (%)	Average	1.28	1.06	0.85	0.71	0.53	0.33
	Maximum	1.60	1.23	1.37	1.12	0.86	0.58

Table 4. Summary of 8-group calculation results considering errors due to spectral interference effect and energy collapsing.

		None	LI	SPH	DF	LI + SPH	LI + DF
Control rod: withdrawn
$\Delta k_{inf}$ (pcm)	Average	29	33	14	16	8	3
	Maximum	135	110	60	70	24	8
ΔRf, RMS (%)	Average	0.59	0.50	0.29	0.30	0.20	0.07
	Maximum	0.78	0.63	0.45	0.52	0.35	0.13
Control rod: inserted
$\Delta k_{inf}$ (pcm)	Average	36	38	13	13	6	6
	Maximum	151	115	62	70	24	12
ΔRf, RMS (%)	Average	0.62	0.52	0.31	0.35	0.21	0.08
	Maximum	0.82	0.65	0.48	0.55	0.35	0.14

From Tables 3 and 4, the impacts of the LI correction technique, the SPH factor, and the DF can be discussed.

First, the impact of the LI correction technique is discussed from the comparison of “None” and “LI”. In this comparison, only the error due to the spectral interference effect on coarse group cross sections is focused. For the 4-group calculation, the calculation accuracies of the k-infinity and the pin-by-pin fission rate distribution are improved. On the other hand, for 8-group calculations, the average values of difference of k-infinity become large by the LI correction technique. In order to discuss the reasons for the above observations, we confirm the verification results in [6]. In [6], the same 2D benchmark problems are carried out though the reference calculation results are calculated with the coarse group cross sections, which are obtained by direct collapsing of fine group cross sections in the target colorset assembly geometry. The absolute value of relative difference of k-infinities and the RMS difference of pin-by-pin fission rate distributions are shown in Tables 5 and 6, which are described in [6].

Table 5. Summary of 4-group calculation results only considering spectral interference effect in previous study [6].

		None	LI
Control rod: withdrawn
$\Delta k_{inf}$ (pcm)	Average	40	20
	Maximum	143	48
ΔRf, RMS (%)	Average	0.48	0.13
	Maximum	0.79	0.23
Control rod: inserted
$\Delta k_{inf}$ (pcm)	Average	75	23
	Maximum	187	52
ΔRf, RMS (%)	Average	0.55	0.16
	Maximum	0.86	0.28

Table 6. Summary of 8-group calculation results only considering spectral interference effect in previous study [6].

		None	LI
Control rod: withdrawn
$\Delta k_{inf}$ (pcm)	Average	17	1
	Maximum	72	4
ΔRf, RMS (%)	Average	0.29	0.02
	Maximum	0.51	0.04
Control rod: inserted
$\Delta k_{inf}$ (pcm)	Average	13	1
	Maximum	73	5
ΔRf, RMS (%)	Average	0.33	0.02
	Maximum	0.54	0.04

From Tables 5 and 6, the calculation accuracies of the k-infinity and the pin-by-pin fission rate distribution are improved by the LI correction technique both for 4- and 8-group calculations. However, by comparing Tables 3–6, the improvements of calculation accuracies in Tables 3 and 4 are smaller than those in Tables 5 and 6. Only the error due to the spectral interference effect on coarse group cross sections is included in the “None” of Tables 5 and 6. On the contrary, the errors due to the spectral interference effect on coarse group cross sections and the energy collapsing are included in “None” of Tables 3 and 4. Since these two errors (i.e., the spectral interference effect and the energy collapsing) would cancel each other, “None” of Tables 3 and 4 would show smaller error. Therefore, improvement of calculation accuracies in Tables 3 and 4 are smaller than those in Tables 5 and 6. More detailed discussion on this matter (cancellation of errors) will be described in Section 3.3.2.

Second, through the comparisons between “None”, “SPH”, and “DF”, the impacts of the SPH factor and the DF are discussed. In these comparisons, only the error due to the energy collapsing of cross sections is focused. For both of 4- and 8-group calculations in Tables 3 and 4, the calculation accuracies are improved by the SPH factor or the DF. Moreover, the improvements of calculation accuracies by the SPH factor and the DF are similar. Thus, the SPH factor and the DF, which are calculated in single-assembly geometries, can consistently remove the energy collapsing errors in colorset assembly geometries.

Finally, the applicability of the present LI correction technique with the SPH factor or the DF is discussed. The differences in “LI + SPH” become smaller than those in “None”, “LI”, and “SPH”. The improvements of calculation accuracies by “LI + SPH” are approximately equal to the summation of those by “LI” and “SPH”. Thus, “LI + SPH” can efficiently remove both of the errors due to the spectral interference effect on coarse group cross sections and the energy collapsing. Moreover, the combination of the LI correction technique with the SPH factor does not offset the improvements of calculation accuracies obtained by each correction technique. Similarly tendencies are observed among “None”, “LI”, “DF”, and “LI + DF”. Thus, “LI + DF” (i.e., the present LI correction technique with the DF) also can remove both of the errors due to the spectral interference effect on coarse group cross sections and the energy collapsing without the cancellation of these correction performances. From the comparisons of “LI + SPH” and “LI + DF”, the difference of k-infinity by “LI + DF” is smaller than that by “LI + SPH” and the difference of pin-by-pin fission rate distribution by “LI + SPH” is approximately a few times larger than that by “LI + DF”. Therefore, “LI + DF” reproduces the reference calculation results better than “LI + SPH”. The reason for this difference is discussed in the next subsection.

Using the calculation results shown in Tables 3–6, breakdown of differences between the reference fine group and the coarse group calculations are analyzed as shown in Tables 7 and 8.

Table 7. Breakdown of calculation errors by LI correction technique, SPH factor, and DF in 4-group.

		Spectral interference effect		Energy collapsing
			With correction		With correction	With correction
	Total	Uncorrected	by LI	Uncorrected	by SPH	by DF
Control rod: withdrawn
$\Delta k_{inf}$ (pcm)	106	40	20	66	17	0
ΔRf, RMS (%)	1.19	0.48	0.13	0.71	0.36	0.13
Control Rod: Inserted
$\Delta k_{inf}$ (pcm)	137	75	23	62	23	8
ΔRf, RMS (%)	1.28	0.55	0.16	0.73	0.37	0.17

Table 8. Breakdown of calculation errors by LI correction technique, SPH factor, and DF in 8-group.

		Spectral interference effect		Energy collapsing
			With correction		With correction	With correction
	Total	Uncorrected	by LI	Uncorrected	by SPH	by DF
Control rod: withdrawn
$\Delta k_{inf}$ (pcm)	29	17	1	12	7	2
ΔRf, RMS (%)	0.59	0.29	0.02	0.30	0.18	0.05
Control rod: inserted
$\Delta k_{inf}$ (pcm)	36	13	1	23	5	5
ΔRf, RMS (%)	0.62	0.33	0.02	0.29	0.19	0.06

Values shown in Tables 7 and 8 are estimated by the averaged differences of k-infinity and pin-by-pin fission rate distribution, which are represented as “Average” in Tables 3–6. Details of estimations are described as follows.

1. Total differences between the reference fine group and the coarse group calculations are represented as “Total”, which correspond to “None” in Tables 3 and 4.

2. Errors due to the spectral interference effect on coarse group cross sections are represented as “Uncorrected” in “Spectral interference effect”, which correspond to “None” in Tables 5 and 6.

3. Residual errors after the LI correction are represented as “With correction by LI”. These values correspond to “LI” in Tables 5 and 6.

4. Errors due to the energy collapsing are represented as “Uncorrected” in “Energy collapsing”, which are calculated by subtracting “Uncorrected” in “Spectral interference effect” from “Total”.

5. Residual errors after the SPH correction are represented as “With correction by SPH”. These values are calculated by subtracting “LI” in Tables 5 and 6 from “LI + SPH” in Tables 3 and 4.

6. Residual errors after the DF correction are represented as “With correction by DF”. These values are calculated by subtracting “LI” in Tables 5 and 6 from “LI + DF” in Tables 3 and 4.

The errors due to the spectral interference effect on coarse group cross sections and the energy collapsing are not generally independent. Moreover, they would cancel out each other as described previously. Thus, the breakdown in Tables 7 and 8 cannot be rigorously estimated. However, in the present paper, we approximately estimate the breakdown of errors in Tables 7 and 8 in order to compare the performances of improvements of calculation accuracies by each correction technique.

From Tables 7 and 8, first, the errors due to the spectral interference effect on coarse group cross sections (i.e., “Uncorrected” in “Spectral interference effect”) are reduced by the LI correction technique. The degree of freedom for the LI correction technique in 8-group is greater than that in 4-group, which can be found from Equation (3) and is also discussed in [6]. Thus, as the number of energy groups becomes larger, the residual errors after the LI correction (i.e., “With correction by LI”) become smaller. Next, the errors due to the energy collapsing (i.e., “Uncorrected” in “Energy collapsing”) are removed by the SPH factor or the DF. As mentioned above, the residual errors (i.e., “With correction by SPH” or “With correction by DF”) become smaller when the number of energy groups becomes larger. In the present study, the SPH factor and the DF, which are calculated in single-assembly geometries, are used in colorset assembly geometries. Namely, the variations of the SPH factor and the DF due to the spectral interference effect are assumed to be small in the present study. Since the impact of this assumption in 4-group calculations typically becomes larger than that in 8-group calculations, the SPH factor and the DF obtained in single-assembly geometries would show better performance as the number of energy groups becomes larger.

In 4-group calculations, the improvements by the SPH factor are approximately 60%–70% of those by the DF as shown in Table 7. Moreover, in 8-group calculations shown in Table 8, the improvements by the SPH factor are approximately 50% of those by the DF. In other words, the DF shows better performance than the SPH factor. The reason is discussed in the next subsection together with the reason for better performance of “LI + DF” than “LI + SPH” in Tables 3 and 4.

3.3.2. Comparisons of detailed pin-by-pin fission rate distribution

In order to discuss the improvements of calculation accuracies by the LI correction technique, the SPH factor, and the DF in more detail, we compare the pin-by-pin fission rate distributions on 2×2 colorset assembly geometry with the periodic boundary condition shown in Figure 5.

Figure 5. Geometry of 2×2 colorset assemblies.

We use the 2×2 colorset assembly geometry shown in Figure 5 in this subsection for simplicity.

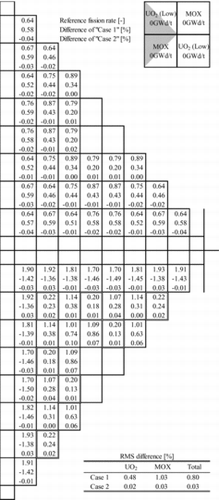
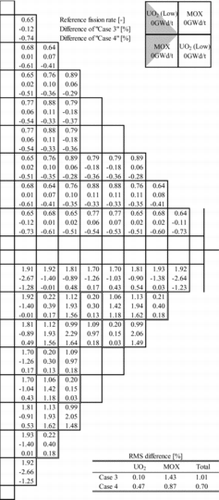
As shown in Figure 5, the 2×2 colorset assembly geometry consists of the low-enrichment UO₂ (1.0 wt% ²³⁵U) and the MOX (4.0 wt% Pu-fissile) fuel assemblies, in which large spectral interference effect can be observed. In the 2×2 colorset assembly geometry, the control rod is withdrawn and the assembly-averaged exposure is 0 GWd/t. Thus, the RMS differences of pin-by-pin fission rate distribution in the 2×2 colorset assembly geometry, which are shown in latter, become larger than those in the 4×4 colorset assembly geometry shown in Tables 3 and 4. The energy collapsing of cross sections from 47 to 8 energy groups is considered.

First, we discuss that the improvements of calculation accuracies in Tables 3 and 4 are smaller than those in Tables 5 and 6. The following four types of difference of pin-by-pin fission rate distribution are discussed in order to address the differences in calculation accuracies.

• Case 1: Difference of “None” in Tables 5 and 6.

• Case 2: Difference of “LI” in Tables 5 and 6.

• Case 3: Difference of “None” in Tables 3 and 4.

• Case 4: Difference of “LI” in Tables 3 and 4.

It would be reminded that only errors of coarse group cross sections due to the spectral interaction are included in Tables 5 and 6, but not only the errors of coarse group cross sections due to the spectral interaction but also errors due to the energy collapsing are also included in Tables 3 and 4. These calculation results are shown in Figures 6 and 7. Note that the reference calculation results used in “Case 1” and “Case 2” (i.e., “Reference fission rate” in Figure 6) are obtained with the reference coarse group cross sections and those used in “Case 3” and “Case 4” (i.e., “Reference fission rate” in Figure 7) are obtained with the reference fine group cross sections, respectively.

Figure 6. Difference of pin-by-pin fission rate distribution (Cases 1 and 2).

Figure 7. Difference of pin-by-pin fission rate distribution (Cases 3 and 4).

In Figure 6, from the comparison of “Case 1” and “Case 2”, the differences due to the spectral interference effect on coarse group cross sections are mainly observed in the assembly peripheral regions and they are reduced by the LI correction technique on both of UO₂ and MOX fuel assemblies. On the other hand, while the RMS difference on MOX fuel assemblies in “Case 3” becomes larger than that in “Case 4”, the RMS difference on UO₂ fuel assemblies in “Case 3” becomes smaller than that in “Case 4” in Figure 7. From this result, in UO₂ fuel assemblies, errors due to the spectral interference effect on coarse group cross sections and the energy collapsing would cancel out each other. This cancellation is also confirmed by the comparison of “Case 1”, “Case 2”, and the differences of “SPH” and “DF” in Tables 3 and 4. In UO₂ fuel assemblies, though the differences of pin-by-pin fission rates of “Case 2” generally show negative values, those of “SPH” and “DF” in Tables 3 and 4 show positive values. Thus, the errors due to the spectral interference effect on coarse group cross sections and the energy collapsing cancel out each other. Let us focus on the differences of several meshes located around Gd-bearing fuels framed by double line in MOX fuel assemblies. Improvements of these differences in Figure 7 become smaller than those in Figure 6. Namely, the several meshes located around the Gd-bearing fuels would have larger impact by the energy collapsing error than other meshes. Therefore, the improvements of calculation accuracies by the LI correction technique in Tables 3 and 4 become smaller than those in Tables 5 and 6. Similar tendencies caused on fuel meshes located around the Gd-bearing fuels are observed in other 2×2 colorset assembly geometries (e.g., 2×2 colorset assembly geometries, which consist of the low-enrichment and the high-enrichment UO₂ fuel assemblies).

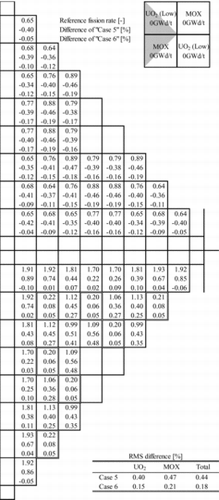
Next, we discuss that the LI correction technique with the DF performs better than the LI correction technique with the SPH factor in Tables 3 and 4. We compare the following two types of difference of pin-by-pin fission rate distribution in addition to “Case 3” and “Case 4” as described above. By comparing the four types of differences, we address the difference in the performances of the SPH factor and the DF.

• Case 5: Difference of “LI + SPH” in Tables 3 and 4.

• Case 6: Difference of “LI + DF” in Tables 3 and 4.

These calculation results are shown in Figure 8. Note that the reference calculation results used in the above two cases (i.e., “Reference fission rate” in Figure 8) are obtained with the reference fine group cross sections.

Figure 8. Difference of pin-by-pin fission rate distribution (Cases 5 and 6).

From the comparison among “Case 3”, “Case 4”, and “Case 5”, the calculation accuracies are improved by the SPH factor. Thus, the application of the SPH factor can reduce the errors due to energy collapsing. By comparing “Case 3”, “Case 4”, and “Case 6”, the differences also become smaller; thus, the DF also can reduce the energy collapsing errors. Furthermore, the improvements of calculation accuracies in “Case 6” are larger than that in “Case 5” for every fuel meshes.

The assembly-averaged SPH factor, which is calculated in single-assembly geometries, is approximately unity [7]. However, in general, that calculated in colorset assembly geometries is different from unity (i.e., the assembly-averaged SPH factor is perturbed by the spectral interference effect). As discussed in [14], even though the spatial shape of pin-by-pin fission rate distribution on each fuel assembly can be approximately reproduced in “Case 5”, the assembly-averaged fission rate distribution cannot be accurately reproduced since the variation of SPH factor due to the spectral interference effect is assumed to be small in the present study. Therefore, it is indicated that the LI correction technique with the SPH factor would not be useful to accurately reproduce the calculation results of the reference fine group calculations as long as the variation of SPH factor due to the spectral interference effect is not taken into account.

On the other hand, though the variation of DF due to the spectral interference effect is also assumed to be small, the DF has larger degree of freedom than that of the SPH factor (i.e., the SPH factor and the DF are calculated in each pin-cell mesh and in every surface of pin-cell mesh, respectively). Furthermore, for the spatial homogenization, the DF at the fuel assembly surface depends on the type of fuel assembly. Thus, the “level” of surface flux at the heterogeneous calculations is approximately preserved in the homogeneous calculations by the DF. Similar to the spatial homogenization, for the energy collapsing, the “level” of surface flux at the fine group calculations is approximately preserved in the coarse group calculations by the DF. These would contribute to the robustness of the DF to the spectral interference effect.

From the above discussions, the combination of the LI correction technique with the DF reproduces the reference fine group calculation results better than that of the LI correction technique with the SPH factor. The application of DF for the pin-by-pin core analysis would have difficulty from the viewpoint of the computational load since the DF requires larger memory storage than that of the SPH factor. However, the computational performance becomes higher year by year. In this context, difficulty on the memory requirement is reducing and the usefulness of the LI correction technique with the DF is increasing from the viewpoint of calculation accuracies.

4. Conclusions

In this paper, we combine the LI correction technique, which can consider the spectral interference effect on coarse group cross sections, with the SPH factor or the DF, which can reduce the errors due to energy collapsing.

In the LI correction technique, the variations of coarse group cross sections due to the spectral interference effect are represented by the linear combination of variations of coarse group LIs and the reference coarse group cross sections are well reproduced. However, though the reference coarse group calculation results are well reproduced, errors due to the energy collapsing of cross sections still exist (i.e., the reference fine group calculation results are not reproduced). In order to reduce the energy collapsing errors, it is necessary to combine other correction methods to reduce the energy collapsing errors with the LI correction technique. In the present study, we focus on the SPH factor and the DF. In general, similar to coarse group cross sections, the SPH factor and the DF are also perturbed by the spectral interference effect in core geometries. However, our preliminary investigations suggested that if the variations of SPH factor and DF due to the spectral interference effect are considered in the calculation procedure of LI correction technique, the LI correction technique would be more complicated and become unstable from the viewpoint of numerical calculations. Thus, in the present study, the SPH factor and the DF calculated in single-assembly geometries are used with the LI correction technique.

In order to verify the combination uses of the LI correction technique, the SPH factor, and the DF, 4×4 colorset assembly calculations including the control cell, which consist of typical BWR fuel assemblies, are carried out. The energy collapsing from 47 to 4 and 8 energy groups is considered. The pin-by-pin fine mesh calculations based on the diffusion theory are performed and the k-infinity and the pin-by-pin fission rate distribution are compared. In the present verification, the calculations results obtained with fine group cell-homogeneous cross sections are considered as the reference. The calculation results indicate that the energy collapsing errors are reduced by the SPH factor or the DF. Moreover, the reference calculation results are well reproduced by the combination of the LI correction technique, the SPH factor, and the DF. The LI correction technique with the SPH factor or the DF shows similar improvement for the k-infinity. However, from the viewpoint of the pin-by-pin fission rate distribution, the LI correction technique with the DF outperforms the LI correction technique with the SPH factor. Namely, error reduction of “LI + DF” is a few times larger than that of “LI+SPH”.

In order to discuss the difference between the SPH factor and the DF, we carry out the 2×2 colorset assembly calculations and compare the pin-by-pin fission rate distribution. The calculation results indicate that though the spatial shape of pin-by-pin fission rate distribution on each fuel assembly can be reproduced in “LI + SPH”, the assembly-averaged fission rate distribution cannot be well reproduced. In general, the assembly-averaged SPH factor calculated in colorset assembly geometries is different from unity due to the spectral interference effect. However, in the present study, we use the SPH factor calculated in single-assembly geometries and the variation of SPH factor due to the spectral interference effect is assumed to be negligible. Similar to the SPH factor, the variation of the DF due to the spectral interference effect is also assumed to be negligible (i.e., the DF calculated in single-assembly geometries is used). However, since the SPH factor and the DF are calculated in each pin-cell mesh and in every surface of pin-cell mesh, respectively, the DF has larger degree of freedom than the SPH factor. Furthermore, since the DF depends on the type of fuel assembly, the “level” of surface flux at the fine group calculations is approximately preserved in the coarse group calculations by the DF (i.e., the DF is more robust over the spectral interference effect than the SPH factor). Therefore, “LI + DF” reproduces the reference calculation results better than “LI + SPH”.

Consequently, the LI correction technique with the DF is useful to capture the spectral interference effect on coarse group cross sections and to reduce the energy collapsing errors on pin-by-pin BWR core analysis. On the other hand, the applicability of LI correction technique for the reduction of spatial homogenization errors has not been investigated in the present study. Thus, such additional investigations are necessary on this point for practical use of the LI correction technique.