Monte Carlo uncertainty quantification of the effective delayed neutron fraction

ABSTRACT

The applicability of Monte Carlo techniques, namely the Monte Carlo sensitivity method and the random-sampling method, for uncertainty quantification of the effective delayed neutron fraction β_eff is investigated using the continuous-energy Monte Carlo transport code, MCNP, from the perspective of statistical convergence issues. This study focuses on the nuclear data as one of the major sources of β_eff uncertainty. For validation of the calculated β_eff, a critical configuration of the VENUS-F zero-power reactor was used. It is demonstrated that Chiba's modified k-ratio method is superior to Bretscher's prompt k-ratio method in terms of reducing the statistical uncertainty in calculating not only β_eff but also its sensitivities and the uncertainty due to nuclear data. From this result and a comparison of uncertainties obtained by the Monte Carlo sensitivity method and the random-sampling method, it is shown that the Monte Carlo sensitivity method using Chiba's modified k-ratio method is the most practical for uncertainty quantification of β_eff. Finally, total β_eff uncertainty due to nuclear data for the VENUS-F critical configuration is determined to be approximately 2.7% with JENDL-4.0u, which is dominated by the delayed neutron yield of ²³⁵U.

KEYWORDS:

• Effective delayed neutron fraction
• uncertainty quantification
• sensitivity
• Bretscher's prompt k-ratio method
• Chiba's modified k-ratio method
• random-sampling method
• MCNP
• VENUS-F

1. Introduction

The effective delayed neutron fraction β_eff performs a key role in reactor design and safety analysis. For a reliable evaluation of the design parameters related to β_eff including control-rod worth and the margin of prompt criticality, it is necessary to conduct the uncertainty quantification (UQ) of β_eff.

Recently, continuous-energy Monte Carlo transport codes such as the Monte Carlo N-Particle transport code (MCNP) [1] have been identified as powerful tools in calculating not only the effective neutron multiplication factor k_eff but also its nuclear data sensitivities and kinetic parameters such as β_eff (without any geometric modeling approximation). Although these codes do not have the capability to directly calculate the sensitivity of β_eff due to their technical shortcomings, the sensitivity of β_eff can be expressed approximately as a function of two different k_eff sensitivities; this means that the uncertainty in β_eff due to nuclear data can be quantified by the Monte Carlo sensitivity method using the approximate β_eff sensitivities and evaluated covariance data of the nuclear data library, as proposed by Chiba et al. [2]. In addition, a random-sampling-based approach known as the random-sampling method has also attracted significant interest and has been studied extensively in recent years [3–5]; this approach directly calculates the propagation of evaluated nuclear data and/or model parameter uncertainties without the need for the sensitivities. However, when both of these techniques are applied with the Monte Carlo transport code, they inevitably involve statistical uncertainty and therefore require a long computation time to reduce it; because of β_eff's numerical complexity, this problem is more prominent for β_eff than for k_eff. Therefore, the β_eff UQ using the Monte Carlo method is yet to be attempted.

In this study, the applicability of the two Monte Carlo techniques, the Monte Carlo sensitivity method and the random-sampling method, to the UQ of β_eff were investigated from the statistical convergence perspective. In this study, we have dealt exclusively with the nuclear data although various uncertainties (for example, nuclear data, material compositions, geometry, and the computational method) would each affect the calculation of β_eff. For the Monte Carlo sensitivity method, we focused on two methods for calculating the β_eff sensitivities: (1) Bretscher's prompt k-ratio method [6], a conventional method used to calculate β_eff in the Monte Carlo analysis, and (2) the modified k-ratio method which was proposed by Chiba [7]. The theoretical basis for the prompt k-ratio method can be found in the studies of Meulekamp and Van der Marck [8], and the theoretical basis for the modified k-ratio method can be found in the studies of Chiba [7] and Nagaya and Mori [9]. β_eff and its sensitivities to the nuclear data were calculated by the MCNP version 6.1.1. For validation of the calculated β_eff, we employed a critical configuration of the VENUS-F zero-power reactor at the SCK•CEN site [10], an experimental fast reactor fueled with 30 wt.% enriched metallic uranium and reflected by pure solid lead. In this study, the core geometry was modeled precisely based on small details, and JENDL-4.0u [11,12] was used as the nuclear data library because it contains the covariance data of the delayed neutron yield ${\bar{\nu }}^d$ although there are no covariances for the delayed neutron spectrum χ^d.

This paper is organized as follows. Section 2 is devoted to the Monte Carlo sensitivity method, where explanations of the two methods, Bretscher's prompt k-ratio method and Chiba's modified k-ratio method, are provided along with the VENUS-F MCNP model, and the UQ through the use of the Monte Carlo sensitivity method. Next, the calculated β_eff and their sensitivities and uncertainties are discussed in terms of the statistical issues. Section 3 is devoted to the random-sampling method. In this study, randomly perturbed nuclear data files were produced with the random-sampling code SANDY [5]. Therefore, initially, we describe the process of random sampling by SANDY; then its applicability to the UQ of β_eff is examined; finally, our conclusions are presented in Section 4.

2. Monte Carlo sensitivity method

2.1. The β_eff sensitivities

2.1.1. Prompt k-ratio method

Bretscher's prompt k-ratio method (which from now on will be referred to as the conventional method) describes β_eff as (1) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq 1-\frac{k_p}{k},\end{array}$$(1) where k is the effective neutron multiplication factor calculated in the usual way with the Monte Carlo transport code. This is obtained by solving the neutron transport equation: (2) $$\begin{array}{c}\hfill (\mathcal{T}-\mathcal{S})\psi =\frac{1}{k}\mathcal{F}\psi ,\end{array}$$(2) where ψ( = ψ(r, Ω, E)) is the angular neutron flux at position r with direction Ω and energy E. The operators $\mathcal{T}$, $\mathcal{S}$, and $\mathcal{F}$ represent the transport, scattering, and fission operator, respectively, which are expressed as (3) $$\mathcal{T}=\mathit{\Omega }·\nabla +{\Sigma }_t(\mathit{r},E),$$(3) (4) $$\mathcal{S}=\int d{\mathit{\Omega }}^{\text{'}}\int d{E}^{\text{'}}{\Sigma }_s(\mathit{r},\mathit{\Omega },E\leftarrow {\mathit{\Omega }}^{\text{'}},E^{\text{'}}),$$(4) (5) $$\mathcal{F}=\int d{\mathit{\Omega }}^{\text{'}}\int d{E}^{\text{'}}\chi (\mathit{\Omega },E)\bar{\nu }\left(E^{\text{'}}\right){\Sigma }_f(\mathit{r},E^{\text{'}}),$$(5) where Σ_t and Σ_s are the macroscopic total and scattering cross sections, respectively; χ, $\bar{\nu }$, and Σ_f are the fission neutron spectrum, the fission neutron yield, and the macroscopic fission cross section, respectively, each of which is totaled with respect to fissionable materials. In Equation (1(1) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq 1-\frac{k_p}{k},\end{array}$$(1) ), k_p is the effective neutron multiplication factor induced by prompt neutrons; which is obtained by solving the following equation: (6) $$\begin{array}{ccc}& & (\mathcal{T}-\mathcal{S}){\psi }_p=\frac{1}{k_p}{\mathcal{F}}_p{\psi }_p,\hfill \end{array}$$(6) where ψ_p is an angular neutron flux induced by the prompt neutrons; ${\mathcal{F}}_p$ is a fission (by prompt neutrons) operator expressed as follows: (7) $$\begin{array}{ccc}& & {\mathcal{F}}_p=\int d{\mathit{\Omega }}^{\text{'}}\int d{E}^{\text{'}}{\chi }^p(\mathit{\Omega },E){\bar{\nu }}^p\left(E^{\text{'}}\right){\Sigma }_f(\mathit{r},E^{\text{'}}).\hfill \end{array}$$(7) In Equation (7(7) $$\begin{array}{ccc}& & {\mathcal{F}}_p=\int d{\mathit{\Omega }}^{\text{'}}\int d{E}^{\text{'}}{\chi }^p(\mathit{\Omega },E){\bar{\nu }}^p\left(E^{\text{'}}\right){\Sigma }_f(\mathit{r},E^{\text{'}}).\hfill \end{array}$$(7) ), χ ^p and ${\bar{\nu }}^p$ are the prompt neutron spectrum and the prompt neutron yield, respectively. In the MCNP calculation, k_p is obtained with the TOTNU card, an input card which is used to determine if the delayed neutrons are considered in the criticality calculation. The statistical uncertainty of β_eff defined in Equation (1(1) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq 1-\frac{k_p}{k},\end{array}$$(1) ) is expressed as (8) $$\begin{array}{c}\hfill \delta {\beta }_{\mathrm{eff}}\simeq \frac{k_p}{k}\sqrt{{\left(\frac{\delta k_p}{k_p}\right)}^2+{\left(\frac{\delta k}{k}\right)}^2},\end{array}$$(8) where the notation δ stands for the absolute statistical uncertainty in a particular parameter. Namely, δk and δk_p are the statistical uncertainties in k and k_p, respectively; the values of both δk and δk_p are calculated by MCNP. Although the propagated statistical uncertainties should ideally include correlations between the variables, for the sake of simplicity, they were disregarded throughout this study. Using the definition of the sensitivity and Equation (1(1) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq 1-\frac{k_p}{k},\end{array}$$(1) ), the sensitivity of β_eff to parameter x can be written as follows: (9) $$\begin{array}{c}\hfill S_x^{{\beta }_{\mathrm{eff}}}\equiv \frac{\partial {\beta }_{\mathrm{eff}}}{\partial x}\frac{x}{{\beta }_{\mathrm{eff}}}\simeq \frac{k_p}{k-k_p}\left(S_x^k-S_x^{k_p}\right),\end{array}$$(9) where S^k_x( ≡ (∂k/∂x)/(x/k)) and S^kp_x( ≡ (∂k_p/∂x)/(x/k_p)) are the sensitivities of k and k_p to the parameter x, respectively; these are obtained with the KSEN card of MCNP, a card dedicated to calculating the k_eff sensitivities. The statistical uncertainty in S^βeff_x is expressed as follows: (10) $$\begin{array}{ccc}& & \delta S_x^{{\beta }_{\mathrm{eff}}}\simeq \left|S_x^{{\beta }_{\mathrm{eff}}}\right|\hfill \\ & & ·\sqrt{{\left(\frac{\delta k_p}{k_p}\right)}^2+\frac{{\left(\delta k\right)}^2+{\left(\delta k_p\right)}^2}{{\left(k-k_p\right)}^2}+\frac{{\left(\delta S_x^k\right)}^2+{\left(\delta S_x^{k_p}\right)}^2}{{\left(S_x^k-S_x^{k_p}\right)}^2}},\hfill \end{array}$$(10) where δS^k_x and δS^kp_x are statistical uncertainties in S^k_x and S^kp_x, respectively; these are also obtained with MCNP.

2.1.2. Modified k-ratio method

Chiba's modified k-ratio method (which from now on will be referred to as the modified method) determines β_eff as follows: (11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) where a is a scaling factor introduced by Chiba; $\bar{k}$ is the effective neutron multiplication factor obtained by solving the following equation: (12) $$\begin{array}{ccc}& & (\mathcal{T}-\mathcal{S})\bar{\psi }=\frac{1}{\bar{k}}\bar{\mathcal{F}}\bar{\psi },\hfill \end{array}$$(12) where $\bar{\psi }$ is a fictitious angular neutron flux obtained from Equation (12(12) $$\begin{array}{ccc}& & (\mathcal{T}-\mathcal{S})\bar{\psi }=\frac{1}{\bar{k}}\bar{\mathcal{F}}\bar{\psi },\hfill \end{array}$$(12) ); $\bar{\mathcal{F}}$ is a fission operator defined as (13) $$\begin{array}{ccc}\hfill \bar{\mathcal{F}}& =& \int d{\mathit{\Omega }}^{\text{'}}\int d{E}^{\text{'}}(\chi (\mathit{\Omega },E)\bar{\nu }\left(E^{\text{'}}\right)\hfill \\ & & +a{\chi }^d(\mathit{\Omega },E){\bar{\nu }}^d\left(E^{\text{'}}\right)){\Sigma }_f(\mathit{r},E^{\text{'}}).\hfill \end{array}$$(13) Using the relationship between prompt, delayed, and total neutrons: (14) $$\begin{array}{ccc}\hfill \chi \bar{\nu }& =& {\chi }^p{\bar{\nu }}^p+{\chi }^d{\bar{\nu }}^d,\hfill \end{array}$$(14) Equation (13(13) $$\begin{array}{ccc}\hfill \bar{\mathcal{F}}& =& \int d{\mathit{\Omega }}^{\text{'}}\int d{E}^{\text{'}}(\chi (\mathit{\Omega },E)\bar{\nu }\left(E^{\text{'}}\right)\hfill \\ & & +a{\chi }^d(\mathit{\Omega },E){\bar{\nu }}^d\left(E^{\text{'}}\right)){\Sigma }_f(\mathit{r},E^{\text{'}}).\hfill \end{array}$$(13) ) can be rewritten as (15) $$\begin{array}{ccc}\hfill \bar{\mathcal{F}}& =& \int d{\mathit{\Omega }}^{\text{'}}\int d{E}^{\text{'}}({\chi }^p(\mathit{\Omega },E){\bar{\nu }}^p\left(E^{\text{'}}\right)\hfill \\ & & +(a+1){\chi }^d(\mathit{\Omega },E){\bar{\nu }}^d\left(E^{\text{'}}\right)){\Sigma }_f(\mathit{r},E^{\text{'}}).\hfill \end{array}$$(15) In the MCNP calculation, $\bar{k}$ is obtained using a nuclear data library in which ${\bar{\nu }}^d$ is multiplied with (a + 1). As a approaches zero, the limit of the right-hand side of Equation (11(11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) ) equals the exact β_eff value [9]; in other words, the approximation in Equation (11(11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) ) is poorer when a departs from zero. In addition, setting a = −1 in Equation (15(15) $$\begin{array}{ccc}\hfill \bar{\mathcal{F}}& =& \int d{\mathit{\Omega }}^{\text{'}}\int d{E}^{\text{'}}({\chi }^p(\mathit{\Omega },E){\bar{\nu }}^p\left(E^{\text{'}}\right)\hfill \\ & & +(a+1){\chi }^d(\mathit{\Omega },E){\bar{\nu }}^d\left(E^{\text{'}}\right)){\Sigma }_f(\mathit{r},E^{\text{'}}).\hfill \end{array}$$(15) ) and in Equation (11(11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) ) turns Equation (11(11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) ) into Equation (1(1) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq 1-\frac{k_p}{k},\end{array}$$(1) ); to summarize, we see that the conventional method is a special case (a = −1) of the modified k-ratio method. Using Equation (11(11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) ), the statistical uncertainty in β_eff is expressed as follows: (16) $$\begin{array}{c}\hfill \delta {\beta }_{\mathrm{eff}}\simeq \frac{\bar{k}}{k}\sqrt{{\left(\frac{\delta \bar{k}}{\bar{k}}\right)}^2+{\left(\frac{\delta k}{k}\right)}^2}·\frac{1}{\left|a\right|}.\end{array}$$(16) It can be seen from Equations (8(8) $$\begin{array}{c}\hfill \delta {\beta }_{\mathrm{eff}}\simeq \frac{k_p}{k}\sqrt{{\left(\frac{\delta k_p}{k_p}\right)}^2+{\left(\frac{\delta k}{k}\right)}^2},\end{array}$$(8) ) and (16(16) $$\begin{array}{c}\hfill \delta {\beta }_{\mathrm{eff}}\simeq \frac{\bar{k}}{k}\sqrt{{\left(\frac{\delta \bar{k}}{\bar{k}}\right)}^2+{\left(\frac{\delta k}{k}\right)}^2}·\frac{1}{\left|a\right|}.\end{array}$$(16) ) that, if the statistical uncertainties in k, k_p, and $\bar{k}$ are similar, the statistical uncertainty in β_eff calculated using the modified method is |a| times smaller than that derived using the conventional method. Using the definition of the sensitivity and Equation (11(11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) ), the β_eff sensitivity to the parameter x is expressed as follows: (17) $$\begin{array}{ccc}\hfill S_x^{{\beta }_{\mathrm{eff}}}& \equiv & \frac{\partial {\beta }_{\mathrm{eff}}}{\partial x}\frac{x}{{\beta }_{\mathrm{eff}}}\simeq \frac{\bar{k}}{k}\frac{1}{{\beta }_{\mathrm{eff}}}\left(S_x^{\bar{k}}-S_x^k\right)·\frac{1}{a}\hfill \\ & =& \frac{\bar{k}}{\bar{k}-k}\left(S_x^{\bar{k}}-S_x^k\right),\hfill \end{array}$$(17) where $S_x^{\bar{k}}(\equiv (\partial \bar{k}/\partial x)/(x/\bar{k}))$ is the sensitivity of $\bar{k}$ to the parameter x. The statistical uncertainty in S^βeff_x is expressed as (18) $$\begin{array}{ccc}& & \delta S_x^{{\beta }_{\mathrm{eff}}}\simeq \left|S_x^{{\beta }_{\mathrm{eff}}}\right|\hfill \\ & & ·\sqrt{{\left(\frac{\delta \bar{k}}{\bar{k}}\right)}^2+\frac{{\left(\delta \bar{k}\right)}^2+{\left(\delta k\right)}^2}{{(\bar{k}-k)}^2}+\frac{{\left(\delta S_x^{\bar{k}}\right)}^2+{\left(\delta S_x^k\right)}^2}{{\left(S_x^{\bar{k}}-S_x^k\right)}^2}}\hfill \end{array}$$(18) By comparing Equation (9(9) $$\begin{array}{c}\hfill S_x^{{\beta }_{\mathrm{eff}}}\equiv \frac{\partial {\beta }_{\mathrm{eff}}}{\partial x}\frac{x}{{\beta }_{\mathrm{eff}}}\simeq \frac{k_p}{k-k_p}\left(S_x^k-S_x^{k_p}\right),\end{array}$$(9) ) with Equation (17(17) $$\begin{array}{ccc}\hfill S_x^{{\beta }_{\mathrm{eff}}}& \equiv & \frac{\partial {\beta }_{\mathrm{eff}}}{\partial x}\frac{x}{{\beta }_{\mathrm{eff}}}\simeq \frac{\bar{k}}{k}\frac{1}{{\beta }_{\mathrm{eff}}}\left(S_x^{\bar{k}}-S_x^k\right)·\frac{1}{a}\hfill \\ & =& \frac{\bar{k}}{\bar{k}-k}\left(S_x^{\bar{k}}-S_x^k\right),\hfill \end{array}$$(17) ), and Equation (10(10) $$\begin{array}{ccc}& & \delta S_x^{{\beta }_{\mathrm{eff}}}\simeq \left|S_x^{{\beta }_{\mathrm{eff}}}\right|\hfill \\ & & ·\sqrt{{\left(\frac{\delta k_p}{k_p}\right)}^2+\frac{{\left(\delta k\right)}^2+{\left(\delta k_p\right)}^2}{{\left(k-k_p\right)}^2}+\frac{{\left(\delta S_x^k\right)}^2+{\left(\delta S_x^{k_p}\right)}^2}{{\left(S_x^k-S_x^{k_p}\right)}^2}},\hfill \end{array}$$(10) ) with Equation (18(18) $$\begin{array}{ccc}& & \delta S_x^{{\beta }_{\mathrm{eff}}}\simeq \left|S_x^{{\beta }_{\mathrm{eff}}}\right|\hfill \\ & & ·\sqrt{{\left(\frac{\delta \bar{k}}{\bar{k}}\right)}^2+\frac{{\left(\delta \bar{k}\right)}^2+{\left(\delta k\right)}^2}{{(\bar{k}-k)}^2}+\frac{{\left(\delta S_x^{\bar{k}}\right)}^2+{\left(\delta S_x^k\right)}^2}{{\left(S_x^{\bar{k}}-S_x^k\right)}^2}}\hfill \end{array}$$(18) ), we conclude that the expressions for the sensitivity and its statistical uncertainty calculated using the modified method are similar to those calculated using the conventional method.

2.1.3. Calculation procedure

The β_eff value and its sensitivities were obtained from k, $\bar{k}$, and k_p and their sensitivities computed by the KSEN card. The calculation procedure of $\bar{k}$ is as follows. The values of ${\bar{\nu }}^d$ of the VENUS-F fissionable materials (i.e. ²³⁵U and ²³⁸U) stored, according to ENDF-6 format rules [13], in a section MT=455 of a file MT=1, were multiplied with (a + 1). The values of $\bar{\nu }$ (MF = 1, MT = 452) as the sum of ${\bar{\nu }}^p$ (MF = 1, MT = 456) and ${\bar{\nu }}^d$ was adjusted accordingly. The alternated nuclear data files for ²³⁵U and ²³⁸U were processed into the ACE format (a pointwise-nuclear-data format for MCNP) using the nuclear data processing code NJOY [14]. Using these ACE-formatted files, the $\bar{k}$ value and its sensitivities were calculated using MCNP.

2.2. The β_eff uncertainties

Using the sensitivity profile obtained by the two different methods, the β_eff uncertainty (standard deviation) due to nuclear data was evaluated for each method by the uncertainty propagation law, which is expressed as (19) $$\begin{array}{c}\hfill U^{{\beta }_{\mathrm{eff}}}=\sqrt{{\sum }_x{\sum }_{x^{\text{'}}}{\sum }_g{\sum }_{g^{\text{'}}}{S}_{x,g}^{{\beta }_{\mathrm{eff}}}\mathrm{cov}(x,g;x^{\text{'}},g^{\text{'}})S_{x^{\text{'}},g^{\text{'}}}^{{\beta }_{\mathrm{eff}}}},\end{array}$$(19) where cov(x, g; x′, g′) denotes a (g, g′; x, x′) component of variance–covariance matrix (g, g′: energy group, x, x′: reaction), which was obtained by processing covariance data stored in JENDL-4.0u with NJOY and ERRORJ [15]. In this analysis, we employed eight parameters: fission, neutron capture, elastic scattering, inelastic scattering, and (n, 2n) reaction cross sections, prompt and delayed neutron yields, and prompt neutron spectra for seven major constituent materials: ²³⁵U, ²³⁸U, ⁵⁶Fe, ²⁰⁴Pb, ²⁰⁶Pb, ²⁰⁷Pb, and ²⁰⁸Pb. Correlations between the reactions were also taken into account. Even though Kodeli [16] proposed that the contribution of χ ^d to the β_eff uncertainty should not be disregarded, we did not include this parameter due to the absence of its covariance data in JENDL-4.0u. The statistical uncertainty in $U^{{\beta }_{\mathrm{eff}}}$ for parameter x is expressed as (20) $$\begin{array}{c}\hfill \delta U_x^{{\beta }_{\mathrm{eff}}}\simeq \frac{1}{2}\sqrt{{\sum }_{x^{\text{'}}}{\sum }_g{\sum }_{g^{\text{'}}}{\left\{S_{x,g}^{{\beta }_{\mathrm{eff}}}\mathrm{cov}(x,g;x^{\text{'}},g^{\text{'}})S_{x^{\text{'}},g^{\text{'}}}^{{\beta }_{\mathrm{eff}}}\sqrt{{\left(\frac{\delta S_{x,g}^{{\beta }_{\mathrm{eff}}}}{S_{x,g}^{{\beta }_{\mathrm{eff}}}}\right)}^2+{\left(\frac{\delta S_{x^{\text{'}},g^{\text{'}}}^{{\beta }_{\mathrm{eff}}}}{S_{x^{\text{'}},g^{\text{'}}}^{{\beta }_{\mathrm{eff}}}}\right)}^2}\right\}}^2}.\end{array}$$(20)

2.3. VENUS-F MCNP model

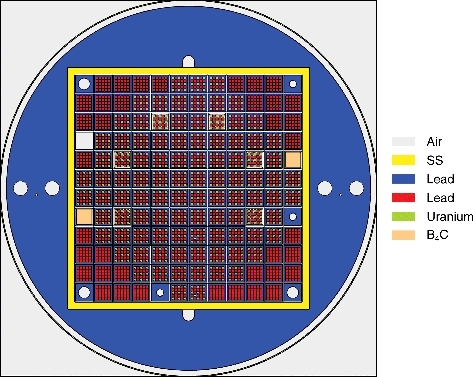
The MCNP model of the zero-power VENUS-F critical core used in the β_eff measurement [17] is illustrated in Figure 1. The core consists of a cylindrical vessel filled with pure solid lead reflector and a 12 × 12 square grid where fuel and lead assemblies as well as safety and control rods are loaded longitudinally. The fuel assembly has a 5 × 5 lattice structure piled up with lead blocks and fuel rodlets made of 30 wt.% metallic uranium. The detailed design of the VENUS-F core is provided by Fridman et al. [18].

Figure 1. Horizontal sectional view of the VENUS-F MCNP model.

2.4. Results and discussions

2.4.1. Effective delayed neutron fraction

Table 1 shows the calculated k and k_p, and $\bar{k}$ with different scaling factors (a = 1, 2, 5, 10, 15, and 20), which include 1σ statistical uncertainties. For each case, the k_eff value was calculated with 1.0 × 10⁸ histories (1.0 × 10⁵ source histories per cycle times 10³ cycles), that resulted in the statistical uncertainty of ∼7 pcm. Figure 2 shows a comparison of the calculated β_eff and C/E values for these different scaling factors. The experimental β_eff value was estimated to be 730 ± 11 pcm using neutron noise techniques [17,18]. The value calculated directly using the adjoint weighting function [19] (from now on referred to as the direct method) for the same number of histories was 731 ± 10 pcm. On first inspection, the direct method appears to agree well with the experimental data; however, the statistical uncertainty is rather too large. In contrast, as expected from Equation (16(16) $$\begin{array}{c}\hfill \delta {\beta }_{\mathrm{eff}}\simeq \frac{\bar{k}}{k}\sqrt{{\left(\frac{\delta \bar{k}}{\bar{k}}\right)}^2+{\left(\frac{\delta k}{k}\right)}^2}·\frac{1}{\left|a\right|}.\end{array}$$(16) ), the statistical uncertainty calculated by the modified method decreases with increase in a; which is about |a| times smaller than that derived using the conventional method. It was also observed that, with increase in a, the calculated β_eff values decreased and the agreement worsened. A similar trend can be seen in the benchmark results for fast neutron systems conducted by Chiba [7] using a deterministic transport code CBG [20]; this is linked to a limitation in the approximation of Equation (11(11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) ).

Figure 2. Comparison of calculated β_eff (lower) and C/E (upper) values with different scaling factors. In the lower panel, the band with pale color and the error bars indicate 1σ experimental uncertainty and 1σ statistical uncertainty, respectively; in the upper panel, the error bars indicate 1σ uncertainty considering both experimental and calculational uncertainties.

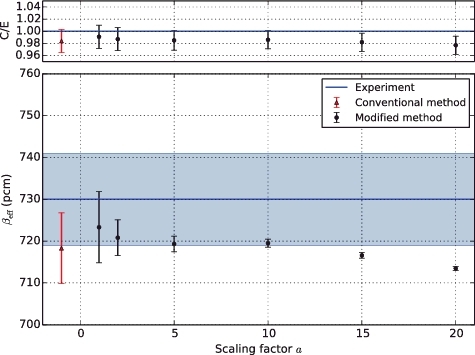
Table 1. Calculated k, $\bar{k}$, and k_p with 1σ statistical uncertainties

	a	keff
k	—	1.00234 ± 0.00007
kp	—	0.99514 ± 0.00006
$\bar{k}$	1	1.00959 ± 0.00006
	2	1.01679 ± 0.00006
	5	1.03839 ± 0.00007
	10	1.07446 ± 0.00007
	15	1.11008 ± 0.00007
	20	1.11454 ± 0.00007

2.4.2. Sensitivity profile

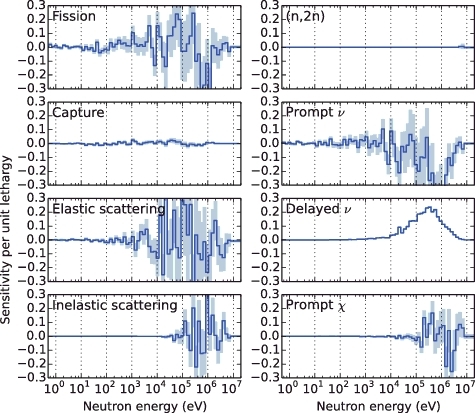
Figures 3 and 4 show profiles of the β_eff sensitivities with respect to ²³⁸U and ²³⁵U reaction parameters, respectively, with the 70-energy-group structure calculated using the conventional method. As supposed in Chiba et al. [2], the statistical uncertainty is very large for all reaction parameters except for ${\bar{\nu }}^d$; this is a result of the small difference between S^kp_x and S^k_x. On the contrary, the statistical uncertainty for ${\bar{\nu }}^d$ is negligible because $S_{{\bar{\nu }}^d}^{k_p}$ and $\delta S_{{\bar{\nu }}^d}^{k_p}$ are each zero in Equations (9(9) $$\begin{array}{c}\hfill S_x^{{\beta }_{\mathrm{eff}}}\equiv \frac{\partial {\beta }_{\mathrm{eff}}}{\partial x}\frac{x}{{\beta }_{\mathrm{eff}}}\simeq \frac{k_p}{k-k_p}\left(S_x^k-S_x^{k_p}\right),\end{array}$$(9) ) and (10(10) $$\begin{array}{ccc}& & \delta S_x^{{\beta }_{\mathrm{eff}}}\simeq \left|S_x^{{\beta }_{\mathrm{eff}}}\right|\hfill \\ & & ·\sqrt{{\left(\frac{\delta k_p}{k_p}\right)}^2+\frac{{\left(\delta k\right)}^2+{\left(\delta k_p\right)}^2}{{\left(k-k_p\right)}^2}+\frac{{\left(\delta S_x^k\right)}^2+{\left(\delta S_x^{k_p}\right)}^2}{{\left(S_x^k-S_x^{k_p}\right)}^2}},\hfill \end{array}$$(10) ), respectively.

Figure 3. Sensitivity profile of ²³⁸U for β_eff calculated by the conventional method. The pale color around the line indicates 1σ statistical uncertainty.

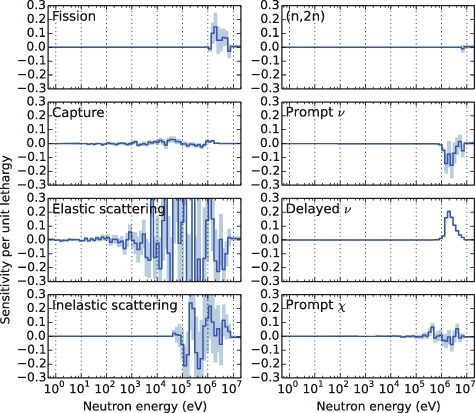
Figure 4. Sensitivity profile of ²³⁵U for β_eff calculated by the conventional method. The pale color around the line indicates 1σ statistical uncertainty.

As examples of the sensitivity profiles calculated by the modified method, a comparison of the β_eff sensitivity profiles of ²³⁵U elastic scattering and ${\bar{\nu }}^p$ with different scaling factors is shown in Figure 5. It is observed that the β_eff sensitivities converge and that their statistical uncertainties decrease with increase in a. By comparing with the trend of the β_eff values to a in Figure 2, it follows that the β_eff sensitivities change within their own 1σ statistical uncertainties, while the nominal values of β_eff tend to exceed their 1σ statistical uncertainties. This indicates that the influence of the change in the β_eff sensitivities that results from increasing a on the UQ of β_eff is expected to be small, while the approximation of Equation (11(11) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\simeq \left(\frac{\bar{k}}{k}-1\right)·\frac{1}{a},\end{array}$$(11) ) worsens. Although these statistical uncertainties can be reduced using the conventional method by simply increasing the number of source histories, an unacceptably large number of source histories or an excessive amount of computing time would be needed to achieve acceptably small statistical uncertainties. For example, Figure 6 illustrates the sensitivity profile of ²³⁵U for β_eff; this is the same as Figure 4 but calculated by increasing the number of source histories by a factor of 3 (3 × 10⁸ histories). In this case, the total elapsed time resulted in 41 days. Therefore, although the number of source histories was increased to an almost acceptable limit, taking into consideration the computing time and storage capacity, the statistical uncertainty remained large.

Figure 5. Comparisons of sensitivity profile of ²³⁵U elastic scattering (left) and ${\bar{\nu }}^p$ (right) for β_eff with different scaling factors. The pale color around the line indicates 1σ statistical uncertainty.

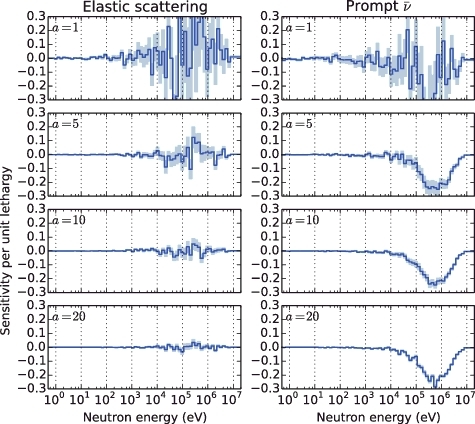
Figure 6. Sensitivity profile of ²³⁵U for β_eff calculated by the conventional method with 3 × 10⁸ histories. The pale color around the line indicates 1σ statistical uncertainty.

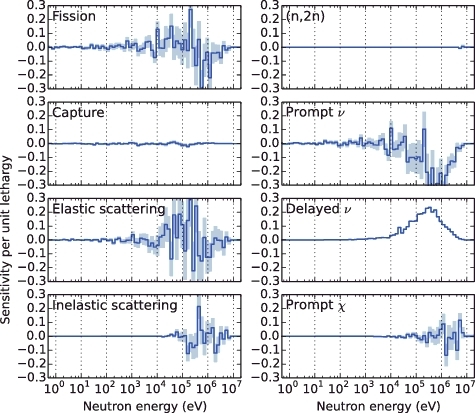
Figure 7. Comparison of calculated nuclide-wise contributions to β_eff uncertainty with different scaling factors. The error bars indicate 1σ statistical uncertainty.

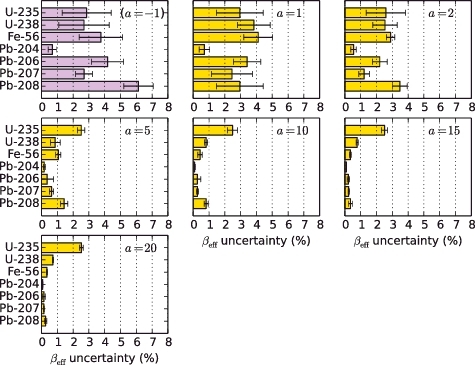
Figure 8. Comparison of calculated reaction-wise contributions to uncertainty in β_eff between the conventional method (upper) and the modified method (lower). The error bars indicate 1σ statistical uncertainty.

Figure 9. Schematic block diagram of UQ using the random sampling method.

Figure 10. Random files of ${\bar{\nu }}^d$ of ²³⁵U produced with SANDY from JENDL-4.0u (bottom), difference in the cross sections with JENDL-4.0u (middle), and standard deviations of the random files and JENDL-4.0u (top).

Figure 11. Statistical uncertainty in ${\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{ef}\mathrm{f}}}$ as a function of N_total and $\overline{\delta {\beta }_{\mathrm{ef}\mathrm{f}}}$.

Figure 12. Convergence of β_eff (upper) and its uncertainty (lower) with respect to ${\bar{\nu }}^d$ of ²³⁵U.

2.4.3. Uncertainty due to nuclear data

The β_eff uncertainties, caused by nuclear data, between the conventional method and the modified method using different scaling factors are summarized in Table 2; their nuclide-wise contributions are shown in Figure 7. It can be seen that the conventional method and the modified method with small scaling factors tend to estimate both uncertainty values and their statistical uncertainties to be larger than that calculated by the modified method with large scaling factors. This arises due to the large sensitivities with large statistical uncertainties in the sensitivity profile as previously described; these statistical uncertainties can be reduced by increasing a and appear to be sufficiently small at a = 20. In addition, Table 2 shows that, as a increases, the calculated total β_eff uncertainty approaches a value of 2.7%.

Table 2. Comparison of calculated β_eff uncertainty, caused by nuclear data, between the conventional method and the modified method with different scaling factors

	a	Relative value (%)
Conventional method	−1	9.2 ± 3.0
Modified method	1	8.7 ± 2.9
	2	6.2 ± 1.7
	5	3.2 ± 0.6
	10	2.8 ± 0.5
	15	2.7 ± 0.3
	20	2.7 ± 0.2

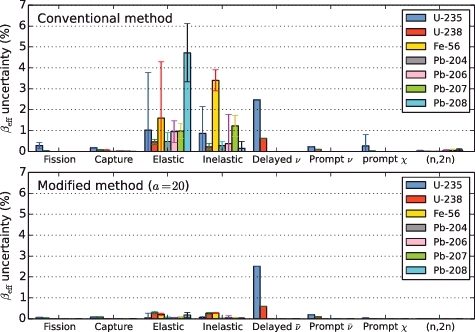
Figure 8 shows a reaction-wise breakdown of the β_eff uncertainties due to nuclear data calculated by the conventional and modified methods (at a = 20). For the same reason as explained previously, the contributions of the scattering cross sections and their statistical uncertainties were reduced by increasing the scaling factor. This indicates that the contribution of the scattering cross sections to the total uncertainty should not be too significant. Although there are no ways to experimentally validate uncertainty in β_eff, we concluded that, for the VENUS-F critical configuration, the total β_eff uncertainty due to nuclear data yielded ∼2.7% in relative value (∼22 pcm in absolute value) which is dominated by ${\bar{\nu }}^d$ of ²³⁵U (∼18 pcm) followed by that of ²³⁸U (∼4 pcm).

3. Random-sampling method

3.1. Calculation procedure

3.1.1. Calculation flow

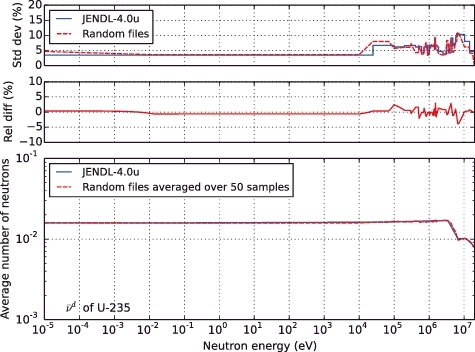
As mentioned earlier, the uncertainty due to nuclear data was estimated using SANDY. Details of its theoretical methodology and verification can be found in the studies of Fiorito et al. [5]. Since considerable computing time is involved, in this study, we have focused only on the ${\bar{\nu }}^d$ of ²³⁵U, which was the major contributor to the β_eff uncertainty predicted by the Monte Carlo sensitivity method. Figure 9 illustrates a schematic block diagram of UQ with the random-sampling method. First, N pointwise random files, in which reaction parameters were normally distributed in accordance with the evaluated covariance data, were produced by SANDY from JENDL-4.0u. As an example of the files produced, a comparison of ${\bar{\nu }}^d$ of ²³⁵U between the random files and JENDL-4.0u is presented in Figure 10. Note that the $\bar{\nu }$ of ²³⁵U is also modified according to the summation rule, MT452 = MT455 + MT456. The files were subsequently processed into the ACE format with NJOY, and N MCNP runs were carried out using these ACE-formatted files. The β_eff and its statistical uncertainty δβ_eff were obtained using the direct method. Finally, reaction-wise uncertainties due to nuclear data were quantified by conducting statistical processing using the resultant β_eff values with their statistical uncertainties.

3.1.2. Statistical processing

The statistical processing procedure adopted is as follows. Assuming that MCNP computes δβ_eff properly and accurately, the uncertainty due to nuclear data σ^βeff_ND can be obtained from the following equation: (21) $$\begin{array}{c}\hfill {\left({\sigma }_{\mathrm{ND}}^{{\beta }_{\mathrm{eff}}}\right)}^2\simeq {\left({\sigma }_{\mathrm{observed}}^{{\beta }_{\mathrm{eff}}}\right)}^2-{\left(\overline{\delta {\beta }_{\mathrm{eff}}}\right)}^2,\end{array}$$(21) where σ^βeff_observed is the observed statistical uncertainty in β_eff obtained from N times MCNP runs with the random files; $\overline{\delta {\beta }_{\mathrm{eff}}}$ indicates δβ_eff averaged over N samples.

In this study, to determine the number of source histories per sample n_s and the total number of samples N_total beforehand, a simple Monte Carlo simulation was conducted, and the statistical uncertainty in the β_eff uncertainty due to nuclear data $\delta {\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ was deduced from the simulation result, whose methodology is as follows. First, β_eff was distributed normally with mean μ and variance σ²: (22) $$\begin{array}{c}\hfill {\beta }_{\mathrm{eff}}\sim \mathcal{N}(\mu ,{\sigma }^2).\end{array}$$(22)

For μ, we chose the value of 731 pcm, which was estimated by the direct method as described earlier. The variance σ² was defined as (23) $$\begin{array}{c}\hfill {\sigma }^2\equiv {\left({\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}\right)}^2+{\left(\overline{\delta {\beta }_{\mathrm{eff}}}\right)}^2,\end{array}$$(23) where ${\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ is the β_eff uncertainty due to nuclear data with respect to ${\bar{\nu }}^d$ of ²³⁵U, for which the value of 18 pcm estimated by the Monte Carlo sensitivity method was used. In this case, the $\overline{\delta {\beta }_{\mathrm{eff}}}$, the average statistical uncertainty in β_eff as defined previously, is a variable used to determine $\delta {\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ and N_total. Next, ${\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ and its statistical uncertainty $\delta {\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ were estimated conversely from the distributed β_eff values by statistical processing over a large number of trials. 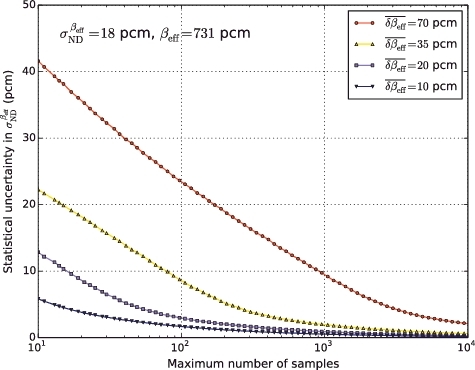Figure 11 shows $\delta {\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ as a function of $\overline{\delta {\beta }_{\mathrm{eff}}}$ and N_total simulated for 40,000 trials. As anticipated, with decrease in $\overline{\delta {\beta }_{\mathrm{eff}}}$ and/or increase in N_total, $\delta {\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ decreases. For example, if $\overline{\delta {\beta }_{\mathrm{eff}}}$ is as large as 70 pcm, an unacceptable number of samples (>10⁴) is required to obtain a reliable ${\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$. From this figure and by compromising on the computing resources and time spent, we chose N_total = 50 and n_s = 1.0 × 10⁸ (1.0 × 10⁵ source histories per cycle times 10³ cycles) in which each resultant δβ_eff value was almost 10 pcm. In this case, $\delta {\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ was expected to be 2 pcm.

3.2. Results and discussions

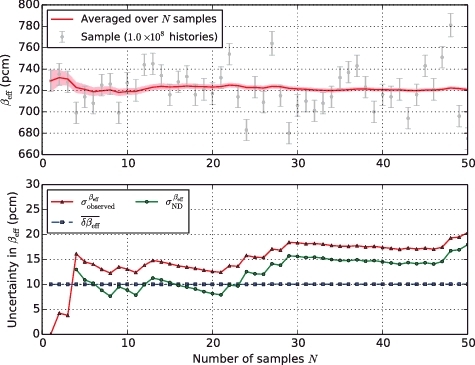
Figure 12 shows the convergence of β_eff and its uncertainty with respect to ${\bar{\nu }}^d$ of ²³⁵U, where the β_eff value averaged over N_total( = 50) and the ${\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}$ value at N_total were 721 and 18 pcm, respectively. From the Monte Carlo simulation as outlined earlier (with μ = 721 pcm, $\overline{\delta {\beta }_{\mathrm{eff}}}=10$ pcm, and ${\sigma }_{\mathrm{ND},{\bar{\nu }}^d}^{{\beta }_{\mathrm{eff}}}=18$ pcm as the input parameters), the statistical uncertainty was estimated to be 2 pcm.

Table 3 provides a comparison of the calculation results between the Monte Carlo sensitivity method and the random-sampling method. It can be seen that the difference between the two results is within the 1σ uncertainty. The total number of histories shown in Table 3 demonstrates that the random-sampling method is much slower than the Monte Carlo sensitivity method in estimating the uncertainty due to nuclear data. In addition, despite the large number of trials or source histories, the random-sampling method still involves larger statistical uncertainties than the Monte Carlo sensitivity method. Although the random-sampling method has the advantage of not needing to compute the sensitivities, these results indicate that this method currently has a limitation attributable to the use of UQ of β_eff.

Table 3. Comparison of β_eff uncertainty and its statistical uncertainty with respect to ${\bar{\nu }}^d$ of ²³⁵U and the total number of source histories used

	Monte Carlo sensitivity method	Random-sampling method
Uncertainty ${\sigma }_{\mathrm{ND},{\bar{\nu }}_d}^{{\beta }_{\mathrm{ef}\mathrm{f}}}$ (pcm)	18	18
Statistical uncertainty^a $\delta {\sigma }_{\mathrm{ND},{\bar{\nu }}_d}^{{\beta }_{\mathrm{ef}\mathrm{f}}}$ (pcm)	<1	2
Total number of histories	2 × (1 × 10^8)	50 × (1 × 10^8)

^a One standard deviation.

4. Conclusions

We investigated the applicability of the two types of Monte Carlo techniques, the Monte Carlo sensitivity method and the random-sampling method, in the UQ of β_eff from the prospective of statistical convergence issues. For the Monte Carlo sensitivity method, we demonstrated that Chiba's modified k-ratio method is superior to Bretscher's prompt k-ratio method in terms of reducing the statistical uncertainty in calculating not only β_eff but also its sensitivities and uncertainty due to nuclear data. Although the approximation of β_eff in the modified method becomes poorer as a increases, it was revealed that the β_eff sensitivities are more stable with respect to the a change than the nominal β_eff values. In addition, it was shown that the random-sampling method agrees with the Monte Carlo sensitivity method for the ${\bar{\nu }}^d$ of ²³⁵U; it was also shown that the Monte Carlo sensitivity method is more practical for the UQ of β_eff in terms of reducing the statistical uncertainty and reducing computing time. Finally, we demonstrated that the total β_eff uncertainty for the VENUS-F critical configuration is approximately 2.7%, and that it is dominated by the ${\bar{\nu }}^d$ of ²³⁵U. It is noted that the impact of the χ^d uncertainty was not estimated because of the lack of covariance data in JENDL-4.0. For more reliable UQ of β_eff, covariance data evaluation of χ^d is required.

Acknowledgments

The authors are grateful to Drs K. Nishihara and T. Sugawara of the Japan Atomic Energy Agency (JAEA) and Prof. G. Chiba of Hokkaido University for providing useful comments and suggestions. One of the authors (H. Iwamoto) would like to thank Dr S. Meigo of JAEA for encouraging his work at SCK•CEN.

Disclosure statement

No potential conflict of interest was reported by the authors.