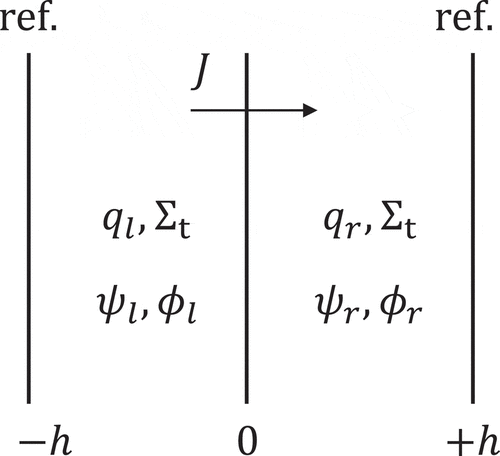Transport consistent diffusion coefficient for CMFD acceleration and comparison of convergence properties

ABSTRACT

A diffusion coefficient for the coarse mesh finite difference (CMFD) acceleration is derived from the semi-analytic solution of one-group, one-dimensional, even-parity transport equation. The derived diffusion coefficient, i.e., the transport consistent diffusion coefficient (TCD), depends on the optical length of a mesh and shows similar behavior with the artificial grid diffusion (AGD) and the effective diffusion (EffD) coefficients for an optically thick mesh. Convergence properties of typical diffusion coefficients are evaluated using the linearized Fourier analysis. Analyses of the C5G7 3D benchmark problems with and without voided region are carried out to compare the convergence properties. The number of transport sweeps to reach convergence using TCD is smaller than that using EffD or AGD.

KEYWORDS:

• CMFD acceleration
• MOC
• convergence
• even-parity transport equation
• linearized Fourier analysis
• C5G7 benchmark problem

View correction statement:

Correction

1. Introduction

The CMFD and the generalized coarse mesh rebalance (GCMR) acceleration methods are widely used for convergent acceleration of transport calculation based on the method of characteristics (MOC) [1–9]. The original idea of the CMFD method was developed by Smith for the acceleration of the advanced nodal method [1]. Later, it has been applied to various neutronics analysis codes due to its efficiency with improvements and generalizations [2–9]. The CMFD and GCMR methods utilize the finite difference approximation based on the diffusion theory. Thus, the acceleration scheme depends on the diffusion coefficient used in the finite-difference approximation. It is well known that the CMFD and the GCMR methods show instability for a thick and diffusive mesh. In more detail, these non-linear acceleration methods generally show instability when the optical thickness of a mesh exceeds 1.0 when conventional diffusion coefficient is used [4].

Various stabilization methods have been proposed and implemented, e.g., increasing the number of transport sweeps between CMFD accelerations, application of a damping factor, corrections on a diffusion coefficient [10]. Among them, the present study focuses on the correction of diffusion coefficient.

Larsen et al. proposed the effective diffusion (EffD) coefficient to preserve the net current obtained by the step characteristics transport solution using the spatially discretized transport solution with the weighted diamond-difference scheme [11]. Jarrett et al. introduced the artificial grid diffusion (AGD) coefficient to make the CMFD acceleration and the partial current based CMFD (pCMFD) acceleration [12] equivalent [10]. The EffD and the AGD coefficients make the CMFD and GCMR acceleration stable [13]. The EffD and AGD coefficients are larger than the conventional diffusion coefficients. Stabilization of CMFD/GCMR acceleration with artificially increased diffusion coefficient is also pointed out by one of the authors [4].

In this paper, the transport consistent diffusion (TCD) coefficient that preserves the semi-analytic solution of the one-group, one-dimensional, even-parity transport equation is derived. The two-node problem, which is commonly used in the CMFD acceleration method for the advance nodal method, is used for derivation. The even-parity transport equation is used for derivation due to its similarity with the diffusion equation.

In Section 2, derivation of the transport consistent diffusion coefficient and convergence analysis methodology of the CMFD acceleration using the linearized Fourier analysis are described. Numerical results are shown in Section 3. Finally, concluding remarks are described in Section 4.

2. Theory

2.1. Derivation of transport consistent diffusion coefficient

The derivation of TCD coefficient is explained in this section. Firstly, the even-parity transport equation is derived followed by the explanation on the analytic solutions of even-parity and odd-parity angular fluxes. Secondly, the spatially averaged even-parity angular flux inside a mesh is obtained using the analytic solution of even-parity angular flux. Then, the spatially averaged scalar flux inside a mesh is obtained by solid angle integration of the average even-parity angular flux. Thirdly, the neutron net current at mesh interface is derived by the solid angle integration of the odd-parity angular flux at the interface. Finally, the TCD coefficient is derived using Fick’s law.

The transport equation for one-group, one-dimensional, homogeneous geometry with an isotropic source is written as:

(1) $\mu \frac{d}{dx}\psi \left(x,\mu \right)+{\mathrm{\Sigma }}_{\mathrm{t}}\psi \left(x,\mu \right)=\frac{1}{2}q,$(1)

where

$\mu$: direction cosine,

$x$: position,

${\mathrm{\Sigma }}_{\mathrm{t}}$: macroscopic total cross section,

$\psi \left(x,\mu \right)$: angular flux for direction $\mu$ and position $x$,

$q$: fixed source.

The transport equation for the opposite direction is given by:

(2) $-\mu \frac{d\psi }{dx}+{\mathrm{\Sigma }}_{\mathrm{t}}\psi \left(x,-\mu \right)=\frac{1}{2}q.$(2)

By adding and subtracting Equations (1)(1) $\mu \frac{d}{dx}\psi \left(x,\mu \right)+{\mathrm{\Sigma }}_{\mathrm{t}}\psi \left(x,\mu \right)=\frac{1}{2}q,$(1) and (2(2) $-\mu \frac{d\psi }{dx}+{\mathrm{\Sigma }}_{\mathrm{t}}\psi \left(x,-\mu \right)=\frac{1}{2}q.$(2) ), the following equations are obtained:

(3) $\mu \frac{d{\psi }^{-}}{dx}+{\mathrm{\Sigma }}_{\mathrm{t}}{\psi }^{+}\left(x,\mu \right)=\frac{1}{2}q,$(3)

(4) $\mu \frac{d{\psi }^{+}}{dx}+{\mathrm{\Sigma }}_{\mathrm{t}}{\psi }^{-}\left(x,\mu \right)=0,$(4)

where ${\psi }^{+}\mathrm{a}\mathrm{n}\mathrm{d}{\psi }^{-}$ are the even- and odd-parity angular fluxes defined as:

(5) ${\psi }^{+}\left(x,\mu \right)\equiv \frac{\psi \left(x,\mu \right)+\psi \left(x,-\mu \right)}{2},$(5)

(6) ${\psi }^{-}\left(x,\mu \right)\equiv \frac{\psi \left(x,\mu \right)-\psi \left(x,-\mu \right)}{2}.$(6)

By eliminating ${\psi }^{-}$ using Equations (3)(3) $\mu \frac{d{\psi }^{-}}{dx}+{\mathrm{\Sigma }}_{\mathrm{t}}{\psi }^{+}\left(x,\mu \right)=\frac{1}{2}q,$(3) and (4(4) $\mu \frac{d{\psi }^{+}}{dx}+{\mathrm{\Sigma }}_{\mathrm{t}}{\psi }^{-}\left(x,\mu \right)=0,$(4) ), the even-parity transport equation is obtained:

(7) $-{\mu }^2\frac{d}{dx}\frac{1}{{\mathrm{\Sigma }}_{\mathrm{t}}}\frac{d{\psi }^{+}}{dx}+{\mathrm{\Sigma }}_{\mathrm{t}}{\psi }^{+}\left(x,\mu \right)=\frac{1}{2}q.$(7)

Now let us consider a two-node problem shown in Figure 1, which is usually used to derive the coupling coefficient of CMFD acceleration in the advanced nodal method [1]. Here, $q_l$ and $q_r$ are spatially uniform isotropic neutron sources, ${\psi }_l$ and ${\psi }_r$ are angular fluxes, ${\varphi }_l$ and ${\varphi }_r$ are scalar fluxes, respectively. Sizes for the left and the right meshes are h, and the origin is set at the mesh boundary between the left and right meshes. Spatially uniform total cross section ${\mathrm{\Sigma }}_{\mathrm{t}}$ is considered. Reflective boundary condition is applied both for the left and right boundaries.

Figure 1. Two-node problem.

Equation (7)(7) $-{\mu }^2\frac{d}{dx}\frac{1}{{\mathrm{\Sigma }}_{\mathrm{t}}}\frac{d{\psi }^{+}}{dx}+{\mathrm{\Sigma }}_{\mathrm{t}}{\psi }^{+}\left(x,\mu \right)=\frac{1}{2}q.$(7) can be analytically solved using the following boundary conditions:

${\psi }_l^{-}\left(-h,\mu \right)=0,$

${\psi }_r^{-}\left(+h,\mu \right)=0,$

${\psi }_l^{+}\left(0,\mu \right)={\psi }_r^{+}\left(0,\mu \right),$

(8) ${\psi }_l^{-}\left(0,\mu \right)={\psi }_r^{-}\left(0,\mu \right),$(8)

where $h$ is the mesh width as shown in Figure 1. The first two are the reflective boundary condition. The third and fourth ones correspond to the continuity condition at material interface.

The analytic solutions of even-parity angular fluxes are given by:

(9) ${\psi }_l^{+}\left(x,\mu \right)=\frac{2q_l-\left(q_l-q_r\right)\frac{cosh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}\left(h+x\right)}{\mu }\right)}{cosh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}}{4{\mathrm{\Sigma }}_{\mathrm{t}}},$(9)

(10) ${\psi }_r^{+}\left(x,\mu \right)=\frac{2q_r+\left(q_l-q_r\right)\frac{cosh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}\left(h-x\right)}{\mu }\right)}{cosh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}}{4{\mathrm{\Sigma }}_{\mathrm{t}}},$(10)

where $q_l$ and $q_r$ are fixed sources as shown in Figure 1.

Using Equations (9)(9) ${\psi }_l^{+}\left(x,\mu \right)=\frac{2q_l-\left(q_l-q_r\right)\frac{cosh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}\left(h+x\right)}{\mu }\right)}{cosh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}}{4{\mathrm{\Sigma }}_{\mathrm{t}}},$(9) and (10(10) ${\psi }_r^{+}\left(x,\mu \right)=\frac{2q_r+\left(q_l-q_r\right)\frac{cosh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}\left(h-x\right)}{\mu }\right)}{cosh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}}{4{\mathrm{\Sigma }}_{\mathrm{t}}},$(10) ), the odd parity angular flux at the mesh interface ${\psi }^{-}\left(0,\mu \right)$, the spatially averaged even parity angular fluxes ${\bar{\psi }}_l^{+}\left(\mu \right)$ and ${\bar{\psi }}_r^{+}\left(\mu \right)$ are given by:

(11) ${\psi }_l^{-}\left(0,\mu \right)={\psi }_r^{-}\left(0,\mu \right)=\frac{\left(q_l-q_r\right)tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4{\mathrm{\Sigma }}_{\mathrm{t}}},$(11)

(12) ${\bar{\psi }}_l^{+}\left(\mu \right)=\left({\int }_{-h}^0{\psi }_l^{+}\left(x,\mu \right)dx\right)/h=\frac{2h{\mathrm{\Sigma }}_{\mathrm{t}}{q}_l-\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4h{\mathrm{\Sigma }}_{\mathrm{t}}^2},$(12)

(13) ${\bar{\psi }}_r^{+}\left(\mu \right)=\left({\int }_0^{+h}{\bar{\psi }}_r^{+}\left(\mu \right)dx\right)/h=\frac{2h{\mathrm{\Sigma }}_{\mathrm{t}}{q}_r+\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4h{\mathrm{\Sigma }}_{\mathrm{t}}^2}.$(13)

Using Equations (11)(11) ${\psi }_l^{-}\left(0,\mu \right)={\psi }_r^{-}\left(0,\mu \right)=\frac{\left(q_l-q_r\right)tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4{\mathrm{\Sigma }}_{\mathrm{t}}},$(11) , (12(12) ${\bar{\psi }}_l^{+}\left(\mu \right)=\left({\int }_{-h}^0{\psi }_l^{+}\left(x,\mu \right)dx\right)/h=\frac{2h{\mathrm{\Sigma }}_{\mathrm{t}}{q}_l-\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4h{\mathrm{\Sigma }}_{\mathrm{t}}^2},$(12) ), and (13(13) ${\bar{\psi }}_r^{+}\left(\mu \right)=\left({\int }_0^{+h}{\bar{\psi }}_r^{+}\left(\mu \right)dx\right)/h=\frac{2h{\mathrm{\Sigma }}_{\mathrm{t}}{q}_r+\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4h{\mathrm{\Sigma }}_{\mathrm{t}}^2}.$(13) ), the net neutron current $J$ at the mesh interface, the average scalar fluxes for the left and the right meshes ${\bar{\varphi }}_l,{\bar{\varphi }}_r$ are given by:

(14) $J={\int }_{-1}^{+1}\frac{\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4{\mathrm{\Sigma }}_{\mathrm{t}}}d\mu ,$(14)

(15) ${\bar{\varphi }}_l={\int }_{-1}^{+1}\frac{2h{\mathrm{\Sigma }}_{\mathrm{t}}{q}_l-\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4h{\mathrm{\Sigma }}_{\mathrm{t}}^2}d\mu ,$(15)

(16) ${\bar{\varphi }}_r={\int }_{-1}^{+1}\frac{2h{\mathrm{\Sigma }}_{\mathrm{t}}{q}_r+\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4h{\mathrm{\Sigma }}_{\mathrm{t}}^2}d\mu .$(16)

Forcing the Fick’s law, the following relation is obtained:

(17) $J=-D^{TCD}\frac{\left({\bar{\varphi }}_r-{\bar{\varphi }}_l\right)}{h},$(17)

where $D^{TCD}$ is the transport consistent diffusion (TCD) coefficient.

By substituting Equations (14)(14) $J={\int }_{-1}^{+1}\frac{\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4{\mathrm{\Sigma }}_{\mathrm{t}}}d\mu ,$(14) , (15(15) ${\bar{\varphi }}_l={\int }_{-1}^{+1}\frac{2h{\mathrm{\Sigma }}_{\mathrm{t}}{q}_l-\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4h{\mathrm{\Sigma }}_{\mathrm{t}}^2}d\mu ,$(15) ), and (16(16) ${\bar{\varphi }}_r={\int }_{-1}^{+1}\frac{2h{\mathrm{\Sigma }}_{\mathrm{t}}{q}_r+\left(q_l-q_r\right)\mu tanh\left(\frac{{\mathrm{\Sigma }}_{\mathrm{t}}h}{\mu }\right)}{4h{\mathrm{\Sigma }}_{\mathrm{t}}^2}d\mu .$(16) ) into Equation (17)(17) $J=-D^{TCD}\frac{\left({\bar{\varphi }}_r-{\bar{\varphi }}_l\right)}{h},$(17) , $D^{TCD}$ can be expressed as:

(18) $D^{TCD}=-\frac{Jh}{{\bar{\varphi }}_r-{\bar{\varphi }}_l}=\frac{1}{{\mathrm{\Sigma }}_{\mathrm{t}}}\frac{{\tau }^2{\int }_{-1}^{+1}\mu tanh\left(\frac{\tau }{\mu }\right)d\mu }{4\tau -2{\int }_{-1}^{+1}\mu tanh\left(\frac{\tau }{\mu }\right)d\mu },$(18)

where $\tau ={\mathrm{\Sigma }}_{\mathrm{t}}h$ is the optical length of a mesh. It should be noted that $D^{TCD}$ depends on ${\mathrm{\Sigma }}_{\mathrm{t}}$ and $\tau$, and but it does not depend on $q_{\mathrm{l}}$ and $q_{\mathrm{r}}$.

2.2. Convergence analysis

Convergence analysis of the CMFD acceleration is carried out using the linearized Fourier analysis. The analysis procedure has been published in many previous works [14–16] but somewhat complicated. Therefore, the detailed description of the linearized Fourier analysis is provided as the supplemental material of this paper. In the following, the fundamental equations used for the linearized Fourier analysis are described in order to clarify the condition of convergence analysis.

The neutron transport equation in one-dimensional slab geometry assuming the step characteristics is written as:

(19) ${\mu }_n\frac{{\psi }_{n,k+\frac{1}{2}}^{l+\frac{1}{2}}-{\psi }_{n,k-\frac{1}{2}}^{l+\frac{1}{2}}}{h}+{\mathrm{\Sigma }}_{\mathrm{t}}\left(f_n{\psi }_{n,k+\frac{1}{2}}^{l+\frac{1}{2}}+\left(1-f_n\right){\psi }_{n,k-\frac{1}{2}}^{l+\frac{1}{2}}\right)={\mathrm{\Sigma }}_{\mathrm{s}}{\varphi }_k^l+q,$(19)

$f_n=-\frac{{\mu }_n}{h{\mathrm{\Sigma }}_{\mathrm{t}}}+\frac{1}{1-e^{-\frac{h{\mathrm{\Sigma }}_{\mathrm{t}}}{{\mu }_n}}},$

(20) $1-f_n=\frac{{\mu }_n}{h{\mathrm{\Sigma }}_{\mathrm{t}}}-\frac{e^{-\frac{h{\mathrm{\Sigma }}_{\mathrm{t}}}{{\mu }_n}}}{1-e^{-\frac{h{\mathrm{\Sigma }}_{\mathrm{t}}}{{\mu }_n}}},$(20)

(21) ${\varphi }_k^{l+\frac{1}{2}}=\frac{1}{2}\sum _n{w}_n\left(f_n{\psi }_{n,k+\frac{1}{2}}^{l+\frac{1}{2}}+\left(1-f_n\right){\psi }_{n,k-\frac{1}{2}}^{l+\frac{1}{2}}\right),$(21)

where

${\mu }_n$: direction cosine for direction n,

$\psi$: angular flux,

$\varphi$: scalar flux,

$h$: mesh width,

${\mathrm{\Sigma }}_{\mathrm{t}}$: macroscopic total cross section,

${\mathrm{\Sigma }}_{\mathrm{s}}$: macroscopic scattering cross section,

$q$: neutron source,

$f_n$: weighting factor to calculate average angular flux,

$w$: quadrature weight,$\sum _n{w}_n=2,$

$l$: index of iteration,

$k$: index of mesh, $k+\frac{1}{2}$ indicates mesh interface between $k+1$ and $k$,

$n$: index of direction.

In the CMFD acceleration, the following difference equation is used to represent the neutron net current.

$J_{i+\frac{1}{2}}^{l+1}=-D^{FD}\left({\varphi }_{i+1}^{l+1}-{\varphi }_i^{l+1}\right)+D_{i+\frac{1}{2}}^{cor,l+\frac{1}{2}}\left({\varphi }_{i+1}^{l+1}+{\varphi }_i^{l+1}\right),$

(22) $J_{i-\frac{1}{2}}^{l+1}=-D^{FD}\left({\varphi }_i^{l+1}-{\varphi }_{i-1}^{l+1}\right)+D_{i-\frac{1}{2}}^{cor,l+\frac{1}{2}}\left({\varphi }_i^{l+1}+{\varphi }_{i-1}^{l+1}\right),$(22)

where

(23) $D^{FD}=\frac{D}{ph},$(23)

$J_{i+\frac{1}{2}}^{l+\frac{1}{2}}=\frac{1}{2}\sum _n{w}_n{\mu }_n{\psi }_{n,i+\frac{1}{2}}^{l+\frac{1}{2}},$

(24) $J_{i-\frac{1}{2}}^{l+\frac{1}{2}}=\frac{1}{2}\sum _n^{\hspace{0.17em}}{w}_n{\mu }_n{\psi }_{n,i-\frac{1}{2}}^{l+\frac{1}{2}},$(24)

$D_{i+\frac{1}{2}}^{cor,l+\frac{1}{2}}=\frac{J_{i+\frac{1}{2}}^{l+\frac{1}{2}}+D^{FD}\left({\varphi }_{i+1}^{l+\frac{1}{2}}-{\varphi }_i^{l+\frac{1}{2}}\right)}{{\varphi }_{i+1}^{l+\frac{1}{2}}+{\varphi }_i^{l+\frac{1}{2}}},$

(25) $D_{i-\frac{1}{2}}^{cor,l+\frac{1}{2}}=\frac{J_{i-\frac{1}{2}}^{l+\frac{1}{2}}+D^{FD}\left({\varphi }_i^{l+\frac{1}{2}}-{\varphi }_{i-1}^{l+\frac{1}{2}}\right)}{{\varphi }_i^{l+\frac{1}{2}}+{\varphi }_{i-1}^{l+\frac{1}{2}}},$(25)

$J_{i+\frac{1}{2}}^{l+\frac{1}{2}}=\frac{1}{2}\sum _n{w}_n{\mu }_n{\psi }_{n,i+\frac{1}{2}}^{l+\frac{1}{2}},$

(26) $J_{i-\frac{1}{2}}^{l+\frac{1}{2}}=\frac{1}{2}\sum _n{w}_n{\mu }_n{\psi }_{n,i-\frac{1}{2}}^{l+\frac{1}{2}},$(26)

and

$D$: diffusion coefficient, $i$: index of coarse mesh, $i+\frac{1}{2}$ indicates mesh interface between $i+1$ and $i$, $p$: number of fine meshes in a coarse mesh.

Using Equation (22)(22) $J_{i-\frac{1}{2}}^{l+1}=-D^{FD}\left({\varphi }_i^{l+1}-{\varphi }_{i-1}^{l+1}\right)+D_{i-\frac{1}{2}}^{cor,l+\frac{1}{2}}\left({\varphi }_i^{l+1}+{\varphi }_{i-1}^{l+1}\right),$(22) , the CMFD equation is written as:

(27) $-D_{i+\frac{1}{2}}\left({\varphi }_{i+1}^{l+1}-{\varphi }_i^{l+1}\right)+D_{i+\frac{1}{2}}^{cor,l+\frac{1}{2}}\left({\varphi }_{i+1}^{l+1}+{\varphi }_i^{l+1}\right)+D_{i-\frac{1}{2}}\left({\varphi }_i^{l+1}-{\varphi }_{i-1}^{l+1}\right)-D_{i-\frac{1}{2}}^{cor,l+\frac{1}{2}}\left({\varphi }_i^{l+1}+{\varphi }_{i-1}^{l+1}\right)+ph{\mathrm{\Sigma }}_{\mathrm{a}}{\varphi }_i^{l+1}=phq,$(27)

where ${\mathrm{\Sigma }}_{\mathrm{a}}={\mathrm{\Sigma }}_{\mathrm{t}}-{\mathrm{\Sigma }}_{\mathrm{s}}$.

Once the CMFD solution is obtained, the scalar flux is normalized as:

(28) ${\varphi }_k^{l+1}={\varphi }_k^{l+\frac{1}{2}}\frac{{\varphi }_i^{l+1}}{{\varphi }_i^{l+\frac{1}{2}}}.$(28)

Equations (19)(19) ${\mu }_n\frac{{\psi }_{n,k+\frac{1}{2}}^{l+\frac{1}{2}}-{\psi }_{n,k-\frac{1}{2}}^{l+\frac{1}{2}}}{h}+{\mathrm{\Sigma }}_{\mathrm{t}}\left(f_n{\psi }_{n,k+\frac{1}{2}}^{l+\frac{1}{2}}+\left(1-f_n\right){\psi }_{n,k-\frac{1}{2}}^{l+\frac{1}{2}}\right)={\mathrm{\Sigma }}_{\mathrm{s}}{\varphi }_k^l+q,$(19) , (25(25) $D_{i-\frac{1}{2}}^{cor,l+\frac{1}{2}}=\frac{J_{i-\frac{1}{2}}^{l+\frac{1}{2}}+D^{FD}\left({\varphi }_i^{l+\frac{1}{2}}-{\varphi }_{i-1}^{l+\frac{1}{2}}\right)}{{\varphi }_i^{l+\frac{1}{2}}+{\varphi }_{i-1}^{l+\frac{1}{2}}},$(25) )–(28(28) ${\varphi }_k^{l+1}={\varphi }_k^{l+\frac{1}{2}}\frac{{\varphi }_i^{l+1}}{{\varphi }_i^{l+\frac{1}{2}}}.$(28) ) consist a set for CMFD acceleration. These equations are used for the convergence analysis using the linearized Fourier analysis.

3. Numerical results and discussions

3.1. Comparison of diffusion coefficients

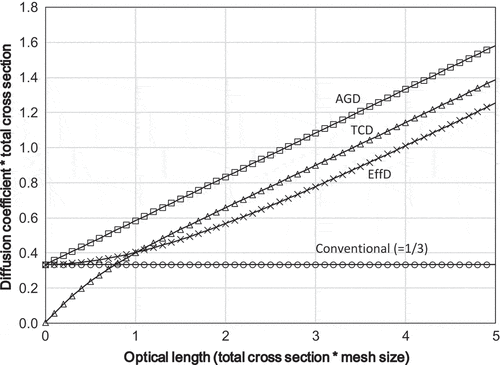
The transport consistent diffusion (TCD) coefficient derived in Section 2.1 is compared with the conventional diffusion coefficient (ConvD), the effective diffusion coefficient (EffD), and the artificial grid diffusion coefficient (AGD). The definitions of ConvD, EffD, and AGD are as follows:

(29) $D^{ConvD}=\frac{1}{3{\mathrm{\Sigma }}_{\mathrm{t}}},$(29)

(30) $D^{EffD}=\frac{1}{3{\mathrm{\Sigma }}_{\mathrm{t}}}+\frac{\tau }{4{\mathrm{\Sigma }}_{\mathrm{t}}}{\int }_{-1}^{+1}\left(\frac{1+exp\left(-\frac{\tau }{\mu }\right)}{1-exp\left(-\frac{\tau }{\mu }\right)}-\frac{2\mu }{\tau }\right)\mu d\mu ,$(30)

(31) $D^{AGD}=\frac{1}{3{\mathrm{\Sigma }}_{\mathrm{t}}}+\frac{\tau }{4{\mathrm{\Sigma }}_{\mathrm{t}}}.$(31)

Comparison of the diffusion coefficients is shown in Figure 2. Note that dimensionless parameter, $D{\mathrm{\Sigma }}_{\mathrm{t}}$, is shown. Behavior of $D^{TCD}$ is similar to those of $D^{EffD}$ and $D^{AGD}$ while that of $D^{ConvD}$ is different.

Figure 2. Comparison of diffusion coefficients ($\tau ={\mathrm{\Sigma }}_{\mathrm{t}}h$ versus $D{\mathrm{\Sigma }}_{\mathrm{t}})$.

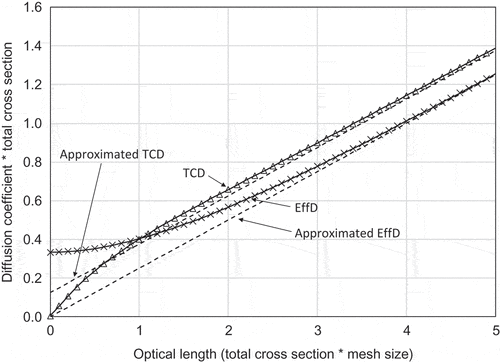
When the optical thickness of a mesh $\tau$ is large, $D^{TCD}$ and $D^{EffD}$ can be approximated by:

(32) $D^{TCD}\approx \frac{1}{{\mathrm{\Sigma }}_{\mathrm{t}}}\frac{{\tau }^2}{4\tau -2}\approx \frac{1}{4{\mathrm{\Sigma }}_{\mathrm{t}}}\left(\tau +\frac{1}{2}\right),$(32)

(33) $D^{EffD}\approx \frac{1}{3{\mathrm{\Sigma }}_{\mathrm{t}}}+\frac{1}{4{\mathrm{\Sigma }}_{\mathrm{t}}}\left(\tau -\frac{4}{3}\right).$(33)

The approximated $D^{TCD}$ and $D^{EffD}$ are shown in Figure 3.

Figure 3. Approximated $D^{TCD}$ and $D^{EffD}$ ($\tau ={\mathrm{\Sigma }}_{\mathrm{t}}h$ versus $D{\mathrm{\Sigma }}_{\mathrm{t}})$.

By comparing Equations (31)(31) $D^{AGD}=\frac{1}{3{\mathrm{\Sigma }}_{\mathrm{t}}}+\frac{\tau }{4{\mathrm{\Sigma }}_{\mathrm{t}}}.$(31) , (32(32) $D^{TCD}\approx \frac{1}{{\mathrm{\Sigma }}_{\mathrm{t}}}\frac{{\tau }^2}{4\tau -2}\approx \frac{1}{4{\mathrm{\Sigma }}_{\mathrm{t}}}\left(\tau +\frac{1}{2}\right),$(32) ), and (33(33) $D^{EffD}\approx \frac{1}{3{\mathrm{\Sigma }}_{\mathrm{t}}}+\frac{1}{4{\mathrm{\Sigma }}_{\mathrm{t}}}\left(\tau -\frac{4}{3}\right).$(33) ), the dependence of these diffusion coefficients on the optical mesh size $\tau$ is characterized by $\frac{\tau }{4{\mathrm{\Sigma }}_{\mathrm{t}}}$. Ref. [13] revealed that the stabilization effect of $D^{EffD}$ and $D^{AGD}$ is similar. This suggests that utilization of $D^{TCD}$ will also contribute to improve stability of the CMFD/GCMR acceleration methods.

Figure 4 indicates the relation between optical length and $D/h$. It is interesting that $D^{TCD}/h$ converges to a finite value (~0.586) when $\tau$ approaches 0. It means that $D^{TCD}$ gives a finite diffusion coefficient for a void region with a finite mesh size, which would have a positive impact on convergence of the CMFD/GCMR acceleration.

Figure 4. Comparison of diffusion coefficients ($\tau ={\mathrm{\Sigma }}_{\mathrm{t}}h$ versus $D/h)$.

3.2. Convergence estimation using the linearized fourier analysis

Three major parameters affecting the convergence of the CMFD acceleration are considered in the linearized Fourier analysis as follows:

• Scattering ratio (${\mathrm{\Sigma }}_{\mathrm{s}}/{\mathrm{\Sigma }}_t$): 0.99

• Number of fine meshes in a coarse mesh: 1, 4

• Optical thickness of a coarse mesh: 10⁻²–10²

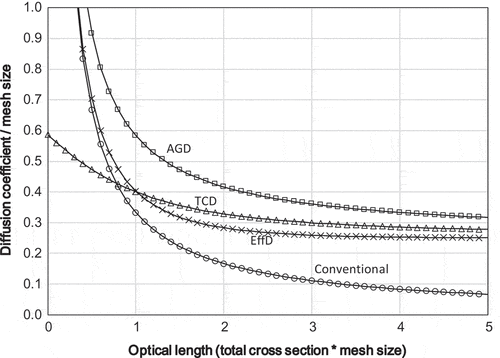
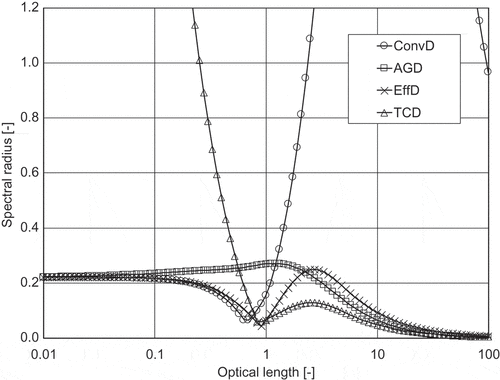
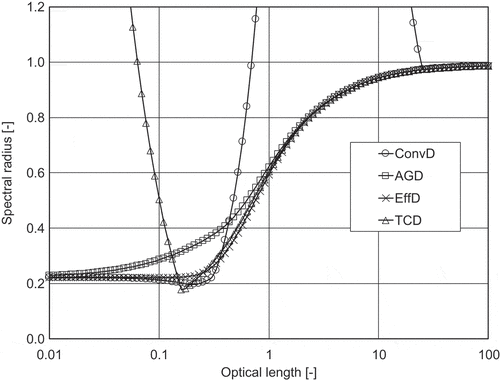
The results of linearized Fourier analysis for four different diffusion coefficients are shown in Figures 5 and 6. The results indicate that $D^{EffD}$, $D^{AGD}$, and $D^{TCD}$ show similar convergent behavior for optically thick meshes, which increases convergence stability. Contrary, the spectral radius of $D^{TCD}$ becomes large for an optically thin mesh. The numerical result shows that $D^{TCD}/h$ approaches approximately 0.6 for an optically thin mesh. The previous study [4] revealed that the CMFD acceleration method is consistent with the coarse mesh rebalance (CMR) when $D/h=1/2$. Therefore, the performance of $D^{TCD}$ would be similar to that of CMR for optically thin meshes. Performance of these diffusion coefficient in actual heterogeneous geometry will be confirmed in Section 3.2.

Figure 5. Comparison of spectral radius (c= 0.99, p= 1).

Figure 6. Comparison of spectral radius (c= 0.99, p= 4).

3.3. Convergence estimation in C5G7 3D benchmark problem

The TCD is derived assuming a very simplified condition (one-group, one-dimensional slab geometry with a uniform fixed source in each region), and the linearized Fourier analysis also assumes a simplified condition. Therefore, its performance evaluation in more realistic conditions is desirable. In this section, the impact of diffusion coefficient on the convergence of the CMFD acceleration is verified through the C5G7 3D benchmark problem [17]. In the original C5G7 benchmark problem, the non-voided condition is specified, but the voided condition is also considered in this study. The GENESIS code, which is a three-dimensional transport code based on the Legendre polynomial Expansion of Angular Flux (LEAF) method, is used [18]. The calculation conditions are as summarized as follows:

• Number of azimuthal angles:    8 for 2π

• Number of polar angles (Gauss-Legendre): 4 for π

• Ray trace width:        0.2 cm

• Axial mesh size:         3.0 cm

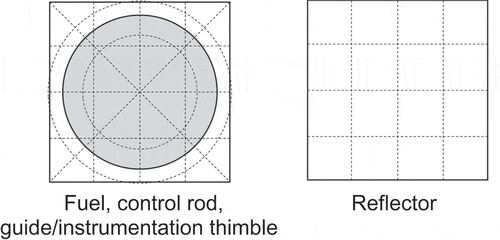
• Radial mesh division      Figure 7

  Figure 7. Mesh division used in the C5G7 3D benchmark problem.

  

• Number of inner iterations:    1 or 2

• Convergence criterion for k-effective:$5\times {10}^{-6}$

• Convergence criterion scalar flux: $1\times {10}^{-5}$

• Mesh size for CMFD:   1 cell and 3.0 cm for radial and axial directions, respectively

The above discretization parameters are too coarse to obtain the converged results [18], but they are appropriate in the present study since the evaluation of convergence behavior of the CMFD acceleration is the major purpose in this paper, and the convergence behavior of the CMFD acceleration is not very sensitive to the discretization parameters. It should be also noted the damping factor [10,13] is not used to stabilize the CMFD acceleration. The specification of the voided condition is taken from Ref. [18].

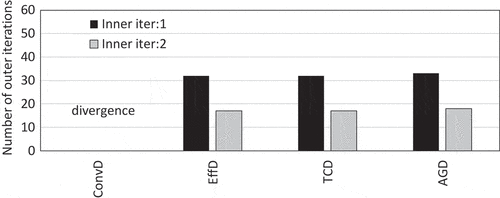
Calculation results are shown in Figures 8 and 9. Note that each CMFD calculation has been fully converged in each acceleration. Performances of $D^{EffD}$, $D^{AGD}$, and $D^{TCD}$ are similar in the non-voided case, while $D^{TCD}$ shows better performance in the voided case. This result seems to be somewhat inconsistent with that of the linearized Fourier analysis since convergence performance of $D^{TCD}$ is worse than $D^{EffD}$ and $D^{AGD}$ for an optically thin mesh. A possible reason for the better convergence of $D^{TCD}$ would be the value of diffusion coefficients. The value of $D^{EffD}$, $D^{AGD}$, and $D^{ConvD}$ could become large for voided region, which has a negative impact on the convergence of a diffusion calculation, while that of $D^{TCD}$ is finite. This might be a cause of the difference of convergence behavior observed in the voided case. However, further study on the convergence property of CMFD acceleration in realistic heterogeneous geometry will be desirable to clarify and to understand this issue. For example, linearized Fourier analysis considering different total cross sections and the periodic boundary condition would be an approach to address this question. Such a study, unfortunately, requires considerable new development works thus is considered as a future task.

Figure 8. Comparison of number of outer iterations of the C5G7 benchmark problem (non-voided case).

Figure 9. Comparison of number of outer iterations of the C5G7 benchmark problem (voided case).

4. Conclusion

The transport consistent diffusion (TCD) coefficient is derived using the even-parity transport equation and the two-node problem in one-dimensional geometry. TCD depends on the optical mesh size and shows similar behavior with the effective diffusion (EffD) and the artificial grid diffusion (AGD) coefficients for an optically thick mesh.

Convergence performances of TCD, AGD, EffD, and conventional diffusion coefficient (ConvD) are compared through the linearized Fourier analysis and numerical calculations in the C5G7 3D benchmark problem. The linearized Fourier analysis indicates that TCD, AGD, and EffD show similar theoretical convergence behavior for an optically thick mesh. In the C5G7 3D benchmark problem, TCD, AGD, and EffD show better performance than ConvD in the non-voided and voided conditions. In the voided condition, TCD is superior to AGD and EffD. This reason would be the limited value of TCD, which does not become very large for a voided region. However, further investigation on better performance of TCD in highly voided condition would be desirable, e.g., linearized Fourier analysis considering different total cross sections and the periodic boundary condition.

The above results suggest that the TCD will be a candidate for the CMFD acceleration which can be robustly used not only for conventional calculation conditions but also for highly voided conditions.

Acknowledgments

This work was supported by the JSPS KAKENHI, Grant-in-Aid for Scientific Research (C) [16K06956].

Disclosure statement

No potential conflict of interest was reported by the authors.

Supplementary material

Supplemental data for this article can be accessed here.

Additional information

Funding

This work was supported by the JSPS KAKENHI, Grant-in-Aid for Scientific Research (C) [16K06956].