Accelerating the coupled-cluster singles and doubles method using the chain-of-sphere approximation

ABSTRACT

In this paper, we present a chain-of-sphere implementation of the external exchange term, the computational bottleneck of coupled-cluster calculations at the singles and doubles level. This implementation is compared to standard molecular orbital, atomic orbital and resolution of identity implementations of the same term within the ORCA package and turns out to be the most efficient one for larger molecules, with a better accuracy than the resolution-of-identity approximation. Furthermore, it becomes possible to perform a canonical CC calculation on a tetramer of nucleobases in 17 days, 20 hours.

KEYWORDS:

• CCSD
• COSX
• exchange term

1. Introduction

The chain-of-sphere (COS) approximation [1,2] was originally proposed for the evaluation of the Fock exchange term in Hartree–Fock self-consistent field (HF-SCF) calculations. It has since been implemented for a variety of correlation methods, including Møller–Plesset perturbation theory at the second-order (MP2) [3] and third-order (MP3) [4], explicitly correlated methods (F12) [5], for the so-called singles Fock term in local pair natural orbital (LPNO) coupled-cluster singles and doubles (CCSD) method [6] and for the equation of motion (EOM) CCSD method [7] for excited states. The singles Fock term in LPNO-CCSD can be efficiently accelerated using the resolution of identity technique (RI) for the Coulomb (J) term (RIJ) and COS for the exchange term (COSX), but the main advantage of the method lies in its use of PNOs and in canonical CCSD the singles Fock term is not the bottleneck. It is also clear that a COSX-based canonical implementation could not compete with the LPNO [8] and the more recent domain-based LPNO or DLPNO approaches [9,10] in terms of speed. For this reason, a COSX-CCSD implementation has never been published for the highest scaling four external terms, although the same term is implemented in our spin-component-scaled (SCS) COSX-MP3 code in a non-iterative fashion for ground states, and in the COSX-EOM-CCSD implementation for excited states, for which a DLPNO variant is currently unavailable. This omission has been repeatedly pointed out to us, and in the present paper, we correct this shortcoming. Indeed, a COSX-CCSD implementation will expand the range of applicability for the canonical method to some degree, and it is interesting to investigate the accuracy of the resulting method. Since COSX-MP3 is non-iterative and COSX-EOM is iterative but linear in terms of the amplitudes, the question of accuracy for a nonlinear iterative scheme like ground-state COSX-CCSD is not a trivial one even in light of our experience with the other methods discussed so far.

The coupled-cluster method [11] itself has arguably become the most accurate wave-function-based method for the computation of molecular electronic energies and properties in the last decades. It is systematically improvable and yields reliable results for a variety of chemical systems, but this accuracy comes with a steep computational scaling with system size and a prohibitive cost for larger systems. In its canonical form, the CCSD method scales as O(N⁶) and requires a disk space proportional to N⁴ for storage. For full triples and quadruples, the scaling becomes even worse (O(N⁸) and O(N¹⁰)) [12], although there are various lower scaling treatments to include these effects perturbatively [13–18]. Given the success of the CC hierarchy of methods, the development of lower scaling coupled-cluster methods is currently one of the most active areas of quantum chemical methodological research. There are various approaches reported in the literature that can be classified into two broad categories. The first family of methods makes use of localisation and natural orbitals to exploit the R⁻⁶ decay behaviour of the correlation energy. The various schemes developed by a variety of groups include the cluster-in-molecule (CIM) [19–21], Divide and Conquer [22], Divide–Expand–Consolidate (DEC) [23], Frozen Natural Orbital (FNO) [24], Projected Atomic Orbital (PAO) [25], Orbital Specific Virtual (OSV) [26] and PNO [8–10,27–32]-based local CCSD approaches.

The alternative approach involves approximating the two electron repulsion integrals (ERIs), since the most time-consuming steps in a CC computation involve the contraction of higher rank tensors with the ERIs. Again, various solutions have been described in the literature to achieve this purpose, ranging from integrals pre-screening techniques, the resolution of identity approximation [33–38] and Cholesky decomposition [39–41]-based approaches to semi-numerical approximations like the pseudo-spectral method [42], the tensor hyper-contraction scheme [43] and the COS approximation [1,2]. For coupled-cluster calculations, the storage of ERIs in the molecular orbital (MO) basis starts to become the limiting factor as the basis set size increases, well before the O(N⁶) scaling could become prohibitive. Therefore, initial attempts of reducing the storage bottleneck of the wave-function-based method concentrated on the atomic orbital (AO) direct construction of integrals with three and four external indices. One of the very first implementation is described in the work of Meyer on self-consistent electron pair (SCEP) [44] theory, in which the three and four external integrals are directly constructed from the AO integrals stored on disk. This approach was later used for various configuration interaction [45] and coupled-cluster methods [46]. On the other hand, later approaches by Koch et al. [47,48] and Schütz et al. [49] calculate the AO integrals on the fly in each iteration, thereby removing the need to store them, although at the expense of additional computational time. Although the storage problem is thus averted, the required O(N⁵) scaling transformation from the MO to AO basis increases the pre-factor of the scaling, since it needs to be performed in each iteration step. The computational timing can then be improved by combining integral pre-screening techniques with AO direct implementations. Alternatively, the storage requirement can be reduced using the resolution of identity (RI) or the Cholesky decomposition (CD) techniques as demonstrated by the work of various groups [50–55], but in terms of computational scaling, these methods are better suited to the evaluation of Coulomb terms. For some approximate CC methods, this is perfectly enough, see, for example, the very efficient RI-CC2 implementation of Hättig and co-workers [51] which can be used to study the excited states of molecules with more than 100 atoms. Recently, Krylov and co-workers [56] have also reported an RI- and CD-based implementation of EOM-CCSD. Despite these improvements, the evaluation of exchange terms remains problematic for coupled-cluster methods since the most expensive term in CCSD is of this kind and involves the contraction of the doubles amplitudes with four external ERIs. Efficient approximations to accelerate this term are much fewer, initial attempts were reported by Martínez and Carter [57,58] using pseudo-spectral methods. Martínez and co-workers latter implemented tensor hyper-contraction (THC) method [43,59–62] as a generalised scheme to speed up both Coulomb and exchange terms in many-body perturbation theory and coupled-cluster methods. Recently, Grüneis and co-workers [63] have come up with a THC-based implementation of periodic coupled cluster. The COS exchange (COSX) approximation [1,2] is also a relative of pseudo-spectral methods, and as noted above, it has also been used extensively with correlation methods [3–7], but not with the ground-state CCSD method. The aim of this paper is then to investigate the efficiency and accuracy of the COSX method for this purpose.

2. Theory

The external exchange term for ground-state CCSD can be written in the molecular orbital (MO) basis as follows: (1) using the (11|22) notation and real quantities. The labels i, j, k denote occupied orbitals, while a, b, c, d is reserved for virtual orbitals. The above terms also contain the single (t^k_b) and ‘dressed’ double CC amplitudes related to the bare CC doubles amplitudes t^ij_cd as (2) Defining an AO external exchange intermediate as (3) all MO exchange terms in Equation (1(1) ) can be obtained by the appropriate transformation of the AO labels (μ, ν, …), (4) i.e. one-index transformations of the of the intermediate defined in Equation (3(3) ) using the MO coefficients c^a_μ and the quantity (5) The double excitation amplitudes have been transformed to the AO basis and they will serve as an effective density for the evaluation of the COSX exchange, (6)

The COS semi-numerical formula can now be applied to the external exchange to yield (7) with the analytic part of the integral defined as (8) while the basis functions are evaluated and weighed on a grid with points at r_g, (9) Finally, the matrix elements Q _μg may be defined as (10) in which S is the analytic overlap matrix. Then, Q _μq may replace X _μg in Equation (7(7) ) to ensure better numerical accuracy. The formal scaling of COSX for a single density is O(MN ²), where M is the number of grid points, which in practice is reduced by various prescreening techniques. While in the SCF case, the A matrix is never constructed, a special algorithm is available for more than a few densities in which A is kept in memory for a given small batch of grid points to avoid recalculating it several times. Parallelisation in this case may proceed through distributing for parallel processing for a given range of the pair labels ij, unlike the usual single density solution which relies on the loop over grid point batches.

The scheme discussed so far is compatible with any chosen method for the treatment of the remaining contributions in the CC residual equations. We will outline our choice in Section 3.

3. Numerical results

All calculations were carried out using the development version of the ORCA quantum chemistry program package [64]. Two different COSX grid settings are used in this work: one called COSXTIGHT corresponds to a Lebedev angular grid with 110 points (ORCA parameter 2) and a Gauss–Chebyshev radial grid with a resolution parameter of 3.34, the other called COSXLOOSE with a 50-point Lebedev grid (ORCA parameter 1) and a Gauss–Chebyshev radial integration accuracy of 2.34. All CCSD calculations are done using the frozen core approximation.

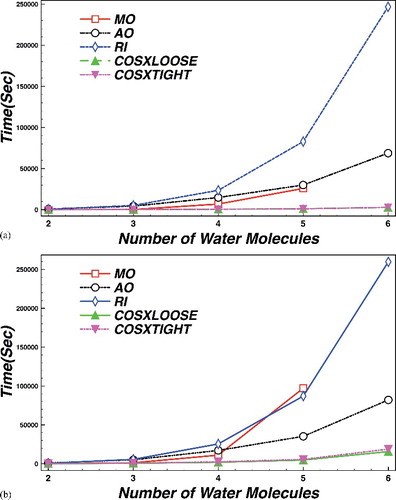
To evaluate the efficiency of the COSX approximation for the four external integral term, we have calculated the ground-state CCSD energy of water clusters ((H₂O)_n, n = 1–6), using MO-, AO-, RI- and COSX-based evaluation schemes for the external exchange. The geometries used are provided in the supporting information. Timing results are reported in Table 1 and also in Figure 1. All the calculations were performed on four cores with 10,000 MB maximum amount of memory per core on a dedicated node with two Xeon E5-2640 processors (eight cores each, 2.6 GHz, 21 MB cache) and 120 GB of total memory. The calculations would certainly also run on machines with much more modest memory, at the expense of increasing the number of batches required for the completion of the external exchange term. The batching arises from the need to hold as many amplitudes and exchange operators in memory as available core memory allows. The def2-QZVPP basis set and def2-QZVPP/C auxiliary basis set were chosen for the calculations. In the MO case, the integrals are transformed and stored in the MO basis, which turns out to be very costly for larger molecules as seen from the total timings in Table 1, only a fraction of which is due to the cost of the external exchange term. In the AO case, the AO integrals are stored and used in each iteration and only the contributions to the residual vector are transformed into the MO basis. While the AO scheme is somewhat slower in the evaluation of the external exchange itself, its main advantage over the MO scheme lies in the savings in the integral transformation step and in the significantly reduced storage burden for the much more sparse AO integrals. Thus, eventually the MO calculation becomes more expensive than the AO one and unfeasible with the given resources. It should be noted that it is also possible to store partially transformed integrals on disk [65]. This might also be useful for three external integrals in combination with our COSX scheme, although we have chosen a different solution, as discussed below. In the RI case, all terms are evaluated using the MO scheme with four index integrals generated from three index MO integrals stored on disk, except the external exchange. In our implementation, this method quickly becomes more costly than the AO-based approach for all but the smallest of molecules. While the RI scheme saves even more on the cost of integral transformation than the AO procedure, the cost of evaluating the external exchange becomes prohibitive. For the COSX implementation, the four external integrals need not be generated and stored. For the remaining terms, here again the MO scheme is used with the various two electron integrals generated when necessary from RI integrals transformed to the MO basis and stored on disk. This reduces the integral transformation time for the remaining terms and also diminishes the storage requirements. For this reason, both the total timing and the time required for exchange evaluation improves significantly. For the tight grid settings, the COSX implementation outperforms the MO one with a factor of 17 for the total, and with a factor of 13 for the exchange term. For the loose settings, the results are even better, a factor of 20 and 23, respectively.

Figure 1. Increase in computational time with number of water molecules in def2-QZVPP basis set.

Table 1. Timings for various CCSD schemes in seconds using the QZVPP basis set for water clusters of n water molecules. Total times indicate the amount of time spent in the correlation module, of which the time required for the integral transformation is indicated under Trafo while the number of CC iteration is shown under Iter. The ratio in brackets indicates how much faster the given implementation is than the MO reference.

n-mer	Iter	term	MO	AO	RI	COSXLOOSE	COSXTIGHT
2	11	Total	197	962 (×0.20)	620 (×0.32)	137 (×1.43)	195 (×1.01)
		Trafo	93	9(×10.33)	3(×31)	3(×31)	3(×31)
		4e	42	833 (×0.05)	551 (×0.08)	73 (×0.58)	130 (×0.32)
3	12	Total	1131	5095 (×0.22)	5614 (×0.20)	631 (×1.79)	846 (×1.34)
		Trafo	522	41(×12.73)	15(×34.80)	15(×34.80)	15(×34.80)
		4e	253	4389 (×0.06)	5218 (×0.05)	269 (×0.94)	483 (×0.52)
4	11	Total	11,084	17,094 (×0.65)	25,467 (×0.44)	1899 (×5.84)	2363 (×4.69)
		Trafo	2856	141(×20.26)	55(×51.93)	55(×51.93)	55(×51.93)
		4e	6892	14,835 (×0.46)	23,593 (×0.29)	597 (×11.54)	1055 (×6.53)
5	12	Total	97,289	35,257 (×2.76)	87,087 (×1.12)	4733 (×20.55)	5586 (×17.42)
		Trafo	67,735	267(×253.69)	181(×374.22)	178(×380.53)	167(×405.6)
		4e	25,854	30,042 (×0.86)	82,840 (×0.31)	1120 (×23.08)	1960 (×13.19)
6	11	Total	–	82,117	259,856	15,669	18,821
		Trafo	–	630	411	408	430
		4e	–	68,798	246,692	2845	5187

To investigate the accuracy of the COSX approximation for the four external terms, we relied on the test set originally used to investigate the accuracy of the overlap-fitted COSX approximation. It consists of 23 reactions involving 47 closed-shell species up to 32 atoms. Sixteen of the reactions are isomerisations of organic molecules taken from the ISO34 test set of GMNTK24 database [66], supplemented with seven more challenging reactions taken from the same database. The def2-TZVP basis set and the def2-TZVP/C auxiliary basis set were used for the calculations and canonical CCSD results were used as reference. The CCSD energies for individual species are presented in the SI. The statistical analysis of the results using the RI and COSX approximations are provided in Table 2. One immediate conclusion is that the reaction energies remain practically unaffected by these approximations, even though the error in the total electronic energy can be significant. The RI approximation yields larger errors, which may be as large as 1.7 m Hartree in our test set, while COSX gives maximum absolute errors of 0.5 m Hartree with tight settings and 0.9 m Hartree with loose settings. The difference between the accuracy of the RI and COSX schemes comes from the accuracy of the external exchange term, since all other terms are evaluated in the same way.

Table 2. Energetic errors and timing data for schemes of evaluation of four external terms is CCSD. Average (μ), variance (σ²) and maximum absolute errors (MAE) values are indicated for various quantities. The error in the correlation energy normalised to the number of correlated electrons (E_c/n_e) is indicated in microHartree/electron units; the error in correlation energy (E_c) in micro-Hartrees; reaction energy errors (ΔE_r) are in kJ/mol. Variance values have the corresponding squared unit.

	μ(Ec/ne)	MAE (Ec)	MAE (ΔEr)	RMSD (ΔEr)	μ (ΔEr)	σ^2 (ΔEr)
RI	−16.73	1742.43	0.15	0.06	−0.01	0.00
COSXLOOSE	5.19	884.14	0.34	0.13	0.04	0.00
COSXTIGHT	3.86	470.51	0.17	0.08	− 0.03	0.00

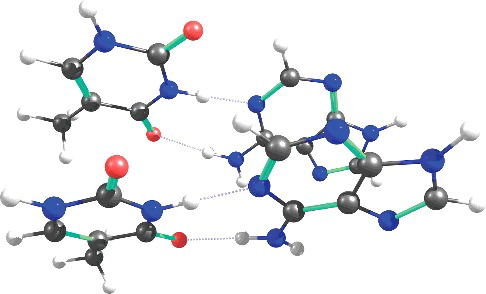
To demonstrate the efficiency of our COSX-based implementation, we have calculated the coupled-cluster energy of the AATT tetramer (See Figure 2) using the 6-311+G(d,p) basis set and the cc-pVTZ/C auxiliary basis set. This system has 272 electrons and 966 basis functions and it was used by Krylov and co-workers to report the efficiency of their RI/CD-based EOM-CCSD implementation. The calculation was run using four cores and COSXLOOSE settings on a dedicated node with two Xeon E5-2640 V3 processors (eight cores each, 2.6 GHz, 21 MB cache) and 256 GB of total memory. The total coupled-cluster calculation takes 432 hours of which one and half hours are spent on integral transformation and it takes only 26 hours to evaluate the external exchange term. The RI implementation of Krylov and co-workers took 699.2 hours on 12 cores even after using the frozen natural orbital approximation. Although the two calculations were carried out on different hardware, this result clearly shows that our COSX-based implementation can be used to do accurate CCSD calculations for medium-sized molecules.

Figure 2. Adenine–thymine–adenine–thymine tetramer.

4. Conclusions

We have proposed a COS implementation of the coupled-cluster external exchange term and tested it for accuracy and efficiency. As expected, COSX outperforms not only the MO and AO implementations, but also the RI scheme which for this particular term scales very badly. In terms of accuracy, the COSX method even with loose grid settings is again superior to RI with the auxiliary basis set chosen in this study. The improved scaling and storage requirements associated with the COSX scheme allow us to carry out a canonical CCSD calculation for systems involving about a thousand basis functions in about two and half weeks on four cores.

Disclosure statement

No potential conflict of interest was reported by the authors.