Assessment of time-dependent density functional theory with the restricted excitation space approximation for excited state calculations of large systems

ABSTRACT

The restricted excitation subspace approximation is explored as a basis to reduce the memory storage required in linear response time-dependent density functional theory (TDDFT) calculations within the Tamm–Dancoff approximation. It is shown that excluding the core orbitals and up to 70% of the virtual orbitals in the construction of the excitation subspace does not result in significant changes in computed UV/vis spectra for large molecules. The reduced size of the excitation subspace greatly reduces the size of the subspace vectors that need to be stored when using the Davidson procedure to determine the eigenvalues of the TDDFT equations. Furthermore, additional screening of the two-electron integrals in combination with a reduction in the size of the numerical integration grid used in the TDDFT calculation leads to significant computational savings. The use of these approximations represents a simple approach to extend TDDFT to the study of large systems and make the calculations increasingly tractable using modest computing resources.

KEYWORDS:

• TDDFT
• large systems
• restricted subspace approximation

1. Introduction

Kohn–Sham density functional theory (DFT) [1] has emerged as an extremely popular and successful approach for modelling molecular systems and solids. Within the framework of DFT, electronically excited states are usually studied though linear response time-dependent density-functional theory (TDDFT) [2]. In many studies, for example in biological chemistry or organic photovoltaics, there is a requirement to study the excited states of large molecular-based systems. For the study of excited states, it is often important to have an ab initio based approach since it is more difficult to parameterise reliable empirical methods for excited states. The application of TDDFT to study large systems is challenging owing to the computational cost, both in terms of the time for the calculations and memory required. Efficient schemes for solving the Casida equations for TDDFT and determining the excitation energies and associated oscillator strengths have been developed [3,4]. However, to study large system comprising of hundreds of atoms often requires further approximations to be made. The density functional tight binding (DFTB) method is a semi-empirical form of DFT which can be several orders of magnitude faster than DFT, and a linear response form of DFTB has been reported [5]. Another approach to extend TDDFT to study very large systems is the simplified TDDFT method of Grimme [6]. The approach exploits a Löwdin monopole based approximation to the two electron integrals and single excitation space selection and can be applied to systems of 500–1000 atoms. Other time-dependent semi-empirical approaches have been developed [7–9]. The low lying excited states of large systems have been studied with pseudo spectral TDDFT [10,11] which leads to a significant speedup in the calculations.

Another important factor in applying TDDFT to study large systems is the memory required by the calculations. TDDFT calculations typically use an iterative eigensolver method, such as Davidson's algorithm [12,13], to solve for the lowest lying excited states. The advantage of Davidson-based approaches is that they are computationally fast but they have the limitation that they are memory intensive. Within the Davidson's method it is necessary to store L vectors of length n_occ × n_virt where L is the size of the excitation subspace, n_occ is the number of occupied orbitals and n_virt is the number of virtual orbitals. This can limit the applicability of TDDFT, particularly when studying large systems with good quality basis sets. Different formalisms of TDDFT can address this problem, for example complex polarisation [14,15], damped response approaches [16] and real-time TDDFT [17,18]. A symmetric Lanczos algorithm and a kernel polynomial method were introduced for low memory determination of absorption spectra within TDDFT [19]. However, within this approach, determining state specific properties is challenging. Other approaches included energy specific TDDFT that allows excited states above a predefined energy threshold to be determined [20] and Krylov-space-based algorithms [21].

A pragmatic approach to extend the applicability of Davidson type algorithms is to apply a restriction to the excitation space. This has been explored in the context of the algebraic-diagrammatic approach by Yang and Dreuw [22]. It was shown that a reduction of the virtual space by up to 40% could be imposed without introducing a large error in the excitation energies. Restriction of the excitation space has also been used with TDDFT, primarily in systems where the excited states of interest are spatially localised, for example, for molecules on a surface or chromophores in a biological environment [23–25]. Recently, the reduction in excitation space, along with integral screening and modification of the numerical integration grid, were exploited to enable the calculation of the X-ray absorption spectra of large systems [26,27]. In this paper, we investigate restriction of the excitation space along with other approximations to enable TDDFT calculations of the UV/vis absorption spectra of large systems and to make calculations of the UV spectra increasingly tractable with modest computational resources.

2. Computational details

The calculations have been performed using TDDFT with the Tamm–Dancoff approximation (TDA) since this approach is computationally less expensive than full TDDFT. However, the principles also apply to full TDDFT. Within the TDA, the excitation energies and associated transition dipole moments are obtained from the following equation [28]: (1) The matrix A is given by (2) where (3) (4) and ε_i are the orbital energies, and E_XC is the exchange correlation functional. For the simulation of UV/vis spectra, only the low energy roots, typically between 0 and 10 eV, are of interest. The Davidson procedure [13] is a computationally fast algorithm that allows these low energy roots to be determined. A more detailed analysis of the Davidson and related methods can be found elsewhere [29].

A major factor that limits the application of this approach to study large systems is the large amount of memory that is required. The Davidson diagonalisation procedure is an iterative subspace approach where for a given root k the eigenvectors of interest are expanded in an orthonormal vector space (5) where x^k is the approximation to X^k for the current iteration. A subspace matrix is diagonalised (6) As the number of expansion vectors b_i is increased, the eigenvalues and eigenvectors of the subspace matrix will approach the exact (within the model) eigenvalues and eigenvectors. On each iteration, if the root is not converged, the subspace is expanded by adding a correction vector (7) The correction vector is orthogonalised with respect to the existing expansion vectors and added to the subspace. A consequence of this is that it is necessary to store all subspace vectors b_i, and this corresponds to L vectors of length n_occ × n_virt, where n_occ is the number of occupied orbitals and n_virt is the number of virtual orbitals. Clearly, for large systems where it may be necessary to converge a large number of roots the memory storage required will become considerable. This can make the calculation intractable or make the use of substantial high performance computing resources necessary.

In the restricted excitation subspace approximation, A is constructed in a reduced orbital subspace. This subspace is defined as the single excitations from a subset of the occupied orbitals to a subset of the virtual orbitals which naturally leads to a reduction in the length of the subspace vectors, greatly reducing the storage required. Here we use a modification of the code implemented for the study of core excitations [27] where A is constructed in the reduced orbital subspace. If there are and in the occupied and virtual orbital subspaces, respectively, the memory storage for the subspace vectors becomes . This can be implemented within existing TDDFT/TDA implementations by expanding the subspace vectors where necessary, which can be done on a root by root basis to avoid large memory requirements. For the occupied subspace, a simple approximation is to exclude the core orbitals. For the virtual subspace, we omit the high energy orbitals, where 25% means that a quarter of the orbitals (those with the highest energy) have been excluded from the virtual orbital subspace. The structures of the molecules have been optimised at the B3LYP/6-311G^** level of theory and the calculations were performed with a development version of the Q-Chem software package [30]. Representation of the spectra is generated by convoluting the calculated transition energies and intensities with gaussian functions with a full width at half maximum of 0.2 eV.

3. Results and discussion

Before examining the effect of the restriction of the virtual orbital space, we will explore the role of the numerical quadrature grid used in the TDDFT calculation. Studies of core excitations have shown that it is possible to employ small (reduced quality) integration grids with little effect on the computed excitation energies and oscillator strengths whilst significantly reducing the time for the calculation and making the study of large systems more accessible. For the case of core excitations, the grid could be reduced to 10 point Euler–McClaurin radial grid and 18-point Lebedev angular grid, denoted as (10,18), without introducing significant changes in the excitation energies and oscillator strengths. We note that, in this approach, the integration grid is only reduced in the TDDFT calculation and the grid used in the Kohn–Sham DFT calculation is unchanged. Table 1 shows the effect of successively reducing the quality of the integration grid from a standard (50,194) grid. The data is for the lowest 30 states for the four molecules benzene, N-acetylglycine-N-methyl-amide (NAGNMA), histidine and Cr(CO)₆. Considering 30 states for these molecules includes a variety of different types of excitations such as nπ^*, ππ^*, metal-ligand charge transfer and Rydberg. It also means that states of relatively high energy (up to 10 eV) are considered since the restricted excitation approximation is likely to predominantly affect states with high energy. Results are shown for two different types of exchange-correlation functional, the generalised gradient approximation functional (GGA) PBE and the Coulomb attenuated functional CAM-B3LYP, and the 6-311+G^* basis set which includes diffuse basis functions is used.

Table 1. Effect of quadrature grid relative to the (50,194) grid for TDDFT calculations for the lowest 30 states of benzene, diamide, histidine and Cr(CO)₆. The 6-311+G* basis set is used, and the percentage error in the oscillator strength of the most intense transition is shown.

	(40,146)	(30,110)	(20,86)	(10,18)	(10,18)+τ = 10^−5
PBE functional
Mean absolute error (eV)	<0.01	<0.01	<0.01	0.02	<0.01
Max. error (eV)	<0.01	<0.01	0.01	0.25	0.01
Max. error in f (%)	<1	<1	<1	3	<1
Average time saving (%)	24	37	45	52	52
CAM-B3LYP functional
Mean absolute error (eV)	<0.01	<0.01	<0.01	0.01	<0.01
Max. error (eV)	<0.01	<0.01	0.01	0.25	<0.01
Max. error in f (%)	<1	<1	<1	3	<1
Average time saving (%)	13	22	28	33	46

The data shows that there is little difference in the behaviour observed for the two functionals. Reducing the size of the grid to (10,18) leads to an average absolute error of 0.01–0.02 eV. This level of error is not significant in the context of the error associated with other approximations made in the calculations, such as the approximate exchange-correlation functional and finite basis set. However, while this average error is small, some large errors are evident in some of the transitions. In particular, an error of 0.25 eV is found for a transition in Cr(CO)₆ and it is important to note that this is not a high energy transition. For the (10,18) grid, there is also some variation evident in the computed oscillator strengths. The larger (20,86) grid provides a consistently low error with respect to the (10,194) grid whilst providing a significant reduction in the computational time. For the PBE and CAM-B3LYP functionals, the time for the calculations is reduced by 45% and 28%, respectively. We note that there are well-documented problems associated with the use of GGA functionals with TDDFT [31,32]. The value for CAM-B3LYP is lower because the evaluation of the integrals associated with the exchange-correlation functional comprises a smaller fraction of the computational time since additional two-electron integrals need to be evaluated. In TDDFT implementations, it is standard to screen the two-electron integrals based upon the Schwarz inequality (8) where (9) The default cut-off used in Q-Chem is 1×10⁻¹⁰; Table 1 also shows the effect of increasing the threshold (τ) to 1 × 10⁻⁵ in the TDDFT calculation. With this value for the threshold parameter, there is no significant change in the computed values for the transition energies and oscillator strengths and reduces the time for the calculation for both PBE and CAM-B3LYP functionals by about a factor of two, and this would become more significant for larger systems. We note that increasing the value of τ further can lead to spurious states with low energy or negative transition energies, and if such roots appear in a calculation, the value of τ should be increased.

Table 2 shows the effect on the computed excitation energies and oscillator strengths when the size of the virtual orbital space is successively reduced. These calculations have been performed with the CAM-B3LYP functional, 6-311+G^* basis set and the (50,194) integration grid. Here 10% means that excitations to the highest energy 10% of virtual orbitals are excluded from the excitation space in the TDDFT calculation, i.e. the excitation subspace consists of excitation from the occupied orbitals to the lowest 90% of there virtual orbitals. Excluding up to 30% of the virtual orbitals introduces no significant error, with the maximum error in the transition energies being less than 0.01 eV and the error in the oscillator strength of the most intense transition is less than 1%. In a previous study with the algebraic diagrammatic construction (ADC) method, it was found that up to 40% of the virtual orbital subspace could be frozen. At the 40% level for TDDFT, the size of the errors begin to increase but remain well within acceptable limits. On further reduction of the virtual orbital space, the error in the transition energies remains small up to truncation levels of 60%. At this level of truncation, there is a significant error of 0.18 eV for benzene. Benzene is the smallest system studied and as a consequence has the smallest number of virtual orbitals with 129. For molecules of this size, the high levels of virtual orbital truncation leaves relatively few virtual orbitals remaining in the calculation, resulting in significant errors. In general, for all of the molecules the oscillator strength shows a greater sensitivity to the restriction of the excitation space, with significant errors that would alter the appearance of the computed spectra being observed at the higher levels of orbital exclusion. In addition to restriction of the virtual orbitals, the exclusion of the core orbitals (1s for the first row of the periodic table, 1s, 2s and 2p for heavier elements) does not result in significant errors.

Table 2. Effect of truncation of the virtual subspace with the CAM-B3LYP exchange-correlation functional and 6-311+G* basis set for the lowest 30 states. The percentage error in the oscillator strength of the most intense transition is shown.

	10%	20%	30%	40%	50%	60%	70%	80%
Benzene
Mean absolute error (eV)	0.000	0.000	0.001	0.003	0.007	0.018	0.039	0.107
Max. error (eV)	0.000	0.001	0.006	0.026	0.077	0.180	0.290	0.461
Error in f (%)	<1	<1	<1	<1	<1	2.3	5.6	7.6
NAGNMA
Mean absolute error (eV)	0.000	0.000	0.001	0.002	0.004	0.009	0.016	0.043
Max. error (eV)	0.000	0.001	0.003	0.007	0.019	0.037	0.065	0.140
Error in f (%)	<1	<1	<1	1.8	6.9	16.7	63.8	76.4
Histidine
Mean absolute error (eV)	0.000	0.000	0.001	0.003	0.006	0.011	0.020	0.044
Max. Error (eV)	0.001	0.001	0.007	0.010	0.019	0.027	0.051	0.088
Error in f (%)	<1	<1	1.7	6.6	14.2	16.7	63.8	76.4
Cr(CO)6
Mean absolute error (eV)	0.000	0.000	0.001	0.002	0.005	0.008	0.019	0.023
Max. Error (eV)	0.001	0.001	0.007	0.010	0.019	0.027	0.051	0.088
Error in f (%)	<1	<1	<1	<1	1.9	5.2	7.9	13.5

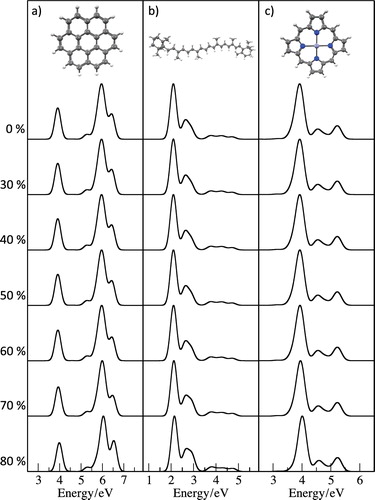
The molecules considered in Table 2 show how the computed excitation energies and intensities are insensitive to significant restrictions of the excitation space. However, these molecules are relatively small and are not representative of the types of system where restriction of the excitation space would be required. Figure 1 shows the computed spectra for three larger molecules, coronene, β-carotene and zinc prophyrin, with varying sizes of virtual subspace. These calculations have been performed with the PBE functional and 6-31+G^* basis set and include 50–120 states, and the occupied orbital space excludes the core orbitals. For these larger systems, the low energy regions of the spectra (<10 eV) are remarkably insensitive to the exclusion of a large fraction of the high-energy virtual orbitals. Closer inspection of the spectra for coronene shows some small changes in the high-energy band at >60% levels. However, for all of the molecules, the spectra with the exclusion of 80% of the virtual orbitals are nearly indistinguishable from the full virtual orbital subspace (0%). In general, for molecules of this size, 70% of the virtual orbitals can be excluded without any effect on the computed spectra in this region.

Figure 1. Variation in the computed PBE/6-31+G* spectra for (a) coronene, (b) β-carotene and (c) zinc porphyrin with the size of the virtual orbital subspace. X% indicates that excitations to the highest energy X% of virtual orbitals are excluded from the excitation space in the TDDFT calculation.

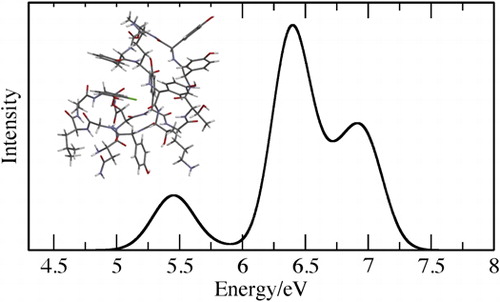
To illustrate the application of the methodology, the UV spectra of the three large molecules, shown in Figure 2, have been computed. These include C₆₀, P3B2 which has been studied previously with real-time TDDFT [18] and semi-empirical methods [9] and ramoplanin (PDB code: 1DSR) which is an antibiotic drug. The computed spectra are shown in Figure 3 and have been computed using the 6-31G* basis set and PBE functional for C₆₀ and CAM-B3LYP functional for P3B2 and ramoplanin, and exclude the core orbitals and 70% of the virtual orbitals from the excitation subspace. For P3B2 and ramoplanin, it was necessary to use the CAM-B3LYP functional because for these systems the PBE functional has a large number of low-energy charge-transfer transitions that have very low intensities. A consequence of this is that it is necessary to converge a large number of roots in order to determine the transitions with intensity. The energy of these charge-transfer states are predicted to be too low with the PBE functional but are described correctly by the CAM-B3LYP functional. Ramoplanin is the largest of these systems with 271 atoms and 2483 basis functions and the calculations were performed on a PC with 125 GB of RAM. The computed spectrum for C₆₀ is in excellent agreement with experiment, and the spectrum for P3B2 is consistent with the low-energy region of the real-time TDDFT spectrum which also shows an intense band at  3 eV. The spectrum for ramoplanin also qualitatively agrees with experiment.

Figure 2. Molecular structures of the large molecules studied.

Figure 3. Computed spectra for (a) C₆₀, (b) P3B2 and (c) ramoplanin. For (a) and (c) experimental data from references [33,34] is also shown.

4. Conclusions

It has been shown that the computational cost of linear-response TDDFT/TDA calculations that use the Davidson procedure to determine the low energy eigenvalues can be reduced significantly. First, exploiting a larger integral screening threshold in conjunction with reduced quality numerical integration grid can significantly reduce the time for the calculations. Furthermore, a limitation of approaches based upon Davidson-type algorithms is the memory required to store all of the subspace vectors. It has been demonstrated that restriction of the excitation subspace by excluding the core orbitals and up to 70% of the virtual orbitals can greatly reduce the length of the subspace vectors without adversely affecting the computed spectra. The limiting factor of the calculations is the evaluation of the two-electron integrals, however, solutions to this problem have been proposed [10]. Overall, the modifications described can extend the size of system that can be studied with linear-response TDDFT and make the calculations increasingly tractable using modest computing resources.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Engineering and Physical Sciences Research Council [grant number EP/N002148/1].