The characterization of electronic defect states of single and double carbon vacancies in graphene sheets using molecular density functional theory

ABSTRACT

A detailed picture of the electronic states manifolds of single- and double-vacancy defects in molecular models of graphene based on polycyclic aromatic hydrocarbons (PAHs) is presented. DFT calculations using various density functionals including long-range corrected ones have been performed for pyrene, circumpyrene and 7a,7z-periacene. It has been found for pyrene defect models that DFT results reproduced well the set of closely-spaced singlet and triplet states predicted by the CCSD(T) and previous MRCI + Q calculations, indicating the applicability of DFT for accessing the excited states manifolds also for larger graphene models. For the single-carbon vacancy defect, all structures have a triplet ground state. As expected, in the largest system, 7a,7z-periacene-1C, the lowest lying states are much closer in energy. For all double-vacancy defect structures, a significant rearrangement of the electronic states with increasing size of the sheet is observed. The closed-shell ¹A_g state in the smallest systems is destabilised in the extended 7a,7z-periacene system, which has the ³B_2u state as the ground state. As observed for the single-vacancy defect, the lowest lying states are closer in energy for the larger systems, since there are more π orbitals close in energy available. For all states, the formation of the bridging bonds for the double vacancy leads to distances shorter than for the single vacancy defect indicating a larger rigidity of the former structure which does not allow stronger distortions.

GRAPHICAL ABSTRACT

KEYWORDS:

• Excited states
• polycyclic aromatic hydrocarbons
• pyrene
• Periacenes
• DFT

1. Introduction

Graphene became one of the most promising materials since its discovery in 2004 by Geim and Novoselov [1]. It possesses exceptional electronic, thermal, and mechanical properties with promising applications in electronics, optoelectronics and photonics [2–9]. Since graphene is a semimetal, it is necessary to modify its band gap in order to create appropriate semiconductor properties. This band gap engineering is frequently accomplished by the introduction of defects. Among the wide range of approaches to generate defects such as physi- and chemisorption, vacancy defects constitute an interesting possibility by which strong variations in the electronic properties of a graphene sheet can be obtained. These defects arise in graphene or in graphitic nanostructures during defective growth and can also be created after ion irradiation [10–17]. Experimentally, the structural details of these defects have been observed using transmission electron microscopy (TEM) [18–22] and scanning tunnelling microscopy (STM) [23,24]. Because of the removal of carbon atoms from the regular honeycomb network, dangling bonds appear, inducing a magnetic behaviour in graphene [25–27]. For the same reason, a radical character is expected to occur in such defective-graphene materials leading to a high chemical reactivity. The characterisation of the electronic structure of the defect states, their structures and energetics is of great significance and constitutes a fascinating and challenging field important for modulating the electronic properties of graphene [28]. Recently, the possibility to use similar defect structures in hexagonal boron nitride (h-BN) for the purpose of quantum computing applications have been explored in the literature with several studies, as one can see in these referenced works and others cited by them [29–31].

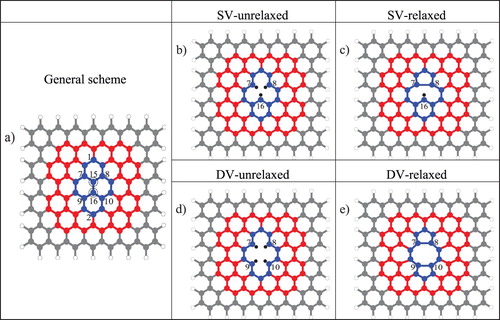
The present work focuses on prototypes of graphene molecular fragments with single and double carbon vacancies using pyrene, circumpyrene and 7a,7z-periacene (a and z denote armchair and zig-zag boundaries) as model structures (Figure 1). Figure 1a shows colour-coded the original unperturbed structures of increasing size, whereas in Figure 1b and Figure 1d one and two carbon atoms have been removed to form single-(SV) and double (DV) vacancy defects without further structural relaxation, thus maintaining the regular graphene network. In the first case, three dangling bonds are created in the σ system, and one hole in the π system. In the second, four dangling bonds are created in the σ orbital system and two holes in the π system. In Figure 1c and Figure 1e geometry relaxation has occurred. The basic features of these defects have been explained many years ago on the basis of a tight binding model taking into account the π system and the dangling bonds formed in the σ orbitals [32,33]. More detailed investigations on the ground state electronic structure of graphene with single and double vacancies have been performed later on [34–40]. These representative works are based on the extended Hückel approach [34], tight binding [35] and several density functional theory (DFT) methods [35–40]. Also, the excited states have been calculated using TD-DFT [41–43].

Figure 1. a) General scheme for unrelaxed structures with numbering of selected carbon atoms; the circles indicate the carbon atoms to be removed; different colours indicate different PAH subsystems formed: pyrene (blue), circumpyrene (blue plus red) and 7a,7z-periacene (total system), b) structures-1C-unrel, c) structures-1C-relaxed, d) structures-2C-unrel, e) structures-2C-relaxed.

Recently, using pyrene as a model, we have shown by means of multireference configuration interaction (MRCI) calculations that SV and DV defects induce a complex set of several closely spaced singlet and triplet electronic states leading to geometry relaxation effects with carbon–carbon bond formation (Figure 1c and Figure 1e) [44,45]. The MRCI calculations performed showed that the complexity of the electronic states was in fact significantly more pronounced than anticipated in previous work. The DV relaxed structure has a ¹A_g ground state with almost negligible unpaired electron density. This stability distinguishes the double vacancy from the single vacancy defect where we have found that even for the relaxed structure a substantial unpaired density existed primarily due to the occurrence of a dangling bond. We also had found in our previous work that B3LYP calculations gave similar results in comparison to the just-mentioned MRCI calculations.

Even though the pyrene model is certainly able to describe the main characteristics of the different electronic states induced by the dangling bonds, extension of the sheet sizes is desirable to study the effects on the defect structures and the energetic spacings of the different electronic states. The purpose of the present work is to investigate these questions by comparing the pyrene results with those obtained from the already introduced circumpyrene and 7a,7z-periacene structures. Since the MRCI calculations performed before [44,45] become computationally increasingly expensive when used for the larger molecular fragments of graphene, we decided to investigate here the possibilities of DFT methodology for describing the manifold of electronic states.

2. Methods

All geometry optimizations were performed using the B3LYP hybrid functional [46–48] together with the 6–311G (2d,1p) basis [49,50]. For all system, the structures were optimised keeping them in plane to retain a higher molecular symmetry for the purpose of computational efficiency. Although, it has been shown that for the case of the1C-vancancy the dangling bond carbon (C₁₆ in Figure 1) is dislocated out-of-plane in most cases only by 0.05 Å and only for one state by 0.3 Å [44]. In the case of 2-vacancy defect the structures for pyrene was previously calculated to stay in the plane [45]. Following the already mentioned MRCI calculations on the pyrene single- and double vacancy defect model [44,45], the low-lying electronic states of singlet and triplet spin multiplicities have been investigated. For the open shell systems, unrestricted (U)DFT/B3LYP was used. As will be discussed below for specific examples of the pyrene systems, open shell high- and low-spin states were constructed by enforcing non-Aufbau orbital occupations according to symmetry. Excitation energies are then determined by total energy differences between the ground state and the symmetry constrained excited states, as in the widely used ΔSCF-DFT method [31,51–54]. The state symmetry determined from the direct product of the irreducible representations of the respective open shell orbitals was maintained throughout the SCF procedure, thus preventing a variational collapse of the wave function to the lowest energy configuration. Besides the low computational cost, this method still offers an advantage of accessing double excited states by the adequate choice of orbital occupations.

The construction of three different carbon sheet sizes (pyrene, circumpyrene and 7a,7z-periacene) is shown in Figure 1. The respective subsystems have been cut out from the graphene sheet with hydrogen-saturated edges to form polycyclic aromatic hydrocarbons (PAHs). From the three template structures, one and two innermost carbon atoms, respectively, (Figure 1a, atoms nos. 15 and 16) were then removed, resulting in the unrelaxed structures denoted structure-1C-unrel and structure-2C-unrel (Figure 1b and Figure 1d). In these names, ‘structure’ stands for pyrene, circumpyrene and 7a,7z-periacene, respectively. (U)DFT/B3LYP/6-311G(2d,1p) geometry optimizations were performed for each electronic state separately to obtain the structure-1C-relaxed and structure-2C-relaxed structures (Figure 1c and Figure 1e). For some states, using the B3LYP optimised geometries we have also used the long-range (LR) corrected HSE06 [55–59] and CAM-B3LYP [60] functionals to perform single point calculations. For the smallest systems, single point unrestricted UCCSD(T) [61] and TDDFT calculations were also carried out.

All the structures were arranged in the yz plane with the long axis oriented along the z axis (vertical axis). All the geometry optimizations using B3LYP were performed using the TURBOMOLE programme [62]. The TDDFT and single point B3LYP, HSE06, CAM-B3LYP and CCSD(T) calculations were carried out using Gaussian09 programme [63]. The Cartesian geometries can be found in the Supplemental Material.

3. Results and discussion

3.1. Pyrene system

B3LYP geometry optimizations for the planar pyrene-1C structures have been performed and the excitation energies and optimised bridging bond (C₇-C₈) distances for the five lowest states are displayed in Table S1 together with results from our previous complete active space self-consistent field (CASSCF) and MR-CISD + Q calculations [44]. The main feature of this optimisation is the formation of the bridging bond (see Figure 1 for atomic numbering) and of a dangling bond at C₁₆, as already found previously in our CASSCF geometry optimizations. In agreement with the CASSCF results, one finds a strong reduction of the C₇-C₈ distance at DFT level from originally 2.47 Å in the unrelaxed structure also. The structures of the A₂ states have shorter C₇-C₈ distances (1.45 Å) than those for the B₁ states (1.58 Å), but the ³B₁ state which has one electron in the 25a₁ dangling bond orbital is the lowest state by both DFT and MRCI calculations. The DFT calculations reproduce the quasi-degeneracy of the four lowest states found at MRCI + Q level within ∼0.2 eV. For pyrene-2C, as observed to pyrene-1C structures, we have shown previously [45] a strong reduction of the C₇–C₈ (C₉–C₁₀) distances from originally 2.47 Å in the unrelaxed structure to distances between 1.45 Å and 1.54 Å for all states, with similar results obtained at CASSCF and DFT/B3LYP levels. They indicate the formation of the pentagon–octagon–pentagon (5–8–5) structure shown in Figure 1e.

Additionally, DFT calculations using the HSE06 and LR corrected CAM-B3LYP functionals and the UCCSD(T) method were performed at the B3LYP optimised geometries. In Table 1, corresponding excitation energies are presented for the pyrene-1C and in Table 2 for the pyrene-2C defect. As one can see, despite of minor numerical differences, the HSE06 and CAM-B3LYP results are close to the B3LYP values. Compared to the MRCI + Q calculations, the DFT results for the five lowest states are slightly overestimated; the CCSD(T) are much closer for these states but somewhat underestimated. The closed shell state ¹A₁ is located above the ground state by about 1.0 eV in all methods, except for CCSD(T) and B3LYP values, which are smaller, 0.72 and 0.86 eV, respectively. The resulting excitation energies (Table 2) obtained with the HSE06 and the CAM-B3LYP functionals for the pyrene-2C defect are quite similar to the ones obtained with B3LYP. The CCSD(T) calculations also present the same energetic order and the closed shell ¹A₁ state as the ground state. Compared to the MRCI + Q results, all DFT and CCSD(T) results are underestimated, but the CCSD(T) results are much closer to MRCI + Q.

Table 1. Excitation energies ΔE (eV) for the relaxed pyrene-1C structure using DFT/6-311G(2d,1p)//B3LYP/6-311G(2d,p) and MRCI + Q(6,6)/6-31G(d)//CASSCF(6,6)/6-31G(d) methods.

State	B3LYP	HSE06^b	CAM^b	CCSD(T)^b	MRCI + Q^a	Configuration^c
^3B1(b1xa1)	0.000	0.000	0.000	0.000	0.000	25a1^13a2^219b2^05b1^1
^1B1(b1xa1)	0.108	0.131	0.107	0.051	0.069	25a1^13a2^219b2^05b1^1
^3A2 (a2xa1)	0.227	0.224	0.219	0.047	0.054	25a1^13a2^119b2^05b1^2
^1A2 (a2xa1)	0.252	0.257	0.254	0.012	0.063	25a1^13a2^119b2^05b1^2
^1A1 (closed)	0.864	0.944	1.009	0.722	1.187	25a1^03a2^219b2^05b1^2

^aOptimized for each state symmetry.

^bHSE06, CAM-B3LYPand CCSD(T) at B3LYP/6-311G(2d,1p) optimised geometries.

^cAt CASSCF(6,6)/6-31G(d) optimised geometries. Ref. [44].

^dclosed shell part: 24a₁²2a₂²18b₂²4b₁².

Table 2. Excitation energies ΔE (eV) for the relaxed pyrene-2C structure using DFT/6-311G(2d,1p)//B3LYP/6-311G(2d,p) and MRCI + Q(8,8)/6-31G(d)//CASSCF(8,8)/6-31G(d) methods.

State	B3LYP	HSE06^b	CAM^b	CCSD(T)^b	MRCI + Q^a	Configuration^c
^1Ag	0.000	0.000	0.000	0.000	0.000	12ag^211b1u^210b2u^03b3u^02b2g^22b1g^2
^3B2u	0.445	0.684	0.565	0.991	1.053	12ag^211b1u^210b2u^03b3u^12b2g^22b1g^1
^1B2u	0.493	0.632	0.614	0.860	1.323	12ag^211b1u^210b2u^03b3u^12b2g^22b1g^1
^3B1u	1.433	1.460	1.334	1.609	1.630	12ag^211b1u^210b2u^03b3u^12b2g^12b1g^2

^aAt CASSCF(8,8)/6-31G(d) optimised geometries. Ref. [45].

^bHSE06, CAM-B3LYP and CCSD(T) at B3LYP/6-311G(2d,1p) optimised geometries.

^cClosed shell part: 11a_g²10b_1u²9b_2u²8b_3g²2b_3u²1b_2g²1b_1g²1a_u².

As a preliminary study, TDDFT calculations were also performed for pyrene-1C (Tables S2 to S4) and pyrene-2C (Table S5) systems. These calculations are compared with the vertical ΔE-DFT excitation energies obtained with B3LYP, HSE06 and CAM-B3LYP, also presented in Tables S2 – S4 and S5. In general, the TDDFT results overestimate the triplet states, mainly for CAM-B3LYP in the pyrene-2C vacancy. In the case of pyrene-1C, the calculations carried out using the ¹A₁ state as reference (Table S2) overestimate the stability of this state for all functionals. Also, these TDDFT results are quite different from the vertical excitation energies, mainly compared with those calculated with CCSD(T). Since the ground state has ³B₁ symmetry and these states present a significant multireference character [44], the TDDFT calculated with the closed shell reference state should not be reliable, as already have pointed out by Reimers et al [31]. in their calculation in hexagonal boron nitride (h-BN) defects. TDDFT and vertical ΔE-DFT calculations were also carried out using the ³B₁ and ¹B₁ as reference state (Tables S3 and S4), which present results reasonably comparable. From these calculations one can see that the ¹A₁ state is located above the ground state ³B₁ by 0.7 or 1.2 eV predicted with CCSD(T) or MRCI + Q at the geometries optimised for each state using B3LYP/6-311G(2d,p) or CASSCF(6,6)/6-31G*, respectively. The result obtained with the CCSD(T) vertical energies is around 1.4 eV. A more conclusive picture on the merits of the TDDFT results by comparing the effects of the underlying exchange–correlation approximations is an important extension of this work that should be addressed in future studies.

The calculations using different density functionals show that they can reproduce quite well the set of closely-spaced singlet and triplet states predicted by the CCSD(T) and previous MRCI + Q calculations for the local defects of both the SV and DV pyrene models. Based on this finding, we continued with DFT to investigate the single and double vacancies using significantly larger graphene sheet models, which should provide more detailed insight into the embedding effects and their consequences on the electronic and geometrical structures. However, for the larger systems, HSE06 and CAM-B3LYP long-range correction is expected to be important, which was tested for some lowest states in the relaxed structures, as discussed below.

3.2. Circumpyrene and periacene systems

3.2.1. Single vacancy

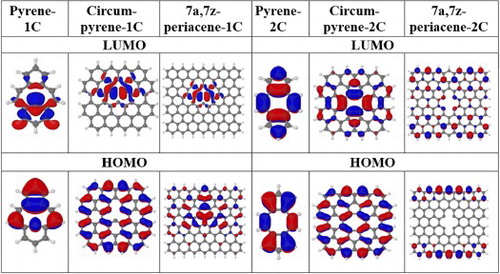
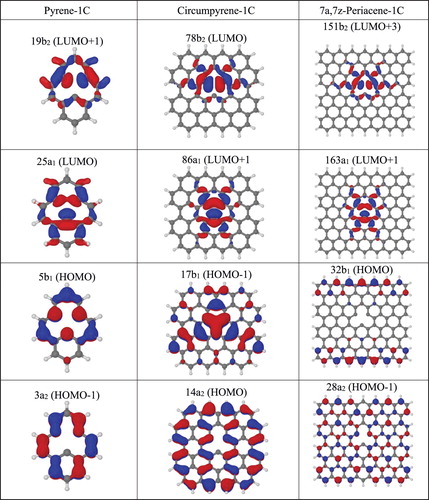
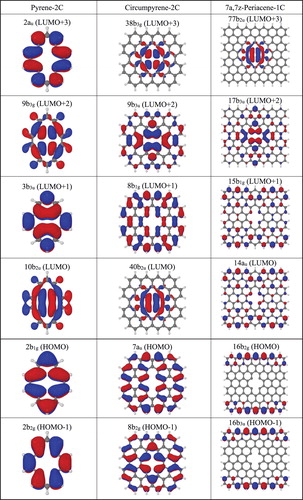
The evolution of the shape of the four active orbitals for the series of pyrene, circumpyrene and 7a,7z-periacene in their unrelaxed structure is shown in Figure 2. Orbital occupations are given with respect to the closed shell configuration of the ¹A₁ state. These four active orbitals in pyrene-1C are the frontier orbitals (HOMO-1 to LUMO + 1), but for the extended systems their localisation features do not follow the same order. However, it is important to note that the lowest lying states for all systems have these orbitals occupied, as discussed below. In particular, the virtual orbitals a₁ and b₂ possess a σ character which describe the dangling bonds and remain localised throughout the expanded embedding. The π(a₂) orbital, which is already located at the perimeter of the ring for pyrene-1C, becomes delocalised at the edges of the PAH sheet. The π(b₁) orbital has significant contribution from the dangling bond atoms for pyrene-1C, but it obtains a more delocalised character in the circumpyrene and has a completely different character for periacene. Thus, these a₂ and b₁ π orbitals are delocalised in the extended system whereas the other two orbitals (a₁ and b₂) describe the local defect in the σ system. The a₁ orbital is bonding in the C₇-C₈ distance and contains a dangling bond on C₁₆ whereas the b₂ orbital is antibonding in C₇-C_8. According to these orbital analyses, the orbital excitations b₁→ b₂ and b₁→ a₁ (both of type π → σ_loc) for the A₂ and B₁ states, respectively, (as seen from the closed shell configuration) represent charge transfer (CT) states arising from delocalised π orbitals to the σ orbital of the local defect structure.

Figure 2. The four-orbital system HOMO, HOMO-1, LUMO and LUMO + 1 for the unrelaxed pyrene-1C, circumpyrene-1C and 7a,7z-periacene-1C structures calculated for the ¹A₁ state using the B3LYP/6-311G (2d,1p) approach.

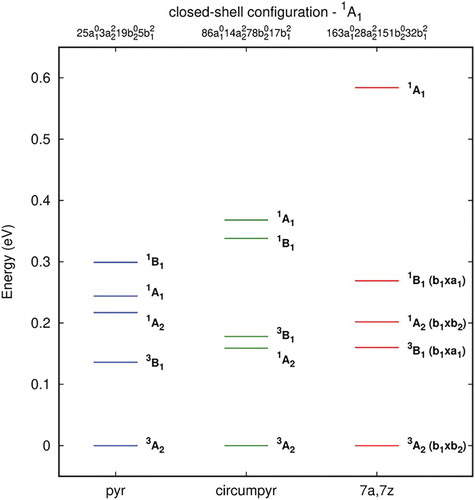
In Figure 3 (Table S6) the relative energies calculated with B3LYP are presented for the first five lowest states of the one-carbon vacancy defect. These states are the first lowest states for all system, but not at the same ordering. The DFT calculations predict a triplet ground state ³A₂ for all single vacancy structures. The triplet and singlet A₂ and B₁ states comprise the first four lowest states, except for pyrene-1C, and they are separated by no more than 0.35 eV from the ground state. The closed shell A₁ state increases in energy when expanding the graphene flakes; it falls in the range of 0.2–0.6 eV above the ground state in all systems.

Figure 3. Single point excitation energies (ΔE, in eV) for the first five states for unrelaxed pyrene-1C, circumpyrene-1C and 7a,7z-periacene-1C structures calculated with the B3LYP/6-311G(2d,1p) method. The single electron occupations are similar for the correspondent states with the same symmetry.

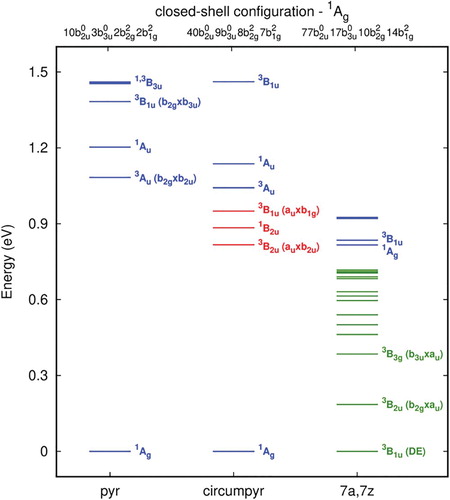
The orbitals computed for the relaxed structure resemble the ones of the unrelaxed one (Figure 2) closely and are displayed in Figure S1. Energy scheme, electronic configuration and optimised bridging bond (C₇-C₈) distances are displayed in Figure 4 and Figure 5 (Table S7) for the planar relaxed structures of pyrene-1C, circumpyrene-1C and 7a,7z-periacene-1C with an energy below 1.00 eV. In Figure 5 the results for some selected states are presented only. Similarly, to pyrene-1C, there is a reduction of the C₇-C₈ distance from originally 2.47 and 2.46 Å in the unrelaxed structure of circumpyrene-1C and 7a,7z-periacene-1C to up to 1.64 and 1.74 Å, respectively, due to the occupation of the σ bond orbital. These results suggest a larger rigidity of the extended carbon networks (Figure 5 and Table S7). In contrast, the closed shell (¹A₁) and the states (^1,3A₂ and ^1,3B₂) which have the antibonding orbital (b₂) singly occupied, show the C₇-C₈ distance larger than the original unrelaxed structure. These states exhibit a repulsive character, as discussed in the case of pyrene-1C, whereas for the ^1,3A₂ states there is a tendency to stabilise the energies at larger C₇-C₈ distances (≥ 2.70 Å) as compared to the unrelaxed structures. Naturally, as the sheet size grows towards 7a,7z-periacine-1C, the density of π orbitals increases, thus resulting in a higher accessibility of π states, as shown in Figure 4 and Table S7. Some of them can be seen as a double excitation (DE) from the closed shell state. In particular, the ³A₂ state with four open shell occupation, corresponding to a π → π* from the ³B₁ ground state, is the second excited state. Also, one can see a small decrease in the singlet–triplet splitting going from 0.1 eV (pyrene-1C) to about 0.06 eV in the extended systems, following the same trend as in the pristine structures [64–66].

Figure 4. Excitation energies (ΔE, in eV) for pyrene-1C, circumpyrene-1C and 7a,7z-periacene-1C calculated with the B3LYP/6-311G(2d,1p) method. The colours represent the state having the same occupation for equivalent orbitals. DE means double excitation.

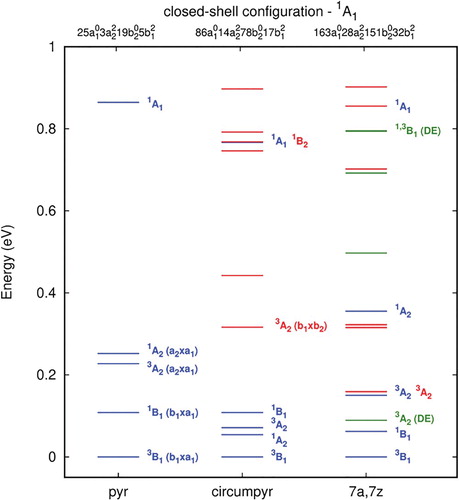
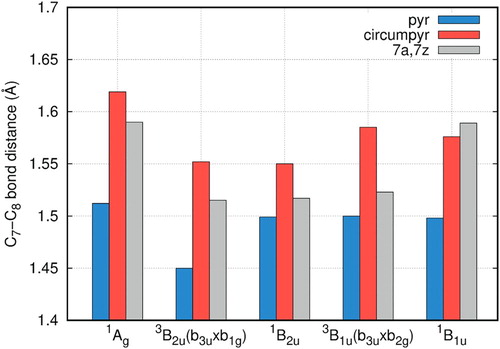
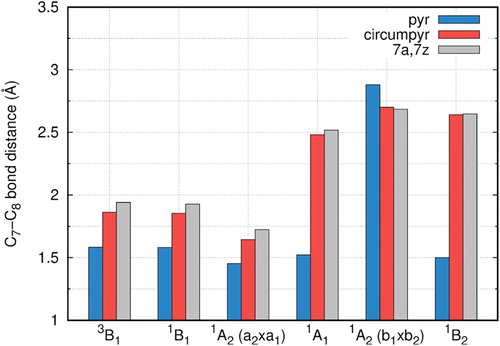
Figure 5. Optimised C₇-C₈ distances (Å) calculated with the B3LYP/6-311G(2d,1p) method for pyrene-1C, circumpyrene-1C and 7a,7z-periacene-1C.

For the relaxed structures, the results obtained with HSE06 and CAM-B3LYP (Table S8) present to some extent a different picture as compared to the B3LYP results. For circumpyrene-1C, the ³B₁ ground state and the ³A₂ state, which represent charge transfer (CT) states arising from delocalised π orbitals to the σ orbital of the local defect structure, were almost degenerate at B3LYP level, differing by 0.07 eV. However, HSE06 and CAM-B3LYP predict ³A₂ as the ground state whereas the ³B₁ state lies above by 0.137 and 0.010 eV. The closed shell ¹A₁ state, which was 0.767 eV above the ground state at B3LYP is around 1.5 eV above with HSE06 and CAM-B3LYP. For the 7a,7z-periacene-1C, B3LYP and the range-separated functionals agree in predicting a triplet multiplicity for the ground state, although they differ with respect to the state symmetries and excitation energies. While ³B₁ is found to be the ground state at the B3LYP level followed by the four-fold open shell state ³A₂ state 0.09 eV higher. This symmetry order is reversed using HSE06 and CAM-B3LYP with the ³B₁ state lying above by 0.411 and 0.366 eV, respectively. The closed shell ¹A₁ state, which was 0.855 eV above the ground state with B3LYP, is much higher now above the ground state at HSE06 and CAM-B3LYP levels (2.131 and 3.680 eV, respectively).

It is important to note that, in the case of single vacancy defects, all systems are characterised by a triplet ground state, even for the relaxed geometries. This result is consistent with the experimentally and theoretically observed magnetism in defected graphene induced by the formation of single vacancies [25,67,68]. It is gratifying that the present DFT calculations can reproduce correctly the general feature of orbital exchange in the course of the structural relaxation process.

3.2.2. Double vacancy

The evolution of the frontier orbitals with system size is illustrated in Figure 6 for the unrelaxed defect in the closed shell ¹A_g state. From this scheme one can distinguish three types of orbitals: the σ and π orbitals localised in the defect and the delocalised π orbitals with higher zig-zag edge contribution on the extended system. These latter correspond to the HOMO-1 and HOMO orbitals. The localised σ orbital (b_2u) corresponds to the LUMO for pyrene-2C and circumpyrene-2C and to the LUMO + 3 in the 7a,7z-periacene-2C, thus anticipating a possible change in the excited states ordering. Similarly, the localised π orbital (b_3u) with C₇-C₈ bonding character undergoes also an upward shift in energy, changing from LUMO + 1 in the pyrene-2C to the LUMO + 2 in the extended systems.

Figure 6. The frontier molecular orbitals for the unrelaxed pyrene-2C, circumpyrene-2C and 7a,7z-periacene-2C calculated for the ¹A_g state with B3LYP/6-311G(2d,1p).

The energy scheme for the unrelaxed structures is shown in Figure 7 (Table S7). For pyrene-2C the lowest six states are listed, and for the extended structures all the states below 1.00 eV. The lowest state is given by the closed shell configuration for the pyerene-2C and circumpyrene-2C, however for 7z,7z-periacene-2C the closed shell is 0.8 eV above the triplet ground state (³B_1u). This state corresponds to a double excitation from HOMO-1 (b_3u) and HOMO (b_2g) to LUMO (a_u) of the closed shell (¹A_g) taken as reference (Table S9). Again, as observed for the single-vacancy case, this is consistent with the tendency to form polyradical structures by increasing the carbon sheet along the zig-zag direction. Interestingly, the states described by a single occupation of the localised σ orbital (³A_u and ¹A_u), which correspond to the second and third states in pyrene-2C, appear as a fingerprint of the double vacancy defect since the energy of these states is almost independent of the sheet size. They lie around one eV above the ground state for all three structures. However, for the extended systems, the formation of a dense set of π orbitals give rise to several lower excited states other than the ³A_u and ¹A_u states.

Figure 7. Excitation energies (ΔE, in eV) for the unrelaxed pyrene-2C, circumpyrene-2C and 7a,7z-periacene-2C structures calculated with the B3LYP/6-311G(2d,1p). The colours represent the state having the same occupation for equivalent orbitals. DE means double excitation.

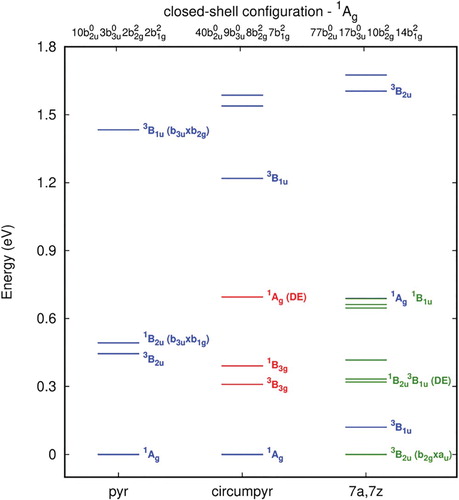
In Figure 8, the frontier orbitals are shown for the relaxed double-vacancy structures of the closed shell ¹A_g state. In this scheme, the main feature of the highest π occupied orbitals in terms of symmetry and delocalisation are preserved as in the unrelaxed double-vacancy defect structures. As expected, the bonding character of these orbitals contributes to the formation of the bridging CC bonds leading to a pentagon-octagon-pentagon structure. Moreover, the geometry relaxation stabilises the unoccupied π orbitals, while the σ* orbitals localised in the defect are shifted upwards to higher energies (LUMO + 3 for 7a,7z-periacene-2C and higher for the small systems). Therefore, the lowest LUMO orbital for the relaxed structures are the π orbitals with the C₇-C₈ bonding and antibonding character for the smaller systems, but in the case of 7a,7z-periacene-2C they are orbitals localised at the zig-zag edge. The energy scheme for the relaxed double vacancy defect presented in Figure 9 (Table S10) shows a significant rearrangement of the electronic states with increasing size of the sheet, as already observed for the unrelaxed case. For pyrene-2C, the four lowest lying states are presented which are the same discussed previously [45]. For circumpyrene-2C and 7a,7z-periacene-2C, besides these four states, the low-lying states below 1 eV and below the ¹A_g state, respectively, are shown. As observed for the unrelaxed structures, the closed shell ¹A_g state is significantly destabilised when going from the circumpyrene-2C to the 7a,7z-periacene-2C. In this latter system, the two most stable states are the near-degenerate triplet ³B_2u and ³B_1u states. Both are formed by single occupation of the HOMO orbital (b_2g) with the other electron promoted to the delocalised zig-zag edge orbital (b_2g) for the ground state (³B_2u); for the ³B_1u state it is in the localised defect orbital (CC bonding orbital, b_3u). The corresponding singlet states are 0.32 and 0.69 eV above the ground state, respectively. One should also note that between these singlet states there are several other states due to the accessibility of others π orbitals close in energy. This ³B_1u state which is the first excited state in 7a,7z-periacene-2C, is lying more than one eV above the ground state for the smaller structures. In the case of the circumpyrene-2C, the singlet and triplet states (^1,3B_3g) having also one electron occupied in the local bonding orbital (b_3u) and the other in the HOMO π delocalised orbital (a_u), are the second and the third excited state. From the stabilisation of the open shell states one would expect a significant enhancement of the chemical reactivity of the DV defect for larger graphene sheets. Using HSE06 and CAM-B3LYP for the relaxed structures, the results present the same picture as observed by B3LYP (Table $S11). The main difference is obtained using CAM-B3LYP for the closed shell ¹A₁ state of the 7a,7z-periacene-2C structure, which is much higher, 2.287 eV above the ground state.

Figure 8. The frontier orbitals for the relaxed pyrene-2C, circumpyrene-2C and 7a,7z-periacene-2C calculated for the ¹A_g state with B3LYP/6-311G(2d,1p).

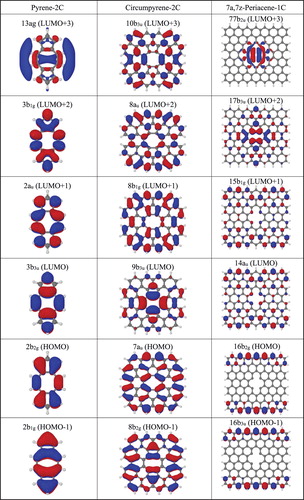
Figure 9. Excitation energies (ΔE, in eV) for pyrene-2C, circumpyrene-2C and 7a,7z-periacene-2C) calculated with the B3LYP/6-311G(2d,1p) method. The colours represent the state having the same occupation for equivalent orbitals. DE means double excitation.

Large reductions of the C₇-C₈ distance from originally 2.47 Å to ∼1.5 Å as compared to the unrelaxed structure are observed for pyrene-2C (Figure 10, Table S7). Increases in the bond distance between the smallest and the largest defect structures amount to about 0.05 Å (0.09 Å for the ¹B_1u state). These values are significantly smaller than the increases found for the single vacancy defect indicating a larger rigidity of the double vacancy structure.

Figure 10. Optimised C₇-C₈ distances (Å) calculated with the B3LYP/6-311G(2d,1p) method for pyrene-2C, circumpyrene-2C and 7a,7z-periacene-2C.

4. Conclusions

A detailed picture of the manifold of electronic states has been obtained for single- and double-vacancy structures constructed for from PAH sheets with increasing size. For the pyrene defect models, it was shown that density functional calculations performed at different computational levels could reproduce well the set of closely-spaced singlet and triplet states predicted by the CCSD(T) and previous MRCI + Q calculations, which provided the reason for using the computationally more efficient DFT method also to describe manifolds of excited states also for significantly larger graphene models.

In the case of single vacancy defects, all systems are characterised by a triplet ground state, ³A₂ for unrelaxed and ³B₁ for the relaxed geometries. This result is consistent with the magnetic response due to the formation of single vacancy defects in graphene. In the relaxed structures, these two triplet (³B₁ and ³A₂) states and the correspondent singlet states have one singly electron occupation always in the a₁ dangling bond orbital. The other electron is either occupying also a local defect orbital or else in a delocalised π orbital, respectively. A strong reduction of the bridging bond C₇-C₈ distance from originally 2.46–2.47 Å in the unrelaxed structures to up to 1.45, 1.64 and 1.74 Å for pynene-1C, circumpyrene-1C and 7a,7z-periacene-1C, respectively, is observed.

For the unrelaxed and relaxed double vacancy defects, a significant rearrangement of the electronic states with increasing size of the sheet is observed. The closed shell ¹A_g state is significantly destabilised when going from the circumpyrene defect to the one in 7a,7z-periacene. In this latter case, the lowest states are triplets (³B_2u and ³B_1u) and a singlet state is also close by, suggesting a high chemical reactivity due to the open-shell character of these states. The two former states are lying more than one eV above the ground state for the smaller structures. On the other hand, the first excited state in pyrene-2C, which is based on single occupation of a π* orbital at the defect, corresponds to a higher order excited state in the extended systems due to the appearance of more π* delocalised orbitals accessible. For all presented states, the optimised structures have the bridging bond C₇-C₈ (C₉-C₁₀) distances between 1.45 and 1.67 Å, which corresponds to a strong reduction compared to the unrelaxed structure (2.46–2.47 Å). These values are smaller than the ones found for the single vacancy defect indicating a larger rigidity of the double vacancy structure.

The results using HSE06 and CAM-B3LYP functionals present a partially different picture compared to the B3LYP results, mostly for the largest system of the 1C-vacancy case due to its open-shell character. Since the long-range correction should play a major role in the extended system, the CAM-B3LYP results are expected to give a more reliable description especially of the charge transfer states within a DFT based approach.

Acknowledgments

The financial assistance of the Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) under Projects Nos. 307052/2016-8, 404337/2016-3, Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) under Project Nos. 2012/11857-7, 2017/07707-3, Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) under Project CAPES/ITA Project No. 88882.161993/2017-01 are gratefully acknowledged. Authors are thankful to Vienna Scientific Cluster (VSC) under project 70376 and to the computer cluster Arran of the School of Pharmaceutical Science and Technology (Tianjin University) for providing the high-performance computational infrastructure and to FAPESP/Tianjin University SPRINT program (project no. 2017/50157-4) for travel support.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico: [Grant Number 307052/2016-8,404337/2016-3]; Coordenação de Aperfeiçoamento de Pessoal de Nível Superior: [Grant Number 88882.161993/2017-01]; Fundação de Amparo à Pesquisa do Estado de São Paulo: [Grant Number 2012/11857-7,2017/07707-3,2017/50157-4].