Representation of the virtual space in extended systems – a correlation energy convergence study

Abstract

We present an investigation of the convergence behaviour of the local second-order Møller-Plesset perturbation theory (MP2) correlation energy toward the canonical result for three insulating crystals with either projected atomic orbitals (PAOs) or various orthonormal representations of the virtual orbital space. Echoing recent results for finite molecular systems, we find that significantly fewer PAOs than localised orthonormal virtual orbitals are required to reproduce the canonical correlation energy. We find no clear-cut correlation between conventional measures of orbital locality and the ability of the representation to span the excitation space of local domains. We show that the PAOs of the reference unit cell span parts of the excitation space that can only be reached with distant local orthonormal virtual orbitals.

GRAPHICAL ABSTRACT

Keywords:

• Local correlation
• periodic systems
• pao
• localisation

1. Introduction

Orbital localisation is a powerful tool in molecular and solid-state quantum chemistry, providing both intuitively appealing interpretations and visualisations of electronic structure [1–3], and opportunities for efficient implementations of correlated theories. Spatially localised orbitals can be obtained either by a suitably chosen unitary transformation of the inherently delocalised canonical Hartree-Fock (HF) or Kohn-Sham orbitals [4] or directly through a restrained noncanonical self-consistent optimisation [5]. From an algorithmic perspective, localised orbitals pave the way for the implementation of orbital-based embedding/fragment schemes [6, 7] and for exploiting the short-range character of electron correlation effects to greatly reduce the computational complexity of post-HF methods [8–10]. In this work, we will be concerned with the latter aspect.

The concept of ‘localized orbitals’ is not uniquely defined, however, and different localisation functionals have been proposed. Among the oldest and most widely used proposals are the Foster-Boys [11, 12], Pipek-Mezey [13], and Edmiston-Ruedenberg [14, 15] functionals, which produce localised orbitals that minimise the orbital spread, maximise the orbital partial Mulliken charges over as few atoms as possible, and maximise the Coulomb self-repulsion of the orbitals, respectively. Neither of these locality measures is directly related to the electron-correlation problem, i.e. they are not defined through a quantity that directly enters an expression for the correlation energy. Consequently, it is far from obvious which localisation functional leads to the most efficient general-purpose local-correlation algorithm.

Local electron-correlation methods rely on at least two features:

1. The occupied and virtual orbitals should be confined within a small volume in space [16], such that the differential overlap between them decay as rapidly as possible with distance.

2. At the same time, the virtual orbitals should be constructed in such a way that a very small number of them is sufficient to accurately represent the excitation space of each pair of occupied orbitals.

The latter has been tackled mainly through the introduction of orbital-specific [17] or pair-specific [18] virtual orbitals. These sets are constructed from an initial set of localised virtual orbitals by means of first-order estimates of the correlation amplitudes – that is, they are constructed directly from features of the electron correlation effects of the system at hand.

Much effort has been devoted to point (1), albeit using measures not directly related to electron correlation effects. It is an open question whether nonorthonormal local orbitals are preferable to orthonormal ones [19–21]. Relaxing the orthogonality constraint leads to simpler nodal structures, which, in particular, may lead to smoother and more rapid decay of the tails of the functions. At the same time, however, the resulting set will be linearly dependent, which one might fear can lead to a larger number of orbitals required to span a given subspace. The most widely-used approach in local correlation theories is to choose an orthonormal set for the occupied space, obtained through localisation of the occupied HF orbitals, while nonorthogonal, linearly dependent projected atomic orbitals (PAOs) are used to represent the virtual manifold. The PAOs are easily computed from the converged HF density matrix and, historically, the choice of PAOs as virtual orbital basis has more to do with the lack of robust algorithms for the localisation of orthonormal virtual orbitals than superior performance in local correlation treatments. With the robust localisation algorithms developed in recent years by Høyvik, Jørgensen, and coworkers [4, 22–24], orthonormal virtual-orbital localisation can be performed reliably and efficiently, warranting a comparison of the performance of PAOs versus localised orthonormal virtual orbitals (LVOs) in local correlation treatments.

Recently, Werner and coworkers [25–27] reported that PAOs outperform LVOs in molecular calculations. While the LVOs are more local than PAOs in terms of orbital spread, significantly fewer PAOs than LVOs are required in the excitation domains to recover the same fraction of the exact correlation energy. The authors did not present a definitive reason for this somewhat counterintuitive result, however.

The central role of locality in electron correlation treatments is even more pertinent in 3D periodic systems, where the canonical orbitals are forced by translation symmetry to be delocalised over the entire infinite solid. The dense packing of 3D periodic systems enhances the effectiveness of locality-based screening procedures, leading to even more pronounced computational savings than for finite molecular systems.

In this work, we compare the performance of PAOs and different sets of LVOs for local second-order Møller-Plesset (MP2) theory of representative insulators: the covalent diamond crystal, the ionic lithium hydride crystal, and the molecular prussic acid crystal.

2. Theoretical background

The electronic correlation energy of a weakly correlated system can be written in the coupled-cluster (CC) formalism as [28] (1) $E_{\mathrm{c}}=\sum _{\mathrm{ij}}\sum _{\mathrm{ab}}(t_{\mathrm{ij}}^{\mathrm{ab}}-t_i^a{t}_j^b)(2(\mathrm{ia}\mid \mathrm{jb})-(\mathrm{ib}\mid \mathrm{ja})),$(1) where we have assumed a closed-shell system for simplicity. We use latin letters i, j, k to denote occupied spatial orbitals and a, b, c to denote virtual spatial orbitals obtained from a preceeding HF calculation. With real orbitals, the electron repulsion integrals (ERIs) are defined as (2) $(\mathrm{ia}\mid \mathrm{jb})=\iint \frac{{\phi }_i(\mathit{r}){\phi }_a(\mathit{r}){\phi }_j({\mathit{r}}^{\mathrm{\prime }}){\phi }_b({\mathit{r}}^{\mathrm{\prime }})}{|\mathit{r}-{\mathit{r}}^{\mathrm{\prime }}|}\mathrm{d}{\mathit{r}}^{\mathrm{\prime }}\mathrm{d}\mathit{r}.$(2) The single- and double-excitation amplitudes, $t_i^a$ and $t_{\mathrm{ij}}^{\mathrm{ab}}$, respectively, are determined from a nonlinear equation system that, for an n-electron system, may involve up to n-tuple excitations, depending on the chosen CC model. The simplest model is second-order Møller-Plesset (MP2) theory [28] where the single-excitation amplitudes vanish due to the Brillouin condition. The double-excitation amplitudes are obtained from the set of equations [23] (3) $\begin{array}{rl}{r}_{\mathrm{ij}}^{\mathrm{ab}}& =\sum _c(f_{\mathrm{ac}}{t}_{\mathrm{ij}}^{\mathrm{cb}}+t_{\mathrm{ij}}^{\mathrm{ac}}{f}_{\mathrm{cb}})-\sum _k(f_{\mathrm{ik}}{t}_{\mathrm{kj}}^{\mathrm{ab}}+t_{\mathrm{ik}}^{\mathrm{ab}}{f}_{\mathrm{kj}})\\ & +(\mathrm{ia}\mid \mathrm{jb})=0,\end{array}$(3) where f is the Fock matrix and all orbitals are assumed to be orthonormal. Solving the MP2 equations scales as $O(N^5)$ with N a measure of system size such as the number of atom-centred basis functions used to expand the occupied and virtual orbitals. The MP2 energy, Equation (1(1) $E_{\mathrm{c}}=\sum _{\mathrm{ij}}\sum _{\mathrm{ab}}(t_{\mathrm{ij}}^{\mathrm{ab}}-t_i^a{t}_j^b)(2(\mathrm{ia}\mid \mathrm{jb})-(\mathrm{ib}\mid \mathrm{ja})),$(1) ), and amplitude equations, Equation (3(3) $\begin{array}{rl}{r}_{\mathrm{ij}}^{\mathrm{ab}}& =\sum _c(f_{\mathrm{ac}}{t}_{\mathrm{ij}}^{\mathrm{cb}}+t_{\mathrm{ij}}^{\mathrm{ac}}{f}_{\mathrm{cb}})-\sum _k(f_{\mathrm{ik}}{t}_{\mathrm{kj}}^{\mathrm{ab}}+t_{\mathrm{ik}}^{\mathrm{ab}}{f}_{\mathrm{kj}})\\ & +(\mathrm{ia}\mid \mathrm{jb})=0,\end{array}$(3) ), are invariant to rotations among occupied and among virtual orbitals separately. For insulators, this can be exploited to bring forth significant sparsity in the Fock matrix and ERIs which, in turn, imply sparsity in the amplitudes. This observation dates back to Pulay [8] and forms the basis for linear-scaling implementations that today approach a near-black-box level of sophistication [23, 27, 29–33].

Linear scaling can be achieved as the following simple argument shows. Given suitably localised occupied and virtual orbitals, the integral $(\mathrm{ia}\mid \mathrm{jb})$ will be negligible unless a is centred in the vicinity of i in the sense that the product ${\phi }_i(\mathit{r}){\phi }_a(\mathit{r})$ must be non-vanishing in some region of space for the integral to be nonzero. A similar argument applies to j and b, of course. This alone leads to quadratic scaling of the number of significant ERIs. Furthermore, multipole expansion of $(\mathrm{ia}\mid \mathrm{jb})$ reveals an asymptotic decay rate proportional to $R^{-3}$, where R is a measure of the distance between i and j, leading to linear scaling of the number of significant integrals [34, 35]. The amplitudes and the residuals in Equation (3(3) $\begin{array}{rl}{r}_{\mathrm{ij}}^{\mathrm{ab}}& =\sum _c(f_{\mathrm{ac}}{t}_{\mathrm{ij}}^{\mathrm{cb}}+t_{\mathrm{ij}}^{\mathrm{ac}}{f}_{\mathrm{cb}})-\sum _k(f_{\mathrm{ik}}{t}_{\mathrm{kj}}^{\mathrm{ab}}+t_{\mathrm{ik}}^{\mathrm{ab}}{f}_{\mathrm{kj}})\\ & +(\mathrm{ia}\mid \mathrm{jb})=0,\end{array}$(3) ) inherit the decay property of the integrals, paving the way for a linear-scaling algorithm. By the same token, it follows that the correlation-energy contribution from pairs of occupied orbitals decays asymptotically as $R^{-6}$, consistent with the decay of London dispersion forces. This argument can be extended to cover also higher-order CC models.

The arguments underpinning linear-scaling correlation treatments thus rely heavily on the concept of orbital locality. As mentioned in the Introduction, this concept is not uniquely defined and a number of localisation functionals have been proposed. In this work, we will consider the central-moment functionals of Høyvik and Jørgensenalong with their statistics-based measures of orbital locality [4]. The mth power of the second central moment (PSM-m) functionals are defined in terms of the second moment orbital spread of each orbital p, (4) ${\sigma }_2(p)=⟨p|{(\mathbf{r}-⟨p|\mathbf{r}|p⟩)}^2|p{⟩}^{1/2},$(4) as (5) ${\xi }^{\mathrm{PSM}-\mathrm{m}}=\sum _p{\sigma }_2(p{)}^{2m},$(5) where the summation over orbitals should be restricted to either occupied or virtual orbitals to maintain the Brillouin condition. The PSM-1 functional is identical to the Foster-Boys functional [36, 37]. Minimising the PSM-1 functional with respect to unitary rotations of the (orthonormal) orbitals leads to the set of orbitals with the smallest possible sum of orbital spreads. In the context of periodic systems, such orbitals are commonly referred to as maximally localised Wannier functions [38].

Similarly, the PSM-2 orbitals are computed by minimising the objective function in Equation (5(5) ${\xi }^{\mathrm{PSM}-\mathrm{m}}=\sum _p{\sigma }_2(p{)}^{2m},$(5) ) with m = 2. The PSM-2 objective function reduces the spread of the least local orbitals at the expense of the most local ones. The motivation behind the PSM-2 functional is the conjecture that the least local orbitals in the PSM-1 set lead to excessive computational effort in a local correlation treatment [22]. Increasing the value of m does not bring any further advantages with respect to the least local orbital(s).

The PSM-m objective functions do not address the problem of long-range tails of the orbitals. The tail of orbital p can be measured by the fourth moment orbital spread ${\sigma }_4$: (6) ${\sigma }_4(p)=⟨p|{(\mathbf{r}-⟨p|\mathbf{r}|p⟩)}^4|p{⟩}^{1/4},$(6) and letting this quantity take the role of ${\sigma }_2(p)$ leads to the mth power of the fourth central moment (PFM-m) class of localisation functionals [4, 16] (7) ${\xi }^{\mathrm{PFM}-\mathrm{m}}=\sum _p{\sigma }_4(p{)}^{4m}.$(7) Minimising the PFM-1 objective function leads to ‘minimally tailed’ orthonormal orbitals and, in analogy with the PSM-2 case above, heavy-tailed outliers may be removed by putting m = 2. Following Høyvik and Jørgensen [4], we use the tail spread $\beta (p)$, defined as the fourth root of the kurtosis, (8) $\beta (p)=\frac{{\sigma }_4(p)}{{\sigma }_2(p)},$(8) to measure tail thickness. The more heavy-tailed an orbital is, the greater the value of its tail spread.

In this work, we will focus on orthonormal orbitals obtained by minimising the PSM-1, PSM-2, and PFM-2 objective functions.

The by far most commonly used virtual basis is composed of PAOs [8], which are straightforwardly constructed by projecting out the occupied orbitals from the atomic orbital (AO) basis, so that a normalised PAO $|\tilde{\mu }⟩$ is given by (9) $|\tilde{\mu }⟩=N_{\mu }(1-\sum _i|i⟩⟨i|)|\mu ⟩,$(9) where $|\mu ⟩$ are the AOs and $N_{\mu }=⟨\mu |(1-\sum _i|i⟩⟨i|){|\mu ⟩}^{-1/2}$. In this way, a redundant set of orbitals is obtained, having in principle the same size as the AO basis. The PAOs inherit a certain degree of locality from the HF density matrix used for the projection and are free from the delocalisation (tail) effects resulting from the orthogonality constraint [24].

We are in this work mainly interested in the impact of the choice of virtual orbitals on the efficiency and accuracy of periodic local MP2 calculations. Although the choice of virtual orbitals can not be entirely decoupled from the choice of localised occupied orbitals, we will use the PSM-1 localised occupied orbitals in conjunction with different sets of either LVOs or PAOs. As proposed by Pinski et al. [30], we may then characterise the so-called multiplicative sparsity between the occupied and virtual sets of orbitals through differential overlap integrals (DOIs). The DOI for an occupied orbital ${\phi }_i$ and a virtual orbital ${\phi }_a$ is defined as (10) ${\mathrm{\Omega }}_{\mathrm{ia}}=\sqrt{\int {\phi }_i(\mathit{r}{)}^2{\phi }_a(\mathit{r}{)}^2\mathrm{d}\mathit{r}}.$(10) The DOIs measure the extent to which the occupied and virtual orbitals have a non-vanishing intersection in ${\mathbb{R}}^3$ and thus can be used to map the sparsity of the ERIs, Equation (2(2) $(\mathrm{ia}\mid \mathrm{jb})=\iint \frac{{\phi }_i(\mathit{r}){\phi }_a(\mathit{r}){\phi }_j({\mathit{r}}^{\mathrm{\prime }}){\phi }_b({\mathit{r}}^{\mathrm{\prime }})}{|\mathit{r}-{\mathit{r}}^{\mathrm{\prime }}|}\mathrm{d}{\mathit{r}}^{\mathrm{\prime }}\mathrm{d}\mathit{r}.$(2) ), with the chosen virtual orbital basis.

While the focus of the localising objective functions and construction procedures is on the spatial distribution of the orbitals, they are each implicitly assumed to bring forth a condition where the significant part of the correlation can be attributed to a subset of the full amplitude space, determined from locality considerations. Although most modern implementations of local correlation theories reduce the impact of the initial choice of virtual basis through further refinements like orbital-specific virtuals [39] or pair-natural orbitals [30, 32, 33], it is of fundamental importance to compare the behaviour of PAOs and orthonormal virtual orbitals in the context of computing the ground-state correlation energy. It is, however, not trivial to devise a fair comparison between different types of orbitals (orthonormal or non-orthonormal, atom-centred or not), where the correlation energy is closely related to the number of virtual orbitals used in the calculation. In this work, we have chosen to treat the excitation space in the following manner:

1. For each occupied orbital a list of atomic centres in its vicinity is compiled, and PAOs centred on such atoms constitute the initial excitation domain. This list is built by taking the n atoms closest to the occupied-orbital centroid, and then rounding up such that all atoms within the same distance are included (within a numerical threshold).

2. Through the orbital-specific virtuals (OSV) methodology [39], a set of virtuals is built as a linear combination of the initial set by diagonalising the MP2 pair density matrices ${\mathbf{D}}^{\mathrm{ii}}$ corresponding to diagonal pairs ii in the reference unit cell: (11) $D_{\mathrm{ab}}^{\mathrm{ii}}=\sum _c{t}_{\mathrm{ii}}^{\mathrm{ac}}{t}_{\mathrm{ii}}^{\mathrm{cb}}$(11)

3. The resulting set of orbitals is trimmed to keep the error in the total correlation energy within a threshold.

4. The number of OSVs retained for each domain is then a function of (i) the size of the original PAO domain, and (ii) the number of orbitals significantly contributing to the correlation energy.

5. Finally, the virtual space of a local pair domain (which, for diagonal pairs, coincides with the orbital domain) is transformed into a local orthonormal (LON) space for the pair-domain amplitudes, in which redundant orbitals are discarded according to a threshold of ${10}^{-4}$ on the overlap eigenvalue.

While thresholds on the LON redundancy check in point (5) above are generally tighter in molecular applications, the closer packing of bulk solids makes the algorithm more sensitive to linear dependencies and, by experience, the chosen value is reasonable. Sets of LON orbitals are constructed in the same manner starting from each initial set of LVOs (PSM-1, PSM-2, or PFM-2 LVOs). In this procedure, each LVO is associated with the atom nearest to its orbital centroid. The convergence of the local MP2 correlation energy toward the exact (canonical) result as a function of the average number of LON orbitals retained in the diagonal domains provides a measure of the ability of the initial virtual-orbital (PAO or LVO) set to capture the main correlation effects.

3. Computational details

We shall consider MP2 energy calculations for three simple bulk insulators: diamond, LiH, and HCN. These are chosen as representatives of the different chemical situations that can be found in a nonmetallic (and non-magnetic) solid: a purely covalently bonded, a purely ionic, and a molecular crystal. The systems are also chosen to keep the complexity low enough to facilitate analysis of the orbitals and their effect on correlation energies.

The localised occupied orbitals are obtained from the Wannierization algorithm [40] implemented in the Crystal program [41]. This procedure includes a Foster-Boys localisation [11, 12] that minimises the PSM-1 objective function given in Equation (5(5) ${\xi }^{\mathrm{PSM}-\mathrm{m}}=\sum _p{\sigma }_2(p{)}^{2m},$(5) ). The PAOs are constructed as in Equation (9(9) $|\tilde{\mu }⟩=N_{\mu }(1-\sum _i|i⟩⟨i|)|\mu ⟩,$(9) ) and those with norm below ${10}^{-3}$ are discarded.

As opposed to many other codes developed for ab initio studies of solid-state materials, Crystal adopts atom-centred Gaussian basis sets, making it comparable with molecular programs – and, in fact, fully equivalent when zero–dimensional periodicity is invoked. A 6-31G** basis was used for HCN [42, 43], 6-21G* for diamond [44], while a simpler basis set was adopted for LiH (3-11G** on H [45], 6-1G** on Li [46]). Detailed structures (nuclear coordinates, unit cell parameters) and technical details regarding the initial HF calculations are provided in the Appendix. In all cases the experimental lattice parameters have ben adopted. The lattice constants of the cubic diamond and LiH crystal structures are 3.56679 Å [47] and 4.0834 Å [48], respectively, while those of the tetragonal HCN crystal structure are a = 4.13 Å, b = 4.85 Å, and c = 4.34 Å [49]. Note that we use primitive unit cells in all calculations.

The LVO orbitals are generated by the same Wannierization algorithm in Crystal, yielding the PSM-1 LVOs (see the Appendix for more technical details). The PSM-2 and PFM-2 LVOs are obtained by further optimisation of the PSM-1 LVOs in a stochastic procedure where only unitary transformations amongst the virtual orbitals in the reference unit cell are permitted. The LVOs associated with all other unit cells of the crystal are then obtained by simple translations.

For each representation of the virtual space, we quantify locality by computing second- and fourth moment orbital spreads, Equations (4(4) ${\sigma }_2(p)=⟨p|{(\mathbf{r}-⟨p|\mathbf{r}|p⟩)}^2|p{⟩}^{1/2},$(4) ) and (6(6) ${\sigma }_4(p)=⟨p|{(\mathbf{r}-⟨p|\mathbf{r}|p⟩)}^4|p{⟩}^{1/4},$(6) ), as well as the tail spread, Equation (8(8) $\beta (p)=\frac{{\sigma }_4(p)}{{\sigma }_2(p)},$(8) ). Further analysis of sparsity in the orbital sets is performed by estimating the DOIs, Equation (10(10) ${\mathrm{\Omega }}_{\mathrm{ia}}=\sqrt{\int {\phi }_i(\mathit{r}{)}^2{\phi }_a(\mathit{r}{)}^2\mathrm{d}\mathit{r}}.$(10) ), using the Monte Carlo integration scheme outlined in appendix II.

Periodic local MP2 calculations are performed with the Cryscor suite [50–54]. Within the present Cryscor implementation [54], the initial excitation domains are constructed by means of the OSV method as outlined in the previous section with the default number of neighbouring atoms n = 30. This number is incrementally increased for each of the systems under consideration, recording the local MP2 correlation energy as a function of the average number of LON orbitals in the domains of diagonal pairs. As in Refs. [17, 54], symmetric OSV pair domains are used in the evaluation of the MP2 correlation energy.

4. Results and discussion

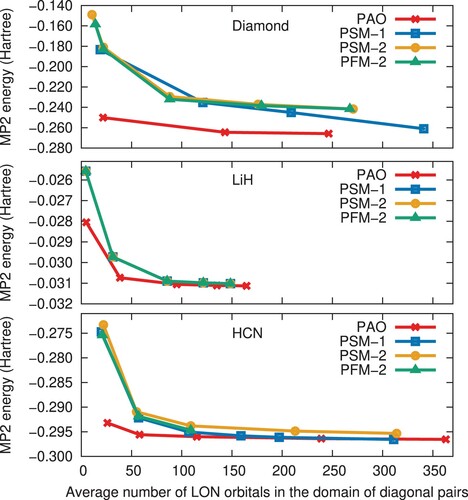
Figure 1 shows the convergence behaviour of the local MP2 correlation energy with respect to the average size of the LON space for each set of initial virtual orbitals. The convergence is strikingly better with PAOs than with LVOs for all three systems. Across a range of chemically distinct systems – covalent diamond, ionic LiH and molecular HCN – we thus observe that the PAOs capture more of the correlation energy within smaller domains than the PSM-1, PSM-2, and PFM-2 LVOs.Overall, the performance of the three LVO sets is equally poor. For LiH, the PAO set yields an essentially converged correlation energy with an average LON dimension of about 40, whereas roughly twice as many LON orbitals are required with the LVO sets. For HCN, the LON dimension required for convergence with the LVO sets is roughly thrice that of the PAO set. The diamond crystal is more challenging, also with PAOs, which yield convergence at a LON dimension just below 150, wheras LVOs require at least about 350 LON orbitals.

Figure 1. Convergence of the MP2 correlation energy with respect to the average number of LON orbitals in the diagonal pairs. The panels from top to bottom show results for bulk diamond, LiH and HCN, respectively, for the PAO and various LVO sets.

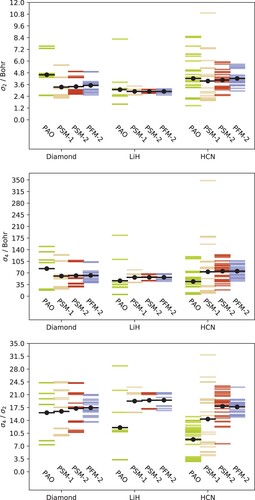
As apparent from the locality measures compiled in Figure 2, the superior convergence of the PAOs can not be unambiguously attributed to their being more local or light-tailed than the LVOs.The ${\sigma }_2$ data show that the PAOs are on average the least local choice and, consequently, orbital spreads can not explain the very different convergence behaviours. This agrees with the observations for molecules by Krause and Werner [25]. Nor can a clear distinction of the PAOs be made from the ${\sigma }_4$ data. While the PAOs do have the smallest average ${\sigma }_4$ for LiH and HCN, they also show the greatest maximum value for LiH and diamond. In all cases, the smallest maximum ${\sigma }_4$ is observed for the PFM-2 set. The average β values, on the other hand, are smaller for the PAOs than for the LVO sets across all three systems. While this is fully consistent with the observed correlation-energy convergence behaviour in Figure 1, we note that the maximum β value is greater for the PAOs than for the PFM-2 sets for both diamond and LiH. Judging from the β values alone, one would expect the correlation-energy convergence behaviour to be similar for PAOs and either of the LVO sets in the case of diamond, while the PAOs should be vastly superior to the LVOs in the case of HCN. As seen from Figure 1, however, the LVO sets struggle even more for diamond than for HCN and LiH. We thus conclude that neither second moment spread, fourth moment spread, nor tail spread can unambiguously explain the observed convergence behaviour.

Figure 2. Second- and fourth moment orbital spreads and tail spreads for the various sets of virtual orbitals for diamond, LiH, and HCN. Horizontal lines give the value for each orbital in each set, while average values are indicated by the horizontal black lines.

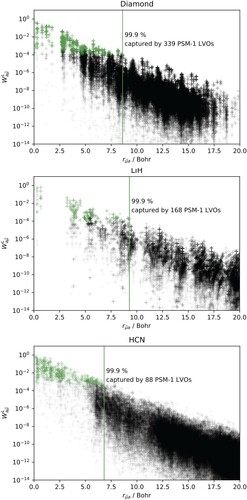
An alternative explanation might be that the PAOs provide greater multiplicative sparsity, translating into smaller diagonal excitation domains by allowing for a smaller cutoff distance from each occupied orbital. According to this hypothesis, the PAOs should show few important DOIs at short range followed by rapid decay at longer distances, whereas the LVOs should decay more slowly with distance. The estimated DOIs for PAOs and PSM-1 virtual orbitals are plotted in Figure 3. For each crystal, the overall DOI decay rates are comparable for both sets of virtual orbitals, although the DOIs of the PAOs are more scattered with values at each distance both above and below those of the PSM-1 orbitals. A DOI cutoff threshold of ${10}^{-2}$, as recommended by Pinski et al. [30], would suggest that about the same or even more PAOs than PSM-1 orbitals must be included in the correlation treatment.

Evidently, neither the statistics-based locality measures nor the DOIs provide a clear-cut explanation of the more rapid correlation-energy convergence with the PAOs. Although the LVOs span the same space as the PAOs when the entire crystal is considered, a distance-based truncation of the PAOs clearly captures more of the correlation energy. From the viewpoint of the LVOs, this implies that the PAOs of a given cell must contain components that are only present in more distant orbitals in the orthonormal representation. To investigate this effect, we expand the PAOs of the reference unit cell, denoted $|0\tilde{\mu }⟩$ where 0 indicates that the parent AO $|\mu ⟩$ is located in the reference unit cell, in a basis defined by a given set of LVOs, (12) $|0\tilde{\mu }⟩=\sum _L\sum _a|\mathrm{La}⟩⟨\mathrm{La}\mid 0\tilde{\mu }⟩\equiv \sum _L\sum _a|\mathrm{La}⟩C_{a\tilde{\mu }}^L,$(12) where L is a lattice index (including 0, the reference unit cell). The expansion coefficients can be computed directly from their definition. In order to measure the extent to which distant LVOs are represented in the PAO set of the reference unit cell, we introduce the ‘weight’ of each virtual orbital $|\mathrm{La}⟩$ as the square of the corresponding expansion coefficient, (13) $W_{a\tilde{\mu }}^L={\left(C_{a\tilde{\mu }}^L\right)}^2.$(13) These weights are plotted in Figure 4 as a function of the inter-orbital distance $r_{\tilde{\mu }a}$ between the PAOs in the reference cell and PSM-1 LVOs throughout the crystal.

Figure 3. Differential overlap integrals between the occupied orbitals of the reference unit cell and the PAO and PSM-1 virtual orbital spaces for diamond (top), LiH (center), and HCN (bottom), as a function of the inter-orbital distance $r_{\mathrm{ia}}$ between occupied orbitals in the reference cell and PAOs or PSM-1 virtual orbitals throughout the crystal. The graphs show the maximum DOI for each orbital set above a given distance.

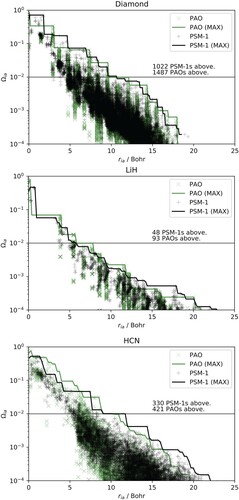
Figure 4. Expansion coefficients squared, Equation (13(13) $W_{a\tilde{\mu }}^L={\left(C_{a\tilde{\mu }}^L\right)}^2.$(13) ), of the PSM-1 virtual orbitals for the reference-cell PAOs as a function of the distance between the reference cell PAOs and each virtual orbital for diamond (top panel), LiH (middle panel), and HCN (bottom panel). Green points indicate expansion coefficients that are required to recover 99.9% of the norm of every single PAO. There are 26, 11 and 32 such PAOs for diamond, LiH, and HCN, respectively. The most distant orbital that has to be included to capture the same span is indicated with a vertical green line.

Only plots for the PSM-1 set are shown. Essentially identical plots are obtained for the PSM-2 and PFM-2 sets. While the weights decay quite rapidly, significant contributions ($W_{a\tilde{\mu }}^L⪆{10}^{-3}$) may indeed be observed between 5 and $10\mathrm{bohr}$ from the origin of the reference cell. This is consistent with the observed correlation-energy convergence behaviour. Furthermore, it is evident from the vertical lines of Figure 4 that a distance-based truncation of the LVOs leads to the inclusion of a large number of redundant components, ultimately resulting in inefficient (but still linear-scaling) calculations of the MP2 correlation energy. Interestingly, the distribution of the green points suggests that a more sparse subspace of LVOs may be chosen based on their importance in spanning the same space as the reference-cell PAOs.

5. Concluding remarks

We have studied the impact of the initial choice of virtual-orbital basis, PAOs and three different sets of LVOs, on the convergence of the local MP2 correlation energy toward the canonical result for three insulating crystals with qualitatively different chemical bonding situations, diamond (covalent crystal), LiH (ionic crystal), and HCN (molecular crystal). Our results confirm recent findings by Werner and coworkers [25–27] for molecules: the performance of PAOs is significantly better than LVOs.

This result is somewhat counterintuitive since the LVOs are generally more local according to second moment orbital spread data, have thinner tails according to fourth moment orbital spread data, and provide comparable or even greater multiplicative sparsity in conjunction with localised orthonormal occupied orbitals than the PAOs. Although we do observe a certain agreement with tail spread data for the PAOs and LVOs, correctly indicating superiority of the former, there is no one-to-one mapping between β values and the observed convergence behaviour. Inspecting the expansion of the reference-cell PAOs in the LVO basis, we find that the PAOs contain surprisingly large components of distant LVOs. It seems, therefore, that the efficiency of the PAOs can be traced to their being sufficiently local and linearly dependent such that by choosing a subset of them based on the location of the atomic centres of the parent AOs, we get a greater fraction of the excitation space than we would have obtained with the LVOs centred in the same spatial region.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Research Council of Norway (RCN)–Norges Forskningsråd through its Centres of Excellence scheme, project number 262695, by the RCN Research Grant No. 240698, and by the Norwegian Supercomputing Program NOTUR Grant No. NN4654K.

Appendices

Appendix 1. Geometries

The reader is referred to the Crystal manual [55] for details regarding the keywords given in the following discussion. All calculations was performed for 3D periodicity. In all cases the two-electron integrals was treated exactly (invoked with keyword NOBIPOLA) when setting up the Fock-matrix.

Diamond was computed with space group 227 and lattice parameter 3.56679 Å. With a standard shift of the origin (IFSO set to 1), a carbon was placed in ${\mathbf{r}}_{\mathrm{C}}=(0,0,0)$. The Hartree-Fock optimisation was performed with SHRINK set to 8 and an energy tolerance of ${10}^{-10}$. The intergral tolerances was 8 8 8 10 20. For the Wannierization, we used a NEWK of 9.

For LiH we used space group 225 with lattice parameter 4.0834 Å. Lithium was placed at ${\mathbf{r}}_{\mathrm{Li}}=(0,0,0)$ and hydrogen at ${\mathbf{r}}_{\mathrm{H}}=(\frac{1}{2},\frac{1}{2},\frac{1}{2})$, both in units given as fractions of the lattice vectors. For the Hartree-Fock optimisation we used a SHRINK factor of 7 with a convergence tolerance on the energy (TOLDEE) ${10}^{-12}$. Integral tolerances (ITOL) was set to 8 8 8 25 50. For the Wannierization we used a NEWK of 11.

For HCN we used space group 44 and lattice parameters 4.13 Å, 4.85 Å, 4.34 Å, ${90}^{\circ }$, ${90}^{\circ }$, and ${90}^{\circ }$. The fractional coordinates of hydrogen, carbon and nitrogen were ${\mathbf{r}}_{\mathrm{H}}=(0,0,-0.2459793977425)$, ${\mathbf{r}}_{\mathrm{C}}=(0,0,0.003572703972826)$, and ${\mathbf{r}}_{\mathrm{N}}=(0,0,0.2701066937697)$, respectively. For the Hartree-Fock optimisation we used a SHRINK factor of 7 and integral tolerances of 7 7 7 20 40. The energy tolerance (TOLDEE) was set to ${10}^{-10}$. The subsequent Wannierization was performed with NEWK 11.

Appendix 2. DOI estimates

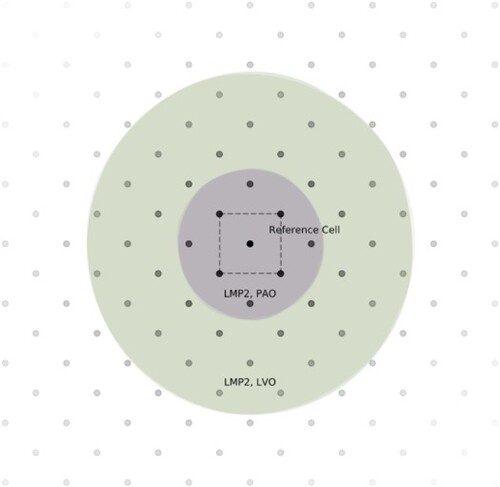
The differential overlap integrals (DOIs) [30] were estimated using Monte Carlo (MC) integration [56] within finite volumes of the full integration domain (${\mathbb{R}}^3$).

For each pair of unit cells, the full integration domain is divided into concentric spherical shells as illustrated in Figure A1, with their origin situated halfway between the lattice vectors associated with the relevant cells. The outermost layer is placed at 50 Bohr, with its interior divided into 121 shells uniformly spaced in the radial direction.

The overlap and differential overlap integrals are computed 20 times for all orbitals associated with the two cells using MC integration with 2000 random samples uniformly distributed inside every finite volume. The integrals over every volume are then summed, and the final integrals are estimated as the average of the 20 separate estimates.

In total, each integrand is sampled in $4.84\times {10}^6$ coordinates. The discretisation of the integration domain can be considered a discrete importance sampling [56], with the consequence of more dense sampling in regions where higher variance in the integrand is expected. The assumption of the concentric spherical shells being a reasonable sample distribution thus relies on the orbitals being localised to their associated cells, so that the products of orbitals have most of their significant distribution between the cells.

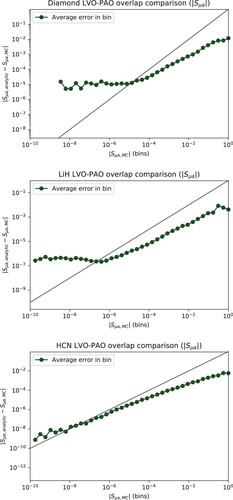
Confidence in the estimates can be established by (1) assessment of the error in the PAO-LVO overlap matrix, and (2) assuming that the same error applies to the DOIs due to the similarities in the integrand with respect to variance. While we can not directly infer the error in the DOIs from the error in the PAO-LVO overlaps, it is clear that the regions with most variance in the integrands coincide in these cases. Hence, if the sampled coordinates has the ability to reproduce the overlaps they should be an equally reasonable choice for the DOIs.

The absolute deviation of the MC estimates of the PAO-LVO overlap matrix elements is compared to their magnitude in Figure A2, where we observe a significant loss of relative accuracy below ${10}^{-4}$ for diamond, and below ${10}^{-6}$ for LiH and HCN. We thus conclude that the DOI estimates presented in Figure 3 are reliable.

Figure A.1. Illustration of Monte Carlo integration within concentric shells. The density of samples is higher in the centre. The final integral is estimated by $I=\sum _{n=1}^{N_{\mathrm{shells}}}{I}_n$.

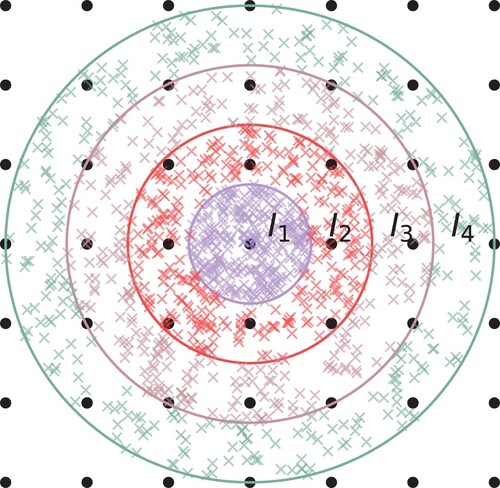
Figure A.2. Absolute difference of analytical and MC estimates for the PAO-LVO ($S_{\mathrm{\mu a}}$) overlap matrix elements. The elements are sorted into bins depending on the absolute value of the MC-estimates, whereby the average error within each bin is calculated and plotted. The diagonal line shows where the absolute deviation equals the MC-estimate. The intersection between the diagonal and the average can be used to identify a lower bound at which the loss of precision in the MC estimates becomes too severe to draw any conclusions. This intersection appears well below ${10}^{-4}$ in all three cases.