Topological and threading effects in polydisperse ring polymer solutions

ABSTRACT

We explore effective interactions in dilute polydisperse ring polymer solutions. Based on a topological and threading analysis, we deduce the steric, topological and threading contributions to the effective potentials for differently sized rings. Additionally, we quantify the contribution of topological constraints for different asymmetries of the ring length. Further, we compare how the effective potentials change when mutual ring threading is restricted and we characterise the threading depth distributions at different center-of-mass ring separations.

GRAPHICAL ABSTRACT

Keywords:

• Ring polymers
• coarse-graining
• effective models
• Monte Carlo simulation
• topological potential
• threading

1. Introduction

The universal properties of ring polymers, which are frequently found in nature in the form of plasmid, bacterial, mitochondrial or extra-chromosomal circular DNA, are being progressively unravelled [1]. The fixed topology, restricting the available phase space in comparison to linear polymers, is difficult to include in effective theories, but has profound consequences on the properties of ring melts and solution in comparison to linear polymer systems. One of such properties is the effective interaction between two long polymer loops that exhibits a part originating solely from the topology [2]. The presence of the topological non-concatenation condition, in contrast to linear chains, generates an interesting non-Gaussian shape of the effective potential with a plateau at small centre-of-mass separations r and a higher amplitude of the interaction potential at r = 0. As a consequence, for example, dilute ring polymer solutions feature a higher tendency to structure at confining walls in comparison to dilute linear polymer solutions [3]. The topological interaction at dilute conditions is the focus of the present work too.

Naturally, topological effects manifest themselves stronger at high system densities, where the rings are forced to reconcile high overlap concentration and many simultaneous non-concatenation conditions. This balance then leads to compact globular ring conformations and their territorial arrangement is reminiscent of out-of-equilibrium (linear) chromosome conformations found in eukaryotes with long genomes. The similarity is conjectured to be not coincidental, but arising from biological times being short in comparison to the time scale required to reach relaxed state of linear chains [4,5]. The latter are so long precisely because of the constraints preventing the chains to cross each other and hence topology governs the physical properties of chromosomes. This is one of the reasons why a lot of effort has been put forth to understand the behaviour of nonconcatenated rings in melt. Some scaling theories, in order to find a proper form of the nonconcatenation free energy cost, build on understanding a simpler case of a few loops at lower densities where rings are not strongly deformed [6]. Such attempts are also useful in the context of chromatin [7], because at scales smaller than the whole chromosomes, the chromatin features loops that, although being possibly quite long, are typically shorter than the entanglement length scale and hence are not subject to strong topological compression. The loopy domains and their mutual interactions have biological importance [8]. They arise by the process of extrusion by the action of a group of specialised protein complexes (structure maintenance of chromosomes) that stops at particular locations on the genome. Therefore, their size and locations vary and hence their interactions as well. For these reasons, in this paper we focus on the characterisation of the effective potential of loops of different sizes with the emphasis on the topological part of the interaction.

The interaction between topologically constrained polymers has in addition particular consequences on their dynamics. In dense systems, the so-called threading conformations, where one polymer segment is intersecting the loop opening of another, slow down the polymer diffusive dynamics. Such threading events are correlated with a slower dynamics of equilibrium systems of rings [9,10], significantly impact viscosity when the rings are long [11] or when the threadings are enhanced by out-of-equilibrium conditions [12,13]. The threadings form a particular subset of the topologically allowed conformations and therefore we investigate how they impact the effective interaction potential in general and its topological part in particular.

In  [14,15], the authors extend the work [16] and study the effective potential of differently sized rings of different topologies. The effective potential $V_{\mathrm{eff}}(r)$ is obtained from Monte Carlo (MC) simulations by Boltzmann inversion of the radial distribution function. The simulations were performed with polymer length limited to N = 100 hard-sphere monomers and the effect of size was studied for different topologies only ($0_1$ and $3_1$ in the classical knot terminology). The work reports a small range of attraction for small separations if the larger ring is unknot and for two equally sized unknots. This effect is caused by an excess entropy of the smaller ring in comparison to a smaller entropy loss of the larger ring that swells a bit to accommodate the other one at small separation. These effects are, however, N-dependent and the limited polymer lengths do not allow to deduce accurately the universal potential features and the topological contribution to the potential. In this regard, the work [7] reaches significantly longer lengths N = 2048 using lattice bond fluctuation model and approaches the universal form of the effective potential for equally sized rings. By comparing the effective potentials for rings that can concatenate with those that are not allowed to, the authors of  [7] deduced the form of the topological part of the effective potential $V_{\mathrm{top}}(r)$. The topological potential for equally sized rings has been also investigated in the form of the linking probabilities in  [17] on a model of self-avoiding polygons of length up to N = 256 and in  [18] for a soft and hard sphere models of rings up to N = 100. It has been found that the $V_{\mathrm{eff}}(r)$ has a local shallow minimum at zero separation and depends for these lengths on N and the excluded volume. Based on the effective potential, the latter work also proposed a coarse-grained model where a number of monomers where blobbed to form a single unit. The model was able to reproduce the full monomer results up to about three overlap concentrations using 20–50 blobs for each ring in a solution of rings with N = 100, but was not tested on solutions with longer chains.

Here we use MC, introduced in Section 2, to study single ring static properties, the effective interaction potential and its topological component between two unknotted rings in dilute conditions. The main results are in Section 3. In Section 3.1, we consider properties of an ensemble of isolated rings. More specifically, we present knotting probability, scaling of the ring's radius of gyration and its minimal surface area. We continue in Sections 3.2–3.4 with two-ring properties. Namely, we detail the computation of the effective potentials, systematically study the role of ring length asymmetry and judge on the impact of threading events on the potential. The methods we use allow us to reach ring lengths sufficient to deduce the asymptotic forms of several interesting quantities. We discuss the results and outline further open questions in Section 4.

2. Models and methods

We generated a series of independent conformations of single ring polymers in good solvent conditions using a Metropolis MC scheme. The single ring conformations were subsequently used in computing the effective potentials between pairs of mono- and polydisperse rings in the infinite dilution regime.

The fully flexible polymer chains were modelled using the standard, Kremer and Grest bead-spring model [19] with absent bending potential. The excluded volume interaction between monomers was given by the purely repulsive Weeks–Chandler–Andersen (WCA) potential [20], thereby mimicking good solvent conditions: (1) $V_{\mathrm{WCA}}(r)=4ϵ[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6+\frac{1}{4}]\mathrm{\Theta }(2^{1/6}\sigma -r)$(1) with $\mathrm{\Theta }(\cdot )$ being the Heaviside step function. Two neighbouring monomers were connected with a finitely extensible nonlinear elastic (FENE) potential (2) $\begin{array}{rl}& V_{\mathrm{FENE}}(r)\\ & =\{\begin{array}{ll}-15ϵ{\left(\frac{R_0}{\sigma }\right)}^2\ln [1-{\left(\frac{r}{R_0}\right)}^2],& \mathrm{for}r\le R_0,\\ +\mathrm{\infty },& \mathrm{for}r>R_0,\end{array}\end{array}$(2) where $R_0=1.5\sigma$. The bead diameter σ was chosen as the unit of length ($\sigma =1$) and the simulations were performed at the reduced temperature $k_B{T}^{\ast }\equiv k_{B}T/ϵ=1$.

Metropolis MC simulations of single ring polymers were performed using translational displacements of separate monomers in combination with collective rotations of ring arcs, the so-called crankshaft moves, as described in  [18,21]. A series of such collective crankshaft rotations can potentially result in a knotted ring configuration, thereby making the topological state of the ring variable in the course of a whole simulation run. Nevertheless, the ring's topology can be preserved by imposing additional checks for bond crossing after every trial MC move [3,18,21], which naturally slows down the sampling of independent ring configurations and also limits the magnitude of rotations that can be performed during a typical crankshaft move [18,21]. In this work, we have adopted a slightly different strategy: instead of performing bond crossing checks at every single trial MC move, we simply generated a set of independent ring conformations and then determined their topology separately using the KymoKnot software [22] based on the Alexander polynomial. This enabled us to efficiently sample configurations of relatively large rings with contour length up to $N={10}^4$ and also get insight into the knotting probability in the currently employed off-lattice ring model. We define one MC step as a sequence of N trial translational displacements and one crankshaft move with arbitrarily large rotations of arcs that had maximal length N/3. In such case, almost uncorrelated configurations, as evidenced by the autocorrelation function of the ring radius of gyration, defined below in Equation (3(3) ${\hat{R}}_{\mathrm{g}}^2=\frac{1}{N}\sum _{i=1}^N{({\mathbf{r}}_i-{\mathbf{r}}_{\mathrm{cm}})}^2,$(3) ), were sampled every 500 MC steps. For every N considered, we generated two independent runs, each having $M={10}^4$ single ring states.

3. Results

3.1. Single ring properties

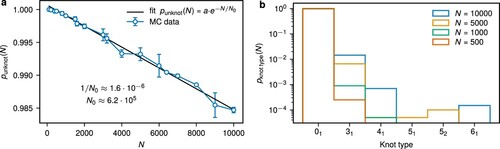
We are primarily interested in the properties of unknotted rings, and therefore we measure the fraction of knotted conformations and the knot spectrum. As shown in  [23], the probability of a random closed loop being unknotted follows an exponential law, $p_{\mathrm{unknot}}=a\cdot \exp (-N/N_0)$. Here, the characteristic length of random knotting $N_0$ is model dependent and grows with the excluded volume from about 300 for flexible infinitely thin segments. For our model with a significant excluded volume, we find $N_0\simeq 6.2\cdot {10}^5$ (Figure 1 a), meaning that our rings have length $N\ll N_0$. Hence, our rings are mostly unknotted, which makes the chosen method suitable for efficient generating the ensembles of unknots. For the knotted content, we also evaluated the knot spectrum confirming that the longer rings allow for more complex knots (Figure 1 b).

Figure 1. (a) Probability of finding an unknotted configuration in the sample of simulated rings. The black solid line indicates the best fit $p_{\mathrm{unknot}}(N)=a\cdot {\mathrm{e}}^{-N/N_0}$ for $N\ge 500$ ($a\simeq 1.0007$). The error bars indicate the standard error over two independent simulation runs. (b) Probability of finding a specific knot configuration in the sample of simulated rings for few N.

For the single ring properties we measured the exponent ν characterising the scaling of the ensemble-averaged radius of gyration $R_{\mathrm{g}}\equiv ⟨{\hat{R}}_{\mathrm{g}}^2{⟩}^{1/2}$ with the polymer length $N)$, where (3) ${\hat{R}}_{\mathrm{g}}^2=\frac{1}{N}\sum _{i=1}^N{({\mathbf{r}}_i-{\mathbf{r}}_{\mathrm{cm}})}^2,$(3) and ${\mathbf{r}}_i$ is the position of the bead i, ${\mathbf{r}}_{\mathrm{cm}}=N^{-1}\sum _{i=1}^N{\mathbf{r}}_i$ is the position of the ring's center of mass and the brackets $⟨\dots ⟩$ generally denote the ensemble average. To a good accuracy (Figure 2 a) we find the $\nu ={\nu }_{\mathrm{SAW}}=0.588$ in agreement with the values found for unknots without excluded volume [24] and the self-avoiding walk in three dimensions. For our model, the exponent is the consequence of the latter due to the large $N_0$. Note that $R_{\mathrm{g}}$ values in Figure 2(a) were computed over the ensemble of all configurations, however, almost identical $R_{\mathrm{g}}$ and therefore ν were obtained for unknotted states alone. As shown in [1,24,25] the size of an unknot without excluded volume interactions of $N\ll N_0$ is governed by a random-walk exponent $\nu =1/2$, because the random walk is typically unknotted on these scales. The topological origin of $\nu ={\nu }_{\mathrm{SAW}}$ is manifested only if $N\gg N_0$, hence the $\nu ={\nu }_{\mathrm{SAW}}$ we observe is the consequence of the self-avoidance. The inset of Figure 2(a) shows the normalised distribution of the ${\hat{R}}_{\mathrm{g}}^2/R_{\mathrm{g}}^2$. While a small finite size effects are visible for N<500, for longer rings we see a good collapse to a universal distribution.

Figure 2. (a) Scaling of the ring's mean square radius of gyration with the polymerisation degree N. The black line is the fit $R_{\mathrm{g}}^2\sim N^{2\nu }$ of the MC results (open blue circles), yielding $\nu =0.588\pm 0.001$ for $N\gtrsim {10}^3$. Right inset: normalised distributions of $X={\hat{R}}_{\mathrm{g}}^2/R_{\mathrm{g}}^2$ for different ring lengths N. Left inset: snapshot of a ring with $N={10}^4$. (b) Scaling of the mean area of the ring's minimal surface with N. The black line is the fit $⟨A⟩\sim N^x$ of the simulation results (open blue circles), yielding $x=1.25\pm 0.01$ for $N\gtrsim 200$. Right inset: normalised distributions of $X=A/⟨A⟩$ for different ring lengths N. Left inset: snapshot of a minimal surface of a ring with $N=6400$.

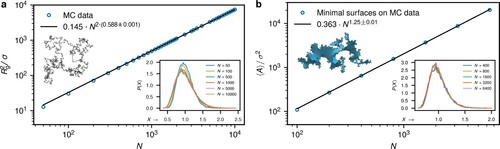
Another interesting static property of the ensemble of unknotted ring conformations is the minimal area of a surface spanned by the ring's contour. The (minimal) surfaces, typically constrained to disk-like topology, have been found useful to investigate static, dynamic and threading properties in entangled regimes of systems of nonconcatenated rings in equilibrium [10,26–28], out of equilibrium [13,29–31], tadpole-shaped polymers [32,33] or ‘lasso’ proteins [34]. A threading, as we define it here, is a conformation for which a polymer segment pierces through the minimal surface spanned on a ring segment of another polymer. Later below we will investigate the threading contribution to the effective topological potential between two rings. The threading probability is related to the minimal surface area that we investigate as a function of polymer length N in Figure 2(b). We minimise the surfaces using the procedure detailed in  [27] and for long rings we find the scaling $A\sim N^x$ with the exponent x = 1.25 consistent with the one found in  [10] for lattice rings. There, it was conjectured the area scaling is governed by the scaling of $R_{\mathrm{g}}$ as $A\sim {\hat{R}}_{\mathrm{g}}^2$ and hence the true value of the exponent x was suspected to be $2\nu =1.176$. The simulations presented here concern rings off lattice that are eight times longer than the ones in  [10], hence the exponent is less likely to be affected by small-scale features and finite-size effects. Yet, we find the values of x and ν with the accuracy that does not support the conjecture. A more thorough future investigation of this feature is necessary to rule out also systematic errors that could, in principle, be connected to the surface minimisation procedure. The distribution of the normalised minimal area $A/⟨A⟩$ exhibits a good collapse to a universal form for longer rings N>400 (inset of Figure 2 b).

3.2. Effective interaction of two monodisperse rings

Next we examine the effective potential arising from the interaction of two rings whose centres of mass are kept fixed at distance r. We adopt the procedure detailed in  [18]. Letting aside the topology, the effective steric potential $V_{\mathrm{ste}}(r)$, which accounts for the steric effects only, of two rings whose centres of mass are at a distance r is defined as (4) $\exp [-\beta V_{\mathrm{ste}}(r)]=\frac{\mathcal{Z}(r)}{\mathcal{Z}(r\to \mathrm{\infty })},$(4) where β is the inverse temperature and $\mathcal{Z}(r)$ is the constrained partition function characterising ring conformations at a fixed center-of-mass distance r, i.e. (5) $\mathcal{Z}(r)=\int \mathrm{d}{\mathbf{R}}_1\mathrm{d}{\mathbf{R}}_2\exp (-\beta \mathcal{H}({\mathbf{R}}_1,{\mathbf{R}}_2))\delta (\mathrm{\Delta }{r}_{\mathrm{cm}}-r),$(5) with $\mathcal{H}({\mathbf{R}}_1,{\mathbf{R}}_2)$ being the full Hamiltonian governing the interaction of two rings, as described by a set of monomer positions ${\mathbf{R}}_i=({\mathbf{r}}_{i,1},{\mathbf{r}}_{i,2},\dots ,{\mathbf{r}}_{i,N})$, $\mathrm{\Delta }{r}_{\mathrm{cm}}=|{\mathbf{r}}_{1,\mathrm{cm}}-{\mathbf{r}}_{2,\mathrm{cm}}|$, and ${\mathbf{r}}_{i,\mathrm{cm}}$ being the centre-of-mass position of the corresponding ring i. Furthermore, $\mathcal{H}({\mathbf{R}}_1,{\mathbf{R}}_2)$ can be rewritten as $\mathcal{H}({\mathbf{R}}_1,{\mathbf{R}}_2)={\mathcal{H}}_{11}({\mathbf{R}}_1)+{\mathcal{H}}_{22}({\mathbf{R}}_2)+{\mathcal{H}}_{12}({\mathbf{R}}_1,{\mathbf{R}}_2)$, where ${\mathcal{H}}_{11}$ and ${\mathcal{H}}_{22}$ entail the respective intra-ring interactions and ${\mathcal{H}}_{12}$ includes the inter-ring interaction terms. As the rings at infinite distance do not interact, the partition function $\mathcal{Z}(r\to \mathrm{\infty })$ simply decomposes into a product of two single-ring partition functions. Hence, the steric effective potential in Equation (5(5) $\mathcal{Z}(r)=\int \mathrm{d}{\mathbf{R}}_1\mathrm{d}{\mathbf{R}}_2\exp (-\beta \mathcal{H}({\mathbf{R}}_1,{\mathbf{R}}_2))\delta (\mathrm{\Delta }{r}_{\mathrm{cm}}-r),$(5) ) can be recast as (6) $\exp [-\beta V_{\mathrm{ste}}(r)]=⟨\exp (-\beta {\mathcal{H}}_{12})\delta (\mathrm{\Delta }{r}_{\mathrm{cm}}-r){⟩}_0,$(6) where the angles $⟨\dots ⟩$ denote the average in the ensemble of non-interacting ring conformations.

In practice, the latter is performed using the Widom's insertion method [35,36]. We take two distinct rings from the set of M single-ring conformations generated using the MC procedure detailed above, which ensures they are representatives of the ensemble corresponding to the single-chain Hamiltonian. The rings are placed, after a random rotation around their centre of mass, at a mutual centre-of-mass distance r, and the corresponding inter-ring interaction energy ${\mathcal{H}}_{12}$ is evaluated. Averaging the Boltzmann factor in Equation (7(7) $\beta V_{\mathrm{ste}}(r)=-\ln [\frac{1}{\mathcal{M}}\sum _{k=1}^{\mathcal{M}}\exp (-\beta {\mathcal{H}}_{12}({\mathbf{R}}_1^k,{\mathbf{R}}_2^k;r))],$(7) ) over a set of randomly chosen $\mathcal{M}$ ring pairs gives the effective steric potential irrespective of whether the rings are linked together or not (in practice, in every case we used $\mathcal{M}={10}^6$). Therefore, (7) $\beta V_{\mathrm{ste}}(r)=-\ln [\frac{1}{\mathcal{M}}\sum _{k=1}^{\mathcal{M}}\exp (-\beta {\mathcal{H}}_{12}({\mathbf{R}}_1^k,{\mathbf{R}}_2^k;r))],$(7) where ${\mathcal{H}}_{12}({\mathbf{R}}_1^k,{\mathbf{R}}_2^k;r)$ is the interaction energy between two single-ring configurations given by ${\mathbf{R}}_1^k$ and ${\mathbf{R}}_2^k$ that are at the centre-of-mass distance r.

To evaluate the effective potential between nonconcatenated rings we have to assess the mutual linking. To do that, we evaluate the standard Gauss linking integral (8) $m=\frac{1}{4\pi }{\oint }_{{\mathcal{C}}_1}{\oint }_{{\mathcal{C}}_2}\frac{\mathrm{d}{\mathbf{s}}_1\times \mathrm{d}{\mathbf{s}}_2\cdot ({\mathbf{s}}_1-{\mathbf{s}}_2)}{|{\mathbf{s}}_1-{\mathbf{s}}_2{|}^3},$(8) computed over the contours of the two rings inserted at a centre-of-mass distance r. The linking number m is zero for unlinked rings. A linked configuration can have m = 0 too, such as Whitehead link, which however requires a knotted conformation of one of the rings. For simple links that are expected in the present case of freely fluctuating configurations, m works well for determining the linking. Using this procedure on all $\mathcal{M}$ ring pairs, we compute the effective potential in analogy to Equation (7(7) $\beta V_{\mathrm{ste}}(r)=-\ln [\frac{1}{\mathcal{M}}\sum _{k=1}^{\mathcal{M}}\exp (-\beta {\mathcal{H}}_{12}({\mathbf{R}}_1^k,{\mathbf{R}}_2^k;r))],$(7) ), but with a Boltzmann factor only of the conformations that have m = 0, i.e. (9) $\begin{array}{rl}& \beta V_{\mathrm{eff}}(r)\\ & =-\ln [\frac{1}{\mathcal{M}}\sum _{k=1}^{\mathcal{M}}\exp (-\beta {\mathcal{H}}_{12}({\mathbf{R}}_1^k,{\mathbf{R}}_2^k;r)){\delta }_{m,0}],\end{array}$(9) equivalent to assigning an infinite energy penalty to linked ring pairs. 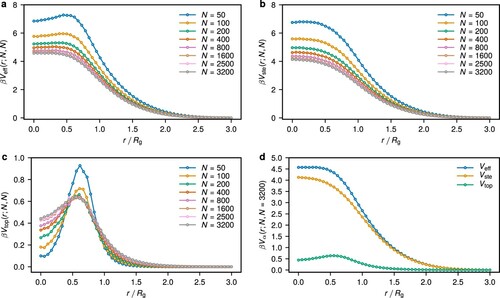The topological part of the effective potential is then given as the difference between the effective potential and the steric effective potential (10) $V_{\mathrm{top}}(r)=V_{\mathrm{eff}}(r)-V_{\mathrm{ste}}(r).$(10) The effective potentials, as well as their respective steric and topological contributions, between rings of the same length N are shown in Figure 3(a)–(c), respectively. For lengths of $N\gtrsim 2000$ the potentials converge to an asymptotic non-Gaussian profile. The asymptotic barrier at zero separation is about $4.5k_{\mathrm{B}}T$, which is consistent with  [7] and lower than previously reported $6k_{\mathrm{B}}T$ [15,16]. This is likely because of longer ring lengths used in  [7] and even longer ones we use here, which allow for a more accurate estimate of the conformational entropy, while shorter and coarse-grained rings systematically underestimate the ring crumpling. Consistent with that we observe a strong N-dependence on the $V_{\mathrm{top}}(r=0)$, as longer rings at small separations are more likely to get linked than shorter ones. In accordance with previous observations [15], we also observe a non-monotonic profile of the $V_{\mathrm{top}}(r)$ with a part causing attractive force component between the rings close to r = 0. The highest topological barrier for large N is about $0.6k_{\mathrm{B}}T$ close to the separation $r=R_{\mathrm{g}}/2$ where the highest linking probability occurs. The maximum is of the order of $1k_{\mathrm{B}}T$ in accordance with the conjecture in  [37] and [6] for the free energy cost of the nonconcatenation between two overlapping rings in melt. This term in the corresponding Flory theories generates a scaling of the ring sizes in accordance with the simulation results in  [6,38], but only in the intermediate length regimes when the topological deformation of the rings is weak. Figure 3(d) shows the comparison of the different components and the total effective potential for the case of N = 3200, the largest ring length for which we were able to extract the effective interactions.

Figure 3. Effective interactions between monodisperse ring polymers at infinite dilution. (a) The effective potential $V_{\mathrm{eff}}(r)$ between a pair of rings of the same length N for different N. (b) The steric part of the effective potential $V_{\mathrm{ste}}(r)$ that does not account for the non-concatenation condition. (c) The topological part of the effective potential $V_{\mathrm{top}}(r)=V_{\mathrm{eff}}(r)-V_{\mathrm{ste}}(r)$. (d) The comparison between $V_{\mathrm{eff}}(r)$, $V_{\mathrm{ste}}(r)$, and $V_{\mathrm{top}}(r)$ for $N=3200$.

3.3. Effective interaction of two polydisperse rings

The effective potentials for rings of different lengths are presented in Figure 4(a)–(c). Expectedly, we find that the amplitude of the effective interaction decreases with increasing the asymmetry in the ring length (Figure 4 a). For a fixed size ratio $N_2/N_1$, the potentials appear to converge to the universal form if both $N_1$ and $N_2$ are large enough. In comparison to the monodisperse case ($N_2/N_1=1$) with the amplitude $V_{\mathrm{eff}}(r=0)$ at about 4.5 $k_{\mathrm{B}}T$, in the limit of large $N_1$ and $N_2$ we obtain $V_{\mathrm{eff}}(r=0)\simeq 3.5,2,1k_{\mathrm{B}}T$ for size ratios $N_2/N_1=2,4,8$, respectively. The effective potential $V_{\mathrm{eff}}(r)$ becomes almost entirely determined by the steric contribution $V_{\mathrm{ste}}(r)$ with increasing the length ratio $N_2/N_1$ (Figure 4 b). The latter is due to the fact that the tendency to find linked ring states decreases with increasing $N_2/N_1$, which makes the topological contribution $V_{\mathrm{top}}(r)$ vanishing for large size ratios (Figure 4 c). Even for $N_2/N_1=2$, we find that the maximum of $V_{\mathrm{top}}$ about three times smaller than in the case of $N_2/N_1=1$.

Figure 4. Effective interactions between polydisperse ring polymers at infinite dilution. (a) The effective potential $V_{\mathrm{eff}}(r)$ between a pair of rings of length $N_1$ and $N_2$. The same length ratios $N_2/N_1$ are shown with the same color. (b) The steric part of the effective potential $V_{\mathrm{ste}}(r)$ that does not account for the non-concatenation condition. (c) The topological part of the effective potential $V_{\mathrm{top}}(r)=V_{\mathrm{eff}}(r)-V_{\mathrm{ste}}(r)$. (d) The amplitude of the effective potential, $V_{\mathrm{eff}}(r=0)$ shown for different $N_1$ as a function of $N_2/N_1$. The dashed gray line indicates the apparent scaling $V_{\mathrm{e}\mathrm{f}\mathrm{f}}(r=0)\sim (N_2/N_1{)}^{-0.89\pm 0.01}$. The inset highlights the fact that the behaviour of the zero-separation value of the effective potential as a function of $z\equiv N_1/N_2<1$ is bracketed between the asymptotic behaviours $\sim z$ and $\sim z^{0.76}$, see the text.

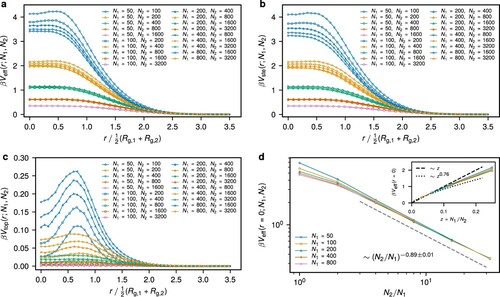
The plateau $V_{\mathrm{eff}}(r=0)$ decreases with increasing length asymmetry ratio as an apparent power-law $(N_2/N_1{)}^{-0.89\pm 0.01}$ (Figure 4 d). We try to rationalise this result by the following scaling considerations where, without a loss of generality, we assume $N_2\ge N_1$. The effective potential is proportional to $k_{\mathrm{B}}T$ times the number of contacts $C_{1,2}$ between the two chains. The latter is proportional to the number of monomers in the overlap volume, being the pervaded volume of the entire smaller chain $R_{\mathrm{g},1}^3$, times the contact probability for each monomer, hence $C_{1,2}=N_{1}p(n)$. The contact probability $p(n)$ of monomers with excluded volume $v_0$ at concentration n scales in three dimensions as (11) $p(n)\sim (n{v}_0{)}^{1/(3\nu -1)}\sim (N{v}_0/R_{\mathrm{g}}^3{)}^{1/(3\nu -1)}\sim N^{-1},$(11) where the exponent $1/(3\nu -1)$ takes into account the connectivity correction to the nave mean-field estimate $n{v}_0$, as detailed in  [39–41]. For the monodisperse case, using (11(11) $p(n)\sim (n{v}_0{)}^{1/(3\nu -1)}\sim (N{v}_0/R_{\mathrm{g}}^3{)}^{1/(3\nu -1)}\sim N^{-1},$(11) ) gives the correct result $\beta V_{\mathrm{eff}}(r=0)\simeq 1$ in the limit of large N. In the polydisperse case, we consider contacts between the two chains, therefore we take as the contact probability $p(n_2)\sim N_2^{-1}$ and we find $\beta V_{\mathrm{eff}}(r=0)\sim (N_2/N_1{)}^{-1}$. Note that our argument is only approximate because the form of the contact probability (11(11) $p(n)\sim (n{v}_0{)}^{1/(3\nu -1)}\sim (N{v}_0/R_{\mathrm{g}}^3{)}^{1/(3\nu -1)}\sim N^{-1},$(11) ) assumes both chains occupy the same volume. In our case, however, we consider only a smaller volume $R_{\mathrm{g},1}^3$, while the second chain lives in a bigger volume $R_{\mathrm{g},2}^3$, hence the connectivity correlations of the second chain can be violated when it exits the volume of interest, which subsequently impacts the form of the contact probability. To see that this matters, one can reverse the roles of the two chains in the above argument. Then one has $N_2{R}_{\mathrm{g},1}^3/R_{\mathrm{g},2}^3$ monomers of chain 2 in the volume of chain 1, interacting with $N_1$ monomers chain 1. Assuming (11(11) $p(n)\sim (n{v}_0{)}^{1/(3\nu -1)}\sim (N{v}_0/R_{\mathrm{g}}^3{)}^{1/(3\nu -1)}\sim N^{-1},$(11) ) for chain 1, we get $\beta V_{\mathrm{eff}}\sim (N_2/N_1{)}^{1-3\nu }$, where the exponent is $1-3\nu \simeq -0.76$. Attempting another exponent in the contact probability also does not lead to a consistent result for the scaling of the effective potential with the length asymmetry, which signifies that the broken correlations change the form of the contact probability significantly. Although we cannot determine the form exactly, we find it interesting to note that the measured exponent of the apparent power-law $\beta V_{\mathrm{eff}}\sim (N_2/N_1{)}^{-0.89}$ is bounded by $-1$ and $-0.76$ obtained above, and is close to their average. We surmise that the observed scaling $\beta V_{\mathrm{eff}}\sim (N_2/N_1{)}^{-0.89}$ is not the expression of a genuine underlying power-law dependence but rather the result of a superposition of power-laws with similar yet different exponents, resulting into an apparent such dependence.

To assess the relative importance of the topological contribution for different length asymmetries $N_2/N_1$, in Figure 5 we plot the ratio $V_{\mathrm{top}}(r;N_1,N_2)/V_{\mathrm{eff}}(r;N_1,N_2)$. For small separations, the topological part diminishes even faster than $V_{\mathrm{eff}}$, while the opposite holds for large separations. There exists a fixed point of 0.025 at around $0.875(R_{\mathrm{g},1}+R_{\mathrm{g},2})$ and the whole profile flattens for growing asymmetry. The maximum close to the average gyration radius is expected as many monomers are located there and linking is relatively likely. We observe that while steric part is still about $1k_{\mathrm{B}}T$ for $N_2/N_1=8$ the topological part is almost negligible.

Figure 5. The ratio between the topological and effective potential $V_{\mathrm{top}}(r)/V_{\mathrm{eff}}(r)$ as a function of the centre-of-mass separation between two rings r for different length ratios $N_2/N_1$.

3.4. The effect of threading on the effective interaction between rings

In addition to the topological contribution to the effective potential we want to evaluate the influence of threading states. We distinguish whether the two rings in question thread or not by analysing the piercings of one ring's minimal surface by the contour of the other ring. As we show in Figure 6(a), the threading probability $p_{ij}$ that ring i threads ring j exhibits a high plateau at small separations, which agrees with the expectation that many of the topologically unlinked states are threading. The plateau level grows with N and it is natural to expect that it asymptotically goes to unity for longer rings as locally flat 2D surfaces cross at small separations in 3D space with probability one. For $N_1=N_2$ the probability is symmetric $p_{12}=p_{21}$, while for asymmetric rings the probability of being threaded is higher for higher N (Figure 6 b), because a larger surface area is exposed to the threading.

Figure 6. Threading properties as a function of ring centre-of-mass separation r and the length ratio $N_2/N_1$. Probability of finding a threading conformation as a function of r for (a) monodisperse and (b) polydisperse ring pairs. $p_{ij}$ is the probability that the ring i threads the ring j placed at a given centre-of-mass distance r. $⟨Q_{ij}⟩$, which quantifies the depth of threading, computed on the threading ring pairs ($Q_{ij}\ne 0$, solid lines) and all ring pairs (dashed lines) as a function of r for (c) monodisperse and (d) polydisperse ring pairs. (e) Distribution of $Q_{12}=Q_{21}$ (including cases with $Q_{ij}=0$) at different fixed distances between the rings' centres of mass for the case with $N_1=200$ and $N_2=200$. Distribution of (f) $Q_{12}$ and (g) $Q_{21}$ (including cases with $Q_{ij}=0$) at different fixed distances between the rings' centres of mass for the case with $N_1=100$ and $N_2=200$.

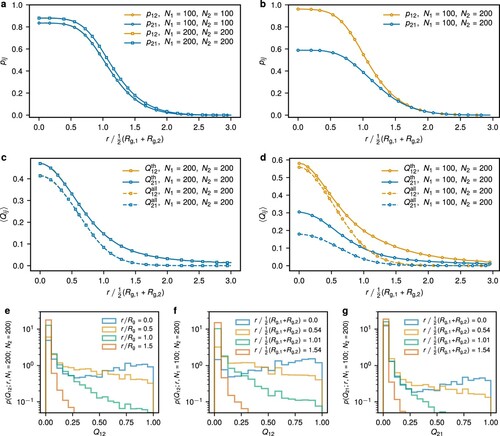
Besides the threading probability, we also quantify each threading state by a depth ratio of threading, defined as $Q_{ij}$. In a threading configuration, the minimal surface of ring j can be pierced multiple times, effectively splitting the threading ring i of length N into segments, of lengths $L_{{\mathrm{t}}_{\mathrm{k}}}$, between two penetrations. Typically, for nonconcatenated rings, the segments with index of different parity reside on different sides of the surface (see also discussion in  [10]). $Q_{ij}$ then expresses the fraction of the monomeric material of the threading ring i on one side of the surface of the threaded ring j versus the other side. We define $Q_{ij}=L_{\mathrm{sep}}/(N_i-L_{\mathrm{sep}})$ where (12) $L_{\mathrm{sep}}=min(\sum _{k=\mathrm{even}}{L}_{{\mathrm{t}}_k},\sum _{k=\mathrm{odd}}{L}_{{\mathrm{t}}_k}).$(12) The rings' surfaces can also avoid each other, in which case $Q_{ij}=0$. As we show with solid lines in Figure 6(c), the topologically allowed conformations exhibit a slower decay for $r>(R_{\mathrm{g},1}+R_{\mathrm{g},2})/2$ of mean threading depth ratio $⟨Q⟩$ in comparison to a normal distribution (dashed lines in Figure 6 c), when evaluated on all conformations irrespective of their topological state. The normal distribution is not surprising, as $⟨Q⟩$ is closely related to a sum of randomly varying, finite-variance lengths due to random orientations of the rings. Similarly to the case of threading probability (Figure 6 b), $⟨Q_{12}⟩$ is increased as compared to $⟨Q_{21}⟩$ because of a larger surface area of ring 2 in the asymmetric case with $N_1=100,N_2=200$ (Figure 6 d). In Figure 6(e), we present the distribution of $Q_{ij}$ for $N_1=N_2=200$ for different separations evaluated on all ring conformations, i.e. including cases with $Q_{ij}=0$. We observe dominating zero threading depth, i.e. unthreading, states at large separation, with a second peak at high values of threading depth for zero separations. This agrees with the observed trends for fraction of the topological interaction in Figure 5, where it is lower at large separations in comparison to small separations. Similar distributions are recovered for $Q_{12}$ and $Q_{21}$ if asymmetric rings pairs are considered (Figure 6f and 6g for $N_1=100$ and $N_2=200$).

In analogy to topological part of the effective potential, we evaluate how do the threading states contribute to the effective potential. In comparison to the effective potential in Equation (9(9) $\begin{array}{rl}& \beta V_{\mathrm{eff}}(r)\\ & =-\ln [\frac{1}{\mathcal{M}}\sum _{k=1}^{\mathcal{M}}\exp (-\beta {\mathcal{H}}_{12}({\mathbf{R}}_1^k,{\mathbf{R}}_2^k;r)){\delta }_{m,0}],\end{array}$(9) ), there is an additional restriction on the non-threading state, i.e.: (13) $\begin{array}{rl}& \beta V_{\mathrm{eff}}^{\mathrm{no}-\mathrm{th}}(r)\\ & =-\ln [\frac{1}{\mathcal{M}}\sum _{k=1}^{\mathcal{M}}\exp (-\beta {\mathcal{H}}_{12}({\mathbf{R}}_1^k,{\mathbf{R}}_2^k;r)){\delta }_{m,0}{\delta }_{Q,0}],\end{array}$(13) where the additional term ${\delta }_{Q,0}$ enforces the non-threading constraint. 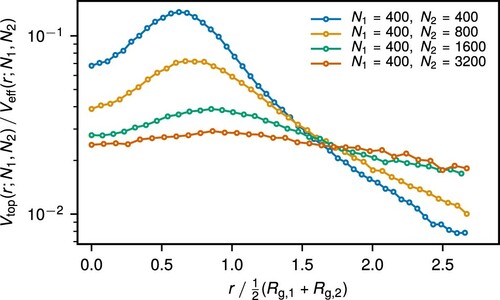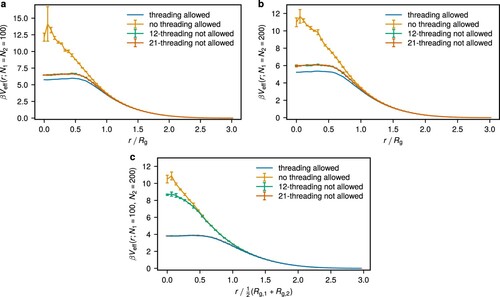Then the threading contribution $V_{\mathrm{th}}$ can be calculated as the difference $V_{\mathrm{th}}(r)=V_{\mathrm{eff}}^{\mathrm{no}-\mathrm{th}}(r)-V_{\mathrm{eff}}(r).$ In Figure 7, we plot the total effective potential under different threading conditions. For the rings of the same length considered in Figure 7(a) and 7(b), conditioning the rings on keeping non-threaded states increases the barrier at zero separation significantly in comparison to the case with any kind of threading allowed. When only one of the two threadings is allowed (threaded or threading), the barrier is higher by about $1k_{\mathrm{B}}T$, that is obviously symmetric for $N_1=N_2$. On the other hand, for a pair of asymmetric rings (Figure 7 c), we find that the threading of a smaller ring of the larger one, $Q_{12}$, is dominant. Once this contribution is restricted, the barrier at zero separations increases significantly, similarly to prohibiting all threading. In contrast, restricting $Q_{21}$ has little effect on the effective interaction potential, which is quite similar to the case when all threading is allowed.

Figure 7. Threading contributions to the effective potentials in the case of (a) $N_1=100$, $N_2=100$, (b) $N_1=200$, $N_2=200$, (c) $N_1=100$, $N_2=200$. Note that ij-threading implies that ring i threads ring j.

4. Discussion and conclusion

We investigated single ring static properties and effective potentials of disperse unknotted and nonconcatenated rings in a dilute limit. The large knotting length allows us to use MC scheme that does not need to check for bond crossings and we effectively sampled long ring lengths that reach asymptotic characteristics in various properties, such as $R_{\mathrm{g}}$ or the minimal surface area.

The scaling exponent of the latter can be useful in characterising threading constraints. For example, the work [26] uses a free energy term proportional to $R_{\mathrm{g}}^2$ to characterise the nonconcatenation condition cost in semidilute solutions. There, the $R_{\mathrm{g}}^2$ is assumed for the scaling of the area of the minimal surface spanned by the ring. In semidilute solution $R_{\mathrm{g}}^2\sim N$ which agrees with the simulation results for the fraction of concatenated rings when crossing is allowed [6] in long $N\sim {10}^3$ limit. In contrast, here we find that the exponent of the area scaling with N is larger than $2\nu$ for freely fluctuating rings. We find two possible reasons for the discrepancy: (i) the surfaces of the ideal-like rings ($\nu =1/2$) are inherently different from the ones of the freely fluctuating rings and indeed display area scaling $2\nu =1$ and (ii) due to the lattice nature of the ring conformations in  [26], the area scaling can be affected by the area present close to the ring boundary. To resolve the question one would have to simulate longer ideal-like rings, because as shown in  [26] and [10], for the area close to the boundary is comparable to the inner area for lengths up to about ${10}^3$ for the two simulated models, which is about the maximum length in  [26]. Here we showed at least, that for the freely fluctuating rings, the area exponent appears larger than $2\nu$ also for the inner area, because as shown in  [10] the inner area strongly dominates the total area for the lengths we investigate here.

Using insertion methods we computed the effective potential between two rings. Comparing the potentials with and without linking and threading allows us to deduce the topological and threading contributions. We computed these for rings with the same, and with different number of monomers, reaching the asymptotic limits in some of them. Using these, we showed that the multi-blob coarse-graining method [18] parametrised on a relatively short rings and with a limited number of blobs ($\le 50$) gives the correct effective potentials only for the lower N's ($6k_{\mathrm{B}}T$ instead of $4.5k_{\mathrm{B}}T$ at zero separation). For longer rings, the crumpling of the rings would be underestimated if only 50 blobs were used, giving a rise to higher effective repulsion. Using more blobs would likely make up for the crumpling freedom and the asymptotic $4.5k_{\mathrm{B}}T$ would be recovered.

We observe that the topological contribution diminishes faster than the steric one for small separations and vice versa for large separations as the length asymmetry ratio grows, generating a fixed point at intermediate separations. Although the topological interaction becomes almost negligible for $N_2/N_1\ge 8$, these effects are still interesting when considering linking probabilities in the asymptotic length limit for fixed asymmetry. However, we have to take the results with caution as the Gauss linking number (8(8) $m=\frac{1}{4\pi }{\oint }_{{\mathcal{C}}_1}{\oint }_{{\mathcal{C}}_2}\frac{\mathrm{d}{\mathbf{s}}_1\times \mathrm{d}{\mathbf{s}}_2\cdot ({\mathbf{s}}_1-{\mathbf{s}}_2)}{|{\mathbf{s}}_1-{\mathbf{s}}_2{|}^3},$(8) ) might be differently sensitive at different ring separation due to the fact that the spectrum of links (including ones not recognised by the linking number) likely depends on the separation [1,17]. We consider this being an interesting open problem.

The comparison of the effective potentials for differently sized rings makes it interesting to investigate bidisperse solutions at higher densities. The same interaction between like-sized rings as opposed to differently sized makes it the system an interesting candidate for a size and topology-induced separation. Clustering in ring polymer solutions has been observed before, for shorter, semi-flexible rings, where it occurs as a result of enhanced threading propensity and anisotropic effective interactions [42–44]. In contrast to the work [42], where the clusters can arise despite of polydispersity, our present work suggests a possible clustering due to the polydispersity through a different mechanism. We leave for future study whether the effective difference in the interactions can trigger such separation at various densities.

Another novel point in this work is the quantification of the threading contributions to the effective potential. For the finite lengths we simulated, the states that are not threading despite zero ring separation constitute a small, but finite fraction of all possible states, as signified by the barrier of about $12k_{\mathrm{B}}T$ in Figure 7. Whether this remains finite also in the $N\to \mathrm{\infty }$ limit remains a yet another interesting open question. Furthermore, it is interesting to estimate the impact of threading on the effective interaction in dilute systems of other topologically restricted polymer architectures, like tadpoles [33] or catenanes [45–47]. Finally, these results, in dilute conditions, are the first steps towards a better understanding of the threading constraints in dense systems. There, the understanding of the threading costs hinders the construction of an equilibrated melt of rings from first principles [27]. This would further enable the development of appropriate scaling theory that would take threading explicitly into account, allowing for a reliable predictions on the existence of an equilibrium topological glass.

Acknowledgments

We are honoured and happy to present this work as a contribution to the scientific celebration of the birthday of Michael Klein. Michael's pioneering work in computational physics, with its vast impact in the broad areas of computational statistical mechanics, molecular interactions, soft matter and biophysics has inspired us all. J.S. acknowledges discussions with Angelo Rosa and the support from the Austrian Science Fund (FWF) through the Lise-Meitner Fellowship No. M 2470-N28.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

J.S. acknowledges discussions with Angelo Rosa and the support from the Austrian Science Fund (FWF) through the Lise-Meitner Fellowship No. M 2470-N28.