Vibrational effects in the quantum dynamics of the H + D₂⁺ charge transfer reaction

Abstract

The H + D${}_2^{+}$(v = 0,1 and 2) charge transfer reaction is studied using an accurate wave packet method, using recently proposed coupled diabatic potential energy surfaces. The state-to-state cross section is obtained for three different channels: non-reactive charge transfer, reactive charge transfer, and exchange reaction. The three processes proceed via the electronic transition from the first excited to the ground electronic state. The cross section for the three processes increases with the initial vibrational excitation. The non-reactive charge transfer process is the dominant channel, whose branching ratio increases with collision energy, and it compares well with experimental measurements at collision energies around 0.5 eV. For lower energies the experimental cross section is considerably higher, suggesting that it corresponds to higher vibrational excitation of D${}_2^{+}$(v) reactants. Further experimental studies of this reaction and isotopic variants are needed, where conditions are controlled to obtain a better analysis of the vibrational effects of the D${}_2^{+}$ reagents.

GRAPHICAL ABSTRACT

Keywords:

• Charge transfer
• quantum dynamics
• non-adiabatic dynamics

1. Introduction

H${}_2$ is the most abundant molecule in the interstellar medium. The gas phase routes to form molecular hydrogen present very slow rate constants, and its formation in local galaxies is attributed to reactions on cosmic grains and ices [1,2]. However, in environments where grains and ice do not exist, like in the Early Universe, one key process is the formation of H${}_2$ in the gas phase. One of such processes is the charge transfer reaction (1) $\mathrm{H}+{\mathrm{H}}_2^{+}\to {\mathrm{H}}_2+{\mathrm{H}}^{+}.$(1) This reaction has been studied experimentally at rather high energies, > 1 keV, by Karpas et al.[3] and by McCartney et al. [4]. Andrianarijaona et al. [5,6] measured the H + D${}_2^{+}$ $\to$ H${}^{+}$ +D${}_2$ charge transfer cross section in a broad energy range, from 0.1 eV/u to 10 keV/u, thus including energies more relevant for the astrophysical environment. At this point it is worth mentioning that the D${}_2^{+}$ reactant is excited vibrationally since it is generated by photoionisation or electronic impact. The main goal of this work is to compare the simulated cross sections for each D${}_2^{+}$(v) vibrational state with the experimental measurements. In this line, the measurements made in the H + D${}_2^{+}$ reaction [5,6] can then be considered as benchmark for the comparison with the theoretical simulations, which conclusions can be generalised to other isotopes and to similar reactions for other cations.

From the theoretical point of view, reaction (1(1) $\mathrm{H}+{\mathrm{H}}_2^{+}\to {\mathrm{H}}_2+{\mathrm{H}}^{+}.$(1) ) has been studied by several authors [7–13], using different and increasingly more accurate coupled diabatic potential energy surfaces (PESs) [14–18]. Last et al. [7] used a quantum method based on negative imaginary potential combined with a variational quantum method in a L${}^2$ basis set, with the helicity decoupling approximation, and using approximated PESs. Krstic [9] used a close coupling method based on the infinite order sudden approximation (IOSA) with Delves hyperspherical coordinates. Gosh et al. [12] and Sanz-Sanz et al. [13] used accurate quantum wave packet methods, in hyperspherical and Jacobi coordinates respectively, and used different coupled diabatic PESs based on accurate ab initio calculations. All these calculations showed an important enhancement on a particular vibrational state of H${}_2$ due to a quasi-degeneracy of ${\mathrm{H}}_2^{+}(\mathrm{v}=0)$ and ${\mathrm{H}}_2({\mathrm{v}}^{\prime }=4)$. This effect depends strongly on the long-range behaviour of the PESs, very accurately described in the work of Aguado et al [19], and already used by Sanz-Sanz et al. [13]. In this latter work, the charge transfer reaction was studied for several isotopic variants. Among them the $\mathrm{H}+{\mathrm{D}}_2^{+}(\mathrm{v}=0)\to {\mathrm{H}}^{+}+{\mathrm{D}}_2$ charge transfer reaction was studied and compared with the experimental values [5,6], showing good agreement for collision energies around 0.5 eV, but some differences appear at lower energies. These differences were attributed to vibrational excitation of the ${\mathrm{D}}_2^{+}$, not taken into account by Sanz-Sanz et al. [13]. The goal of this work is to analyse the effect of vibrational excitation of ${\mathrm{D}}_2^{+}$, which is expected to present important discrepancies due to the variation of the energy difference between the initial ${\mathrm{D}}_2^{+}(\mathrm{v})$ and final ${\mathrm{D}}_2({\mathrm{v}}^{\prime })$ vibrational levels.

The manuscript is distributed as follows. A brief description of the theoretical method is presented in Section 2. In Section 3, the quantum results are described and compared with the experimental results. Finally, in Section 4 are outlined some conclusions.

2. Theoretical method

In this work, we use the coupled diabatic PESs developed by Aguado et al. [19] based on a Diatomics-in-Molecules (DIM) 3×3 matrix description [20,21], corrected with diagonal and non-diagonal three body-terms [22] to fit the energies obtained in Multi-Reference Configuration interaction (MRCI) calculations with complete basis set extrapolation (CBS). Dealing with a system of two electrons, MRCI calculations give full configuration interactions (FCI) results within the space spanned by the orbital set. To obtain near FCI results for complete basis set, a complete basis set extrapolation method was performed. These PESs include the long-range interaction very accurately. The dominant terms for reactants H + H${}_2^{+}$ channel are the charge-induced dipole and charge-induced quadrupole dispersion interactions, varying as $R^{-4}$ and $R^{-6}$ respectively. For the products H${}^{+}$ + H${}_2$ channel, the main long-range terms are the charge-quadrupole and the charge-induced dipole dispersion energies, which vary as $R^{-3}$ and $R^{-4}$ respectively. 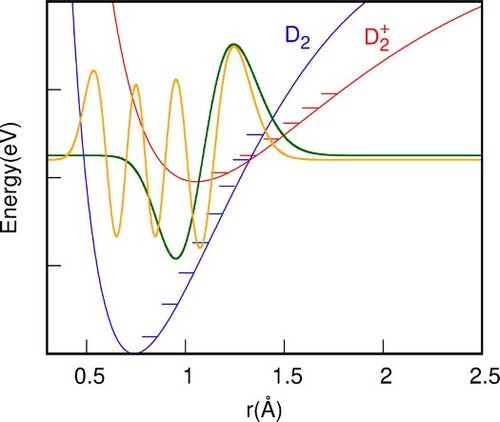The DIM diabatic representation is non diagonal for the description of any H${}_2^{+}$ + H fragment. Therefore, a transformation to a new diabatic representation should be done, in which the PESs are diagonal in the reactants channel while they are non-diagonal in the two product rearrangement channels, as described by Sanz-Sanz et al. [13]. The features of the potential in the reactant channel, as a function of Jacobi r variable, are shown in Figure 1. At long distances, the potentials of D${}_2$ and D${}_2^{+}$ cross at $r=r_c$=1.323Å, as shown in Figure 1(a). The amplitude of D${}_2^{+}(v)$ vibrational state is non-zero at this distance, and, in this outer classical turning point region, the D${}_2^{+}(v)$ levels have a matching overlap with different D${}_2$(v') vibrational states. As the two reactants approach each other, the degeneracy between the two first adiabatic states dissappears: the ground state gets stabilised forming the very stable HD${}_2^{+}$ system, which correlates to H${}^{+}$+D${}_2$ and D${}^{+}$+HD adiabatic asymptotes, while the excited adiabatic state becomes repulsive (see Figure 1(b)).

Figure 1. Features of the 3 x 3 PES's describing the H+D${}_2^{+}$ $\to$ H${}^{+}$ + D${}_2$ charge transfer process, where r is the D${}_2$ internuclear distance and R is the distance between H and the centre-of-mass of D${}_2$. (a) Potential of D${}_2$ and D${}_2^{+}$ at very long distance of H atom, showing the vibrational levels on each. The energies of D${}_2^{+}$(v) are 2.056, 2.251 and 2.439 eV, for v = 0, 1 and 2, respectively. The energies of D${}_2$(v') are 1.902, 2.202, 2.487 and 2.758 for v' = 5,6, 7 and 8, respectively. (b) Adiabatic potential energies of the first 2 singlet electronic states as a function of R, for $r=r_c$ and at a T-shaped configuration. The diabatic coupling between the two diabatic energies are also shown.

The reactive and charge transfer collisions have been studied with a quantum wave packet method using the MADWAVE3 code [23,24], using the parameters listed in Table 1 of Ref. [13]. The wave packet is propagated for each total angular momentum J, using a modified Chebyshev propagator [25–29]. The wave packet is represented in reactant Jacobi coordinates and is transformed to product Jacobi coordinates [30] at each iteration to extract the individual state-to-state reaction probabilities, $P_{\alpha vj\mathrm{\Omega }\to {\alpha }^{\prime }{v}^{\prime }{j}^{\prime }{\mathrm{\Omega }}^{\prime }}^J(E)$, where α denotes the rearrangement channel and the electronic state, v, j correspond to the vibrational and rotational state of the diatomic fragment, and Ω is the projection of the total angular momentum in the z-axis of the body-fixed frame. The integral state-to-state reactive and inelastic cross sections are calculated using the partial wave expansion as (2) $\begin{array}{rl}{\sigma }_{\alpha vj\to {\alpha }^{\prime }{v}^{\prime }{j}^{\prime }}(E)& =q_e\frac{\pi k_{\alpha vj}^{-2}}{(2j+1)}\\ & \times \sum _{J\mathrm{\Omega }{\mathrm{\Omega }}^{\prime }}(2J+1)P_{\alpha vj\mathrm{\Omega }\to {\alpha }^{\prime }{v}^{\prime }{j}^{\prime }{\mathrm{\Omega }}^{\prime }}^J(E),\end{array}$(2) where $q_e=1/4$ is the electronic partition function – note that this factor was not included in the previous study [13]. There are four electronic states correlating to H(${}^2$S)+D${}_2^{+}{(}^2{\mathrm{\Sigma }}_g^{+})$ asymptote, one singlet and three triplet states. The three triplet states are not connected to the H${}^{+}$ + H${}_2$(X${}^1{\mathrm{\Sigma }}_g^{+}$) channel, and therefore cannot undergo charge transfer reactions. In this study, $P^J(E)$ are calculated with the MADWAVE3 code for all values with J<15 and for J = 20, 30, 40, 50, 60, 70 and 80. The rest of reaction probabilities for all the intermediate $J^{\prime }s$ are obtained by a linear interpolation based on the J-shifting approximation, as described before [31,32], to save computational effort. In these calculations, the maximum projection, Ω, considered in the dynamic calculations is 23. In a previous study [13], the role of the trunction of ${\mathrm{\Omega }}_{max}$ was checked, giving excellent results for the NCRT channel, and an accuracy better than 2–3 $\mathrm{\%}$ for the other two channels.

In what follows, three processes are distinguished (3) $\begin{array}{rl}& \mathrm{H}+{\mathrm{D}}_2^{+}(v,j=0,J)\\ & ⟶{\mathrm{H}}^{+}+{\mathrm{D}}_2(v^{\prime },j^{\prime })\\ & \mathrm{non}-\mathrm{reactive}\mathrm{charge}\mathrm{transfer}(\mathrm{NRCT})\\ & ⟶{\mathrm{HD}}^{+}(v^{\prime },j^{\prime })+\mathrm{D}\mathrm{exchange}\mathrm{reaction}(\mathrm{ER})\\ & ⟶\mathrm{HD}(v^{\prime },j^{\prime })+{\mathrm{D}}^{+}\mathrm{reactive}\mathrm{charge}\mathrm{transfer}(\mathrm{RCT}).\end{array}$(3) Charged diatomic products correspond to the first excited electronic singlet adiabatic state, 2${}^1{A}^{\prime }$, while the product with a charged atomic fragment corresponds to the ground adiabatic electronic singlet state, 1${}^1{A}^{\prime }$.

The H(${}^{2}S$)+ H${}_2^{+}{(}^2{\mathrm{\Sigma }}_g^{+})$ entrance channel also correlates with the lowest triplet state of H${}_3^{+}$(${}^3{A}^{\prime }$). This triplet state presents a shallow well at collinear geometry, and has access to the exchange products, as described before [19,33]. Therefore, the triplet state contributes to the exchange reaction, ER, but does not contribute to the other two charge transfer processes, NRCT and RCT. In the present calculations dynamical calculations are all performed for the singlet states. Therefore, the cross section for the RCT channel presented below is not complete, since they should include the contributions arising from the triplet states.

3. Results

The vibrationally resolved reaction probabilities for J = 0 are shown in Figure 2 for H+D${}_2^{+}$(v) collisions, for v = 0,1 and 2, in the left, middle and right panels, respectively. The probabilities for the individual final vibrational states, v', are included for the three different processes, NRCT (top panels), ER (middle panels) and RCT (bottom panels). The reaction in the excited adiabatic electronic state has an extremely high barrier. However, as the two fragments get closer, the electronic couplings bring a large portion of the wave packet to the ground adiabatic state correlating to the two charge transfer channels, NRCT and RCT. The NRCT reaction probabilities are very close to those of RCT at low energies, except when the D${}_2$(v') level is close to the D${}_2^{+}$(v) state considered, D${}_2$(v' = 6) for v = 0 and 1 and D${}_2$(v' = 7) for v = 2. According to Figure 1(a), the final population of D${}_2$(v') with an energy slightly above than that of the initial D${}_2^{+}$(v) is always enhanced. This is due to the interaction with the H atom, which stabilises the ground electronic state, connected to H${}^{+}$+ D${}_2$ asymptote, while the excited state becomes repulsive (see Figure 1(b)).

Figure 2. Vibrationally resolved reaction probability for J = 0 H+D${}_2^{+}$(v = 0,j = 0) (left panels), H+D${}_2^{+}$(v = 1,j = 0) (middle panels), and H +D${}_2^{+}$(v = 2,j=0) (right panels), towards the inelastic charge transfer, NRCT (H${}^{+}$+D${}_2$, in the top panels), the exchange reactive channel, ER (H+HD${}^{+}$, in the middle panels) and reactive charge transfer, RCT, channels (D${}^{+}$ +HD, in the bottom panels).

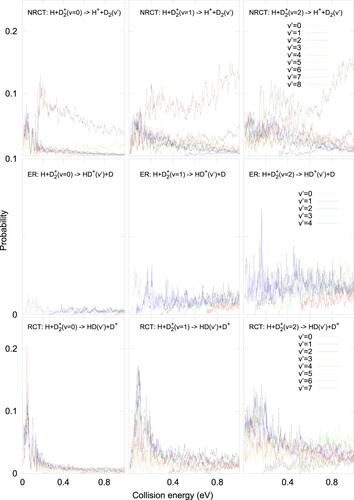
For lower energies, the amplitude transfered to the ground electronic state enters the deep well of HD${}_2^{+}$, forming long lived resonances. In this well, the energy is transfered among all possible modes and the reaction becomes nearly statistical, as reported for the reaction dynamics in the ground electronic state [29,34,35]. This explains why NRCT and RCT show similar populations, except for near-resonant v' levels. This also allows the transition back to the excited electronic state and explains the appearance of the ER probabilities in the middle panels of Figure 2, that cannot reach directly the excited adiabatic electronic state.

The amplitude of the D${}_2^{+}$(v) vibrational state extends over larger radial distances as v increases, becoming larger at the region of the crossing between the two electronic states. This can explain why all the probabilities, NRCT, ER and RCT, increase with v.

As the total angular momentum J increases, the situation gradually changes. The reaction probabilites for the three vibrational states studied are shown in Figure 3 for the three different rearrangent channels. As the rotational barrier increases, the reaction probabilities shift towards higher energy, as expected. This shift, however, depends on the mechanism. Thus, the two reactive processes, ER and RCT, have always larger shifts or effective barriers. As the barrier increases with J, the reaction probabilities decreases.

Figure 3. Reaction probability for different J values in H+D${}_2^{+}$(v=0) (left panels), H+D${}_2^{+}$(v = 1) (middle panels), and H +D${}_2^{+}$(v = 2) (right panels), towards the inelastic charge transfer, NRCT (H${}^{+}$+D${}_2$), in the top panels, the exchange reactive channel, ER (H+HD${}^{+}$), in the middle panels and the reactive charge transfer, RCT, channels (D${}^{+}$ +HD), in the bottom panels.

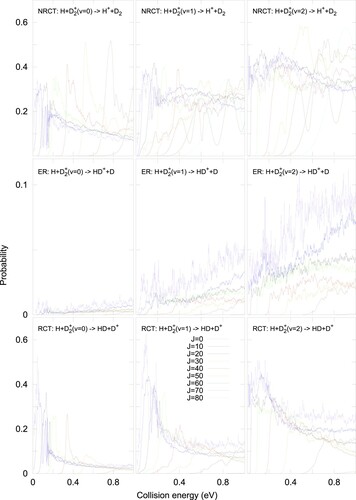
This situation is somehow different for the NRCT channel, which is essentially inelastic and has lower effective barriers. As shown in the top panel of Figure 3, the effective barrier decreases progressively when going from v = 0 to v = 2. The reason is that the energy difference between the initial (v) and final (v') vibrational levels also decreases. Thus, the electronic coupling becomes more effective at longer distances for higher v', because lower couplings can induce the transition.

The resonant structure appearing at low energy progressively disappears as J increases because the rotational barrier increases and the wave packet can not reach the deep well in the ground electronic state. Finally, as the reactive processes decrease, the NRCT process increases in intensity with J, becoming dominant. The lower effective barriers observed for the NCRT channel makes necessary to include more partial waves J to converge the corresponding cross section in Equation (2(2) $\begin{array}{rl}{\sigma }_{\alpha vj\to {\alpha }^{\prime }{v}^{\prime }{j}^{\prime }}(E)& =q_e\frac{\pi k_{\alpha vj}^{-2}}{(2j+1)}\\ & \times \sum _{J\mathrm{\Omega }{\mathrm{\Omega }}^{\prime }}(2J+1)P_{\alpha vj\mathrm{\Omega }\to {\alpha }^{\prime }{v}^{\prime }{j}^{\prime }{\mathrm{\Omega }}^{\prime }}^J(E),\end{array}$(2) ), up to J=140, and they were extrapolated using the J-shifting approximation from the calculated J = 80.

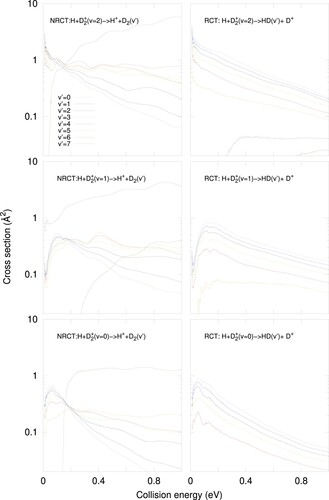
The cross section for the NRCT, ER, and RCT channels are shown in Figure 4. Clearly the ER channel is one order of magnitude lower than the other two. NRCT and RCT are of the same order at low energies, but as collision energy increases, RCT decreases while NRCT is either constant or increases for v = 1 and 2. At higher energy, it is expected that this difference increases, becoming dominant the NRCT channel. It should be noted that in the case of H+H${}_2^{+}$ the two charge transfer processes, RCT and NRCT, are indistinguishable [13].

Figure 4. Reaction cross section for H+D${}_2^{+}$(v = 0, 1 and 2) towards the inelastic charge transfer, NRCT (H${}^{+}$+D${}_2$, in the top panel), the exchange reactive channel, ER (H+HD${}^{+}$, in the middle panel) and the reactive charge transfer, RCT, channels (D${}^{+}$ +HD, in the bottom panel). The experimental values are taken from Ref.[5,6].

The present theoretical results for each initial v are compared with the experimental cross sections in the top panel of Figure 4. In the experimental work by Andrianarijaona et al. [5,6] on the H + D${}_2^{+}$ collisions, the H${}^{+}$ products were detected, i.e. they provide a direct evidence on the NRCT cross section. The theoretical NRCT cross section increases as the initial D${}_2^{+}$(v) vibrational state increases, and, for v = 2 at collision energies around 0.5 eV, it matches the corresponding experimental measurements. This seems to indicate that measurements made at lower temperature could be due to more vibrationally excited initial D${}_2^{+}$ reactants. In the experiments, the D${}_2^{+}$ were produced by a CEA/Grenoble all-permanent magnet Electron Cyclotron Resonance ion source (ECR) [5,6], and their vibrational distributions depend on the ECR ion source parameters, which are not coupled with the ion beam energy. Unfortunately, these experiments did not include any direct nor indirect measurement of the vibrational distributions of these D${}_2^{+}$ ions. It is expected, though, that slight changes in the ion source conditions affect the vibrational distributions of the ions as observed in the case of molecular ions, including D${}_2^{+}$, produced by Duoplasmatron sources [36]. A more detailed experimental work needs to be done with controlled conditions on the vibrational excitation of the D${}_2^{+}$ reactant ions, specially at low collision energies, before a factual conclusion could be drawn. The 3-D imaging technique similar to the one used by Urbain et al. [37] was proven to be efficient to measure vibrational distributions of H${}_2^{+}$ issued from the primary reaction H${}^{+}$ +H${}_2$. In this technique, two position sensitive detectors detect the positions and time of flights of fragments, giving access to the kinetic energy release, which definitely contains information on the vibrational state of the molecular ions. Given the similarity between Urbain et al..'s molecular ions and the ones in Andrianarijaona et al,'s experiment [5,6], the 3-D imagine technique would be an appropriate fit to provide data that will accomplish our goal. The theoretical simulations presented in this work are expected to provide a good guidance to interpret such measurements. Moreover, this should also be extended to the H${}_2^{+}$ + H reaction due to its astrophysical relevance, especially in Early Universe models.

In all the mechanisms, the cross section increases with the vibrational excitation. This is explained, as in the reaction probabilities, by the increase of the overlap between the initial D${}_2^{+}$(v) and dominant D${}_2$(v') (see Figure 1(a)), which acts as a doorway for the three mechanisms. The amplitude of the initial vibrational D${}_2^{+}$(v) wave function around the electronic curve crossing region increases, thus favouring the electronic transition.

The vibrationally resolved state-to-state cross sections for the NRCT and RCT channels are shown in Figure 5. There is a clear difference between the two mechanisms. For RCT, all cross sections decrease with energy, which could be explained by the near statistical mechanisms, due to the presence of many resonances associated to the deep HD${}_2^{+}$ well that mediate the reactivity. For NRCT, however, there are several cases: there is always a dominant v': v'=6 and 7 for the cases of v=0,1 and v=2, respectively. This inelastic channel is formed by an electronic transition taking place at rather long distances. The rest of v' in the NRCT channel show a progressively decreasing cross section with decreasing v', probably due to transitions from v${}_d$'.

Figure 5. Vibrationally resolved state-to-state cross section for H+D${}_2^{+}$(v=0, 1 and 2) towards the inelastic charge transfer, NRCT (H${}^{+}$+D${}_2$(v'), in the left panels), and the reactive charge transfer, RCT, channels (D${}^{+}$ +HD(v'), in the right panels).

The reason why the NRCT channels ${\mathrm{v}}^{\prime }=6$ and 7 for ${\mathrm{D}}_2^{+}(\mathrm{v}=0,1)$ and ${\mathrm{v}}^{\prime }=7$ for ${\mathrm{D}}_2^{+}(\mathrm{v}=2)$ are dominant at high energy can be easily interpreted in terms of the reaction probabilities at high energies and high angular momentum. As J increases, the rotational barrier also increases. This barrier avoids the wave packet to reach short distances between the two reactants, and therefore to enter in the deep insertion well of the ground electronic state, where the reaction takes place. However, the charge transfer between the initial ${\mathrm{D}}_2^{+}$(v) and nearly resonant D${}_2$(v') can takes places at rather long distances, at which small electronic couplings can induce transitions between close lying electronic states. Under these circumstances, as reaction probabilities decreases, the inelastic NRCT becomes dominant towards a particular final D${}_2$(v') state.

In order to check this model, we have performed approximate time-independent close coupling (TICC) calculations, using reactant Jacobi coordinates, including only one vibrational channel in the initial excited electronic state, ${\mathrm{D}}_2^{+}(\mathrm{v}=2)$, and one vibrational state in the final ground electronic state, D${}_2$(v'=7), with 20 rotational channels in each, even j values from 0 to 40. The differential equations are integrated using the renormalised Numerov method [38,39] for distances between 2 and 20 bohr, with 300 grid points. Also, the centrifugal sudden approximation is assumed, keeping only one helicity, Ω=0, since the Coriolis coupling are expected to play a negligible role at the long distances for which the electronic transition takes place at high total angular momentum. These TICC calculations include the NRCT only, and moreover, only consider a possible CT vibrational product, D${}_2$(v'=7). However, the WP presented above include all rearrangement channels, ER and RCT, and all accessible vibrational states of the products, becoming much more demanding computationally.

The NRCT probabilities obtained in these model calculations are compared in Figure 6 with the accurate wave packet calculations described before for J = 50, 60 and 70 (denotd by WP). Clearly, as J increases, the agreement between the two methods improves. This demonstrate the validity of the model. The oscillations obtained as a function of collision energy are due to the interference between the entrance and final channels energy difference[40,41].

Figure 6. NRCT probabilities obtained in $\mathrm{H}+{\mathrm{D}}_2^{+}(\mathrm{v}=2)$ collisions at several J values using the ‘exact’ wave packet results (WP) and the approximated time independent close coupling (TICC) results, as described in the text.

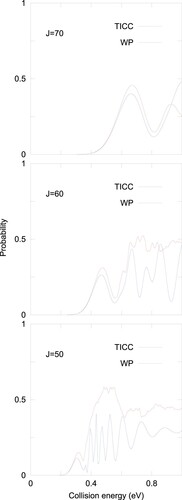
Figure 7. NRCT cross section obtained in H + D${}_2^{+}$(v = 2) collisions comparing the total NRCT ‘exact’ wave packet results (WP), the state-to-state wave packet cross section for D${}_2$(v' = 7), and the approximated time independent close coupling (TICC) results. The experimental values are taken from Ref.[5,6].

This behaviour obtained at high J values shows that NRCT is the dominant reaction channel at high energy. This is valid not only for the reaction studied in this work but also for all the other isotopic variants, since it is attributed to the crossing between the neutral and cationic diatomic fragments, which takes place at very long distances between the reactants.

The TICC model has been extended to calculate the NRCT cross section in a wider energy range, by solving the close-coupling equations for J = 0 to 300. The simulated NRCT cross sections are compared with the experimental results of Andrianarijaona et al. [5,6]. The TICC cross section is very close to the wave packet results for ${\mathrm{D}}_2({\mathrm{v}}^{\prime }=7)$ below 1 eV, but is lower than the total WP NRCT cross section, since it does not take into account the other v' levels. As discussed above, the quasi degeneracy between initial ${\mathrm{D}}_2^{+}(\mathrm{v}=2)$ and final ${\mathrm{D}}_2({\mathrm{v}}^{\prime }=7)$ produces a very efficient electronic transition giving rise to the charge transfer. At low energy, for which relatively low total angular momentum J are dominant, the rotational barriers are low and the dynamics in the ground electronic state can access to the deep well of ${\mathrm{H}}_3^{+}$. Within this well there is an effective energy transfer towards the vibrational levels of D${}_2$(v') and also access to HD products in other rearrangment channels. This explains why TICC results are so different to the accurate WP results below 1eV, since TICC neglects these processes. However, at high angular momenta, which dominate at high collision energy, the rotational barrier does not allow the H and ${\mathrm{D}}_2^{+}$ or H${}^{+}$+D${}_2$ reactants to approach each other at distances where the vibrational energy transfer or the exchange reaction can take place. This explains why the TICC approximation yields results in rather good agreement with the experimental results for collision energies between 3 and 9 eV.

4. Conclusions

The reactive cross sections for the $\mathrm{H}+{\mathrm{D}}_2^{+}$ charge transfer reaction increase with the initial vibrational excitation of the ${\mathrm{D}}_2^{+}$(v) reactant, due to the increase of the amplitude of the vibrational wavefunctions of D${}_2^{+}$ and D${}_2$ in the curve crossing and their mutual overlaps. The dynamics is dominated by the electronic transition from the excited to the ground electronic state, where the reaction takes place in the deep insertion well of ${\mathrm{H}}_3^{+}$. The charge transfer electronic transition is dominated by the crossing of the two ${\mathrm{D}}_2/{\mathrm{D}}_2^{+}$ occurring at rather large distance between reactants, where it can take place between close lying vibrational states. For this reason, the reaction shows a rather marked dependency on the initial vibrational excitation. Moreover, this feature determines that the non-reactive charge transfer becomes the dominant channel as the collision energy increases, for which the high total angular momentum introduces a barrier avoiding the access to the insertion minimum.

The non-reactive charge transfer cross section is compared to the experimental measurements in the 0.01–1 eV collision energy range studied theoretically. A good agreement is found around 0.5 eV. At lower collision energies, the experimental cross-section are larger than the experimental ones. This is attributed to a possible higher vibrational excitation in the generation of ${\mathrm{D}}_2^{+}$ reagents. Also, a TICC model, including only the initial D${}_2^{+}(v=2)$ and the near resonant ${\mathrm{D}}_2({\mathrm{v}}^{\prime }=7)$ vibrational states, shows good agreement with the experimental cross-section in the 3–9 eV collision energy range. It is concluded that a more detailed experimental study, focusing on the control of experimental conditions used to generate D${}_2^{+}$, are needed to further analyse the vibrational effects of reagents on the charge transfer reaction, specially at low energies. For these studies, the theoretical simulations can be of important help.

Acknowledgments

We acknowledge computing time at Cibeles (UAM) under RES computational grant AECT-2021-1-0011.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

The research leading to these results has received fundings from Ministerio de Ciencia e Innovación (MICINN) (Spain) under grant FIS2017-83473-C2. V. Andrianarijaona is supported by the National Science Foundation (NSF) through Grant No. PHY - 1530944.